Push-broom hyperspectral imaging for elemental mapping with glow discharge optical emission spectrometry
Gerardo
Gamez
*,
Damian
Frey
and
Johann
Michler
Swiss Federal Laboratories for Materials Science and Technology, Laboratory for Mechanics of Materials and Nanostructures, Feuerwerkerstrasse 39, 3602, Thun, Switzerland. E-mail: gerardo.gamez@empa.ch; Fax: +41 33 2284490; Tel: +41 58 7656201
First published on 7th November 2011
Abstract
Glow discharge optical emission spectroscopy (GDOES) has been recognized for allowing direct solid sample elemental analysis with high depth resolution. However, the lateral resolution it affords has been historically restricted to some millimetres or the diameter of the sputtered area. Recently, it was shown that one can obtain laterally resolved information from within the sputtered area by operating the discharge in pulsed power mode. The newly available data dimensions require a new approach to the collection of the GDOES signal with lateral (to recover X and Y positions), spectral (to qualify and quantify elemental information), and temporal resolution (to improve lateral resolution and allow depth profiling). Previous studies have utilized spectral imagers of whisker-broom and staring geometries. In this study we characterize the advantages and disadvantages of using a push-broom geometry hyperspectral imager for GDOES elemental mapping. The results show that the higher light throughput of the push-broom geometry allows faster image acquisition times, compared to other spectral imaging systems with the same components, and thus maintain depth resolutions below 10 nm.
Introduction
Glow discharge optical emission spectroscopy has gained much attention as a surface analysis technique due to the high depth resolution it affords. Nevertheless, the lateral resolution of the elemental composition information, which is obtained via cathodic sputtering of the solid sample surface, can be very poor. Indeed, the lateral resolution has been historically limited to the diameter of the sputtered area which is in itself limited by the inner diameter of the anode in Grimm-type glow discharge sources. Thus, in a GDOES typical commercial system, the only way of obtaining a map of the elemental composition of the surface would be to mount the sample, analyze/sputter the area limited by the anode (down to 1 mm, but typically 4 mm), dismount the sample and restart the sequence in an adjacent sample area. It is clear that this type of rastering analysis would be too time consuming, to the point of impracticality, and still yield not very good lateral resolution.However, recently it was found that one can get laterally resolved information from within the sputtered area of the sample. Hoffman and Ehrlich showed that the lateral profile of the glow discharge emission from heterogeneous samples is not homogeneous.1 In this way, it was clear that the emission from the discharge can keep some kind of “memory” of the origin of the sputtered atoms from the sample. Webb et al. showed that by operating the glow discharge in pulsed DC mode it is possible to obtain laterally resolved information from within the sputtered area.2 Gamez et al. showed this could also be accomplished with pulsed RF discharges and demonstrated the first application of the technique for analysis of proteins on blotting membranes.3
Meanwhile, it is evident that the newly available data dimensions require a new approach to the collection of the GDOES signal. The requirements are to have lateral resolution to recover X and Y position, spectral resolution to qualify and quantify elemental information, and temporal resolution to improve lateral resolution3 and allow depth profiling. Hence, this technique requires multi/hyper-spectral imaging. Previous studies have utilized spectral imagers of whisker-broom and staring geometries.1,2 In the whisker-broom configuration, one collects the light coming from one point of the object (the glow discharge) which is passed through a light dispersion system to obtain the spectral information. The collection point is then rastered throughout the object to get the full image. When using a monochromator, one has to scan in two spatial dimensions and one spectral dimension to get the full picture; when using a spectrograph, one still has to scan in two spatial dimensions. This geometry affords very high light throughput but it is very time consuming. On the other hand, in the staring geometry the object is imaged onto a 2D array detector while the collected light is passed through a bandpass filter. The two spatial dimensions are obtained simultaneously but multiple spectral information can only be obtained by using several filters sequentially or by using a dispersion system as a filter, e.g.monochromator, and scanning the spectral dimension.
In this study we characterize the utility of a push-broom geometry hyperspectral imager for GDOES elemental mapping. The push-broom configuration is analogous to the whisker-broom but it uses a spectrograph with a 2D array detector that allows collection of the spectral dimension and one spatial dimension simultaneously. In addition, the high light throughput of the whisker broom configuration is kept while only one spatial dimension has to be scanned to obtain the full picture. A comparison of the advantages and disadvantages of this geometry against others is discussed.
Experimental
Push-broom hyperspectral imaging system
The push-broom hyperspectral system (Fig. 1) is based on a 140 mm focal length spectrograph (microHR manual, Jobin Yvon Horiba, France) equipped with a 1200 g per mm grating blazed at 250 nm (5.25 nm mm−1 reciprocal linear dispersion and f/3.88 aperture). The entrance slit has a maximum height of 8 mm and slits of different widths can be mounted (here 25 μm unless otherwise noted). An ICCD (PI-Max 3 1024i, Princeton Instruments, USA) was mounted on the spectrograph. The ICCD has 1024 × 1024 pixels which are 12.8 μm × 12.8 μm and typically binned 2 × 2 for all experiments. The resulting spectral window is approximately 68.5 nm. The ICCD has 32 MHz (16 MHz × 2)/16-bit digitization.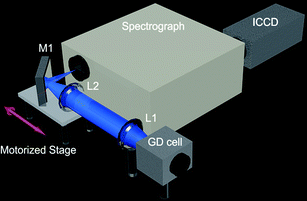 | ||
| Fig. 1 Schematic of push-broom hyperspectral imaging system for GDOES elemental mapping. For details please refer to Experimental section in the text. | ||
The collection optics consist of two triplet lenses to minimize chromatic aberrations (CaF2/fused silica/CaF2, 135 mm effective focal length, f/6, Edmund Optics Ltd, UK), with a typical chromatic shift of 0.55 mm over the spectrograph's spectral window in the UV region and 0.07 mm in the Vis-NIR region, and a broadband metallic mirror (Newport Corporation, USA) with >90% reflectivity from 200–650 nm. The first triplet lens (L1) serves to collimate the light coming from the GD source. The second triplet lens (L2) serves to focus the light onto the entrance slit of the spectrograph. The mirror (M1) allows positioning the axis of the focusing lens and the axis of the entrance slit at 90° from each other. Both focusing lens and turning mirror are mounted on a motorized stage such that the image can be scanned through the entrance slit without having to move the spectrograph or the source, thus allowing push-broom scanning in a practical manner. The stage motor (MTS25/M-Z8, Thorlabs Ltd, UK) has a maximum velocity of 3.0 mm s−1, maximum acceleration of 4.5 mm s−2, bidirectional repeatability of 1.6 μm, and backlash <6 μm. It is equipped with a Hall effect encoder feedback where the linear displacement of the lead screw per encoder count is equivalent to 29 nm. The imaging system was characterized with an Hg(Ar) pencil style calibration lamp (Oriel Instruments) and a USAF 1951 negative resolution target on fused silica substrate (Edmund Optics Ltd, UK). A deuterium lamp/tungsten–bromine lamp combination continuum source (LLC2, Lambda Scientific Systems, Inc., FL, USA) was also used for spatial resolution characterization and to perform flat field correction. WinSpec32 software (Roper Scientific, USA) was used to record the images for the spectral and spatial characterization of the imaging system. A LabVIEW program (National Instruments Corporation, Austin, TX, USA), described below, was developed for the acquisition automation, display and analysis of hyperspectral cube images.
Glow discharge cell
The glow discharge cell is based on a modified commercial lamp from JY Horiba with a Grimm-type geometry and power applied to the back of the sample. The lamp features interchangeable hollow anodes with inner diameters (here 7 mm). The end-on geometry lamp was modified such that the outer surface facing the collection optics could fit an o-ring to mount a 40 mm diameter CaF2 window held in place with an Al plate. The pressure was measured with a Baratron gauge (100 mbar range, MKS Instruments, Inc., USA) and maintained with a metering valve (SS-4L-MH, Swagelok, USA) and a rotary vane pump (Trivac D16A, Oerlikon Leybold Vacuum GmbH, Germany). The plasma gas used was Ar (99.9999% purity). The discharge was powered with a DC power supply with upper limits of 1250 V and 500 mA (MCP 700-1250, FUG Electronik GmbH, Germany) through a ballast resistor of 4 kΩ. The pulsed power studies were performed with an in-house built high voltage pulser driven by a 30 MHz synthesized function generator (DS345, Stanford Research Systems, Inc., USA).Results and discussion
The justification for exploring the use of a push-broom system becomes evident when comparing in a simple fashion its light throughput, which can also be translated to image acquisition times, against the whisker-broom and staring configurations. The image acquisition time is important because it will limit the depth resolution of the GDOES analysis. The same components, as described above (lenses and spectrograph/monochromator), will be used for theoretical comparison of all the different configurations. Furthermore, the same spectral and spatial resolution requirements will be applied to all different arrangements.To compare the systems one can determine the geometric entendue (G), or geometric extent, of each system to describe the light collecting capabilities. In short, the entendue is a limiting function of light throughput based on the area of the source and the solid angle (for further information about geometric entendue please see ref. 4–7). The G of the system will be limited by the component with the lowest geometric entendue which in the case of the whisker- and push-broom configurations, with the components herein, is the triplet lens. The G of the lenses can be approximated by G ≈ As × AL/DLS, where As is the area of the entrance slit, AL is the illuminated area of the lens, and DLS is the distance from the lens to the entrance slit. In the spectrograph the area of the slit is equivalent to the area of one camera pixel (0.0256 × 0.0256 mm, when binned 2 × 2) which is the same for both whisker- and push-broom configurations to maintain the same spectral and spatial resolution. The effective diameter of the lenses is 22.5 mm and DLS is the same as the focal distance of the lens. In the case of the staring geometry with a monochromator as a filtering device AL is equivalent to the area of the entrance slit because this is the component acting as the limiting aperture stop. The width of the slit would be 0.0256 mm, to keep the same spectral resolution, but the height can be the maximum allowed by the system which is 8 mm in this monochromator. As, in this case, would also be equivalent to the area of one camera pixel which is 0.0256 × 0.0256 mm to maintain the same spatial resolution between the systems. These conditions yield G that is higher in the whisker- and push-broom configurations by more than three orders of magnitude compared to the staring configuration based on a monochromator as a filter.
In terms of time required to collect a 2D image at a given wavelength, one would have to restrict the spatial and spectral resolution, as well as the pixel exposure time, to compare image acquisition times between systems. If one were to obtain an image of 512 × 512 pixels, then one would need to scan over 512 columns in the push-broom system but one would have to raster over 262′144 positions with a whisker-broom system. In theory they both have the same geometric entendue; thus it would take 512 times as long to collect an image with the whisker-broom configuration compared to the push-broom configuration at a single wavelength. In the case of the staring configuration it would take three orders of magnitude more exposure time to capture the same amount of light per pixel compared to the whisker- and push-broom systems, according to the geometric entendue calculations above. However, this is not the whole story because the staring configuration would give a full 2D image at a given wavelength but one would still have to scan or raster in the other configurations to get a full 2D image. Nevertheless, to get one monochromatic 2D image it would still take about twice as long as in the staring configuration compared to the push-broom configuration in spite of the scanning requirements. On the other hand, the push-broom configuration does not only yield one monochromatic image but it gives many monochromatic images over the spectral window (68.5 nm, under current operating conditions) of the spectrograph. Taking the linear dispersion and pixels size into account one could estimate the bandpass at ∼0.5 nm (or 3 pixels). In principle, this push-broom configuration would allow easily getting more than 100 monochromatic 2D images simultaneously and to get the same amount of information with the staring geometry one would have to spend more than 200 times as long.
A step further in the comparison would be to take into account how this applies directly to the GDOES case. For example, typically, commercial GDOES instruments are equipped with a polychromator that allows simultaneous measurement of up to 60 channels from around 100 nm to 800 nm. Thus, it is clear that the number of simultaneous bands which the push-broom system affords is above the typical requirements but it is also evident that the spectral window here falls short of the typical requirements. Thus, one can take a specific spectral window, for example from 220 nm to 288.5 nm, and see that the emission lines of approximately 12 elements typically used in GDOES lie within this window, plus about 12 more emission lines from different elements which are not so typically used.8 Then, one could say that with the staring geometry (monochromator-based) one could get the same amount of useful GDOES images in about 50 times as long as with the push-broom geometry (with the same spectral and spatial resolution, and the same amount of light collected), hence the use of a push-broom spectral imaging system. It is worth noting that other types of staring or push-broom imagers may perform better but going over every single type of configuration is outside of the scope of this manuscript.
Characterization of the imaging system
In principle, the imaging system has a given spatial and spectral resolution but in reality this is not always achieved. Thus, one needs to characterize the spectral resolution and the imaging fidelity. It is critical first to align as best as possible the ICCD camera with respect to the focal plane of the spectrograph. For this purpose, an Hg(Ar) pen lamp serves to position the camera where the best spectral resolution is found (cf.Fig. 2A). However, it is evident that at the optimum ICCD position the spectral resolution is not the same at every spatial position. If one places a grid at the entrance slit of the spectrograph and gets an image with a continuum source (cf.Fig. 2B), the change in the point spread function across the field becomes clearer. Classical Czerny-Turner spectrographs, with plane gratings, suffer from several aberrations such as astigmatism, coma, spherical aberration, and defocusing, all of which have a dependence on the numerical aperture.4 Such aberrations not only affect the spatial and spectral resolution but cause a decrease in signal because they prevent the light collected to be focused at the detector. It is outside of the scope of this manuscript to treat in detail such aberrations (for more on imaging spectrograph artifacts see ref. 4 and 9), but it is clear from Fig. 2C and D that as one increases the f/# of the spectrograph (by decreasing the size of the grating with masks) the aberrations decrease. The spectrograph without a grating mask, 32 mm × 32 mm grating size, has a maximum spectral resolution of 0.4 nm (in pixels, row: 225, column: 300) and gets worse (down to 1.35 nm FWHM) as one moves toward the edges of the field. On the other hand, the 8 mm × 8 mm grating mask yields a more homogeneous spectral resolution (best: 0.4 nm; worst: 0.8 nm). In terms of spatial resolution, however, the effect of the mask is more significant, for example, without the mask there is a considerable portion of the field where one cannot even resolve 3.56 lp mm−1. With the 8 mm × 8 mm mask one can resolve 3.56 lp mm−1 everywhere in the field and there is a 25 nm window where the spatial resolution is as good as 10.10 lp mm−1. Conversely, without a mask one cannot get down to 10.10 lp mm−1 anywhere in the field. It is worth noting that these aberrations are instrument specific and that the spectrograph in this study was chosen because of its availability rather than its imaging capabilities. Furthermore, there are many examples of Czerny-Turner spectrographs where the aberrations are minimized by use of toroidal mirrors or corrective lenses. In addition, one can use a concave imaging grating7 or a different kind of spectrograph, e.g. Offner configuration, to achieve better imaging fidelity.9 Other options would include the use of prisms7 or even lenses with circular blazed gratings. | ||
| Fig. 2 (A) Spectral image of the spectrograph slit illuminated with the Hg(Ar) pen lamp. (B) Spectral image of a grid on the spectrograph slit illuminated with a continuum lamp. (C) and (D) are taken under same conditions as (A) and (B) but with a grating mask that only allows an 8 mm × 8 mm central portion to be illuminated. | ||
Image correction
A way of getting around the smile problem is to make the unit pixel size in the spectral dimension big enough to make the smile insignificant with respect to the size of the wavelength channel (in other words degrade the image to have a uniform point spread function), however, this would come at a premium cost of spectral resolution.11 There are several methods to correct for the smile;12 herein the smile is corrected by projective transformation.13 In short, the method uses a function to chart and amend distorted images. In the case of the smile, a polynomial function is justified due to the dependence of the curvature on the square of the vertical position.4 The polynomial function is obtained by establishing control points in the sample image that correspond to model positions in an ideal image. For this purpose, a spectrum of the Hg(Ar) pen lamp was measured. Line peak positions for each spatial position were obtained with a Matlab (R2011a, The MathWorks, Inc., Natick, MA) program called iPeak,14 thus giving a set of control points. This was followed by resampling the spectra for all the spatial positions to the central spatial position parameters (across the track row corresponding to the pixel where the aberrations are at a minimum and thus the spectral and spatial resolution is highest) which gave a set of model points. The sets of points serve as input in Matlab which can yield the appropriate structure (viacp2tform) that can then be used for the image transformation (via imtransform).
It should be noted that before the smile correction the image is rotated to correct for the remaining camera rotation misalignment (in this case 0.38 degrees). This is characterized via imaging a section of a USAF 1951 target mask illuminated with the deuterium/tungsten halogen continuum source onto the spectrograph's entrance slit. The same images can be used to measure the keystone distortion, which is a change in magnification with the spectral channel. Fortunately, our system does not have an observable keystone distortion.
However, in a push-broom system one obtains a spatial and a spectral dimension and so the ideal flat-field source would have to be homogeneous in these two dimensions for the correction to take the effects of the imaging system into account. A source that emits a perfectly even intensity through a large wavelength range is not accessible but some alternatives can be pursued. In our case, the emission from the D2 lamp is spatially homogenized via a “spatial averaging”17 optical collection system and imaged onto a diffuser. The spectral heterogeneity, which should not be extreme within the spectrograph's wavelength window, can be removed by obtaining an average spectrum from the smoothed spectra over the spatial dimension and dividing element-wise the original image over the average spectrum. The resulting image is the one used for flat-field correction.
Image acquisition and analysis
As previously mentioned, push-broom imaging systems allow simultaneous measurement of the spectral dimension and one spatial dimension. It is necessary to scan the remaining spatial dimension to reconstruct the monochromatic 2D images. The image reconstruction requires one to know the exact position of the scanning motorized stage for each camera frame. Also, it is clear that for practical reasons, taking into account the spatial resolution requirements, the data collection needs to be automated. Thus, a LabVIEW program was developed for data collection automation, which incorporates the image correction routines from Matlab and allows the reconstruction of the full hyperspectral data cube where 2D monochromatic images can be extracted at the wavelengths of interest. The part of the program concerning the ICCD control was developed with the assortment of VIs provided in the Scientific Imaging Toolkit (SITK®, R Cubed Software, NJ, USA). The part concerned with the stage motor control was accomplished with the Advanced Positioning Technology software (APT, ThorLabs, UK). Fig. 3A shows the hyperspectral cube image of a USAF 1951 transmission target illuminated from behind with the Hg(Ar) lamp through a fused silica diffuser. The 2D image at 404.7 nm can be observed in Fig. 3B.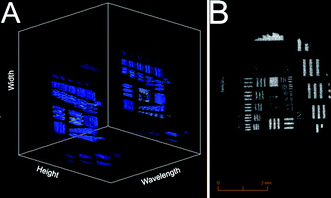 | ||
| Fig. 3 (A) Hyperspectral data cube of a transmission 1951 USAF target situated at the position of the cathode surface in the GD cell and illuminated with the Hg(Ar) pen lamp. (B) Monochromatic 2D image from data above at 404.7 nm. | ||
GDOES elemental mapping
It is now appropriate to see how the system performs for GDOES elemental mapping. For this purpose a model sample consisting of a copper pin inserted in a nickel substrate was used. The glow discharge pulsing frequency was 1 kHz and the pulse width was 10 μs. The pressure was maintained at 900 Pa and the peak voltage was 1250 V. The ICCD gate width was set at 10 μs to coincide with the GD pulse and there were a total of 34 gates accumulated per frame. Under these conditions it takes 56 ms to obtain a single ICCD frame (22 ms for the ICCD to be read, binned 2 × 2, plus the 34 ms due to the accumulated gates at 1 kHz) corresponding to a given motor position. The scan motor speed was set at 0.5 mm s−1, thus we obtain a frame every 28 μm which is the effective pixel size in terms of the spatial resolution. One aspect to keep in mind in scanning systems is the forward motion blur (FMB) which is the loss of resolution that may appear due to the motion of the object with respect to the detection system. With the above-mentioned operating conditions the FMB is 0.66 pixel, thus the system's resolution in the scanning direction is not limited by this effect. Fig. 4A shows the Cu emission image obtained at 324.7 nm and Fig. 4B shows the Ni emission image at 341.5 nm. The position from the Cu pin is clear from the 324.7 nm image. Also, there is a dip in the Ni emission intensity at the Cu pin position. Fig. 5 shows images under the same conditions as Fig. 4 but with the use of the 8 mm mask in the spectrograph. Although the collected emission intensity is approximately 5.5 times less, it is evident that the improved spatial resolution afforded by the mask is necessary to avoid blurring of the GD laterally resolved emission. The Cu pin is not symmetrical but it was measured under an optical microscope to be 1.58 mm in the long direction. The FWHM of the Cu pin emission in this direction is 1.85 mm (Fig. 5). It should be noted that the GD operating conditions were not optimized to obtain the best spatial resolution but were chosen only to illustrate the advantages of the push-broom imaging system. To put this into perspective, the optimum conditions for GDOES elemental mapping found in previous studies used 10 times smaller pulse widths, 10 times lower pulse frequencies, and up to five times greater pressures, all of which have been shown to have a significant effect on the obtained lateral resolution. A parametric study will be performed in the future to find the optimum GD operating conditions that yield the best lateral resolution with this particular GD cell. It is noteworthy that this is the first time that pulsed GDOES elemental mapping is used to obtain a multi-elemental qualitative image of the surface composition of a single laterally heterogeneous sample.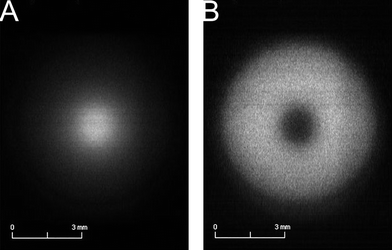 | ||
| Fig. 4 GDOES elemental mapping of Cu pin in the Ni substrate sample without a grating mask. (A) Monochromatic image of the GD at 324.7 nm. (B) Monochromatic image of the GD at 341.5 nm. | ||
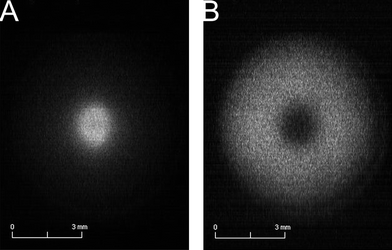 | ||
| Fig. 5 GDOES elemental mapping of Cu pin in the Ni substrate sample with a 8 mm × 8 mm grating mask. (A) Monochromatic image of the GD at 324.7 nm. (B) Monochromatic image of the GD at 341.5 nm. | ||
To have an idea of the expected depth resolution under the current operating conditions one must take into account the erosion rate. The erosion rate for a pure Cu sample under the same conditions for a period of 8 h was measured to be 12.5 nm min−1. In our case, a 7 mm scan (size of the anode) takes approximately 14.1 s (0.5 mm s−1motor speed, plus acceleration and deceleration time), which means that the size of one pixel in the depth dimension is equal to 2.9 nm for Cu. This shows that the resolution in the depth dimension is still very high and, in fact, this is not the limit. The depth resolution could be improved by optimizing the glow discharge operating parameters such as pulse width, voltage, or pressure, as well as the ICCD exposure conditions such as the amount of accumulated ICCD gates per frame or increasing the binning to reduce the time it takes to read each frame.
One important aspect to keep in mind is that the optimum conditions for lateral resolution may not be the optimum conditions for depth resolution. Nevertheless, GDOES elemental mapping gives more flexibility in terms of depth resolution compared to the typical GDOES arrangement. In the latter, the emission is basically an average from the sputtered species that are excited in the plasma and as such a major emphasis has to be placed on having the very best crater shape (flat) over a very large area to prevent mixing of different layers from the sample. This is not the case with GDOES elemental mapping (within the limits of lateral resolution) where the laterally resolved information allows us to determine from which part of the crater the emission is coming. This concept, however, requires further study currently underway in our laboratory.
One last aspect to note is that the Cu pin/Ni substrate sample is a very simple model but it serves well the main objective here. Besides Cu, and Ni in this study, only emission from Ag containing samples has been reported in the literature of GDOES elemental mapping.3 It is clear that these elements have very strong emission lines and it remains to be seen how other samples behave in terms of sensitivity, which is also ongoing work in our laboratory. It is not straightforward to come up with an expected limit of detection because it depends on many things (operating conditions, type of imaging system and spatial resolution, elemental line, etc.) which still have to be optimized for the application. Keeping this in mind, one can compare the typical GDOES arrangement to the push-broom elemental mapping by keeping all experimental conditions the same except using a PMT detectorvs. a CCD. Thus, under the conditions used in this study the emission from the 7 mm anode is distributed vertically over ∼300 pixels along the slit while it would be collected by a single detector in the typical GDOES arrangement. In this case, the limits of detection would be expected to be about two orders of magnitude lower for the elemental mapping in the detector limited background case. Nevertheless, this is only the starting point in this discussion because one also has to consider that in typical GDOES depth profiling the experimental conditions are optimized for best crater shape not for best detection limits; likewise in elemental mapping the conditions would be optimized for best lateral resolution. Finally, it is worth noting that there are applications of GDOES elemental mapping where current limits of detection are already remarkable, for example it was shown that bovine serum albumin could be detected down to 1 fmol when blotted onto PVDF membranes and stained with silver enhanced colloidal gold by measuring the Ag emission with a monochromator-based staring imaging spectrometer.3
Conclusion
Push-broom hyperspectral imaging has been shown to have several advantages with respect to other spectral imaging systems when applied to GDOES elemental mapping. In particular, monochromator based whisker-broom and staring spectral imaging systems require longer acquisition times to obtain a comparable image. On the other hand, we have also shown that push-broom systems may suffer from some distortions, which can be significant and in the one presented above required decreasing the aperture as well as implementing image correction routines. The true advantage of push-broom systems can be harnessed when the aberrations are originally minimized, such that there is no compromise in light throughput, and when multi-elemental maps of the same sample have to be obtained simultaneously.Acknowledgements
The authors would like to acknowledge funding from the Swiss National Science Foundation through SNF-project 206021_128738/1.References
- V. Hoffmann and G. Ehrlich, Spectrochim. Acta, Part B, 1995, 50, 607–616 CrossRef.
- M. R. Webb, V. Hoffmann and G. M. Hieftje, Spectrochim. Acta, Part B, 2006, 61, 1279–1284 CrossRef.
- G. Gamez, S. J. Ray, F. J. Andrade, M. R. Webb and G. M. Hieftje, Anal. Chem., 2007, 79, 1317–1326 CrossRef CAS.
- D. J. Schroeder, Astronomical Optics, Academic Press, San Diego, 2000 Search PubMed.
- J. M. Lerner and A. Thevenon, The Optics of Spectroscopy, Horiba Scientific, 1998 Search PubMed.
- R. G. Bingham, Proceedings of SPIE, The International Society for Optical Engineering, 1984, vol. 445, pp. 516–521 Search PubMed.
- J. M. Lerner, Cytometry, Part A, 2006, 69, 712–734 CrossRef.
- T. Nelis and R. Payling, Glow Discharge Optical Emission Spectroscopy: A Practical Guide, The Royal Society of Chemistry, Cambridge, 2004 Search PubMed.
- P. Mouroulis, R. O. Green and T. G. Chrien, Appl. Opt., 2000, 39, 2210–2220 CrossRef CAS.
- J. M. Sasián, Appl. Opt., 2000, 39, 34–39 CrossRef.
- D. Schläpfer, J. Nieke and K. I. Itten, IEEE. Trans. Geosci. Rem. Sens., 2007, 45, 458–468 CrossRef.
- X. Ceamanos and S. Douté, IEEE. Trans. Geosci. Rem. Sens., 2010, 48, 3951–3959 Search PubMed.
- F. W. L. Esmonde-White, K. A. Esmonde-White and M. D. Morris, Appl. Spectrosc., 2011, 65, 85–98 CrossRef CAS.
- T. O'Haver, Version 1.4, http://terpconnect.umd.edu/%7Etoh/spectrum/PeakFindingandMeasurement.htm, 2011 Search PubMed.
- T. C. Williams and C. R. Shaddix, Rev. Sci. Instrum., 2007, 78, 123702 CrossRef.
- C. A. Monnig, B. D. Gebhart and G. M. Hieftje, Appl. Spectrosc., 1989, 43, 577–579 CrossRef CAS.
- M. R. Winchester, Appl. Spectrosc., 1996, 50, 245–251 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
