Molecular structure and acid/base properties of 1,2-dihydro-1,3,5-triazine derivatives†
Vjekoslav
Štrukil
a,
Ivica
Đilović
b,
Dubravka
Matković-Čalogović
b,
Jaan
Saame
c,
Ivo
Leito
c,
Primož
Šket
de,
Janez
Plavec
def and
Mirjana
Eckert-Maksić
*a
aRuđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia. E-mail: mmaksic@emma.irb.hr; Fax: +385-1-4680-195; Tel: +385-1-4680-197
bFaculty of Science, Department of Chemistry, Horvatovac 102A, 10000 Zagreb, Croatia
cUniversity of Tartu, Institute of Chemistry, Ravila 14a, 50411 Tartu, Estonia
dSlovenian NMR Centre, National Institute of Chemistry, Hajdrihova 19, SI-1000 Ljubljana, Slovenia
eEN-FIST Centre of Excellence, Dunajska 156, SI-1000 Ljubljana, Slovenia
fFaculty of Chemistry and Chemical Technology, University of Ljubljana, Askerceva cesta 5, SI-1000 Ljubljana, Slovenia
First published on 25th October 2011
Abstract
It is shown that guanidine and its N,N-dimethyl-derivative react with substituted carbodiimides, affording hitherto unknown 1,2-dihydro-1,2,3-triazine derivatives. The structures of three novel compounds of this type and their perchlorate salts were elucidated by spectroscopic (IR, 1H and 13C NMR and 15N solid-state NMR) and X-ray diffraction methods. The acid/base properties were also determined experimentally and by using DFT calculations with the B3LYP functional. The most basic compound was found to be dihydrotriazine 3, the basicity of which with the pKa value of 23.3 is of the same order of magnitude as that of tetramethylguanidine. Acidity measurements revealed that all the compounds studied are very weak acids with pKa values in the range of 25.8–30.8 pKa units in acetonitrile.
Introduction
Dihydrotriazine derivatives comprising a variety of substituents have been extensively studied in the past due to their broad biological activity. Some of these compounds have been used as antibacterial,1 anti-inflammatory,2antimalarial,3 anti-diabetic4 and antitumor5 agents (Scheme 1).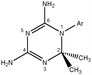 | ||
| Scheme 1 The structure of cycloguanil, an antimalarial1,2-dihydrotriazine inhibitor of dihydrofolate reductase (Ar = 4-ClC6H4).3 | ||
Other successful applications include use as herbicides,6insecticides7 and corrosion inhibitors.8 Consequently, their syntheses and the evaluation of their biological activity continue to attract considerable attention.9 In the course of our ongoing project on the design and reactivity of strong guanidine bases,10 we became interested in exploring the possibility of preparing some specifically substituted dihydrotriazines using guanidine derivatives and carbodiimides as reactants. This approach, as well as the reaction of biguanide derivatives and carbodiimides, has been extensively explored in the past. In all the reports published so far, only the formation of melamine or isomelamine derivatives was reported.11–13 The reaction was proposed to proceed through the primary addition of the reactants, followed by the cyclization of the resulting intermediate triguanide, with the loss of amine, to the heterocyclic end-product.11 However, although this approach to melamine and isomelamine derivatives has been known for a long time, no thorough study of a reaction mechanism and a structure of the so obtained products has been published as yet.11,12 Therefore, we considered it of interest to address some of these questions in the present work. Furthermore, an additional focus of our interest in the properties of dihydrotriazines concerned their acid–base properties. Namely, due to the presence of guanidine-type subunits in their molecular framework, they are expected to exhibit basicity of a similar order of magnitude as guanidine or biguanide derivatives.14
Herewith, we report on the synthesis and structural features of three novel 1,2-dihydro-1,3,5-triazine derivatives, namely 1–3 (Scheme 2). It should be noted that they differ from previously reported members of this family of compounds by the presence of the exo-cyclic imino group at ring position 2. We were particularly interested in establishing the structure of compound 1, for which the isomelamine geometry (see Scheme 5) from UV spectral analysis was previously proposed.11,12 Our second aim in this work was to evaluate their basicity and acidity experimentally by employing quantum chemical calculations. This is of considerable importance since due to the presence of exo-cyclic imino- and amino-type nitrogen atoms, they are expected to have the ability either to donate or accept a proton, i.e., to act as either an acid or a base (Scheme 2). In addition, the results of a computational study of the effect of p-substituents in aryl-substituted species on the protonation energies, with the goal of designing potentially stronger acids/bases belonging to this class of compounds, will be presented. To the best of our knowledge, this has been the first comprehensive study of the structural features and acid/base properties of 1,2-dihydro-1,3,5-triazine derivatives so far.
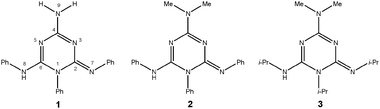 | ||
| Scheme 2 The 1,2-dihydro-1,3,5-triazine derivatives 1–3 studied in this work. | ||
Results and discussion
Synthesis and characterization of products
Compounds 1–3 were prepared in an excellent yield by applying a modified one-pot procedure based on a protocol reported earlier by Kurzer and Pitchfork.11Guanidine (4) or N,N-dimethylguanidine (5) was first treated with two equivalents of N,N′-diphenylcarbodiimide (6) in refluxing THF (Scheme 3), affording the phenyl derivatives 1 and 2 in moderate yields (60% and 51%, respectively), accompanied by the corresponding biguanide derivative and N,N′,N′′-triphenylguanidine (8) (Fig. S1, ESI†; Scheme 4). This suggests that the aniline molecule liberated during cyclization competes with the in situ formed biguanide derivative for N,N′-diphenylcarbodiimide (6), yielding by-product 8. To increase the yield, the reaction was repeated using three equivalents of N,N′-diphenylcarbodiimide (6), which led to a complete consumption of the biguanide intermediate and an increase in the isolated yield of the cyclic product to 98% (1) and 94% (2), respectively (Fig. S2, ESI†). After removing the solvent, the main product was isolated by suspending the crude reaction mixture in diethylether followed by filtration (1 and 2). In the case of the isopropyl derivative 3, the reaction was carried out using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of 5 and 7, and a pure product was isolated by high-vacuum distillation in 80% yield. Moreover, no N,N′,N′′-triisopropylguanidine (9) was observed, presumably due to the lower reactivity of dialkylcarbodiimide 7 (R2 = i-Pr) and high volatility of isopropylamine (bp 32 °C) under the applied experimental conditions. Another important observation is that an intermediate triguanide derivative could not be identified in any of the reactions studied in this work, which is in accordance with the available literature studies.11,12
2 ratio of 5 and 7, and a pure product was isolated by high-vacuum distillation in 80% yield. Moreover, no N,N′,N′′-triisopropylguanidine (9) was observed, presumably due to the lower reactivity of dialkylcarbodiimide 7 (R2 = i-Pr) and high volatility of isopropylamine (bp 32 °C) under the applied experimental conditions. Another important observation is that an intermediate triguanide derivative could not be identified in any of the reactions studied in this work, which is in accordance with the available literature studies.11,12
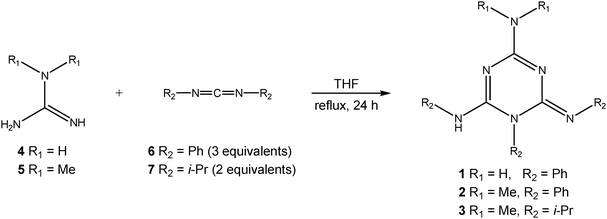 | ||
| Scheme 3 Synthesis of triazines 1–3. | ||
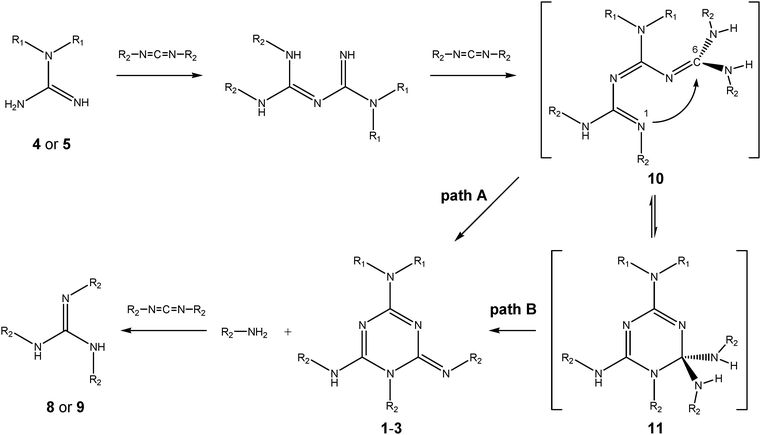 | ||
| Scheme 4 Possible mechanisms of the formation of 1,2-dihydro-1,3,5-triazine derivatives 1–3 (R1 = H or Me, R2 = Ph or i-Pr). | ||
This confirms the previous proposition11,12 that an intermediately formed triguanide derivative undergoes spontaneous cyclization accompanied by the elimination of amine R2NH2 (aniline in the reaction of N,N′-diphenylcarbodiimide (6) or isopropylamine when N,N′-diisopropylcarbodiimide (7) is used). From a mechanistic point of view, two modes of cyclization to 1,2-dihydrotriazines could be envisaged (Scheme 4): one starting directly from the triguanide moiety 10 (path A) or from its ring tautomer intermediate 11, which is formed by a nucleophilic attack of the lone pair at the imino nitrogen N1 to the carbon atom C6 in triguanide 10, followed by the elimination of the R2NH2 molecule (path B). This type of tautomerism is well known from, e.g., sugar chemistry.15 More recently, chain–ring tautomerism, which, in fact, corresponds to thermally allowed 6π-electrocyclization, has also been invoked to explain the mechanism of the cyclization of some unsaturated hetero chains of the oligonitrile type into 1,2-dihydro-1,3,5-triazine derivatives.16
However, in this work, we could not confirm the presence of these intermediates experimentally due to their obvious instability. Therefore, we calculated the energies of both types of tautomers for the model compounds in which R1 and R2groups were replaced by methyl groups, using the B3LYP/6-311+G(d,p)//B3LYP/6-31G(d,p) method. In addition to the gas phase, calculations were carried out in THF as the solvent. The geometries of the fully optimized species are shown in Fig. S3 and Table S1 (see ESI†) and the computed energies are listed in Table 1. A glance at the calculated energies in Table 1 clearly shows that the open-chain and cyclic tautomers 10 and 11 are of similar stability, with the latter being slightly more stable in THF (by 1.07 kcal mol−1). Thus, based on these data, albeit qualitative, we presume that path B would be favored.
| Structurea | E el/a.u. | E ZPV/a.u. | E tot/a.u. | E rel/kcal mol−1 |
|---|---|---|---|---|
| a R1 = R2 = CH3, see Scheme 4. TS corresponds to the transition structure for chain-tautomer cyclization. | ||||
| Gas phase | ||||
| 10 | −739.06485 | 0.32223 | −738.74262 | 0.00 |
| TS | −739.04652 | 0.32210 | −738.72442 | 11.42 |
| 11 | −739.06342 | 0.32486 | −738.73856 | 2.55 |
| THF solution | ||||
| ΔGsolv/kcal mol−1 | E solvrel/kcal mol−1 | |||
| 10 | 11.61 | 0.00 | ||
| TS | 8.81 | 8.62 | ||
| 11 | 7.99 | −1.07 | ||
The 1,2-dihydrotriazine products were fully characterized by elemental analysis and spectroscopic methods (IR, HRMS, 1H and 13C solution and 1H, 13C and 15N solid-state NMR). The structures of compounds 1 and 2 were ultimately confirmed by X-ray diffraction analysis. In the mass spectra, all three compounds gave the expected molecular ion [MH+] along with some fragment ions. The proposed structures were supported by analysis of the solution and solid-state NMR spectra. For instance, taking the 1H NMR spectra in the solution of compound 3 as an example, we observe a broad doublet at 6.15 for the C–NHproton, a singlet for the protons of the N–CH3 group at 2.96 ppm, three multiplets for the N–CHprotons in the range of 3.96–4.76 ppm and three doublets for the CH–CH3 protons in the range of 0.96–1.41 ppm. The corresponding 13C NMR spectrum in solution displays three signals between 159.2–148.2, three signals between 45.3–42.8 ppm, one signal at 35.5 ppm and three signals between 24.5–19.4 ppm assigned to the ring carbon atoms, CH carbon atoms of three chemically different isopropyl groups, N–CH3 and C–CH3 carbon atoms, respectively.
Similar chemical shifts for carbon atoms have been observed in the solid state as well (Fig. 1). The 1H and 13C NMR spectra of triphenyl derivatives 1 and 2 (see the Experimental section) in solution, as well as in the solid state (Fig. S4–S7 and S19–S22 in ESI†), are also fully consistent with the 1,2-dihydro-1,3,5-dihydrotriazine structures. Notably, the signals for the NHproton in the 1H NMR spectra of 1 and 2, taken in DMSO, appear in the same region (7.61 ppm in 1 and 7.75 ppm in 2 in DMSO), thereby confirming that the imino proton is in the same chemical environment in both compounds (Fig. S4 and S6 in ESI†).
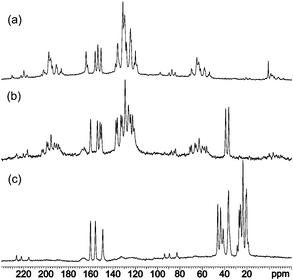 | ||
| Fig. 1 13C CP-MAS NMR spectra of compounds 1 (a), 2 (b) and 3 (c). | ||
Furthermore, in the 15N CP-MAS NMR spectra, the most upfield signals between −290 and −300 ppm indicate the presence of the amino/dimethylamino group attached to the C4 atom (Fig. 2).
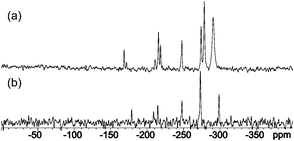 | ||
| Fig. 2 15N CP-MAS NMR spectra of compounds 1 (a) and 2 (b). | ||
Even more importantly, the signals for N3 and N5 atoms have different chemical shifts. In the case of 1, this excludes the existence of the quinoid and isomelamine structures 1T2 and 1T3 (Scheme 5), in which we would expect to observe a single resonance for both atoms due to the symmetry of the molecule. In order to obtain insights into the intrinsic stabilities of tautomers 1T1–1T3 of compound 1, their energies were calculated using the B3LYP/6-311+G(d,p)//B3LYP/6-31G(d) method. At this level of theory, tautomer 1T1 was found to be more stable than 1T2 and 1T3 by 15.2 and 11.6 kcal mol−1, thus being in accordance with NMR data (see Table S3 for energies in ESI†).
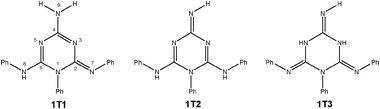 | ||
| Scheme 5 Possible tautomeric structures of molecule 1. 1T1-imino, 1T2-quinoid and 1T3-isomelamine structures. | ||
Finally, an interesting feature observed in the 15N CP-MAS NMR spectrum of compound 1 concerns the presence of a larger number of signals than in compound 2, indicating that two molecules are present in the asymmetric unit of compound 1, while a single molecule is present in the asymmetric unit of compound 2 in the solid state. This, as will be shown below, was confirmed by X-ray diffraction data.
X-Ray structure determination of 1 and 2
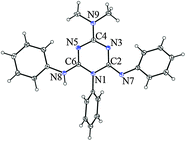
The crystal and molecular structures of the methanol solvate of compound 1 (1·0.5 MeOH) and compound 2 were determined by the single crystal X-ray diffraction method (Table 3). The asymmetric unit of 1·0.5 MeOH consists of two different conformers of 1 (1a and 1b) and a methanol molecule, while that of 2 contains a single molecule (Fig. 3 and 4). The selected bond lengths are given in Table 2. Their perusal clearly indicates that imino tautomer 1T1 is present in both compounds. The carbon–nitrogen bond distances within the triazine ring range from 1.302(2) Å to 1.433(2) Å, and are also in agreement with this tautomeric form, albeit with extensive delocalization. Such delocalized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds were also reported for the structurally related 1,6-dihydro-1,3,5-triazine derivative.17
N bonds were also reported for the structurally related 1,6-dihydro-1,3,5-triazine derivative.17
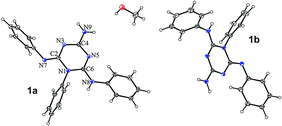 | ||
| Fig. 3 ORTEP drawing of 1·0.5 MeOH. Thermal ellipsoids are at the 30% probability level. | ||
 | ||
| Fig. 4 ORTEP drawing of 2. Thermal ellipsoids are at the 30% probability level. | ||
| Bond | 1a | 1b | 2 |
|---|---|---|---|
| a For numeration of atoms see Fig. 3 and 4. | |||
| N1–C2 | 1.416(2) | 1.419(2) | 1.433(2) |
| N1–C6 | 1.374(2) | 1.372(2) | 1.371(2) |
| C2–N3 | 1.360(2) | 1.370(2) | 1.354(2) |
| N3–C4 | 1.331(2) | 1.329(2) | 1.328(2) |
| C4–N9 | 1.325(2) | 1.333(2) | 1.346(2) |
| C4–N5 | 1.367(2) | 1.366(2) | 1.362(2) |
| N5–C6 | 1.302(2) | 1.317(2) | 1.308(2) |
| C2–N7 | 1.292(2) | 1.287(2) | 1.292(2) |
| C6–N8 | 1.359(2) | 1.343(2) | 1.361(2) |
| N1–Ph | 1.447(2) | 1.444(2) | 1.444(2) |
| N7–Ph | 1.423(2) | 1.416(2) | 1.411(2) |
| N8–Ph | 1.418(2) | 1.433(2) | 1.424(2) |
| 1·0.5 MeOH | 2 | 2·HClO4 | 3·HClO4 | |
|---|---|---|---|---|
| a R = ∑||Fo| − |Fc||/∑Fo, w = 1/[σ2(F2o) + (g1P)2 + g2P] where P = (F2o + 2F2c)/3, S = Σ[w(F2o – F2c)2/(Nobs − Nparam)]1/2. b wR = [Σ(F2o − F2c)2/Σ(F2o)2]1/2. | ||||
| Empirical formula | 2(C21H18N6), CH4O | C23H22N6 | C23H23N6, ClO4 | C14H29N6, ClO4 |
| Formula weight | 740.87 | 382.47 | 482.92 | 380.88 |
| Crystal system, space group | Monoclinic, P 21/c | Orthorhombic, P bca | Orthorhombic, P 212121 | Monoclinic, P 21/c |
| Unit cell dimensions (Å, °) | ||||
| a | 14.1696(2) | 19.0976(8) | 6.9133(5) | 9.4056(10) |
| B | 17.3971(4) | 9.1823(3) | 15.5643(12) | 9.3787(9) |
| c | 15.0518(3) | 21.9471(8) | 20.7086(14) | 22.2736(18) |
| α | 90.00 | 90.00 | 90.000 | 90.00 |
| β | 91.7700(20) | 90.00 | 90.000 | 98.682(7) |
| γ | 90.00 | 90.00 | 90.000 | 90.00 |
| Volume/Å3 | 3708.65(12) | 3848.6(2) | 2228.3(3) | 1942.3(3) |
| Z | 4 | 8 | 4 | 4 |
| D calc/g cm−3 | 1.327 | 1.320 | 1.440 | 1.303 |
| T/K | 100(2) | 100(2) | 150(2) | 110(2) |
| Reflections observed/independent (Rint) | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085/6866 (0.0366) 085/6866 (0.0366) |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 539/3363 (0.0426) 539/3363 (0.0426) |
5090/3659 (0.0297) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999/3799 (0.0317) 999/3799 (0.0317) |
| Observed reflections [I > 2σ(I)] | 4991 | 2698 | 2760 | 3083 |
| Goodness-of-fit on F2 | 0.979 | 1.072 | 1.033 | 1.121 |
| R/wR [I > 2σ(I)]a | 0.0443/0.1067 | 0.0454/0.0892 | 0.0632/0.1065 | 0.0488/0.1235 |
| R/wR (all data)b | 0.0642/0.1172 | 0.0642/0.0958 | 0.0910/0.1167 | 0.0624/0.1317 |
| Flack parameter | — | — | −0.04(12) | — |
It is important to note that the NH2 group (NMe2 in 2) is practically coplanar with the triazine moiety, thus enabling effective delocalization of the nitrogen lone pair in the triazine ring. Another notable feature concerns the difference in the length of the exocyclic C2–N7 and C6–N8 bonds. While the length of the C2–N7 bond (1.292(2) Å and 1.287(2), 1.292(2) Å in 1a, 1b, and 2, respectively) corresponds to a typical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond, the C6–N8 bond (ranging from 1.343(2) to 1.361(2) Å) has a value closer to a typical Nsp2–Csp2 single bond, such as in ref. 18.
N double bond, the C6–N8 bond (ranging from 1.343(2) to 1.361(2) Å) has a value closer to a typical Nsp2–Csp2 single bond, such as in ref. 18.
In the crystal structure of 1·0.5 MeOH, the two conformers are connected by hydrogen bonds of the type N–H⋯N (2.912(2) and 3.053(2) Å), forming a ring that can be described by the graph-set notation R22(8).
The methanol molecule is a donor in the hydrogen bond O–H⋯N (2.915(2) Å) to molecule 1a and is an acceptor of a weak hydrogen bond C–H⋯O from a neighboring 1a molecule (Fig. 5). Such supramolecular assemblies are interconnected in the crystal structure by weak interactions of the type C–H⋯O, C–H⋯N, C–H⋯π and N–H⋯π.
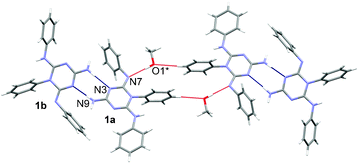 | ||
| Fig. 5 A supramolecular assembly in the structure of 1·0.5 MeOH showing molecules interconnected by hydrogen bonds (blue and red lines). Symmetry code * = 1 − x, −y, −z. | ||
In contrast, packing in the crystal structure of 2 is achieved through weak interactions, mostly of the C–H⋯π type. The protonated nitrogen atom N8 is sterically hindered and not involved in hydrogen bonding.
The effect of protonation on the molecular structure of 1–3
In order to confirm the site of proton attack and to obtain insights into the effect of protonation on the structure of the compounds considered, we measured the X-ray structure of the monocrystals of the perchlorate salts of 2 and 3 (Fig. 6). All attempts to prepare single crystals of the perchlorate salt of 1 suitable for X-ray measurements were unsuccessful. Therefore, in order to obtain insights into the structure of protonated 1, its geometry was optimized using the B3LYP/6-31G(d) method. The key structural parameters of the calculated and experimentally determined structures of the protonated species, 2·HClO4 and 3·HClO4, are listed in Table 4, while the summary of all the calculated parameters and relevant parameters for the neutral molecules is presented in Tables S4–S6 in the ESI.†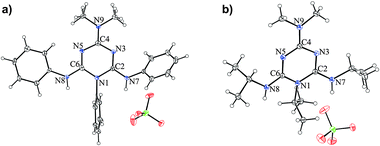 | ||
| Fig. 6 ORTEP drawings of (a) 2·HClO4 and (b) 3·HClO4. The thermal ellipsoids are at the 30% probability level. | ||
| Bond | d/Å | ||||
|---|---|---|---|---|---|
| Theory | Measured | Theory | Measured | Theory | |
| 1H++ | 2·HClO4 | 2H++ | 3·HClO4 | 3H++ | |
| a For numbering of the atoms see Scheme 2 and Fig. 6. | |||||
| N1–C2 | 1.401 | 1.397(5) | 1.401 | 1.393(2) | 1.400 |
| N1–C6 | 1.402 | 1.401(6) | 1.401 | 1.389(2) | 1.401 |
| C2–N3 | 1.317 | 1.304(5) | 1.311 | 1.320(3) | 1.317 |
| N3–C4 | 1.349 | 1.376(6) | 1.357 | 1.347(2) | 1.354 |
| C4–N9 | 1.336 | 1.318(5) | 1.340 | 1.336(2) | 1.341 |
| C4–N5 | 1.349 | 1.350(5) | 1.357 | 1.349(3) | 1.355 |
| N5–C6 | 1.317 | 1.307(5) | 1.311 | 1.322(2) | 1.316 |
| C2–N7 | 1.343 | 1.352(6) | 1.347 | 1.330(3) | 1.340 |
| C6–N8 | 1.343 | 1.333(5) | 1.347 | 1.333(3) | 1.344 |
| N1–Ph (i-Pr) | 1.449 | 1.446(5) | 1.448 | 1.503(2) | 1.505 |
| N7–Ph (i-Pr) | 1.432 | 1.437(5) | 1.432 | 1.478(3) | 1.483 |
| N8–Ph (i-Pr) | 1.432 | 1.429(6) | 1.432 | 1.479(3) | 1.484 |
Before analyzing the effect of protonation on 1–3 in detail, we note that the trend of the changes in the calculated structural parameters in 2H++ and 3H++ closely resembles those found in the X-ray structures of their perchlorate salts. The same holds for the comparison of the experimental and calculated structures of 1 and 2 and their protonated forms with those of the corresponding perchlorate salts. This, in turn, lends credence to the structural parameters calculated for the other species studied in this work.
The most striking feature of the experimental structures of the protonated species concerns the elongation of the C2–N7 bond relative to that in the neutral molecule, confirming that protonation occurs at the N7 atom. This results in a near equalization of the exocyclic C2–N7 and C6–N8 bonds, accompanied by changes in the bond lengths within the triazine ring, which assumes a paraquinonoid character with the C2–N3 and N5–C6 bond lengths being close to typical Csp2–Nsp2 bonds.
Basicity and acidity determination
The results of basicity and acidity measurements are presented in Tables 5 and 6, respectively. Also included in Tables 5 and 6 are the reference bases and acids used in this work. The basicity and acidity of a wide range of neutral heterocyclic and acyclic nitrogen-containing compounds have been measured previously in acetonitrile by several groups,19–21 resulting in well-defined acidity scales covering 24 orders of acidity20a,b and a base scale covering 28 orders of basicity,20c,d thus facilitating comparison of the pKa values of the compounds studied in this work with previously measured ones.| Compd. (B) | Reference base (Rb) | pKa (Rb) | ΔpKaa | pKa (B) | Assigned pKa(B) |
|---|---|---|---|---|---|
| a pKa(Rb) − pKa(B). b The standard uncertainties of the pKa values relative to the acetonitrile pKa scale are estimated as 0.05 pKa units (see ref. 20e). | |||||
| 1 | 2-Cl–C6H4P1(pyrr) | 20.17 | 1.69 | 18.48 | 18.51 |
| 2-Cl–C6H4P1(dma) | 19.07 | 0.59 | 18.48 | ||
| 2,6-Cl2–C6H3P1(pyrr) | 18.56 | 0.00 | 18.56 | ||
| 2 | PhP1(dma)2Me | 21.03 | 1.89 | 19.14 | 19.14 |
| 2-Cl–C6H4P1(pyrr) | 20.17 | 1.01 | 19.16 | ||
| 2-Cl–C6H4P1(dma) | 19.07 | −0.05 | 19.12 | ||
| 3 | 2-Cl–C6H4P2(dma) | 24.23 | 1.23 | 23.00 | 23.02 |
| PhP1(pyrr) | 22.34 | −0.72 | 23.06 |
| Compd. (A) | Reference acid (Ra) | pKa (Ra) | ΔpKaa | pKa (A) | Assigned pKab (A) |
|---|---|---|---|---|---|
| a pKa(Ra) − pKa(A). b The standard uncertainties of the pKa values relative to the acetonitrile pKa scale are estimated as 0.06 pKa units for 1 and 0.2 pKa units for 2 and 3 (see ref. 20e). | |||||
| 1 | (C6F5)(C6H5)CHCN | 26.14 | 0.31 | 25.83 | 25.83 |
| (C5F4N)(C6H5)NH | 26.34 | 0.51 | 25.83 | ||
| 2 | (C6F5)(C6H5)CHCN | 26.14 | −0.47 | 26.61 | 26.6 |
| (C5F4N)(C6H5)NH | 26.34 | −0.32 | 26.66 | ||
| (4-Me-C6F4)(C6F5)NH | 24.94 | −1.48 | 26.42 | ||
| 3 | 9-C6F5-Fluorene | 28.11 | −2.7 | 30.8 | 30.8 |
| 2,3,4,5,6-(CF3)5-Toluene | 28.7 | −2.1 | 30.8 |
Analysis of the results for the basicity measurements of 1–3 (Table 5) reveals that the basicity of 3 is the highest among the studied dihydrotriazines. Its pKa value lies between those for the 2-Cl-C6H4P2(dma) and PhP1(pyrr) reference bases. In relation to our current interest in the basicity of guanidine compounds,19 which, similarly to the present compounds, undergo protonation at the imino group, we note that this pKa value is of the same order of magnitude as that of tetramethylguanidine (23.3 pKa units)20f and 3.9 pKa units smaller than the pKa value of N,N′,N′′-tris(3-dimethylaminopropyl)guanidine, which is the most basic acyclic guanidine derivative studied so far.19 It should be, however, emphasized that the high basicity of the latter compound is to a large extent due to the presence of cooperative intramolecular hydrogen bonds and their impact on the stabilities of the base and its conjugated acid,19 which are not present in dihydrotriazines studied in this work. Replacement of the isopropyl groups with the electron-withdrawing phenyl rings, leading to 2 and 1, leads to a decrease in basicity of 3.9 and 4.5 pKa units (in acetonitrile), respectively. It is noteworthy that replacement of the amino group with the dimethylamino moiety in 1 leading to 2 causes partial cancellation of the electron-withdrawing effect of the phenyl rings, resulting in a slight enhancement of basicity.
Comparison of the measured acidity data (Table 6) with those encompassed by the previously published acidity scale of the neutral compounds indicates that the acidity of the NH proton in 1–3 has been among the lowest measured in acetonitrile so far. Thus, the acidity of 3 is ca. 2 pKa units lower than that of 9-C6F5-fluorene (28.11), which has the lowest acidity in the previously reported acidity scale20a and thus 3 extends the previously established pKa scale of acidity in acetonitrile. The acidity of the respective protons in 1 and 2 is 5.0 and 4.2 pKa units higher relative to 3. The observed enhancement in acidity can be understood by comparing the calculated charge density distribution in the molecules considered. Due to the delocalization of electronic density on the deprotonation site into the neighboring phenyl ring in molecules 1 and 2, the loss of the proton from this site becomes easier and the resulting anion more stabilized than in the case of 3, where such delocalization is not possible (Tables S8–S10 in the ESI†).
Comparison of the measured and calculated pKa values of bases 1–3 in acetonitrile
Due to the wide interest in the design of strong organic bases in synthetic work, considerable efforts have been devoted in the past to the development of practical theoretical methods capable of predicting pKa values in organic solvents. The a priori estimates of the pKa values from the first principles22 are, unfortunately, still not feasible in larger molecules of practical interest. Therefore, it is necessary to resort to simpler models of the polarized continuum (PCM)23 and its isodensity (IPCM) variant form.24 We have recently demonstrated that the latter approach in conjunction with the B3LYP/6-311+G(d,p)//B3LYP/6-31G(d) method for a large number of strong neutral nitrogen bases yields a fair correlation with the experimental pKa values of a large number of nitrogen bases.25Having measured the pKa values of guanidines 1–3, we decided to test the applicability of such correlations for calculating the pKa values of these types of bases. For this purpose, we used a slightly modified approach as employed in ref. 25. Specifically, the IEF-PCM model was used for calculating solvation energies instead of the IPCM method, due to a problem in the convergence of the isodensity surfaces for several structures. The same approach was subsequently used to evaluate the effect of a series of selected substituents in the para position of the phenyl rings, using molecule 2 as an example. All the optimized geometries were verified to be minima by vibrational analysis at the same level of theory. The resulting internal coordinates of all the optimized species are shown in Table S11 in the ESI.† The electronic energies and Gibbs energy corrections were calculated by the B3LYP/6-311+G(d,p) and B3LYP/6-31G(d) methods, respectively. Zero point vibrational energies were used unscaled. pKa values for the examined dihydrotriazines were calculated using linear eqn (1).26
| pKa(calc) = 0.617 × GB′(B)AN − 155.585 | (1) |
| GB′(AN) = GB′(B)gas + ΔG(BH+)AN − ΔG(B)AN | (2) |
The parameters for eqn (1) were evaluated from the linear relationship calculated for the test set of the 57 different nitrogen bases also used in our previous calculations, which span a range of ca. 40 pKa units. The calculated GB′(B)AN and pKa(calc) values of the compounds considered (as bases) are summarized in Table 7.
| Molecule | GB(B)gas | GB′(B)gas | ΔG(X)AN/kcal mol−1 | GB′(B)AN/kcal mol−1 | pKa(calc) | pKa (exp) | Δ(pKa) | |
|---|---|---|---|---|---|---|---|---|
| (kcal mol−1) | X = B | X = BH+ | ||||||
| a For numeration of atoms see Scheme 2. | ||||||||
| 1 | 247.35 | 253.63 | 3.80 | −25.18 | 282.61 | 18.78 | 18.51 | −0.27 |
| 2 | 249.49 | 255.77 | 9.30 | −18.36 | 283.43 | 19.29 | 19.14 | −0.15 |
| 3 | 250.42 | 256.70 | 14.66 | −18.50 | 289.86 | 23.26 | 23.02 | −0.24 |
| 2-NO2 | 226.77 | 233.05 | −0.26 | −42.10 | 274.89 | 14.02 | ||
| 2-CN | 230.09 | 236.37 | 1.10 | −39.37 | 276.84 | 15.23 | ||
| 2-Cl | 242.59 | 248.87 | 10.82 | −22.57 | 282.26 | 18.57 | ||
| 2-F | 243.97 | 250.25 | 10.41 | −22.53 | 283.19 | 19.14 | ||
| 2-Me | 253.53 | 259.81 | 13.42 | −12.68 | 285.91 | 20.82 | ||
| 2-OMe | 255.71 | 261.99 | 8.67 | −16.43 | 287.09 | 21.55 | ||
| 2-NH2 | 260.28 | 266.56 | 0.27 | −22.49 | 289.32 | 22.93 | ||
| 2-NMe2 | 264.77 | 271.05 | 13.68 | −6.46 | 291.19 | 24.08 | ||
| 2-N7PhNMe2 | 255.46 | 261.74 | 10.60 | −14.52 | 286.86 | 21.41 | ||
| 2-N7,N8PhNMe2 | 259.37 | 265.65 | 11.92 | −10.82 | 288.39 | 22.35 | ||
Before considering the effect of substituents on the basicity of compound 2, we note that the calculated pKa values for bases 1–3 are in excellent agreement with the experimentally measured values. Analysis of the data calculated for compound 2 substituted in the para position of the phenyl rings shows the strong impact of the electronic properties of the substituents on basicity. As expected, the effect of strong electron-donating dimethylamino groups is the most profound, causing an increase in basicity by ca. 5 pKa units. It is interesting to note that the effect of the dimethylamino group is additive; the largest contribution arises from the dimethylamino group at the phenyl ring attached to the N7 (2.12 pKa units), at which protonation takes place. This is followed by the contribution of the dimethylamino group at the N1 (1.73 pKa units) and N8 (0.94 pKa units) (Table 7). A somewhat weaker effect is observed for the amino substituted species, while methoxy and methyl groups increase basicity only moderately. On the other hand, substitution by the electron-accepting groups lowers basicity, with the largest effect encountered for the nitro-substituted species. To summarize, the chosen set of substituents facilitates fine-tuning of the basicity of the examined compound in the range of ca. 10 pKa units. It is quite plausible that all of these species can be easily prepared. Their use in further studies could lead to fine refinement of the existing scales of basicity in the range of ca. 14 to 24 pKa values.
Conclusions
One-pot synthesis of hitherto unknown 1,2-dihydro-1,2,3-triazine derivatives, starting from the corresponding guanidine and carbodiimide derivatives and their characterization using spectroscopic (IR, 1H and 13C solution-state and 13C and 15N solid-state NMR) methods, is described. The structures of two of the prepared compounds and their perchlorate salts were also confirmed by the X-ray diffraction method. This is, to the best of our knowledge, the first report on the preparation and structural determination of 1,2-dihydro-1,3,5-triazines possessing exo-cyclic imino group at ring position 2, thus opening a new avenue in exploring chemistry of this family of compounds. Due to the presence of exo-cyclic imino- (N7) and amino-type (N8) nitrogen atoms, the parent compounds were assumed to possess the ability either to donate or accept a proton, i.e., to act as either an acid or a base. This was confirmed by measuring basicity and acidity in acetonitrile and quantum chemical calculations. The most basic species was found to be compound 3, the basicity of which was of the same order of magnitude as that of tetramethylguanidine. Acidity measurements revealed that all the compounds studied behave like very weak acids, having pKa values in the range of 25.8–30.8 pKa units in acetonitrile. Finally, the pKa values were also calculated by the IEF-PCM model employing the B3LYP/6-311+G(d,p)/B3LYP/6-31G(d) method and were found to be in excellent agreement with the measured values, confirming high predictive power of the theoretical approach used. The same method was used to calculate the effect of a series of substituents in the para positions of the aromatic rings in 2, suggesting that in this way a fine-tuning of the basicity of the examined compound in the range of ca. 10 pKa units could be attained. It is quite plausible that all of these species can be easily prepared and their use in further basicity measurements could have significant impact on fine refinement of the existing scales of basicity in the range of ca. 14 to 24 pKa values, and could presumably lead to new types of strongly basic organocatalysts.Experimental section
Materials and methods
All reagents and solvents were purchased from commercial sources and were further purified by the standard methods, if necessary. 1H and 13C NMR spectra were recorded on Brucker Avance (300 and 600 MHz) spectrometers with tetramethylsilane as an internal standard, while IR spectra were obtained on an ABB Bomem MB102 spectrophotometer (CsI optics, DTGS detector, KBr pellets technique).
NMR spectra of solid samples were recorded on a Varian NMR System 600 MHz NMR spectrometer equipped with a 3.2 mm NB Double Resonance HX MAS Solids Probe. The Larmor frequencies of protons, carbon and nitrogen nuclei were 599.77 MHz, 150.83 MHz and 60.78 MHz, respectively. The 1H MAS NMR spectra were externally referenced using adamantane. The 13C CP-MAS NMR spectra were externally referenced using hexamethylbenzene (HMB). The 15N CP-MAS NMR spectra were externally referenced using ammonium sulfate (δ −355.7 ppm regarding nitromethane at δ 0.0 ppm). Samples were spun at the magic angle at 20 kHz during 1H measurement and 10 kHz during 13C and 15N measurements. The 1H spectra were acquired using an echo pulse sequence. The repetition delay was 5 s and the number of scans was 16. The pulse sequences used for acquiring the 13C and 15N spectra were standard cross-polarization MAS pulse sequences with high-power proton decoupling during acquisition. The repetition delay was 5 s. The numbers of scans were between 600 and 2200 for the 13C measurements and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 27
000 and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for 15N measurements.
000 for 15N measurements.
HPLC analyses were performed on a Varian ProStar Instrument supplied with a UV/Vis detector using a Restek UltraIBD C18 (reversed phase) 5 μm 250 × 4.6 mm column operated at room temperature with a flow rate of 1 mL min−1; gradient of 2% acetic acid (solvent A) and methanol (solvent B): 95% A + 5% B, 0–5 min; 85% A + 15% B, 5–45 min, 35% A + 65% B, 45–55 min, 5% A + 95% B, 55 min. Melting points were determined on a Kofler hot-stage apparatus and are uncorrected. Elemental analyses were performed on a Perkin Elmer 2400 Series II CHNS/O Analyzer.
Synthesis
υ max/cm−1 3352, 1638, 1430, 1070. δH(600 MHz; d6-DMSO; Me4Si) 2.74 (6 H, s, CH3), 4.30–4.70 (3 H, br s, NH). δC(150 MHz, d6-DMSO; Me4Si) 37.5, 160.0.
Guanidine to N,N′-diphenylcarbodiimide molar ratio = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 2.
To a solution of N,N′-diphenylcarbodiimide (6), (0.98 g, 5.0 mmol, prepared as previously described) in dry THF (10 cm3) guanidine (4) (0.15 g, 2.5 mmol) was added and the reaction mixture was heated under reflux for 24 hours. The pale yellowish crude mixture remaining upon the removal of the solvent was suspended in acetonitrile (10 cm3), the precipitated white solid was filtered off, washed with cold acetonitrile (5 cm3) and dried in air (0.45 g, 51%). Evaporation of the filtrate yielded a yellow residue, which was suspended in 3.0 cm3 of acetonitrile. The crystals that precipitated were separated by filtration and washed with 2.0 cm3 of cold acetonitrile, affording 0.53 g (60%) of product 1 in total.
2.
To a solution of N,N′-diphenylcarbodiimide (6), (0.98 g, 5.0 mmol, prepared as previously described) in dry THF (10 cm3) guanidine (4) (0.15 g, 2.5 mmol) was added and the reaction mixture was heated under reflux for 24 hours. The pale yellowish crude mixture remaining upon the removal of the solvent was suspended in acetonitrile (10 cm3), the precipitated white solid was filtered off, washed with cold acetonitrile (5 cm3) and dried in air (0.45 g, 51%). Evaporation of the filtrate yielded a yellow residue, which was suspended in 3.0 cm3 of acetonitrile. The crystals that precipitated were separated by filtration and washed with 2.0 cm3 of cold acetonitrile, affording 0.53 g (60%) of product 1 in total.
Guanidine to N,N′-diphenylcarbodiimide molar ratio = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 3.
To a solution of N,N′-diphenylcarbodiimide (6), (0.314 g, 1.6 mmol, prepared as previously described) in dry THF (3 cm3) guanidine (4) (0.031 g, 0.53 mmol) was added and the mixture was refluxed for 24 hours. The crude reaction mixture remaining upon the removal of the solvent was first suspended in diethylether (5 cm3), the precipitated white solid was filtered off and then again suspended in acetonitrile (2 cm3), followed by filtration and additional washing with acetonitrile (2 cm3). The solid was dried in air to afford pure dihydrotriazine 1 (0.184 g, 98%).
3.
To a solution of N,N′-diphenylcarbodiimide (6), (0.314 g, 1.6 mmol, prepared as previously described) in dry THF (3 cm3) guanidine (4) (0.031 g, 0.53 mmol) was added and the mixture was refluxed for 24 hours. The crude reaction mixture remaining upon the removal of the solvent was first suspended in diethylether (5 cm3), the precipitated white solid was filtered off and then again suspended in acetonitrile (2 cm3), followed by filtration and additional washing with acetonitrile (2 cm3). The solid was dried in air to afford pure dihydrotriazine 1 (0.184 g, 98%).
Evaporation of the filtrate afforded a pale yellowish residue as a mixture of N,N′-diphenylbiguanide (∼8%) and N,N′,N′′-triphenylguanidine (8) (∼92%, by HPLC). An analytically pure sample of guanidine by-product 8 was obtained by the recrystallisation of the residue from ethanol.
A single crystal suitable for X-ray crystallographic measurement was obtained by dissolving a sample of 1 (0.10 g) in an ethanol–methanol 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (15 cm3). After 4 days of slow evaporation, the product was crystallized in the form of colorless prisms (65 mg, 65%).
1 mixture (15 cm3). After 4 days of slow evaporation, the product was crystallized in the form of colorless prisms (65 mg, 65%).
mp 277–278 °C (from EtOH–MeOH 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture) (lit.,1 270–271 °C). Found: C, 70.0%; H, 5.4%; N, 23.0% C21H18N6·0.5CH3OH requires C, 69.7%; H, 5.45%; N, 22.7%. υmax/cm−1 3393, 3154, 1637, 1588, 1534, 1463, 1362, 1295, 1143, 772, 743, 700. δH(600 MHz; d6-DMSO; Me4Si) 6.40–7.40 (12 H, m, overlapped Ph and NH2 protons), 7.44–7.46 (3 H, m, Ph), 7.52–7.55 (2 H, m, Ph), 7.61 (1 H, s, NH). δC(150 MHz, d6-DMSO; Me4Si) 119.5–121, 123–125 (br), 127.9, 128.4, 129.62, 129.64, 136.5, 162.4. HRMS-MALDI found: 355.1683; calc. for C21H19N6 (MH+): 355.1666.
1 mixture) (lit.,1 270–271 °C). Found: C, 70.0%; H, 5.4%; N, 23.0% C21H18N6·0.5CH3OH requires C, 69.7%; H, 5.45%; N, 22.7%. υmax/cm−1 3393, 3154, 1637, 1588, 1534, 1463, 1362, 1295, 1143, 772, 743, 700. δH(600 MHz; d6-DMSO; Me4Si) 6.40–7.40 (12 H, m, overlapped Ph and NH2 protons), 7.44–7.46 (3 H, m, Ph), 7.52–7.55 (2 H, m, Ph), 7.61 (1 H, s, NH). δC(150 MHz, d6-DMSO; Me4Si) 119.5–121, 123–125 (br), 127.9, 128.4, 129.62, 129.64, 136.5, 162.4. HRMS-MALDI found: 355.1683; calc. for C21H19N6 (MH+): 355.1666.
N,N-Dimethylguanidine to N,N′-diphenylcarbodiimide molar ratio = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 2.
To a solution of N,N′-diphenylcarbodiimide (6), (1.01 g, 5.2 mmol) in dry THF (10 cm3) N,N-dimethylguanidine (5) (0.22 g, 2.5 mmol, prepared as previously described) was added and the reaction mixture was heated under reflux for 24 hours. The mixture of yellow oil and solid remaining upon removal of the solvent was removed and the residue suspended in diethylether (5 cm3). The precipitated white solid was filtered off and washed with ether (0.44 g, 46%). Evaporation of the filtrate produced yellow oil, which solidified upon standing at room temperature (0.83 g, contains approximately 12% of the product according to HPLC analysis). Subsequent crystallization from the mother liquor afforded an additional 0.05 g of product 2, thus increasing the yield to 51%.
2.
To a solution of N,N′-diphenylcarbodiimide (6), (1.01 g, 5.2 mmol) in dry THF (10 cm3) N,N-dimethylguanidine (5) (0.22 g, 2.5 mmol, prepared as previously described) was added and the reaction mixture was heated under reflux for 24 hours. The mixture of yellow oil and solid remaining upon removal of the solvent was removed and the residue suspended in diethylether (5 cm3). The precipitated white solid was filtered off and washed with ether (0.44 g, 46%). Evaporation of the filtrate produced yellow oil, which solidified upon standing at room temperature (0.83 g, contains approximately 12% of the product according to HPLC analysis). Subsequent crystallization from the mother liquor afforded an additional 0.05 g of product 2, thus increasing the yield to 51%.
N,N-Dimethylguanidine to N,N′-diphenylcarbodiimide molar ratio = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 3.
To a solution of N,N′-diphenylcarbodiimide (6), (0.314 g, 1.6 mmol, prepared as previously described) in dry THF (3 cm3) N,N-dimethylguanidine (5) (0.047 g, 0.53 mmol) was added and the mixture was refluxed for 24 hours. The crude reaction mixture remaining upon the removal of the solvent was suspended in diethylether (4 cm3), the precipitated white solid was filtered off and dried in air to afford pure dihydrotriazine 2 (0.193 g, 94%).
3.
To a solution of N,N′-diphenylcarbodiimide (6), (0.314 g, 1.6 mmol, prepared as previously described) in dry THF (3 cm3) N,N-dimethylguanidine (5) (0.047 g, 0.53 mmol) was added and the mixture was refluxed for 24 hours. The crude reaction mixture remaining upon the removal of the solvent was suspended in diethylether (4 cm3), the precipitated white solid was filtered off and dried in air to afford pure dihydrotriazine 2 (0.193 g, 94%).
Evaporation of the filtrate yielded a pale yellowish residue of N,N′,N′′-triphenylguanidine (8) (>95% by HPLC analysis, crude product yield 97%).
A single crystal suitable for X-ray crystallographic studies was obtained by dissolving a sample of 2 (0.10 g) in methanol (8.0 cm3). The product crystallized in the form of pale yellowish prisms (66 mg, 66%).
mp 197–198 °C (from MeOH). Found: C, 71.4%; H, 5.7%; N, 21.9% C23H22N6 requires C, 72.2%; H, 5.8%; N, 22.0%. υmax/cm−1 3390, 2923, 2853, 1629, 1611, 1584, 1534, 1487, 1467, 1401, 1218, 765, 694. δH(600 MHz; d6-DMSO; Me4Si) 2.97 (6 H, s, CH3), 6.60–7.60 (15 H, m, overlapped Ph protons), 7.75 (1 H, s, NH). δC(150 MHz, d6-DMSO; Me4Si) 35.7, 120, 123, 124, 127.7, 128.5, 129.58, 129.63, 136.3, 137, 150, 151, 155, 160.0. HRMS-MALDI found: 383.1971; calc. for C23H23N6 (MH+): 383.1979.
mp 203–205 °C (from H2O–EtOH mixture). υmax/cm−1 3402, 3063, 2930, 1657, 1622, 1589, 1543, 1462, 1411, 1225, 1120, 1095, 764, 745, 722, 692, 623, 561. δH(600 MHz; d6-DMSO; Me4Si) 3.01 (6 H, s, CH3), 7.22–7.27 (2 H, m, Ph), 7.32–7.41 (8 H, m, Ph), 7.70–7.84 (5 H, m, Ph), 8.81 (2 H, s, NH). δC(150 MHz, d6-DMSO; Me4Si) 36.1, 125.7, 126.1, 128.1, 129.4, 130.8, 131.62, 131.64, 136.3, 154.1, 159.9.
mp 42–43 °C. υmax/cm−1 3301, 3214, 2969, 2931, 2874, 1602, 1565, 1547, 1491, 1410, 1168, 778. δH(600 MHz; d6-DMSO; Me4Si) 0.96 (6 H, d, J 6.3, (CH3)2CH), 1.17 (6 H, d, J 6.6, (CH3)2CH), 1.41 (6 H, d, J 6.8, (CH3)2CH), 2.96 (6 H, s, CH3), 3.96–4.03 (1 H, m, (CH3)2CH), 4.16–4.24 (1 H, m, (CH3)2CH), 4.68–4.76 (1 H, m, (CH3)2CH), 6.15 (1 H, d, J 7.2, NH). δC (150 MHz, d6-DMSO; Me4Si) 19.4, 22.1, 24.5, 35.5, 42.8, 45.0, 45.3, 148.2, 155.1, 159.2. HRMS-MALDI found: 281.2437; calc. for C14H29N6 (MH+): 281.2448.
mp 178–179 °C (from MeOH). Found: C, 44.15%; H, 7.25%; N, 21.4% C14H29N6O4Cl requires C, 44.15%; H, 7.7%; N, 22.05%. υmax/cm−1 3215, 2969, 1607, 1559, 1453, 1411, 1166, 1140, 1118, 1087, 778, 627. δH(300 MHz; d6-DMSO; Me4Si) 1.24 (12 H, d, J 6.6, (CH3)2CH), 1.49 (6 H, d, J 7.0, (CH3)2CH), 3.12 (6 H, s, CH3), 4.27–4.40 (2 H, m, (CH3)2CH), 4.51–4.64 (1 H, m, (CH3)2CH), 7.13 (2 H, d, J 7.5, NH). δC(75 MHz, d6-DMSO; Me4Si) 19.1, 21.3, 36.1, 44.7, 48.7, 153.5, 159.3.
X-Ray structure determination
Crystallographic data were collected on an Oxford Diffraction Xcalibur CCD diffractometer with graphite-monochromated Mo Kα radiation at low temperature (Table 3) and room temperature (only for 2, Table S7 in ESI†). The programs CrysAlis CCD and CrysAlis RED27 were used for data collection, cell refinement and data reduction. The structure was solved by direct methods. A refinement procedure by full-matrix least squares methods based on F2 values against all reflections included anisotropic displacement parameters for all non-H atoms. The positions of hydrogen atoms were geometrically optimized applying the riding model except in 1·0.5 MeOH where they were found in the difference Fourier map and isotropically refined (only those on MeOH were geometrically optimized). Calculations were performed with SHELXS9728 and SHELXL9729 (both operating under the WinGX30 program package). The molecular graphics were done with PLATON9831 and Mercury.32 Supplementary crystallographic data sets for the structures 1·0.5 MeOH, 2 (at low and room temperature), 2·HClO4 and 3·HClO4 are available through CCDC 830994–830998.pKa determination
The UV-Vis spectrophotometric titration method used in this work was described in detail in ref. 20a, c, and d. For each investigated compound, the relative acidity and basicity were measured against at least two (mostly three) different reference compounds with known pKa values in AN.20a,b,d To determine the relative acidity of two compounds, a mixture of two different acids was titrated with UV-Vis radiation non-absorbing acidic and basic titrants to obtain several spectra of solutions containing both neutral and anionic forms of the two acids in different proportions. Both of the acids were also titrated separately to obtain the spectra of the neutral and anionic forms of the pure compounds. The relative basicities were determined in a similar way, although in this case the solutions contained neutral and cationic forms. From the titration data, the relative acidity of the acids or the relative acidity of the conjugate acids of the bases—the difference between the pKa values (ΔpKa values)—was calculated (see ref. 20a, c, d). During titrations, the protonation–deprotonation processes were reversible with all the compounds and sharp isosbestic points (at which the absorption of neutral and ionic forms are the same) were obtained. All the compounds investigated in this work have significantly different spectra of protonated and deprotonated forms in the UV region (major changes between 250–300 nm for 1 and 250–350 nm for 2 and 3) and calculation methods using only spectral data obtained from the titration of pure compounds and mixture were used to obtain ΔpKa values. From the ΔpKa values of measurements carried out in this work and from the absolute pKa values assigned to the reference compounds in previous works,20a,b,d the absolute pKa values of the investigated compounds were obtained as the average of absolute values. From each titration experiment of the mixture of two compounds, the ΔpKa value was determined as the mean of 10–20 values. Concentrations of the measured compounds were mostly in the order of n·10−5 M and never exceeded 2 × 10−4 M, while concentrations of acidic and basic titrants were in the 3 × 10−3 M range.Quantum chemical calculations
Quantum calculations were carried out with the GAUSSIAN-03 program package33 using Becke's three-parameter exchange functional with the correlation functional of Lee, Yang and Paar (B3LYP).34 Geometries were fully optimized with the 6-31G(d) valence double ξ-basis set of Pople and Hariharan, and were confirmed to be minima by computing their analytical vibrational frequencies. Single-point calculations were then performed with the 6-311+G(d,p) basis set. The zero point vibrational energies computed at the B3LYP/6-31G(d) level used in the proton affinity calculations are unscaled. Proton affinities are calculated at the B3LYP6-311+G(d,p)//B3LYP/6-31G(d) level employing the general equation: PA(B) = (ΔEel) + (ΔZPVE), where (ΔEel) = [E(B) − E(BH+)] and (ΔZPVE) = [ZPVE(B) − ZPVE(BH+)] are the electronic and the zero-point vibrational energy contributions to the proton affinity, respectively. Here, B and BH+ denote the base in question and its conjugate acid, respectively. Solvation energies were calculated at the IEF-PCM/HF/6-31G(d) level of theory using radii optimized for COSMO-RS35 for cavity construction. All the calculations were performed using the Gaussian 03 program package with default parameters.Acknowledgements
Financial support of this work by the Ministry of Science, Education and Sports of Croatia (Project No. 098-0982933-2920 (M.E.-M.) and 119-119079-1084 (D.M.-Č.) is acknowledged. The work of I. L. and J. S. was supported by Grant No. 7374 from the Estonian Science Foundation. We also thank Dr Z. Glasovac for assistance in calculations of basicities and Dr Mario Cindrić (Center for Proteomics and Mass Spectrometry, Rudjer Bošković Institute) for HRMS analyses.References
- (a) S. Mehrotra, V. Pandey, R. Lakhan and P. K. Srivastava, J. Indian Chem. Soc., 2002, 79, 176 CAS; (b) P. Mamalis, Ger. Offen., 1934, 120, 1970 Search PubMed.
- A. Gopalsamy and H. Y. Yang, US Pat. Appl., 49,320, 2002 Search PubMed.
- (a) T. Vilaivan, N. Saesaengseerung, D. Jarprung, S. Kamchonwongpaisan, W. Sirawaraporn and Z. Yuthavong, Bioorg. Med. Chem., 2003, 11, 217 CrossRef CAS; (b) P. Mamalis and D. J. Outred, Ger. Offen., 1,957,769, 1970 Search PubMed; (c) P. Mamalis and D. J. Outred, Ger. Offen., 1,965,711, 1970 Search PubMed; (d) P. Mamalis, Ger. Offen., 1,963,759, 1970 Search PubMed; (e) A. Nzila, J. Antimicrob. Chemother., 2006, 57, 1043 CrossRef CAS.
- G. Moinet, D. Cravo, L. Doare, M. Kergoat and D. Mesangeau, PCT Int. Appl., WO 01 55 122, 2001 Search PubMed.
- S. Hayashi, M. Furukawa, J. Yamamoto, Y. Nishizima, E. Sannomiya and H. Ueki, Kumamoto Pharm. Bull., 1966, 7, 7 CAS.
- (a) M. D. Turnbull, P. J. Crowley, E. J. T. Chrystal, J. M. Clough, I. B. Bryan, K. Beautement, S. P. Barnett, R. J. Ponsford and D. J. Outred, PCT Int. Appl., WO 9615671, 1966 Search PubMed; (b) R. Smrz, J. Cech, J. Auerhan and A. Simek, Czech Patent, 119,884, 1966 Search PubMed.
- (a) C. J. Peake and S. Y. Lin, Patent US, 5,565,451 Search PubMed; (b) C. J. Peake, T. G. Cullen and A. C. Lew, Patent US, 5,300,503, 1994 Search PubMed.
- (a) A. Kummar, S. K. Patnaik and M. M. Singh, Mater. Chem. Phys., 1998, 56, 243 CrossRef; (b) M. M. Singh and A. Gupta, Bull. Electrochem., 1996, 12, 511 CAS.
- (a) A. Rosowsky, K. K. N. Chen, R. St. Amand and E. J. Modest, J. Pharm. Sci., 1973, 62, 477 CrossRef CAS; (b) E. Rossi, G. Abbiati and D. Nava, Heterocycles, 1999, 51, 1401 CrossRef CAS; (c) G. Lowe, C. Carr and R. Quarrell, Chem. Commun., 2001, 737 RSC; (d) H.-K. Lee and T. M. Rana, J. Comb. Chem., 2004, 6, 504 CrossRef CAS; (e) M. Kidwai, P. Mothsra, R. Mohan and S. Biswas, Bioorg. Med. Chem. Lett., 2005, 15, 915 CrossRef CAS; (f) M. V. Vovk, A. V. Bol'but, P. S. Lebed and N. V. Mel'nichenko, Zh. Org. Khim., 2007, 43, 929 Search PubMed; (g) D. Gravestock, A. L. Rousseau, A. C. U. Lourens, S. S. Moleele, R. L. Van Zyl and P. A. Steenkamp, Eur. J. Med. Chem., 2011, 46, 2022 CrossRef CAS.
- (a) Z. Glasovac, B. Kovačević, E. Meštrović and M. Eckert-Maksić, Tetrahedron Lett., 2005, 46, 8733 CrossRef CAS; (b) A. Tintaru, J. Roithová, D. Schröder, L. Charles, I. Jušinski, Z. Glasovac and M. Eckert-Maksić, J. Phys. Chem. A, 2008, 112, 12097 CrossRef CAS; (c) Z. Glasovac, V. Štrukil, M. Eckert-Maksić, D. Schröder, M. Kaczorowska and H. Schwarz, Int. J. Mass Spectrom., 2008, 270, 39 CrossRef CAS; (d) Z. Glasovac, V. Štrukil, M. Eckert-Maksić, D. Schröder, M. Schlangen and H. Schwarz, Int. J. Mass Spectrom., 2010, 291, 22 Search PubMed; (e) V. Štrukil, L. Fabian, D. G. Reid, M. J. Duer, G. J. Jackson, M. Eckert-Maksić and T. Friščić, Chem. Commun., 2010, 46, 9191 RSC.
- F. Kurzer and E. D. Pitchfork, J. Chem. Soc., 1964, 3459 RSC.
- F. Kurzer and E. D. Pitchfork, The Chemistry of Biguanides, in Fortschr. Chem. Forshung, Springer Verlag, Berlin-Heidelberg, edn. 10/3, 1968, p. 375 Search PubMed.
- F. Kurzer and K. Douraghi-Zadeh, Chem. Rev., 1967, 67, 107 CrossRef CAS.
- (a) Z. Maksić and B. Kovačević, J. Org. Chem., 2000, 65, 3303 CrossRef; (b) B. Kovačević, Z. B. Maksić and R. Vianello, J. Chem. Soc., Perkin Trans. 2, 2001, 886 Search PubMed; (c) K. Kovačević and Z. B. Maksić, Chem.–Eur. J., 2002, 8, 1694 CrossRef; (d) B. Kovačević, Z. Glasovac and Z. B. Maksić, J. Phys. Org. Chem., 2002, 15, 765 CrossRef.
- See, e.g., (a) R. E. Valters and W. Flitsch, Ring–Chain Tautomerism, ed. A. R. Katritzky, Plenum Press, New York, 1985 Search PubMed; (b) R. E. Valters, F. Fülöp and D. Korbonits, Adv. Heterocycl. Chem., 1995, 64, 251 CrossRef CAS; (c) R. E. Valters, F. Fülöp and D. Korbonits, Adv. Heterocycl. Chem., 1996, 66, 1–71 CrossRef CAS.
- (a) N. Hesse, R. Frölich, B. Wibbeling and E.-U. Würthwein, Eur. J. Org. Chem., 2006, 3923 CrossRef CAS; (b) M. Buhmann, M. H. Möller and E.-U. Würthwein, Chem. Ber., 1993, 126, 957 CrossRef; (c) M. Buhmann, M. H. Möller, U. Rodewald and E.-U. Würthwein, Chem. Ber., 1993, 126, 2467 CrossRef CAS.
- P. V. Gushchin, N. A. Bokach, K. V. Luzyanin, A. A. Nazarov, M. Haukka and V. Y. Kukushkin, Inorg. Chem., 2007, 46, 1684 CrossRef CAS.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, G. A. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1 RSC.
- M. Eckert-Maksić, Z. Glasovac, P. Trošelj, A. Kütt, T. Rodima, I. Koppel and I. A. Koppel, Eur. J. Org. Chem., 2008, 5176 CrossRef.
- (a) A. Kütt, I. Leito, I. Kaljurand, L. Sooväli, V. M. Vlasov, L. M. Yagupolskii and I. A. Koppel, J. Org. Chem., 2006, 71, 2829 CrossRef; (b) A. Kütt, V. Movchun, T. Rodima, T. Dansauer, E. B. Rusanov, I. Leito, I. Kaljurand, J. Koppel, V. Pihl, I. Koppel, G. Ovsjannikov, L. Toom, M. Mishima, M. Medebielle, E. Lork, G.-V. Röschenthaler, I. A. Koppel and A. A. Kolomeitsev, J. Org. Chem., 2008, 73, 2607 CrossRef; (c) I. Leito, I. Kaljurand, I. A. Koppel, L. M. Yagupolskii and V. M. Vlasov, J. Org. Chem., 1998, 63, 7868 CrossRef CAS; (d) I. Kaljurand, A. Kütt, L. Sooväli, T. Rodima, V. Mäemets, I. Leito and I. A. Koppel, J. Org. Chem., 2005, 70, 1019 CrossRef CAS; (e) L. Sooväli, I. Kaljurand, A. Kütt and I. Leito, Anal. Chim. Acta, 2006, 566, 290 CrossRef; (f) E.-I. Rõõm, A. Kütt, I. Kaljurand, I. Koppel, I. Leito, I. A. Koppel, M. Mishima, K. Goto and Y. Miyahara, Chem.–Eur. J., 2007, 13, 7631 CrossRef; (g) V. Palm, Tables of Rate and Equilibrium Constants of Heterocyclic Organic Reactions, ed. VINITI, Moscow-Tartu, 1975–1985 Search PubMed.
- e.g., (a) N. Uchida, A. Taketoshi, J. Kuwabara, T. Yamamoto, Y. Inoue, Y. Watanabe and T. Kanbara, Org. Lett., 2010, 12, 5242 CrossRef CAS; (b) K. T. Leffek, P. Pruszynski and K. Thanapaalasingham, Can. J. Chem., 1989, 67, 590 CrossRef CAS.
- for more recent papers, see, e.g. Z.-K. Jia, D.-M. Du, Z.-Y. Zhou, A.-G. Zhang and R.-Y. Hou, Chem. Phys. Lett., 2007, 439, 374 CrossRef CAS and references cited therein.
- (a) M. T. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032 CrossRef; (b) S. Miertuš, E. Scrocco and J. Tomasi, J. Chem. Phys., 1981, 55, 117 Search PubMed; (c) S. Miertuš and J. Tomasi, J. Chem. Phys., 1982, 65, 239 Search PubMed.
- (a) K. B. Wiberg, P. R. Rablen, D. J. Rush and T. A. Keith, J. Am. Chem. Soc., 1995, 117, 4261 CrossRef CAS; (b) J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098 CrossRef CAS.
- Z. Glasovac, M. Eckert-Maksić and Z. B. Maksić, New J. Chem., 2009, 33, 588 RSC.
- Z. Glasovac, M. Eckert-Maksić and Z. B. Maksić, to be published.
- Oxford Diffraction (2010). Oxford Diffraction Ltd., Xcalibur CCD system, CrysAlis Software system, Version 1.171.34.44.
- (a) G. M. Sheldrick, SHELXS, Program for the Solution of Crystal Structures, University of Göttingen, Germany, 1997 Search PubMed; (b) G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112 CrossRef CAS.
- (a) G. M. Sheldrick, SHELXL97, Program for the Refinement of Crystal Structures, University of Göttingen, Germany, 1997 Search PubMed; (b) G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112 CrossRef CAS.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837 CrossRef CAS.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.03, Gaussian, Inc., Pittsburgh, PA, 2003 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- A. Klamt, V. Jonas, T. Buerger and J. C. W. Lohrenz, J. Phys. Chem., 1998, 102, 5074 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Spectra, X-ray CIF files, tables of bond length, angles and Cartesian coordinates of the optimized structures. CCDC 830994–830998. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1nj20595a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2012 |
