DOI:
10.1039/C1RA01108A
(Paper)
RSC Adv., 2012,
2, 1927-1935
Dynamics and thin film drainage of a deformable droplet moving towards a solid wall with finite inertia†
Received
16th November 2011
, Accepted 17th November 2011
First published on 6th January 2012
Abstract
Direct numerical simulations of a deformable droplet approaching a planar solid wall through another fluid are performed to investigate the droplet dynamics and thin film drainage. The numerical approach solves the full Navier–Stokes equations and the interface is located by a moving mesh interface tracking method with high fidelity. Cases with Reynolds numbers of 25 and 50 and capillary numbers of 5 × 10−3 and 1 × 10−2 are simulated for both head-on and oblique approaching scenarios. The front head of the droplet is flattened as the droplet nearly touches the wall, and a dimpled thin film is observed. Because of the great viscous forces of the flow inside the thin film, the droplet slows down dramatically which leads to a significant jump in the drag force. A detailed study of the thinning of the thin film is presented, and an asymmetric thin film is observed for the oblique approach. The numerical prediction on the central separation at which a dimple is formed agrees fairly well with previous analysis based on the lubrication theory. The simulated thinning rate is slower than the rate predicted by previous approximate models. The differences are mainly due to the finite Reynolds number of the simulated cases.
1 Introduction
When a deformable droplet approaches a solid wall through another stationary liquid, the droplet decelerates and deforms. As the droplet becomes very close to the wall, a thin film is usually formed between the droplet and the wall, and some of the surrounding fluid is trapped inside this thin film. The viscous resistance of the trapped fluid dramatically slows down the motion of the drop towards the wall. The film becomes thinner as the liquid inside the thin film drains, and the thin film usually takes a shape of a dimple before it ruptures. The underlying physics of this process is very intriguing due to its wide applications in industrial processes and real life, such as ink-jet printing, droplet deposition, and raindrops impacting the ground.
The motion and the drainage of the thin film of a droplet/bubble approaching a surface have been studied by a number of researchers, however, most of these investigations are limited to slow motion, i.e. in the Stokes regime. Bart3 theoretically solved the unsteady settling of a fluid sphere towards a flat fluid surface at low Reynolds numbers with continuity of shear stresses applied to the interfaces, and the theory compared well with experimental results. Beshkov4 analyzed the drag coefficient of a droplet approaching a solid plane, and they reported that the drag of the droplet towards a solid wall was much different from the drag for two approaching droplets. The thin film drainage of a small spherical drop/bubble approaching a solid surface was modeled by Dimitrov and Ivanov10 and Lin and Slattery,19 respectively. Dimitrov and Ivanov10 argued that the two sides of the thin film were flat and parallel for sufficiently thin liquid films, while a dimpled thin film was predicted by Lin and Slattery19. Lin and Slattery's19 theoretical predictions based on the immobile interface assumption were validated well in early stages with the experimental work by Platikanov,25 while these authors pointed out that the immobile assumption might fail for later stages. The deformation of a droplet moving towards a plane wall by gravitational forces was studied numerically using boundary integral methods.1,26 In these works, dimpled thin films were observed between the droplet and the wall, and the smallest thickness of the thin film at the rim was around 10% of the undeformed drop radius. Yiantsios and Davis36 studied the buoyancy-driven motion of a drop toward a rigid surface using a combination of asymptotic analysis, lubrication theory, and boundary integral calculations. The smallest thin film thickness at the rim reported by these authors was 0.1%. Steinhaus et al.32 studied droplet size effects on film drainage between a drop and a solid surface and used the Stefan–Reynolds equation to predict the film rupture time. They found that for millimetre-scale droplets the experimental and analytical rupture times agreed well, while for micrometre sized drops there were large differences. A modified Stefan–Reynolds equation is proposed to minimize the differences.
Using a surface force apparatus (SFA), Connor and Horn8 measured the evolution of the deformation and the thickness of the thin film of a mercury drop approaching a mica surface with sub-nanometre resolution. By varying the electrical potential applied to the drop, the effects of surface forces were studied. These experimental data were analyzed by Horn et al.17 using a drainage model based on the coupling of the local curvature of the interface and the Young–Laplace equation. Using the model developed for analyzing force measurements between two deformable droplets,5 Manica et al.21 further modeled the experimental data by Connor and Horn.8 With the assumption of no-slip boundary condition on the interface, the theoretical predictions agreed well with the experiments. The effects of electrolyte and surfactant on the film drainage between an oil droplet and a silica surface were investigated by Goodall et al.14 and Tan et al.33 using an imaging reflectometry method. The interaction between a rising bubble and a hydrophilic surface was experimentally examined by Parkinson and Ralston24 and then was theoretically modeled by Manica et al.23 Parkinson and Ralston24 reported a transition of the interface condition from full-slip to no-slip. As the thickness of the thin film reached nanometre-scale in all the experiments mentioned above, double-layer forces were considered. It is also noticed that all of the experiments were in the small capillary number limit, and the inertia was usually neglected. Chan et al.7 reviewed the thin film drainage between the drop/bubble and a flat surface in the slow motion regime, and they indicated that the drainage rates of both stable and coalescing films were consistent with theoretical predictions based on the tangentially immobile condition on the interface. These authors also pointed out that more efforts are needed to study the problems with finite Reynolds numbers.
Compared to the large volume of literature on the slow motion of the interaction between droplets and solid surfaces, the literature on problems with finite Reynolds numbers is very limited. However, interactions between bubbles/droplets and flat surfaces in many industrial processes occur at finite Reynolds numbers. Studies in this area are needed to reveal the interesting underlying physics. The goal of this work is to shed some light on the understanding of the dynamics and the thin film drainage of a deformable droplet approaching a solid surface with finite inertia using a CFD (Computational Fluid Dynamics) approach. The full Navier–Stokes equations are solved using a finite volume method and the interface between the drop and the surrounding gas is located by the moving mesh interface tracking (MMIT) method developed by Quan and Schmidt.29 The evolutions of the drag force and the deformation as the drop moving towards the surface are examined. The detailed drainage of the thin film is also investigated.
2 Problem formulation and numerical methods
The problem of interest is a droplet moving toward a solid planar wall with an initial centroid velocity of U0 in negative y direction as shown in Fig. 1. The drop has a viscosity of μd and a density of ρd and the viscosity and the density of the surrounding fluid are μs and ρs, respectively. The initial spherical droplet has a radius of R0. Two configurations of the problem are simulated with one being head-on (the drop moves normal to the wall as shown in Fig. 1(a)) and another one being oblique (the angle between the drop moving direction and the normal of the wall is α = arctan(0.25) = 14° as shown in Fig. 1(b)), where the thick line denotes the planar wall. The droplet centroid is 4R0 away from the bottom wall for the head-on case, and is 6R0 for the oblique approach. The computational domain is a cylinder for the head-on case and a cut cylinder for the oblique approaching. Fig. 2 (a) shows the mesh near the center of the domain on the xy plane for the oblique case. The cylinder has a radius of 8R0 and the drop is located on the axis of the cylinder (y axis). The distance from the top base to the droplet centroid is 8R0 to minimize the wall effects as in the simulations wall boundary conditions are applied to all the bases and the side. To save computing time, the mesh near and inside the drop is much finer than the mesh in other regions. Fig. 2 (b) shows the velocity field on the xy plane, and the velocity vectors are colored by their magnitude. A vortex ring is observed by considering that the domain is cylindrical. It should be noted that all the lengths reported hereafter are non-dimensionalized by R0.
 |
| | Fig. 1 Sketch of a droplet approaching a planar wall. (a) head-on and (b) oblique. The thick line stands for the planar wall. | |
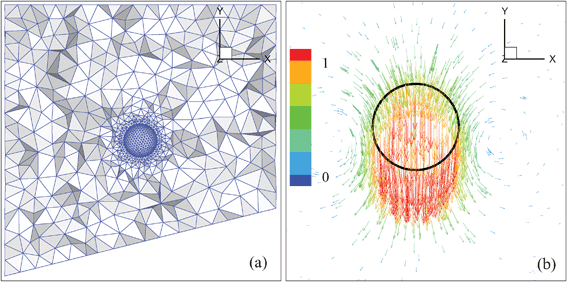 |
| | Fig. 2 (a) The domain and the mesh, and (b) the velocity field near the center on the xy plane for the oblique approach. The outer domain is a cut cylinder with the y axis as the axis of the cylinder. The thick circle in (b) denotes the droplet. | |
The two fluids are assumed immiscible and the flow is incompressible. As the interface is moving and deforming, an integral form of the Navier–Stokes in a moving control volume35 is employed
| |  | (1) |
| | 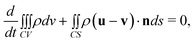 | (2) |
| | 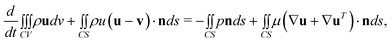 | (3) |
where
CV and
CS stand for a control volume and the surfaces of the control volume,
u and
v denote the fluid velocity and the surface moving velocity,
n is the unit normal vector of the control surface,
p is the pressure, and the superscript T stands for the transpose. As the control volume not only moves but also deforms, a consistency requirement for the volume of a control volume (
eqn 1) is necessary and it can be derived from Leibnitz's theorem. Gravitational forces are neglected in this work.
The boundary conditions across the interface between two immiscible fluids are
| |  | (5) |
| | 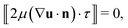 | (6) |
where

denotes the difference across the interface,
R1 and
R2 are the local principle radii of the surface,
τ is the unit tangential vector of the surface, and
σ stands for the surface tension coefficient. These boundary conditions can be derived from the above governing equations by treating the interface as an internal boundary. Please note that as the fluid normal velocities (
us,n and
ud,n) of the two phases near the interface are continuous and are equal to the normal velocity (
vn) of the moving surface (
eqn 4), the convection terms in
eqn 2 and 3 are identically zero on the interfacial surfaces.
A finite volume/moving mesh interface tracking method based on unstructured tetrahedral meshes is employed to solve the full Navier–Stokes equations, and this method has been extensively validated against a number of experimental observations and theoretical predictions of multiphase flow problems.28–31 In the method, the interface is represented by the triangular surfaces of the interior tetrahedral elements, and thus is zero-thickness. The nodes on the interface move with the fluid velocity in a Lagrangian fashion to avoid any mixing and to automatically satisfy the boundary condition in eqn 4. Therefore the interfacial meshes always align with the physical interface. The mesh quality becomes worse as the mesh moves which induces large errors or even discontinues the simulation. To address this challenge, a number of mesh adaptation schemes are developed and applied locally to obtain good mesh quality and to achieve computing efficiency.9,29 As the length scale inside the thin film is several orders of magnitude smaller than the droplet radius when the droplet is very close to the wall, the nominal length scale based on the surface normal by Quan27 is employed to distribute much finer mesh near and inside the thin film while making the mesh in the region away from the thin film much coarser.
The mean curvature ( ) in eqn 5 is calculated using a least-squares parabola fitting in a local coordinate system9 to compute the surface tension forces, and the jump in the normal viscous stresses is calculated directly by using Taylor series expansion to the first order for multivariable functions.29 The jump in normal stresses is implemented directly as a pressure boundary condition. To satisfy the continuity of shear stresses across the interface, i.e.eqn 6, the second-order geometric harmonic mean method29 is used to calculate the viscous shear stresses on the interfacial surfaces. The convection term is computed by a central difference scheme, and the viscous term is calculated by a predictor-corrector method. The time integration is advanced by a three-step, second-order Runge–Kutta scheme.
) in eqn 5 is calculated using a least-squares parabola fitting in a local coordinate system9 to compute the surface tension forces, and the jump in the normal viscous stresses is calculated directly by using Taylor series expansion to the first order for multivariable functions.29 The jump in normal stresses is implemented directly as a pressure boundary condition. To satisfy the continuity of shear stresses across the interface, i.e.eqn 6, the second-order geometric harmonic mean method29 is used to calculate the viscous shear stresses on the interfacial surfaces. The convection term is computed by a central difference scheme, and the viscous term is calculated by a predictor-corrector method. The time integration is advanced by a three-step, second-order Runge–Kutta scheme.
3 Numerical results
Simulations have been performed for a density ratio (η = ρd/ρs) of 50 and a viscosity ratio of (λ = μd/μs) of 50. Two cases with initial Reynolds number of (Re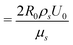 ) 25 and 50 have been computed to investigate the inertia effects on the droplet deformation and the thin film drainage for the head-on and oblique scenarios, respectively. The corresponding Weber numbers (We
) 25 and 50 have been computed to investigate the inertia effects on the droplet deformation and the thin film drainage for the head-on and oblique scenarios, respectively. The corresponding Weber numbers (We ) are 0.125 and 0.5. Therefore, the Capillary numbers (Ca
) are 0.125 and 0.5. Therefore, the Capillary numbers (Ca ) are 5 × 10−3 and 1 × 10−2, respectively.
) are 5 × 10−3 and 1 × 10−2, respectively.
3.1 Deformation and drag force
As the droplet moves toward the planar wall, the drop deforms due to the viscous forces by the surrounding gaseous flow. The evolution of the droplet shape for the head-on case with Re = 25 and We = 0.125 is shown in Fig. 3 (a). The droplet does not deform very much until the distance (d) from the droplet centroid to the wall in the approaching direction is less than one. The huge viscous resistance in the gas phase due to the existence of the solid wall dramatically slows down the motion of the front head of the droplet toward the wall, while the rear portion of the droplet continues moving downward with much less resistance from the wall. Therefore, the front head of the droplet is flattened, and a thin film is formed between the droplet and the wall. With the increase of the inertia, i.e. a larger Weber number of 0.5, we expect a greater deformation which is demonstrated in Fig. 3 (b). The droplet is elongated in the moving direction in the earlier stages, and the tail of the droplet is more curved than the head. At d = 1.05, a thin film is also observed, and compared to case (a) with smaller Weber number, the droplet is slimmer.
 |
| | Fig. 3 Shape evolution for the head-on approaching cases. (a) Re = 25, We = 0.125, Ca = 5 × 10−3 at d = 1.41, 1.05, 0.99, and 0.87; (b) Re = 50, We = 0.5, Ca = 1 × 10−2 at d = 1.35. 1.13, 1.05, and 1.0. | |
The shape evolution of the oblique approaching is demonstrated in Fig. 4. Similar to the head-on cases, the droplet with a smaller Weber number deforms much less than the drop with a larger Weber number. Again, a thin film is observed for each case, and the thin film is sloped and aligned with the wall.
 |
| | Fig. 4 Shape evolution for the oblique approaching cases. (a) Re = 25, We = 0.125, Ca = 5 × 10−3 at d = 1.35, 1.1, 0.98, and 0.88; (b) Re = 50, We = 0.5, Ca = 1 × 10−2 at d = 1.48. 1.16, 1.07, and 0.99. | |
To quantify the deformation, a deformation factor (D) is employed and defined as  (see Fig. 3 for the definition of H and L), i.e. the length ratio between the maximum length in the moving direction and the largest length perpendicular to the moving direction. The deformation factors (D) versus d for the four cases are displayed in Fig. 5, where the head-on cases are plotted on the left hand side while the oblique cases are demonstrated on the right hand side. In the earlier stages where the drop is far away from the planar wall, the droplet is elongated in the direction of motion, and the droplet with a larger Weber number is much more elongated due to the smaller surface tension forces which allow larger deformations. For the head-on cases, the droplet with smaller inertia experiences relaxation for d < 2.6. The relaxation occurs for both cases of oblique approaching as the droplet travels longer distance before it is very close to the wall. For all the four case, when d < 1.2, the deformation factor decreases dramatically due to the flattening of the droplet's head by the greater viscous forces of the surrounding flow in the thin film.
(see Fig. 3 for the definition of H and L), i.e. the length ratio between the maximum length in the moving direction and the largest length perpendicular to the moving direction. The deformation factors (D) versus d for the four cases are displayed in Fig. 5, where the head-on cases are plotted on the left hand side while the oblique cases are demonstrated on the right hand side. In the earlier stages where the drop is far away from the planar wall, the droplet is elongated in the direction of motion, and the droplet with a larger Weber number is much more elongated due to the smaller surface tension forces which allow larger deformations. For the head-on cases, the droplet with smaller inertia experiences relaxation for d < 2.6. The relaxation occurs for both cases of oblique approaching as the droplet travels longer distance before it is very close to the wall. For all the four case, when d < 1.2, the deformation factor decreases dramatically due to the flattening of the droplet's head by the greater viscous forces of the surrounding flow in the thin film.
 |
| | Fig. 5 Droplet deformation versus the distance (d) in y direction from the droplet centroid to the wall. | |
The droplet is slowed down as it moves towards the wall mainly due to the viscous dissipation at earlier stages. The non-dimensional droplet centroid velocity (Uc/U0) versus the distance (d) between the droplet and the wall for all the cases is displayed in Fig. 6. The droplet centroid velocity is computed using a volume average method.28 For d > 1.2, the droplet velocity decreases smoothly although there are some small oscillations for the oblique case with Re = 50 and We = 0.5. However, for d < 1.2, the velocity decreases abruptly, and this dramatic change in the velocity is mainly due to the huge viscous forces and pressure inside the thin film.
 |
| | Fig. 6 Non-dimensional droplet centroid velocity versus the distance (d) in y direction from the droplet centroid to the wall. | |
To measure the total drag forces that the droplet experiences, a total drag coefficient is defined as28,34
| |  | (7) |
The drag coefficients for all the cases are shown in Fig. 7, where the insets are the enlarged views of CD when the droplet is very near the wall. The drag coefficient oscillates for d > 1.2, and then CD jumps dramatically. The maximum CD of the simulated cases is above 100. According to the work by Barnocky and Davis,2 the hydrodynamics resistance force for drops moving towarsd a free surface after the formation of thin films can be 100 times larger than the drag forces of the Hadamard–Rybczynski solution for an isolated drop moving in an infinite domain.
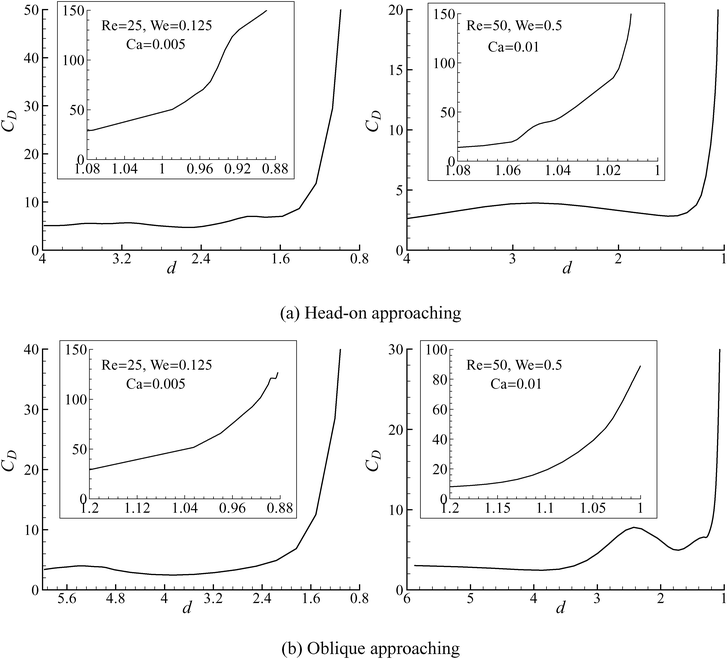 |
| | Fig. 7 Drag coefficients (CD) for all the cases. The inset displays the enlarged view of CD when the droplet is very near to the wall, i.e. d ≤ 1.2 for the head-on cases and d ≤ 1.08 for the oblique approaching. | |
3.2 Thin film dynamics
It was shown in the previous section that a thin film is formed between the drop and the wall at later stages. It is of great interest to demonstrate the evolution of the thin film drainage, and Fig. 8 shows the evolution for all the cases. The thick straight line in the figure denotes the planar wall. Fig. 8 (a) and (b) shows the thin film evolution for the two head-on cases with Re = 25 and Re = 50, respectively, while Fig. 8 (c) and (d) are for the two oblique approaching cases. In the simulations, the different Reynolds numbers are achieved by changing the initial inertia. It should be noted that the data in the oblique approaching cases have been rotated 14° clockwise to make the oblique wall horizontal for the convenience of observation. It is observed that for all the cases, the interface is convex when the interface is far away from the wall. As the interface moves closer to the wall, it becomes flattened, and further approaching the wall leads to a concave shape which is called a dimple. The formation of the dimple is due to the slow motion of the central region of the interface compared to the approaching speed of the rim. For the two cases with smaller inertia, the thin film is wider in the radial (r) direction compared to the thin film of the two cases with larger inertia. This is partially due to the elongation of the drop in the earlier stages which in turn makes the drop head more curved as shown in Fig. 3 and 4. An asymmetric evolution of the thin film is observed for the two oblique approaching cases, and as expected the right side is closer to the wall at each instance after the formation of the dimple. It is also observed that the spreading of the thin film in the radial direction is much faster than the approaching the wall, and this implies that the fluid motion inside the thin film is mainly tangential.
 |
| | Fig. 8 Evolution of the thin film for all the cases. | |
To investigate the thin film drainage evolution as a function of time (drainage rate), we define the thin film thickness, h0 at the central the thin film, hrim at the rim for the head-on cases, hrrim at the right rim and hlrim at the left rim for the oblique approach, and a sketch of these definitions is demonstrated in Fig. 9. The drainage rates of the thin films for all cases are shown in Fig. 10. From the figure, we can see that the smallest thin film thickness resolved in the simulations is around 1%. The dimpling for the two cases with smaller Reynolds numbers occurs at hdimple = 0.029 and 0.028, while the dimpling for the two cases with larger Reynolds number happens at smaller thickness, i.e. hdimple = 0.022 and 0.024 for the head-on motion and the oblique approaching, respectively. Here, hdimple is defined as the point where h0 and hrim start to deviate from each other. According to the numerical solutions by Manica et al.22 for two identical drops approaching each other at a constant velocity,
where
k is a constant and has a value in a range between 0.3 and 0.5 for 10
−10 ≤ Ca ≤ 10
−4. For a drop approaching a solid plate, the constant
k is between 0.4 and 0.7 for the same range of the Capillary number.
6,22 In the simulations, Ca = 5 × 10
−3 for the slower motion drop, then
hdimple = 0.049 according to
eqn 8 if we take
c = 0.7. The simulations predict smaller central separation of the thin film for the dimpling. It is believed that the finite inertial of the simulation cases might be a key reason for the difference, as
eqn 8 is mainly for the slow motion scenarios,
i.e. the Stokes regime and based on the lubrication theory. Another reason for the difference is that the continuity of shear stresses is forced on the interface in the simulations, while the immobile interface condition is assumed in the work by Manica
et al.6,22 For Ca = 0.01, the differences in
hdimple between the predictions by
eqn 8 and the simulations are even larger,
i.e. in the simulations the dimples are formed at much smaller
hdimple. A larger Reynolds number and the large deformation of the drop which results in more curved head of the drop are the two key reasons. The more curved front head of the droplet leads to a smaller local radius, and thus a smaller local capillary number.
 |
| | Fig. 9 Sketch of the definition of the thin film thickness at the centerline and at the rim. | |
 |
| | Fig. 10 Time history of the thin film drainage at the central line (h0) and at the rim (hrim for the head-on approach, hrrim being at the right rim and hlrim denoting the thickness at the left rim for the oblique approaching). The dash-dot-dot green lines represents the thin film drainage rate being , and here t is non-dimensionalized by , and here t is non-dimensionalized by  . . | |
A number of approximate models have been developed for the decay of the thin film thickness which were reviewed by Fisher et al.12 and Hewitt et al.16 Frankel and Mysels,13 Hartland and Robinson,15 and Yiantsios Davis36 found that h0 ∝ t−1/4 and hrim ∝ t−1/2, while Dimitrov10 and Jain and Ivanov18 reported h0 ∝ t−1/2 and hrim ∝ t−1/2. The simulated thin film thickness has been correlated with time for the head-on and oblique approaching cases with Re = 25, and the correlation indicates hrim ∝ t−1/4 which is shown in Fig. 10 (a) and (c) by the dash-dot-dot line. The simulations compute a slower thinning rate of the thin film than the models. Furthermore, the central part of the thin film thins much slower than the rim, and it is noticed that for the oblique approach h0 increases a little bit after the dimple is formed. It is also noted that Fisher et al.12 concluded that comparison of the thin film decay with the models is “an ill-advised endeavour”. Recently, by solving the Stokes–Reynolds–Young–Laplace equations with a tangentially immobile interface, Manica and Chan20 modelled the experimental data by Fisher et al.,11,12 and Hewitt et al.,16 and a good agreement was obtained. Manica and Chan20 also pointed out that the predictions by solving the Reynolds thin film model without considering the film deformation are “qualitatively incorrect”.
3.3 Velocity field
The overall velocity field of the oblique approach with Re = 50 is displayed in Fig. 11, where the streamlines are plotted to better observe the vortex. The flow field is asymmetric. The majority of the fluid inside the droplet moves towards the wall and the fluid near the thin film starts to turn to the direction parallel to the wall. To clearly observe the flow inside the thin film, an enlarged view of this region is plotted in Fig. 12. From the figure, it can be seen that the fluid inside the thin film moves parallel to the wall and is flowing out of the thin film. The fluid on the interface also moves tangentially. The tangential motion of the fluid on the interface of thin films was also reported in the work by Ascoli et al.29 for a buoyancy-driven drop moving toward a planar wall.
 |
| | Fig. 11 Streamlines of the oblique approaching with Re = 50, We = 0.5 when the drop is very close to the sloped wall. | |
 |
| | Fig. 12 Enlarged view of the velocities near the thin film of Fig. 11. | |
4 Conclusion and discussion
Numerical simulations of a droplet moving towards a planar solid wall are presented. The dynamics of the droplet and thinning process of the dimpled thin film are investigated. The droplet slows down dramatically as the thin film is formed due to the huge drag forces mainly from the viscous forces of the flow inside the thin film. For the small Reynolds number cases, the simulated central separation (hdimple) at which the dimple starts to form agrees fairly well with the previous predictions by considering the large difference in the range of the capillary number, while for the large Reynolds number cases, the simulated dimple starts to form at a much smaller central separation. Compared to the previous approximate models for slow motion problems, the simulations for finite Reynolds numbers predict a slower thinning rate.
In the simulations, the smallest thickness resolved is around 1%, and there are around four layers of tetrahedral elements inside the thin film region. To simulate with a higher resolution, more layers of mesh elements are needed, and the numerical schemes have the capability to distribute even finer mesh in the region. However, the total number of mesh elements in the whole domain for a typical case reported in this work is around 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 with the majority of the mesh near and inside the thin film, and it takes several minutes for one time step as the current CFD code is serial. If the mesh size inside the thin film decreases to half, then the total number of elements would be at least quadrupled. This will dramatically slow down the simulations. Parallelization can significantly speed up the code and can help run the problems with higher resolution and to even thinner thin films, and will be addressed in the future.
000 with the majority of the mesh near and inside the thin film, and it takes several minutes for one time step as the current CFD code is serial. If the mesh size inside the thin film decreases to half, then the total number of elements would be at least quadrupled. This will dramatically slow down the simulations. Parallelization can significantly speed up the code and can help run the problems with higher resolution and to even thinner thin films, and will be addressed in the future.
Acknowledgements
The author would like to thank Rogerio Manica, Evert Klaseboer, and Derek Y. C. Chan for numerous helpful discussions and valuable suggestions.
References
- E. P. Ascoli, D. S. Dandy and L. G. Leal, J. Fluid Mech., 1990, 213(0), 287 CrossRef CAS
 Buoyancy-driven motion of a deformable drop toward a planar wall at low Reynolds number..
Buoyancy-driven motion of a deformable drop toward a planar wall at low Reynolds number..
- G. Barnocky and R. H. Davis, Int. J. Multiphase Flow, 1989, 15(4), 627–638 CrossRef CAS
 The lubrication froce between spherical drops, bubbles and rigid particles in a viscous fluid..
The lubrication froce between spherical drops, bubbles and rigid particles in a viscous fluid..
- E. Bart, Chem. Eng. Sci., 1968, 23(0), 193–210 CrossRef
 The slow unsteady settling of a fluid sphere toward a flat fluid interface..
The slow unsteady settling of a fluid sphere toward a flat fluid interface..
- V. N. Beshkov, B. P. Radoev and I. B. Ivanov, Int. J. Multiphase Flow, 1978, 4(5–6), 563–570 CrossRef
 Slow motion of two droplets and a droplet towards a fluid or solid interface..
Slow motion of two droplets and a droplet towards a fluid or solid interface..
- S. L. Carnie, D. Y. C. Chan, C. Lewis, R. Manica and R. R. Dagastine, Measurement of dynamical forces between deformable drops using the atomic force microscope. I. Theory, Langmuir, 2005, 21(7), 2912–2922 CrossRef CAS
 .
.
- D. Y. C. Chan, E. Klaseboer and R. Manica, Soft Matter, 2009, 5(15), 2858–2861 RSC
 Dynamic deformations and forces in soft matter..
Dynamic deformations and forces in soft matter..
- D. Y. C. Chan, E. Klaseboer and R. Manica, Soft Matter, 2011, 7(6), 2235–2264 RSC
 Film drainage and coalescence between deformable drops and bubbles.
Film drainage and coalescence between deformable drops and bubbles.
- J. N. Connor and R. G. Horn, Faraday Discuss., 2003, 123, 193–206 RSC
 The influence of surface forces on thin film drainage between a fluid drop and a flat solid.
The influence of surface forces on thin film drainage between a fluid drop and a flat solid.
- M. Z. Dai and D. P. Schmidt, J. Comput. Phys., 2005, 208(1), 228–252 CrossRef
 Adaptive tetrahedral meshing in free-surface flow.
Adaptive tetrahedral meshing in free-surface flow.
- D. S. Dimitrov and I. B. Ivanov, J. Colloid Interface Sci., 1978, 64(1), 97–106 CrossRef
 Hydrodynamics of thin liquid films. On the rate of thinning of microscopic films with deformable interfaces.
Hydrodynamics of thin liquid films. On the rate of thinning of microscopic films with deformable interfaces.
- L. R. Fisher, E. E. Mitchell, D. Hewitt, J. Ralston and J. Wolfe, Colloids Surf., 1991, 52, 163–174 CrossRef CAS
 The drainage of a thin aqueous film between a solid surface and an approaching gas bubble.
The drainage of a thin aqueous film between a solid surface and an approaching gas bubble.
- L. R. Fisher, D. Hewitt, E. E. Mitchell, J. Ralston and J. Wolfe, Adv. Colloid Interface Sci., 1992, 39, 397–416 CrossRef CAS
 The drainage of an aqueous film between a solid plane and an air bubble.
The drainage of an aqueous film between a solid plane and an air bubble.
- S. P. Frankel and K. J. Mysels, J. Phys. Chem., 1962, 66(1), 190–191 CrossRef CAS
 On the dimpling during the approach of two interfaces.
On the dimpling during the approach of two interfaces.
- D. G. Goodall, M. L. Gee and G. W. Stevens, Langmuir, 2002, 18(12), 4729–4735 CrossRef CAS
 An imaging reflectometry study of the effect of electrolyte on the drainage and profile of an aqueous film between an oil droplet and a hydrophilic silica surface.
An imaging reflectometry study of the effect of electrolyte on the drainage and profile of an aqueous film between an oil droplet and a hydrophilic silica surface.
- S. Hartland and J. D. Robinson, J. Colloid Interface Sci., 1977, 60(1), 72–81 CrossRef CAS
 A model for an axisymmetric dimpled draining film.
A model for an axisymmetric dimpled draining film.
- D. Hewitt, D. Fornasiero, J. Ralston and L. R. Fisher, J. Chem. Soc., Faraday Trans., 1993, 89(5), 817–822 RSC
 Aqueous film drainage at the quartz/water/air interface.
Aqueous film drainage at the quartz/water/air interface.
- R. G. Horn, M. Asadullah and J. N. Connor, Langmuir, 2006, 22(6), 2610–2619 CrossRef CAS
 Thin film drainage: hydrodynamic and disjoining pressures determined from experimental measurements of the shape of a fluid drop approaching a solid wall.
Thin film drainage: hydrodynamic and disjoining pressures determined from experimental measurements of the shape of a fluid drop approaching a solid wall.
- R. K. Jain and I. B. Ivanov, J. Chem. Soc., Faraday Trans., 1980, 2, 76(0), 250–266 Search PubMed
 Thinning and rupture of ring-shaped films.
Thinning and rupture of ring-shaped films.
- C. Y. Lin and J. C. Slattery, AIChE J., 1982, 28(1), 147–156 CrossRef CAS
 Thinning of a liquid film as a small drop or bubble approaches a solid plane.
Thinning of a liquid film as a small drop or bubble approaches a solid plane.
- R. Manica and D. Y. C. Chan, Phys. Chem. Chem. Phys., 2011, 13(4), 1434–1439 RSC
 Drainage of the air–water-quartz film: experiments and theory. ISSN 1463-9084S.
Drainage of the air–water-quartz film: experiments and theory. ISSN 1463-9084S.
- R. Manica, J. N. Connor, S. L. Carnie, R. G. Horn and D. Y. C. Chan, Langmuir, 2007, 23(2), 626–637 CrossRef CAS
 Dynamics of interactions
involving deformable drops: Hydrodynamic dimpling under attractive and repulsive electrical double layer interactions.
Dynamics of interactions
involving deformable drops: Hydrodynamic dimpling under attractive and repulsive electrical double layer interactions.
- R. Manica, E. Klaseboer and D. Y. C. Chan, Soft Matter, 2008, 4(8), 1613–1616 RSC
 Dynamic interactions between drops - a critical assessment.
Dynamic interactions between drops - a critical assessment.
- R. Manica, L. Parkinson, J. Ralston and D. Y. C. Chan, J. Phys. Chem. C, 2010, 114(4), 1942–1946 CAS
 Interpreting the dynamic interaction between a very small rising bubble and a hydrophilic titania surface.
Interpreting the dynamic interaction between a very small rising bubble and a hydrophilic titania surface.
- L. Parkinson and J. Ralston, J. Phys. Chem. C, 2010, 114(5), 2273–2281 CAS
 The interaction between a very small rising bubble and a hydrophilic titania surface.
The interaction between a very small rising bubble and a hydrophilic titania surface.
- D. Platikanov, J. Phys. Chem., 1964, 68(12), 3619–3624 CrossRef CAS
 Experimental investigation on the dimpling of thin liquid films.
Experimental investigation on the dimpling of thin liquid films.
- C. Pozrikidis, J. Fluid Mech., 1990, 215(0), 331–363 CrossRef CAS
 The deformation of a liquid drop moving normal to a plane wall.
The deformation of a liquid drop moving normal to a plane wall.
- S. P. Quan, J. Comput. Phys., 2011, 230(13), 5430–5448 CrossRef CAS
 Simulations of multiphase flows with multiple length scales using moving mesh interface tracking with adaptive meshing.
Simulations of multiphase flows with multiple length scales using moving mesh interface tracking with adaptive meshing.
- S. P. Quan and D. P. Schmidt, Phys. Fluids, 2006, 18(10), 102103 CrossRef
 Direct numerical study of a liquid droplet impulsively accelerated by gaseous flow.
Direct numerical study of a liquid droplet impulsively accelerated by gaseous flow.
- S. P. Quan and D. P. Schmidt, J. Comput. Phys., 2007, 221(2), 761–780 CrossRef
 A moving mesh interface tracking method for 3d incompressible two-phase flows.
A moving mesh interface tracking method for 3d incompressible two-phase flows.
- S. P. Quan, J. Lou and D. P. Schmidt, J. Comput. Phys., 2009, 228(7), 2660–2675 CrossRef CAS
 Modeling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations.
Modeling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations.
- S. P. Quan, D. P. Schmidt, J. S. Hua and J. Lou, J. Fluid Mech., 2009, 640, 235–264 CrossRef
 A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid.
A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid.
- B. Steinhaus, P. T. Spicer and A. Q. Shen, Langmuir, 2006, 22(12), 5308–5313 CrossRef CAS
 Droplet size effects on film drainage between droplet and substrate.
Droplet size effects on film drainage between droplet and substrate.
- C. S. Tan, M. L. Gee and G. W. Stevens, Langmuir, 2003, 19(19), 7911–7918 CrossRef CAS
 Optically profiling a draining aqueous film confined between an oil droplet and a solid surface: Effect of nonionic surfactant.
Optically profiling a draining aqueous film confined between an oil droplet and a solid surface: Effect of nonionic surfactant.
- S. Temkin and M. K. Mehta, J. Fluid Mech., 1982, 116(0), 297–313 CrossRef CAS
 Droplet drag in an accelerating and decelerating flow..
Droplet drag in an accelerating and decelerating flow..
-
Z. U. A. Warsi
Fluid dynamics: Theoretical and computational approaches.
CRC press
1998
Search PubMed
 .
.
- S. G. Yiantsios and R. H. Davis, J. Fluid Mech., 1990, 217(0), 547–573 CrossRef CAS
 On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface.
On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ra01108a |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 


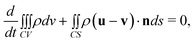
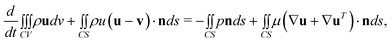

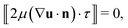
 denotes the difference across the interface, R1 and R2 are the local principle radii of the surface, τ is the unit tangential vector of the surface, and σ stands for the surface tension coefficient. These boundary conditions can be derived from the above governing equations by treating the interface as an internal boundary. Please note that as the fluid normal velocities (us,n and ud,n) of the two phases near the interface are continuous and are equal to the normal velocity (vn) of the moving surface (eqn 4), the convection terms in eqn 2 and 3 are identically zero on the interfacial surfaces.
denotes the difference across the interface, R1 and R2 are the local principle radii of the surface, τ is the unit tangential vector of the surface, and σ stands for the surface tension coefficient. These boundary conditions can be derived from the above governing equations by treating the interface as an internal boundary. Please note that as the fluid normal velocities (us,n and ud,n) of the two phases near the interface are continuous and are equal to the normal velocity (vn) of the moving surface (eqn 4), the convection terms in eqn 2 and 3 are identically zero on the interfacial surfaces.
 ) in eqn 5 is calculated using a least-squares parabola fitting in a local coordinate system9 to compute the surface tension forces, and the jump in the normal viscous stresses is calculated directly by using Taylor series expansion to the first order for multivariable functions.29 The jump in normal stresses is implemented directly as a pressure boundary condition. To satisfy the continuity of shear stresses across the interface, i.e.eqn 6, the second-order geometric harmonic mean method29 is used to calculate the viscous shear stresses on the interfacial surfaces. The convection term is computed by a central difference scheme, and the viscous term is calculated by a predictor-corrector method. The time integration is advanced by a three-step, second-order Runge–Kutta scheme.
) in eqn 5 is calculated using a least-squares parabola fitting in a local coordinate system9 to compute the surface tension forces, and the jump in the normal viscous stresses is calculated directly by using Taylor series expansion to the first order for multivariable functions.29 The jump in normal stresses is implemented directly as a pressure boundary condition. To satisfy the continuity of shear stresses across the interface, i.e.eqn 6, the second-order geometric harmonic mean method29 is used to calculate the viscous shear stresses on the interfacial surfaces. The convection term is computed by a central difference scheme, and the viscous term is calculated by a predictor-corrector method. The time integration is advanced by a three-step, second-order Runge–Kutta scheme.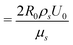 ) 25 and 50 have been computed to investigate the inertia effects on the droplet deformation and the thin film drainage for the head-on and oblique scenarios, respectively. The corresponding Weber numbers (We
) 25 and 50 have been computed to investigate the inertia effects on the droplet deformation and the thin film drainage for the head-on and oblique scenarios, respectively. The corresponding Weber numbers (We ) are 0.125 and 0.5. Therefore, the Capillary numbers (Ca
) are 0.125 and 0.5. Therefore, the Capillary numbers (Ca ) are 5 × 10−3 and 1 × 10−2, respectively.
) are 5 × 10−3 and 1 × 10−2, respectively.


 (see Fig. 3 for the definition of H and L), i.e. the length ratio between the maximum length in the moving direction and the largest length perpendicular to the moving direction. The deformation factors (D) versus d for the four cases are displayed in Fig. 5, where the head-on cases are plotted on the left hand side while the oblique cases are demonstrated on the right hand side. In the earlier stages where the drop is far away from the planar wall, the droplet is elongated in the direction of motion, and the droplet with a larger Weber number is much more elongated due to the smaller surface tension forces which allow larger deformations. For the head-on cases, the droplet with smaller inertia experiences relaxation for d < 2.6. The relaxation occurs for both cases of oblique approaching as the droplet travels longer distance before it is very close to the wall. For all the four case, when d < 1.2, the deformation factor decreases dramatically due to the flattening of the droplet's head by the greater viscous forces of the surrounding flow in the thin film.
(see Fig. 3 for the definition of H and L), i.e. the length ratio between the maximum length in the moving direction and the largest length perpendicular to the moving direction. The deformation factors (D) versus d for the four cases are displayed in Fig. 5, where the head-on cases are plotted on the left hand side while the oblique cases are demonstrated on the right hand side. In the earlier stages where the drop is far away from the planar wall, the droplet is elongated in the direction of motion, and the droplet with a larger Weber number is much more elongated due to the smaller surface tension forces which allow larger deformations. For the head-on cases, the droplet with smaller inertia experiences relaxation for d < 2.6. The relaxation occurs for both cases of oblique approaching as the droplet travels longer distance before it is very close to the wall. For all the four case, when d < 1.2, the deformation factor decreases dramatically due to the flattening of the droplet's head by the greater viscous forces of the surrounding flow in the thin film.






 , and here t is non-dimensionalized by
, and here t is non-dimensionalized by  .
.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 with the majority of the mesh near and inside the thin film, and it takes several minutes for one time step as the current CFD code is serial. If the mesh size inside the thin film decreases to half, then the total number of elements would be at least quadrupled. This will dramatically slow down the simulations. Parallelization can significantly speed up the code and can help run the problems with higher resolution and to even thinner thin films, and will be addressed in the future.
000 with the majority of the mesh near and inside the thin film, and it takes several minutes for one time step as the current CFD code is serial. If the mesh size inside the thin film decreases to half, then the total number of elements would be at least quadrupled. This will dramatically slow down the simulations. Parallelization can significantly speed up the code and can help run the problems with higher resolution and to even thinner thin films, and will be addressed in the future.Buoyancy-driven motion of a deformable drop toward a planar wall at low Reynolds number..
The lubrication froce between spherical drops, bubbles and rigid particles in a viscous fluid..
The slow unsteady settling of a fluid sphere toward a flat fluid interface..
Slow motion of two droplets and a droplet towards a fluid or solid interface..
.
Dynamic deformations and forces in soft matter..
Film drainage and coalescence between deformable drops and bubbles.
The influence of surface forces on thin film drainage between a fluid drop and a flat solid.
Adaptive tetrahedral meshing in free-surface flow.
Hydrodynamics of thin liquid films. On the rate of thinning of microscopic films with deformable interfaces.
The drainage of a thin aqueous film between a solid surface and an approaching gas bubble.
The drainage of an aqueous film between a solid plane and an air bubble.
On the dimpling during the approach of two interfaces.
An imaging reflectometry study of the effect of electrolyte on the drainage and profile of an aqueous film between an oil droplet and a hydrophilic silica surface.
A model for an axisymmetric dimpled draining film.
Aqueous film drainage at the quartz/water/air interface.
Thin film drainage: hydrodynamic and disjoining pressures determined from experimental measurements of the shape of a fluid drop approaching a solid wall.
Thinning and rupture of ring-shaped films.
Thinning of a liquid film as a small drop or bubble approaches a solid plane.
Drainage of the air–water-quartz film: experiments and theory. ISSN 1463-9084S.
Dynamics of interactions involving deformable drops: Hydrodynamic dimpling under attractive and repulsive electrical double layer interactions.
Dynamic interactions between drops - a critical assessment.
Interpreting the dynamic interaction between a very small rising bubble and a hydrophilic titania surface.
The interaction between a very small rising bubble and a hydrophilic titania surface.
Experimental investigation on the dimpling of thin liquid films.
The deformation of a liquid drop moving normal to a plane wall.
Simulations of multiphase flows with multiple length scales using moving mesh interface tracking with adaptive meshing.
Direct numerical study of a liquid droplet impulsively accelerated by gaseous flow.
A moving mesh interface tracking method for 3d incompressible two-phase flows.
Modeling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations.
A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid.
Droplet size effects on film drainage between droplet and substrate.
Optically profiling a draining aqueous film confined between an oil droplet and a solid surface: Effect of nonionic surfactant.
Droplet drag in an accelerating and decelerating flow..
.
On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface.
