Zone-selective photoelectronic measurements of the local bonding and electronic dynamics associated with the monolayer skin and point defects of graphite
Chang Q
Sun
*ab,
Yanguang
Nie
a,
Jisheng
Pan
c,
Xi
Zhang
a,
S. Z.
Ma
a,
Yan
Wang
d and
Weitao
Zheng
*e
aSchool of Electrical and Electronic Engineering, Nanyang Technological University, Singapore 639798. E-mail: Ecqsun@ntu.edu.sg
bFaculty of Materials, Photoelectronics and Physics, Xiangtan University, Changsha, 400073, China
cInstitute of Materials Research and Engineering, A*Star, Singapore 117602
dSchool of Information and Electronic Engineering, Hunan University of Science and Technology, Xiangtan, 411201, China
eSchool of Materials Science, Jilin University, Changchun, 130012, China. E-mail: wtzheng@jlu.edu.cn
First published on 30th January 2012
Abstract
Zone-resolved photoelectron spectroscopy (ZPS) has enabled us to gain local and quantitative information (and hence confirm our theoretical expectations) on the bonding and electronic dynamics associated with the monolayer skin and atomic vacancy defects of graphite. The ZPS revealed: (i) the 1s energy level of an isolated carbon atom is located at 282.57 eV, which increases by 1.32 eV upon diamond bulk formation; (ii) the graphite surface bonds contract by 18% with a 165% gain in energy compared with a C–C bond in bulk diamond; the surface C 1s energy increases by 2.08 eV from the 1s level of an isolated carbon atom; and (iii) the defect bonds are ∼26% shorter and 215% stronger with a binding energy shift of ∼2.85 eV. An additional polarization peak centered at 1.28 eV below the C 1s level is present when a vacancy is formed. In association with the scanning tunneling microscopy/spectroscopy observations and density functional theory calculations, the ZPS measurements clarify, for the first time, that the graphitic Dirac–Fermi polarons at an atomic vacancy or on graphene’s zigzag edge arise from the polarization of the unpaired dangling-bond electrons by the under-coordination-induced local densification and quantum entrapment of the bonding electrons. The theory-enabled ZPS complements scanning tunneling microscopy/spectroscopy and conventional photoelectron emission techniques in understanding the bond and electronic dynamics at the atomic scale.
I Introduction
Bonds and electrons associated with under-coordinated atoms dictate the unusual performance of materials at surfaces, defects, and at the nanoscale 1 in catalytic reactivity,2,3 crystal growth,4 adsorption,5decomposition,6 doping,7 interface formation,8,9 wettability,10 thermal stability,11etc. Although the chemistry and physics of materials associated with under-coordinated atoms have been extensively investigated for decades, the laws governing the performance of local bonds and electrons remain to be established.12,13,14 Collection and purification of such local, atomistic zone selective, and quantitative information has been increasingly in demand but it remains, as yet, the “black hole” of the community.As a powerful detection tool, scanning tunneling micro/spectroscopy (STM/S) maps local electrons in the open side of a too-thin subatomic layer of a surface with energies of a few eVs close to the Fermi energy (EF). Understanding the intriguing STM/S attributes of high protrusions and the additional resonant spectral peak near EF of a graphite atomic vacancy 15 and the graphene edge,16 for instance, as well as the driving force for the unusual protrusions and the EF resonance, remains a challenge. One urgently needs to identify what the “root” of the STM/S attributes is, and what the quantitative information could be about the length and strength of the annexed bonds and the energies of the associated electrons. On the other hand, a photoelectron spectroscopy (PES with ultraviolet or X-ray as the source are called UPS or XPS, respectively) probes the statistical and volumetric information of electrons with binding energies in the valence band and below within a too-thick layer of 10 nanometres or thicker.13,17,18,19 The interplay of STM/S and XPS could provide qualitative information about the surface and the bulk to a degree, however, the extraction of localized, atomistic zone selective, quantitative information from a sheet of atomic thickness is beyond what STM/S can measure.
In order to solve this challenging issue, we have developed a special yet simple technique of zone-resolved photoelectron spectroscopy (ZPS), which has enabled us to overcome the aforementioned limitations. Applying ZPS to a graphite surface with and without atomic vacancies, we have been able to derive important findings as elaborated in the following.
II Principles
2.1 The Hamiltonian determined core level shift
Firstly, according to the energy band theory,20 the energy shift of a specific (the C 1s) core band from that of an isolated atom is proportional to the crystal potential energy at equilibrium or the cohesive energy per bond. Any perturbation to the crystal potential will shift the C 1s band away from the bulk value. The energy shift can be positive or negative depending on the perturbation resulting from bond relaxation, bond nature alteration, charge polarization, “initial-final states” effect, etc. Secondly, according to the bond order–length–strength (BOLS) correlation21 extended from the premise of Pauling22 and Goldschmidt,23 bonds between under-coordinated atoms become shorter and stronger, as confirmed in Au clusters.24,25 The spontaneous process of bond contraction and strengthening will cause local densification and quantum entrapment of bonding charge and binding energy and hence the positive core level shift results. Thirdly, the densely and locally entrapped bonding electrons will polarize the weakly bound sp2 dangling-bond electrons. These polarized and unpaired electrons neither follow the regular dispersion relation nor occupy the allowed energy states in the valence band and below as defined by the Hamiltonian; however, they add impurity states in the vicinity of EF and follow the Dirac equation,26 generating the STM/S probed Dirac–Fermi polarons (DFPs).27,28,29,30 Finally, the polarized and unpaired electrons with non-zero spin will in turn screen and split the crystal potential and consequently generate extra component in the upper edge of the core band. Fig. 1(a) and (b) illustrate the BOLS correlation and the associated entrapment and polarization effect.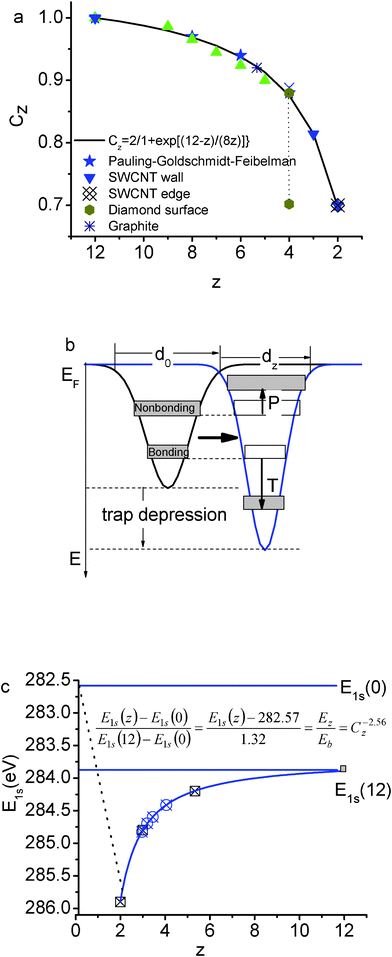 | ||
| Fig. 1 Illustration of (a) the “atomic CN-radius” correlation of Goldschmidt–Pauling–Feibelman with the scattered data of observations and the formation of the bond contraction coefficient;47 (b) the BOLS correlation indicating that the shorter and stronger bonds between under-coordinated atoms cause local quantum entrapment and densification of the binding energy and the bonding and core electrons, which in turn polarize the nonbonding edge electrons;48 and, (c) the positive core level shift of graphene edge (z = 2), graphene (z = 3), few-layer graphene, graphite and diamond with respect to the E1s(0),21 in comparison with experimental results 34,49. | ||
Analytically, the Hamiltonian for the 1s electrons of carbon can be formulated by the combination of the band theory 20 and the BOLS correlation21 with inclusion of the polarization effect,
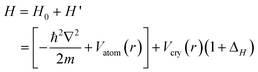 | (1) |
The perturbation to the Hamiltonian ΔH contains the following terms:21
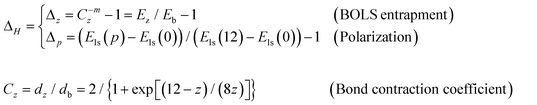 | (2) |
The C 1s level of an isolated carbon atom and its shift upon the crystal potential involved follow the relations,20,21
 | (3) |
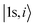 is the C 1s eigenwave function at the ith atomic site with z neighbors.
is the C 1s eigenwave function at the ith atomic site with z neighbors. 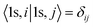 because of the strong localization of the core electrons.
because of the strong localization of the core electrons.
For the diamond, the effective z is 12 instead of 4 because the diamond structure is an interlock of two fcc unit cells.21 With the C–C bond lengths in graphite (0.142 nm) and in diamond (0.154 nm), one can derive that the effective z = 5.335 for an atom in bulk graphite using the Goldschmidt–Pauling coefficient Cz.
Thus, correlation between the XPS components follows the criterion,
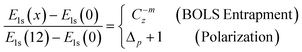 | (4) |
The x represents z or p. If the polarization-entrapment coupling effect is apparent, the term C−mzis then replaced by pC−mz, the entrapped states will be moved up from the otherwise low-z position to an energy close to that of the bulk. For situations without apparent polarization, the relation evolves,
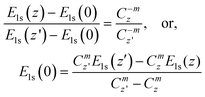 | (5) |
The BOLS reproduction21 of the elastic modulus enhancement31 and the melting point depression32 of carbon nanotubes,33 and the C 1s core level shifts of graphene edge, graphene, graphite, and diamond34 have consistently confirmed that the C–C bond between two-coordinated edge atoms contracts by 30% from 0.154 nm to 0.107 nm and the bond become 252% stronger than that in diamond, giving a generalized form for the z-resolved C 1s energy shift with the optimized bond nature indicatorm = 2.56,21 as illustrated in Fig. 1(c),
| Els(z) = Els(0) + [Els(12) − Els(0)] C−256z = 282.57 + 1.32C−256z (eV) | (6) |
The discovery12 that the minimal energy (7.5 eV bond−1) required for breaking a bond of the two-coordinated carbon atom near a vacancy is 32% times higher than that (5.67 eV bond−1) required for breaking a bond of a three-coordinated carbon atom in a suspended graphene sheet confirms the BOLS formulation of under-coordination-induced bond strength gain.
2.2 Zone-resolved photoelectron spectroscopy (ZPS)
One can imagine what will happen by considering the difference between two spectra collected: (i) from the same defect-free surface at different emission angles; or (ii) from the same surface after and before the surface has been conditioned (such as defect generation and chemisorption) under the same measurement conditions. Upon conducting the standard processes of background correction and spectral area normalization, the ZPS in (i) retains the spectral features due to the skin by filtering out the bulk information as the XPS collects more information from the surface at larger emission angles.35 Likewise, the ZPS in (ii) purifies merely the spectral features due to the conditioning. The ZPS also filters out all the artifact background such as the charging effect and the “initial–final states” relaxation effect that exist throughout the course of the measurements. This technique can be used for monitoring surface processes such as crystal growth, defect generation, chemical reactions, alloy formation, etc., both statically and dynamically.III Experimental procedures
STM/S measurements have uncovered the graphitic DFPs as extraordinarily high protrusions and resonant peaks at the EF from sites surrounding atomic vacancies15,29,36,37 and at the edges of monolayer graphite terraces and graphene nanoribbons (GNRs).12,16,38 The DFPs demonstrate anomalies including the extremely low effective mass, extremely high group velocity, and non-zero spin, following the Dirac equation with a nearly linear dispersion crossing the Fermi energy.39,40 Our recent density functional theory (DFT) calculations41 revealed that the DFPs with a high-spin-density are preferably created at a zigzag-GNR edge and at an atomic vacancy because of the isolation and polarization of the dangling σ-bond electrons of the identical √3d (d is the C–C bond length) distance along the edge. The locally and densely entrapped bonding electrons provide the force pinning the DFPs. However, along the armchair-GNR edge and the reconstructed-zigzag-GNR edge, the formation of a quasi-triple-bond between the nearest edge atoms of distance d prevents the DFPs from being generated.In order to test the power of ZPS and confirm the DFT calculations, we applied ZPS to the XPS analysis in combination with the BOLS and the energy band theory to identify the nature, origin, and consequences of the graphitic DFPs with quantitative information by distilling the surface and defect states from the mixture of bulk and surface states.
The XPS data were collected at different emission angles at room temperature from a graphite surface with and without artificial vacancies using the Sigma Probe Instrument (Thermal Scientific) with monochromatic Al Kα(1486.6 eV) as the X-ray source. The XPS facility was firstly calibrated using pure gold, silver, and copper standard samples by setting the Au 4f7/2, Ag 3d5/2 at binding energies of 83.98 ± 0.02 eV and 368.26 ± 0.02 eV, respectively. Highly oriented pyrolytic graphite (HOPG) was cleaved using adhesive tape, and then, transferred quickly into the XPS chamber.
In order to control the generation and density of the surface atomic vacancy, we sprayed the graphite surface using Ar+ ions with 0.5 keV energy incident along the surface normal. The ion dose was controlled by the sample current and the duration of spraying. The energetic Ar+ bombardment creates only under-coordinated atoms at the surface without any chemical reaction in high vacuum.42 We firstly collected the spectra at different emission angles (between the surface normal and photoelectron beam) from the defect-free surface to discriminate the skin from the bulk. We then collected the spectra from the conditioned surface at different Ar+ ion doses under the same conditions and the same emission angle.
The spectra were corrected using the standard process of Shirley background correction and then the spectral peak areas were normalized using the standard process under guidelines of spectral area conservation. As the total number of electrons excited from the specimen each time is proportional to the area, the spectral area was normalized to minimize the effect of scattering by the rough surface or by the surface atoms at larger emission angles. The spectra collected from the defect-free surface at larger emission angles up to 75° were then subtracted by the reference spectrum collected from the freshly-cleaved surface at the lowest available emission angle (25°). For the defect density dependence, we simply repeat the process at 50° without changing the emission angle. The difference between the spectra collected at 75° from the surface with and without defects were also collected for comparison.
IV Results and discussion
Fig. 2(a) and (b) show the well-resolved XPS spectra collected (a) from the defect-free surface at different emission angles and (b) from the surface of different defect densities represented by the Ar+ doses at the emission angle of 50°. The data sets gained here are consistent with those previously reported.17,18,43,44 The angle-resolved spectra show a small positive shift while the defects give rise to a slight negative shift of the spectrum. The overall weakened intensities of the raw spectra collected at larger emission angles or from those of higher defect densities arise from the scattering loss.45 This effect can be compensated by the spectral area normalization correction under the guidelines of spectral area conservation. It is noted that the energy change remains the same for angles approaching to 75° or higher vacancy densities. As the extent of the core-level shift depends on the atomic CN instead of the number of such atoms, the lack of change of the core level energy suggests that the spectral information becomes dominated by the surface skins as the emission angle increases.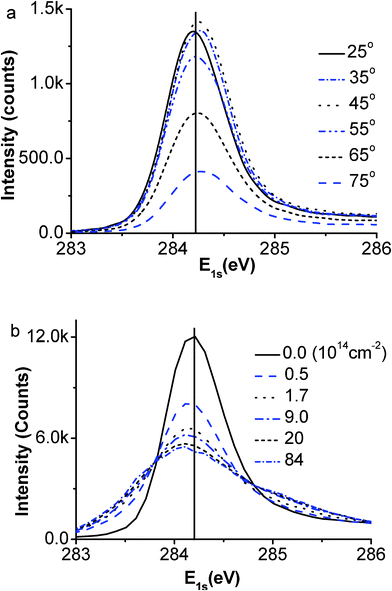 | ||
| Fig. 2 The raw XPS spectra collected from (a) defect-free graphite surface at different emission angles and (b) the defect surface at 50° with different Ar+ ion doses. One can hardly resolve a difference in the value of the binding energy but the spectral intensity variation in marked, which leads us to initiate the ZPS technique. | ||
The ZPS results in Fig. 3 show the evolution of (a) the defect-free surface and (b) the surface with different defect densities as represented by the doses of Ar+ ions. The areas above and below the x-axis are, respectively, the gain and loss of the energy states under the given conditions.
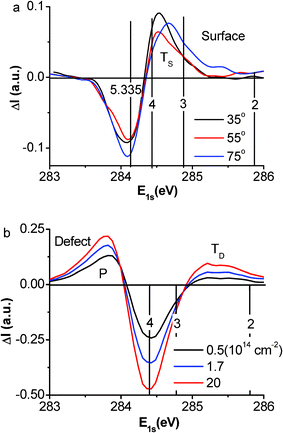 | ||
| Fig. 3 (a) The purified ZPS results show only the trapped (TS) surface states evolving from z ∼ 4 to z ∼ 3 with emission angle increasing from 25° to 75° and (b) both the trapped (TD) and polarized (P) states coexist due to the vacancy defects. The TD energy well is deeper than that of TS, indicating that the defect bonds are shorter and stronger than those of the surface. The surface bonds are shorter and stronger than those in the bulk. | ||
According to the tight binding approximation, the separation between the spectral features and the atomic C 1s level (282.57 eV) is proportional to the bond energy. The valleys at 284.20 eV in Fig. 3(a) and 284.40 eV in Fig. 3(b) are the subtracted graphite bulk and the mixture of surface and bulk components. In addition to the spectral valleys, one trapped peak (for state TS) is present in the defect-free surface at the bottom edge of the C 1s band, which shifts to a lower binding energy corresponding to the evolution of the effective atomic CN from z ∼ 4 to z ∼ 3.2, as the emission angle increases from 35° to 75°. As the vacancy defects are generated, the TS state moves to an even deeper energy and evolves into the TD state. Surprisingly, the TD state is associated with the emergence of both the DFPs at the Fermi energy as identified using STM/S12,15,16,29,36,37,38 and the P component at the upper edge of the C 1s band.
As the defect density is increased, the intensity of the peak from the TD component grows but remains stable in energy; the peak for the P component moves up in both energy and intensity. This finding indicates that the atomic CN has reached the lowest value and stabilized and the extent of polarization increases with the defect density. The core level position depends on the effective atomic CN but not the density of such under-coordinated atoms. The presence and evolution of the TS state to the TD component is referred to as a positive core level shift due to the surface- and defect-induced quantum entrapment making the C 1s band deeper when the atomic CN is decreased, which further verify the Goldschmidt–Pauling–Feibelman premise of bond contraction and the BOLS prediction. The presence of the P states is referred to as the negative core level shift, which results from the screening of the crystal potential by the presence of the DFPs at the defect sites. The DFPs screen and partially split the crystal potential and hence the core band into the TD and the P components. However, such a process of screening and splitting does not happen to the defect-free surface because of the lack of unpaired dangling bond electrons at the smooth surface.
Fig. 4 and Table 1 summarize our ZPS findings from graphite surfaces. The ZPS for the clean surface is obtained by differentiating the XPS data collected at 75° from that collected at 25°. The defect ZPS is the difference between the two spectra collected at 75° from the surface after and before high-density defect generation. The insets show the zones (in color) dominating the extra states in each case. The atomic CN for the outermost layer of graphite is estimated as 3.1 close to the ideal case of 3.0 in graphene. The atomic CN for the vacancy extends from 2.2 to 2.4, which indicates that the next nearest neighbors to the vacancy contribute to the ZPS features. It is exciting that the atomic CN of the atoms next to the vacancy are comparable to that of the GNR edge (2.0) because of the weak interface interaction. From Fig. 4 and the BOLS numerical expressions in eqn (3) and (4), we can evaluate the length and strength of the bonds and the binding energy shift associated with the under-coordinated atoms, as summarized in Table 1. Consistency in the expected effective coordination and the specific energy between the current results and previous observations (see Table 1 in ref. 21 and Fig. 1(c) in this paper) provides evidence that the accuracy of the derivatives is sufficient. Strikingly, the ratio of the energy shift of the 2- and 3-coordinated atoms agrees exceedingly well with the trend of energy requirement for 2- and 3-coordinated graphene bond breaking.12
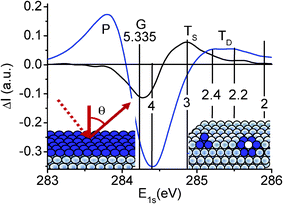 | ||
| Fig. 4 Comparison of the purified XPS C 1s spectrum collected at 75° from the surface with (9 × 1014 cm−2 dosed Ar+ ions) and without defects. The valleys centered around 284.20 eV and 284.40 eV correspond, respectively, to the removed obvious graphite bulk and the mixture of surface–bulk information; the extra components are the energy states due to the surface skin, TS (z ∼ 3.1), within the outermost atomic layer and sites surrounding vacancy defects, TD (z ∼ 2.2–2.4). G denotes the bulk graphite (z = 5.335). The P component at the upper edge arises from the screening and splitting of the crystal potential by the DFPs that originate from the polarization of the dangling bond electrons by the trapped (TD in the bottom of the core band) core electrons. Insets illustrate the emission angle and the atomic diameter thick zones (in blue) dominating the extra core band components in each situation. | ||
| z | C z | d z (nm) | E z (eV) | C 1s (eV) | P (eV) | |
|---|---|---|---|---|---|---|
| Atom | 0 | — | — | — | 282.57 | |
| GNR edge | 2.00 | 0.70 | 0.107 | 1.548 | 285.89 | |
| GraphiteVacancy | 2.20 | 0.73 | 0.112 | 1.383 | 285.54 | 283.85 |
| 2.40 | 0.76 | 0.116 | 1.262 | 285.28 | ||
| GNR interior | 3.00 | 0.81 | 0.125 | 1.039 | 284.80 | |
| Graphite Surface | 3.10 | 0.82 | 0.127 | 1.014 | 284.75 | |
| Graphite | 5.335 | 0.92 | 0.142 | 0.757 | 284.20 | |
| Diamond | 12.00 | 1.00 | 0.154 | 0.615 | 283.89 |
As compared in Fig. 5(a) and (b), the high protrusions and the STS resonant peak of a graphite surface’s atomic vacancy15 are naturally the same to that of the graphene zigzag edge16 despite the sharpness of the resonant EF peak. The peak sharpness is subject to the STM/S tip conditions and the temperature. The STM/S similarity and the close values of atomic CNs between the graphite atomic vacancy and the graphene edge suggest that both are the same in nature. Therefore, we can focus on the graphite surface vacancy as a more convenient mimic of the GNR edge. Fig. 5(c) compares the density functional theory calculations of the local density of states of the vacancy and edge atoms. The polarized protrusions with alternative spin directions indicate that the z-edge and atomic vacancy share the same mechanism of Dirac–Fermi polaron generation as the isolation and polarization of the dangling σ-bond electrons of √3d distance along the edge by the locally densely trapped core and bonding electrons, however quasi-triple bond forms between the nearest d separated σ-bond electrons along the arm-chaired edge or the reconstructed (5 or 7 atomic rings) z-edge prevents the DFPs formation41.
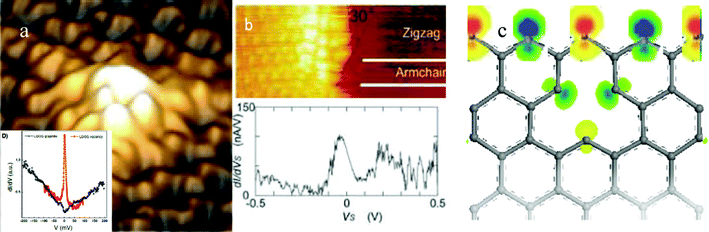 | ||
| Fig. 5 The STM/S profiles of (a) the graphite surface with and without atomic vacancies (reprinted from ref. 15 with permission) and of (c) the graphene zigzag edge (reprinted from ref. 16 with permission) in comparison with the density functional theory derived edge states of asymmetric-dumbbell shaped unpaired and polarized dangling bond electrons with spin up and down by the locally densified and entrapped bonding and core electrons.41 | ||
It has been found recently that46 the graphene coating of an electrode could insignificantly improve the function of charge transfer that was indicated to occur mostly around its edges and at any defects. This finding corroborates that the edge and defect limited charge transportation may be dominated by the Dirac–Fermi polarons at the zigzag edges arising from the polarization of the dangling bond electrons by the nearby trapped core charge.
V Conclusion
We have demonstrated the power of ZPS in gaining the local, atomistic zone selective, and quantitative information about the length and energy of the local bonds and the binding energy shift of electrons associated with under-coordinated defects and surface atoms of graphite. It has been confirmed that DFPs are generated in the following processes: (i) the shorter and stronger bonds between under-coordinated atoms cause local densification and quantum entrapment of bonding charge and binding energy that produces an entrapped component in the core band; (ii) the entrapped core charge polarizes the unpaired dangling-bond electrons to produce the DFPs; and (iii) the DFPs in turn screen and split the potential and then generate the P component in the upper edge of the core band. For s clean surface, no polarization happens although the TS state remains because of the lack of dangling bond electrons. ZPS is therefore demonstrated to be more revealing than using either of STM/S or XPS alone in obtaining bond and electronic information limited to selected atomic zones.Financial supports from MOE (RG15/09), Singapore, and NSF (No. 11172254, 11002121and 10802071) of China are gratefully acknowledged.
References
- D. W. Wang, Y. L. Chang, Q. Wang, J. Cao, D. B. Farmer, R. G. Gordon and H. J. Dai, Surface chemistry and electrical properties of germanium nanowires, J. Am. Chem. Soc., 2004, 126, 11602–11611 CrossRef CAS.
- C. G. Long, J. D. Gilbertson, G. Vijayaraghavan, K. J. Stevenson, C. J. Pursell and B. D. Chandler, Kinetic evaluation of highly active supported gold catalysts prepared from monolayer-protected clusters: an experimental Michaelis–Menten approach for determining the oxygen binding constant during CO oxidation catalysis, J. Am. Chem. Soc., 2008, 130, 10103–10115 CrossRef CAS.
- S. W. Lee, S. Chen, J. Suntivich, K. Sasaki, R. R. Adzic and Y. Shao-Horn, Role of surface steps of Pt nanoparticles on the electrochemical activity for oxygen reduction, J. Phys. Chem. Lett., 2010, 1, 1316–1320 CrossRef CAS.
- Q. S. Wei, K. Tajima, Y. J. Tong, S. Ye and K. Hashimoto, Surface-segregated monolayers: a new type of ordered monolayer for surface modification of organic semiconductors, J. Am. Chem. Soc., 2009, 131, 17597–17604 CrossRef CAS.
- N. Koch, A. Gerlach, S. Duhm, H. Glowatzki, G. Heimel, A. Vollmer, Y. Sakamoto, T. Suzuki, J. Zegenhagen, J. P. Rabe and F. Schreiber, Adsorption-induced intramolecular dipole: correlating molecular conformation and interface electronic structure, J. Am. Chem. Soc., 2008, 130, 7300–7304 CrossRef CAS.
- T. Kravchuk, L. Vattuone, L. Burkholder, W. T. Tysoe and M. Rocca, Ethylene decomposition at undercoordinated sites on Cu(410), J. Am. Chem. Soc., 2008, 130, 12552 CrossRef CAS.
- O. Seitz, A. Vilan, H. Cohen, C. Chan, J. Hwang, A. Kahn and D. Cahen, Effect of doping on electronic transport through molecular monolayer junctions, J. Am. Chem. Soc., 2007, 129, 7494 CrossRef CAS.
- J. J. Blackstock, C. L. Donley, W. F. Stickle, D. A. A. Ohlberg, J. J. Yang, D. R. Stewart and R. S. Williams, Oxide and carbide formation at titanium/organic monolayer interfaces, J. Am. Chem. Soc., 2008, 130, 4041–4047 CrossRef CAS.
- T. He, H. J. Ding, N. Peor, M. Lu, D. A. Corley, B. Chen, Y. Ofir, Y. L. Gao, S. Yitzchaik and J. M. Tour, Silicon/molecule interfacial electronic modifications, J. Am. Chem. Soc., 2008, 130, 1699–1710 CrossRef CAS.
- M. Paneru, C. Priest, R. Sedev and J. Ralston, Static and dynamic electrowetting of an ionic liquid in a solid/liquid/liquid system, J. Am. Chem. Soc., 2010, 132, 8301–8308 CrossRef CAS.
- D. A. Ricci, T. Miller and T. C. Chiang, Controlling the thermal stability of thin films by interfacial engineering, Phys. Rev. Lett, 2005, 95 Search PubMed.
- C. O. Girit, J. C. Meyer, R. Erni, M. D. Rossell, C. Kisielowski, L. Yang, C. H. Park, M. F. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Graphene at the edge: stability and dynamics, Science, 2009, 323, 1705–1708 CrossRef CAS.
- T. T. Fister, D. D. Fong, J. A. Eastman, H. Iddir, P. Zapol, P. H. Fuoss, M. Balasubramanian, R. A. Gordon, K. R. Balasubramaniam and P. A. Salvador, Total-reflection inelastic X-ray scattering from a 10-nm thick La0.6Sr0.4CoO3 thin film, Phys. Rev. Lett., 2011, 106, 037401 CrossRef CAS.
- Saad Hebboul, Synopsis: X-raying the skin, http://physics.aps.org/synopsis-for/10.1103/PhysRevLett.106.037401.
- M. M. Ugeda, I. Brihuega, F. Guinea and Gómez-J. M. Rodríguez, Missing atom as a source of carbon magnetism, Phys. Rev. Lett., 2010, 104, 096804 CrossRef CAS.
- T. Enoki, Y. Kobayashi and K. I. Fukui, Electronic structures of graphene edges and nanographene, Int. Rev. Phys. Chem., 2007, 26, 609–645 CrossRef CAS.
- G. Speranza and L. Minati, The surface and bulk core line's in crystalline and disordered polycrystalline graphite, Surf. Sci., 2006, 600, 4438–4444 CrossRef CAS.
- D. Q. Yang and E. Sacher, Carbon 1s X-ray photoemission line shape analysis of highly oriented pyrolytic graphite: the influence of structural damage on peak asymmetry, Langmuir, 2006, 22, 860–862 CrossRef CAS.
- I. Aruna, B. R. Mehta, L. K. Malhotra and S. M. Shivaprasad, Size dependence of core and valence binding energies in Pd nanoparticles: Interplay of quantum confinement and coordination reduction, J. Appl. Phys., 2008, 104, 064308–064305 CrossRef.
- M. A. Omar, Elementary Solid State Physics: Principles and Applications. 1993, New York: Addison-Wesley Search PubMed.
- C. Q. Sun, Y. Sun, Y. G. Nie, Y. Wang, J. S. Pan, G. Ouyang, L. K. Pan and Z. Sun, Coordination-resolved C–C bond length and the C 1s binding energy of carbon allotropes and the effective atomic coordination of the few-layer graphene, J. Phys. Chem. C, 2009, 113, 16464–16467 CAS.
- L. Pauling, Atomic radii and interatomic distances in metals, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- V. M. Goldschmidt, Crystal structure and chemical correlation, Ber. Dtsch. Chem. Ges., 1927, 60, 1263–1296 CrossRef.
- W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Coordination-dependent surface atomic contraction in nanocrystals revealed by coherent diffraction, Nat. Mater., 2008, 7, 308–313 CrossRef CAS.
- J. T. Miller, A. J. Kropf, Y. Zha, J. R. Regalbuto, L. Delannoy, C. Louis, E. Bus and J. A. van Bokhoven, The effect of gold particle size on Au–Au bond length and reactivity toward oxygen in supported catalysts, J. Catal., 2006, 240, 222–234 CrossRef CAS.
- C. Q. Sun, Dominance of broken bonds and nonbonding electrons at the nanoscale, Nanoscale, 2010, 2, 1930–1961 RSC.
- B. Uchoa, V. N. Kotov, N. M. R. Peres and A. H. C. Neto, Localized magnetic states in graphene, Phys. Rev. Lett., 2008, 101, 026805 CrossRef.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- G. Li and E. Y. Andrei, Observation of Landau levels of Dirac fermions in graphite, Nat. Phys., 2007, 3, 623–627 CrossRef CAS.
- K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Stormer and P. Kim, Observation of the fractional quantum Hall effect in graphene, Nature, 2009, 462, 196–199 CrossRef CAS.
- M. R. Falvo, G. J. Clary, R. M. Taylor, V. Chi, F. P. Brooks, S. Washburn and R. Superfine, Bending and buckling of carbon nanotubes under large strain, Nature, 1997, 389, 582–584 CrossRef CAS.
- B. An, S. Fukuyama, K. Yokogawa and M. Yoshimura, Surface superstructure of carbon nanotubes on highly oriented pyrolytic graphite annealed at elevated temperatures, Jpn. J. Appl. Phys., 1998, 37, 3809–3811 CrossRef CAS.
- C. Q. Sun, H. L. Bai, B. K. Tay, S. Li and E. Y. Jiang, Dimension, strength, and chemical and thermal stability of a single C–C bond in carbon nanotubes, J. Phys. Chem. B, 2003, 107, 7544–7546 CrossRef CAS.
- K. J. Kim, H. Lee, J. H. Choi, Y. S. Youn, J. Choi, T. H. Kang, M. C. Jung, H. J. Shin, H. J. Lee, S. Kim and B. Kim, Scanning photoemission microscopy of graphene sheets on SiO2, Adv. Mater., 2008, 20, 3589–3591 CrossRef CAS.
- T. Balasubramanian, J. N. Andersen and L. Wallden, Surface-bulk core-level splitting in graphite, Phys. Rev. B: Condens. Matter, 2001, 64, 205420 CrossRef.
- T. Matsui, H. Kambara, Y. Niimi, K. Tagami, M. Tsukada and H. Fukuyama, Phys. Rev. Lett., 2005, 94, 226403 CrossRef CAS.
- T. Kondo, Y. Honma, J. Oh, T. Machida and J. Nakamura, Edge states propagating from a defect of graphite: Scanning tunneling spectroscopy measurements, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 153414 CrossRef.
- Y. Niimi, H. Kambara and H. Fukuyama, Localized distributions of quasi-two-dimensional electronic states near defects artificially created at graphite surfaces in magnetic fields, Phys. Rev. Lett., 2009, 102, 026803–026804 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Two-dimensional gas of massless Dirac fermions in graphene, Nature, 2005, 438, 197–200 CrossRef CAS.
- S. Y. Zhou, G. H. Gweon, J. Graf, A. V. Fedorov, C. D. Spataru, R. D. Diehl, Y. Kopelevich, D. H. Lee, S. G. Louie and A. Lanzara, First direct observation of Dirac fermions in graphite, Nat. Phys., 2006, 2, 595–599 CrossRef CAS.
- X. Zhang, Y. G. Nie, W. T. Zheng, J. L. Kuo and C. Q. Sun, Discriminative generation and hydrogen modulation of the Dirac–Fermi polarons at graphene edges and atomic vacancies, Carbon, 2011, 49, 3615–3621 CrossRef CAS.
- K. Ostrikov, Colloquium: Reactive plasmas as a versatile nanofabrication tool, Rev. Mod. Phys., 2005, 77, 489–511 CrossRef CAS.
- S. R. Haines, K. H. Williams, N. Almond, M. Schwitters, D. S. Martin, J. E. Butler and P. Weightman, The initial stages of graphite formation on the diamond (100) 2 × 1 surface, J. Electron Spectrosc. Relat. Phenom., 2006, 152, 33–36 CrossRef CAS.
- R. A. P. Smith, C. W. Armstrong, G. C. Smith and P. Weightman, Observation of a surface chemical shift in carbon 1s core-level photoemission from highly oriented pyrolytic graphite, Phys. Rev. B: Condens. Matter, 2002, 66, 245409 CrossRef.
- D. Q. Yang and E. Sacher, s–p hybridization in highly oriented pyrolytic graphite and its change on surface modification, as studied by X-ray photoelectron and Raman spectroscopies, Surf. Sci., 2002, 504, 125–137 CrossRef CAS.
- D. A. C. Brownson, L. J. Munro, D. K. Kampouris and C. E. Banks, Electrochemistry of graphene: not such a beneficial electrode material?, RSC Adv., 2011, 1, 978–988 RSC.
- C. Q. Sun, Size dependence of nanostructures: impact of bond order deficiency, Prog. Solid State Chem., 2007, 35, 1–159 CrossRef CAS.
- W. T. Zheng and C. Q. Sun, Underneath the fascinations of carbon nanotubes and graphene nanoribbons, Energy Environ. Sci., 2011, 4, 627–655 CAS.
- H. Hibino, H. Kageshima, M. Kotsugi, F. Maeda, F. Z. Guo and Y. Watanabe, Dependence of electronic properties of epitaxial few-layer graphene on the number of layers investigated by photoelectron emission microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125431 CrossRef.
| This journal is © The Royal Society of Chemistry 2012 |
