Differences in electron densities of phenoxazine and phenothiazine derivatives—charge density studies†
Maura
Malińska
a,
Jacek
Nowacki
a,
Andrzej
Kapturkiewicz
b and
Krzysztof
Woźniak
*a
aDepartment of Chemistry, University of Warsaw, Pasteura, 1, 02-093, Warszawa, Poland
bInstitute of Physical Chemistry, Polish Academy of Science, Kasprzaka, 44/52, 01-224, Warszawa, Poland
First published on 28th March 2012
Abstract
High resolution X-ray studies for three single crystals of derivatives of phenoxazine and phenothiazine, 1-(4-phenothiazin-10-yl-phenyl)-ethanone (PAS), 1-(4-phenoxazin-10-yl-phenyl)-ethanone (PAO), and (4-phenoxazin-10-yl-phenyl)phenyl-methanone (PBO), have been carried out and the experimental charge densities for these crystals have been established. A significant intramolecular charge redistribution is observed for the studied moieties. It appears that the donor parts of the molecules studied in all three cases are negatively charged (−0.715, −0.313 and −0.218) and the acceptor fragments carry significant positive charges (0.696, 0.316 and 0.224) for PBO, PAS and PAO, respectively. Separation of the charge between the donor and the acceptor parts in the solid state is in the opposite direction in comparison to the molecules’ behaviour in the solution. Analysis of the geometry of these compounds allowed the explanation of the differences in the values of the electronic coupling element V0. The three most important factors influencing the coupling element are the following: hybridization of the nitrogen atom, conformation of the heterocyclic ring and the torsion angle between the acceptor and the donor parts of the molecules. Theoretical calculations support the charge properties obtained from experiment. The calculated highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) indicate that the charge transfer in the excited state takes place from the donor to the acceptor molecular fragments.
Introduction
Phenoxazine and phenothiazine derivatives are of interest as potential physiologically active compounds and they also have interesting physicochemical properties. Drugs of the phenothiazine type include the antipsychotic agents, chlorpromazine and thioridazine, the long-acting antihistamine promethazine, and ethopropazine, used in treatment of parkinsonism and a variety of different applications (e.g., antidepressants, antispasmodics, analgesics, and antiarrhythmics).1,2 Phenothiazine has been used as an antiworming agent for livestock and as an insecticide.3 A large group of dyes have the phenothiazine structure, methylene green, thionine and methylene blue, a substance widely used as a biological stain and an oxidation–reduction indicator.3 Phenothiazinium dyes exhibit intense absorption maxima in the 600–660 nm region of the spectrum and have other advantages, therefore they can be used in photodynamic therapy (PDT).4The phenoxazine system is the chromophoric (colour-imparting) part of the molecular structures of the naturally occurring actinomycin antibiotics.5 Phenoxazine derivatives have been studied as antitumor agents6 and in PDT.7 Many polycyclic compounds containing a phenoxazine ring are used as biological stains, fabric dyes, and light-emitting materials in dye lasers (e.g., cresyl violet and nile blue).8 Organic dyes with a core phenoxazine chromophore have been used as sensitizers in dye-sensitized solar cells (DSCs).9 A great variety of phenothiazine and phenothiazine applications is possible due to their photophysical properties.
The concept of excited-state intramolecular electron transfer in acceptor–donor (A–D) molecular fragments linked by a formal single bond plays a central role in the discussion of their photophysical properties.10,11 Investigations of large aromatic donor–acceptor compounds12,13 show a possibility to predict the photophysical behaviour of a particular A–D system from the properties of its donor and acceptor subunits alone.
One of the most important factors describing the properties of a given donor–acceptor pair is connected with the manner in which the A and D subunits are bonded together and, correspondingly, with the interactions between the donor and acceptor subunits. The respective electron transfer coupling elements describing the electronic interaction between the charge transfer (CT) state and the ground state and/or the locally excited states are mainly determined by the interaction between the atoms forming the A–D bond.10–12
A simple kinetic model of an irreversible excited charge transfer state formation (100% efficiency) allows for the determination of the radiation-less and radiative rate constants and then the values of the electronic transition dipole moment, M, from the CT fluorescence. The electronic transition dipole model can be applied for the estimation of the contributions:
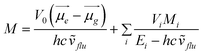 | (1) |
The values of the electronic coupling element V0 are found to correlate with the position of the accepting subunit with respect to the A–D bond. According to the formalism proposed by Dogonadze et al.,14 this coupling element can be estimated according to the formula:
| V0 = CALUMOCDHOMOβADcos(θAD) + const |
The photophysical chemistry of phenothiazine and phenoxazine derivatives (Fig. 1) 1-(4-phenothiazin-10-yl-phenyl)-ethanone (PAS), 1-(4-phenoxazin-10-yl-phenyl)-ethanone (PAO), and (4-phenoxazin-10-yl-phenyl)phenyl-methanone (PBO) has already been studied.15,16 A charge transfer band has only been observed for phenoxazine derivatives in the UV-Vis spectroscopic experiment in the solution. The molecules were divided into two fragments; donor and acceptor. The donor in the phenothiazine, or phenoxazine, derivatives is the triple ring and the acceptor is the acetylphenyl (PAO and PAS) or the benzoylphenyl (PBO) fragment.
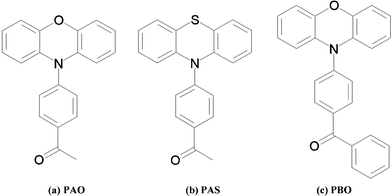 | ||
| Fig. 1 Phenothiazine and phenoxazine derivatives: (a) 1-(4-phenoxazin-10-yl-phenyl)-ethanone (PAO), (b) 1-(4-phenothiazin-10-yl-phenyl)-ethanone (PAS), (c) (4-phenoxazin-10-yl-phenyl)phenyl-methanone (PBO). | ||
It appeared that the coupling elements V0, obtained from the experimental spectroscopic data, were in good agreement with those calculated from a simple LCAO molecular orbital (MO) model, which assumes that V0 is mainly determined by interactions between the atoms forming the A–D bond. The values of V0 obtained for the phenoxazine derivatives in the butyl ether and butyl acetate solutions are as follows: 0.14 and 0.12 eV (PAO), 0.15 and 0.11 eV (PBO), correspondingly. The respective values for the phenothiazines were 0.07 and 0.06 eV (PAS).15
The aim of this work is to investigate the differences in the geometry of the phenoxazine and phenothiazine derivatives (see Fig. 1) and to find out the relationship between the conformation and the electronic coupling element. Moreover, we are interested in details of the charge density distributions in all the examined molecules and the degree of intramolecular charge redistribution.
Experimental
Synthesis
The synthesis of PAS, PAO and PBO was previously reported.15Data collection
Single-crystal high resolution X-ray measurements of the scattered intensities of the reflections for PAS, PAO and PBO were performed using the Bruker AXS KAPPA-APEX II diffractometer at a 0.5 Å resolution at 100 K. Indexing and integration were performed with the original Bruker Apex software.17 The multi-scan absorption correction was applied in the scaling procedure using the SORTAV Program.18 Conventional spherical atom refinement was carried out using SHELX9719 with the full-matrix least-squares on the F2 method for all data sets. The least-squares refinement applied for PAO, PAS and PBO was based on F2, with the resolution limited to 0.5 Å for PAO and PAS and 0.55 Å for PBO, to gain data completeness of around 100%, 96% and 100%, respectively. All equivalent reflections for PAS, PAO and PBO were averaged out (Friedel pairs and symmetry equivalents). The lattice parameters and the final R-indices obtained from the spherical refinement (IAM) are presented in Table 1.| Compound | PAS | PAO | PBO |
|---|---|---|---|
| Formula | C20H15NOS | C20 H15NO2 | C25H17NO2 |
| Formula weight | 317.39 | 301.33 | 363.40 |
| Temperature / K | 100 | 100 | 100 |
| Wavelength / Å | 0.71073 | 0.71073 | 0.71073 |
| Crystal system | Monoclinic | Triclinic | Monoclinic |
| Space group | P21/n | P-1 | P21/c |
| Unit cell dimensions | |||
| a / Å | 8.8508(1) | 7.6407(3) | 8.3769(3) |
| b / Å | 7.6650(1) | 9.6786(4) | 29.7404(11) |
| c / Å | 22.6191(3) | 10.6854(4) | 7.7536(3) |
| α / ° | 90 | 65.630(2) | 90.00 |
| β / ° | 91.7340(10) | 89.433(2) | 117.130(2) |
| γ / ° | 90 | 89.894(2) | 90.00 |
| Volume / Å3 | 1533.81(3) | 719.75(5) | 1719.14(11) |
| Z | 4 | 2 | 4 |
| Calculated density / g cm3 | 1.374 | 1.39 | 1.404 |
| μ / cm−1 | 2.15 | 0.9 | 0.9 |
| F(000) | 664 | 316 | 760 |
| Theta range for data collection | 1.8–45.29 | 2.09–45.22 | 1.37–39.88 |
| Index ranges | h: −17, 17; k: −14, 15; l: −45, 45 | h: −14, 14; k: −17, 19; l: −21, 21 | h: −15, 14; k: −53, 52; l: −13,13 |
| Reflections collected/unique | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293/17 293/17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162 162 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754/11 754/11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672/10 672/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
| Completeness to theta (max) | 100% | 96% | 100.00% |
| Rint | 0.033 | 0.016 | 0.073 |
| Absorption correction | Multi-scan | Multi-scan | Multi-scan |
| IAM refinement | |||
| Refinement method | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 |
| Data/restraints/parameters | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602/0/268 602/0/268 |
8836/0/209 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528/0/304 528/0/304 |
| Goodness-of-fit on F2 | 1.031 | 1.072 | 1.045 |
| Final R indices [I > 2σ(I)] | R 1 = 0.0470 | R 1 = 0.0428 | R 1 = 0.0448 |
| wR 2 = 0.1165 | wR 2 = 0.1322 | wR 2 = 0.1172 | |
| R indices (all data) | R 1 = 0.0526 | R 1 = 0.0534 | R 1 = 0.0608 |
| wR 2 = 0.1207 | wR 2 = 0.1425 | wR 2 = 0.1236 | |
| Largest diff. peak and hole | 0.709; −0.241 | 0.713; −0.188 | 0.71; −0.24 |
| Multipole refinement | |||
| No. of reflections [I> 3σ(I)]/parameters | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003/852 = 12 003/852 = 12 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516/714 = 15 516/714 = 15 |
7744/773 = 10 |
| R1/wR1 (for I >3σ(I)) | 0.039/0.043 | 0.021/0.030 | 0.026/0.029 |
| R2/wR2 (for I >3σ(I)) | 0.027/0.030 | 0.032/0.046 | 0.037/0.054 |
| GooF (for I >3σ(I)) | 1.345 | 1.149 | 1.101 |
| Largest residual density peak and hole | −0.145; 0.264 | −0.126; 0.197 | −0.169; 0.219 |
Fourier transform infrared spectroscopy (FTIR)
IR spectra were measured on a Perkin Elmer Spectrum 100 Series instrument and the attenuated total reflectance (ATR) method for PAO, PAS and PBO powder was applied.Multipole refinement
Multipole refinement of PAS, PAO and PBO has been accomplished using the XD program suite20 based on the Hansen & Coppens formalism.21 In this formalism the total atomic electron density is a sum of the three components;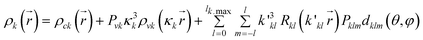 | (2) |
Atomic positions and mean-square displacement parameters of the non-H atoms were refined using high order X-ray diffraction data (sinθ/λ > 0.6). Atomic coordinates x, y, z and anisotropic displacement parameters (ADPs) were fixed after the high order refinement. The C–H bond distances were fixed at the averaged distances for similar groups taken from single crystal neutron diffraction data. The hydrogen thermal displacement parameters were estimated by the SHADE222 program and fixed for all compounds. In these multipole refinements, multipoles up to the hexadecapole level were refined for the non-H atoms. For the H atoms, only monopoles and dipoles were used. All parameters κ and κ' were refined for the non-H atoms for all compounds; for the sp2 carbon atoms the κ and κ' parameters were restricted to be the same. For hydrogen atoms the κ and κ' parameters were fixed at the recommended values.23 The advantage of the approach with mixed high order refinement and rigid body refinement was previously discussed by Hoser et al.24 In the last refinement only the positions of the non-H atoms were refined. Each refinement cycle was considered fully converged at the point at which the maximum shift/standard uncertainty (s.u.) ratio was less than 10−5. Hirshfeld's rigid-bond test25 was applied after each step. The DMSDA (difference of the mean-square displacement amplitude) values are less than 0.0010 Å2, except for the C(1)–O(1) bond in PBO where this value is 0.0011 Å2.
Atoms-in-Molecules (AIM) integrated atomic charges
All calculations were performed using the TOPXD program, a part of the XD package.20 All grid parameters are presented in the ESI† (Table 2S, 8S and 14S for PAO, PAS and PBO, respectively). The error in the atomic Lagrangian measures the accuracy of the numerical integration and was less than 10−3–10−4 au for all the studied compounds.Computations
All ab initio calculations were performed using the Gaussian03 program.26 Two different quantum methods were used to calculate the electronic properties of the PAO, PAS and PBO molecules for comparison with the experimental charge density data. The density functional theory (DFT) method with the B3LYP27,28 6-311G**29,30 basis set applied for all atoms was used with full geometry optimization of these molecules. Also energy scans over the torsion angle [C(6)–C(5)–N(8)–C(20)] were performed for PAO, PAS and PBO. 18 steps (each step equal to 10°) from 81°, −168°, −88° were used for PAO, PAS and PBO, respectively. After each change in the torsion angle, full optimization of the geometry was executed. Then single point calculations with the Becke's density functional method with the Perdew's gradient-corrected functional31 (BP86) and the aug-cc-pVDZ32 basis set were performed to get the charge density. Next, approximate charge density analysis was performed using DGRID-4.5.33Results and discussion
X-Ray structures of PAS, PAO and PBO
ORTEP illustrations of all the structures studied, with atomic labels, are presented in Fig. 2.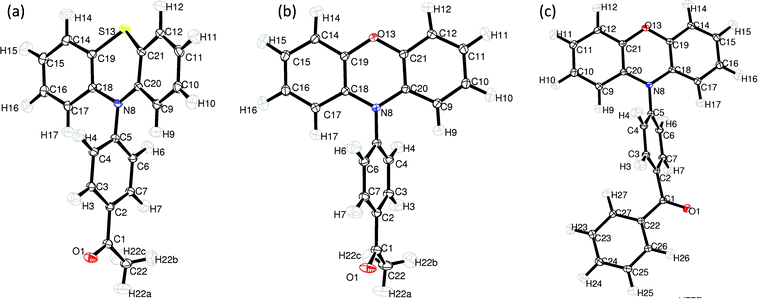 | ||
| Fig. 2 The molecular structure of PAS (a), PAO (b) and PBO (c) and atomic labelling. Thermal displacement ellipsoids are drawn at the 50% probability level (ORTEP-3).34 | ||
The first difference between these molecules is the conformation of the heterocyclic ring—which is almost flat in the phenoxazine derivatives and in the boat conformation for the phenothiazine derivative. In the PAS molecule only atoms C(18), C(19), C(20) and C(21) are in-plane, whereas the S(1) and N(8) atoms are bent from the plane in the same direction. For the phenoxazine derivatives the C(19), O(13), C(21) angles and C(18), N(8), C(20) angles are close to 120°, 117.07(4)° and 118.43(4)° for PBO, and 117.79(4)° and 118.87(3)° for PAO. The respective angles for PAS are 122.20(2)° and 99.88(1)°. The ring puckering analysis was made by Platon software35 for the 6-membered ring S(13), C(19), C(18), N(8), C(20), C(21) and the obtained values were Theta = 76.27°, Phi = 359.3°, which are close to the ideal boat conformation—Theta = 90.0°; Phi = k·60° (k = natural number).
For investigations of the planarity of the donor part, two mean planes were determined: the first one going through the S(13)/O(13), N(8), C(9), C(10), C(11), C(12), C(20), C(21) atoms and the second one through the S(13)/O(13), N(8), C(14), C(15), C(16), C(17), C(18), C(19) atoms. The angle between these planes is 7.135(8)°, 24.635(8)° and 12.582(9)° for PAO, PAS and PBO, respectively. The dihedral angle ΘAD: C(18), N(8), C(5) and C(4) in the PAS molecule is −77.51(2)° and −69.02(3)° for PAO, for PBO the analogous value of the dihedral angle is −58.41(4)°. For a more clear analysis of the angle between the acceptor and donor part, two mean planes were determined, the donor plane and the acceptor plane. The first one going through all non-hydrogen atoms of the donor part (14 atoms: N(8), C(9), C(10), C(11), C(12), O(13)/S(13),…, C(21)) and the acceptor plane going through C(1), C(2), C(3), C(4), C(5), C(6), C(7), N(8). The interplane angle is 68.28(1)°, 63.49(1)° and 89.12(1)° for PAO, PBO and PAS, respectively.
These geometrical arguments suggest that charge transfer is possible in the PAO and PBO molecules. The conformation of the donor part in the phenothiazine derivative disables the electron transfer between the two parts of the PAS molecule.
The C(1)–O(1) bond length in the carbonyl group is similar for the phenoxazine derivatives, 1.2216(5) Å for PAO and 1.2249(6) Å for PBO. The situation for the N(8)–C(5) bond is quite similar. The distance between N(8) and C(5) is 1.4242(5) Å and 1.4235(4) Å for PBO and PAO, respectively.
The PAS, PAO and PBO molecules crystallize in the P21/n, P-1, P21/c space groups, respectively, with one molecule at a general position in the unit cell. The packing modes of the PAO and PBO molecules are similar (see ESI† Fig. 1S and 2S). π⋯π stacking is possible because the phenoxazine part is flat. The distance between the two closest carbon atoms in the PAO molecules is 3.585 Å [C(14)⋯C(20)_1 + x, y, z]. In the PBO molecules, the distances between the opposite rings are longer and close to 4 Å. Moreover, PAS and PAO have similar packing motifs (see ESI† Fig. 2S).
For all structures, a network of weak C–H⋯π interactions is present, but there is a difference between the phenothiazine derivative and the phenoxazine derivatives in the arrangement of the connected groups. The C–H⋯π contacts in PAS link the perpendicular donor parts (see ESI† Fig. 2S). For example, the distance between C(14) and C(10) is 3.6353(6) Å in the PAS structure. In the phenoxazine derivatives two types of these interactions between the donor and acceptor molecular fragments are present.
Weak C–H⋯O interactions are present for all the molecules. Both PAO and PAS are similar in this aspect. The C–H⋯O contacts are between the oxygen atom in the carbonyl group and the hydrogen atom in the acceptor unit. The distance from O(1) to the carbon atom in the next neighbouring molecule is 3.4055(4) Å in the PAO structure, and 3.3904(5) in the PAS structure. In PBO, the packing around the carbonyl group is different because of the size of the acceptor unit. The C–H⋯O interaction connects the oxygen atom from the carbonyl group and the hydrogen atom in the donor part from the next nearest molecule. The distance from O(1) to C(16) is 3.6101(8) Å. The interaction lines and critical points for these interactions can be found, but the values of the charge density at the critical points are very small (less than 0.15 eÅ−3).
Topological analysis
The values of electron density ρ(r) and the Laplacian of electron density ∇2ρ(r) at the bond critical points were found for all compounds (Fig. 3). The carbonyl bond C(1)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1) is strongest in the PAO molecule. The value of the electron density at the critical point for this bond is 2.97(2) eÅ−3 and the Laplacian is −27.16(9) eÅ−5. The carbonyl bond in the PAS and PBO derivatives is weaker, with the values of the density at the critical points being 2.93(2) eÅ−3 and 2.60(3) eÅ−3, and the Laplacian at the bond critical points being −22.5(1) eÅ−5 and −4.3(2) eÅ−5, respectively.
O(1) is strongest in the PAO molecule. The value of the electron density at the critical point for this bond is 2.97(2) eÅ−3 and the Laplacian is −27.16(9) eÅ−5. The carbonyl bond in the PAS and PBO derivatives is weaker, with the values of the density at the critical points being 2.93(2) eÅ−3 and 2.60(3) eÅ−3, and the Laplacian at the bond critical points being −22.5(1) eÅ−5 and −4.3(2) eÅ−5, respectively.
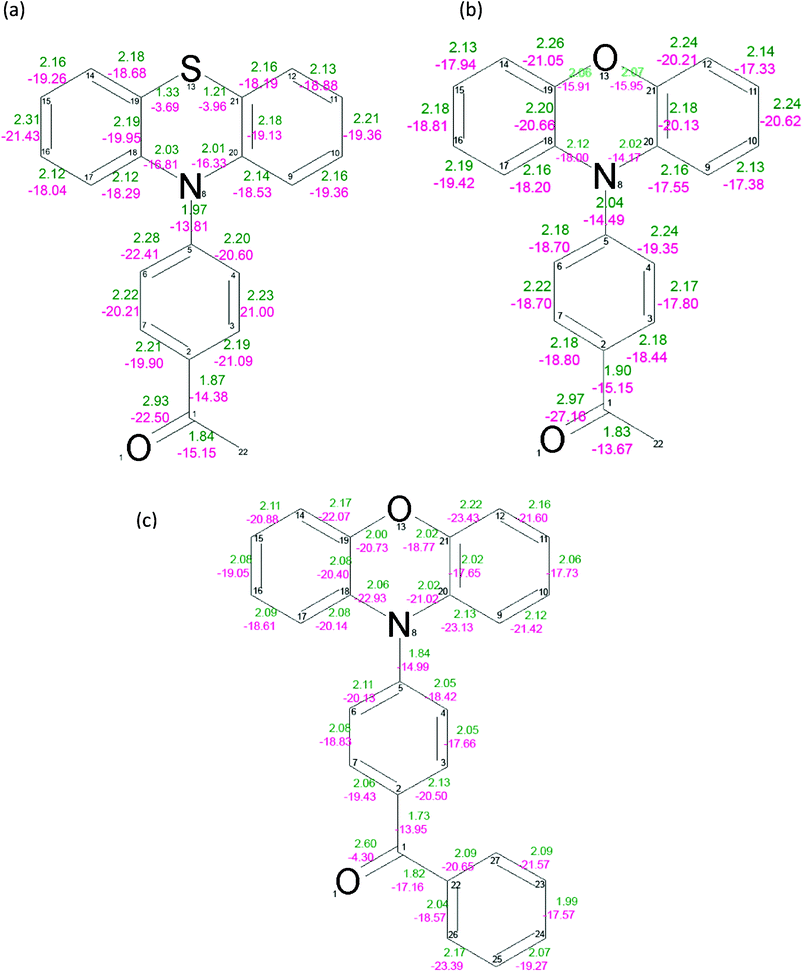 | ||
| Fig. 3 Values of the electron density at the bond critical points (green) and the Laplacian of the electron density at the bond critical points for PAS (a), PAO (b) and PBO (c). The mean error for the BCP electron density is equal to 0.02 eÅ−3, 0.02 eÅ−3, 0.04 eÅ−3 for PAS, PAO and PBO, respectively. The mean error for the BCP Laplacian values is equal to 0.06 eÅ−5, 0.07 eÅ−5 and 0.13 eÅ−5 for PAS, PAO and PBO, respectively. | ||
The values of ρ(r) and ∇2ρ(r) at the N(8)–C(5) BCP are 1.97(1) eÅ−3, 2.04(1) eÅ−3 and 1.84(2) eÅ−3, −13.81(4) eÅ−5, −14.49(5) eÅ−5 and −14.99(13) eÅ−5 for PAS, PAO and PBO, respectively. The ρ(r) and ∇2ρ(r) values suggest that the C(5)–N(8) bond is the strongest in the acetyl derivative of phenothiazine, and similar to the same bond in the acetyl derivative of phenoxazine. It is weaker in PBO. However, the bond connecting the donor and acceptor units is longest for the PAS molecule.
Integration over atomic basins was carried out by using the TOPXD20 software. Atomic Lagrangian values for each atom were about 10−3 or less (see ESI† Table 2S, 8S and 14S for PAO, PAS and PBO, respectively). This supports the proper integration of atomic basins. The AIM charges for all atoms are presented in Fig. 4.
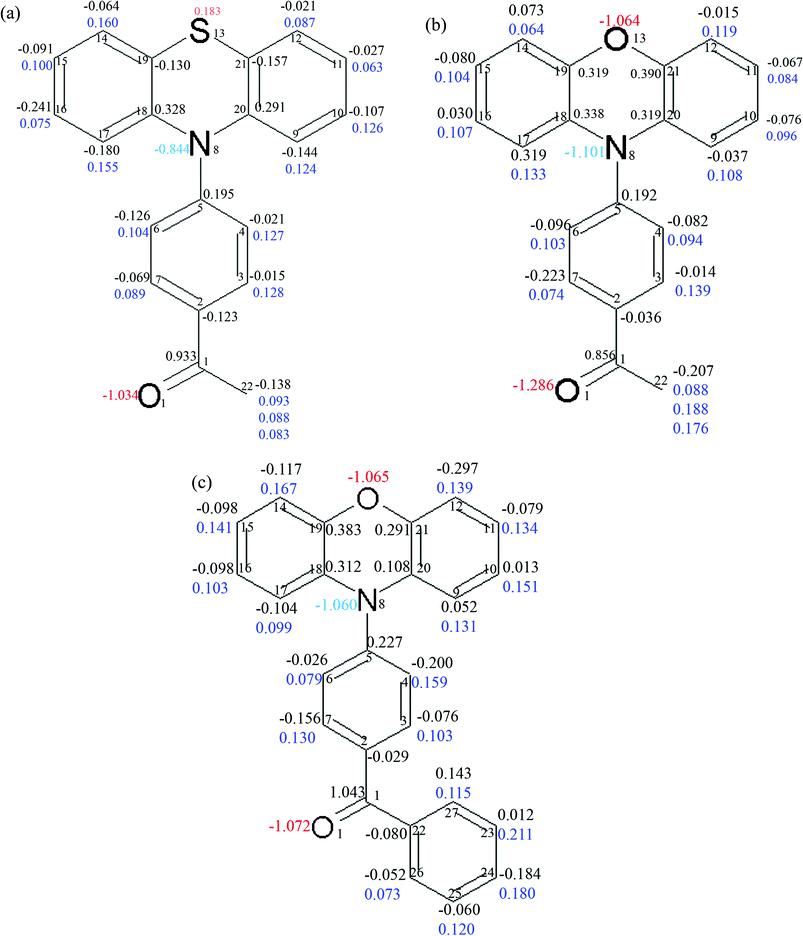 | ||
| Fig. 4 The integrated charges for the atoms in the molecules of PAS (a), PAO (b) and PBO (c). The charges for the carbon atoms are written in black, hydrogen atoms in blue, nitrogen atoms, cyan and oxygen atoms in red. | ||
The charges for atoms heavier than carbon are quite reasonable. For the oxygen atoms in the carbonyl groups the charges are close to −1. The largest integrated charge for the oxygen atom in the carbonyl bond (−1.29) is found in PAO. In PBO and PAS they are slightly smaller (−1.07 and −1.03, respectively). The oxygen atom charge in the heterocyclic ring in the phenoxazine derivatives is similar, −1.06 for PAO and −1.07 for PBO. The sulphur atom in PAS has a positive charge (0.18). The sulphur atom’s positive charge was obtained for all models used in the different multipole refinement strategies for this data set.
The integrated atomic charges for the atoms in the bond connecting the donor and acceptor units are as follows: for the nitrogen atom −1.06, −0.84 and −1.10, and for the C(5) atom 0.23, 0.20 and 0.19 for PBO, PAS and PAO, respectively. The high charge value of the N(8) atom in the PAO and PBO molecules is associated with a large concentration of electron density there. This suggests that the difference in the electron density in this region of molecules is significant.
The donor part of the phenothiazine or phenoxazine derivatives consists of the three fused rings, whereas the acceptor fragment is the acetylphenyl or benzoylphenyl substituent. The charges were summed up for these parts. The sums of the atomic charges for the whole molecules were close to zero. Only the sum of charges for the PBO molecule is quite unsatisfactory (equal to 0.019). The results obtained are summarized in Table 2. In the PBO molecule, there is the largest separation of charge and it is two times bigger than for the PAS and PAO molecules. For the acetyl derivatives the separation is quite similar, and the charges are as follows: for the donor part −0.32 and −0.22, whereas for the acceptor part 0.31 and 0.23, for PAS and PAO, respectively.
| PBO | PAS | PAO | ||
|---|---|---|---|---|
|
Donor | −0.715 | −0.313 | −0.218 |
| Acceptor | 0.696 | 0.316 | 0.225 | |
| ∑ | 0.019 | 0.003 | 0.007 |
Energy scans over the torsion angle [C(6)–C(5)–N(8)–C(20)] were performed using 18 steps of 10° from 81°, −168° and −88° for PAO, PAS and PBO, respectively. After each change of the torsion angle full optimization of the geometry was executed. All torsion angles for which the geometry optimization was applied are listed in the ESI† (Table 19S). The shapes of the energy scan dependences for PAO and PBO are very similar (Fig. 5).
![The variation of the energy Ei over an 18 step change (step = 10 degrees) in the torsion angle C(6)–C(5)–N(8)–C(20) for PAS, PAO and PBO. The starting [C(6)–C(5)–N(8)–C(20)] torsion angle values are: 81°, −168° and −88° for PAO (black solid line), PAS (red dashed line) and PBO (green dotted line), respectively. The corresponding torsion angles with the step numbers are in the ESI (Table 19S).](/image/article/2012/RA/c2ra01148d/c2ra01148d-f5.gif) | ||
| Fig. 5 The variation of the energy Ei over an 18 step change (step = 10 degrees) in the torsion angle C(6)–C(5)–N(8)–C(20) for PAS, PAO and PBO. The starting [C(6)–C(5)–N(8)–C(20)] torsion angle values are: 81°, −168° and −88° for PAO (black solid line), PAS (red dashed line) and PBO (green dotted line), respectively. The corresponding torsion angles with the step numbers are in the ESI† (Table 19S). | ||
The optimal torsion angle values are close to the angles obtained from the X-ray analysis (PAO3 and PBO3). An increase in the torsion angle results in a decrease in the aromaticity of the donor part. This part of the molecule is not flat, which reduces the distances between the hydrogen atoms, and, in consequence, contributes to the increase in energy (see Fig. 6.). The first maximum for PAO and PBO (PAO8 and PBO8) is obtained for the non-planar donor part, and the acceptor and donor fragments are very close in space to each other. With an increasing torsion angle, the steric effect for the hydrogen atoms is too strong and the butterfly structure is broken, the nitrogen atom approaches sp3 hybridization and the energy decreases (the second minimum on the diagram—PAO9 and PBO9). Next, the acceptor unit is rotated and the distance between the hydrogen atoms decreases again, which leads to the second maximum (PAO12 and PBO12). The next value of the torsion angle allows the flattening of the geometry of the donor.
![Visualization of the maxima and minima on energy scans over the torsion angle [C(6)–C(5)–N(8)–C(20)] of the PAO, PBO and PAS molecules after geometry optimization in the Gaussian03 program.](/image/article/2012/RA/c2ra01148d/c2ra01148d-f6.gif) | ||
| Fig. 6 Visualization of the maxima and minima on energy scans over the torsion angle [C(6)–C(5)–N(8)–C(20)] of the PAO, PBO and PAS molecules after geometry optimization in the Gaussian03 program. | ||
The diagram for PAS is different. The donor part is not aromatic and the energy cost for the decrease in the angle between the aromatic rings in the donor part is smaller. Again, the distance between the hydrogen atoms is the most significant factor taken into account. The first maximum is obtained for the geometry with the torsion angle −118 deg. (PAS5). Next, the butterfly geometry is broken and the energy decreases. However this change is not destructive because the donor part is more flexible (PAS8). Then, the distance between the hydrogen atoms decreases and the energy rises again (the second maximum—PAS13) to go back to the same minimum as for the PAO and PBO scans.
The single point calculations to obtain the charge density and then its analysis were accomplished for chosen geometries from the energy scans. We selected the following single points for the calculations: the starting ones for PAO0, PBO0 and PAS0, PAO2, PAO4, PBO2, PBO4, the first maxima (PAO8, PBO8 and PAS5), the second minima (PAO9, PBO9 and PAS8) and the second maxima (PAO12, PBO12 and PAS13).
The total sum of the atomic integrated charges and the charges of the donor and acceptor units are summarized in Table 3. In all examined cases, the charge of the acceptor is positive and the charge of the donor is negative. This is exactly as it was in the experimental topological analyses. In the starting geometries, the PAO0 molecule has the largest separation in the charge in comparison to PBO0—the donor has the charge −0.543 and the acceptor part 0.532. However, when the torsion angle changes and the donor and acceptor planes are closer to each other, the charge in the subunits changes. In the case of PAO, a charge transfer takes place from the acceptor to the donor, and for PAO4 the acceptor takes the value −0.419 and the donor 0.434. For PBO0, the angle between the donor and the acceptor plane is close to 90°, and thus charge transfer by the mesomeric effect is forbidden. Then, separation of the charge is possible because the planes of the molecular donor and acceptor fragments are closer to each other. This results in the following charges for the acceptor and donor units: 0.488 and −0.506, respectively (for the PBO4 geometry). In the next cases PAO8, PAO9 and PAO12, charge transfer by the mesomeric effect is forbidden, because the donor part is not aromatic and the hybridization of the nitrogen atom N(8) is close to sp3. From this analysis it is possible to show that the inductive effect in PAO seems to be independent of the geometry. It is very strong and present because of the differences in the electronegativity of the atoms forming the bond between the donor and acceptor parts [N(8)–C(5)]. The mesomeric effect is possible only in PAO0–PAO4 and it causes a bigger separation in the charge. The donor is more negative and the acceptor more positive in the case of PAO0 compared to PAO12. Analysis of the values of ρ(r) and ∇2ρ(r) at the BCP of the N(8)–C(5) bond shows that the change in torsion angle between the donor and acceptor fragments in the first four steps of the relative rotation do not influence these values strongly. However, in the case of PAO8 and PBO8, the ρ(r) and ∇2ρ(r) values are smaller and this indicates a weaker conjugated double bond system. The highest value of ρ(r) and smallest value of the Laplacian is for PAO9 and PBO9—for the “broken butterfly” conformation. In those cases the mesomeric effect is forbidden and the lack of the steric effect between the hydrogen atoms permits the shortening of the distance between the nitrogen atom N(8) and the carbon atom C(5), which leads to the increase of ρ(r) and ∇2ρ(r) at the BCP of this bond.
| PAO0 | PAO2 | PAO4 | PAO8 | PAO9 | PAO12 | |
| Donor | −0.543 | −0.651 | −0.419 | −0.489 | −0.453 | −0.475 |
| Acceptor | 0.532 | 0.505 | 0.434 | 0.319 | 0.260 | 0.487 |
| SUM | −0.011 | −0.146 | 0.015 | −0.169 | −0.193 | 0.012 |
| ρ(BCP [N(8)–C(5)]). | 1.861 | 1.859 | 1.863 | 1.859 | 1.894 | 1.866 |
| ∇2ρ(r) BCP [N(8)–C(5)]. | −17.82 | −17.76 | −17.84 | −17.58 | −18.24 | −17.64 |
| PBO0 | PBO2 | PBO4 | PBO8 | PBO9 | PBO12 | |
| Donor | −0.240 | −0.553 | −0.506 | −0.098 | −0.212 | −0.274 |
| Acceptor | 0.181 | 0.382 | 0.488 | 0.469 | 0.498 | 0.249 |
| SUM | −0.060 | −0.171 | −0.018 | 0.371 | 0.285 | −0.025 |
| ρ(BCP [N(8)–C(5)]). | 1.859 | 1.858 | 1.860 | 1.858 | 1.892 | 1.861 |
| ∇2ρ(r) BCP [N(8)–C(5)]. | −17.79 | −17.76 | −17.77 | −17.55 | −18.19 | −17.50 |
| PAS0 | PAS5 | PAS8 | PAS13 | |||
| Donor | −0.227 | −0.282 | −0.252 | 0.144 | ||
| Acceptor | 0.298 | 0.472 | 0.563 | 0.470 | ||
| SUM | 0.071 | 0.190 | 0.311 | 0.614 | ||
| ρ(BCP [N(8)–C(5)]). | 1.850 | 1.854 | 1.907 | 1.897 | ||
| ∇2ρ(r) BCP [N(8)–C(5)]. | −17.47 | −17.48 | −18.61 | −18.24 | ||
Analysis of the ATR IR spectra showed slight differences between the PAO and PAS molecules (IR spectra for PAO, PAS and PBO are in the ESI† in Fig. 18S). The stretching vibrations (Table 4) for the carbonyl bond occur at 1680 cm−1 and 1682 cm−1 for PAO and PAS, respectively. These bands for the PBO molecules are shifted to a lower energy, which is caused by the neighbouring phenyl ring. Similarities between the PAO and PAS molecules occur in the entire infrared region. The most significant shift is for the stretching vibrations for the bond connecting the donor and acceptor units (C–N). The wavenumbers for this band are 1290 cm−1, 1287 cm−1 and 1275 cm−1 for PAO, PAS and PBO, respectively. This shift indicates a separation of the charge between the carbon and nitrogen atoms in the C–N bond.
| Compound/Frequency | PAS | PAO | PBO |
|---|---|---|---|
ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) O) O)
|
1682 | 1680 | 1659 |
ν(CAr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) CAr) CAr)
|
1588 | 1595 | 1593 |
ν(CAr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) CAr) CAr)
|
1488 | 1487 | 1488 |
ν(CAr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) CAr) CAr)
|
1440 | 1465 | 1464 |
| δ(C(22)–H) | 1353 | 1355 | — |
| γ(C–H)para | 842 | 835 | 844 |
| γ(C–H)ortho | 747 | 730 | 737 |
| γ(C–H)mono | — | — | 693 |
| ν(C–N) | 1287 | 1290 | 1275 |
| ν(C–O–C) | — | 868 | 869 |
We want to stress that the partition of these molecules into acceptor and donor fragments comes from the literature9 and is based on the results of experiments in solution. In the excited state there is a transfer of the electron density from the donor fragment to the acceptor. It appears that in the solid state, the intramolecular charge redistribution is taking place in the opposite direction. One of the reasons for this effect is the difference in the electronegativity of the atoms connecting the donor and acceptor units, namely N(8) and C(5). In the acetyl derivatives, the separation of the charge is slightly bigger for the PAS molecule. The hybridization of the nitrogen atoms in PAO and PBO is close to sp2 and for PAS it is close to sp3. Bond lengths for PAO and PBO from the nitrogen atom to the surrounding atoms are shorter compared to the PAS molecule, e.g., the aforementioned bond length N(8)–C(5). The angles; C(5)N(8)C(18), C(5)N(8)C(20) and C(18)N(8)C(20) are 116.22(2)°, 116.20(2)°, 122.20(2)° for the PAS molecules. The respective values for PBO are 120.97(4)°, 119.99(4)°, 118.43(3)°, and for PAO 119.58(2)°, 121.45(2)°, 118.87(2)°. The inductive effect is even stronger in the PAO and PBO molecules because of the oxygen atom in the central ring of the donor.
The mesomeric effect also influences the charge separations in these molecules with conjugated double bond systems. However, in the PAS molecules it is blocked, due to a hybridisation of the nitrogen atom, and a flat conformation of the heterocyclic ring in the phenoxazine derivatives. This effect is very strong in the benzoic derivatives of phenoxazine (PBO). The N(8)–C(5) bond lengths in the PAO and PBO molecules are similar. The analysis of the FTIR spectra of these compounds indicates the stronger aromatic character and a bigger conjugated system for the PBO molecules, e.g., ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and ν(C–N). The conjugated double bond system enables the propagation of electronic effects over the whole moiety and the geometry of the moieties permits charge transfer between the donor and acceptor units.
O) and ν(C–N). The conjugated double bond system enables the propagation of electronic effects over the whole moiety and the geometry of the moieties permits charge transfer between the donor and acceptor units.
The HOMO and LUMO orbitals have been calculated for the isolated PAO3 and PBO3 geometries of both molecules using Gaussian03 with the BP86 and aug-cc-pVDZ basis set. As expected, the HOMO orbital for PBO and PAO is mainly localised on the donor subunit and the LUMO on the acceptor subunit. The separation of the charge between the donor and acceptor units in the opposite direction to that expected does not indicate the opposite charge transfer in the excited state. This is due to the fact that the hydrogen atoms (positively charged) and their s orbitals have a small contribution to the HOMO and LUMO orbitals. Moreover, it is observed in the illustration below (Fig. 7), that the N(8) nitrogen atom and the C(5) carbon atom also contribute to the HOMO and LUMO. The dipole moments calculated from topological analysis and from the Gaussian03 calculations are included in the ESI† (see Table 4S, 10S and 16S).
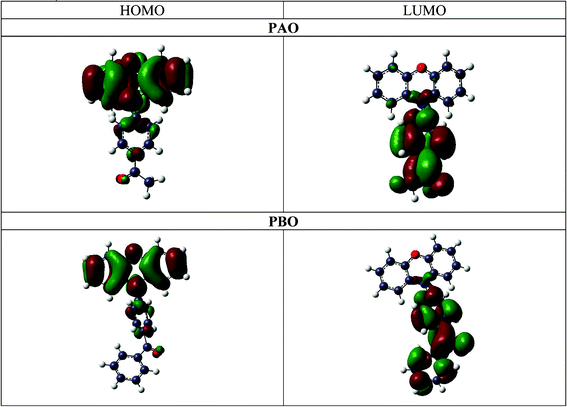 | ||
| Fig. 7 The calculated HOMO and LUMO orbitals for PAO and PBO. | ||
Conclusions
Applications of phenothiazine and phenoxiazine derivatives can be found in medicine, chemistry and physics. Geometry analysis of the studied compounds [1-(4-phenothiazin-10-yl-phenyl)-ethanone (PAS), 1-(4-phenoxazin-10-yl-phenyl)-ethanone (PAO), and (4-phenoxazin-10-yl-phenyl)phenyl-methanone (PBO)] allows an explanation of the differences in the values of the electronic coupling element V0 for the phenothiazine and phenoxazine derivatives. The three most important factors influencing the V0 values are: hybridization of the nitrogen atom, conformation of the heterocyclic ring and the torsion angle between the acceptor and donor parts. The biggest value of the parameter V0 is obtained for molecules where the hybridization of the nitrogen atom is close to sp2; a flat conformation of the heterocyclic ring and the torsion angle is far from 90 degrees between the donor and acceptor parts. The donor part in PAS is non-planar, which ‘breaks’ the conjugated double bond system and the electronic coupling element is smaller than that for the phenoxazine derivatives.Intramolecular charge redistribution was investigated by topological analysis of estimated electron density from high resolution X-ray experiments. Separation of the charge between the donor and acceptor parts in the solid state is in the opposite direction in comparison to the molecule's behaviour in solution after exposure to light. Commonly, electron density redistribution takes place from the donor to the acceptor part. However in the solid state, charge redistribution takes place from the formal acceptor to the donor unit. The acceptor part is positively charged and the donor negatively charged. The biggest difference between the acceptor and donor parts occurs in the benzoic derivative of phenoxazine, which has the largest system of coupled double bonds. Two effects, inductive and mesomeric, result from intramolecular charge separation. The first is present between the two atoms connecting the acceptor and donor parts: the nitrogen atom N(8) and the carbon atom C(5). The degree of charge redistribution depends on the hybridization of the nitrogen atom. The hybridisation of the N atom in the phenoxazine derivatives is close to sp2 and in phenothiazine it is close to sp3. Also, hybridization of the nitrogen atom close to sp2 hybridization allows the creation of a coupled system of double bonds in the phenoxazine derivatives. Theoretical calculations support the charge properties obtained from the topological analysis for the donor and acceptor units. The calculated HOMO and LUMO orbitals indicate that the charge transfer in the excited state is from the donor to the acceptor molecular fragments.
Our quantitative experimental charge density results agree very well with the photo-physical effects exhibited by the molecules studied and allow a simpler interpretation of the previous spectroscopic results. Previously, the blue shift of the CT absorption band was interpreted as a consequence of the terminal location of the –CN and –CO groups,10 and was based on the wrong direction of the dipole moment in the ground state.
Apparently, the A–D molecules can be formally treated as formed from neutral A and D moieties by deprotonation of the A and D units, which are next joined together. Conservation of the HOMO and LUMO orbitals in the molecule A–D results in a negative charge on the donor D fragment and a positive one on the acceptor. In consequence, the dipole moment of the ground state should have an opposite orientation in comparison to the dipole moment in the excited state when an electron is transferred from D to A. Also solvatochromic effects can be expected: the CT emission band should be shifted towards lower energy (the IR shift) and the reverse shift can be expected for the CT absorption band (the blue shift towards UV). In fact, such effects are observed experimentally.15 Conservation of the HOMO and LUMO levels allows rationalization of the differences between the PAO and PBO molecules and the similarities between PAS and PAO.
Acknowledgements
The X-ray single-crystal measurements were accomplished at the Structural Research Laboratory (Department of Chemistry, University of Warsaw, Poland), established with financial support from the European Regional Development Fund (grant number WKP_1/1.4.3./1/2004/72/72/165/2005/U, Sectoral Operational Programme, Improvement of the Competitiveness of Enterprises, 2004–2006). KW thanks the Foundation for Polish Science for financial support within the “Master” (“Mistrz” in Polish) program and the Ministry of Science and Higher Education for financial support within the grant N N204 135138. The authors gratefully acknowledge the Interdisciplinary Centre for Mathematical and Computational Modelling in Warsaw (grant no. G33-14) for providing computer facilities on which most of the calculations were done.References
- M. J. Ohlow and B. Moosmann, Drug Discovery Today, 2011, 16, 119–131 CrossRef CAS.
- A. D. Mosnaim, V. V. Ranade, M. E. Wolf, J. Puente and M. Antonieta Valenzuela, Am. J. Ther., 2006, 13, 261–13273 CrossRef.
- G. Sudeshna and K. Parimal, Eur. J. Pharmacol., 2010, 648, 6–14 CrossRef CAS.
- O. M. New and D. Dolphin, Eur. J. Org. Chem., 2009, 2675–2686 CrossRef CAS.
- S. Imai, A. Shimazu, K. Furihata, K. Furihata, Y. Hayakawa and H. Seto, J. Antibiot., 1990, 43, 1606–1607 CrossRef CAS.
- J. Koshibu-Koizumi, M. Akazawa, T. Iwamoto, M. Takasaki, F. Mizuno, R. Kobayashi, A. Abe, A. Tomoda, M. Hamatake and R. Ishida, J. Cancer Res. Clin. Oncol., 2002, 128, 363–368 CrossRef CAS.
- N. Zacal and A. J. Rainbow, Photochem. Photobiol., 2007, 83, 730–737 CrossRef CAS.
- K. H. Drexhage, Chem. Abstr., 1974, 80, 114727 Search PubMed.
- K. M. Karlsson, X. Jiang, S. K. Eriksson, E. Gabrielsson, H. Rensmo, A. Hagfeldt and L. Sun, Chem.–Eur. J., 2011, 17, 6415–6424 CrossRef CAS.
- A. Kapturkiewicz, H. Herbich, J. Karpiuk and J. Nowacki, J. Phys. Chem. A, 1997, 101, 2332–2344 CrossRef CAS.
- J. Herbich and A. Kapturkiewicz, Chem. Phys. Lett., 1997, 273, 8–17 CrossRef CAS.
- J. Herbich and A. Kapturkiewicz, J. Am. Chem. Soc., 1998, 120, 1014–1029 CrossRef CAS.
- A. Kapturkiewicz and J. Nowacki, J. Phys. Chem. A, 1999, 103, 8145–8155 CrossRef CAS.
- R. R. Dogonadze, A. M. Kuznetsov and T. A. Marsagishvili, Electrochim. Acta, 1980, 25, 1–28 CrossRef CAS.
- P. Borowicz, J. Herbich, A. Kapturkiewicz, M. Opallo and J. Nowacki, Chem. Phys., 1999, 249, 49–62 CrossRef CAS.
- P. Borowicz, J. Herbich, A. Kapturkiewicz, R Anulewicz-Ostrowska, J. Nowacki and G. Grampp, Phys. Chem. Chem. Phys., 2000, 2, 4275–4280 RSC.
- Apex2 v. 2.1-0, 2003, 2004; Bruker Nonius, 2005, 2006 Bruker AXS.
- R. H. Blessing, Crystallogr. Rev., 1987, 1, 3–58 CrossRef.
- G. M. Sheldrick, SHELXL97. Program for Crystal Structures Refinement, University of Göttingen, Göttingen, Germany, 1997. Release 97-2 Search PubMed.
- A. Volkov, P. Macchi, L. J. Farrugia, C. Gatti, P. Mallinson, T. Richter and T. Koritsanszky, XD2006 - A Computer Program Package for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental and Theoretical Structure Factors, 2006 Search PubMed.
- N. K. Hansen and P. Coppens, Acta Cryst., 1978, A34, 909–921 CrossRef CAS.
- A. Madsen, J. Appl. Crystallogr., 2006, 39, 757–758 CrossRef CAS.
- A. Volkov, Y. A. Abramov and P. Coppens, Acta Cryst., 2001, A57, 272–282 CrossRef CAS.
- A. Hoser, P. M. Dominiak and K. Wozniak, Acta Cryst., 2009, A65, 300–311 CAS.
- F. L. Hirshfeld, Acta Cryst., 1976, A32, 239–244 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burantet al., Gaussian 03, Revision B.01, Gaussian, Inc., Pittsburgh PA, 2003 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–48 CrossRef CAS.
- K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- M. Kohout, DGrid, version 4.5, Radebeul, 2009 Search PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565–565 CrossRef CAS.
- A. L. Spek, PLATON, A Multipurpose Crystallographic Tool; Utrecht University, Utrecht, The Netherlands, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: residual density maps, static deformation density maps, normal probability plots, scale plots, selected topological parameters (rBCP) and (rBCP) at BCPs, integrated atomic charges and integrated Laplacian, fractional dimension vs. residual density plots for selected planes, minima and maxima of residual density, dipole moments related to experimental charge density analysis for PAO, PAS and PBO molecules. Also tables and figures related to the theoretical calculations and theoretical charge density analyses of the PAO, PAS and PBO molecules: Cartesian coordinates, dipole moments and experimental IR spectra for PAO, PAS and PBO. CCDC reference numbers 852714, 852715 and 852716. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2ra01148d |
| This journal is © The Royal Society of Chemistry 2012 |
