Nanocellular foaming of fluorine containing block copolymers in carbon dioxide: the role of glass transition in carbon dioxide
Cédric
Dutriez
a,
Kotaro
Satoh
b,
Masami
Kamigaito
b and
Hideaki
Yokoyama
*cd
aGlaizer Group, 32 rue Guy Moquet, 92240, Malakoff, France
bDepartment of Applied Chemistry, Graduate School of Engineering, Nagoya University, Nagoya, Japan
cDepartment of Advanced Materials Science, Graduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwa-no-ha, Kashiwa, Chiba 277-8561, Japan. E-mail: yokoyama@molle.k.u-tokyo.ac.jp; Fax: +81-4-7136-3766; Tel: +81-4-7136-3766
dPrecursory Research for Embryonic Science and Technology (PRESTO), Japan Science and Technology Agency, 3-5, Sanbancho, Chiyoda-ku, Tokyo, 102-0075, Japan
First published on 8th February 2012
Abstract
Carbon dioxide foaming in polymeric materials has been recognized as an environmentally friendly method to introduce microfoam consisting of cells of micrometre size (microcells). Our group has demonstrated that CO2-philic fluorinated block domains of block copolymers worked as nuclei of foams and further decreased the size of cells to around 10 nm (nanocells). In this study, we introduced nanocells to poly[(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PMMA–PFMA, MF) and poly[(perfluorooctylethyl methacrylate)-b-(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PFMA–PMMA–PFMA, FMF), and compared the resultant porosity with those of polystyrene-based fluorinated block copolymers previously studied. The temperature providing a maximum porosity for the PMMA based copolymers was lower than that for the PS based copolymers. We further measured the glass transition temperatures, Tg, of skeleton blocks, i.e. PS and PMMA, in the presence of CO2 using a quartz crystal resonator and revealed that the temperature of maximum porosity is correlated to the decreased Tg of the skeleton polymers in CO2.
Introduction
Block copolymers, assembling themselves in nanodomains, have been attracting a great deal of interest over the past few decades.1 A variety of nanostructured domains appear dependent on molecular weight and block fraction. Such self-assembled nanodomains of block copolymers have often been employed as templates for a variety of nanopatterning techniques. Carbon dioxide (CO2) has been used for a variety of polymer processes,2 in particular, it has been used to create foams in polymeric materials.3 However, conventional methods can only introduce foams with a size greater than 1 micrometre.3We have previously reported4–7 the successful build up of empty cells with a size of tens of nanometres (nanocells) by CO2 foaming using block copolymers with fluorinated blocks, which have high affinity toward carbon dioxide8 and hence are selectively swollen. Upon depressurization, foaming of CO2 is geometrically restricted within the CO2-philic fluorinated block domains. For example, poly(styrene-b-perfluorooctylethyl methacrylate) (PS-PFMA) successfully accommodated nanocells with diameters in the range 10–30 nm depending on the CO2 processing pressure. The successful introduction of nanocells in polystyrene based fluorinated block copolymers using CO2 requires two-temperature-step foaming processes, an example of which is composed of saturating a block copolymer with CO2 at 20 MPa and 60 °C, followed by an isobaric temperature quench to 0 °C before CO2 pressure release. While the two-temperature-step foaming processes successfully fabricated unique nanocellular structures, the mechanism has not yet been clearly understood.
In this paper, we studied the conditions for the successful introduction of nanocells in poly[(methyl methacrylate)-b-perfluorooctylethyl methacrylate] (PMMA–PFMA) and poly[(perfluorooctylethyl methacrylate)-b-(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PFMA–PMMA–PFMA, FMF) and compared the results with those of polystyrene-based fluorinated block copolymers in our previous study. We further related the optimum process temperature to a decreased glass transition temperature of skeleton block (PS or PMMA) in the presence of CO2 that was measured using a quartz crystal resonator (QCR).
Experimental section
Polymer synthesis and sample preparation
Poly[(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PMMA–PFMA, MF) and poly[(perfluorooctylethyl methacrylate)-b-(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PFMA–PMMA–PFMA, FMF) were synthesized by sequential living radical polymerization using a ruthenium catalyst.9 A typical example for the preparation of FMF with Ru(Ind)Cl(PPh3)2 as the catalyst coupled with CHCl2(COPh) as the bifunctional initiator is given below. In a 50 mL round-bottomed flask was placed Ru(Ind)Cl(PPh3)2 (39.7 mg, 0.051 mmol), toluene (11.9 mL), MMA (10.9 mL, 102 mmol), CHCl2(COPh) (0.128 mL of 800 mM solution in toluene, 0.102 mmol), and nBu3N (2.56 mL of 400 mM solution in toluene, 1.02 mmol) at room temperature. The flask was placed in an oil bath and kept at 80 °C under stirring. After 19 h, the monomer conversion determined by 1H NMR reached 80.6%. The product was precipitated into hexane and isolated by centrifugation to give the telechelic PMMA as a macroinitiator (5.70 g, 71% yield; Mn = 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, Mw/Mn = 1.13). In another 50 mL vessel, the macroinitiator (1.5 g, 0.0198 mmol), Ru(Ind)Cl(PPh3)2 (8.7 mg, 0.011 mmol), perfluorooctylethyl methacrylate (0.45 mL, 1.33 mmol), and nBu3N (0.56 mL of 400 mM solution in toluene, 0.224 mmol) were dissolved in the solvent mixture of toluene (1.1 mL) and perfluorocumylalcohol [(CF3)2C(Ph)OH] (2.0 mL). After 215 h at 80 °C, the monomer conversion determined by 1H NMR reached 95.2%. The reaction mixture was diluted with CHCl3 and the product was precipitated into hexane and isolated by centrifugation to give the triblock copolymer FMF30 (1.7 g, 87% yield). For the synthesis of the diblock copolymers, H–(MMA)2–Cl was employed as the monofunctional initiator in place of CHCl2(COPh).
500, Mw/Mn = 1.13). In another 50 mL vessel, the macroinitiator (1.5 g, 0.0198 mmol), Ru(Ind)Cl(PPh3)2 (8.7 mg, 0.011 mmol), perfluorooctylethyl methacrylate (0.45 mL, 1.33 mmol), and nBu3N (0.56 mL of 400 mM solution in toluene, 0.224 mmol) were dissolved in the solvent mixture of toluene (1.1 mL) and perfluorocumylalcohol [(CF3)2C(Ph)OH] (2.0 mL). After 215 h at 80 °C, the monomer conversion determined by 1H NMR reached 95.2%. The reaction mixture was diluted with CHCl3 and the product was precipitated into hexane and isolated by centrifugation to give the triblock copolymer FMF30 (1.7 g, 87% yield). For the synthesis of the diblock copolymers, H–(MMA)2–Cl was employed as the monofunctional initiator in place of CHCl2(COPh).
The synthesized block copolymers have various weight fractions of fluorinated block (17.6%, 30.9% and 37%) with diblock (MF) and triblock (FMF) architectures as listed in Table 1. Polystyrene-b-poly(perfluorooctylethyl methacrylate) (SF) was synthesized by a sequential anionic polymerization in tetrahydrofurane at −78 °C for our previous study3 and used as a reference in this study. The molecular weights of PS and PFMA blocks are 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 13
000 and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. The block copolymers dissolved in α-α-α-trifluorotoluene were spun-coated on silicon wafers (Shinetsu Co.) using a spin coater (MIKASA Spin Coater 1H-D7) to form 200 to 300 nm thick films.
000, respectively. The block copolymers dissolved in α-α-α-trifluorotoluene were spun-coated on silicon wafers (Shinetsu Co.) using a spin coater (MIKASA Spin Coater 1H-D7) to form 200 to 300 nm thick films.
| Code | Block type | PMMA prepolymer | Unit ratio (m/n) (NMR) | ||
|---|---|---|---|---|---|
| M n | M w/Mn | MMA | Rf8EMA | ||
| MF15 | di- | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.14 | 754 | 32 |
| FMF15 | tri- | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.13 | 790 | 30 |
| MF30 | di- | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.14 | 790 | 66 |
| FMF30 | tri- | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.13 | 754 | 64 |
| MF40 | di- | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.14 | 790 | 88 |
| FMF40 | tri- | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.13 | 760 | 84 |
CO2 process for nanofoaming
CO2 process for nanofoaming was carried out using a stainless steel vessel linked to a high pressure liquid chromatographic pump (JASCO PU 2086plus) with a cooling head, and to a back pressure controller (JASCO SCF-Bpg). The vessel was temperature controlled in a water bath during the process. The CO2 process is composed of two successive steps: the first step is a saturation step which introduces CO2 in order to swell the block copolymer film. The saturation temperature was set to 45 °C unless otherwise stated. The range of saturation pressure was between 0 and 30 MPa. The second step is a depressurization step which removes CO2 from the films in order to leave empty nanocells in the film. This step proceeded at lower temperature, such as 0 °C, with a fixed depressurization rate of 0.57 MPa min−1 for all our experiments.Ellipsometry
Block copolymer thin films on silicon wafers before and after the CO2 process were analyzed using a polarization modulated spectroscopic ellipsometer JASCO M150 using a range of wavelengths from 300 to 800 nm. The angle of reflection was set to 60° from the normal to the substrate. The ellipsometry measurement provides the values for the thickness and refractive index of the thin films before and after the CO2 process, which relate to the porosity of the films.Quartz crystal resonator (QCR)
AT cut quartz crystals with a fundamental frequency of 5 MHz and diameter of 14 mm with aluminum electrodes were custom designed and purchased from Kyocera Co. Thin polymer films of PS, PSMMA and PMMA were deposited on the quartz crystals by spin-casting toluene solutions of these polymers. The characteristics of these homopolymers and random copolymers are shown in Table 2. The specimens were placed in a stainless steel high-pressure vessel having two channels of electric feedthrough, which allow us to simultaneously monitor frequency shifts of a bare quartz crystal and polymer-coated quartz crystal in pressurized CO2. The whole vessel was immersed in a temperature controlled water bath. The frequency and bandwidth of the resonance were determined by impedance analysis using a 250B network analyzer (Saunders & Associates, Inc., Scottsdale, AZ) in conjunction with the software package QTZ (Resonant Probes, Goslar, Germany).| Code | Polymer | Molecular weight (g mol−1) | M w/Mn |
|---|---|---|---|
| PMMA | Poly(methyl methacrylate) | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.06 |
| PSMMA 50 | Poly(styrene-r-methyl methacrylate) | 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
2.3 |
| PS | Polystyrene | 354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.07 |
Scanning electron microscopy
The structures of nanocellular thin films were observed using an environmental scanning electron microscope (ESEM) (Phillips XL20 ESEM-FEG) equipped with a field emission gun with an electron beam energy of 10 and 15 keV and working distance of 10 mm without conductive coating. To expose the embedded cells to the surface for SEM, we etched the films with a reactive ion etcher (Plasma Etching System SAMCO FA-1) under controlled rate (ca. 1 nm min−1) with a CF4 flow rate of 2 mL min−1, a pressure of 10 Pa, and a power density of 10 W cm−2.Results and discussion
Poly[(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PMMA–PFMA, MF) and poly[(perfluorooctylethyl methacrylate)-b-(methyl methacrylate)-b-(perfluorooctylethyl methacrylate)] (PFMA–PMMA–PFMA, FMF) were synthesized and used as thin films on silicon wafers. A series of MF and FMF were pressurized with CO2 at 30 MPa and 45 °C for 1 h, followed by a temperature quench to 0 °C and subsequent depressurization. Examples of SEM images of the nanocellular structures obtained by the process are shown in Fig. 1. These SEM images, observed after plasma etching to remove the surface-covering layer, show closed nanocellular structures in the films. The apparent size of the cells are distributed across the range 20 to 70 nm. The nanocells in the triblock copolymers are smaller than those in the diblock copolymers with the same total molecular weights, and the number of cells is greater in the triblock copolymers. In the case of polystyrene based block copolymers in our previous studies, a variety of structures other than cell structure, such as stacked thin sheets, originated from swollen lamellae in CO2 were observed.10 However, PMMA based block copolymers only showed cell structures, even when highly pressurized. We speculate that this is due to the relatively high affinity of PMMA for CO2 compared to that of PS; therefore, selectivity of CO2 to PFMA is smaller.11 We are currently conducting an in situ small angle scattering study of block copolymers in CO2 to reveal the morphological transitions. | ||
| Fig. 1 Examples of SEM images of nanocellular films of diblock copolymers (MF30, above) and triblock copolymers (FMF30, below). | ||
Ellipsometry was employed to measure the thickness and refractive index of the films before and after the CO2 process to estimate the porosity of the films. In the thickness range of our experiment, the thin film effect is negligible12 and no influence of thickness on porosity was found. From the measured initial thickness, hi, and the final thickness of the film, hf, porosity of the films, p, is estimated by eqn (1) by assuming that the increment of the volume of the film is solely due to the volume of the introduced nanocells:
 | (1) |
Similarly, the refractive index is lowered with the porosity introduced into the film since the air filling the pores has a refractive index of unity. The obtained refractive index agreed well with the porosity defined in eqn (1). Since the porosities estimated from the thickness differences give smaller deviations from the mean values than those estimated using the refractive index, we use the porosity defined in eqn (1) in this report. The validity of this method for estimating porosity has been discussed in our previous report.4,6,7Fig. 2 shows the dependence of porosity on the block fraction of PFMA for diblock or triblock copolymers. CO2 is expected to be localized in the CO2-philic fluorinated domains, and hence the higher molecular weights of PFMA result in higher porosity after the process, as shown in Fig. 2. Triblock copolymers show a slightly smaller porosity under the conditions that the total molecular weights for diblock and triblock copolymers are equal. In addition, the molecular weights of fluorinated blocks in the triblock copolymers, and hence their domain and cell sizes, are smaller than those of diblock copolymers, as can be seen in Fig. 1. It should be noted that the conditions we employed for this experiment is for maximum porosity, as described detail later.
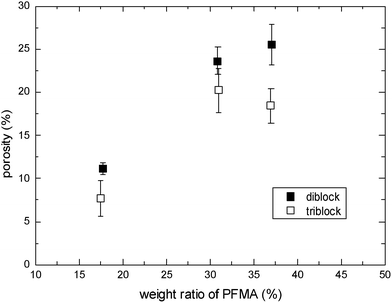 | ||
| Fig. 2 Porosity as a function of weight ratio of PFMA block for diblock and triblock copolymers. Saturation temperature and pressure were set to 45 °C and 30 MPa, respectively. | ||
Process parameters (pressure and temperature) also control the final porosity of the films. The two-step foaming process, consisting of saturation and depressurization processes, was employed with a saturation temperature T1 = 45 °C at a pressure P1, followed by thermal quenching to a depressurization temperature T2 = 0 °C and subsequent slow depressurization 0.57 MPa min−1. A saturation pressure P1 has a significant influence on the final porosity of each sample. In the range of pressures from 6 to 30 MPa, the porosity increases linearly with saturation pressure, as shown in Fig. 3. This dependence is in good contrast to that of PS based block copolymers in which porosity reaches a maximum at 20 MPa.4 The appearance of maximum porosity at 20 MPa for PS based copolymers was explained by the balance between increasing affinity, which increases porosity and the hydrostatic pressure effect, which decreases porosity as pressure increases. In the case of PMMA based block copolymers, increasing affinity with pressure seems to dominate over the hydrostatic pressure effect in the pressure range since PMMA has a higher affinity for CO2 than PS.12
 | ||
| Fig. 3 Porosity as a function of process pressure for MF30 and FMF30 copolymers. | ||
To understand the role of the two-step foaming process described above with saturation, T1, and depressurization, T2, temperatures, MF30 films were processed using the following two protocols: (1) Saturation temperature T1 was fixed at 45 °C and depressurization temperature T2 was varied; (2) Depressurization temperature T2 was fixed at −40 °C and saturation temperature T1 was varied. The porosities were plotted as a function of either T1 or T2 in Fig. 4. For a pressurizing step, there is a lower boundary of approximately 10 °C for T1 to obtain the maximum porosity. In contrast, for a depressurization process, there is an upper boundary of approximately 20 °C for T2 to reach the maximum porosity. This result clearly indicates that the saturation process requires temperatures higher than 10 °C and depressurization temperatures lower than 20 °C.
 | ||
| Fig. 4 Porosity of MF30 as a function of process temperatures. The hollow circles (○) represent the dependence on saturation temperature (T1) with a fixed depressurization temperature of 40 °C. The filled triangles (▼) represent the dependence on depressurization temperature (T2) with a fixed saturation temperature of 45 °C. | ||
We also directly compared the porosities of PMMA–PFMA with PS–PFMA at a constant process temperature (T1 = T2) and the resultant porosities are plotted in Fig. 5. We can point out the existence of an optimum temperature (Tmax) for each material, depending on the species of the non-fluorinated part of the block copolymers, i.e. PS or PMMA. The process for PMMA–PFMA is qualitatively similar to the process required to obtain nanocells in PS–PFMA in our previous studies, but the optimum process temperature is significantly lower. In the case of PMMA–PFMA (MF30), this optimum temperature is approximately 10 °C, which is located between the upper and lower bounds for T2 and T1, respectively. The same value of optimum temperature was observed for different architectures, such as diblock, triblock and different ratios of PFMA. In the case of PS–PFMA, however, the optimum temperature is approximately 30 °C, higher than the 10 °C for PMMA–PFMA. The chemical composition of non-fluorinated part of the block copolymer determines the optimum temperature for the maximum porosities.
 | ||
| Fig. 5 Dependence of porosity of the films after the CO2 process on temperature. Temperature was fixed during the whole process (T1 = T2). | ||
The nanocellular process requires either the two-step process with a saturation temperature T1 and depressurization temperature T2, or a one-step process temperature in the narrow optimum temperature window. We speculate that the glass transition of the non-fluorinated part of the block copolymer in CO2 is playing an important role as the non-fluorinated part of the block copolymer must be rubbery in order to allow the PFMA domains to swell in the saturation step, but must also be glassy to sustain the swollen structure in the depressurization step; otherwise, the swollen structure would shrink back and lose its porous structure. However, such speculation is based solely on the result of PS–PFMA and the reported glass transition temperature of PS in CO2. To justify this hypothesis, we looked for a correlation between the optimum temperature, Tmax, during the CO2 process and the glass transition temperature of the non-fluorinated part of the block copolymer.
Condo et al.,13–16 as well as Wang et al.,17,18 studied the glass transition temperature (Tg) of polymers under CO2 pressure. The glass transition temperature of a polymer in CO2 decreases by absorption of CO2. Conversely, hydrostatic pressure itself tends to increase the Tg. In addition to a direct temperature effect on glass transition, temperature changes the affinity of CO2 to polymers and indirectly affects the glass transition.
Wang et al.17,18 studied the glass transition of PS under higher pressure and evaluated the glass transition to be almost pressure independent, approximately 35 °C in the pressure range 10 to 30 MPa of CO2. Condo et al. found an existence of retrograde vitrification, which presents a glass-to-rubber transition on heating in addition to another glass-to-rubber transition on cooling of PS in CO2. A similar result was also obtained for a random copolymer of PS and PMMA (PSMMA) containing 60% of PMMA for a CO2 pressure under 10 MPa. In pressurized CO2, lowering the temperature increases the absorbed amount of CO2 in polymers and induces a glass-to-rubber transition, which is the origin of retrograde vitrification. However, their results were only in a low pressure range (a vicinity of critical point) and the glass transition of PMMA in the pressure range from 10 to 30 MPa, which is relevant to our experiment, has not been reported.
We used a quartz crystal resonator (QCR) to monitor the glass transition of PMMA and PS, in a relatively high pressure range from 10 to 30 MPa of CO2. QCR is normally called quartz crystal microbalance (QCM) since QCR is generally used as a microbalance for measuring a small change of mass. To determine a mass change on a quartz crystal, one can employ the Sauerbrey equation:
 | (2) |
Δf, f, and ff are frequency shift, resonant frequency and the fundamental frequency, respectively.19Zq and m are the acoustic impedance of quartz and mass per unit area, respectively. The Sauerbrey equation holds under the conditions that the small load approximation is valid, where the stress induced by the added thin film is caused by inertia only. However, the Sauerbrey equation is invalid for thick, soft films, in which the deformation of film dominates over inertia. For a viscoelastic film in liquid, such as a polymer thin film in CO2, a viscoelastic correction must be introduced into the Sauerbrey equation:
 | (3) |
 | (4) |
 | (5) |
When a polymer film goes into glass-to-rubber transition upon swelling with CO2, the shear modulus of the film decreases by several orders of magnitude, while the mass of the film by absorption changes by much less than an order of magnitude. The resonance frequency of a relatively thicker film is hence dominated by the change in the modulus of the film deposited on the quartz crystal. Therefore, by monitoring the shift of resonance frequency of quartz covered by a thick polymer layer, one can detect a large change of modulus due to glass transition.
QCR is also sensitive to the temperature and pressure of a system either directly or through the change of density and viscosity of CO2, as well as the changes in weight and viscosity of the film deposited on a quartz surface. For our experiments, we used two sets of quartz crystals in a high pressure vessel, a bare quartz crystal and a quartz crystal coated with a 2-micron-thick polymer film. Such a thick polymer film was deposited on quartz crystals in order to emphasize the change in shear modulus instead of the change in mass. The bare crystal was simultaneously used to discriminate the direct effects of pressure and temperature on a quartz resonant frequency, and to extract the change in modulus of polymer films deposited on quartz crystals. All experiments were carried out at fixed pressures of CO2 in a temperature range from −10 °C to 60 °C. We measured frequency shifts for the third and fifth overtones (15 MHz and 25 MHz) as a function of temperature. Measurements were carried out on PMMA, PSMMA and PS, as listed in Table 2.
Examples of frequency shift curves as a function of temperature under 20 MPa CO2 pressure are shown in Fig. 6. The bare quartz showed linearly decreasing frequency with increasing temperature, which suggests smoothly decreasing density and viscosity of CO2 with increasing temperature. On the other hand, polymer-coated quartz crystals show distinct kinks on the frequency shift curves. Such behavior was independent of the choice of overtone, i.e. 3rd or 5th overtone. These kinks are related to the glass transition of polymers because the frequency shifts are dominated by the change in shear modulus in the case of soft thick films deposited on quartz crystal.
 | ||
| Fig. 6 Examples of frequency shift curves obtained by QCR experiments with three different polymer films with thicknesses in the range of 1.5 to 2 μm under a CO2 pressure of 20 MPa. The points A, B, and C designate the glass transition temperatures observed for the polymers. The data are shifted vertically for comparison. | ||
We extracted the glass transition temperatures as indicated by arrows in Fig. 6 and plotted them in Fig. 7. The glass transition temperatures of PS were measured using QCR and show a good agreement with the work of Condo et al.13–16 and Wang et al.,17,18 as shown in Fig. 7. Based on this good agreement, we used the QCR analysis to estimate semi-quantitatively the glass transition temperatures of PSMMA and PMMA, which has not been reported at a higher pressure range. Although, in the pressure range from gas to supercritical fluid (0 MPa to 7.5 MPa), a unique retrograde vitrification, which presents a glass-to-rubber transition on heating in addition to another glass-to-rubber transition on cooling, is shown in Condo's reproduced plot in Fig. 7, note that Tgs of PS and PMMA are almost independent on pressure in the higher pressure range of supercritical state (7.5 MPa to 30 MPa). Therefore, in our working pressure range, Tgs of PS and PMMA are considered to be constant. We can conclude from the QCR experiments that PMMA based copolymers become glassy at 10 °C, whilst PS based copolymers become glassy at 30 °C. The random copolymer of PS and PMMA, PSMMA, also shows lower glass transition relative to PS. Such reduction clearly indicates enhanced affinity of CO2 towards the copolymer with added MMA segments. However, it is interesting that the glass transition temperature of PSMMA is almost the same as PMMA, despite the MMA fraction of only 50% in PSMMA. Since we have only one random copolymer to be compared, we avoid further discussion of this trend.
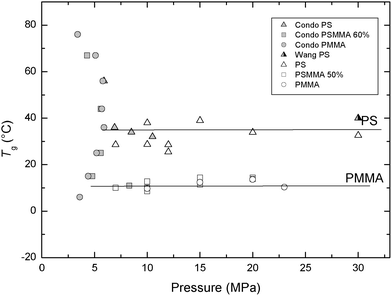 | ||
| Fig. 7 Comparison of the glass transition temperatures estimated from the quartz crystal resonance measurement with those of Condo et al.8–11 and Wang et al.12–13 | ||
We found that the glass transition temperatures are well correlated to the Tmax of PMMA–PFMA of 10 °C. Considering this correlation between the optimum temperature, Tmax, and the glass transition, Tg, of the block copolymer, we can propose the following explanation of the effect of the glass transition on nanocellular formation. At a given pressure, we will consider a saturation temperature (T1): if T1 is higher than the Tg of the matrix polymer, the PFMA domains are allowed to swell with CO2. However, when T1 is lower than the Tg of the matrix polymer, the PFMA domains are confined in the glassy matrix and are not allowed to swell with CO2. Similarly, at a given pressure, we will consider a depressurization temperature (T2): when T2 is higher than the Tg of the matrix polymer, the swollen PFMA domains shrink back during depressurization. If the sample is thick enough, microfoaming occurs under these conditions instead of shrinking. However, when T2 is lower than the Tg of the matrix polymer, the swollen PFMA domains are frozen and nanocellular structures appear during depressurization. We have mostly worked for polystyrene based copolymers with the temperatures T1 = 45 °C and T2 = 0 °C, which satisfy the above conditions for successful introduction of nanocellular structures, but PMMA based copolymers requires a lower T2, i.e. −10 °C, due to their lower Tg .
Conclusions
We found that the cell formation in CO2 requires the non-fluorinated part of the block copolymer to be in a rubber state to allow CO2 to diffuse into and to swell the nuclei of fluorinated blocks. When depressurized, on the other hand, the glassy state of the non-fluorinated part of the block copolymer prevents collapsing of the swollen cells of the non-fluorinated block. Therefore, to achieve such conditions, either selecting different temperatures for saturation and depressurization processes or choosing a narrow temperature band is required. We measured the glass transition temperatures of PS and PMMA and confirmed that such optimum temperatures are strongly correlated to the glass transition temperatures of the non-fluorinated block in CO2.Acknowledgements
This work has been financially supported by PRESTO-JST.References
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32 CrossRef CAS.
- A. I. Cooper, J. Mater. Chem., 2000, 10, 207–234 RSC.
- A. I. Cooper, Adv. Mater., 2003, 15, 1049–1059 CrossRef CAS.
- H. Yokoyama, L. Li, T. Nemoto and K. Sugiyama, Adv. Mater., 2004, 16, 1542 CrossRef CAS.
- H. Yokoyama, K. Sugiyama and L. Li, Macromolecules, 2005, 38, 10516 CrossRef CAS.
- L. Li, H. Yokoyama, T. Nemoto and K. Sugiyama, Adv. Mater., 2004, 16, 1226 CrossRef CAS.
- L. Li, T. Nemoto, K. Sugiyama and H. Yokoyama, Macromolecules, 2006, 39, 4746–4755 CrossRef CAS.
- J. M. DeSimone, Z. Guan and C. S. Elsbernd, Science, 1992, 257, 945–947 CAS.
- (a) M. Kato, M. Kamigaito, M. Sawamoto and T. Higashimura, Macromolecules, 1995, 28, 1721–1723 CrossRef CAS; (b) H. Takahashi, T. Ando, M. Kamigaito and M. Sawamoto, Macromolecules, 1999, 32, 3820–3823 CrossRef CAS; (c) T. Shibata, K. Satoh, M. Kamigaito and Y. Okamoto, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 3609–3615 CrossRef CAS; (d) M. Kamigaito, T. Ando and M. Sawamoto, Chem. Rev., 2001, 101, 3689–3745 CrossRef CAS.
- H. Yokoyama, L. Li, C. Dutriez, Y. Iwakura, K. Sugiyama, H. Masunaga, S. Sasaki and H. Okuda, Macromolecules, 2008, 41, 8626–8631 CrossRef CAS.
- D. L. Tomasko, H. B. Li, D. H. Liu, X. M. Han, M. J. Wingert, L. J. Lee and K. W. Koelling, Ind. Eng. Chem. Res., 2003, 42, 6431–6456 CrossRef CAS.
- J. Q. Pham, K. P. Johnston and P. F. Green, J. Phys. Chem. B, 2004, 108, 3457–3461 CrossRef CAS.
- P. D. Condo and K. P. Johnston, Macromolecules, 1992, 25, 6730–6732 CrossRef CAS.
- P. D. Condo, I. C. Sanchez and C. G. Panayiotou, Macromolecules, 1992, 25, 6119–6127 CrossRef CAS.
- P. D. Condo and K. P. Johnston, J. Polym. Sci., Part B: Polym. Phys., 1994, 32, 523–533 CrossRef CAS.
- P. D. Condo, D. R. Paul and K. P. Johnston, Macromolecules, 1994, 27, 365–371 CrossRef CAS.
- W. C. Wang and E. J. Kramer, Bull. Am. Phys. Soc., 1981, 26, 367–367 Search PubMed.
- W. C. Wang and E. J. Kramer, J. Polym Sci. Part B, 1982, 20, 1371–1384 CAS.
- For example: see Chapter 4 in Models for Resonant Sensors in Piezoelectric Transducers and Applications, ed. A. Arnau, Springer-Verlag Berlin Heidelberg, 2004.
| This journal is © The Royal Society of Chemistry 2012 |
