Direct measurements of the saturated vapor pressure of water confined in extended nanospaces using capillary evaporation phenomena†
Takehiko
Tsukahara
a,
Taku
Maeda
b,
Akihide
Hibara
b,
Kazuma
Mawatari
b and
Takehiko
Kitamori
*b
aResearch Laboratory for Nuclear Reactors, Tokyo Institute of Technology, Tokyo, Japan. E-mail: ptsuka@nr.titech.ac.jp; Fax: +81-3-5734-3061; Tel: +81-3-5734-3061
bDepartment of Applied Chemistry, School of Engineering, The University of Tokyo, Tokyo, Japan. E-mail: kitamori@icl.t.u-tokyo.ac.jp; Fax: +81-3-5841-6039; Tel: +81-3-5841-7233
First published on 15th February 2012
Abstract
Direct measurements of the saturated vapor pressures of water confined in extended nanospaces (10–100 nm scale) were realized using capillary evaporation phenomena. These results verified that the saturated vapor pressure was reduced with decreasing space sizes and that Kelvin's equation was applicable even in extended nanospaces.
A 10–100 nm scale space (referred to as an extended nanospace) has attracted much attention as an innovative research tool, because the extended nanospace is a transition region of molecular behavior from single molecules to bulk condensed liquids and corresponds to the electric double layer (EDL) thickness associated with surface charges.1–3 Unique liquid properties such as an increase in liquid viscosity, a slowing of molecular motions, and an enhancement of proton mobility, and formation of well-ordered hydrogen bonding networks have been recognized in extended nanospaces,4–6 and various nanofluidic devices have been designed by controlling the confinement-induced nanospatial properties, including selective ion transports, DNA handling, and single molecule detection.2,3,7–10 Recently, we found that the capillary condensation of water from vapor occurred in extended nanospaces even at 100 °C, and succeeded to demonstrate an efficient distillation of a water–ethanol solution using 270 nm sized pillars.11 From this vapor–liquid phase transition result, the equilibrium vapor pressures of liquids in extended nanospaces appear to be different from those in bulk space, but have never been explored experimentally.
The saturated vapor pressure of a liquid in a nanoconfinement environment (P) are theoretically described by the Kelvin eqn (1),12
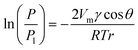 | (1) |
where P1, Vm, γ, θ, R, T and r are the saturated vapor pressure on a flat surface, the molar volume, the surface tension, the contact angle (about 10° for water on a fused-silica surface), the gas constant, the temperature, and the capillary radius of the nanospaces, respectively. A few studies have measured the vapor pressure of capillary-condensed liquids with meniscus radii in the range of 1–10 nm and above 1 μm, and discussed the applicability of Kelvin's equation to the liquids.13–16 However, the correlation between the saturated vapor pressure of liquids in extended nanospaces and the Kelvin equation has never been explored, because there have been no experimental methods for examining nanospace-confinement effects on the vapor–liquid phase transition. Therefore, in this study, we aimed to construct a novel experimental system, which can provide strictly controlled equilibrium vapor pressures and temperatures in extended nanospaces, and to clarify the space size dependence of the saturated vapor pressure of water from the observation of capillary evaporation phenomena.
As detailed information on the fabrication processes is available in our previous papers,6 only a simple explanation is given here. Two microchannels (200 μm wide (W) and 10 μm deep (D)) were fabricated using photolithographic patterning and plasma etching methods, and extended nanospace channels (W: 120–840 nm and D: 90–370 nm) were made by electron beam lithography and plasma etching methods on a fused-silica glass substrate. The rectangular-shaped extended nanospace channels, which can be determined to have a capillary radius of r = 103, 262, and 514 nm, according to the mean curvature of the meniscus 2/r = (1/D + 1/W),17 were bridged between the microchannels (Table S1† in the Supplementary Information). The fabricated substrate was washed repeatedly and then thermally bonded with a cover glass in a vacuum furnace at 1080 °C.
Fig. 1 shows a schematic diagram of the vapour–liquid phase transition measurement apparatus equipped with micro and extended nanospace channels on a chip. Air was pressurized into a water filled vial using the air-pressure controller, and the water was transferred to a second vial. Since the pressure in the second vial was slightly increased due to the transport of water, the saturated water vapor could be introduced into the micro and extended nanospace channels. This system consisting of two vials made it possible to produce stably the water vapor at lower pressures (∼5 kPa) and without bubbles. Further, the temperatures in the vials and in the micro and extended nanospace channels on a chip were individually controlled by individual Peltier stages. Actually, when the temperatures in a microchannel were measured using a thermocouple inserted into a hole drilled from the side of a chip, and compared with those on the chip surface, the two temperatures were found to be controlled with an accuracy of ± 0.01 °C. Since the plot of temperatures in a chip against those on a chip surface gave a linear relationship with a correlation coefficient of 0.999, the difference in temperatures between in chip and on chip could be corrected using this linear relationship (Fig. S1†). Moreover, in order to confirm whether the water vapor generated in the vials still provided a saturated vapor pressure at the target temperature, the humidity of the water vapor flowing from the vials to the microchannels was measured at a microchannel outlet using a capacitive hygrometer (HygroFlex, ROTRONIC AG, Switzerland) in the temperature range of 22.0 to 24.7 °C. We could confirm that the vapor pressures calculated from the experimental humidities and temperatures were in good agreement with the theoretical values obtained using Wagner's equation (Fig. S2†).18
 | ||
| Fig. 1 (a) Schematic illustration of vapor–liquid phase transition measurement apparatus. (b) Picture of the fabricated chip equipped with micro and nanochannels. | ||
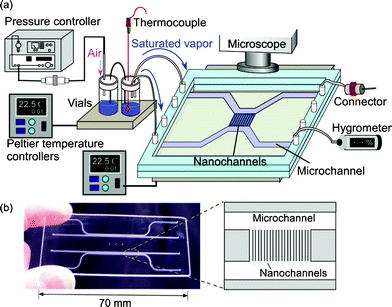
The observation of capillary evaporation phenomena of water in micro and extended nanospace channels was performed using the above experimental system in the following manner. After the water was introduced into the microchannels and extended nanospace channels (nanochannels) by capillary filling, the air-pressure controller, Peltier stages, and dual-exit vials were connected. Next, a saturated water vapor (2.645 kPa) was produced in vials at 22.0 °C and introduced from the vials into the microchannels on a chip at 21.9 °C by pressurizing at a pressure that is significantly lower than the capillary pressure. In this case, the water in the microchannels could be almost completely replaced with the saturated vapor, whilst the only water that remained was that in nanochannels and at nano–micro intersections (Fig. 2 (a)). Then, the time courses of capillary evaporation of the remaining water in the nanochannels and micro–nano intersections at temperatures between 22.0 and 22.5 °C were examined using a phase-contrast microscope (IX70, Olympus, Tokyo, Japan), with an objective lens (Olympus, ×20, NA 0.45), and a cooled CCD camera (Pentamax Gen IV, Roper. Scientific GmbH, Ottobrunn, Germany).
 | ||
| Fig. 2 (a) An illustration and a micrograph of the initial condition in micro and nanochannels at 21.9 °C. (b) Time courses of capillary evaporation of water in nano–micro intersections. | ||
Fig. 2 (b) shows typical micrographs from the video capture of the capillary evaporation of water in micro and nanochannels. When the temperature on chip was increased gradually from 21.9 to 22.0 °C in 0.01 °C steps, the evaporation of the remaining water in the nano–micro intersections began at 22.0 °C and was completed in a period of 62 s, while the water confined in the nanochannels did not evaporate. This observation means that water in the microspace has the same vapor pressure as the bulk water. As the water-filled nanochannels became vacant by evaporation, the micrograph images of the channel region should change from light to dark patterns, because of the difference in the refractive indices of water and glass. Therefore, the temperature was raised from 22.0 to 22.2 °C, and the evaporation temperatures of the confined water were examined.
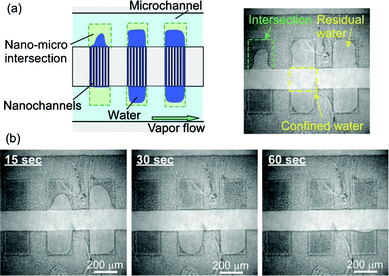
As shown in Fig. 3, changes from light to dark colors in the channel region were found to suddenly appear once the temperature reached 22.2 °C. Since part of the water-filled channels gradually evaporated, the percentage of dark colors in the whole channel region increased with the elapse of time. After a wait of 32 s, the 103 nm sized nanochannels emptied; the confined water had completely evaporated.
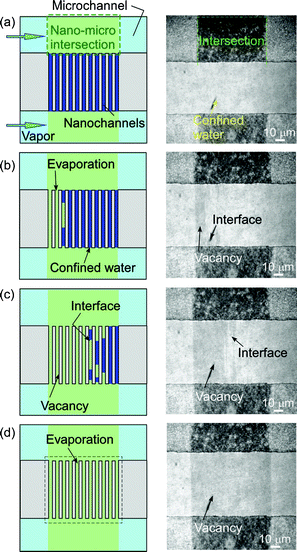 | ||
| Fig. 3 Typical illustrations and micrographs for time courses of capillary evaporation of water confined in 103 nm sized nanochannels. (a) Before reaching 22.2 °C, (b) 8 s after reaching 22.2 °C, (c) 16 s after reaching 22.2 °C, and (d) 32 s after reaching 22.2 °C. | ||
Furthermore, we were able to measure the space size dependence of the capillary evaporation temperatures of water using the same methods. The differences in the saturated vapor pressure of water for each space size could be accurately observed from the changes of evaporation temperatures in this experimental system. We found that the evaporation of water in 262 nm sized and 514 nm sized nanochannels occurred at 22.09 and 22.05 °C, respectively. These observations indicated that the saturated vapor pressure of water in the nanochannels was different from those in the bulk and micro spaces, and that the vapor pressure values were reduced by nanospace confinement.
Since the experimental saturated vapor pressure (P) at which water in the nanochannels was evaporated at certain temperatures (T) corresponded to the saturated vapor pressure (2.645 kPa) in vials at 22.0 °C regardless of the channel sizes, the P values should be significantly smaller than the saturated vapor pressure values (P1) of bulk water at each T. Therefore, the experimental P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 ratios at 22.05, 22.09, and 22.2 °C are plotted against the channel sizes and compared with the theoretical P
P1 ratios at 22.05, 22.09, and 22.2 °C are plotted against the channel sizes and compared with the theoretical P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 values calculated from the Kelvin eqn (1) at 22.0 °C in Fig. 4. Both experimental and theoretical P
P1 values calculated from the Kelvin eqn (1) at 22.0 °C in Fig. 4. Both experimental and theoretical P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 values showed a similar size dependence in which the P
P1 values showed a similar size dependence in which the P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 values decreased with decreasing channel sizes. It followed from these results that a developed experimental system made it possible to determine the correct saturated vapor pressure of liquids, and that Kelvin's equation was applicable for characterizing the vapor–liquid phase transition of liquids even in extended nanospaces.
P1 values decreased with decreasing channel sizes. It followed from these results that a developed experimental system made it possible to determine the correct saturated vapor pressure of liquids, and that Kelvin's equation was applicable for characterizing the vapor–liquid phase transition of liquids even in extended nanospaces.
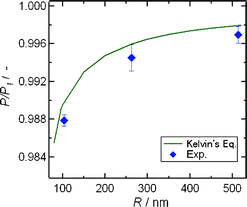 | ||
Fig. 4 Size-dependence of the experimental P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 values and theoretical P P1 values and theoretical P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 curves calculated from Kelvin's equation at 22.0 °C. P1 curves calculated from Kelvin's equation at 22.0 °C. | ||
It may be noteworthy that the experimental P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P1 value for the 103 nm sized nanochannel was not entirely in agreement with the theory, and were smaller than the theoretical value, because the slight difference between experimental and theoretical values was beyond the range of experimental errors. Such slight discrepancies would be caused by the assumption of a uniform surface tension of water in Kelvin's equation, because as mentioned above, the water confined in extended nanospaces has high viscosity, high negative pressure, and well-defined hydrogen bonding networks across the charged surfaces. Namely, the meniscus of curvature with a radius of r and pressure drop (ΔP) at the vapor–liquid interface will be changed by space size-confinement, and the surface tension (γ) of the confined water according to the Young–Laplace relationship ΔP = 2γ/r may be also different from that of bulk water.
P1 value for the 103 nm sized nanochannel was not entirely in agreement with the theory, and were smaller than the theoretical value, because the slight difference between experimental and theoretical values was beyond the range of experimental errors. Such slight discrepancies would be caused by the assumption of a uniform surface tension of water in Kelvin's equation, because as mentioned above, the water confined in extended nanospaces has high viscosity, high negative pressure, and well-defined hydrogen bonding networks across the charged surfaces. Namely, the meniscus of curvature with a radius of r and pressure drop (ΔP) at the vapor–liquid interface will be changed by space size-confinement, and the surface tension (γ) of the confined water according to the Young–Laplace relationship ΔP = 2γ/r may be also different from that of bulk water.
Conclusions
In conclusion, we succeeded in developing an experimental system for the direct observation of vapor–liquid phase transition phenomena in extended nanospaces, and found that the saturated vapor pressure of confined water decreased with decreasing space sizes. The results verified that the vapor–liquid phase transition of water in extended nanospaces could be explained well by the classical Kelvin's equation for the first time. These techniques and findings have the potential to provide a deeper understanding of vapor–liquid phase transition phenomena of liquids and for realizing nanofluidic heat exchangers as novel cooling devices.Acknowledgements
The present work was partially supported by the Grant of Core Research for Evolutional Science and Technology (CREST) from the Japan Science and Technology Agency (JST) and the Funding Program for Next Generation World-Leading Researchers (NEXT Program) from the Japan Society for the Promotion of Science (JSPS).References
- T. Tsukahara, K. Mawatari and T. Kitamori, Chem. Soc. Rev., 2010, 39, 1000 RSC.
- P. Abgrall and N. T. Nguyen, Anal. Chem., 2008, 80, 2326 CrossRef CAS.
- R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839 CrossRef CAS.
- A. Hibara, T. Saito, H-B. Kim, M. Tokeshi, T. Ooi, M. Nakao and T. Kitamori, Anal. Chem., 2002, 74, 6170 CrossRef CAS.
- N. R. Tas, J. Haneveld, H. V. Jansen, M. Elwenspoek and A. van den Verg, Appl. Phys. Lett., 2004, 85, 3274 CrossRef CAS.
- (a) T. Tsukahara, A. Hibara, Y. Ikeda and T. Kitamori, Angew. Chem., Int. Ed., 2007, 46, 1180 CrossRef CAS; (b) T. Tsukahara, W. Mizutani, K. Mawatari and T. Kitamori, J. Phys. Chem. B, 2009, 113, 10808 CrossRef CAS.
- Q. Pu, J. Yun, H. Temkin and S. Liu, Nano Lett., 2004, 4, 1099 CrossRef CAS.
- H. Daiguji, P. Yang and A. Majumdar, Nano Lett., 2004, 4, 137 CrossRef CAS.
- M. Kato, M. Inaba, T. Tsukahara, K. Mawatari and T. Kitamori, Anal. Chem., 2010, 82, 543 CrossRef CAS.
- N. Kaji, Y. Tezuka, Y. Takamura, M. Ueda, T. Nishimoto, H. Nakanishi, Y. Horiike and Y. Baba, Anal. Chem., 2004, 76, 15 CrossRef CAS.
- A. Hibara, K. Toshin, T. Tsukahara, K. Mawatari and T. Kitamori, Chem. Lett., 2008, 37, 1064 CrossRef CAS.
- Physical chemistry, ed. P. W. Atkins, Oxford University Press, Oxford, 6th edn, 1998 Search PubMed.
- L. R. Fisher, R. A. Gamble and J. Middlehurst, Nature, 1981, 290, 575 CrossRef CAS.
- H. K. Christenson, J. Colloid Interface Sci., 1985, 104, 234 CrossRef CAS.
- J. C. Melrose, Langmuir, 1989, 5, 290 CrossRef CAS.
- M. M. Kohonen and H. K. Christenson, Langmuir, 2000, 16, 7285 CrossRef CAS.
- G. Barnes, I. Gentle, Interfacial science: an introduction,Oxford University Press, Oxford, 2nd edn, 2011 Search PubMed.
- W. Wagner and A. Pruss, J. Phys. Chem. Ref. Data, 1993, 22, 783 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra01330d/ |
| This journal is © The Royal Society of Chemistry 2012 |
