Recording temporal characteristics of convection currents by continuous and segmented-flow sampling†
Po-Han
Li
a,
Hsu
Ting
a,
Yu-Chie
Chen
ab and
Pawel L.
Urban
*ab
aDepartment of Applied Chemistry, National Chiao Tung University, Hsinchu 300, Taiwan
bInstitute of Molecular Science, National Chiao Tung University, Hsinchu 300, Taiwan. E-mail: plurban@nctu.edu.tw
First published on 12th October 2012
Abstract
Despite the fact that the natural distribution of chemical substances in the three-dimensional world is far from homogeneous, most liquid-phase chemistry involves operations on homogeneous solutions. Here we describe two facile methods for real-time monitoring of liquid-phase chemical heterogeneity induced by convection in millilitre-range volumes. The liquid medium was continuously aspirated from the vial (acting as a “convection chamber”), and driven to online detectors either using continuous or discontinuous (segmented) hydrodynamic flow. In one embodiment, after the initial passage through a flow-through optical detector, the sample was driven to an electrospray ion source—set in front of the orifice of an ion trap mass spectrometer. The system recorded the emergence of chemical waves produced as a result of convection currents from the test substances introduced to the vial. Both variants of the method (using continuous and segmented flow) revealed fluctuations of the analyte concentration before an equilibrium was reached, and the mixture became homogeneous. We believe that this analytical scheme can further be used to study spatiotemporal characteristics of various dynamic chemical systems in liquid phase.
1. Introduction
A vast majority of contemporary developments and applications in liquid-phase chemistry deals with homogeneous solutions. Synthetic chemists pay a lot of attention to adequate mixing of reaction mixtures; inhomogeneities could lead to a decrease in reaction efficiency, or produce system instabilities. Also in analytical chemistry, homogenisation of samples is essential for ascertaining reliable and reproducible results. However, many natural and human-triggered processes are non-homogeneous; examples include the diffusion of atmospheric gases into ocean waters, and dispersion of environmental pollutants in the atmosphere, or in water reservoirs. Chemical gradients are omni-present in the macro-world and micro-worlds: for example, organisms emit signalling molecules in their habitats while individual cells do the same in their microenvironments in order to exert a response of other biological entities. Diffusion (passive transport of molecules from a zone with a high concentration) and convection (collective movement of molecules within fluids) further contribute to the dispersion of these chemical species until an equilibrium is reached. On the sub-cellular and supra-cellular levels, chemical gradients are responsible for the evolution of important physiological processes.Chemical analysis of the convection-driven currents can contribute to better understanding of natural and artificial processes. For example, consider chemical reactions that require high concentrations of reactants—in those cases, a homogeneous reaction environment may incur a dilution of reactants. On the other hand, convection process may allow one to increase the contact area of reactants (or a reactant and a catalyst) without considerable dilution. Thus, recording temporal characteristics of convection currents can provide an insight into chemical processes in heterogeneous mixtures. However, analytical methods for studying the propagation of chemical waves in non-equilibrated mixtures are scarce. For example, the so-called “Hele–Shaw cell” enables observation of convection patterns in a quasi-two-dimensional environment.1 Optical imaging methods provide high lateral resolution but have poor chemical selectivity. On the other hand, when analyzing three-dimensional samples using spectrophotometric tools, one has to assume a perfect homogeneity of a solution, so that the absorption laws are obeyed (cf. Fig. S1A). Therefore, spectrophotometry—in its standard format—is not directly applicable to the analysis of chemical heterogeneity. The same holds for other modern analytical techniques such as mass spectrometry (MS), in which case liquid samples are typically loaded into syringes in order to infuse them via electrospray ionization (ESI) emitter into MS orifice; this normally eliminates the possibility of studying chemical gradients which occur in liquid media.
One way of recording dynamic spatiotemporal gradients in heterogeneous mixtures is continuous sampling of the medium, followed by the transport of the samples to a detection system (cf. Fig. S1B, ESI†). However, the suction of fluids into capillary tubing or microfluidic devices is likely to blur the spatiotemporal gradients present in the sampled media. Although hydrodynamic dispersion (zone broadening) of sample plugs transported in microfluidic channels can be reduced by implementing electrokinetic flow,2 application of electric field is not always feasible or convenient. Another way to reduce dispersion of samples transported in a flow line is by implementing segmented flow, which can readily be achieved by simultaneous injection of two immiscible fluids into a capillary or a microfluidic channel.3,4 Segmented-flow systems can readily be coupled with various types of analytical instruments; in fact, this approach has widely been used in enzyme assays,5,6 analysis of proteins,7,8 small molecules,9–12 and single-cell analysis.13,14 Segmented flow can also be used in conjunction with various detection platforms, including nuclear magnetic resonance (NMR)15 and mass spectrometry (MS).16–19
Building on previous work outlined above, here we show two facile methods for recording spatiotemporal gradients formed during convection of substances in liquid media—used as a model process, which illustrates the dynamics of chemical heterogeneity in the three-dimensional space. The methods presented here are either based on continuous or segmented flow fluid transport, and used in conjunction with visible-range absorbance and/or mass spectrometric detection.
2. Materials and methods
2.1 Materials
Caffeine, ferroin, n-octanol, and reserpine were purchased from Sigma-Aldrich (St Louis, USA). Inks (Simbalion, New Taipei City, Taiwan) were purchased from a local stationery shop. The fused silica capillary with the ID 150 μm (OD 375 μm) was purchased from GL Science (Tokyo, Japan), while the ID 320 μm (OD 435 μm) and the ID 450 μm (OD 673 μm) were purchased from Polymicro (Phoenix, USA). Tygon tubing of different kind was purchased from both Saint Gobain (Akron, USA) and Idex (Oak Harbor, USA).2.2 Experimental set-up
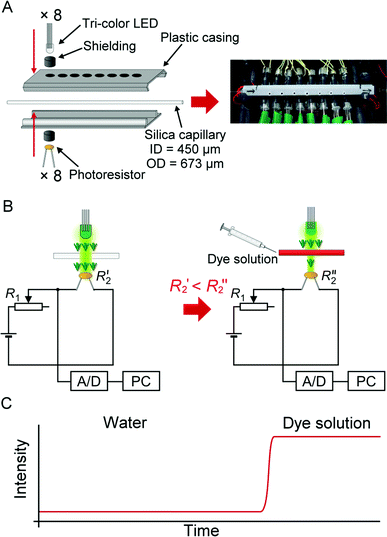 | ||
| Fig. 1 Multi-point multi-wavelength flow-through optical detector. (A) Assembly of the device. (B) Electronic circuit for the absorbance measurement in an individual channel. Note that only up to 3 channels were used in this study. (C) An ideogram showing a typical response of the detector following the injection of a light-absorbing solution. | ||
The optical cell was incorporated into an 8-hole plastic casing (Fig. 1A, left panel). The holes have a diameter of 4.1 mm, and are spaced at 8-mm interval. The inner surface of the casing was lined with aluminium foil. An infrared μs-laser engraving machine (Huahia Laser, Taipei, Taiwan) was used to create eight pinholes (diameter, ∼450 μm) on the aluminium foil. Polyimide coating was removed from a standard GC-type fused silica capillary (length: 12 cm; ID 450 μm, OD 673 μm)—used as the optical cell—and the transparent section of the capillary was precisely aligned with the pinholes along the aluminium foil lining inside the plastic casing. The two parts of the plastic casing were joined together, so that the positions of the LEDs on one side matched the positions of the photoresistors mounted on the opposite side (Fig. 1A, left panel). Smaller holes were drilled on the plastic casing in order to increase air circulation (Fig. 1A, right panel). The optical cell assembly was installed inside a styrofoam box (inner dimensions: 24 × 22 × 10 cm, w/d/h). Three PC-type electric fans were also installed in the box to enhance air circulation, and to facilitate heat dissipation. The fused silica capillary was connected to the upstream and the downstream parts of the flow line with Tygon tubing (ID 0.38 mm, OD 2.2 mm).
The wavelength of the light emitted by the tri-colour LEDs was controlled by the relay board (Denkovi Assembly Electronics, Byala, Bulgaria). An analog/digital data logger (ADC-20; resolution: 20 bits; input range: ± 2.5 V; preset sampling rate: 61–183 ms data-point−1; Pico Technology, St Neots, United Kingdom) was used to record the electric potentials at the outputs of the photoresistor circuits. Both devices were connected to a computer via USB ports, and operated with appropriate software packages. The segmented-flow data were treated using a custom software program written in Free PASCAL (version 1.0.10 2009/04/10; B. Gábor, P. Muller, P. Vreman); the algorithm automatically removed the features due to n-octanol segments, and preserved the features due to the water-based segments.
When using the hyphenated system, several modifications had to be introduced to the convection chamber and the sampling setup: Two fused silica capillaries (length: 6 cm; ID 320 μm; OD 435 μm) were transferred through the septum in the cap (18-MSL-ST3; Thermo Fisher Scientific, Waltham, USA) of the 20-mL glass vial (20-HSV; Thermo Fisher Scientific) acting as the sample/convection chamber. One of these capillaries was connected to the syringe pump, and the other one was connected to the downstream flow line (Tygon tubing) with the optical detector and the mass spectrometer. The fused-silica capillary used as the ESI emitter (length: 2 cm; ID 150 μm; OD 375 μm) was mounted in a tiny hole made in the Tygon tubing (ID 0.38 mm; cf. Fig. S3A, ESI†). The distance between the ESI emitter and the orifice of the ion trap MS was relatively long (∼2 cm) in order to avoid contaminating the instrument when concentrated samples were analyzed. Since the section of Tygon tubing mounted downstream from the ESI emitter exerted a slight backpressure on the liquid in the flow line, a small portion of the liquid was diverted to the fused silica capillary section acting as the ESI emitter. Recently, a method of introducing samples to mass spectrometers without the need for establishing an electrical connection at the emitter has been published.20 In our system, we also skipped the electrical connection at the ESI emitter, which greatly simplified the design and operation of the system without damaging its performance. We used the amaZon speed ion trap mass spectrometer from Bruker Daltonics (Bremen, Germany). The voltage applied to the ion transfer capillary was −5500 V (positive-ion mode), and the end-plate offset was set to 500 V. The flow rate of the dry gas was set to 12 L min−1. The mass range was 70–380 Da, and the accumulation time was 0.5 ms.
At the beginning of the experiment, before acquiring data, the test analyte (ferroin) was injected into the lower part of a glass vial filled with ∼21 mL of an aqueous solution containing caffeine (4.8 × 10−5 M) and acetic acid (0.5%). The data acquisition started when the syringe pump was turned on, and the 0.5%-solution of acetic acid was pumped into the vial. Since the vial was completely filled with the liquid medium, the acetic acid solution—injected with the syringe pump—exerted hydrodynamic pressure on its contents; as a result, the liquid medium was pushed out via the second capillary mounted in the septum. Overall, this setup provided an adequate flow stability for the continuous MS analysis.
In order to measure the effective flow rate of the sample in the ESI emitter, we implemented the experimental setup shown in Fig. S3.† Water was pumped through the flow line by syringe pump at the flow rate of 30 μL min−1. Effluent was collected at the outlet of the Tygon tubing (ID 0.13 mm) during a 10-min interval. The net weight of the effluent aliquots was determined using analytical balance. The procedure was performed with the mass spectrometer turned on and off, and also after the removal of the ESI emitter (Fig. S3B†). The flow rate of liquid sample in the ESI emitter was then calculated by subtraction of the flow rates determined for the eluate collected at the outlet of the Tygon tubing—without and with the ESI emitter installed.
3. Results and discussion
3.1 Monitoring convection-driven currents by optical detector
Here we demonstrate probing chemical waves, which are formed in a liquid medium due to convection, by using continuous flow sampling in conjunction with optical absorption detection. A small amount of medium is sampled and transferred along the capillary flow line towards detector by using either segmented flow or non-segmented (continuous) flow. At the beginning of the experiment, we injected a small aliquot of ferroin solution into the bottom of a 20-mL glass vial. Subsequently, the lower part of the vial was heated up (∼34 °C) in order to develop a temperature gradient, and induce convective mixing of the ferroin solution with the aqueous medium present in the vial. We used a syringe pump operated in the withdrawal mode in order to pull the contents of the vial with the flow rate of 30 μL min−1. An immiscible solvent (n-octanol) was simultaneously injected to the Y-junction (installed along the flow line) by a syringe pump operated in the infusion mode at the flow rate of 6 μL min−1 (Fig. 2A). Taking into account the low ratio of the cross sections of the sampling capillary (ID 0.320 mm) and the convection chamber (ID 20 mm), estimated to 2.6 × 10−4, it is expected that the laminar hydrodynamic flow (∼24 μL min−1, Re < 3) in the sampling tubing does not significantly perturb the spatiotemporal pattern of the convection waves developing in the chamber.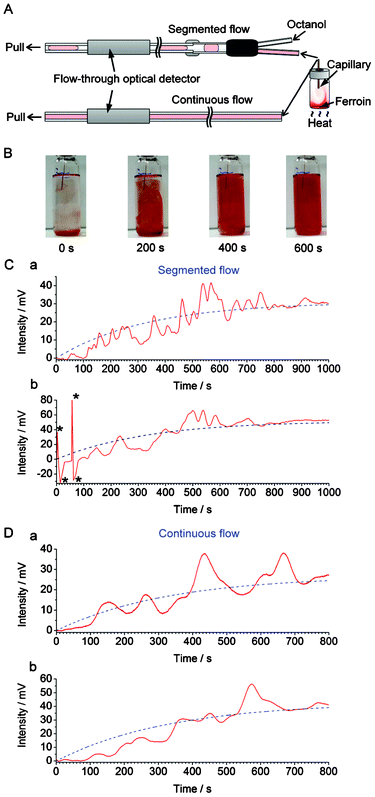 | ||
| Fig. 2 Recording convection with segmented and continuous flow. (A) Experimental setup used in the real-time sampling with/without segmented flow prior to detection by the flow-through optical detector (cf.Fig. 1). The segmented flow was generated by pushing n-octanol towards the Y-junction while the bulk of the liquid was withdrawn by a syringe pump at the outlet of the flow line. (B) Photographs of the vial (nominal volume: 20 mL) during the convective mixing of 100 μL ferroin with 15 mL water (aided by heating). The ID of the capillary used for on-line sampling was 320 μm. Distance from the bottom of the vial to the inlet of the capillary: ∼40 mm. (C) The output data (red solid line) obtained with the segmented flow sampling (2 replicates: (a) and (b)). The blue dashed lines correspond to the exponential functions fitted to the experimental data (after removal of n-octanol-related features from the trace): (a) f(t) = 31 × (1 − e(−0.0030t)); (b) f(t) = 52 × (1 − e(−0.0030t)). The features marked with asterisks (*) are due to air bubbles. (D) The output data (red solid line) obtained with the continuous flow sampling (2 replicates: (a) and (b)). The blue dashed lines correspond to the exponential functions fitted to the raw data: (a) f(t) = 27 × (1 − e(−0.0030t)); (b) f(t) = 43 × (1 − e(−0.0030t)). The ranges of horizontal axes in (C) and (D) were adjusted in order to represent comparable sampling volumes (taking into account differences in the effective sampling rates). | ||
Fig. 2B shows photographs of the inlet vial representing the convection-driven mixing of ferroin (red) with the liquid medium (transparent) while Fig. S4, ESI† shows the corresponding raw data obtained with the optical detector. The “ups” and “downs” in the original signal trace are caused by differences in refractive indices and extinction coefficients of n-octanol and the aqueous samples. The relative heights of the bottom parts of the valleys in Fig. S4† vary according to the absorbance of the plugs sampled from the vial. In order to simplify the representation of the data, a custom software was used to remove the signal of n-octanol, and the treated data is displayed in Fig. 2C (red solid line). From this data it is clear that the signal increased due to the increasing absorbance of ferroin. Interestingly, the increase of the absorbance with time (in relative units) cannot be described by any simple function, as one could do for the diffusion process. The gradual mixing of ferroin with the liquid medium is a random and chaotic process, and the trace in Fig. 2C (red solid line) represents numerous fluctuations before the signal stabilizes at a level when the mixture became a homogeneous solution.
Next, we carried out a similar experiment but using continuous (non-segmented) flow to transfer samples from the glass vial to the detector. This yielded a curve which also represents some fluctuations (Fig. 2D, red solid line). However, in this case, the trace is much smoother than the curve obtained using segmented flow (Fig. 2C, red solid line). This unwanted “smoothing effect” is due to advection and diffusion (e.g.ref. 18,21), taking place in the flow line—between the sample inlet and the detector. By digitizing three-dimensional chemical waves, the segmented flow sampling preserves the temporal characteristics better than continuous flow; this is in agreement with the previous studies implementing segmented flow.10,11 In the present study, the temporal resolution obtained using the segmented flow is defined by the signal rise time equal to ∼8 s (cf. Fig. S5, ESI†). The difference between this value and the duration of the signal of each segment (∼4 s, cf. Fig. S4†) is due to the hydrodynamic dispersion of the sample between the sampling capillary inlet and the Y-junction used to generate the segmented flow.
In both cases, the traces can be fit with exponential functions (Fig. 2C and 2D, blue dashed line), which represent the mixing trends. In all cases, the time constants were ∼333 s (τ = 1/0.0030). Despite the fluctuations caused by convection currents, the equilibriums are reached at similar times (taking into account the small difference between the effective sampling flow rates in the segmented-flow and continuous flow systems). In Fig. S6, ESI,† the experimental data (cf.Fig. 2Ca and 2Da, red solid line) were subtracted with the values predicted by the fitted exponential functions (cf.Fig. 2Ca and 2Da, blue dashed line): this representation highlights the presence of strong fluctuations of relative absorbance due to the convection process. These fluctuations are especially apparent in the middle of the data record, i.e. 400–800 s (segmented flow, Fig. S6A†), and 300–700 s (continuous flow, Fig. S6B†). From Fig. 2C it is also clear that at some points the relative absorbance values (represented by the measured potential) are much higher than the equilibrium-stage absorbance at the end of the data record. This result points out an important feature of the convection current; a momentary concentration of the substance away from the source may be higher than the concentration of this substance after complete mixing with the medium. This feature has implications on the real-world convection systems, for example, the release of pollutants to the environment. Overall, the experiments discussed above show the feasibility of sampling convection-induced waves from liquid media on the scale of micro- to millilitres. In order to realize the possibility of performing measurements at various wavelengths offered by the detector described above (cf.Fig. 1), we further attempted the monitoring of sequential convection of substances with different absorption maxima (Fig. 3). First, an aliquot of 100 μL of a blue ink was injected into to the lower part of the 20-mL glass vial, which was then heated up to induce convection, and segmented flow was then used for sampling (Fig. 3A). The blue ink absorbs green and red light (wavelength range of red: 600–700 nm, green: 490–560) but it does not absorb blue light (wavelength range 450–490 nm, cf. Fig. S7B, ESI†). Therefore, one could observe the fluctuating increase of the signal in the detection channels operating at wavelengths 629 and 518 nm (Fig. 3B). Subsequently, a 100-μL aliquot of ferroin was injected into the lower part of the same vial. This time the detection channels operating at wavelengths 518 and 463 nm produced a significant change in the light absorption traces (Fig. 3C). In a similar experiment, two dyes with different absorption maxima were dispersed in water, and the segmented-flow sampling routine was carried out. Signals were recorded at three different wavelengths. As can be seen in Fig. 4, the convection waves of the two dyes—absorbing light at different wavelengths—did not overlap. This is because the two samples were not delivered in a mixture but separately, and the mixing occurred simultaneously with the convection process.
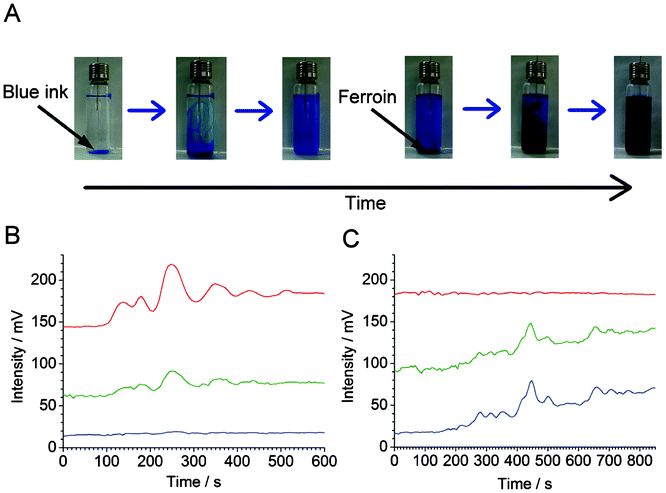 | ||
| Fig. 3 Sequential convection of two substances with different visible light absorption maxima. (A) Photographs of the vial (nominal volume: 20 mL) filled with 15 mL of water after injection of blue link (three pictures to the left), and ferroin (three pictures to the right). (B,C) Sampling and detection of the vial content by segmented flow used in conjunction with the home-made optical detector (cf.Fig. 1). (B) Measurement started after the injection of 100 μL of blue ink (50× diluted original sample). (C) Measurement started after subsequent addition of 100 μL of ferroin sample. In (B) and (C), different wavelength channels are denoted by their apparent colour (red, green, and blue light—top to bottom). Wavelengths: λred = 629 ± 6.5 nm, λgreen = 518 ± 16 nm, λblue = 463 ± 11 nm. The traces were shifted vertically for clarity. The delay time between red/green and green/blue channels is ∼2.5 s. The raw data have been treated with a custom software in order to eliminate the peaks due to the n-octanol plugs. | ||
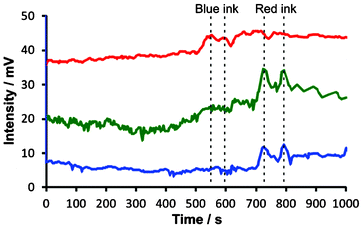 | ||
| Fig. 4 Simultaneous convection of two dyes absorbing light of different wavelength using the optical detector shown in Fig. 1. Blue ink (100 μL, diluted 20×) and red ink (100 μL, diluted 20×) were injected into a beaker containing 50 mL of 25% ethanol solution in water. The lower part of the beaker was heated up to ∼34 °C to speed up convective mixing of the inks with the medium, and the contents of the beaker were constantly aspirated by the sampling capillary and digitized in the segmented flow generator (cf. Fig. S2, ESI†). Different wavelength channels are denoted by their apparent colour (red, green, and blue light—top to bottom). Wavelengths: λred = 629 ± 6.5 nm, λgreen = 518 ± 16 nm, λblue = 463 ± 11 nm. The traces were shifted vertically for clarity. The traces were also shifted horizontally to compensate for the delay caused by sequential detection in the three channels (red, green, and blue). The time “zero” roughly corresponds to the start of the experiment, even though some mixing of the ink with the medium could already be noticed during the introduction of the sample to the beaker. Vertical dashed lines highlight non-overlapping waves of the two inks. | ||
3.2 Monitoring convection-driven currents by optical detector and mass spectrometer
Optical detection benefits from the direct dependence of absorbance on concentration, warranted by the Beer–Lambert law; however, it has poor selectivity. In order to demonstrate the possibility of continuous sampling of chemical waves—such as those due to the convection currents—we have attempted coupling the home-made flow-through optical detector with a mass spectrometer. Several technical problems had to be solved to assure satisfactory performance of the system. When coupling the convection monitoring setup with MS, we opted for using continuous flow because it provided much better signal stability than using segmented flow. Moreover, maintaining a high sampling rate is essential to ensure satisfactory temporal resolution. However, when coupling fluidic systems with MS, it is not desirable to work with high flow rates. Therefore, we have implemented “split-flow” coupling of the sampling setup with MS via an electrode-free ESI interface (Fig. 5A), as described in section 2.2.3. A section of Tygon tubing with a relatively small ID (0.13 mm) was used to produce a backpressure (∼160 mbar), and divert a desired fraction of the flow towards the ESI emitter. In this experiment, the nominal flow rate was set to 30 μL min−1. The flow rate measured in the fused silica capillary (ESI emitter) was found to be ∼6.7 μL min−1 (Table S1, ESI†). Counter-current flow (12 L min−1) of dry gas (N2 at 250 °C) was used to ensure desolvation of microdroplets formed at the ESI emitter.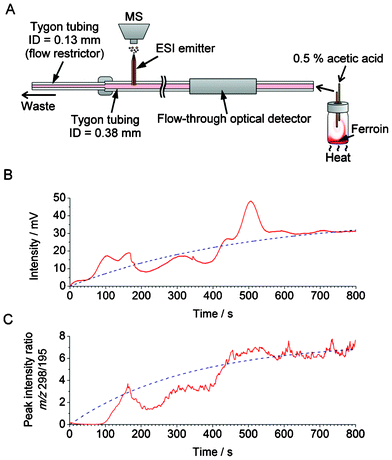 | ||
| Fig. 5 Application of the hyphenated system—incorporating the home-made optical detector (cf.Fig. 1) and mass spectrometer—in the monitoring of the chemical current due to convection. (A) Experimental setup. Nominal volume of the vial is 20 mL. The vial was completely filled with ∼21 mL the aqueous medium containing the internal standard (caffeine). (B,C) Measurement of the relative changes in the concentration of ferroin in the course of convection. (B) Optical detection; the raw data (red solid line) were fitted with an exponential function (f(t) = 31 × (1 − e(−0.0035t)), blue dashed line). (C) MS detection; the smoothed data were fitted with an exponential function (f(t) =7.5 × (1 − e(−0.0030t)), blue dashed line). The data acquisition with MS started 132 s after the start of the data acquisition with the optical detector in order to compensate for the dead-volume delay. | ||
Similarly to the previous experiments, discussed in section 3.1, a 100-μL aliquot of ferroin solution was injected into the lower part of a 20-mL glass vial, and the convective mixing was induced by heating (∼34 °C) (Fig. 5A). Fig. 5B shows the results obtained by the home-made optical detector (wavelength: 518 nm) as well as the mass spectrometer. In this experiment, caffeine was added to the liquid medium present in the glass vial, and used as an internal standard. Fig. 5C shows the resulting plot representing the intensity ratios of ferroin ([M]2+) and caffeine ([M+H]+) peaks at the m/z 298 and 195, respectively. The MS result approximately matches the result obtained from the flow-through optical detector, with the time constants equal to ∼333 and 286 s, respectively. However, exact matching is hindered by the fact that dispersion and diffusion occur as the sample traverses the flow line section between the optical detector and the ESI emitter, non-linear response of the ion-trap MS, and possible ionization biases. In particular, the role of hydrodynamic dispersion in peak deformation is evident from the comparison of the segmented-flow and the continuous-flow sampling (Fig. 2C and 2D). As noted above, we chose to combine continuous (non-segmented) flow with MS, which—in the case of the present study—provided a higher stability of MS signal than the segmented flow. In order to demonstrate the further capabilities of the MS monitoring of convection, we used this experimental setup to monitor convection waves of a substance that does not absorb visible light: using the ESI-MS setup shown in Fig. 5A, convection of reserpine could readily be monitored in the presence of an internal standard (Fig. S8, ESI†).
4. Conclusions
We have demonstrated two simple methods for monitoring liquid-phase chemical heterogeneity induced by convection—in millilitre-range volumes—in real time. In essence, the three-dimensional chemical waves present in the vial acting as a convection chamber were sampled into a one-dimensional flow line, and transferred to single-point (zero-dimensional) detectors. Segmented-flow sampling preserves the characteristics of convective currents to a greater extent than continuous-flow sampling. This is attributed to the occurrence of hydrodynamic dispersion in the continuous-flow system, which is reduced when using the method with segmented flow. However, continuous-flow sampling is better suited for coupling the fluidic system with mass spectrometer.We are currently working on various practical applications of the proposed analytical methods: they include monitoring chemical waves in unstirred reaction vessels, spatiotemporal gradients produced by oscillating reactions, and waves of signalling molecules secreted by biological cells. The proposed methods can be further developed by hyphenating them with other detectors, including UV absorption detection, electrochemical detection, and microscale nuclear magnetic resonance. They can also be used to study other dynamic processes, for example, dissolution of pharmaceutical preparations. The systems described here operate in liquid phase; however, in the future, it would also be interesting to develop them further to probe convection waves in the gas phase.
Acknowledgements
We wish to thank Dr Mathivathani Kandiah for correcting our manuscript. We thank the National Science Council of Taiwan, and the Center of Interdisciplinary Science for the financial support of the work. We also thank the National Chiao Tung University for providing the start-up funds for the purchase of the ion-trap mass spectrometer.References
- C. Almarcha, P. M. J. Trevelyan, P. Grosfils and A. De Wit, Phys. Rev. Lett., 2010, 104, 044501 CrossRef CAS.
- S. J. Haswell and V. Skelton, TrAC, Trends Anal. Chem., 2000, 19, 389 CrossRef CAS.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163 CrossRef CAS.
- M. Joanicot and A. Ajdari, Science, 2005, 309, 887 CrossRef CAS.
- L. Mazutis, J.-C. Baret, P. Treacy, Y. Skhiri, A. F. Araghi, M. Ryckelynck, V. Taly and A. D. Griffiths, Lab Chip, 2009, 9, 2902 RSC.
- L.-F. Cai, Y. Zhu, G.-S. Du and Q. Fang, Anal. Chem., 2012, 84, 446 CrossRef CAS.
- L. S. Roach, H. Song and R. F. Ismagilov, Anal. Chem., 2005, 77, 785 CrossRef CAS.
- C. Martino, M. Zagnoni, M. E. Sandison, M. Chanasakulniyom, A. R. Pitt and J. M. Cooper, Anal. Chem., 2011, 83, 5361 CrossRef CAS.
- D. Chen, W. Du, Y. Liu, W. Liu, A. Kuznetsov, F. E. Mendez, L. H. Philipson and R. F. Ismagilov, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16843 CrossRef CAS.
- M. Wang, T. Slaney, O. Mabrouk and R. T. Kennedy, J. Neurosci. Methods, 2010, 190, 39 CrossRef CAS.
- T. R. Slaney, J. Nie, N. D. Hershey, P. K. Thwar, J. Linderman, M. A. Burns and R. T. Kennedy, Anal. Chem., 2011, 83, 5207 CrossRef CAS.
- O. J. Miller, A. El Harrak, T. Mangeat, J.-C. Baret, L. Frenz, B. El Debs, E. Mayot, M. L. Samuels, E. K. Rooney, P. Dieu, M. Galvan, D. R. Link and A. D. Griffiths, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 378 CrossRef CAS.
- J.-U. Shim, L. F. Olguin, G. Whyte, D. Scott, A. Babtie, C. Abell, W. T. S. Huck and F. Hollfelder, J. Am. Chem. Soc., 2009, 131, 15251 CrossRef CAS.
- S.-Q. Gu, Y.-X. Zhang, Y. Zhu, W.-B. Du, B. Yao and Q. Fang, Anal. Chem., 2011, 83, 7570 CrossRef CAS.
- R. A. Kautz, W. K. Goetzinger and B. L. Karger, J. Comb. Chem., 2005, 7, 14 CrossRef CAS.
- T. Hatakeyama, D. L. Chen and R. F. Ismagilov, J. Am. Chem. Soc., 2006, 128, 2518 CrossRef CAS.
- J. Pei, Q. Li and R. T. Kennedy, J. Am. Soc. Mass Spectrom., 2010, 21, 1107 CrossRef CAS.
- P. Song, N. D. Hershey, O. S. Mabrouk, T. R. Slaney and R. T. Kennedy, Anal. Chem., 2012, 84, 4659 CrossRef CAS.
- S. Sun, T. R. Slaney and R. T. Kennedy, Anal. Chem., 2012, 84, 5794 CrossRef CAS.
- C.-H. Hsieh, C.-H. Chang, P. L. Urban and Y.-C. Chen, Anal. Chem., 2011, 83, 2866 CrossRef CAS.
- M. Trojanowicz (ed.), Advances in Flow Analysis, Wiley, Weinheim, 2008 Search PubMed.
Footnote |
| † Electronic Supplementary Information (ESI) available: additional table and figures. See DOI: 10.1039/c2ra21695g |
| This journal is © The Royal Society of Chemistry 2012 |
