Enhanced oil recovery using the ionic liquid trihexyl(tetradecyl)phosphonium chloride: phase behaviour and properties
Sara
Lago
a,
Héctor
Rodríguez
a,
Mohammad K.
Khoshkbarchi
b,
Ana
Soto
a and
Alberto
Arce
*a
aDepartment of Chemical Engineering, University of Santiago de Compostela, E-15782, Santiago de Compostela, Spain. E-mail: alberto.arce@usc.es
bKimia Process, Calgary, Canada
First published on 7th August 2012
Abstract
With a decrease in world oil reserves and a higher demand for petroleum and its derived products, the effective exploitation of oil reservoirs has become increasingly important. Enhanced oil recovery (EOR) assisted by surfactants is an effective method for recovering the oil from reservoirs that have lost their drive after the application of primary and secondary recovery methods. This research is aimed at showing the suitability of several ionic liquids as effective replacements for conventional surfactants in EOR. The reservoir fluid has been modelled as a ternary system of water (pure water or aqueous solution of NaCl) plus the ionic liquid trihexyl(tetradecyl)phosphonium chloride plus dodecane. Determination of its liquid–liquid phase equilibrium indicates the formation of a Winsor type III system, with a triphasic region and adjacent biphasic regions. The interfacial tensions in the system corroborate the ability of the ionic liquid to act as a surface active agent, as desirable for its use in an EOR process. A relevant transport property such as viscosity, in addition to density, has been experimentally measured for the equilibrium phases.
Introduction
The worldwide diminution of easy-to-access oil, along with an increase in the demand for oil and its high price, has rendered full exploitation of reservoirs (including the recovery of the hard-to-access oil) necessary. Enhanced oil recovery (EOR) methods have proven to be effective in recovering the remaining oil from reservoirs that have lost drive during the application of primary and secondary recovery methods.1Currently, the most commonly used EOR methods can be classified in three categories: thermal, miscible displacement, and chemical flooding. One of the EOR processes whose use is growing at a faster pace is miscible flooding with CO2 as solvent. The main problem with miscible gas flood EOR is the adverse mobility ratio caused by the low viscosity of the typical injecting gas compared to oil, which could be as high as one or two orders of magnitude. This results in the formation of an unstable front between the gas and the oil, leading to the generation and propagation of undesired, viscous fingers in the displaced fluid.
An alternative method that does not suffer from the shortcomings of the miscible flooding is chemical EOR. The most investigated and used chemicals in this technique are surfactants, polymers and alkalis. Surfactant flooding, also known as microemulsion flooding, is based on injecting an aqueous solution of surfactant, of low concentration, into the reservoir. This produces a low interfacial tension between oil and water, which in turn enhances the mobility of the oil trapped inside the reservoir and releases the oil retained in the rocks, letting it be flushed away by the flowing water. The surfactant viscosity should be high enough to decrease the water/oil mobility ratio, but not as much to create pumping problems. Although the surfactant flooding technique is promising, its application to date has been limited due to the high cost of the surfactant and the difficulty in its recovery, as a result of its adsorption onto the oil bearing formation rocks.2 For these reasons, there is growing interest in finding new surfactants whose properties best fit the surfactant EOR requirements, and which optimise the process.
Within the large family of ionic liquids (salts with melting temperatures below 100 °C), some have been found to be surface active agents. Pino et al.3 have described several dozens of ionic liquids that exhibit characteristics of cationic surfactants (long carbon chain substituents appended to a charged cationic headgroup) and summarise their important applications in analytical chemistry and separation science. The amphiphilicity responsible for a remarkable interfacial and aggregation capability of ionic liquid surfactants may be associated with the cation, with the anion, or with both.4 Properties such as the critical micelle concentration or the aggregation number can be controlled by changing the length and shape of the hydrocarbon tail, the type of polar head group, and/or the nature and size of the counter-ion.5
As a result of the above, surface active ionic liquids have the potential to constitute an attractive alternative to the surfactants commonly used in EOR processes, with important advantages over the traditional surfactant or polymer flooding methods; for instance:
• Ionic liquids are often liquid (and essentially non-volatile) over a wide temperature range.
• It is possible, in principle, to “design” an optimum ionic liquid for specific reservoir conditions (considering different fluid and rock properties).
• Ionic liquids have a relatively high viscosity, which is important to prevent the formation of digitations (phase degradation) resulting from unfavourable mobility rates.
• The use of co-surfactants (usually long chain alcohols, which are volatile compounds and pose an environmental risk) may be avoided. This is as a result of the strong cohesive forces in ionic liquids, which enable them to form stable micelles without the need of additional chemicals.
During surfactant-assisted EOR, once the chemicals are injected within the reservoir, the fluid system has three primary constituents: oil, water and surfactant. To analyse the effectiveness of a proposed EOR method, it is critical to have knowledge of the phase behaviour of the ternary system water + surfactant + oil, as well as of the physical and transport properties of each phase. The phase behaviour of ternary systems of this kind was first studied by Winsor,6 who defined three types of ternary phase diagrams at a fixed temperature and pressure. A Winsor type III phase diagram contains a three-phase region surrounded by three biphasic regions (one of which is usually negligible), and a monophasic region. A surfactant forming this type of phase diagram is considered to be in optimum formulation, meaning that its physicochemical properties are such that it can generate an extremely low interfacial tension between phases. Therefore, during the EOR process, this surfactant can eliminate the capillary forces that hold the oil in the porous medium, thus improving the oil recovery. Several Winsor type III diagrams have been found in the literature for water + ionic liquid + oil systems,7–9 although they are not focused on EOR.
Murillo-Hernández and Aburto10 summarised several applications of ionic liquids in the petroleum industry. One of these is the capacity of ionic liquids to solubilise heavy compounds in oil (asphaltenes, paraffins...). Several works on this topic show that the viscosity of oils decreases considerably after being treated for removal of asphaltenes and similar substances.11 Thus, the ability of some ionic liquids to solubilise those heavy compounds may also be advantageous if ionic liquids are used in EOR, where such solubilisation into a distinct phase would contribute to levelling the viscosity of the aqueous and organic phases. Other researchers have investigated the use of ionic liquids to demulsify water-in-crude oil emulsions.12,11a To the best of our knowledge, there are no studies in the literature directly focused on the use of ionic liquids as replacements of conventional surfactants in EOR; only a recent work on the use of these compounds as co-surfactants complementing the action of classical surfactants.13
In this work, experimental measurements have been carried out to evaluate the ability of the IL [P6 6 6 14]Cl to act as a surface active agent (surfactant) to reduce the interfacial tension between water and oil, with the aim of using this IL in EOR. In addition to its intrinsic chemical structure and some appropriate physical properties, the [P6 6 6 14]Cl has been selected for being liquid at room temperature. This ionic liquid-based EOR system has been modelled as a ternary system constituted by water, the ionic liquid and dodecane. The liquid–liquid equilibrium for this ternary system has been determined at 25 °C and atmospheric pressure. The surface activity of [P6 6 6 14]Cl has been studied by measuring the interfacial tension, density, and viscosity of the equilibrium phases formed by various mixtures of water + [P6 6 6 14]Cl + dodecane. To study the effect of salinity, the experimental measurement of the properties was also performed on the same system, just replacing water with a brine solution (4% (w/w) NaCl).
Experimental
Materials
Dodecane (≥99%) was purchased from Merck. In spite of its high purity, the small content of impurities drastically affects the interfacial tension measurements. Prior to use, it was washed with fresh water three times and passed through a column of alumina (Sigma-Aldrich, activated, basic, Brockmann I) several times, until its equilibrated mixture with water yielded an interfacial value in line with literature values. Sodium chloride (≥99%) was purchased from Sigma-Aldrich. Any organic impurities were removed by heating the salt to 450 °C for 12 h. Water was distilled twice. [P6 6 6 14]Cl was obtained from Cytec Industries Inc. with a purity of 96–97%. Prior to use, this ionic liquid was dried under high vacuum (<0.1 mbar) at 70–80 °C for a minimum of 24 h. Its purity was confirmed by 1H NMR and 13C NMR. The CAS number, water content, density, viscosity, and surface tension of the pure compounds used in this work are reported in Table 1 and compared with available literature data.9,14–19| Compound | CAS Number | w H2O (ppm) | ρ/g cm−3 | η (mPa·s) | γ (mN·m−1) | |||
|---|---|---|---|---|---|---|---|---|
| Exp. | Exp. | Lit. | Exp. | Lit. | Exp. | Lit. | ||
| a Interpolated value. | ||||||||
| Water | 7732-18-5 | — | 0.99704 | 0.9970514 | 0.904 | 0.89014 | 72.0 | 71.814 |
| Dodecane | 112-40-3 | 74 | 0.74527 | 0.745315 | 1.356 | 1.36116 | 24.9 | 24.914 |
| 1.37814 | ||||||||
| [P6 6 6 14]Cl | 258864-54-9 | 898 | 0.89103 | 0.89149 | 2014 | 21529 | 32.3 | 30.718 |
| 182417 | 33.619a | |||||||
Methods
Liquid–liquid equilibrium data for the ternary system (water + [P6 6 6 14]Cl + dodecane) were experimentally measured at 25 °C and atmospheric pressure. To perform the measurements, a known composition of the three components (or two in the case of the binary tie-lines) within the biphasic or triphasic region were added into a jacketed equilibrium cell. The content of each cell was vigorously stirred for 2 h maintaining its temperature constant at 25 °C using a Selecta Ultraterm 6000383 thermostatic bath accurate to within ±0.02 °C. The cells were then left to settle for 48 h to ensure that a complete separation of the phases was achieved. Previously, several tests with different settling times were performed to ensure that 48 h was sufficient to reach equilibrium and complete phase separation. A sample of each phase was withdrawn to measure the composition and physical properties.The composition of each phase was analysed using a Hewlett-Packard HP 6890 Series gas chromatograph, equipped with a thermal conductivity detector and a HP-FFAP capillary column (25 m × 0.2 mm × 0.33 μm). Helium was used as the mobile phase, and injection volume was 2 μL, with a split ratio of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The oven temperature was kept at 55 °C for 3.0 min, then increased to 175 °C at a rate of 75 °C min−1, and finally it was kept at 175 °C for 1.0 min. An empty column was placed between the injector and the column to protect the column and collect the ionic liquid that could not be retained by the liner. For calibration, all the weighing was carried out in a Mettler Toledo AE 240 analytical balance with a precision of 10−4 g. Isopropanol was used simultaneously as solvent and as internal standard. The uncertainty in the compositions determined with this procedure is estimated to be ±0.008 mole fraction for the dodecane-rich phase, ±0.001 for the water-rich phase, and ±0.009 for the ionic liquid-rich phase.
1. The oven temperature was kept at 55 °C for 3.0 min, then increased to 175 °C at a rate of 75 °C min−1, and finally it was kept at 175 °C for 1.0 min. An empty column was placed between the injector and the column to protect the column and collect the ionic liquid that could not be retained by the liner. For calibration, all the weighing was carried out in a Mettler Toledo AE 240 analytical balance with a precision of 10−4 g. Isopropanol was used simultaneously as solvent and as internal standard. The uncertainty in the compositions determined with this procedure is estimated to be ±0.008 mole fraction for the dodecane-rich phase, ±0.001 for the water-rich phase, and ±0.009 for the ionic liquid-rich phase.
Densities were measured with an Anton Paar DMA 5000 oscillating U-tube densimeter with automatic viscosity correction and with self-control of temperature to ±0.01 °C. The uncertainty in the density measurements is ±10−5 g cm−3.
Kinematic viscosities were determined with Ubbelohde micro-viscometers. Depending on the viscosity of the samples, two different viscometers (capillaries I and III, manufactured by Schott Instruments) were used to measure the viscosity of the samples. The capillaries were calibrated and certified by the company, and verified by measuring the viscosity of pure compounds with known viscosities. Measurement of the flow time measurement was performed by a Lauda Processor Viscosity PVS1 system, with a resolution of 0.01 s. The temperature of the viscometer was kept constant using a Lauda D 20 KP clear view thermostat with a Lauda DLK 10 through-flow cooler connected. Viscosity measurements were repeated at least 3 times for each sample, and were found to be reproducible to within 0.04 s for times less than 100 s, and ±0.4 s for longer times. The dynamic viscosity is given by the following formula:
| η = v·ρ = K·(t − y)·ρ | (1) |
The interfacial tension of the samples was measured using a Krüss K11 tensiometer. The Wilhelmy plate method was used. In particular, a specially adapted platinum plate with cylindrical shape (Krüss accessory reference PL22; dimensions: 10 mm height × 20 mm base perimeter × 0.1 mm width) was used to carry out reliable measurements with lower amounts of sample than a conventional (flat) plate. For the measurement of the interfacial tension, enough volumes of samples were withdrawn from each phase in the equilibrium cells, and stored at 25 °C. Cylindrical open-top glass vessels with a diameter of 30 mm were used to place the lighter and denser phases during the different steps of the measuring procedure, which was performed according to the instructions by the manufacturer. The sample vessels were placed inside a jacketed oil bath through which refrigerating water from a Julabo F12 cryogenic thermostat was circulated. The actual temperature of the oil bath was determined by a built-in thermometer precise to within 0.1 °C. Every interfacial tension datum reported in this work is the average of ten consecutive immersion measurements, after two previous immersion measurements were systematically discarded. The method described has an estimated uncertainty of ±0.1 mN·m−1.
Results and discussion
To determine the suitability of the ionic liquid [P6 6 6 14]Cl as a potential replacement for conventional surfactants in surfactant-assisted EOR processes, the reservoir fluid was modelled as a mixture of (water + ionic liquid + oil). In a first part of the study, the liquid–liquid equilibrium at 25 °C for the system water + [P6 6 6 14]Cl + dodecane was determined. The results obtained for all equilibrium regions are shown in Table 2 and presented in a ternary diagram in Fig. 1. As it can be seen from this figure, this mixture forms a Winsor type III system, with a triphasic region and two biphasic regions around it (the third biphasic region not being detectable due to the proximity of the triphasic region to the axis representing the mixture of water + dodecane), as well as a monophasic domain. The first biphasic region (marked with circles) implies the coexistence of an excess-water phase and another phase where the ionic liquid solubilises a relevant amount of dodecane. The other biphasic region (marked with squares) corresponds to an excess-oil phase in equilibrium with another phase where the ionic liquid solubilises a relevant amount of water. Although the Winsor type III diagrams do ‘nominally’ contain a third biphasic region, in most cases it has a negligible size and cannot be detected, as it is the case in the modelled system studied herein. In the triphasic region (under the dashed lines), there is an ionic liquid-rich middle phase coexisting with an excess-water phase (consisting of practically pure water) and an excess-dodecane phase (consisting of practically pure dodecane).![Experimental tie-lines for the liquid–liquid equilibrium of the ternary system water + [P6 6 6 14]Cl + dodecane at 25 °C and atmospheric pressure.](/image/article/2012/RA/c2ra21698a/c2ra21698a-f1.gif) | ||
| Fig. 1 Experimental tie-lines for the liquid–liquid equilibrium of the ternary system water + [P6 6 6 14]Cl + dodecane at 25 °C and atmospheric pressure. | ||
| Biphasic region 1 | |||||||||||
| Upper phase | Lower phase | ||||||||||
| x 1 | x 2 | x 3 | x 1 | x 2 | x 3 | ||||||
| 0.824 | 0.176 | 0.000 | 1.000 | 0.000 | 0.000 | ||||||
| 0.776 | 0.176 | 0.048 | 1.000 | 0.000 | 0.000 | ||||||
| 0.718 | 0.182 | 0.100 | 1.000 | 0.000 | 0.000 | ||||||
| 0.683 | 0.173 | 0.144 | 1.000 | 0.000 | 0.000 | ||||||
| Biphasic region 2 | |||||||||||
| Upper phase | Lower phase | ||||||||||
| x 1 | x 2 | x 3 | x 1 | x 2 | x 3 | ||||||
| 0.000 | 0.005 | 0.995 | 0.000 | 0.259 | 0.741 | ||||||
| 0.000 | 0.006 | 0.994 | 0.043 | 0.267 | 0.690 | ||||||
| 0.000 | 0.003 | 0.997 | 0.083 | 0.275 | 0.642 | ||||||
| 0.000 | 0.004 | 0.996 | 0.148 | 0.279 | 0.573 | ||||||
| 0.000 | 0.003 | 0.997 | 0.195 | 0.270 | 0.535 | ||||||
| 0.000 | 0.008 | 0.992 | 0.292 | 0.256 | 0.452 | ||||||
| 0.000 | 0.006 | 0.994 | 0.424 | 0.221 | 0.355 | ||||||
| 0.000 | 0.007 | 0.993 | 0.506 | 0.209 | 0.285 | ||||||
| 0.000 | 0.003 | 0.997 | 0.561 | 0.190 | 0.249 | ||||||
| Triphasic region | |||||||||||
| Upper phase | Middle phase | Lower phase | |||||||||
| x 1 | x 2 | x 3 | x 1 | x 2 | x 3 | x 1 | x 2 | x 3 | |||
| 0.000 | 0.005 | 0.995 | 0.654 | 0.158 | 0.188 | 1.000 | 0.000 | 0.000 | |||
For an effective EOR system, the presence of the ionic liquid should reduce remarkably the interfacial tension between water and oil, and there should not be too much difference between the viscosity of the aqueous and the organic phases. To check these values for the system here investigated, the physical and transport properties were determined for six samples corresponding to both biphasic regions and to the triphasic region (as indicated in Fig. 2). For every sample, the density, dynamic viscosity, and interfacial tension of all phases in equilibrium are presented in Table 3. Due to the presence of salts in the oilfield, the same study was carried out by substituting the water with a brine solution (4% (w/w) NaCl). Results with this brine solution are presented in Table 4. The visual aspect of the six samples analysed is shown in Fig. 3 and 4 for the systems with water and with brine solution, respectively. In both cases, sample number 4 shows the triphasic system.
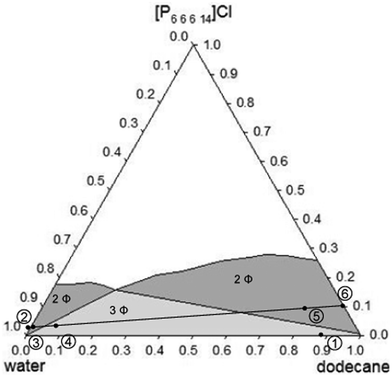 | ||
| Fig. 2 Localisation of the compositions of the samples used to measure properties (see Table 3 and 4). | ||
![Photograph of the biphasic and triphasic mixtures of the ternary system (water + [P6 6 6 14]Cl + dodecane) selected for determination of thermophysical properties. See Fig. 2 for composition and numbering of the samples.](/image/article/2012/RA/c2ra21698a/c2ra21698a-f3.gif) | ||
| Fig. 3 Photograph of the biphasic and triphasic mixtures of the ternary system (water + [P6 6 6 14]Cl + dodecane) selected for determination of thermophysical properties. See Fig. 2 for composition and numbering of the samples. | ||
![Photograph of the biphasic and triphasic mixtures of the ternary system (4% NaCl aqueous solution + [P6 6 6 14]Cl + dodecane) selected for determination of thermophysical properties. See Fig. 2 for composition and numbering of the samples.](/image/article/2012/RA/c2ra21698a/c2ra21698a-f4.gif) | ||
| Fig. 4 Photograph of the biphasic and triphasic mixtures of the ternary system (4% NaCl aqueous solution + [P6 6 6 14]Cl + dodecane) selected for determination of thermophysical properties. See Fig. 2 for composition and numbering of the samples. | ||
| Global composition | Phase | ρ/g cm−3 | η (mPa·s) | γ (mN·m−1) |
|---|---|---|---|---|
| a Negative values are reported by tensiometer due to the light phase being the wetting fluid. | ||||
| Experiment 1 | Upper | 0.74527 | 1.356 | 52.2 |
| x1 = 0.890 , x2 = 0.000 , x3 = 0.110 | Lower | 0.99704 | 0.904 | |
| Experiment 2 | Upper | 0.90408 | 113.3 | 1.8a |
| x1 = 0.970 , x2 = 0.030 , x3 = 0.000 | Lower | 1.00092 | 0.908 | |
| Experiment 3 | Upper | 0.86244 | 49.34 | 1.4a |
| x1 = 0.950, x2 = 0.025 , x3 = 0.025 | Lower | 1.00047 | 0.910 | |
| Experiment 4 | Upper | 0.74578 | 1.363 | 0.3 |
| x1 = 0.885, x2 = 0.025 , x3 = 0.090 | Middle | 0.85795 | 44.99 | 1.4a |
| Lower | 0.99829 | 0.904 | ||
| Experiment 5 | Upper | 0.74583 | 1.370 | 0.4 |
| x1 = 0.118, x2 = 0.088 , x3 = 0.794 | Lower | 0.83619 | 77.73 | |
| Experiment 6 | Upper | 0.74605 | 1.368 | 0.5 |
| x1 = 0.000 , x2 = 0.100, x3 = 0.900 | Lower | 0.81508 | 84.20 | |
| Global composition | Phase | ρ/g cm−3 | η (mPa·s) | γ (mN·m−1) |
|---|---|---|---|---|
| a Negative values are reported by the tensiometer due to the light phase being the wetting fluid. | ||||
| Experiment 1 | Upper | 0.74526 | 1.353 | 53.2 |
| x1 = 0.887, x2 = 0.000, x3 = 0.113 | Lower | 1.02544 | 0.957 | |
| Experiment 2 | Upper | 0.90356 | 122.2 | 2.4a |
| x1 = 0.970, x2 = 0.030, x3 =0.000 | Lower | 1.03248 | 0.971 | |
| Experiment 3 | Upper | 0.86168 | 51.36 | 2.0a |
| x1 = 0.950, x2 = 0.025, x3 = 0.025 | Lower | 1.03186 | 0.968 | |
| Experiment 4 | Upper | 0.74590 | 1.365 | 0.5 |
| x1 = 0.885, x2 = 0.025, x3 = 0.090 | Middle | 0.85607 | 46.54 | 1.7a |
| Lower | 1.03228 | 0.978 | ||
| Experiment 5 | Upper | 0.74598 | 1.368 | 0.6 |
| x1 = 0.142, x2 = 0.088, x3 = 0.770 | Lower | 0.91003 | 78.48 | |
| Experiment 6 | Upper | 0.74605 | 1.368 | 0.5 |
| x1 = 0.000, x2 = 0.100, x3 = 0.900 | Lower | 0.81508 | 84.20 | |
According to Table 3, an interfacial tension of 1.8 mN·m−1 was found for the water + [P6 6 6 14]Cl binary system. A considerable deviation was found with data reported by Carrera et al.,18 who found an interfacial tension of 6.11 mN·m−1. This is probably due to the different method used in the measurement. These authors used a pendant drop method, which requires knowledge of the density of the phases in equilibrium, in order to calculate the interfacial tension. In the case of the ionic liquid phase, it is well known that this physical property is substantially affected by the presence of impurities; in particular, of the water content, which is not stated by Carrera et al. in their work.18
The values in Table 3 also show that the addition of a small concentration of [P6 6 6 14]Cl to the water + dodecane system results in the formation of a third phase in equilibrium with a water-rich lower phase and an oil-rich upper phase. The formation of this third, middle phase is an indication of the formation of bicontinuous microemulsions due to the amphiphilic nature of the cation of the ionic liquid, resulting in a dramatic reduction in the interfacial tension. The binary system water + dodecane has an interfacial tension of 52.2 mN·m−1 (in agreement with literature data20,21). When adding the ionic liquid to form the triphasic system, 1.4 mN·m−1 was found for the lower-middle interface (γac) and 0.3 mN·m−1 for the upper-middle interface (γbc).
At 25 °C, addition of the ionic liquid to a mixture of equal volumes of water and dodecane up to a mass fraction ωIL = 0.008 generates a triphasic system with a minimum interfacial tension between the aqueous and oil phases, that must fulfil the stability condition (γab ≤ γac + γbc). Sottmann and Strey22 worked with alkylpolyglycol ether surfactants in concentrations between ω = 0.015 and ω = 0.05 in a range of temperatures 0 °C < T < 70 °C, finding interfacial tensions in the range 0.0001–1 mN·m−1 for systems with several alkanes, ranging this property over several orders of magnitude as a function of temperature. Although our values are slightly worse than these conventional surfactants, there is a need to find the temperature which leads to a maximum efficiency of the amphiphile in homogenising water and oil, and a minimum of interfacial tension, before establishing comparisons.
With regard to the interfacial tensions in the system with brine instead of water, it is worth noting that the presents of ionic liquid largely shields any effect of the salt.
From Table 3 and 4, it is evident that the addition of [P6 6 6 14]Cl clearly increases the viscosity of the aqueous phases, thus reducing the viscosity ratio between aqueous and organic phases within the system. From comparison of viscosity values in Table 3 and in Table 4, it can be deduced that the presence of the inorganic salt slightly increases the viscosity. These viscosity results, however, must be taken with particular care, since it is hard to extrapolate viscous behaviour from the use of dodecane in the studied model system to a real field case with real (and much more viscous) oil.
Conclusions
The surface activity of the ionic liquid [P6 6 6 14]Cl and the phase behaviour of the system (water + [P6 6 6 14]Cl + dodecane) has been experimentally studied. Liquid–liquid equilibrium data at 25 °C for this ternary system have been determined. The results show a phase diagram similar to the Winsor type III system with one triphasic region, two biphasic regions, and one miscible region.The measured interfacial tensions indicate that, when added to the water–oil mixtures, the ionic liquid [P6 6 6 14]Cl acts as a surface active agent and reduces considerably the interfacial tension in the water–oil interface. Thus, the ionic liquid could be potentially used in an EOR process, in order to increase the production of oilfields in exploitation. The advantages of being liquid at room temperature and avoiding the addition of any co-surfactant should also be taken into account.
The results also show that the addition of the ionic liquid increases the viscosity of the water phase. During an EOR process this behaviour could prevent the water from seeping through fractures or high permeability regions, and therefore decreasing the water–oil mobility ratio within the reservoir and resulting in a more efficient oil recovery.
In principle, the results obtained in this work support the possibility of using the phosphonium ionic liquid to act as a surfactant in chemical flooding EOR. Nevertheless, these are initial research steps that need to be complemented by further research. Work in progress at our research group involves the study of the influence of temperature and pressure in the phase equilibrium and properties of modelled systems. Experiments with real oil, investigation of the adsorption of ionic liquids in rocks, and many others are also needed before envisioning in situ research at the oilfield.
Acknowledgements
The authors are grateful to the Ministry of Economy and Competitiveness of the Spanish Government, and to the European Union, for financial support under project CTQ2009-10776.References
- J. G. Speight, in Enhanced oil recovery methods for heavy oil and tar sands, Gulf Publishing Company, Houston, 2009, 134 Search PubMed.
- L. W. Lake, R. L. Schmidt and P. B. Venuto, Oilfield Review, 1992, 55 Search PubMed.
- V. Pino, M. Germán-Hernández, A. Martín-Pérez and J. L. Anderson, Sep. Sci. Technol., 2012, 47, 264 CrossRef CAS.
- I. R. Collins, M. J. Earle, S. P. Exton, N. V. Plechkova and K. R. Seddon, PCT Int. Appl., 2006, WO 2006111712 A2 Search PubMed.
- (a) J. Bowers, C. P. Butts, P. J. Martin and M. C. Vergara-Gutierrez, Langmuir, 2004, 20, 2191 CrossRef CAS; (b) M. Blesic, M. H. Marques, N. V. Plechkova, K. R. Seddon, L. P. N. Rebelo and A. Lopes, Green Chem., 2007, 9, 481 RSC; (c) M. Blesic, A. Lopes, E. Melo, Z. Petrovski, N. V. Plechkova, J. N. Canongia-Lopes, K. R. Seddon and L. P. N. Rebelo, J. Phys. Chem. B, 2008, 112, 8645 CrossRef CAS; (d) M. Blesic, M. Swadzba-Kwasny, J. D. Holbrey, J. N. Canongia Lopes, K. R. Seddon and L. P. N. Rebelo, Phys. Chem. Chem. Phys., 2009, 11, 4260 RSC.
- (a) P. A. Winsor, Trans. Faraday Soc., 1948, 44, 376 RSC; (b) P. A. Winsor, in Solvent Properties of Amphiphilic Compounds, Butherworth & Co., London, 1954 Search PubMed.
- G. Zhang, X. Chen, Y. Zhao, Y. Xie and H. Qiu, J. Phys. Chem. B, 2007, 111, 11708 CrossRef CAS.
- J. Liu, Y. Li, J. L. Chai, C. K. Kin, X. Y. Yu and Y. Xia, Tenside Surf. Det., 2009, 46, 306 CAS.
- K. Anderson, H. Rodríguez and K. R. Seddon, Green Chem., 2009, 11, 780 RSC.
- J. A. Murillo-Hernández and J. Aburto, in Current knowledge and potential applications of ionic liquids in the petroleum industry, in Ionic liquids: applications and perspectives, ed. A. Kokorin, Intech-Open, 2011 Search PubMed.
- (a) Z. X. Fan, T. F. Wang and Y. H. He, J. Fuel Chem. Technol., 2009, 37, 690 CrossRef CAS; (b) M. Siti-Qurratu'Aini and I. Mohd-Saaid, A review of ionic liquids used for upgrading of heavy oils, in: 3rd CUTSE International Conference, Miri, Sarawak, 2011 Search PubMed.
- (a) R. C. B. Lemos, E. B. da Silva, A. dos Santos, R. C. L. Guimaraes, B. M. S. Ferreira, R. A. Guarnieri, C. Dariva, E. Franceschi, A. F. Santos and M. Fortuny, Energy Fuels, 2010, 24, 4439 CrossRef CAS; (b) D. Guzmám-Lucero, P. Flores, T. Rojo and R. Martínez-Palou, Energy Fuels, 2010, 24, 3610 CrossRef; (c) G. J. Hirasaki, C. A. Miller, O. G. Raney, M. K. Poindexter, D. T. Nguyen and J. Hera, Energy Fuels, 2011, 25, 555 CrossRef CAS.
- Y. Z. Shang, W. J. Song, N. Zhao, H. Li and H. I. Liu, Youtian Huaxue, 2010, 27, 306 CAS.
- J. A. Riddick, W. B. Bunger and T. K. Sakano, in Organic Solvents. Physical Properties and Methods of Purification, 4th ed., John Wiley and Sons, New York, 1986 Search PubMed.
- T. M. Aminabhavi and V. B. Patil, J. Chem. Eng. Data, 1997, 42, 641 CrossRef CAS.
- Y. Liu, R. DiFoggio, K. Sanderlin, L. Perez and J. Zhao, Sens. Actuators, A, 2011, 167, 347 CrossRef.
- http://www.rsc.org/suppdata/cp/b9/b920530f/b920530f-12.pdf, accessed April 2012.
- G. V. S. M. Carrera, C. A. M. Afonso and L. C. Branco, J. Chem. Eng. Data, 2010, 55, 609 CrossRef CAS.
- P. Kilaru, G. A. Baker and P. Scovazzo, J. Chem. Eng. Data, 2007, 52, 2306. CrossRef http://pubs.acs.org/doi/abs/10.1021/je7003098 - je7003098AF1#je7003098AF1.
- S. Zeppieri, J. Rodríguez and A. L. López Ramos, J. Chem. Eng. Data, 2001, 46, 1086 CrossRef CAS.
- D. M. Mitrinovic, A. M. Tikhonov, M. Li, Z. Huang and M. L. Schlossman, Phys. Rev. Lett., 2000, 85, 582 CrossRef CAS.
- T. Sottmann and R. Strey, J. Chem. Phys., 1997, 106, 8606 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
