A programmable transducer self-assembled from DNA

Abstract

A transducer consists of an input/output alphabet, a finite set of states, and a transition function. From an input symbol applied to a given state, the transition function determines the next state, and an output symbol. Using DNA, we have constructed a transducer that divides a number by 3. The input consists of a series of individually addressable 2-state DNA nanomechanical devices that control the orientations of a group of flat 6-helix DNA motifs; these motifs have edge domains tailed in sticky ends corresponding to the numbers 0 and 1. Three-domain DNA molecules (TX tiles) act as computational tiles that correspond to the transitions that the transducer can undergo. The output domain of these TX tiles contains sticky ends that also correspond to 0 or 1. Two different DNA tiles can chelate these output domains: a 5 nm gold nanoparticle is attached to the chelating tile that binds to 0-domains and a 10 nm gold nanoparticle is attached to the chelating tile that binds to 1-domains. The answer to the division is represented by the series of gold nanoparticles, which can be interpreted as a binary number. The answers of the computation are read out by examination of the transducer complexes under a transmission electron microscope. The start or end points of the output sequence can be indicated by the presence of a 15 nm gold nanoparticle. This work demonstrates two previously unreported features integrated in a single framework: a system that combines DNA algorithmic self-assembly with DNA nanomechanical devices that control that input, and the arrangement of non-DNA species, here metallic nanoparticles, through DNA algorithmic self-assembly. The nanomechanical devices are controlled by single-stranded DNA strands, allowing multiple input sequences to be applied to the rest of the system, thus guiding the algorithmic self-assembly to a variety of outputs.

---

Introduction

A collection of synthetic DNA molecules have been designed and shown to assemble into branched motifs,^1–4 as well as more complex species that entail the lateral fusion of DNA double helices.⁵ The second group of motifs includes double crossover (DX) molecules,⁶ triple crossover (TX) molecules⁷ and paranemic crossover (PX) molecules.^8,9 Double¹⁰ and triple⁷ crossover molecules have been used as tiles and building blocks for nanoscale 2D arrays, and tensegrity triangles¹¹ have been used to produce macroscopic 3D crystals.¹²

It can be shown that two dimensional arrays made from DX or TX DNA motifs can simulate the dynamics of a bounded one dimensional cellular automaton and therefore are capable of performing computation as a universal Turing machine.¹³ Successful experiments have confirmed the possibility of computation by DNA self-assembly: binary addition (simulation of a cumulative exclusive OR (called XOR)) using triple cross-over molecules¹⁴ as well as aperiodic Sierpinski triangle assembly by DX molecules have been reported.¹⁵ Although not explicitly mentioned, both of these algorithmic assemblies could be viewed as finite state automata simulations. Further simulations of finite state automata that use duplex DNA molecules and a restriction endonuclease have been reported by Shapiro, Keinan, Benenson and their colleagues.^16,17

In addition to these self-assemblies, a variety of sequence-dependent DNA nanomechanical devices have been reported, including 2-state devices,^18,19 a 3-state device,²⁰ track-based walkers,^21–24 and a combination of devices with a walker that performs the functions of an assembly line.²⁵ These systems all depend on the use of toehold-based fuel strands that unset the state of a device by removing a strand from it isothermally.¹⁸ The PX-JX₂ device¹⁹ has two distinct states and each is obtained by the addition of two DNA strands that hybridize with it, so that the molecule is in either of two states, termed the PX state or the JX₂ state. The two states differ from each other in that one end is rotated relative to the other by a half-turn. A group of these devices can be addressed individually,²⁶ so that different devices can act simultaneously, but independently.²⁷

It is well known that by iteration of generalized sequential machines (finite state machines mapping symbols into strings) all computable functions can be iterated.^28,29 The full computational power depends on the possibility of iterating the finite state machines. Wang tiles³⁰ can simulate iterated transducers and recursive (computable) functions. Wang tiles consist of a set of tiles (usually square) with colored edges; the tiles self-assemble according to the local rule requiring edges with the same color to pair with each other; this type of self-assembly has been shown to simulate a Turing machine, a universal computer.³⁰ Both the XOR simulation¹⁴ and the Sierpinski triangle assembly¹⁵ can be seen as DNA Wang tile assemblies. Here, we have developed this idea further and we report the use of PX-JX₂ devices to assemble the input for a programmable finite state machine that produces an output and potentially has iteration capabilities.

The experiment achieves a previously undemonstrated use of robust DNA nanomechanical devices in the context of DNA algorithmic self-assembly. The single-stranded DNA strands that control the states of the PX-JX₂ DNA nanomechanical devices act to set the input of the transducer and set the state of the rest of the system. The components of the transducer perform the computation by assembling in the predesigned configuration as a consequence of the states of the devices. The output of the system is read out through an arrangement of differently sized gold nanoparticles. To our knowledge, this organization of gold nanoparticles represents the first reported use of algorithmic self-assembly to arrange non-DNA species.

Description of the computational model

A transducer, also known as a finite state automaton with output, is a formal system consisting of an input/output alphabet, a transition function, one designated initial state, and a finite set of other states, some of which are designated terminal. From a given state and an input symbol, the transition function determines the next state, and an output symbol. One computational step, or one transition, is denoted with (q, a) → (a′, q′) meaning that being in state q and scanning an input symbol a, the transducer produces an output symbol a′ and enters state q′. Usually the states of the transducer are presented as the vertices of a graph and the transitions are presented as directed edges with input/output symbols as labels. An example is shown in Fig. 1a. The output in this case is the result of the division of a binary string by three. For example, on inputting the string 10101 (21 in decimal) the transducer gives the output 00111 (7 in decimal). In this computation process, the transducer moves through the following transitions: (S₀, 1) → (0, S₁), (S₁, 0) → (0, S₂), (S₂, 1) → (1, S₂), (S₂, 0) → (1, S₁), (S₁, 1) → (1, S₀) (see Fig. 1a). The transducer is said to accept a string (or a word) if there is a path in the graph from the initial state to a terminal state whose input label is the string. The output labels of the path form the output word corresponding to the accepted input. Finite state automata recognize the class of regular languages.³¹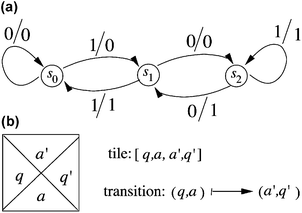

Fig. 1 A finite state machine and a Wang prototile. (a) A finite state machine that accepts binary strings that are divisible by 3. The input and output alphabet of the machine consists of {0, 1}. The starting and terminal states are both s₀. If we end at s₀, we accept the string; if we end elsewhere, the input is rejected. The machine outputs in binary the result of dividing the binary input string by 3. The three states are labelled s₀, s₁ and s₂, each corresponding respectively to a possible remainder, 0, 1 or 2. The arrows represent transitions to new states that accompany the outputs of the computation. The labels of the arrows are the input/output symbols (always signified left/right). Thus, if one were trying to divide 21 (10101 binary) by 3 (11 binary), the result is obtained by the following process: starting at state s₀, read from the right input 1, whose output is 0, and move to state s₁; reading the next symbol, which is 0, leads to state s₂ and produces output 0. The next symbol, 1 leads back to s₂, and produces output 1. The next symbol, 0, leads to output 1 and transitions to state s₁. The last symbol, 1, produces output 1 and leads to state s₀, indicating that the binary string is divisible by 3, and that the answer is 00111, or 7 in decimal. (b) A Wang prototile. This tile represents a computational tile for a transducer. See text for an explanation of the symbols.

Tiles for simulating a transducer

A finite set of distinct unit squares with colored edges is called a set of Wang prototiles. We assume that for each prototile there are an arbitrarily large number of copies in solution that are called tiles. Tiles associate with each other by abutting identically colored edges. A tile τ with left edge colored l, bottom edge colored b, top edge colored t and right edge colored r is denoted by τ = [l, b, t, r]. Two tiles τ = [l, b, t, r] and τ′ = [l′, b′, t′, r′] can be placed next to each other, τ to the left of τ′ if and only if r = l′, and τ′ can be placed on top of τ if and only if t = b′.

Computational tiles

For a transducer with a transition of the form:

(q, a) → (a′, q′),

we associate a prototile [q, a, a′, q′] as shown in Fig. 1b. If there are m transitions in the transducer, we associate m such prototiles with the transducer. These tiles are the computational tiles. For the example of the transducer presented in Fig. 1a, the computational tiles are depicted in Fig. 2b.

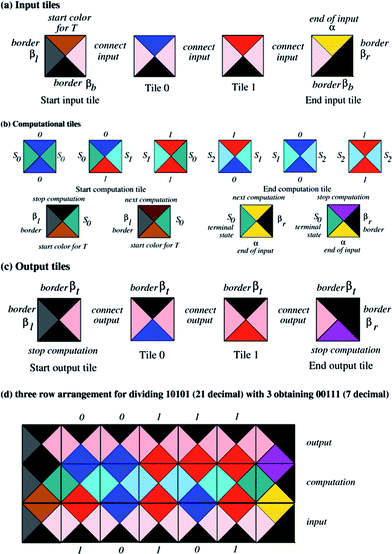Fig. 2 The prototiles needed for performing the computation of the transducer in Fig. 1a. The colors associated with each edge are indicated. (a) The input tiles. (b) The computational tiles. (c) The output tiles. (d) The assembly of tiles representing the division of 21 by 3.

Input and output tiles

Additional colors called ‘border colors’ are added to the set of colors. These colors are not part of the computational assembly, but represent the boundaries of the computational assembly. We denote these with β_l, β_b, β_r, β_t for left, bottom, right and top borders, respectively. There are as many input prototiles as there are input symbols. The bottom color of the input prototiles is β_b and the top color corresponds to one of the input symbols. In all input tiles the left and right sides are colored with the same color, the “connect” color c, as shown in Fig. 2a. For example, an input symbol a is represented with tile τ_a = [c, β_b, a, c]. For the “end of input” symbol α, a prototile τ_α = [c, β_b, α, β_r] is constructed. The output tiles are essentially the same as the input tiles, except they contain the “top” border: for example an output tile for symbol a is τ_a = [c′, a, β_t, c′] where c′ is another “connect” color, as shown in Fig. 2c.

Start tiles and accepting (end) tiles

To initiate the computation and to finish (accept) a computation we add two additional tile types, the start and the end tiles. The start of the input for the transducer is indicated with the start input prototile S_T = [β_l, β_b, T, c], where T is a special color specifying the particular transducer that is being used (Fig. 2a left). The input tiles can then be placed next to such a starting tile. The input ends with end of input tile τ_α (Fig. 2a right). For the starting state s₀ a starting prototile start computation τ₀ = [β_l, T, η, s₀] is constructed that can be placed on top of S_T (Fig. 2b). The color η can be equal to T if we want to iterate the same transducer, or it can indicate another transducer that should be applied afterwards. If the computation is to be ended, η is equal to “finish left” F_l, indicating the start of the output layer with the “top boundary”. For each terminal state f, we associate a terminal end of computation prototile τ_f = [f, α, α, β_r] if another computation (layer of tiles) is required; otherwise, τ_f = [f, α, F_r, β_r] containing a top color “finish right” F_r which stops the computation. Then the output starts with a start output tile τ_out = [β_l, F_l, β_t, c′] followed by a sequence of output tiles. The output layer of tiles then ends with an end output tile τ′_out = [c′, F_r, β_t, β_r]. Although the abstract model we describe allows iteration, it has not been implemented in the work described here. The complete set of tiles for executing a computation for the transducer that performs division by 3 (see Fig. 1a) is depicted in Fig. 2a–c. With these sets of input and output tiles, every computation with the transducer is obtained as a tiled rectangle surrounded by boundary colors.

Computation

Every computation by the transducer on an (m − 2)-bit input string (m ≥ 2) can be obtained as a tiled 3 × m rectangle such that the bottom row starts with tile S_T and a sequence of input tiles ending with τ_α. Tiles in the middle row of the 3 × m block represent the actual execution of the computation of the transducer; this row contains computation tiles aligned according to the input state (to the left) and the input symbol (at the bottom). A computational rectangle for the division of 21 (10101 binary) by 3 (11 binary) is shown in Fig. 2d. This computation row ends with the end tile τ_f, which can lie next to both the last input tile and the last computational tile if and only if the input is accepted (i.e., the input is divisible by 3). The output result is “read” from the sequence of the output colors at the top of the second row of tiles. The top row of the 3 × m block consists of the output tiles containing the top border. In this way the set of all 3 × m rectangles (m ≥ 2) such that the sides of the rectangle are colored with boundary colors corresponds precisely to the set of all one-step computations of the transducer with input of length m − 2.

DNA implementation of the Wang tiles

(a) Setting the input

The input is established through the use of the robust sequence-dependent 2-state nanomechanical device that is called PX-JX₂.¹⁹ Its machine cycle is shown in Fig. 3, where it can be seen that state changes are directed by the addition of set strands to the solution that forms its environment. The set strands, drawn in green and purple, fix which of the two states the device will assume. The states differ by rotation of a half-turn between the ends of the device. The sequence-directed nature of the device means that many different devices can be constructed and combined, each of which is individually addressable; this is done by changing the sequences of the strands connecting the AB end of the device with the CD end of the device, in the region where the green and purple set strands pair with them. The green and purple strands have short, unpaired extensions on them, which are known as toeholds.¹⁸ The state of the device is changed by hybridizing the full complements of the green or purple strands; these duplex complexes are removed from solution by magnetic streptavidin beads, and then the other set strands can be added to obtain the opposite state. It has been shown that the device can change the orientation of large DNA trapezoids;¹⁹ it also has been shown that the devices can be organized in an array and are individually addressable.^20,24,26 We have employed this property of the device to obtain a programmable input for the transducer. Linear arrays of a series of PX-JX₂ devices have been adapted to set the input of the transducer. In the computations performed here, we have assembled the PX-JX₂ devices in the states needed to provide a particular input, rather than starting them in a general state and then setting the inputs through the addition of new set strands.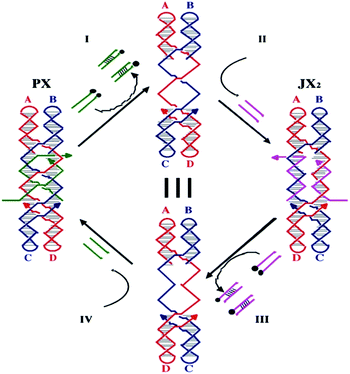

Fig. 3 The machine cycle of the PX-JX₂ device. Starting with the PX device on the left, the green set strands are removed by their complements (Process I) to leave an unstructured frame. The addition of the yellow set strands (Process II) converts the frame to the JX₂ structure, in which the top and bottom domains are rotated a half turn relative to their arrangement in the PX conformation. Processes III and IV reverse this process to return to the PX structure. The black dots on the complements in Processes I and III represent biotin groups that facilitate the removal of the duplex molecules from solution.

A schematic representation of the series of PX-JX₂ devices setting up the input is depicted in Fig. 4. This arrangement corresponds to the bottom and the middle rows of the tile arrangement in Fig. 2d. A new structural unit, the six-domain-flat (6DF) motif, which sets the input in the computational layer as a function of the state of the PX-JX₂ device to its left is also depicted in Fig. 4. These 6DF motifs contain sticky ends for a 1 and a 0 on their top and bottom domains respectively. This 1 or 0 becomes part of the input to the computational layer. Fig. 4 also shows the placement of ‘start’ and ‘end’ tiles.

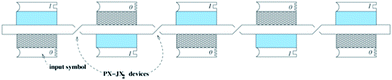Fig. 4 Schematic view of the input. A row of 6DF input tiles connected with PX-JX₂ devices. The 6DF tiles contain a 0 or a 1 symbol (represented as a sticky end) on their top or bottom domains; only their top domains have impact on the calculation. Whether the top domain contains a 1 or a 0 is a function of the state of a PX-JX₂ device that connects the 6DF motifs near their centres. The representation shown illustrates the input corresponding to 10101 binary (21 decimal).

(b) Computation

We have implemented the computational model by tiles that are triple crossover (TX) DNA molecules; these contain three double helical domains in a roughly planar arrangement. The TX molecule contains sticky ends that correspond to the colored sides of the Wang prototile. Since the transducer produces not just an output, but also changes its state, and the next computational tile needs two output sticky ends, we found TX molecules to be an appropriate and simple motif to use. An example of such a molecule is presented in Fig. 5a. The non-rotational nature of the tiles about their long axes is ensured by the coding of their sticky ends. The basic TX computational tile representing one transition of the transducer is depicted schematically with sticky ends indicated by geometrical shapes in Fig. 5b. As noted above in the description of Wang prototiles, the connector is a sticky part that does not contain any information, but it is necessary for the correct assembly of the tiles (see below). It has been shown that TX molecules can self-assemble into a 2D array,⁷ and they have also been assembled in a linear arrangement such that a cumulative XOR operation has been executed.¹⁴Fig. 5c shows the top domain of the 6DF motif representing the input tile, which fits structurally in between two TX computational tiles. The TX tiles have the middle duplex longer than the other two to accommodate for the length of this input domain.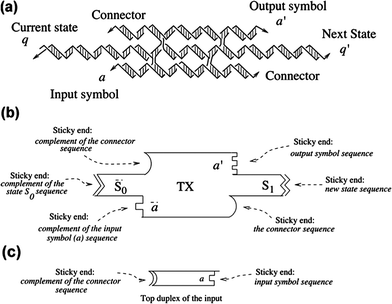

Fig. 5 The TX tile that represents one transition of the transducer. (a) Molecular representation of the TX Tile. The TX tile is shown as a complex of individual strands self-assembled to form three domains. Arrowheads represent the 3′ ends. The sticky ends representing the current state, q, and the next state, q′, are indicated. Similarly the input symbol, a, and the output symbol, a′, are represented by sticky ends. The connector sticky ends present for purposes of stability are also shown. (b) A schematic representation of the TX molecule. The TX is shown with three layers. The current state is shown as S₀ and the next state is shown as S₁. Complementarity is shown in a geometrical form for all six sticky ends. (c) Top duplex domain of the input tile. The sticky ends complementary to the connector and the input signal from the 6DF input tiles are shown geometrically.

The computational set-up corresponding to the Wang tiles in Fig. 2b is illustrated schematically in Fig. 6, where one row of tiles corresponding to the input is depicted; we also show computational tiles made of DNA triple crossover (TX) molecules. This row of TX tiles corresponds to the second row of tiles in Fig. 2d.

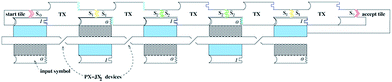Fig. 6 Schematic view of a single-row computation. The TX computational tiles are shown at the top. They are positioned by the start tile at the left, and the 6DF input tiles at the bottoms of the TX tiles. The 6DF tiles connect the TX tiles, and establish which tiles belong in each slot. The representation shown illustrates the computation tiles assembled for input corresponding to 10101 binary (21 decimal).

(c) Obtaining output

The next feature of the system to describe is the readout. A chelator DNA DX motif to which a gold nanoparticle has been attached performs this task. The chelator tile fits on the top of the TX computational tile; there are two different chelator tiles, one that fits on the top of a TX tile whose top (output) domain corresponds to 0 and a different chelator tile that fits on top of a 1-containing output domain. The chelator that binds to 0 contains a 5 nm gold nanoparticle, whereas the chelator that binds to 1 contains a 10 nm gold nanoparticle. Thus, the output can be read in a TEM. This layer of chelator tiles corresponds to the top row of the computation row of numerical symbols depicted in Fig. 2d.

Fig. 7 illustrates schematically how the computation is performed. Fig. 7a shows the complete set of tiles needed to perform division by 3. They demonstrate the transitions between the different states of Fig. 1a (s₀, s₁ and s₂), as well as initiation and termination tiles. Fig. 7b shows the complete assembly that corresponds to the division of 21 (10101 binary) by 3 (11 binary). The 6DF molecules are all connected by PX-JX₂ devices in the JX₂ states (the purple Xs) so the input is 10101. Following the DX initiator tile, the TX computational tiles fit together in the order (s₀ → s₁ [output 0]), (s₁ → s₂ [output 0]), (s₂ → s₂ [output 1]), (s₂ → s₁ [output 1]), (s₁ → s₀ [output 1]), and then comes the end of computation tile. Thus, the output is 00111 binary, or 7 decimal. In a similar fashion, Fig. 7c, 7d and 7e, respectively, illustrate the division of 18 (10010 binary) by 3 to yield 00110 binary, or 6, the division of 15 (1111 binary) by 3 to yield 0101 binary, or 5 and the division of 12 (1100 binary) by 3 to yield 0100 binary, or 4. The different inputs are set by using different combinations of PX and JX₂ states of the devices, as indicated by the color coding of the ‘X’ shapes applied to the same sequence of input 6DF tiles. The last two computations use only four 6DF input tiles, rather than five.

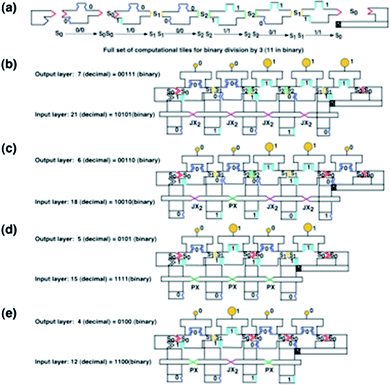Fig. 7 Schematic representations of the calculations performed. (a) Schematic diagrams of the tiles used to divide by 3. From left to right, the schematic representations of the following tiles are shown: the DX starter tile, the s₀ → s₀ TX tile, the s₀ → s₁ TX tile, the TX s₁ → s₂ tile, the TX s₂ → s₂ tile, the TX s₂ → s₁ tile, the TX s₁ → s₀ tile, and the TX end tile. Although the end tile has only two sticky ends, they are separated by a domain, so it is a TX tile. (b) The division of 21 by 3. Five 6DF input motifs are seen at the bottom, connected by five PX-JX₂ devices, all in the JX₂ state (purple set strands). Thus, 10101 (21 in binary) is the input value, on the tops of the 6DF tiles, and the output value is 00111. The chelator tiles can be seen to produce 00111, with two small (5 nm) gold particles, representing 0, followed by three large (10 nm) gold particles, representing 1. (c) The division of 18 by 3. There are five 6DF motifs, but the second device is in the PX (green strand) state, so the input is 10010. 00110 is the output, as can be seen from the gold particles. (d) The division of 15 by 3. There are only four input 6DF tiles, set to 1111, by 3 PX states in a row, and the output is 0101. (e) The division of 12 by 3. There are four 6DF tiles, where alternating PX-JX₂-PX device states set the input to 1100 and the output to 0100.

Fig. 7b–e indicate that these answers are represented by gold nanoparticles of two different sizes, 5 nm, representing 0, and 10 nm, representing 1. As noted above, these gold nanoparticles are attached to chelator DX tiles that fit on the tops of the TX computational tiles, thus giving a readout that can be ascertained in the TEM. We find that it is not possible to rely on AFM to distinguish 5 nm and 10 nm particles, although the sample construct was imaged in the AFM (tapping mode) under native conditions after every annealing stage.

(d) Molecular representation of the components

The molecular components designed to implement the transducer are depicted in a DNA-strand representation in Fig. 8. The top and bottom sticky ends of the six-domain-flat (6DF) motif (Fig. 8a) encode the bits 0 and 1 respectively. The middle duplex (third from the top in the figure) extends to sticky ends complementary to the PX-JX₂ device whose two states are depicted in Fig. 8b and c. As the device changes its state, the top or the bottom sticky end of the 6DF motif is exposed to bind the computational TX tile “reading” the bit 0 or 1, respectively. The start and end tiles are shown in Fig. 8d and 8f, while a computational TX tile is shown in Fig. 8e. The chelator tile is shown in Fig. 8g, where the filled gold circle represents one of the gold nanoparticles. The complete 21/3 computation array (analogous to Fig. 7b) is shown in a DNA strand representation in Fig. 8h.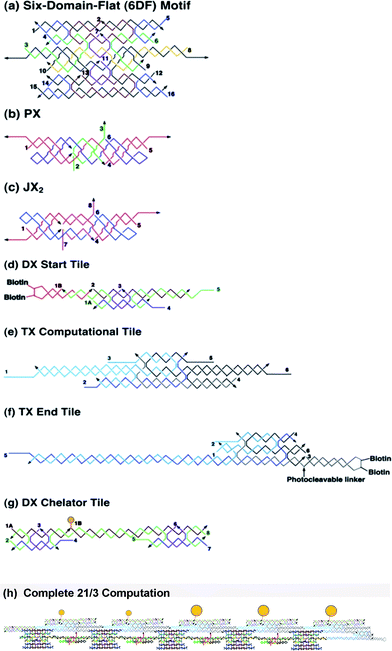

Fig. 8 DNA strand representations of the components in the calculation. Strand numbers are indicated throughout. (a) 6DF motif. This flat 6-helix motif can be thought of as consisting of three DX motifs that are joined by crossovers between them at two positions each. (b) and (c) are the two states of the PX-JX₂ device, the PX state, shown in (b) with green set strands, and the JX₂ state shown in (c) with purple set strands. Note that the right sides of the two motifs are identical, but the left sides are flipped. (d) shows the DX start tile, (e) shows a TX computational tile, and (f) shows a TX end tile. Note the biotin groups indicated on the start and end tiles. (g) shows a chelator tile with a gold particle drawn in yellow that can attach to the top domain of the TX computational tile. (h) DNA strand representation of the division of 21 by 3. This is the DNA strand representation of the calculation shown in Fig. 2(b).

Methods

Design, synthesis, purification and formation of DNA motifs

DNA sequences were designed using the program SEQUIN.³² They were synthesized by standard phosphoramidite techniques³³ and purified from denaturing polyacrylamide gels. Individual components of the transducer and its 2D assembly were constructed by annealing from 90 °C to 4 °C stoichiometric mixtures of the strands (estimated by OD₂₆₀) to a concentration of 1 μM; this was done in a buffer solution containing 40 mM Tris·HCl, pH 8.0, 20 mM acetic acid, 2 mM EDTA, and 10 mM magnesium acetate (TAE/Mg). The chelator DX tiles were connected to the gold particles, and annealed to a concentration of 1 μM in a TAE buffer containing 2 mM EDTA, 5 mM magnesium acetate and 100 mM NaCl from 75 °C to 4 °C.

Formation of gold–DNA conjugates

Citrate-stabilized gold colloids with mean diameters of 5 and 10 nm (Ted Pella) were subsequently passivated with a monolayer of anionic phosphine molecules.^34,35 The colloidal solution was concentrated up to the micromolar range after phosphine coating. Single stranded (ss) DNA/Au conjugates were prepared by mixing gold nanoparticles with 5′-thiolated (–SH) ss-DNA in a molar ratio of 3 : 1, and incubated for 30 min in a TAE buffer containing 2 mM EDTA, 5 mM magnesium acetate and 50 mM NaCl. Au nanoparticles tethered with single DNA strands were purified by gel electrophoresis 2% agarose gel at 75V, 0.5X TAE buffer, and then recovered by cutting and extracting the appropriate band. ∼100 μL of a red solution was collected and then diluted to a final volume of 500 μL in a solution containing 100mM Na and TAE buffer. After further incubation for 5 h the volume was slowly reduced to 100 μL by vacuum centrifugation at room temperature. This process produces a gradual increase in ionic strength, which leads to much more stable DNA/Au conjugates.

Formation of motifs containing gold nanoparticles

The chelatorDX DNA/Au conjugate was prepared by mixing the ssDNA-Au strands and other component DNA strands in 3 mM TAE/Mg²⁺ buffer, followed by overnight annealing from 75 °C to 4 °C.³⁶ The final reaction volume was 50 μL and the concentration of each oligonucleotide was 1 μM.

Formation of the transducer and execution of the computation

To form the first layer, the component tiles, i.e., 6DF tiles, and PX-JX₂ devices in the appropriate state were mixed in a stoichiometric ratio, heated up to 42 °C and cooled to 4 °C to form the input 1D transducer array. In the next step the start DX tile, all computational TX tiles, and the two-chelator DX tiles were all mixed with the pre-formed 1D array and thermocycled between 36 °C and 20 °C 4 or 5 times over a period of 9 h²⁷ and stored at 4 °C. As discussed below, this thermocycling procedure is key to performing the computational assembly with fidelity. Only a start tile complementary to the first input symbol was used to avoid assembly of computational tiles on both sides of the 6DF motifs.

Selection of the complete computations from the incomplete ones

The computations that go to completion, i.e., those that contain the end TX tile, are selected using magnetic streptavidin beads that bind to a biotin group covalently attached to the end TX tile. The mixture is kept for 30 min at 4 °C. The beads are then washed with 3 mM TAE/Mg²⁺ buffer, and an equivalent amount of buffer is added to suspend the streptavidin beads connected with the final computations. Next, the material is irradiated under UV light at 366 nm in the presence of the crosslinking reagent psoralen; the addition of psoralen causes the start DX tile, the computational TX tiles and the end TX tile to be connected covalently in the order of their connectivity; simultaneously, the UV irradiation severs a photocleavable linker (Glen Research, Sterling, VA, USA) that is attached to the end TX tile. Thus, the computations containing the end TX tile can be cleaved from the streptavidin bead support. The beads are then washed two to three times with 3 mM TAE/Mg²⁺ buffer so that the final concentration for TEM examination is 5–10 times lower than 0.2 μM. A low initial temperature is used to ensure the stability of the Au/DNA conjugate and of the whole computation.

Marking the start and end of the computation

To mark the start of the computation, the same protocol was followed, except that the start tile was modified so that a biotinylated loop could be attached after selection of the final products. The biotinylated loop was separately annealed and incubated with 15 nm streptavidin–gold overnight. It was then added to the selected computations and cooled from 37 °C to 4 °C overnight. To mark the end tile with 15 nm streptavidin–gold, the start tile was modified to have no biotin attached to it, and the end tile was modified to have no photocleavable linker attached to it. In this case, only cross-linking with psoralen occurs as a result of UV irradiation. However, the biotin is not cleaved from the computation, so that the computation cannot be selected to find only complete answers if an end-marker is used.

Visualization of the final answers

Following this incubation, visualization of the particles was carried out by transmission electron microscopy (TEM). TEM imaging was performed both at the Neuroscience Department of NYU and at the Chemistry Department of CCNY. The instrument was operated at 60 kV. The particle samples were prepared on 400 mesh formvar-coated nickel grids by dropping 5 μL of 20–50 nM sample solution on grids and then wicking off excess solution with filter paper after 10 min. All grids were dried at least overnight.

Results

Formation and operation of the transducer

To execute the computation, the transducer is first annealed separately using 6DF tiles and the PX and/or JX₂ molecules. At the second stage, all the computational, start, end, and chelator tiles are added to the previously annealed input transducer and put through a thermocycling protocol between 20 °C and 36 °C. Algorithmic assembly requires that measures be taken to ensure that all relevant sticky ends bind correctly, not just one: In contrast to periodic assemblies (e.g., ref. 7 and 10), the inherent problem of algorithmic assemblies is that correct tiles compete not only with incorrect tiles, but also with partially correct tiles. There have been extensive attempts to treat this problem theoretically and experimentally by using sticky-ends of different strengths (e.g., ref. 15). We have shown previously that thermocycling around the melting point of the system ensures correct assembly of the DNA tiles when partially-correct tiles are competing with correct tiles.²⁷ We find that this approach has been applied successfully here, because we have obtained largely correct answers (vide infra). The result is visualized under TEM at a diluted concentration of 20–50 nM, following deposition on the grid for a period of 2–12 h. Initial results showed a lot of partial structures which could have been a consequence of incomplete assembly or of disintegration. To stabilize the structures, the middle domains of the computational TX tiles were joined covalently with a DNA cross-linking agent, psoralen; this procedure linked them with each other and with the start and end tiles along the computation pathway. The construct was irradiated with UV light for ∼10 min and a covalent linkage was formed as described elsewhere.²¹

Structures containing complete assemblies need to be selected away from those containing partial assemblies through a chemical purification/selection for those assemblies containing the end tile. As noted above, the selection was performed by modifying the end tile to contain a hairpin loop in its bottom helical domain and biotin was attached to the loop. A photocleavable linker was connected to the duplex between the tile and the hairpin so that it could be cleaved off the streptavidin support after selection by magnetic streptavidin beads. Following selection, the last step in the procedure was to mark the beginning or end of the computation with a 15 nm nanoparticle, so as to establish the order to read out the answer.

Visualization of the finite state machine readout by TEM

Fig. 9 shows that the answers to the computation can be read in the TEM. As noted above, AFM did not reliably differentiate 5 nm particles from 10 nm particles. Using the TEM, we were able to visualize the pattern of 4 or 5 gold particles in a row, as required by the input length. Fig. 9a shows the division of 21 (10101) by 3 yielding the output 7 (00111); the images contain two 5 nm particles (representing 0), followed by three 10 nm particles (representing 1) in a row. Fig. 9b, 9c and 9d show analogous patterns that contain the results of dividing 3 into 18, with output 6 (00110), into 15, with output 5 (0101), and into 12 with output 4 (0100), respectively. In each case, the proper pattern of 5 nm and 10 nm gold nanoparticles is visible.

Fig. 9 TEM images showing the output of the transducer. In each of these TEM images, the answers established by the chelator tiles attached to the TX computation tiles are visualized. (a) Division of 21 by 3. Note the two small circular objects preceding the three larger ones yielding a binary answer of 00111 (7 decimal). (b) Division of 18 by 3. The binary answer is 00110 (6 decimal). (c) Division of 15 by 3. The binary answer is 0101 (5 decimal). (d) Division of 12 by 3. The binary answer is 0100 (4 decimal). (e) Division of 15 by 3 with the end marked. The end-marker is a 15 nm gold nanoparticle. (f) Division of 12 by 3 with the start marked. (g) Division of 18 by 3 with the start marked. (h) Division of 21 by 3 with the start marked.

Despite cross-linking and selection, only about 15–30% complete answers (four or five nanoparticles, as appropriate) were visible through examination of many fields. Nevertheless, fewer than 5% of the answers had the order of the nanoparticles incorrect, which supports our previous experience with the power of thermocycling to ensure fidelity.²⁷ About 75–80% of the 5-particle answers that were visible could be read completely from the TEM images, and 80–90% of the 4-particle answers could be read; in the other instances, the distinction between 5 and 10 nm particles was unclear. About 11–12 correct complete answers out of ∼15 observable nanoparticle strings were visible for the 5-particle answers and about 16–18 correct complete answers were visible out of ∼20 observable nanoparticle strings were visible for the 4-particle answers.

Of course, we know these answers ahead of time; if we did not, there would be a problem, because the beginning of the string of nanoparticles is not distinct from the end. As noted above, we solve this problem by using a marker streptavidin gold particle of 15 nm diameter. This particle was added through biotin–streptavidin interactions to either the beginning or the end of the complete answers. Fig. 9e shows the output of 15/3 = 5 (0101) connected with the 15 nm gold marker at the end of the calculation, so the direction of reading is clear. Fig. 9f shows the output of 12/3 = 4 (0100), marked with 15 nm gold at the beginning. Fig. 9g demonstrates that the output of 18/3 = 6 (00110) can be marked with 15 nm gold at the beginning of the readout. Fig. 9h shows that the output of 21/3 = 7 (00111) can also be marked with 15 nm gold at the beginning of the string. In the cases where the direction of readout is marked, the 15 nm marker particle appears to dominate the image, and, to some extent, the behavior of the string of nanoparticles reporting the answer.

Discussion

Construction of the transducer

We have demonstrated that the transducer is able to perform division of small numbers by 3, provided the input is set. Setting the input in a varied combination of 0s and 1s was performed efficiently via the use of two-state PX-JX₂ devices connecting the 6DF input tiles. The input number could be changed by changing the states of the devices although, in our experiments, the devices were set to the designated state by applying the appropriate set strands for the given input before the computational tiles were applied. We have also demonstrated the computation in the second layer after the input is set. The binding of the start tile to the first input helix decides the next tile's binding with the information of the current state. We have designed the system so that the computation will reach the end only if every tile has a dual connection with its previous tile. Otherwise, the partially correct tile will fall off during the thermocycling protocol, and only the fully correct tile will survive and lead to the binding of the next tile.²⁷ This approach of sacrificing incorrect assemblies along the way may have led to the relatively small number of observable computations.

Optimization of the system required us to increase the length of some of the sticky ends from 7 nucleotides to 12, especially the sticky ends that encrypt the current-state and next-state information. The stability of the system, rather than its fidelity, was the motivation for this change in the sticky ends. Even after this modification, we found a majority of partial answers. In addition to the instability of the computation tiles, partial answers also may have resulted from poor binding by the chelator tiles or from the gold particles falling off the chelator tiles. We found that adjacent 10 nm particles destabilized the system somewhat, although adjacent 5 nm particles were tolerated quite well. In addition to lengthening the sticky ends, psoralen cross-linking was also added to the protocol, so as to solve this problem. A short irradiation time (10 min) was used to prevent nonspecific crosslinking.

Features of the transducer

In principle, the transducer described here can perform multilayered and multidirectional computing. In this work, we have only demonstrated division performed on one side of the transducer. The other side could also be used, once we alter the start signal for the calculation, while using the rest of the construct. This transducer so far has only divided a number that is exactly divisible by 3. If the sticky ends of the output symbols are chosen to be the same as those of the input symbols, another layer of computation could be performed by iterating the transducer. Similarly applying another layer of computation by another set of computational tiles would provide the composition of transducers. In another modification, we could possibly modify the computational tiles to include certain markers for state “S₁” (for remainder 1) and state “S₂” (remainder 2); this modification of the current device would enable output of the remainder if the number is not evenly divisible by 3.

We have used the gold particles as our readout, but to our knowledge, this is the first time that algorithmic assembly has been used to organize metallic nanoparticles. It is also a clear instance in which algorithmic assembly has been used in conjunction with nanomechanical devices, as done less explicitly by Guet al.²⁷ In another modification of the system, one could imagine including other components to chelate the computational tiles. Of course, the chelator tiles need not bind only metallic nanoparticles. They could be modified to contain other species, such as antibodies or aptamers,³⁷ a variety of biological catalysts, such as enzymes, ribozymes or deoxyribozymes³⁸ that would then be organized algorithmically. Likewise, other nanoparticles,³⁹ other inorganic species that could act as nanoelectronic⁴⁰ or nanophotonic⁴¹ hardware or a variety of organic precursors to small molecules⁴² or polymers⁴³ could be organized in this fashion. Strand displacement DNA logic circuits⁴⁴ could also be organized this way. In a different application, the inclusion of programmable DNA devices chelating the tiles would lead to reciprocal programmable motions;⁴⁵ in this case, a choreographed set of motions would be available [Y. Li, N. J. and N. C. S., work in progress]. Although we do not have a high yield of complete answers, the answers themselves are largely correct. The success of thermocycling this system further demonstrates that it is possible to perform at least a 1-dimensional algorithmic assembly without complex models based on the estimated strengths⁴⁶ of sticky end classes.¹⁵ This successful empirical approach suggests that it is possible to attain a thermodynamic minimum in simple cases.

Conclusions

This work has demonstrated that it is possible to prototype a DNA-based computational device with variable input. Previous examples of DNA-based computations (e.g., ref. 14) have used fixed systems whose tile assemblies determined the answer. Here, we have used the same system with different settings to achieve our results. Thus we have shown a potentially reusable system performing computations by self-assembly on different inputs. To our knowledge all other self-assembly systems perform only one computation without the ability to be reused. The readout of the system is obtained by algorithmically assembling gold nanoparticles. Although arranging gold nanoparticles by DNA self-assembly has been reported,⁴⁷ this is the first time such arrangement of nanoparticles has been obtained as the result of a computation. Furthermore, it should be noted that this system may be considered as a first step in an assembly of a programmed array incorporating nanomechanical devices or other varieties of biochemical, chemical or materials systems that can be organized as the result of a simple computation.

Acknowledgements

We thank Dr Ruojie Sha for valuable discussions and for the synthesis of non-standard oligonucleotides. We thank Prof. George John for the use of the CCNY TEM and Prof. Chiye Aoki for the use of the NYU TEM. We acknowledge support by grant CCF-0726378 from the NSF to both N.J. and N.C.S., grant DMS-0900671 to N.J., and the following grants to N.C.S: GM-29554 from NIGMS, grant CTS-0608889 from the NSF, grant W911FF-08-C-0057 from ARO, via Pegasus Corporation, MURI W911NF-07-1-0439 from ARO, grants N000140910181 and N000140911118 from ONR and a grant from the W.M. Keck Foundation.

Notes and references

1. N. C. Seeman, J. Theor. Biol., 1982, 99, 237.
2. N. R. Kallenbach, R.-I. Ma and N. C. Seeman, Nature, 1983, 305, 829.
3. Y. Wang, J. E. Mueller, B. Kemper and N. C. Seeman, Biochemistry, 1991, 30, 5667.
4. X. Wang and N. C. Seeman, J. Am. Chem. Soc., 2007, 129, 8169.
5. N. C. Seeman, Nano Lett., 2001, 1, 22.
6. T.-J. Fu and N. C. Seeman, Biochemistry, 1993, 32, 3211.
7. T. H. LaBean, H. Yan, J. Kopatsch, F. Liu, E. Winfree, J. H. Reif and N. C. Seeman, J. Am. Chem. Soc., 2000, 122, 1848.
8. Z. Shen, H. Yan, T. Wang and N. C. Seeman, J. Am. Chem. Soc., 2004, 126, 1666.
9. W. Liu, X. Wang, T. Wang, R. Sha and N. C. Seeman, Nano Lett., 2008, 8, 317.
10. E. Winfree, F. Liu, L. A. Wenzler and N. C. Seeman, Nature, 1998, 394, 539.
11. D. Liu, W. Wang, Z. Deng, R. Walulu and C. Mao, J. Am. Chem. Soc., 2004, 126, 2324.
12. J. Zheng, J. J. Birktoft, Y. Chen, T. Wang, R. Sha, P. E. Constantinou, S. L. Ginell, C. Mao and N. C. Seeman, Nature, 2009, 461, 74.
13. E. Winfree, X. Yang and N. C. Seeman, DNA Based Computers, ed. L. Landweber and E. Baum, AMS DIMACS series, 1998, vol. 44, p. 191.
14. C. Mao, T. H. LaBean, J. H. Reif and N. C. Seeman, Nature, 2000, 407, 493.
15. P. W. K. Rothemund, N. Papadakis and E. Winfree, PLoS Biol., 2004, 2, 2041.
16. Y. Benenson, T. Paz-elizur, R. Adar, E. Keinan, Z. Livneh and E. Shapiro, Nature, 2001, 414, 430.
17. Y. Benenson, R. Adar and E. Shapiro, Nature, 2004, 429, 423.
18. B. Yurke, A. J. Turberfield, A. P. Mills, Jr., F. C. Simmel and J. L. Neumann, Nature, 2000, 406, 605.
19. H. Yan, X. Zhang, Z. Shen and N. C. Seeman, Nature, 2002, 415, 62.
20. B. Chakraborty, R. Sha and N. C. Seeman, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17245.
21. W. B. Sherman and N. C. Seeman, Nano Lett., 2004, 4, 1203.
22. J.-S. Shin and N. A. Pierce, J. Am. Chem. Soc., 2004, 126, 10834.
23. P. Yin, H. Yan, X. G. Daniell, A. J. Turberfield and J. H. Reif, Angew. Chem., Int. Ed., 2004, 43, 4906.
24. T. Omabegho, R. Sha and N. C. Seeman, Science, 2009, 324, 67.
25. H. Gu, J. Chao, S. J. Xiao and N. C. Seeman, Nature, 2010, 465, 202.
26. S. Liao and N. C. Seeman, Science, 2004, 306, 2072.
27. H. Gu, J. Chao, S. J. Xiao and N. C. Seeman, Nat. Nanotechnol., 2009, 4, 245.
28. V. Manca, C. Martin-Vide and G. Paun, BioSystems, 1999, 52, 47.
29. G. Paun, Rev. Roum. Math. Pures. Appl., 1978, 23, 921.
30. N. Jonoska, S. Liao and N. C. Seeman, Aspects of Molecular Computing, ed. N. Jonoska, Gh. Paun and G. Rozenberg, Springer LNCS, 2004, vol. 2950, p. 219.
31. J. E. Hopcroft and J. D. Ullman, Introduction to Automata Theory, Languages, and Computing, 1979, Addison-Wesley, Reading, MA.
32. N. C. Seeman, J. Biomol. Struct. Dyn., 1990, 8, 573.
33. M. H. Caruthers, Science, 1985, 230, 281.
34. D. Zanchet, C. Micheel, W. Parak and A. P. Alivisatos, Nano Lett., 2001, 1, 32.
35. D. Zanchet, C. Micheel, A. P. Parak and A. P. Alivisatos, J. Phys. Chem. B, 2002, 106, 11758.
36. J. Zheng, P. E. Constantinou, C. Micheel, A. P. Alivisatos, R. A. Kiehl and N. C. Seeman, Nano Lett., 2006, 6, 1502.
37. C. Lin, E. Katilius, Y. Liu, J. P. Zhang and H. Yan, Angew. Chem., Int. Ed., 2006, 45, 5296.
38. H. Lederman, J. MacDonald, D. Stefanovic and M. N. Stojanovic, Biochemistry, 2006, 45, 1194.
39. R. Freeman, T. Finder and I. Willner, Angew. Chem., Int. Ed., 2009, 48, 7818.
40. B. Robinson and N. C. Seeman, Protein Eng., Des. Sel., 1987, 1, 294.
41. P. K. Dutta, R. Varghese, J. Nangreave, S. Lin, H. Yan and H. Liu, J. Am. Chem. Soc., 2011, 133, 11985.
42. K. Sakurai and D. R. Liu, J. Synth. Org. Chem. Jpn., 2008, 66, 590.
43. S. Liao and N. C. Seeman, Science, 2004, 306, 2072.
44. L. Qian, E. Winfree and J. Bruck, Nature, 2011, 475, 368.
45. C. Liu, N. Jonoska and N. C. Seeman, Nano Lett., 2009, 9, 2641.
46. J. SantaLucia, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460.
47. J. Zheng, P. E. Constantinou, C. Micheel, A. P. Alivisatos, R. A. Kiehl and N. C. Seeman, Nano Lett., 2006, 6, 1502.

---

Footnote

† Electronic supplementary information (ESI) available: Structural diagrams and sequences for the DNA motifs used in this work. See DOI: 10.1039/c1sc00523e

---