One hundred fold overall sensitivity enhancements for Silicon-29 NMR spectroscopy of surfaces by dynamic nuclear polarization with CPMG acquisition†
Aaron J.
Rossini
a,
Alexandre
Zagdoun
a,
Moreno
Lelli
a,
David
Gajan
b,
Fernando
Rascón
b,
Melanie
Rosay
c,
Werner E.
Maas
c,
Christophe
Copéret
b,
Anne
Lesage
a and
Lyndon
Emsley
*a
aCentre de RMN à Très Hauts Champs, Université de Lyon (CNRS/ENS Lyon/UCB Lyon 1), 5 Rue de la Doua, 69100, Villeurbanne, France. E-mail: lyndon.emsley@ens-lyon.fr; Fax: +33 4 78 89 67 61
bDepartment of Chemistry, ETH Zürich, Laboratory of Inorganic Chemistry, 10 Wolfgang Pauli Strasse, CH-8093, Zürich, Switzerland
cBruker BioSpin Corporation, 15 Fortune Drive, Billerica, MA 01821, USA
First published on 10th October 2011
Abstract
Dynamic nuclear polarization (DNP) 29Si solid-state NMR spectra of a hybrid mesoporous silica material impregnated with aqueous biradical solutions have been acquired with cross-polarization (CP) and cross-polarization Carr–Purcell Meiboom–Gill (CP/CPMG) pulse sequences. The integrated intensities (II) and signal to noise ratios (S/N) of the 29Si solid-state NMR spectra are monitored in order to measure the DNP enhancement factors (εSi CP) as well as the overall sensitivity enhancement (ΣSi CP) available from the combination of DNP and CPMG acquisition. Here, 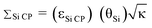 , where θSi is a factor which quantifies reduction of the NMR signal by paramagnetic effects (quenching) and κ is the square root of the ratio of nuclear longitudinal relaxation times of the dry material and material impregnated with radical solution. It is found that ΣSi CP is always substantially lower than the measured value of εSi CP due to paramagnetic effects which reduce the II of the 29Si CP solid-state NMR spectra at high biradical concentrations. In this system, it is observed that the sample preparation which provides optimal DNP signal enhancement does not provide optimal overall signal enhancement. Notably, optimal signal enhancements are obtained for CPMG acquisition of the 29Si solid-state NMR spectra when lower radical concentrations are employed due to slower transverse relaxation rates. To the best of our knowledge this is the first study which seeks to quantify the overall sensitivity enhancements available from DNP solid-state NMR experiments.
, where θSi is a factor which quantifies reduction of the NMR signal by paramagnetic effects (quenching) and κ is the square root of the ratio of nuclear longitudinal relaxation times of the dry material and material impregnated with radical solution. It is found that ΣSi CP is always substantially lower than the measured value of εSi CP due to paramagnetic effects which reduce the II of the 29Si CP solid-state NMR spectra at high biradical concentrations. In this system, it is observed that the sample preparation which provides optimal DNP signal enhancement does not provide optimal overall signal enhancement. Notably, optimal signal enhancements are obtained for CPMG acquisition of the 29Si solid-state NMR spectra when lower radical concentrations are employed due to slower transverse relaxation rates. To the best of our knowledge this is the first study which seeks to quantify the overall sensitivity enhancements available from DNP solid-state NMR experiments.
Introduction
Dynamic nuclear polarization (DNP) has attracted considerable interest as a method to enhance the sensitivity of solution and solid-state NMR experiments.1–3 The original DNP experiments were first proposed and performed in the 1950's at low magnetic fields.4–6 The development of gyrotrons capable of producing high power high frequency microwave (MW) radiation has recently enabled DNP experiments to be extended to high magnetic fields.7–10 In a DNP NMR experiment the polarization of unpaired electrons is transferred to the nuclei of interest by irradiating the electron paramagnetic resonance (EPR). Modern high field DNP NMR experiments are usually accomplished by introducing an exogenous stable radical into the sample as a polarization source. Under continuous wave MW irradiation, all NMR active nuclei in the sample are polarized, although the extent of polarization depends upon the abundance, gyromagnetic ratio and relaxation properties of the nucleus in question; 1H nuclei are usually the most rapidly polarized nuclei11,12 and spin diffusion efficiently distributes polarization over the protons of the solvent/sample.13–19 Enhanced 1H polarization may then be transferred to hetero-nuclei (e.g., 13C, 29Si). DNP NMR experiments in the solid state are usually today accomplished under magic angle spinning (MAS) conditions with sample temperatures around 100 K.Modern DNP solid-state NMR experiments have mainly focused on biological applications such as the characterization of proteins and membrane systems.1,3,20–23 We have recently shown how the NMR signals from the surfaces of materials can be enhanced by DNP if the sample is impregnated24 with a radical containing solution.25,26 In this way DNP signal enhancement factors (ε) from 20 to 40 were obtained. We dub this method DNP Surface Enhanced NMR Spectroscopy (SENS). Since sensitivity is the key barrier to the characterization of surfaces by NMR, this opens up a whole new field of possibilities and should have broad ranging implications for the characterization of a variety of materials. For example, we showed the acquisition of two-dimensional 29Si and 13C CP heteronuclear correlation (HETCOR) solid-state NMR spectra were possible in total experiment times on the order of an hour, at natural isotopic abundance.25,26 Recently Lafon et al. have used this approach to acquire DNP enhanced directly excited 29Si solid-state NMR spectra of the bulk phase of silica nanoparticles.27
In order to better evaluate the applications of DNP SENS experiments it would be beneficial to quantify the overall sensitivity enhancement of the experiments. Quantifying the overall sensitivity enhancements available from DNP is key for several reasons: (i) sources of signal loss or less than optimal signal enhancement in DNP NMR experiments could be identified, and possibly rectified in the future. (ii) The practising chemist could identify the sample preparation conditions which will provide highest sensitivity enhancements, rather than simply the best DNP enhancements. (iii) Without knowledge of the sensitivity enhancement the feasibility of future applications of DNP solid-state NMR cannot be reasonably estimated (e.g., based upon the concentration of NMR active nuclei in materials). Understanding the nature of the overall enhancement would therefore open up new avenues for designing polarizing radicals, conceiving NMR acquisition schemes, or optimizing instrumentation (for lower sample temperatures, for example).
However, to the best of our knowledge there has not been a quantitative study of the overall sensitivity enhancements available from DNP experiments performed with exogenous polarization agents. Thurber and Tycko have recently investigated sensitivity gains provided by DNP in frozen water/glycerol solutions at various temperatures (from 7 to 80 K) and radical concentrations.28 They observed that at higher radical concentrations ε generally increased, while the magnitude of the absolute signal generally decreased. To date, this is the only study in which the absolute signal intensities of the DNP enhanced NMR spectra were reported, in addition to ε and the time constant for build-up of DNP enhanced longitudinal magnetization (TDNP). In other recent solid-state DNP NMR studies by several research groups only ε and TDNP values were reported, rather than absolute signal intensities.22,23,25,26,28–31
In a DNP solid-state NMR experiment, the observed enhancement factor ε, defined here as the ratio of the integrated intensities between MW on and MW off spectra, depends on many factors. To name but a few, the structure and concentration of the polarizing agent, the sample temperature, the spinning frequency, the microwave power, the composition of the frozen solution, and the deuteration level of the substrates.1,17,28,32–34 However ε only encapsulates part of the whole experiment. For example, the radical concentration not only influences ε, but also (i) the fraction of spins residing inside the so-called diffusion barrier,16,35,36 which will not contribute to the NMR signal, and (ii) TDNP, which is linked to the nuclear longitudinal relaxation time (T1).28,33,34,37 Both factors will affect the overall sensitivity enhancement factor provided by the DNP experiment.
In this article, in addition to quantifying the overall signal enhancements available from DNP, we apply the Carr–Purcell Meiboom–Gill (CPMG) acquisition scheme to obtain further signal enhancements for 29Si solid-state NMR spectra. CPMG sequences38,39 are routinely employed to enhance the signal to noise (S/N) ratios of solid-state NMR spectra which are inhomogeneously broadened by some combination of chemical shift anisotropies,40,41 chemical shift distributions,42–44 quadrupolar broadening,45,46 and magnetic field inhomogeneity.47–49 In CPMG experiments a train of refocusing pulses are applied to acquire a series of spin echoes (Fig. 1). CPMG sequences can yield order of magnitude improvements in signal to noise when the effective transverse dephasing time50 (T2′) is relatively long and many spin echoes can be acquired, as was observed for mesoporous silicas.43 However, it is not at first sight obvious that CPMG can be used in DNP SENS experiments, since T2′ is expected to be severely affected by the presence of the paramagnetic polarizing agent.51 This could potentially hinder the application of CPMG pulse sequences. In this regard Ellis and Lipton have shown that it is possible to apply CP/CPMG pulse sequences to acquire spectra of quadrupolar nuclei contained in metalloproteins which are dissolved in frozen solutions doped with paramagnetic metal ions (that act to enhance 1H longitudinal relaxation rates).52–56 Kervern et al. have also demonstrated that the CPMG pulse sequence can be utilized to extend 1H coherence lifetimes of paramagnetic solids under ultra fast MAS.57 These findings suggest that T2′ may remain long enough such that CPMG experiments remain feasible on systems doped with radicals.
![(A) Schematic drawing of the structure of the hybrid material (I) used here. (B) DNP enhanced 1H-29Si CP/MAS spectrum of I impregnated with a 12 mM aqueous TOTAPOL solution. The Tn [(R)n(OSi)4 − n] and Qn [(OSi)n(OR)4 − n] sites are labelled on the spectrum. (C) The CP pulse sequence utilized to acquire the MAS 1H-29Si CP/MAS NMR spectra. (D) The CP/CPMG pulse sequence utilized to acquire the 1H-29Si CP/CPMG MAS NMR spectra. τr is the rotor period and m and N are integers.](/image/article/2012/SC/c1sc00550b/c1sc00550b-f1.gif) | ||
Fig. 1 (A) Schematic drawing of the structure of the hybrid material (I) used here. (B) DNP enhanced 1H-29Si CP/MAS spectrum of I impregnated with a 12 mM aqueous TOTAPOL solution. The Tn [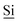 (R)n(OSi)4 − n] and Qn [ (R)n(OSi)4 − n] and Qn [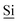 (OSi)n(OR)4 − n] sites are labelled on the spectrum. (C) The CP pulse sequence utilized to acquire the MAS 1H-29Si CP/MAS NMR spectra. (D) The CP/CPMG pulse sequence utilized to acquire the 1H-29Si CP/CPMG MAS NMR spectra. τr is the rotor period and m and N are integers. (OSi)n(OR)4 − n] sites are labelled on the spectrum. (C) The CP pulse sequence utilized to acquire the MAS 1H-29Si CP/MAS NMR spectra. (D) The CP/CPMG pulse sequence utilized to acquire the 1H-29Si CP/CPMG MAS NMR spectra. τr is the rotor period and m and N are integers. | ||
In the following we first evaluate the overall sensitivity enhancements (where sensitivity is defined as the signal to noise ratio per square root of unit time per unit mass)58 obtained by 29Si DNP SENS experiments on a mesoporous hybrid silica material (I, Fig. 1A). By taking into account the loss of signal due to various paramagnetic effects, the effective relaxation times, and the effect of performing experiments at low temperature the overall sensitivity enhancements can be measured. We show that the conditions for optimal sensitivity do not in general correspond to those providing the highest ε, and very importantly, that paramagnetic effects lead to a large reduction in signal intensities. We then show how the CPMG acquisition scheme can be combined with DNP SENS. Under optimum conditions we obtain sensitivity enhancement factors of ca. 100, which corresponds to a ca. 10000 fold reduction in the experiment times. To the best of our knowledge this is the first study which seeks to quantify the overall sensitivity enhancements available from DNP experiments.
Experimental
Sample preparation
Experiments were performed on the hybrid silica material (I, Fig. 1A) with directly incorporated phenol ligands, prepared as previously described.59 The influence of solvent deuteration level on DNP enhancement was tested on a methyl passivated SBA-15 silica, the synthesis of which is described in the ESI†. The biradical TOTAPOL30 was obtained from DyNuPol Inc., Massachusetts, USA. Samples for DNP solid-state NMR experiments were prepared by placing 8.8 to 9.5 mg of dry I onto a disposable weighing boat. With a micro-pipette ca. 12 μL of the aqueous TOTAPOL solution (100% H2O, unless indicated otherwise) was added to the material. The total mass of this (impregnated) material was then recorded and the material was then mixed by hand with a glass stirring rod in order to homogeneously distribute the solution over the powdered sample. The impregnated material was then packed into a 3.2 mm sapphire rotor. The rotors were weighed (empty masses of 329.0 to 325.7 mg) before and after packing. A polyfluoroethylene plug was then inserted to prevent leakage and the rotor was capped with a zirconia drive cap. The mass of dry I material was then determined by calculating the fraction of material inside the rotor corresponding to dry material (Table S1†).DNP surface enhanced NMR experiments
All experiments were performed on a commercial 9.4 T 263 GHz Bruker DNP solid-state NMR instrument (ν0(1H) = 399.82 MHz and ν0(29Si) = 79.43 MHz),34 using a low temperature 3.2 mm double resonance CPMAS probe, sample temperatures of ca. 105 K and sample spinning frequencies (νrot) of 8000 Hz. The field sweep coil of the NMR magnet was set so that MW irradiation occurred at the DNP enhancement maximum of TOTAPOL (263.334 GHz). The estimated power of the MW beam at the output of the probe waveguide was ca. 4 W.34 Hartmann–Hahn matching conditions and contact times were optimized directly on the samples under study in MW on DNP cross-polarization (CP) experiments. For CP, the amplitude of the 1H contact pulse was linearly ramped in order to improve CP efficiency.60,61SPINAL-64 decoupling was employed with 1H rf fields (ν1(1H)) of ∼89 kHz.62 For CP Carr–Purcell Meiboom–Gill (CP/CPMG) experiments40,41,43 the echo delays and acquisition periods were rotor synchronized by setting them to integer multiples of the rotor period. A complete listing of experimental parameters (pulse widths, rf fields, recycle delays, etc.) is given in the ESI† (Table S2). Pulse programs are available upon request. Echo reconstructed CPMG spectra were obtained by summing the whole echoes of the FIDs in the time domain, followed by Fourier transform and magnitude calculation.63,64 All spectral processing, integrated intensity (II) and signal to noise ratio (S/N) measurements were performed with the Topspin software package. εSi CP was observed to be the same for both T and Q sites, so for convenience integrals were taken across the isotropic resonances of I, and S/N measurements utilized the peak of the Q sites.Results and discussion
Part I - Quantification of overall DNP sensitivity enhancements
| [TOTAPOL] (mM) | m Total (mg)a | m SiO2 (mg)b | II MW offc | II MW onc | ε Si CP d | II MW on 30 s e | θ Si e | T 1(1H) or TDNP(1H) (s)g | Σ Si CP f | Σ † Si CP f |
|---|---|---|---|---|---|---|---|---|---|---|
a
m
Total is the total mass of impregnated I material in the rotor. Uncertainties for all the last digit of all quantities are given in parenthesis.
b
m
SiO2
corresponds to the mass of dry I inside the rotor. A detailed explanation of the determination of this mass is given in the ESI†.
c Integrated intensities (II) of all isotropic resonances in the 29Si CP/MAS spectra, with or without MW irradiation. εSi CP is the same for both the T and Q sites, so for convenience the integrals were take over the entire isotropic resonance. All integrals are per unit mass of dry material (mSiO2) and per number of scans. A 2 s recycle delay was employed in all cases. 128 scans were acquired for the MW on spectra and 384 scans were acquired for the MW off.
d
ε
Si CP
is the DNP enhancement factor,  .
e DNP 29Si CP/MAS spectra were acquired with 30 s recycle delays (35 s for pure H2O) in order to allow for greater than 95% longitudinal relaxation and measure the 29Si quenching factor (θSi). All integrals are divided by mSiO2 and the number of scans. 8 scans were acquired for the materials impregnated with radical solution, while 384 scans were acquired for the material impregnated with pure water, .
e DNP 29Si CP/MAS spectra were acquired with 30 s recycle delays (35 s for pure H2O) in order to allow for greater than 95% longitudinal relaxation and measure the 29Si quenching factor (θSi). All integrals are divided by mSiO2 and the number of scans. 8 scans were acquired for the materials impregnated with radical solution, while 384 scans were acquired for the material impregnated with pure water,  .
f
Σ
Si CP
is the overall DNP enhancement factor, .
f
Σ
Si CP
is the overall DNP enhancement factor,  . Σ†Si CP is the overall DNP enhancement factor including Boltzmann enhancement, . Σ†Si CP is the overall DNP enhancement factor including Boltzmann enhancement,  , where 105 K is the estimated sample temperature and 298 K is the sample temperature at which most solid-state NMR experiments are performed.
g
T
1(1H) or TDNP(1H) was measured by fitting saturation recovery curves obtained with a 1H-29Si CP/CPMG pulse sequence which was modified to have a train of saturating 1H π/2 pulses. TDNP(1H) was measured for I impregnated with radical solutions with MW on experiments, and T1(1H) was measured for materials without radicals with MW off experiments. When biradical polarizing agents are utilized, T1 and TDNP are usually equal. , where 105 K is the estimated sample temperature and 298 K is the sample temperature at which most solid-state NMR experiments are performed.
g
T
1(1H) or TDNP(1H) was measured by fitting saturation recovery curves obtained with a 1H-29Si CP/CPMG pulse sequence which was modified to have a train of saturating 1H π/2 pulses. TDNP(1H) was measured for I impregnated with radical solutions with MW on experiments, and T1(1H) was measured for materials without radicals with MW off experiments. When biradical polarizing agents are utilized, T1 and TDNP are usually equal.
|
||||||||||
| Dry material | — | — | — | — | — | — | — | 0.20–0.80 | — | — |
| Degassed, dry | — | — | — | — | — | — | — | 3.9(5) | — | — |
| Pure H2O | 18.6(2) | 8.1(3) | — | — | 1 | 4.2(1) | 1.00 | 12.6(3) | — | — |
| 4.0(2) | 18.2(2) | 7.9(3) | 1.00(4) | 16.2(2) | 16(1) | 35.5(4) | 0.49(4) | 5.3(1) | 6.7(8) | 19(2) |
| 7.8(2) | 18.3(2) | 8.0(3) | 1.31(4) | 19.6(2) | 15(1) | 35.1(4) | 0.52(5) | 4.6(1) | 7.2(9) | 20(3) |
| 12.1(2) | 18.5(2) | 8.1(3) | 0.88(4) | 28.9(3) | 33(1) | 57.8(7) | 0.39(3) | 2.9(1) | 15(1) | 42(4) |
| 16.1(2) | 18.0(2) | 7.7(3) | 0.58(4) | 24.5(2) | 43(1) | 36.9(4) | 0.19(1) | 2.4(1) | 10.4(9) | 29(3) |
| 20.3(2) | 21.9(2) | 8.6(3) | 0.72(3) | 21.3(2) | 30(1) | 35.1(4) | 0.26(2) | 2.5(1) | 9.7(9) | 27(3) |
| 23.9(2) | 16.7(2) | 7.1(3) | 0.47(4) | 11.9(1) | 25(1) | 16.1(2) | 0.14(1) | 2.5(1) | 4.5(5) | 13(1) |
The effect of solvent deuteration ratio on εSi CP was investigated using a methyl passivated mesoporous silica impregnated with 10 mM TOTAPOL solutions of varying H2O:D2O ratios (Figure S1). It was found that fully protonated solutions gave the largest εSi CP values and absolute signal intensities. Therefore 100% H2O solutions were employed for all subsequent measurements. The influence of biradical concentration on εSi CP was investigated by acquiring 1H-29Si CP/MAS spectra of I impregnated with TOTAPOL H2O solutions of varying biradical concentration (Fig. 2, Table 1). The left and middle columns show respectively the 29Si CP/MAS spectra with MW irradiation on and off. The intensities of all of the NMR spectra have been scaled for the mass of dry material contained in each rotor. From Fig. 2 it is clear that DNP provides a substantial enhancement of the 29Si NMR signals, and εSi CP strongly depends on the radical concentration (Fig. 3A). For the TOTAPOL concentrations studied, εSi CP ranges from 16 (4.0 mM) to 25 (23.9 mM) and peaks at a value of 43 (16.1 mM). These εSi CP values are similar to those previously reported by our research group for DNP experiments on other silica materials impregnated with TOTAPOL solutions.25,26
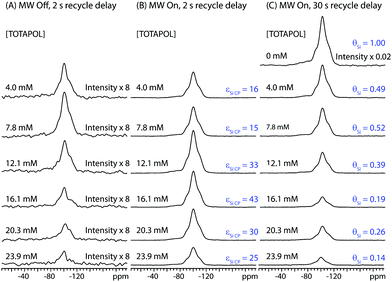 | ||
| Fig. 2 1H-29Si CP/MAS spectra of I impregnated with aqueous TOTAPOL solutions ranging in concentration from 0 mM to 23.9 mM. The intensities of all spectra have been scaled to account for differences in the mass of material inside each rotor and the number of scans (see Table 1). (A) Spectra acquired without MW irradiation with a 2 s delay in between each of 384 scans. (B) Spectra acquired with MW irradiation with a 2 s delay in between each of 128 scans. The corresponding DNP signal enhancement factors (εSi CP) are given for each spectrum. (C) Spectra acquired with MW irradiation (excepting the sample impregnated with pure water) with a 30 s recycle delay in between each of 8 scans (384 scans for the sample impregnated with pure water). The intensity of the spectra impregnated with aqueous TOTAPOL solutions have been scaled down by the corresponding value of εSi CP. The intensity of the spectrum of the sample impregnated with pure water has been scaled by a factor of 8/384. The factor which describes the reduction of the 29Si signal intensities due to paramagnetic effects (θSi) is listed next to each spectrum. Spectra were processed with 200 Hz of exponential line broadening in order to obtain more reliable integrals for the MW off spectra. | ||
![Graphs showing the effect of electron concentration on (A) DNP enhancement factor (εSi CP), (B) the 29Si quenching factor (θSi), (C) DNP enhanced longitudinal relaxation times (TDNP) and (D) the overall enhancement factor (ΣSi CP) and the overall enhancement factor including the Boltzmann enhancement (Σ†Si CP). Uncertainties for all measurements are indicated in Table 1. Note that [e−] = 2 × [TOTAPOL].](/image/article/2012/SC/c1sc00550b/c1sc00550b-f3.gif) | ||
| Fig. 3 Graphs showing the effect of electron concentration on (A) DNP enhancement factor (εSi CP), (B) the 29Si quenching factor (θSi), (C) DNP enhanced longitudinal relaxation times (TDNP) and (D) the overall enhancement factor (ΣSi CP) and the overall enhancement factor including the Boltzmann enhancement (Σ†Si CP). Uncertainties for all measurements are indicated in Table 1. Note that [e−] = 2 × [TOTAPOL]. | ||
The factor θSi is utilized to quantify the reduction or “quenching” of the 29Si signal (Table 1). θSi is calculated by dividing the II per unit mass of the MW on 29Si spectra of the impregnated I by εSi CP and the II of the 29Si spectrum of I impregnated with pure water (Table 1). All measurements of θSi were performed with 30 s recycle delays in order to allow for greater than 95% longitudinal relaxation of the 1H magnetization at all biradical concentrations. The errors associated with measurements of θSi are not easy to quantify,72 however, in general, it can clearly be seen that as the biradical concentration is increased, θSi decreases (Fig. 3B). This is consistent with our hypothesis that the loss of signal is due to paramagnetic effects.
 | (1) |
Note that the pristine dry material possesses extremely short T1(1H) values when it is handled in open air. The short relaxation times are attributed to the presence of paramagnetic molecular oxygen in the pores of the material. When a sample of the pristine dry material is degassed and then packed into a rotor under an inert argon atmosphere, T1(1H) is equal to 3.9 s, which is an order of magnitude longer than T1(1H) of the oxygenated material (Table 1). Since our ultimate goal is the characterization of air sensitive catalyst materials, T1(1H) of the dry degassed material was chosen as the reference point for the calculation of ΣSi CP. TDNP(1H) decreases from 5.3 s at 4 mM biradical concentration to 2.4 s at 16 mM biradical concentration. At higher biradical concentrations TDNP(1H) does not significantly decrease further (Fig. 3C).
In addition to the DNP signal enhancement, signal enhancement is obtained from conducting the experiments at temperatures of 105 K. With respect to NMR experiments performed at 298 K, the overall sensitivity enhancement including the Boltzmann factor (Σ†Si CP) is:
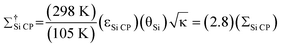 | (2) |
The Boltzmann enhancement was experimentally confirmed by acquiring 29Si CP/MAS spectra of dry I at temperatures of 105 K and 310 K (Figure S2†). It was found that the low temperature spectrum possessed a signal that was 3.7 times larger than that of the high temperature spectrum. The additional signal enhancement is attributed to increased CP efficiency at lower temperature as well as an increase in the probe quality factor (Q). For calculations of Σ†Si CP in the following only the ratios of sample temperatures were employed (i.e., a factor of 2.8), as the other factors are highly variable and difficult to quantify, although they do tend to improve at low temperatures.
For all biradical concentrations it is observed that ΣSi CP is always significantly lower than εSi CP. ΣSi CP and Σ†Si CP peak at a biradical concentration of 12.1 mM, where values of 15 and 42 are observed, respectively (Fig. 3D). Note that a 16.1 mM solution of TOTAPOL actually provides a higher value of εSi CP (43) than the 12.1 mM solution, however, the value of ΣSi CP is lower due to a low θSi (0.19).
Part II - Combining DNP and CP/CPMG for additional 29Si signal enhancement
The DNP 29Si CP/MAS and CP/CPMG spectra of I are shown in Fig. 4A and 4B, respectively, and the corresponding CPMG free induction decays presented in magnitude mode are shown in Fig. 4C. For all CP/CPMG experiments 12 echoes (N) were acquired, which corresponds to a 48 ms acquisition. In the absence of transverse relaxation the acquisition of N echoes would lead to an increase in the II by a factor of 2N, and an increase in the S/N by a factor of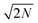 in comparison to a standard CP spectrum. For the dry material and material impregnated with pure water, a slow decay of transverse magnetization is observed (T2′(29Si) > 200 ms), therefore, the enhancement of S/N available from CPMG acquisition (εCPMG) can be estimated to be
in comparison to a standard CP spectrum. For the dry material and material impregnated with pure water, a slow decay of transverse magnetization is observed (T2′(29Si) > 200 ms), therefore, the enhancement of S/N available from CPMG acquisition (εCPMG) can be estimated to be 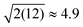 . In line with these results, Pruski and co-workers have previously demonstrated that it is possible to acquire over 200 CPMG echoes (acquisition times of ca. 300 ms) with fast spinning MAS experiments on similar mesoporous silica materials.43,44 This results in a factor of 16 sensitivity enhancement.43 However, rapid sample spinning rates are crucial for these experiments as they enable low power 1H heteronuclear decoupling to be used. This leads to minimal probe duty cycles which allow for long acquisition times. Here it would in principle be possible to acquire many more echoes for the dry and impregnated I, but, this would in practice lead to untenable probe duty cycles.
. In line with these results, Pruski and co-workers have previously demonstrated that it is possible to acquire over 200 CPMG echoes (acquisition times of ca. 300 ms) with fast spinning MAS experiments on similar mesoporous silica materials.43,44 This results in a factor of 16 sensitivity enhancement.43 However, rapid sample spinning rates are crucial for these experiments as they enable low power 1H heteronuclear decoupling to be used. This leads to minimal probe duty cycles which allow for long acquisition times. Here it would in principle be possible to acquire many more echoes for the dry and impregnated I, but, this would in practice lead to untenable probe duty cycles.
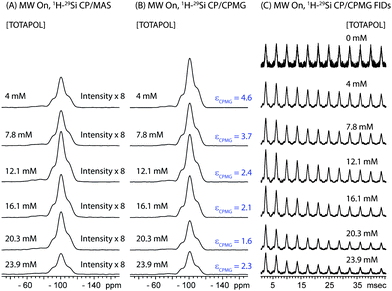 | ||
| Fig. 4 (A) 1H-29Si CP/MAS spectra and (B) 1H-29Si CP/CPMG MAS spectra of I impregnated with aqueous TOTAPOL solutions ranging in concentration from 0 mM to 23.9 mM. The intensities of all spectra have been scaled to account for differences in the mass of material inside of each rotor (see Table 1 for masses). All spectra were acquired with MW irradiation, 128 scans, 2 s recycle delays and νrot = 8000 Hz. For the CPMG spectra, each echo was 3.75 ms in length and 12 echoes were acquired. CPMG enhancement factors (εCPMG) which describe the increase in S/N obtained with CPMG are listed to the right of the CPMG spectra. (C) Magnitude calculated 1H-29Si CP/CPMG free induction decays (FIDs), illustrate the differences in T2′(29Si) at different radical concentrations. | ||
For I impregnated with radical solutions T2′(29Si) ranges from 23 ms to 13 ms and is greatly reduced compared to T2′(29Si) for I materials free of radicals. T2′(29Si) decreases as the concentration of biradicals increases (Table 2), which can likely be attributed to a combination of enhanced paramagnetic relaxation and decreased 1H decoupling efficiency. The enhancements of the S/N provided by CPMG acquisition for impregnated I are still appreciable, although they are less than the theoretical limit. Comparison of the spectra also suggests that εCPMG is the same for both the T and Q sites.
| [TOTAPOL] (mM) | m SiO2 (mg)a | (S/N) CP MW onb | (S/N) CPMG MW onb | ε CPMG c | T 2′ (29Si) (ms)d | Σ Si CPMG e | Σ † Si CPMG e |
|---|---|---|---|---|---|---|---|
a See Table 1 for a determination of these values.
b Signal to noise ratios (S/N) were measured in Topspin and are per unit mass of sample. For both CP and CP/CPMG experiments a 2 s delay was employed in between each of 128 scans. In order to obtain an accurate and unbiased measure of S/N, both the CP and CP/CPMG spectra were processed without any line broadening and only the first 350 points of the CP FIDs were used for Fourier transform.
c
ε
CPMG
is the CPMG sensitivity enhancement factor, . For convenience the S/N of the Q peak was utilized.
d
T
2′(29Si) time constants were measured by fitting the intensity of the echo tops of the CP/CPMG FIDs to monoexponential decay functions [S(t) = (S0)exp(-t/T2′)]. For the dry material and material impregnated with pure water, not enough decay of transverse magnetization could be observed to fit with exponential functions, so the FIDs were fitted with pseudo-linear functions [S(t) = S0(1 − (t/T2′))].
e
Σ
Si CPMG
is the overall sensitivity enhancement obtained from combination of DNP with CPMG acquisition, . For convenience the S/N of the Q peak was utilized.
d
T
2′(29Si) time constants were measured by fitting the intensity of the echo tops of the CP/CPMG FIDs to monoexponential decay functions [S(t) = (S0)exp(-t/T2′)]. For the dry material and material impregnated with pure water, not enough decay of transverse magnetization could be observed to fit with exponential functions, so the FIDs were fitted with pseudo-linear functions [S(t) = S0(1 − (t/T2′))].
e
Σ
Si CPMG
is the overall sensitivity enhancement obtained from combination of DNP with CPMG acquisition, . Σ†Si CPMG includes Boltzmann enhancement, . Σ†Si CPMG includes Boltzmann enhancement, . .
|
|||||||
| Dry | — | — | — | ∼4.9 | 236(44) | — | — |
| Pure H2O | 8.1(2) | ∼4.9 | 354(27) | ∼4.9 | ∼14 | ||
| 4.0 | 7.9(2) | 21(1) | 99(5) | 4.6(4) | 23(3) | 31(3) | 88(9) |
| 7.8 | 8.0(2) | 22(1) | 82(3) | 3.7(2) | 17(2) | 26(3) | 75(8) |
| 12.1 | 8.1(2) | 36(2) | 83(3) | 2.4(1) | 16(2) | 35(2) | 98(9) |
| 16.1 | 7.7(2) | 33(1) | 68(3) | 2.1(1) | 13(1) | 21(2) | 61(7) |
| 20.3 | 8.6(2) | 28(1) | 46(2) | 1.6(1) | 13(1) | 16(2) | 44(5) |
| 23.9 | 7.1(2) | 17(2) | 39(2) | 2.3(1) | 13(2) | 10(1) | 29(2) |
The largest εCPMG is observed for the material impregnated with the 4.0 mM TOTAPOL solution since it possesses the longest T2′(29Si) of the impregnated materials. In this case the S/N of the DNP 29Si CP/CPMG spectrum is 4.6 times larger than the S/N of the corresponding CP spectrum. With knowledge of εCPMG the overall sensitivity enhancement available from the combination of DNP and CPMG acquisition (ΣSi CPMG) can be calculated:
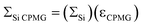 | (3) |
![Graphs showing the effect of electron concentration on (A) the CPMG enhancement factor (εCPMG) and (B) the overall sensitivity enhancement of DNP CP/CPMG experiments (ΣSi CPMG) and the DNP CP/CPMG sensitivity enhancement including Boltzmann enhancement (Σ†Si CPMG). Uncertainties for all measurements are listed in Table 2. (C) Comparison of 1H-29Si CP/CPMG (top) and CP/MAS (bottom) solid-state NMR spectra of I impregnated with 12.1 mM aqueous TOTAPOL solution. CP/CPMG improves the S/N by a factor of 2.4. Note that [e−] = 2 × [TOTAPOL].](/image/article/2012/SC/c1sc00550b/c1sc00550b-f5.gif) | ||
| Fig. 5 Graphs showing the effect of electron concentration on (A) the CPMG enhancement factor (εCPMG) and (B) the overall sensitivity enhancement of DNP CP/CPMG experiments (ΣSi CPMG) and the DNP CP/CPMG sensitivity enhancement including Boltzmann enhancement (Σ†Si CPMG). Uncertainties for all measurements are listed in Table 2. (C) Comparison of 1H-29Si CP/CPMG (top) and CP/MAS (bottom) solid-state NMR spectra of I impregnated with 12.1 mM aqueous TOTAPOL solution. CP/CPMG improves the S/N by a factor of 2.4. Note that [e−] = 2 × [TOTAPOL]. | ||
Conclusions
Quantitative measurements of the integrated intensities of DNP 29Si CP/MAS spectra suggest that paramagnetic effects lead to substantial reductions in the absolute signal of the spectra. For this reason the overall signal enhancement of DNP experiments is far less than that which is expected from ε values alone. However, if Boltzmann enhancement of the signal is also included then it is found that Σ†Si CP and Σ†Si CPMG peak here at values of 42 and 98, respectively. Given these observations it is recommended that rather than focusing on ε values alone when optimizing DNP experiments, quantitative measurements of signal intensities should be performed in order to determine optimal sample preparation conditions, whenever possible. It is also recommended that when similar ε values are obtained from samples prepared with different radical concentrations, the lower radical concentration should be employed. We anticipate that the approach outlined here should be useful for optimizing the signal enhancement available from DNP for a wide variety of systems.Here, we have shown that a major source of loss in DNP experiments in our system is due to quenching. This directly opens up the perspective of developing approaches to reduce it. Several approaches could be possible using either advanced NMR techniques or novel synthetic routes, for example, (i) utilizing fast MAS rates (>30 kHz) as has already been implemented for paramagnetic samples (this requires the construction of a fast MAS DNP probe), or (ii) designing radicals with a “shell” that would exclude the NMR nuclei of interest from the diffusion barrier. Finally, we expect that quenching will be highly variable and dependent upon the precise structure of the system under study. For example for bulk crystalline systems where the radical resides at the surface of the crystals14 or for systems in which the nuclei of interest reside at the center of proteins,20,21 it is expected that θ ≈ 1. Conversely, for small molecules and proteins dissolved in radical containing solutions it is expected that θ ≪ 1.
CPMG pulse sequences can be readily combined with DNP to obtain further improvements in the S/N ratios of 29Si solid-state NMR spectra of mesoporous silicas. However, due to the strong dependence of CPMG signal enhancement on T2′(29Si) the optimal signal enhancement is obtained at low biradical concentrations. Similar to CPMG pulse sequences, many other sequences rely upon T2′ for signal enhancement/coherence transfer, and these experiments are also expected to function better at low radical concentrations. We note that the signal enhancement currently offered by fast spinning CP/CPMG experiments for 29Si approaches that of the DNP experiments, however, in fast MAS experiments small sample quantities are used and we therefore expect that DNP experiments provide better absolute sensitivity. Additionally, CPMG pulse sequences are not generally applicable (e.g., in cases where resonances are narrow or T2′ is short). Conversely, the sensitivity gains afforded by DNP experiments are expected to improve with the design of better radical polarizing agents (such as triradicals),28,73 hardware (probes, cooling systems, etc.), and the development of novel DNP methods (e.g., involving pulsed MW sources).
Acknowledgements
A.J.R. acknowledges support from a EU Marie-Curie IIF Fellowship (PIIF-GA-2010-274574). Financial support is acknowledged from EQUIPEX contract no. ANR-10-EQPX-47-01, and the ETH Zürich. We acknowledge A. Roussey and C. Thieuleux for the development and preparation of I (ref. 59).Notes and references
- T. Maly, G. T. Debelouchina, V. S. Bajaj, K. N. Hu, C. G. Joo, M. L. Mak-Jurkauskas, J. R. Sirigiri, P. C. A. van der Wel, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Chem. Phys., 2008, 128, 052211 CrossRef.
- T. Prisner and W. Kockenberger, Appl. Magn. Reson., 2008, 34, 213–218 CrossRef CAS.
- R. G. Griffin and T. F. Prisner, Phys. Chem. Chem. Phys., 2010, 12, 5737–5740 RSC.
- T. R. Carver and C. P. Slichter, Phys. Rev., 1953, 92, 212–213 CrossRef CAS.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- C. P. Slichter, Phys. Chem. Chem. Phys., 2010, 12, 5741–5751 RSC.
- L. R. Becerra, G. J. Gerfen, R. J. Temkin, D. J. Singel and R. G. Griffin, Phys. Rev. Lett., 1993, 71, 3561–3564 CrossRef CAS.
- L. R. Becerra, G. J. Gerfen, B. F. Bellew, J. A. Bryant, D. A. Hall, S. J. Inati, R. T. Weber, S. Un, T. F. Prisner, A. E. McDermott, K. W. Fishbein, K. E. Kreischer, R. J. Temkin, D. J. Singel and R. G. Griffin, J. Magn. Reson., Ser. A, 1995, 117, 28–40 CrossRef CAS.
- V. S. Bajaj, M. K. Hornstein, K. E. Kreischer, J. R. Sirigiri, P. P. Woskov, M. L. Mak-Jurkauskas, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Magn. Reson., 2007, 189, 251–279 CrossRef CAS.
- A. C. Torrezan, S. T. Han, I. Mastovsky, M. A. Shapiro, J. R. Sirigiri, R. J. Temkin, A. B. Barnes and R. G. Griffin, IEEE Trans. Plasma Sci., 2010, 38, 1150–1159 CrossRef.
- T. Maly, L. B. Andreas, A. A. Smith and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5872–5878 RSC.
- T. Maly, A. F. Miller and R. G. Griffin, ChemPhysChem, 2010, 11, 999–1001 CAS.
- M. Rosay, A. C. Zeri, N. S. Astrof, S. J. Opella, J. Herzfeld and R. G. Griffin, J. Am. Chem. Soc., 2001, 123, 1010–1011 CrossRef CAS.
- P. C. A. van der Wel, K. N. Hu, J. Lewandowski and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 10840–10846 CrossRef CAS.
- A. E. Dementyev, D. G. Cory and C. Ramanathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024413 CrossRef.
- C. Ramanathan, Appl. Magn. Reson., 2008, 34, 409–421 CrossRef CAS.
- A. B. Barnes, B. Corzilius, M. L. Mak-Jurkauskas, L. B. Andreas, V. S. Bajaj, Y. Matsuki, M. L. Belenky, J. Lugtenburg, J. R. Sirigiri, R. J. Temkin, J. Herzfeld and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5861–5867 RSC.
- M. Negoro, K. Nakayama, K. Tateishi, A. Kagawa, K. Takeda and M. Kitagawa, J. Chem. Phys., 2010, 133.
- Y. Hovav, A. Feintuch and S. Vega, J. Chem. Phys., 2011, 134, 074509 CrossRef.
- M. L. Mak-Jurkauskas, V. S. Bajaj, M. K. Hornstein, M. Belenky, R. G. Griffin and J. Herzfeld, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 883–888 CrossRef CAS.
- V. S. Bajaj, M. L. Mak-Jurkauskas, M. Belenky, J. Herzfeld and R. G. Griffin, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9244–9249 CrossRef CAS.
- U. Akbey, W. T. Franks, A. Linden, S. Lange, R. G. Griffin, B. J. van Rossum and H. Oschkinat, Angew. Chem., Int. Ed., 2010, 49, 7803–7806 CrossRef CAS.
- E. Salnikov, M. Rosay, S. Pawsey, O. Ouari, P. Tordo and B. Bechinger, J. Am. Chem. Soc., 2010, 132, 5940–5941 CrossRef CAS.
- J. Haber, J. H. Block and B. Delmon, Pure Appl. Chem., 1995, 67, 1257–1306 CrossRef.
- A. Lesage, M. Lelli, D. Gajan, M. A. Caporini, V. Vitzthum, P. Mieville, J. Alauzun, A. Roussey, C. Thieuleux, A. Mehdi, G. Bodenhausen, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2010, 132, 15459–15461 CrossRef CAS.
- M. Lelli, D. Gajan, A. Lesage, M. A. Caporini, V. Vitzthum, P. Mieville, F. Heroguel, F. Rascón, A. Roussey, C. Thieuleux, M. Boualleg, L. Veyre, G. Bodenhausen, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2011, 133, 2104–2107 CrossRef CAS.
- O. Lafon, M. Rosay, F. Aussenac, X. Lu, J. Trebosc, O. Cristini, C. Kinowski, N. Touati, H. Vezin and J. P. Amoureux, Angew. Chemie. Int. Ed., 2011, 50(36), 8367–8370 CAS.
- K. R. Thurber, Y. Wai-Ming and R. Tycko, J. Magn. Reson., 2010, 204, 303–313 CrossRef CAS.
- J. Z. Hu, M. S. Solum, R. A. Wind, B. L. Nilsson, M. A. Peterson, R. J. Pugmire and D. M. Grant, J. Phys. Chem. A, 2000, 104, 4413–4420 CrossRef CAS.
- C. S. Song, K. N. Hu, C. G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390 CrossRef CAS.
- V. Vitzthum, M. A. Caporini and G. Bodenhausen, J. Magn. Reson., 2010, 205, 177–179 CrossRef CAS.
- M. Rosay, Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, 2001.
- K. N. Hu, C. Song, H. H. Yu, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2008, 128, 052302 CrossRef.
- M. Rosay, L. Tometich, S. Pawsey, R. Bader, R. Schauwecker, M. Blank, P. M. Borchard, S. R. Cauffman, K. L. Felch, R. T. Weber, R. J. Temkin, R. G. Griffin and W. E. Maas, Phys. Chem. Chem. Phys., 2010, 12, 5850–5860 RSC.
- W. E. Blumberg, Phys. Rev., 1960, 119, 79–84 CrossRef CAS.
- G. R. Khutsishvili, Sov. Phys. JETP, 1962, 15, 909–913.
- K. N. Hu, G. T. Debelouchina, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2011, 134, 125105 CrossRef.
- H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630–638 CrossRef CAS.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CAS.
- I. Hung, A. J. Rossini and R. W. Schurko, J. Phys. Chem. A, 2004, 108, 7112–7120 CrossRef CAS.
- R. Siegel, T. T. Nakashima and R. E. Wasylishen, J. Phys. Chem. B, 2004, 108, 2218–2226 CrossRef CAS.
- J. Trebosc, J. W. Wiench, S. Huh, V. S. Y. Lin and M. Pruski, J. Am. Chem. Soc., 2005, 127, 3057–3068 CrossRef CAS.
- J. Trebosc, J. W. Wiench, S. Huh, V. S. Y. Lin and M. Pruski, J. Am. Chem. Soc., 2005, 127, 7587–7593 CrossRef CAS.
- K. Mao, T. Kobayashi, J. W. Wiench, H. T. Chen, C. H. Tsai, V. S. Y. Lin and M. Pruski, J. Am. Chem. Soc., 2010, 132, 12452–12457 CrossRef CAS.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Phys. Chem. A, 1997, 101, 8597–8606 CrossRef CAS.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Magn. Reson., 1998, 131, 144–147 CrossRef CAS.
- G. Goelman and M. G. Prammer, J. Magn. Reson., Ser. A, 1995, 113, 11–18 CrossRef CAS.
- M. D. Hurlimann and D. D. Griffin, J. Magn. Reson., 2000, 143, 120–135 CrossRef CAS.
- I. Hung, K. Shetty, P. D. Ellis, W. W. Brey and Z. H. Gan, Solid State Nucl. Magn. Reson., 2009, 36, 159–163 CrossRef CAS.
- A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987–10993 CrossRef CAS.
- I. Bertini and C. Luchinat, Coord. Chem. Rev., 1996, 150, 1–252 CrossRef CAS.
- F. H. Larsen, A. S. Lipton, H. J. Jakobsen, N. C. Nielsen and P. D. Ellis, J. Am. Chem. Soc., 1999, 121, 3783–3784 CrossRef CAS.
- A. S. Lipton, J. A. Sears and P. D. Ellis, J. Magn. Reson., 2001, 151, 48–59 CrossRef CAS.
- A. S. Lipton, R. W. Heck, J. A. Sears and P. D. Ellis, J. Magn. Reson., 2004, 168, 66–74 CrossRef CAS.
- A. S. Lipton, R. W. Heck, S. Primak, D. R. McNeill, D. M. Wilson and P. D. Ellis, J. Am. Chem. Soc., 2008, 130, 9332–9341 CrossRef CAS.
- A. S. Lipton, R. W. Heck, W. A. de Jong, A. R. Gao, X. J. Wu, A. Roehrich, G. S. Harbison and P. D. Ellis, J. Am. Chem. Soc., 2009, 131, 13992–13999 CrossRef CAS.
- G. Kervern, S. Steuernagel, F. Engelke, G. Pintacuda and L. Emsley, J. Am. Chem. Soc., 2007, 129, 14118–14119 CrossRef CAS.
- R. R. Ernst, G. Bodenhausen and A. Wokaun, in Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford University Press, Oxford, 1987 Search PubMed.
- A. Roussey, D. Gajan, T. K. Maishal, A. Mukerjee, L. Veyre, A. Lesage, L. Emsley, C. Copéret and C. Thieuleux, Phys. Chem. Chem. Phys., 2011, 13, 4230–4233 RSC.
- O. Peersen, X. Wu, I. Kustanovich and S. Smith, J. Magn. Reson., Ser. A, 1993, 104, 334–339 CrossRef CAS.
- G. Metz, X. Wu and S. Smith, J. Magn. Reson., Ser. A, 1994, 110, 219–227 CrossRef CAS.
- B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101 CrossRef CAS.
- F. H. Larsen, J. Skibsted, H. J. Jakobsen and N. C. Nielsen, J. Am. Chem. Soc., 2000, 122, 7080–7086 CrossRef CAS.
- R. Lefort, J. W. Wiench, M. Pruski and J. P. Amoureux, J. Chem. Phys., 2002, 116, 2493–2501 CrossRef CAS.
- Y. Ishii, N. P. Wickramasinghe and S. Chimon, J. Am. Chem. Soc., 2003, 125, 3438–3439 CrossRef CAS.
- N. P. Wickramasinghe, M. Shaibat and Y. Ishii, J. Am. Chem. Soc., 2005, 127, 5796–5797 CrossRef CAS.
- G. Kervern, G. Pintacuda, Y. Zhang, E. Oldfield, C. Roukoss, E. Kuntz, E. Herdtweck, J. M. Basset, S. Cadars, A. Lesage, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2006, 128, 13545–13552 CrossRef CAS.
- W. L. Huang, M. Schopfer, C. Zhang, R. C. Howell, L. Todaro, B. A. Gee, L. C. Francesconi and T. Polenova, J. Am. Chem. Soc., 2008, 130, 481–490 CrossRef CAS.
- N. P. Wickramasinghe, M. A. Shaibat, C. R. Jones, L. B. Casabianca, A. C. de Dios, J. S. Harwood and Y. Ishii, J. Chem. Phys., 2008, 128.
- G. Kervern, A. D'Aleo, L. Toupet, O. Maury, L. Emsley and G. Pintacuda, Angew. Chem., Int. Ed., 2009, 48, 3082–3086 CrossRef CAS.
- I. Bertini, L. Emsley, M. Lelli, C. Luchinat, J. F. Mao and G. Pintacuda, J. Am. Chem. Soc., 2010, 132, 5558–5559 CrossRef CAS.
- The estimated uncertainties provided in Table 1 reflect standard deviations which can be measured (e.g., standard deviations in integrals and sample masses). The uncertainties do not include deviations in other factors (e.g., sample temperature, spectrometer stability, etc.) which will also impact the measured values of θSi. The actual uncertainties are likely to be larger and explain the uneven variation of θSi with biradical concentration.
- K. Hu, Solid State Nucl. Magn. Reson., 2011, 40, 31–41 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: calculations of sample masses, solid-state NMR acquisition parameters, additional 29Si solid-state NMR spectra and details on the synthesis and characterization of the methyl passivated silica. See DOI: 10.1039/c1sc00550b |
| This journal is © The Royal Society of Chemistry 2012 |
