 Open Access Article
Open Access ArticleFluorescence spectroscopy and multi-way techniques. PARAFAC†
Kathleen R.
Murphy
*a,
Colin A.
Stedmon
b,
Daniel
Graeber
c and
Rasmus
Bro
d
aUniversity of New South Wales, Water Research Centre, Sydney, Australia. E-mail: krm@unsw.edu.au; Fax: +61 2 9313 8624; Tel: +61 2 9385 4601
bTechnical University of Denmark, National Institute for Aquatic Resources, Charlottenlund, Denmark. E-mail: cost@aqua.dtu.dk
cAarhus University, Department of Bioscience, Silkeborg, Denmark. E-mail: dgr@dmu.dk
dUniversity of Copenhagen, Dept. Food Science, Frederiksberg, Denmark. E-mail: rb@life.ku.dk
First published on 10th September 2013
Abstract
PARAllel FACtor analysis (PARAFAC) is increasingly used to decompose fluorescence excitation emission matrices (EEMs) into their underlying chemical components. In the ideal case where fluorescence conforms to Beers Law, this process can lead to the mathematical identification and quantification of independently varying fluorophores. However, many practical and analytical hurdles stand between EEM datasets and their chemical interpretation. This article provides a tutorial in the practical application of PARAFAC to fluorescence datasets, demonstrated using a dissolved organic matter (DOM) fluorescence dataset. A new toolbox for MATLAB is presented to support improved visualisation and sensitivity analyses of PARAFAC models in fluorescence spectroscopy.
 Kathleen R. Murphy | Kathleen Murphy studied science and engineering at the Universities of Western Australia and Tasmania, majoring in Zoology and Environmental Engineering. Between 2000 and 2009 she worked for the Smithsonian Environmental Research Center studying chemical tracers of ballast water origin. In 2007, she obtained her doctorate from the University of New South Wales, and since 2010 has been an Australian Research Council Postdoctoral Fellow studying the chemometric analysis of odour datasets. She has given invited presentations on PARAFAC at international conferences and has developed open-sourced MATLAB toolboxes for analysing natural organic matter and odour datasets. |
 Colin A. Stedmon | Colin Stedmon studied chemical oceanography at the Southampton Oceanography Centre, Southampton University, UK, obtaining his doctorate in 2004 from the Climate and Environment school at the University of Copenhagen. From 2005 to 2011 he worked as a Research Scientist and Senior Scientist at the Department of Marine Ecology at the former National Environmental Research Institute (Denmark), now merged with Aarhus University. In 2011 he became an Associate Professor at the Technical University of Denmark, Institute for Aquatic Resources. His research interests include marine biogeochemistry, aquatic optics and UV-Visible spectroscopy. |
 Daniel Graeber | Daniel Graeber studied biodiversity and ecology at the University of Göttingen, Germany. He is currently working on his Ph.D. in the Department of Bioscience at Aarhus University. From 2007 to 2010, he was employed as research scientist at the Leibniz-Institute of Freshwater Ecology and Inland Fisheries in Berlin. His research interests include freshwater ecology and organic biogeochemistry, especially the effects of land use and climate change on both. |
 Rasmus Bro | Rasmus Bro studied mathematics and analytical chemistry at the Technical University of Denmark receiving his M.Sc. in 1994. In 1998 he obtained his Ph.D. (Cum Laude) in multi-way analysis from the University of Amsterdam, The Netherlands. He is currently Professor of chemometrics in the Department of Food Science at the University of Copenhagen, Denmark. He has developed a range of popular chemometrics software and has received numerous prizes for contributions to and achievement in the field of chemometrics, including the third Elsevier Chemometrics Award (2000), the Eastern Analytical Symposium Award (2004), and the 10th Herman Wold Gold Medal (2011). |
Introduction
PARAllel FACtor analysis (PARAFAC) is used in the chemical sciences to decompose trilinear multi-way data arrays and facilitate the identification and quantification of independent underlying signals, termed ‘components’. In 2011–2012, 334 Scopus-indexed journal and conference papers were published with keywords “PARAFAC” or “parallel factor analysis”. In the subset of papers where PARAFAC was used primarily as a tool for data interpretation (n = 238, thus excluding 96 papers concerned primarily with developing or comparing algorithms, tools or statistical methodologies), PARAFAC was applied across research fields (medical, pharmaceutical, food, environmental, social, and information science) and to a wide range of data types, including spectral, NMR, GC-MS, (HP)LC-DAD, EEG, geospatial, radar, sensory, metabolomic and image data. However, PARAFAC was applied more often to fluorescence excitation emission matrices (EEMs) than to all other data types combined. Thus, of the 238 studies in 2011–2012 involving straight-forward applications of PARAFAC to real-world datasets, more than 70% were applications to fluorescence EEMs, and of these, more than 70% related to the study of natural organic matter (NOM) fluorescence. This result reflects the rapid and enthusiastic uptake of a technique that was introduced to the organic matter research field only ten years ago1 (Fig. 1).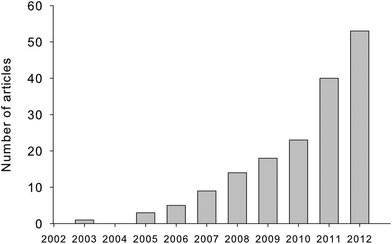 | ||
| Fig. 1 Number of Scopus-indexed articles (2003–2012) in which PARAFAC was used to decompose fluorescence excitation emission matrices (EEMs) of dissolved and natural organic matter samples. | ||
This paper provides a tutorial in the practical application of PARAFAC to fluorescence data. For a comprehensive theoretical description of PARAFAC and other multi-way models, including tutorials in its application to a range of data types, the reader is referred to earlier ref. 2–4. In consideration of current trends in PARAFAC application, this tutorial is primarily intended to provide a deeper practical treatment of preparing, modelling and interpreting fluorescence datasets, particularly when arising from environmental samples in which the number, identity and behaviour of fluorophores is not known at the outset. A number of aspects of this tutorial are therefore specifically relevant to modelling fluorescence datasets in general and organic matter fluorescence in particular, although many aspects are broadly relevant to analysing multi-way datasets, regardless of their type.
Many of the steps described in this tutorial were discussed in the earlier tutorials. Others are new, particularly the demonstration of how hypothesis-testing might be incorporated into PARAFAC analyses to increase insights into the robustness of a PARAFAC model and its chemical interpretation. A demonstration of the application of PARAFAC to real-world data accompanies this tutorial. The tutorial dataset consists of 224 samples collected during four surveys of San Francisco Bay and measured using excitation-emission matrix fluorescence spectroscopy.5 PARAFAC analyses for the tutorial are implemented in MATLAB using two free toolboxes distributed under the terms of GNU General Public Licence: the N-way toolbox6 which provides the PARAFAC engine, and the drEEM toolbox, which supports the application, visualisation and interpretation of PARAFAC when applied to EEM datasets, and is released in conjunction with this tutorial (Table 1). The drEEM toolbox combines and significantly extends the capabilities of two earlier toolboxes: DOMFluor7 and FDOMcorr.8,9 A detailed tutorial in the application of drEEM covering all included functions is provided as an Appendix† to this article. The tutorial dataset together with up-to-date versions of the drEEM and N-way toolboxes may be downloaded at http://www.models.life.ku.dk/.
| Toolbox | Descriptiona |
|---|---|
| a See the main text for reference information. | |
| N-way toolbox | General multi-way analysis toolbox that contains the PARAFAC algorithm |
| DOMFluor | EEM-specific toolbox using the N-way toolbox as an engine for PARAFAC |
| FDOMcorr | EEM-specific toolbox for importing, correcting and assembling EEM datasets in preparation for statistical analysis |
| drEEM | EEM-specific toolbox using the N-way toolbox as a PARAFAC engine and incorporating FDOMcorr. Extends the DOMFluor toolbox to improve dataset manipulation and visualisation and support hypothesis-testing during model validation |
PARAFAC model
PARAFAC2,10 belongs to a family of so-called multi-way methods applicable to data that are arranged in three- or higher-order arrays. Examples of threeway arrays that can be analysed with PARAFAC include fluorescence EEMs (sample × excitation wavelength × emission wavelength; Fig. 2), chromatographic data (GC-MS: sample × elution time × m/z structure), sensory data (sample × attribute × judge) and electroencephalography (space × time × frequency).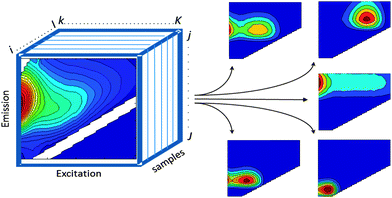 | ||
| Fig. 2 EEM dataset arranged in a threeway structure and decomposed into five PARAFAC components. | ||
PARAFAC of a three-way dataset decomposes the data signal into a set of trilinear terms and a residual array:
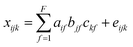 | (1) |
In eqn (1), xijk is the data point corresponding to the ith sample at the jth variable on mode 2 and at the kth variable on mode 3, and eijk is the residual representing the variability not accounted for by the model. In the case of a fluorescence excitation-emission matrix, the i, j and k correspond to the sample, emission and excitation modes, respectively (Fig. 2). Each f corresponds to a PARAFAC component and each such component has I a-values (scores); one for each sample. Each component also has J b-values; one for each emission wavelength as well as K c-values; one for each excitation wavelength.
These model components have a direct chemical interpretation in a valid model. The parameter aif is directly proportional to the concentration of the fth analyte of sample i; the vector bf with elements bjf is a scaled estimate of the emission spectrum of the fth analyte. Likewise, the vector cf with elements ckf is linearly proportional to the specific absorption coefficient (e.g. molar absorptivity) of the fth analyte.
Important assumptions for successfully decomposing a multi-way dataset using PARAFAC include:
(1) Variability: no two chemical components can have perfectly covarying fluorescence intensities or identical spectra.
(2) Trilinearity: the same number of components underlies the chemical variation in each mode (dimension) of the dataset. For fluorescence EEMs, this means that emission spectra are invariant across excitation wavelengths, excitation spectra are invariant across emission wavelengths, and fluorescence increases approximately linearly with concentration.
(3) Additivity: the total signal is due to the linear superposition of a fixed number of components.
The second and third assumptions constitute Beers Law.11 PARAFAC components extracted from data which deviate significantly from Beers Law are neither physically nor chemically meaningful. When modelling real data, difficulties that arise include the presence of strongly correlated components with similar spectral properties, non-trilinear systematic error structures resulting from e.g. light scattered off the sample matrix, and concentration-dependent nonlinearity due to the inner filter effect, described further below. Other issues that may arise in some datasets and make modelling difficult or even impossible are that spectral properties may vary due to chemical reactions, quenching, interactions between fluorophores, or due to changes in the electronic environment of the fluorophores (e.g. with pH).
Approach
The overall approach to obtaining a PARAFAC model is illustrated in the schematic in Fig. 3. The basic steps are (1) import and assemble the dataset; (2) preprocess; (3) explore the data and develop preliminary models (4) develop a final, validated model containing the correct number of components, and (5) export and interpret the results. These steps are detailed below.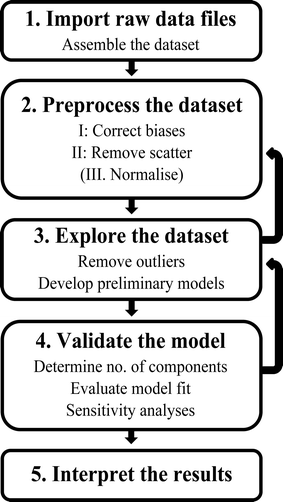 | ||
| Fig. 3 Schematic of the steps involved in PARAFAC analysis of fluorescence excitation emission matrices (EEMs). | ||
Data import
The first step is to transfer the data from the instrument to software supporting PARAFAC analysis. Analysis is frequently performed with the commercial MATLAB (Mathworks, Inc.) software which efficiently handles data arrays. The PARAFAC algorithms are available through third-party MATLAB toolboxes, including N-way6 and Tensorlab.12 Commercial platforms not requiring MATLAB include SOLO (Eigenvector Inc.). Recently, PARAFAC has been enabled for the free R platform,13 but fluorescence applications remain to be demonstrated. Commercial softwares typically allow a range of file types to be imported. In the free software domain, methods and code for importing EEMs and related data (*.txt, *.csv and *.xls) to MATLAB and assembling them into threeway data structures are freely available via the FDOMcorr9 and drEEM toolboxes.Preprocessing
Preprocessing steps are highly dependent upon the type of data being analysed and the goal of the analysis, with some types of data necessitating several preprocessing steps and others requiring little or none. For more comprehensive accounts of preprocessing the reader is referred elsewhere.14–17 In a practical sense, it should be borne in mind that the best way to preprocess a dataset may not be obvious from the outset, and modelling can identify weaknesses in a dataset (e.g. unusual samples, correlated components, residual scatter, systematic errors), which must be dealt with before proceeding. Consequently, it is often necessary to iterate the preprocessing and modelling steps in order to arrive at stable and satisfactory solutions (Fig. 3).The preprocessing phase in PARAFAC modelling has three main aims: (1) correct any systematic biases in the dataset, (2) remove signals unrelated to fluorescence, and (3) normalise datasets having large intensity differences between samples. These are described in Preprocessing I–III below. Steps that do not affect models include applying a linear calibration to convert signals to a standard scale (e.g. Quinine Sulfate Equivalents or Raman Units).9
Linearity in the relationship between concentration and fluorescence intensity can be assumed only for very dilute samples; in all other cases, data should be corrected for the so-called “inner-filter effects (IFE)”. This occurs when radiation is absorbed by the sample matrix on its way in or out of the cuvette, ultimately reducing the amount of excitation light absorbed by chromophores at center of the cuvette and the amount of emitted light incident upon the detector. Chromophores that do not fluoresce also contribute to IFEs. As sample absorbance increases, non-linearity between concentration and fluorescence intensity becomes increasingly severe, to the point where further addition can actually cause a reduction in fluorescence. DOM absorbance spectra typically decrease approximately exponentially with increasing wavelength (Fig. 4A), indicating that IFEs are most severe at short wavelengths. This leads to distorted EEMs in which each emission spectrum depends not only on the fluorophores present, but also on the excitation wavelength at which they are measured.
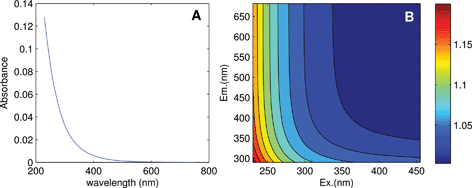 | ||
| Fig. 4 (A) Absorbance of a DOM sample from the tutorial dataset, and (B) calculated correction factors accounting for its inner filter effect. | ||
It is often stated that inner filter effects only impact samples with high optical densities, when in fact IFEs occur in all samples where fluorophores are present in measurable concentrations. Modern fluorometers typically use right-angle excitation/emission geometries and a standard rectangular cuvette with a 1 cm path length, for which it can be deduced that IFEs exceed 6% at wavelengths where A > 0.05.11 In experiments involving known fluorophores having high quantum yields (i.e. high efficiency at converting incident radiation to emitted radiation), it may be possible to avoid significant inner filter effects by keeping concentrations low. However, in natural samples where quantum yields are typically low, inner filter effects are very likely to be significant at least at short wavelengths (Fig. 4B). A recent survey determined that in more than 97% of Swedish lakes (n = 554, D. Kothawala, pers. comm.), fluorescence intensities at 250 nm required correction for inner filter effects (lakes with DOC ≥2.1 mg C L−1).
While there are several different ways to account for inner filter effects, a simple and popular post-hoc method uses only the sample's absorbance spectrum to calculate a matrix of correction factors, with a separate correction factor corresponding to each wavelength pair in the EEM (Fig. 4B).11 The EEM can simply be multiplied element-wise by the correction matrix.9 Absorbance-based correction is typically reported to be accurate within 5% when absorbance is below 2.0 (ref. 21–23) in a 1 cm cell. For samples with absorbance approaching 2.0 or exceeding the linear range of the spectrophotometer, the sample must either be diluted first, or else instrument-specific geometric parameters must be taken into account using a modified algorithm.21 Note that spectral correction prior to IFE correction is always necessary to align the fluorescence spectra with the absorbance spectrum and with the theoretical description of inner filter effects.
The typical treatment for scatter peaks is to excise the affected data, replacing it by either with missing data2,7 or with measurements interpolated from either side of the scatter band.26,27 Primary Rayleigh scatter occurs in a region where there are no chemical signals, so can be handled by setting the scatter-affected region to missing values.4 Raman bands and secondary Rayleigh scatter often cut through fluorescence peaks; for these it is often best to interpolate over the excised area, since too much missing data within the chemical signal region can slow down or prevent model convergence. Care must be taken when interpreting signals bordering interpolated bands since interpolation can broaden the apparent spectra of narrow peaks that cross the edges of the scatter band (e.g. tryptophan fluorescence). Using the smootheem function in the drEEM toolbox, the decision of whether to interpolate or excise a scatter band can be made for each of the primary and secondary Rayleigh and Raman bands independently.
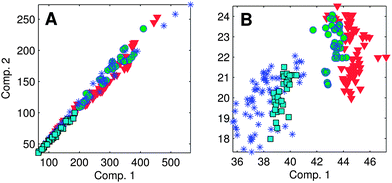 | ||
| Fig. 5 (A) Strongly correlated components violate the variability assumption of the PARAFAC model; (B) normalising each EEM to its total signal improves adherence to the variability assumption. | ||
Normalisation is done by scaling the data in the first (sample) mode to unit norm, i.e. dividing by the sum of the squared value of all variables for the sample. Normalisation can be reversed after validating the model, by multiplying the scores by the same values. The drEEM toolbox contains tools for normalising EEM datasets and subsequently recovering the unscaled model scores.
Exploratory phase
The aim of exploratory data analysis is to settle upon the best possible dataset for modelling and obtain a preliminary idea about how many PARAFAC components it may contain. One of the main goals here is to identify and remove unrepresentative or poor quality data, as well as ‘outlier’ samples or variables (wavelengths) that could otherwise prevent a satisfactory model from being obtained. Outliers can result from sampling or analytical errors, but could equally be unrepresentative of the rest of the dataset for perfectly legitimate reasons. Either way, outliers need to be examined individually to determine the likely reason for their difference, and in extreme cases, it may be necessary to eliminate data.Determining the identity of outlier samples and variables is part of the ‘art’ of PARAFAC modelling, and may need to be revisited several times during model development. One way to identify outliers is through examining the structure in the error residuals (error = data − model). Ideally, residuals will be distributed approximately randomly, or at least will not contain obvious structure (Fig. 6A). Another is to calculate the influence each sample and wavelength has on a model.29 The leverage is a number between zero and one that expresses deviation from the average data distribution. Samples/variables that are not very different to others have leverages near zero, whereas very atypical samples have leverages near one (Fig. 6C–E). Ideally, the samples and wavelengths in a dataset will exhibit roughly similar leverages.
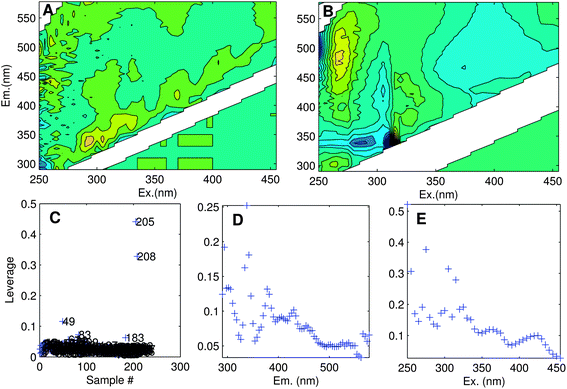 | ||
| Fig. 6 (A) Residuals for an adequately modelled sample with minor peaks along the diagonal, and (B) a poorly modelled sample (no. 205). Leverage plots indicate: (C) unusual samples (205, 208, 49); (D) emission wavelengths with high influence especially near 340 nm; (E) excitation wavelengths with high influence especially near 250, 270 and 310 nm. | ||
Model validation
The valid chemical interpretation of a PARAFAC model relies upon the right number of components being fitted. When models are under-specified, fewer components are used in the model than there are independently varying chemical moieties responsible for the measured signal. When this occurs, the model may approximate the combined signal of chemically distinct components. When models are over-specified, too many components are being fitted. In this case, two or more PARAFAC components may be used to represent a single moiety, often in combination with noise. There are many ways to evaluate whether a PARAFAC model was specified with the correct number of components. No single method is a “silver bullet”, rather, several should be considered in combination wherever possible. This is particularly important for real datasets, because different validation methods can produce conflicting indications about the number of components in a model. For this reason a certain level of subjectivity is unavoidable; however, with careful investigation and reliance upon a diverse range of tools, subjectivity can be minimised.Randomness of residuals
When the correct number of PARAFAC components is chosen, all of the significant systematic variation in the dataset is captured by the model, and the difference between the dataset and the model, termed the residual, contains only random error. In this situation, residual plots for each sample show no consistent pattern. In practice for real datasets, systematic variation is often seen for at least some samples in the form of peaks (representing signals not captured by the model) or troughs (negative peaks). In the case of fluorescence EEMs, small peaks occurring along the diagonal due to incompletely removed scatter can be ignored, since they are not trilinear and should not feature in the model (Fig. 6A). However, adjacent peaks and troughs in the residuals often indicate a problem (Fig. 6B) whereby a peak is modelled using two or more poorly-fitting components.Visualise spectral loadings
If the loadings of a PARAFAC model have a direct chemical interpretation, it should be assessed whether they are physically reasonable with respect to the chemical phenomenon being studied. In the case where the dataset consists of EEMs of non-interacting organic fluorophores, the emission spectrum should exhibit a pronounced shift relative to its excitation spectrum, known as the ‘Stokes Shift’.11 This reflects the fact that the energy with which a molecule fluoresces is lower than the energy at which the molecule was excited, due to energy losses occurring while it is in the excited state. The Stokes shift depends on a fluorophore's type and position within a macromolecule as well as its electronic environment.24 Typically, however, the spectra of independent, non-interacting organic fluorophores in water exhibit the following characteristics:11,30(1) Minimal overlap (usually <50 nm) between the excitation and emission spectra.
(2) Excitation spectra may have multiple peaks, but emission spectra exhibit a single distinct peak.
(3) When an excitation spectrum has two or more peaks indicating consecutive excited state absorption bands, some absorption (excitation) occurs between these peaks.
(4) Excitation and emission spectra do not exhibit abrupt changes over very short wavelength distances.
Fig. 7 depicts the loadings of a five-component PARAFAC model derived from the tutorial dataset, noting atypical characteristics for non-interacting organic fluorophores.
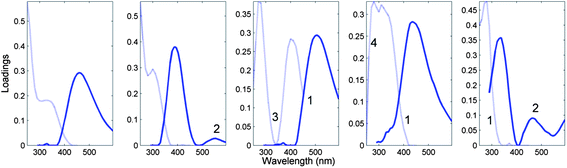 | ||
| Fig. 7 Five-component DOM-PARAFAC model exhibiting atypical spectral features, including (1) excitation spectrum tailing well into the emission spectrum; (2) multiple distinct emission peaks, (3) no evidence of excitation between consecutive absorption bands; (4) abrupt spectral changes over short wavelength distances. The light and dark curves represent excitation and emission spectra, respectively. | ||
Core consistency
An indication of the number of components in a PARAFAC model can be obtained from the core consistency diagnostic, which evaluates the ‘appropriateness’ of the model.31 When a sequence of models is run with an increasing number of components, the core consistency tends to start high (near 100%) then drop abruptly at the point when too many components are selected. The number of components is determined to equal the number in the largest model still having a high core consistency.31 In practice for real-world non-ideal datasets, core consistency is not always a reliable diagnostic of the number of PARAFAC components needed. In the case of fluorescence EEMs derived from organic matter, published models having high core consistencies tend to have two to four components and in many cases, exhibit unusual spectra. Conversely, models with five or more components very often have low or even negative core consistencies even when there are otherwise strong indications that the model is capturing real chemical phenomena.32–34Overall, it seems that core consistency applied to organic matter EEMs may provide too much protection against over-fitting and not enough protection against under-fitting. This may in part reflect the situation that there are likely to be many fluorophores present at low levels in organic matter, in which case there may be no clear-cut number of PARAFAC components to capture them.31 Also, PARAFAC models of natural samples almost invariably contain two or more strongly covarying components,34,35 challenging the variability assumption. Finally on the practical side, it can be difficult or at least very time consuming to eliminate all scatter in a dataset that impacts upon core consistency without also eliminating useful chemical information.
Split-half analysis
One of the most powerful ways to confirm that a PARAFAC model is appropriate is to produce identical models from independent subsamples of the dataset.36,37 This is typically only possible for relatively large datasets, because at some point the number of samples becomes a limiting condition on the number of components that can be identified.Harshman37 proposed validating models using multiple split-half tests, where various models are created and compared after dividing the dataset in half in different ways. In the version of this method implemented in the DOMFluor toolbox,7 each sample is first assigned alternately to one of four splits, then the four splits are assembled into four combined splits (where each combination contains half the samples in the dataset) to produce two split-half comparison tests (Fig. 8). We will refer to this style of validation as an alternating ‘S4C4T2’ (Splits: 4, Combinations: 4, Tests: 2). The method can easily be extended in order to assemble six different dataset ‘halves’ and produce three validation tests ‘S4C6T3’ (Fig. 8). Furthermore, the alternating procedure for assigning the initial groups can be changed in order to keep particular sets of samples together, for example replicates or experimental groups. The drEEM toolbox that accompanies this tutorial includes capability for assembling split-half datasets according to a wide range of user-specified criteria.
 | ||
| Fig. 8 Four quarter splits can be combined in six dataset halves to produce two (S4C4T2) or three (S4C6T3) validation tests. See the ESI† for an elaboration of this figure. | ||
It is often assumed that the best way to split a dataset is via a random process. Consider, however, that if dissimilar samples are deliberately assigned to different splits, models should be harder to validate because splits are less similar than they would be if samples were grouped randomly, or evenly, as when alternating splits are created from a samples ordered in space or time. However, when identical models are obtained from different non-random and non-even splits, this can provide strong evidence of the robustness of the model. Further, when a dataset consists of natural groups (corresponding to e.g. particular sites, dates, sources, high versus low concentration, etc.), then the model validation process can provide an opportunity to examine hypotheses about how sources of variability in the dataset affect the underlying fluorescence components.
The Appendix† to this paper works through the PARAFAC analysis of an EEM dataset obtained from four surveys of San Francisco Bay.5 During these surveys, particular sites were revisited up to four times in February, April, July and October 2006. It is interesting to ask whether there is any difference in PARAFAC component spectra related to time of year. Fig. 9 shows S4C6T3 validations of a 6-component PARAFAC model of the tutorial dataset, where the initial splits were created in two different ways. In the first case, groups of replicate samples were assigned alternately to four splits. In the second, the initial splits consisted entirely of samples from a single cruise. Each row of plots in Fig. 9 depicts a sensitivity analysis indicating which components and parts of excitation or emission spectra are modelled more or less consistently than others. The first validation (Fig. 9 top row) appears most successful in the sense that the components identified in each split combination are most similar. However, the second validation (Fig. 9 bottom row) is potentially more informative, because it provides reasonably strong evidence that the major underlying components responsible for DOM fluorescence in the Bay dataset did not vary seasonally. One possible explanation for the observed differences is that the split model which is least similar to the others was derived from fewer samples (n = 68) and fewer sites (n = 12) than the other split models (n > 100 and n = 24, respectively).
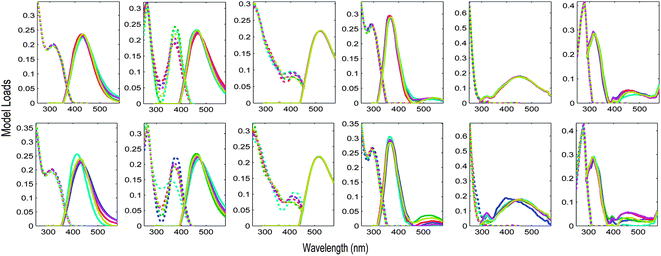 | ||
| Fig. 9 Validation of the tutorial dataset with six dataset halves created in two different ways. Top row: alternating S4C6T3 keeping replicate samples together; bottom row: by-cruise S4C6T3 keeping all samples from the same cruise together. | ||
A few comments are warranted on the topic of replication. It is generally good experimental and statistical practice to obtain replicate measurements of any phenomenon under study.38 For example, subsamples can yield useful data related to the precision of experimental measurements, repeated sampling of the same phenomenon can help to quantify sampling and experimental error, while measurements of different substances, at different sites or over time each yield different types of information that may be necessary to interpret the behaviour of a chemical system. When validating a PARAFAC model as any other type of model, it is simply necessary to be mindful of how the experimental design affects the conclusions that can be drawn from any particular model validation.
The ultimate goal is to obtain a model that fairly represents the problem at hand, i.e. the population of all possible samples from which a particular set of actual samples were obtained. When nearly-identical PARAFAC models are obtained from two replicate halves of a dataset (or even two random halves, if the dataset contains many similar samples) it is possible to conclude only that the two halves of the dataset are spectrally very similar. It does not prove the model is correct, since the same erroneous solution may be located in two similar dataset halves. To demonstrate that the model is representative of the sample population, it must be possible to derive the same PARAFAC components using completely independent data subsets. Also, although replicate samples can be included when modelling, if only some samples in a dataset are replicated, these will influence the model more than unreplicated samples. For these reasons, when validating a model it is good practice to keep replicate samples together in the same split, and eliminate any sample that duplicates another.
Model refinement
Creating a PARAFAC model of a real-world dataset is rarely a linear process, so the exploratory and validation phases of modelling may need revisiting, possibly several times in the case of a large or complex dataset. Aside from any analytical issues, the iterative PARAFAC algorithm itself can cause difficulties.2 Thus, when datasets are difficult to fit or contain a large number of components, PARAFAC can fail to locate the true solution, and repeated model runs may produce different solutions. Unstable models can sometimes be improved by applying appropriate constraints during modelling.4 For example, it is common in fluorescence applications that concentrations and spectra are constrained to be non-negative. It can also work well to constrain spectra to having no more than a single peak (unimodality). The application of constraints can assist PARAFAC in arriving at stable, chemically-sensible solutions especially for real-world, noisy datasets. However, care has to be taken to ensure that the process does not cover up problems that would be better solved with other approaches. Once the modelling constraints and criteria have been decided, the best way to obtain models with the correct solution for any given number of components is to repeat the modelling, each time using a different random starting vector, ultimately adopting only the model that represents the least-squares (minimum error) solution.Interpreting the results
When fluorescence datasets conform to Beers Law, PARAFAC components in validated models can be interpreted to represent independent fluorophores or possibly, groups thereof sharing very similar spectra. If a component can be attributed to a specific chemical analyte, it is possible through the addition of known quantities of the analyte to determine its concentration in each sample. However, if the identity of a PARAFAC component is unknown, it is not possible to convert fluorescence intensities to concentrations. Instead, it is usual to track the fluorescence intensity at the maximum (“Fmax”) for each component. The PARAFAC model loadings obtained using the N-way toolbox are normalised so that all quantitative information is contained in the model scores (“a” in eqn (1)). Fmax is calculated by multiplying the maximum excitation loading and maximum emission loading for each component by its score, producing intensities in the same measurement scale as the original EEMs. Because different fluorophores can have very different efficiencies at absorbing and converting incident radiation to fluorescence, if component A has a higher fluorescence signal than component B it does not follow that A has a higher concentration than B. Quantitative and qualitative information may however be obtained from changes in the intensity of a given component, or in the ratios of any two components, between samples in the dataset. Also, changes in the relative abundance of a component (Fmax/∑Fmax) can indicate changes in its overall importance, although this measure is sensitive to changes in the relative abundances of all the components so must be interpreted with care.In the case of organic matter, the chemical interpretation of PARAFAC components is not completely clear. It is notable, for example, that two-thirds of NOM-PARAFAC studies published between 2003 and 2010 identified fewer than seven PARAFAC components,17 although the number of naturally occurring fluorophores present in natural systems is presumably much greater. This probably results from several factors that vary in importance between studies, including sample size17 and low signal-to-noise ratios making it difficult to resolve all but the most prevalent fluorophores. In some published models, combinations of protein-like and humic-like components are modelled as single components, while others show clear signs of over-fitting. Overall, many larger PARAFAC models deviate significantly from Beers Law, as evidenced by the frequent reports of low core consistencies for PARAFAC models validated by residual and split-half analysis. Future work should formally examine what kind and degree of deviation can be tolerated without unduly impacting the chemical interpretation of NOM-PARAFAC models.
Conclusions
Parallel factor analysis is a powerful tool for resolving underlying structures in multi-way datasets. Rapidly developing technologies for capturing multi-way data are shifting the scientific bottleneck from collecting data to its interpretation. The use of PARAFAC to interpret fluorescence EEMs has expanded correspondingly in recent years. However, the task of obtaining accurate and chemically-meaningful PARAFAC models is not trivial, particularly when datasets contain complex mixtures of highly-correlated components, as appears to be the case for organic matter fluorescence. A range of free and commercial software tools are available to implement and support PARAFAC analyses of fluorescence data; the drEEM toolbox released with this tutorial representing the newest addition. We hope this latest contribution will assist in progressing the understanding and implementation of PARAFAC in fluorescence spectroscopy.Acknowledgements
KRM acknowledges funding by the Australian Research Council (DP1096691). CAS and DG acknowledge funding by the Danish Research Council (DFF 1323-00336 and DFF 09-067335, respectively). RB acknowledges support from the Villum Foundation (http://www.veluxfoundations.dk).Notes and references
- C. A. Stedmon, S. Markager and R. Bro, Mar. Chem., 2003, 82, 239–254 CrossRef CAS.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
- R. Bro, C. A. Andersson and H. A. L. Kiers, J. Chemom., 1999, 13, 295–309 CrossRef CAS.
- C. M. Andersen and R. Bro, J. Chemom., 2003, 17, 200–215 CrossRef CAS.
- K. R. Murphy, J. Boehme, M. Noble, C. Brown, G. Smith, D. Sparks and G. M. Ruiz, J. Mar. Syst., 2013, 111–112, 157–166 CrossRef.
- C. A. Andersson and R. Bro, Chemom. Intell. Lab. Syst., 2000, 52, 1–4 CrossRef CAS.
- C. A. Stedmon and R. Bro, Limnol. Oceanogr.: Methods, 2008, 6, 572–579 CrossRef CAS.
- K. R. Murphy, Appl. Spectrosc., 2011, 65, 62–65 CrossRef.
- K. R. Murphy, K. D. Butler, R. G. M. Spencer, C. A. Stedmon, J. R. Boehme and G. R. Aiken, Environ. Sci. Technol., 2010, 44, 9405–9412 CrossRef CAS PubMed.
- R. A. Harshman, UCLA Working Papers in Phonetics, University Microfilms, Ann Arbor, no. 10,085, 1970, vol. 16, pp. 1–84 Search PubMed.
- J. R. Lakowicz, Principles of fluorescence spectroscopy, Plenum Press, New York, 3rd edn, 2006 Search PubMed.
- L. Sorber, M. V. Barel and L. D. Lathauwer, Tensorlab v1.0, http://esat.kuleuven.be/sista/tensorlab/, accessed 19 July 2013 Search PubMed.
- D. G. Leibovici, J. Stat. Softw., 2010, 34, 1–34 Search PubMed.
- E. V. Thomas, Anal. Chem., 1994, 66, 795A–804A CrossRef CAS.
- R. Bro and A. K. Smilde, J. Chemom., 2003, 17, 16–33 CrossRef CAS.
- T. Naes, T. Isaksson, T. Fearn and T. Davies, A User Friendly Guide to Multivariate Calibration and Classification, NIR Publications, Chichester, 2002 Search PubMed.
- K. R. Murphy, R. Bro and C. A. Stedmon, in Aquatic organic matter fluorescence, ed. P. Coble, A. Baker, J. Lead, D. Reynolds and R. Spencer, Cambridge University Press, New York, accepted 6/6/2011, in press, ISBN: 9780521152594 Search PubMed.
- P. C. DeRose, E. A. Early and G. W. Kramer, Rev. Sci. Instrum., 2007, 78(033107) DOI:10.1063/1.2715952.
- P. C. DeRose and U. Resch-Genger, Anal. Chem., 2010, 82, 2129–2133 CrossRef CAS PubMed.
- A. Gilmore, R. Hurteaux, S. FitzGerald and A. Knowles, WIT Trans. Ecol. Environ., 2012, 160, 295–306 Search PubMed.
- Q. Gu and J. E. Kenny, Anal. Chem., 2009, 81, 420–426 CrossRef CAS PubMed.
- J. F. Holland, R. E. Teets, P. M. Kelly and A. Timnick, Anal. Chem., 1977, 49, 706–710 CrossRef CAS.
- D. R. Christmann, S. R. Crouch, J. F. Holland and A. Timnick, Anal. Chem., 1980, 52, 291–295 CrossRef CAS.
- N. Senesi, Anal. Chim. Acta, 1990, 232, 77–106 CrossRef CAS.
- P. G. Coble, S. A. Green, N. V. Blough and R. B. Gagosian, Nature, 1990, 348, 432–435 CrossRef CAS.
- M. Bahram, R. Bro, C. Stedmon and A. Afkhami, J. Chemom., 2006, 20, 99–105 CrossRef CAS.
- R. G. Zepp, W. M. Sheldon and M. A. Moran, Mar. Chem., 2004, 89, 15–36 CrossRef CAS.
- S. P. Gurden, J. A. Westerhuis, R. Bro and A. K. Smilde, Chemom. Intell. Lab. Syst., 2001, 59, 121–136 CrossRef CAS.
- J. Riu and R. Bro, Chemom. Intell. Lab. Syst., 2003, 65, 35–49 CrossRef CAS.
- C. A. Stedmon, DOMFluor spectral database, http://www.models.life.ku.dk/domfluor, accessed 6 July 2012.
- R. Bro and H. A. L. Kiers, J. Chemom., 2003, 17, 274–286 CrossRef CAS.
- M. V. Bosco, M. Garrido and M. S. Larrechi, Anal. Chim. Acta, 2006, 559, 240–247 CrossRef CAS.
- K. R. Murphy, A. Hambly, S. Singh, R. K. Henderson, A. Baker, R. Stuetz and S. J. Khan, Environ. Sci. Technol., 2011, 45, 2909–2916 CrossRef CAS PubMed.
- K. R. Murphy, C. A. Stedmon, T. D. Waite and G. M. Ruiz, Mar. Chem., 2008, 108, 40–58 CrossRef CAS.
- C. A. Stedmon and S. Markager, Limnol. Oceanogr., 2005, 50, 686–697 CrossRef CAS.
- R. A. Harshman and W. S. DeSarbo, in Research methods for multimode data analysis, ed. H. G. Law, J. C. W. Snyder, J. Hattie and R. P. McDonald, Praeger., New York, 1984, pp. 602–642 Search PubMed.
- R. A. Harshman, in Research methods for multimode data analysis, ed. H. G. Law, J. C. W. Snyder, J. Hattie and R. P. McDonald, Praeger, New York, 1984, pp. 566–591 Search PubMed.
- S. H. Hurlbert, Ecol. Monogr., 1984, 54, 187–211 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Appendix A contains a tutorial on preparing EEM datasets and implementing PARAFAC analysis. The dataset itself may be downloaded from http://www.models.life.ku.dk/. Appendix B illustrates split half analysis. Appendix C is an example output (*.xlsx) for a PARAFAC model developed and validated using the drEEM toolbox. See DOI: 10.1039/c3ay41160e |
| This journal is © The Royal Society of Chemistry 2013 |
