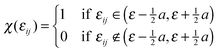First-principles simulation of the absorption bands of fluorenone in zeolite L†
Xiuwen
Zhou
a,
Tomasz A.
Wesolowski
*a,
Gloria
Tabacchi
b,
Ettore
Fois
*b,
Gion
Calzaferri
*c and
André
Devaux
d
aDépartement de Chimie Physique, Université de Genève, 30 quai Ernest-Ansermet, CH-1211 Genève 4, Switzerland. E-mail: tomasz.wesolowski@unige.ch
bDepartment of Science and High Technology, University of Insubria, and INSTM, Via Lucini 3, I-22100 Como, Italy. E-mail: fois@fis.unico.it
cDepartment of Chemistry and Biochemistry, University of Bern, Freiestrasse 3, CH-3012 Bern, Switzerland. E-mail: gion.calzaferri@iac.unibe.ch
dInstitute of Inorganic Chemistry, University of Fribourg, CH-1700 Fribourg, Switzerland
First published on 18th October 2012
Abstract
The absorption spectrum of fluorenone in zeolite L is calculated from first-principles simulations. The broadening of each band is obtained from the explicit treatment of the interactions between the chromophore and its environment in the statistical ensemble. The comparison between the simulated and measured spectra reveals the main factors affecting the spectrum of the chromophore in hydrated zeolite L. Whereas each distinguishable band is found to originate from a single electronic transition, the bandwidth is determined by the statistical nature of the environment of the fluorenone molecule. The K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C motif is retained in all conformations. Although the interactions between K+ and the fluorenone carbonyl group result in an average lengthening of the C
C motif is retained in all conformations. Although the interactions between K+ and the fluorenone carbonyl group result in an average lengthening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and in a redshift of the lowest energy absorption band compared to gas phase or non-polar solvents, the magnitude of this shift is noticeably smaller than the total shift. An important factor affecting the shape of the band is fluorenone's orientation, which is strongly affected by the presence of water. The effect of direct interactions between fluorenone and water is, however, negligible.
O bond and in a redshift of the lowest energy absorption band compared to gas phase or non-polar solvents, the magnitude of this shift is noticeably smaller than the total shift. An important factor affecting the shape of the band is fluorenone's orientation, which is strongly affected by the presence of water. The effect of direct interactions between fluorenone and water is, however, negligible.
1 Introduction
The one-dimensional channel framework of zeolite L,1,2 acting as a host for a large variety of guests, has encouraged syntheses of guest–host composites with remarkable organizational patterns.3–18 These are currently investigated for applications in different fields, ranging from sensing in analytical chemistry, biology, and diagnostics,15–18 to applications in optical and electro optical devices3–5,19–21 and extending to solar energy utilization, e.g. in the form of luminescent solar concentrators.3,4,22–25 Advanced optical microscopy techniques have enabled researchers to obtain detailed information regarding the properties of the guests.11,26–31However, modeling studies needed for interpreting and understanding the experimental data remain challenging, mainly because of the considerable extension of the systems to be handled in the calculations. We have, nevertheless, recently been successful in explaining experimental observations by performing first-principles calculations on systems consisting of hundreds of atoms.32–34
Important organic molecules used in guest–zeolite-L composites bear carbonyl groups. Fluorenone was found to be an excellent probe molecule for studying the behavior and interactions of the carbonyl group of such guests inside the channels of zeolite L, both experimentally and theoretically.33,34 The previously reported computer simulation studies of fluorenone inside dry and hydrated zeolite L channels focused on the structure and interactions of fluorenone with the channels and the charge compensating cations as well as with the water molecules present as co-guests.32 It was comprehensively shown that the water molecules were incapable of displacing the fluorenone out of the zeolite L channel because of the strong interactions between fluorenone's carbonyl group and the extra-framework potassium cations. The K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C arrangement was found to be the leitmotif determining the behavior of fluorenone in the channel. Without breaking this arrangement, the fluorenone molecule can, however, adopt various orientations owing to the sufficiently large diameter of the channel. The ab initio molecular dynamics simulations revealed that the reorientation time of fluorenone in hydrated zeolite L is about twice as long as that in dry zeolite L. Turning to the absorption spectra of fluorenone, the bands in the 200–420 nm range observed in gas phase and in non-polar media are rather well understood. They all originate from four electronic transitions of π → π* character.35 This interpretation was confirmed by Fois et al.32 The shape of the electronic absorption spectrum of fluorenone in zeolite L and in non-polar solvent (cyclohexane) is similar (see Fig. 5 in ref. 33 and the data shown in the present work). However, the former is less structured and the maxima of the bands are red-shifted. It is tempting, therefore, to assign the observed bands of fluorenone in zeolite L to the same electronic transitions as the ones in the gas phase and in cyclohexane. The disappearance of the vibrational features can be due to the structural fluctuations of the environment of fluorenone in zeolite L. In contrast to cyclohexane, the zeolite environment includes components strongly interacting with the chromophore: water molecules, extra framework cations, and the zeolite framework. The shifts in the maxima of the absorption bands could be attributed to the average effect of the interactions between fluorenone and charged atoms (potassium cations) or polar molecules (water) as well as to the effect of long-range interactions between the fluorenone and the zeolite framework. The overall effect of the environment on the absorption spectrum can be considered as resulting from two factors: one being electronic and the other structural. Interactions with the environment affect fluorenone's electronic structure at any instantaneous geometry. On the other hand, these interactions determine both the average internal geometry of the chromophore and its relative orientation in the zeolite channel in a given statistical ensemble. The orientation of fluorenone is especially interesting as it is directly related to the properties of fluorenone as a component of the energy relay system in artificial antennas. Discriminating the direct effects induced by the presence of water molecules in the zeolite channel, which are due to the potential they generated at a given geometry, from the indirect ones such as their impact on the orientation of fluorenone in the channel, is crucial for understanding the experimental data concerning the electronic properties and excited state dynamics of the composite as well as the whole energy relay mechanism in artificial antennae systems based on zeolite L. Experimental estimation of the importance of these two types of effects is rather difficult.3,4 However, availability of an adequate sample of instantaneous geometries generated in numerical simulations for the corresponding statistical ensembles makes it possible to assess directly the relative importance of these two effects. The electronic effect due to the water molecules can be easily monitored by means of comparing the spectrum evaluated from geometries corresponding to the hydrated zeolite L with the one evaluated from the same set of instantaneous geometries but with the water molecules removed. Their structural effect on the other hand, can be also easily monitored once two samples of instantaneous geometries are available: one for the hydrated and the other for the dry composite. The difference between the spectra evaluated without water but for instantaneous geometries corresponding to these two different statistical ensembles provides a direct measure of the structural effect.
C arrangement was found to be the leitmotif determining the behavior of fluorenone in the channel. Without breaking this arrangement, the fluorenone molecule can, however, adopt various orientations owing to the sufficiently large diameter of the channel. The ab initio molecular dynamics simulations revealed that the reorientation time of fluorenone in hydrated zeolite L is about twice as long as that in dry zeolite L. Turning to the absorption spectra of fluorenone, the bands in the 200–420 nm range observed in gas phase and in non-polar media are rather well understood. They all originate from four electronic transitions of π → π* character.35 This interpretation was confirmed by Fois et al.32 The shape of the electronic absorption spectrum of fluorenone in zeolite L and in non-polar solvent (cyclohexane) is similar (see Fig. 5 in ref. 33 and the data shown in the present work). However, the former is less structured and the maxima of the bands are red-shifted. It is tempting, therefore, to assign the observed bands of fluorenone in zeolite L to the same electronic transitions as the ones in the gas phase and in cyclohexane. The disappearance of the vibrational features can be due to the structural fluctuations of the environment of fluorenone in zeolite L. In contrast to cyclohexane, the zeolite environment includes components strongly interacting with the chromophore: water molecules, extra framework cations, and the zeolite framework. The shifts in the maxima of the absorption bands could be attributed to the average effect of the interactions between fluorenone and charged atoms (potassium cations) or polar molecules (water) as well as to the effect of long-range interactions between the fluorenone and the zeolite framework. The overall effect of the environment on the absorption spectrum can be considered as resulting from two factors: one being electronic and the other structural. Interactions with the environment affect fluorenone's electronic structure at any instantaneous geometry. On the other hand, these interactions determine both the average internal geometry of the chromophore and its relative orientation in the zeolite channel in a given statistical ensemble. The orientation of fluorenone is especially interesting as it is directly related to the properties of fluorenone as a component of the energy relay system in artificial antennas. Discriminating the direct effects induced by the presence of water molecules in the zeolite channel, which are due to the potential they generated at a given geometry, from the indirect ones such as their impact on the orientation of fluorenone in the channel, is crucial for understanding the experimental data concerning the electronic properties and excited state dynamics of the composite as well as the whole energy relay mechanism in artificial antennae systems based on zeolite L. Experimental estimation of the importance of these two types of effects is rather difficult.3,4 However, availability of an adequate sample of instantaneous geometries generated in numerical simulations for the corresponding statistical ensembles makes it possible to assess directly the relative importance of these two effects. The electronic effect due to the water molecules can be easily monitored by means of comparing the spectrum evaluated from geometries corresponding to the hydrated zeolite L with the one evaluated from the same set of instantaneous geometries but with the water molecules removed. Their structural effect on the other hand, can be also easily monitored once two samples of instantaneous geometries are available: one for the hydrated and the other for the dry composite. The difference between the spectra evaluated without water but for instantaneous geometries corresponding to these two different statistical ensembles provides a direct measure of the structural effect.
In ref. 32, excitation energies were calculated on molecular models (clusters) extracted from the minimum energy structures of the fluorenone–zeolite system containing fluorenone and the nearest atoms of the zeolite L environment. Due to the statistical nature of the system, we extend these studies of electronic excitations for embedded fluorenone by simulating the theoretical spectra for a model consisting of more than one thousand of atoms in which the structural fluctuations of both the chromophore and the environment are taken into account. The principal objective of the present work is a qualitative and quantitative analysis of the relative significance of the electronic and structural effects of the environment on the absorption bands of fluorenone inside the hydrated zeolite. To this aim, the theoretical absorption spectrum of fluorenone in a hydrated zeolite is obtained as a first step. Subsequently, the relative importance of structural and electronic factors is investigated by selectively switching off and on different effects. The observed broadening of the absorption bands and the ultimate shape of the absorption spectrum result mainly from vibrational effects, i.e., fluctuations of the environment and of the internal geometry of the chromophore. Computer simulation of the band shapes involves, therefore, a large number of evaluations of excitation energies for a relatively large system. In this case, the fluctuation of the absorption energies of the chromophore should be mainly related to its instantaneous environment (zeolite framework, water molecules, cations) which does not absorb light in the investigated spectral range. The embedding strategy is, therefore, an optimal way to evaluate reliably the excitation energies for the corresponding statistical ensemble. In this strategy, the quantum mechanical descriptors are used only for the chromophore, whereas the effect of the environment is taken into account by an additional operator. According to the basic result of Frozen-Density Embedding Theory (FDET),36–40 such an operator has the form of a local potential, which is uniquely determined by the charge distribution in the environment and the electron density of the chromophore. Moreover, recent benchmarking studies demonstrated that the precision of the environment-induced shift of the electronic excitation energy obtained from FDET was remarkable for environments not interacting covalently with the chromophore. The differences between the environment-induced shifts of the excitation energies and their high-quality reference counter-parts are typically in the 150 cm−1 range, corresponding to 0.02 eV.41,42 Such accuracy of the shift values is expected to be retained for the case studied here as the overlap between the electron densities of the chromophore and its environment is rather small. The secondary objective of the present work is to assess the usefulness of the used computational protocol based on FDET as a first-principles method to simulate the shape of the absorption bands. Currently, in order to simulate the absorption spectra of organic chromophores in condensed phases, most of the methods obtain the excitation energies by first-principles based calculations combined with empirical widening of each band.43 In the present work, the inhomogeneous widening of the bands is also obtained from first principles.
2 Computational details
2.1 First-principles molecular dynamics
Density functional theory (DFT) calculations on the dry fluorenone–zeolite-L composite (simulation cell stoichiometry: K18[Al18Si54O144]Fl) and on a hydrated system modeling low water loading conditions (simulation cell stoichiometry: K18[Al18Si54O144]Fl·(H2O)4) were performed by adopting the PBE approximation44 and periodic boundary conditions, as described in detail in ref. 32. The simulation cell was twice the hexagonal experimental unit cell of the zeolite host along c(a = b = 18.466 Å; c = 2 × 7.476 Å; β = 120°).45 Wavefunctions were expanded in planewaves up to a 25 Ry cutoff (200 Ry for the density).46–48 Electron–ion cores interactions were calculated with ultra-soft Vanderbilt pseudopotentials for H, C, O; norm-conserving pseudopotentials for Si, Al, K (semi-core).49–52 Such a calculation scheme for the electronic structure provided a proper description of other large organic–inorganic systems.53–60First-principles molecular dynamics (FPMD)61–63 simulations were performed on both hydrated and dry systems. The room temperature FPMD trajectory of the dry composite was described in ref. 32. In the case of the hydrated system, two trajectories were performed. One (12 ps) was at room temperature, and the fluorenone molecular axis was roughly parallel to the channel axis as described in ref. 32. The other (5 ps) was performed at a 40 K temperature starting with fluorenone oriented approximately perpendicular to the channel axis, in order to sample different fluorenone orientations in the zeolite and to investigate their effect on the electronic spectrum. The target temperature of 40 K (NVT ensemble) was chosen because the perpendicular orientation of fluorenone is not stable under room temperature conditions. Actually, in a 300 K simulation starting with perpendicular fluorenone, the molecule was observed to recover in one picosecond to its energetically favored orientation in the zeolite channel, i.e. approximately parallel to the zeolite channel axis. As in ref. 32, a time step of 0.121 fs and an inertia parameter of 500 au for the electronic states coefficients were adopted.
2.2 Excitation energies of embedded fluorenone from Frozen-Density Embedding Theory based calculations
One of the clusters used for calculating the excitation energies of fluorenone in the hydrated zeolite taken from the trajectory representing the statistical ensemble is shown in Fig. 1. The same cluster size was used to calculate the excitation energies for fluorenone in the dry zeolite. For each instantaneous geometry of the system, the excitation energy of fluorenone was calculated using the method64 combining FDET36–40 with linear-response time-dependent DFT framework.78 This FDET framework was implemented38,65 into the ADF code (2009.01 version)67 allowing for evaluation of various properties of embedded systems and making possible to introduce additional approximations for the frozen density as the ones discussed in ref. 38, 66, 74 for instance. Fluorenone was treated as an embedded system, described by electron density ρA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and embedded orbitals, while the rest of the system (zeolite L framework, cations and water molecules) was treated as an embedding system, described by its electron density ρB(
) and embedded orbitals, while the rest of the system (zeolite L framework, cations and water molecules) was treated as an embedding system, described by its electron density ρB(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ).
).
![Left panel: the fluorenone molecule. Right panel: the cluster used for calculating excitation energies of fluorenone in the hydrated zeolite: K71[Al108Si324O819]Fl·(H2O)12 (1380 atoms in total). Color code: red, O; white, H; light blue, Al; grey, Si; yellow, K+; green, C.](/image/article/2013/CP/c2cp42750h/c2cp42750h-f1.gif) | ||
| Fig. 1 Left panel: the fluorenone molecule. Right panel: the cluster used for calculating excitation energies of fluorenone in the hydrated zeolite: K71[Al108Si324O819]Fl·(H2O)12 (1380 atoms in total). Color code: red, O; white, H; light blue, Al; grey, Si; yellow, K+; green, C. | ||
In the excitation energy calculation, the frequency-dependent response was expanded using only embedded orbitals associated with the chromophore (neglect of the dynamic response of the environment, NDRE, called also uncoupled FDE in the literature68) as described in ref. 38. The STO-type DZP basis set was applied for all the calculations. The Statistical Averaged Orbital Potential (SAOP)69–71 model was used to approximate the exchange–correlation potential evaluated for the density corresponding to fluorenone (embedded or isolated). For the orbital-free embedding potential (eqn (3) in ref. 72):
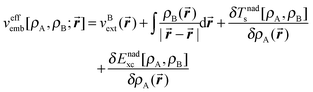 | (1) |
-NDSD approximation73 for the non-additive kinetic energy dependent component of the embedding potential;
-Dirac- and Vosko–Wilk–Nusair expressions were used for the non-additive exchange energy and correlation energy, respectively.
-The choice of ρB used in eqn (1) is a key approximation in any FDET based simulation and lies at the origin of great computational savings compared to the corresponding Kohn–Sham calculations for the whole system. The electronic density of the environment (zeolite L, cations, and water) ρB was approximated by the superposition of spherically symmetric electron densities of individual atoms each integrating to the following net charge: silicon +4e, aluminum +3e, oxygen (zeolite) −2e, oxygen (water) −0.8e, potassium +1e, and hydrogen (water) +0.4e. The net charge of each spherically symmetric atomic density corresponds to the formal ionic charges of the zeolitic material. The applied procedure to generate ρB was validated by performing the following test. For a smaller cluster comprising only the nearest neighbors of fluorenone (Si50Al16K16O163H62, 307 atoms in total), two sets of ρB were generated. The first one was obtained using the above procedure (consisting of superposing spherically symmetric atomic densities) and the other one was obtained from conventional Kohn–Sham calculations. In the subsequent step, the two frozen densities were used in FDET based calculations to evaluate the excitation energies for fluorenone embedded in the small cluster. A graphical representation of the small cluster and the calculated values of the excitation energies are reported in the ESI.† The excitation energies obtained with the two sets of frozen densities (ρB) agree within about 0.03 eV, validating thus the chosen strategy to generate ρB in the larger system simulation.
2.3 Simulation of the absorption spectra
The simulated spectrum was generated through averaging over several hundred configurations representing the corresponding statistical ensemble. For each configuration, a “stick spectrum” was obtained from LR-TDDFT calculations providing vertical excitation energies and intensities. Each simulated spectrum reported in this work is just the envelope of a large number of superimposed “stick spectra”. In this way, the inhomogeneous broadening of each absorption band due to variations of both internal degrees of freedom and intermolecular ones was taken into account. This approach is essentially the same as the one used in ref. 66, which focused on solvatochromism. In the present work, we attempt to simulate not only the solvatochromic shifts of the first excited states but rather the whole shape of the absorption spectrum in the UV/Vis range.For a given energy point ε, the averaged oscillator strength fav(ε) was calculated by summing the oscillator strengths of the excitations for each instantaneous geometry:
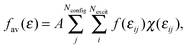 | (2) |
The summation range a was set to be 0.08 eV. The simulated spectra considered in the present work were obtained for Nconfig in the range of 600. Numerical experience with the considered system shows that an ensemble of such size obtained from the equilibrated molecular dynamics trajectory assures a stable shape of the simulated spectrum. Spectra obtained using trajectories with different lengths are provided in ESI.† For samples of this size, the chosen value of a = 0.08 eV ensures smoothness of the spectrum without losing finer features of the bands. Varying the value of the parameter a from 0.06 to 0.14 eV marginally changes the overall shape of the spectrum (see ESI†). This procedure corresponds to finding the envelope of a stick spectrum such as the one shown in Fig. 8 in the Results section. We notice that eqn (2) corresponds to essentially the same procedure to simulate spectra as the one applied in ref. 75, in which the parameter a was set to be 0.01 eV for studies of gas and condensed phase spectra of amides. The narrower width of the energy bin used in ref. 75 was needed because gas-phase spectra of amides are much more structured than the spectra considered in the present work. In this context, it is worthwhile pointing out that the used value of the parameter a exceeds the natural width of the absorption band due to the finite lifetime of the excited state. The shape function for each line in the “stick spectrum” is, therefore, not considered explicitly in such averaging procedures.
In our strategy for simulating the shape of the absorption bands, the excitation energy of the embedded species is obtained as the sum of the excitation energy of the isolated chromophore and of the environment induced shift. For fluorenone embedded in the environment at a given instantaneous geometry {![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}, its excitation energy is obtained as:
i}, its excitation energy is obtained as:
εcalcemb({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) = εcalciso({ i}) = εcalciso({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) + ΔεFDET({ i}) + ΔεFDET({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) i}) | (3) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}), LR-TDDFT excitation energies for small organic chromophores are known to lead to errors in the range of 0.1–0.5 eV if semilocal approximations are used for the exchange–correlation potential.76,77 As far as ΔεFDET({
i}), LR-TDDFT excitation energies for small organic chromophores are known to lead to errors in the range of 0.1–0.5 eV if semilocal approximations are used for the exchange–correlation potential.76,77 As far as ΔεFDET({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) is concerned, the benchmark calculations show that the errors of the FDET calculated environment induced shifts are about 0.02 eV (the relative errors of the FDET shifts lie around 10%).41 It can be expected, therefore, that the shape of the absorption bands of fluorenone in a fluctuating environment can be described rather accurately by means of FDET shifts evaluated for a large number of configurations representing the considered statistical ensemble, whereas the position of the center of the bands depends on the method used to evaluate εcalciso({
i}) is concerned, the benchmark calculations show that the errors of the FDET calculated environment induced shifts are about 0.02 eV (the relative errors of the FDET shifts lie around 10%).41 It can be expected, therefore, that the shape of the absorption bands of fluorenone in a fluctuating environment can be described rather accurately by means of FDET shifts evaluated for a large number of configurations representing the considered statistical ensemble, whereas the position of the center of the bands depends on the method used to evaluate εcalciso({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}). Using LR-TDDFT/FDET excitation energies to simulate the absorption spectra by means of eqn (3) involves also another approximation, namely the neglect of the difference between the position of the maximum of the absorption band and the corresponding vertical excitation energy. Obtaining the numerical value of such a difference from the theoretical model exceeds the scope of the present work. By taking into account these factors affecting the accuracy of the simulated band shapes, the values of εcalcemb({
i}). Using LR-TDDFT/FDET excitation energies to simulate the absorption spectra by means of eqn (3) involves also another approximation, namely the neglect of the difference between the position of the maximum of the absorption band and the corresponding vertical excitation energy. Obtaining the numerical value of such a difference from the theoretical model exceeds the scope of the present work. By taking into account these factors affecting the accuracy of the simulated band shapes, the values of εcalcemb({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) needed in eqn (2) were evaluated not by using eqn (3) but by adopting its empirically corrected formulation:
i}) needed in eqn (2) were evaluated not by using eqn (3) but by adopting its empirically corrected formulation:εcalcemb({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) = εSAOPiso({ i}) = εSAOPiso({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) + Δεiso + ΔεFDET({ i}) + Δεiso + ΔεFDET({![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) i}) i}) | (4) |
2.4 Excitation energies of fluorenone in gas phase
The geometry of fluorenone in the gas phase was optimized at the MP2/6-311++g(d,p) level. Excitation energies were calculated using the LR-TDDFT methodology78 with a STO-type DZP basis set and the SAOP69–71 exchange–correlation potential. Note that all the parameters in the reported calculations were set in such a way that the gas-phase excitation energies from LR-TDDFT calculations are the same as the FDET/LRTDDFT energies obtained when the embedding potential in eqn (1) is set to zero.3 Results and discussions
The Results section is organized as follows. The characterization of the excited states of isolated fluorenone in its equilibrium geometry is followed by the analysis of the simulated absorption spectrum. Different factors which may affect the shape of the absorption bands of fluorenone in hydrated zeolite L are discussed in the subsequent sections. In particular, the effect of water molecules on the calculated absorption spectrum of the composite is analysed in detail by decomposing it into a component due to the fluorenone–water direct interactions at each instantaneous geometry and a component due to the effect of water on fluorenone's orientation in the channel. Additionally, the effect of fluctuations in the internal geometry of fluorenone due to interactions with its environment is analyzed in detail.3.1 Electronic transitions for isolated fluorenone in its equilibrium geometry
The results of LR-TDDFT calculations for isolated fluorenone in its equilibrium geometry and the corresponding results reported in the literature are collected in Table 1. The n → π* transitions are symmetry forbidden and the observed bands correspond to π → π* transitions. The energies of the allowed transitions are systematically lower than their LRTDDFT/B3LYP and PPP counterparts. Such an underestimation is in line with the literature that the SAOP approximation underestimates the energy of the lowest transitions in organic chromophores.77 For this reason, the LR-TDDFT and semiempirical PPP results are expected to be better estimates of the exact excitation energies of the isolated fluorenone. Compared to PPP excitation energies, which are most likely the best estimate, the LR-TDDFT/SAOP excitation energies are underestimated by 0.3 to 0.58 eV (see Table 1).| Type of excitation | ε a | f a | ε b | ε c |
|---|---|---|---|---|
| a This work (LR-TDDFT/SAOP). b Ref. 32 (LR-TDDFT/B3LYP). c Ref. 35 (PPP semi-empirical calculations). | ||||
| π → π* | 2.75 | 0.29 × 10−2 | 3.09 | 3.26 |
| n → π* | 3.04 | 0.35 × 10−9 | 3.13 | — |
| 2π → π* | 3.56 | 0.31 × 10−1 | 4.00 | 4.00 |
| 3π → π* | 3.98 | 0.19 × 10−1 | 4.44 | 4.28 |
| n → 2π* | 4.06 | 0.74 × 10−10 | 4.82 | — |
| 4π → π* | 4.38 | 0.23 × 10−1 | 5.07 | 4.96 |
| π → 2π* | 4.62 | 0.69 | 4.89 | — |
| 3π → 2π* | 4.78 | 0.17 × 10−2 | — | — |
| 2π → 2π* | 4.90 | 0.18 × 10−1 | — | — |
| n → 3π* | 4.95 | 0.26 × 10−3 | — | — |
3.2 Absorption spectra of fluorenone in hydrated zeolite L
Fig. 2 shows the absorption spectra of fluorenone measured in cyclohexane and in hydrated zeolite L as reported originally in ref. 33. Due to the small values of the molecular extinction coefficient at long wavelengths, the intensities are shown on the logarithmic scale in all the figures subsequently discussed in this work.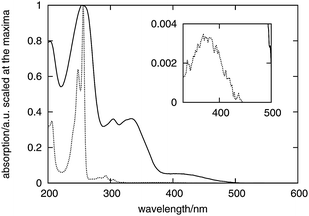 | ||
| Fig. 2 Absorption spectra of fluorenone measured in cyclohexane (dashed curve) and in hydrated zeolite L (solid curve). The extinction coefficients are scaled to 1 at the absorption maximum. The inset shows an enlargement of the weak band at 375 nm in cyclohexane. | ||
The simulated spectrum of fluorenone in the hydrated zeolite together with its experimental counterpart is shown in Fig. 3.
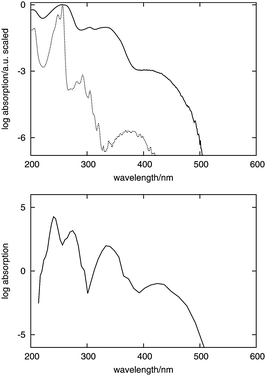 | ||
| Fig. 3 Top: experimental spectra of fluorenone in cyclohexane solution (dashed curve) and in hydrated zeolite L (solid curve). Bottom: simulated spectrum of fluorenone in hydrated zeolite L. The intensity is given on the logarithmic scale in both measured and simulated spectra to visualize the weak bands. | ||
The simulated and measured spectra of fluorenone in hydrated zeolite L feature four intense bands in the low-energy part of the spectrum. The shapes of the two spectra match quite well. The position of the lowest energy band was built into our model to simulate spectra by means of the chosen value of Δεiso in eqn (4). The correct positions and relative intensities of the three subsequent clearly distinguishable bands indicate the strength of the used strategy to simulate absorption band shapes using the FDET embedding potential given in eqn (1) in LR-TDDFT calculations of excitation energies combined with the non-empirical treatment of line broadening (eqn (2)).
The non-shifted (eqn (3)) excitation energies for embedded fiuorenone are collected in Table 2. The analysis of electronic excitations in the instantaneous geometries shows that each electronic transition generates only one peak in the spectrum. The width of each band results from the different excitation energy values due to the fluctuating environment of fluorenone in hydrated zeolite L. Table 2 collects also the range at which each type of excitation occurs in the analyzed sample of conformations. The good agreement between the simulated and observed absorption spectra suggests a more detailed analysis of the factors affecting band shapes. Such analyses are reported in the subsequent sections.
| State | ε iso | ε peakzeo | ε minzeo − εmaxzeo |
|---|---|---|---|
| The order of the excited states corresponds to the LR-TDDFT result for isolated fluorenone. The correspondence of the transitions obtained for fluorenone in different environments is arbitrary because of the large number of single-electron excitations contributing to a given transition in LR-TDDFT based methods. Such attribution is unambiguous only if there is a clear dominant excitation, as it is the case in the lowest transition. εiso is the calculated excitation energy of isolated fluorenone. εpeakzeo is the position of the peak of the simulated absorption band for fluorenone in the hydrated zeolite; εminzeo and εmaxzeo are the lowest and highest values of the calculated excitation energy of a given transition in the sample, respectively. | |||
| 1 | 2.75 | 2.07 | 1.61–2.63 |
| 2 | 3.04 | 2.89 | 2.37–3.27 |
| 3 | 3.56 | 3.15 | 2.67–3.53 |
| 4 | 3.98 | 3.69 | 3.25–3.97 |
| 5 | 4.06 | 3.81 | 3.41–4.11 |
| 6 | 4.38 | 3.95 | 3.61–4.35 |
| 7 | 4.62 | 4.25 | 3.71–4.47 |
| 8 | 4.78 | 4.31 | 3.91–4.53 |
| 9 | 4.90 | 4.35 | 4.17–4.75 |
| 10 | 4.95 | 4.53 | 4.27–5.01 |
3.3 Absorption spectra of fluorenone in hydrated and dry zeolites
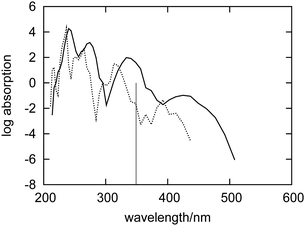
In this section, the spectrum of fluorenone in the dry zeolite is analyzed. Such a spectrum was obtained by using a different sample of configurations corresponding to a different statistical ensemble. In this case, the electronic density of the environment ρB used to evaluate the embedding potential from eqn (1) did not include the contributions from water molecules because they were absent in the corresponding FPMD simulation.Fig. 4 shows the simulated absorption spectra of fluorenone in hydrated and in dry zeolite L. The overall effect (structural and electronic) of the water molecules is significantly smaller than that of the zeolite framework and the counter ions. This is in line with the analysis given in ref. 32 pointing out that the zeolite environment affects fluorenone's excitations primarily by the direct interaction between K+ cations and fluorenone's carbonyl group. The lowest energy band is broader in the dry zeolite, indicating that the structural fluctuations in the system are reduced upon hydration.
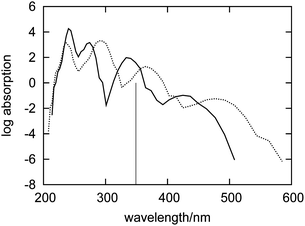 | ||
| Fig. 4 Simulated absorption spectra of fluorenone in dry (dashed curve) and hydrated (solid curve) zeolite L. The vertical line indicates the calculated wavelength of the lowest excitation for isolated fluorenone in its equilibrium geometry. | ||
The differences between the absorption spectra of fluorenone in dry and wet zeolites might originate from direct interactions between fluorenone and water, but also from differences in the overall geometry of the dye–zeolite system in the two statistical ensembles. To distinguish between these two effects, the following computational experiment was made. The spectra were evaluated using the trajectory corresponding to the hydrated zeolite, but with the embedding potential (eqn (1)) evaluated without contributions from water molecules. Both spectra are shown in Fig. 5.
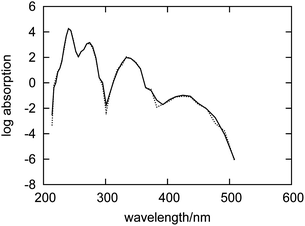 | ||
| Fig. 5 Simulated absorption spectrum for an artificial system comprising only fluorenone, counterions and the zeolite L framework with geometries taken from the FPMD of fluorenone in hydrated zeolite L (dashed curve). The simulated spectrum for fluorenone in hydrated zeolite L is also shown for comparison (solid curve). | ||
The two spectra appear to be almost identical, indicating therefore that the direct interactions between water and fluorenone hardly affect the electronic structure of fluorenone. Actually, during the simulation, water molecules are not directly hydrogen bonded to the fluorenone carbonyl group, but rather preferentially coordinated to other potassium cations in the zeolite channel.32 The differences between the absorption spectra of fluorenone in hydrated and in dry zeolite L shown in Fig. 4 should, therefore, arise from structural factors, i.e., changes of the fluorenone's preferential orientation and average geometry due to the presence of water molecules.
3.4 The effect of the environment on the internal geometry of fluorenone and its consequences on the absorption bands
The absorption spectrum of fluorenone in zeolite L is affected by both fluctuations in the environment and changes of the internal geometry of fluorenone. As highlighted in Fig. 6, the internal geometry of fluorenone fluctuates following the fluctuating environment during the FPMD trajectory. The fact that the instantaneous environment changes in the sampled simulation time is evidenced by the time evolution of the K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances, indicating that the carbonyl oxygen of fluorenone switches coordination between two distinct nearest neighbor potassium cations. As an effect, the average C
C distances, indicating that the carbonyl oxygen of fluorenone switches coordination between two distinct nearest neighbor potassium cations. As an effect, the average C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length, 1.250 Å, is greater than that of isolated fluorenone at the equilibrium geometry (1.220 Å),32 fluctuates between 1.180 Å and 1.325 Å, and the oscillation amplitude is correlated with the shortest K+⋯O
O bond length, 1.250 Å, is greater than that of isolated fluorenone at the equilibrium geometry (1.220 Å),32 fluctuates between 1.180 Å and 1.325 Å, and the oscillation amplitude is correlated with the shortest K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances. It is instructive, therefore, to estimate the importance of such fluctuations compared to the other factors discussed in the previous sections. To this aim, yet another artificial absorption spectrum of fluorenone was generated following a strategy similar to the one adopted to investigate the significance of the direct electronic effects of water molecules. In this case, the FPMD trajectory corresponding to the hydrated zeolite was used, but the embedding potential was switched off. The obtained spectrum is shown in Fig. 7 together with the positions of the excitation levels in the gas phase. The simulated spectrum of fluorenone in hydrated zeolite L is shown as well for reference purposes. Fig. 8 shows the stick spectrum, i.e., the distribution of the narrow absorption lines corresponding to the lowest excitation arising from the instantaneous geometries. The fluctuation of the fluorenone's internal geometry results in the broadening of the band and in a shift of the band maximum for the lowest excitation. In Fig. 8, the spectrum changing from a single line (excitation energy and intensity at equilibrium geometry) to a band (distribution of intensities for the isolated chromophore with fluctuating geometry), can be attributed to vibronic broadening, as the distribution of oscillator strengths correlates with the fluctuations of the C
C distances. It is instructive, therefore, to estimate the importance of such fluctuations compared to the other factors discussed in the previous sections. To this aim, yet another artificial absorption spectrum of fluorenone was generated following a strategy similar to the one adopted to investigate the significance of the direct electronic effects of water molecules. In this case, the FPMD trajectory corresponding to the hydrated zeolite was used, but the embedding potential was switched off. The obtained spectrum is shown in Fig. 7 together with the positions of the excitation levels in the gas phase. The simulated spectrum of fluorenone in hydrated zeolite L is shown as well for reference purposes. Fig. 8 shows the stick spectrum, i.e., the distribution of the narrow absorption lines corresponding to the lowest excitation arising from the instantaneous geometries. The fluctuation of the fluorenone's internal geometry results in the broadening of the band and in a shift of the band maximum for the lowest excitation. In Fig. 8, the spectrum changing from a single line (excitation energy and intensity at equilibrium geometry) to a band (distribution of intensities for the isolated chromophore with fluctuating geometry), can be attributed to vibronic broadening, as the distribution of oscillator strengths correlates with the fluctuations of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length. However, both broadening and shift effects are much smaller than those induced by the full hydrated zeolite L environment. Interestingly, the histograms in Fig. 8 correlate well with the histograms of the C
O bond length. However, both broadening and shift effects are much smaller than those induced by the full hydrated zeolite L environment. Interestingly, the histograms in Fig. 8 correlate well with the histograms of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length and of the shortest K+⋯O
O bond length and of the shortest K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances sampled along the trajectory, reported in Fig. 9. Indeed, the fluctuating C
C distances sampled along the trajectory, reported in Fig. 9. Indeed, the fluctuating C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length mirrors the band broadening due to the fluctuating internal geometry of fluorenone, while the K+⋯O
O bond length mirrors the band broadening due to the fluctuating internal geometry of fluorenone, while the K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distance distribution reproduces the multipeak shape of the calculated absorption band for embedded fluorenone. In summary, the changes in fluorenone's internal geometry provide a minor contribution to the whole effect of the hydrated zeolite L environment on fluorenone's absorption spectrum.
C distance distribution reproduces the multipeak shape of the calculated absorption band for embedded fluorenone. In summary, the changes in fluorenone's internal geometry provide a minor contribution to the whole effect of the hydrated zeolite L environment on fluorenone's absorption spectrum.
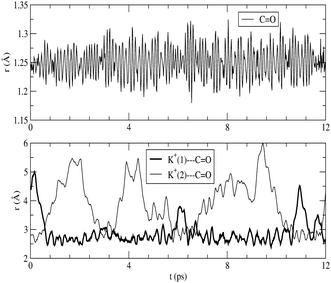 | ||
Fig. 6 Top: fluorenone C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance vs. simulation time. Bottom: K+⋯O O distance vs. simulation time. Bottom: K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distances vs. time for the two K+ closest to the fluorenone carbonyl group. C distances vs. time for the two K+ closest to the fluorenone carbonyl group. | ||
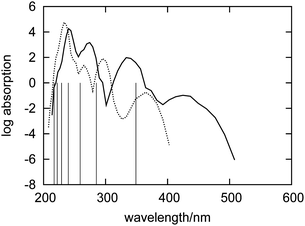 | ||
| Fig. 7 Simulated absorption spectra of an artificial system comprising only fluctuating fluorenone. The geometries are taken from the FPMD of fluorenone in hydrated zeolite L (dashed curve). The simulated spectrum of fluorenone in hydrated zeolite L is also shown for comparison (solid curve). The vertical lines indicate the calculated wavelengths of the excitations of isolated fluorenone in its equilibrium geometry. The forbidden weak transitions are not shown. | ||
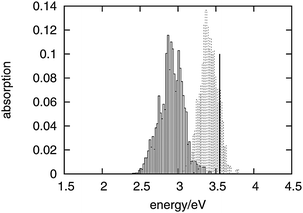 | ||
| Fig. 8 Distribution of the lowest excitation energies for the artificial system of fluctuating fluorenone (dashed boxes) and for fluorenone in hydrated zeolite L (solid boxes) corresponding to the spectra in Fig. 7. The black vertical line indicates the calculated lowest excitation energy for isolated fluorenone in its equilibrium geometry. | ||
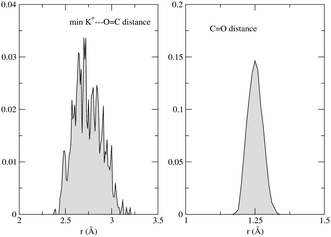 | ||
Fig. 9 Left: shortest K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distance histogram; right: C C distance histogram; right: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance histogram. O distance histogram. | ||
3.5 The effect of the environment on the orientation of fluorenone and its consequences on the absorption bands
The relatively large diameter of the channels in zeolite L leaves some degrees of freedom for fluorenone's orientation. In hydrated zeolite L, however, the fluorenone molecule has a strong preference to orient along the channel instead of perpendicular to the channel.32 In particular, in the case of the hydrated system, a distribution centered at 21° was obtained from the FPMD trajectory for the angle formed by fluorenone's long axis with the zeolite channel axis.32 In order to investigate the effect of fluorenone's preferential orientation on the absorption spectrum, we also calculated the spectrum of fluorenone with its long axis perpendicular to the channel from a 5 ps trajectory. The FPMD simulation of this trajectory was performed at the temperature of 40 K starting with fluorenone oriented approximately perpendicular to the channel. As mentioned in Section 2.1, such a low temperature is needed because the perpendicular orientation is not stable under room temperature conditions.Fig. 10 shows the spectra of fluorenone with different orientations in hydrated zeolite L. The spectrum of fluorenone with perpendicular orientation is redshifted by around 0.2 eV with respect to that of fluorenone with parallel orientation, although the band shapes of the two spectra are not much different. This finding is easily rationalized by taking into account that along the trajectory with fluorenone perpendicular to the channel, the carbonyl oxygen of fluorenone is not bound to potassium cations, but directly interacts with a water molecule via a hydrogen bond. Therefore both the calculated spectra and FPMD results indicate that fluorenone has an orientation preference in the hydrated zeolite and that the coexistence of parallel/perpendicular arrangements should rather be excluded. Such coexistence would result in the appearance of additional bands not visible in the experimental spectrum.
 | ||
| Fig. 10 Simulated absorption spectra of fluorenone in hydrated zeolite L with its long axis perpendicular (dashed curve) and parallel (solid curve) to the zeolite L channel. The vertical line indicates the calculated wavelength of the lowest excitation for isolated fluorenone in its equilibrium geometry. | ||
4 Conclusions
The simulated absorption spectrum reproduces all the main features of the measured spectrum of fluorenone in zeolite L in the region of 250–550 nm. Each distinguishable band in the long wavelength part of the absorption spectrum of fluorenone in zeolite L can be attributed to a single electronic excitation with its width determined by fluctuations of the geometry of the whole system. The adopted computational model provides, therefore, an adequate tool for simulating and interpreting the shape of the absorption bands in such systems. The overall effect of the fluorenone environment on its absorption bands can be decomposed into geometrical factors (orientation of the fluorenone with respect to the zeolite framework, mobility of counter ions and water, and variations of the internal geometry of fluorenone) and the direct electronic effect. The adopted strategy allows one to estimate the relative significance of these factors by selectively switching them off and on. Results obtained using such modified models lead to the following key observations:(i) The overall redshift of the spectrum observed in hydrated zeolite L compared to cyclohexane originates mainly from the interactions between the counter-ions of the zeolite and the carbonyl group of fluorenone. These interactions lie at the origin of the rather conservative arrangement of the K+⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C motif in the statistical ensemble.
C motif in the statistical ensemble.
(ii) The direct effect of water molecules on the excitation energies of fluorenone is negligible at any instantaneous geometry. Water molecules rather affect fluorenone's orientation inside the zeolite channel by stabilizing the parallel arrangement.
(iii) The fluctuations of the internal geometry of fluorenone along FPMD trajectories provide a minor effect on the shape of the absorption bands.
In summary, the simulated absorption bands and the analysis of the factors affecting their position and width support the interpretation that the preferential orientation of fluorenone in hydrated zeolite L is parallel to the zeolite channel. The coexistence of parallel/perpendicular arrangements is rather to be excluded.
Finally, the present study shows that the FDET based simulations of the absorption band shapes can provide an accurate model of the experimental band shapes of chromophores in condensed phases. Such a model is based on first principles except for the offset on the energy scale (Δεiso), which is empirically adjusted due to the intrinsic inaccuracy of the method used to evaluate the vertical excitation energies and the difference between the vertical excitation energy and the absorption energy of the chromophore in the gas phase. The first contribution to Δεiso is strongly dependent on the computational method and the chromophore in question whereas the first-principles based computation part of the second contribution represents a major computational challenge.
Acknowledgements
This work was supported by the grant 200020-134791 from the Fonds National Suisse de la Recherche Scientifique. CINECA supercomputing center (Bologna, Italy) is acknowledged for computing time (ISCRA project 2011 “ZeoDye”, HP10B8FNIH).References
- International Zeolite Association, http://www.izastructure.org.
- T. Ohsuna, B. Slater, F. Gao, J. Yu, Y. Sakamoto, G. Zhu, O. Terasaki, D. E. W. Vaughan, S. Qiu and C. R. A. Catlow, Chem.–Eur. J., 2004, 10, 5031–5040 CrossRef CAS.
- G. Calzaferri, S. Huber, H. Maas and C. Minkowski, Angew. Chem., Int. Ed., 2003, 42, 3732–3758 CrossRef CAS.
- G. Calzaferri, Langmuir, 2012, 28, 6216–6231 CrossRef CAS.
- A. Devaux, F. Cucinotta, S. Kehr and L. De Cola, Functional supramolecular architectures for organic electronics and nanotechnology, Wiley, 2011, vol. 1, pp. 283–242 Search PubMed.
- P. Cao, Y. Wang, H. Li and X. Yu, J. Mater. Chem., 2011, 21, 2709–2714 RSC.
- P. Cao, H. Li, P. Zhang and G. Calzaferri, Langmuir, 2011, 27, 12614–12620 CrossRef.
- M. Woerdemann, S. Gläsener, F. Hörner, A. Devaux, L. De Cola and C. Denz, Adv. Mater., 2010, 22, 4176–4179 CrossRef CAS.
- F. Cucinotta, Z. Popovic, E. A. Weiss, G. M. Whitesides and L. De Cola, Adv. Mater., 2009, 21, 1142–1145 CrossRef CAS.
- A. Guerrero-Martinez, S. Fibikar, I. Pastoriza-Santos, L. Liz-Marzan and L. De Cola, Angew. Chem., Int. Ed., 2009, 48, 1169 CrossRef.
- S. Hashimoto, K. Samata, T. Shoji, N. Taira, T. Tomita and S. Matsuo, Microporous Mesoporous Mater., 2009, 117, 220–227 CrossRef CAS.
- K. B. Yoon, Acc. Chem. Res., 2007, 40, 29–40 CrossRef CAS.
- I. Lopez-Duarte, L.-Q. Dieu, I. Dolamic, M. V. Martinez-Diaz, T. Torres, G. Calzaferri and D. Brühwiler, Chem.–Eur. J., 2011, 17, 1855–1862 CrossRef CAS.
- D. Brühwiler, G. Calzaferri, T. Torres, J. H. Ramm, N. Gartmann, L.-Q. Dieu, I. Lopez-Duarte and M. V. Martinez-Diaz, J. Mater. Chem., 2009, 19, 8040–8067 RSC.
- Z. Popovic, M. Otter, G. Calzaferri and L. De Cola, Angew. Chem., Int. Ed., 2007, 46, 6188–6191 CrossRef CAS.
- M. M. Tsotsalas, K. Kopka, G. Luppi, S. Wagner, M. P. Law, M. Schäfers and L. De Cola, ACS Nano, 2010, 4, 342–348 CrossRef CAS.
- Z. Li, G. Luppi, A. Geiger, H.-P. Josel and L. De Cola, Small, 2011, 7, 3193–3201 Search PubMed.
- J. El-Gindi, K. Benson, L. De Cola, H.-J. Galla and N. Seda Kehr, Angew. Chem., Int. Ed., 2012, 51, 3716–3720 Search PubMed.
- L. Gartzia-Rivero, J. Banuelos-Prieto, V. Martinez-Martinez and I. Lopez- Arbeloa, ChemPlusChem, 2012, 77, 61–70 Search PubMed.
- V. Vohra, G. Calzaferri, S. Destri, M. Pasini, W. Porzio and C. Botta, ACS Nano, 2010, 4, 1409–1416 CrossRef CAS.
- V. Vohra, A. Bolognesi, G. Calzaferri and C. Botta, Langmuir, 2010, 26, 1590–1593 Search PubMed.
- G. Calzaferri, R. Méallet-Renault, D. Brühwiler, R. Pansu, I. Dolamic, T. Dienel, P. Adler, H. Li and A. Kunzmann, ChemPhysChem, 2011, 12, 580–594 CrossRef CAS.
- T. Dienel, C. Bauer, I. Dolamic and D. Brühwiler, Sol. Energy, 2010, 84, 1366–1369 CrossRef CAS.
- G. Calzaferri, D. Brühwiler and A. Kunzmann, Patent, 2008, CH 698333 and WO 2010/009560 Search PubMed.
- M. G. Debije and P. P. C. Verbunt, Adv. Energy Mater., 2012, 2, 12–35 Search PubMed.
- S. Megelski, A. Lieb, M. Pauchard, A. Drechsler, S. Glaus, C. Debus, A. J. Meixner and G. Calzaferri, J. Phys. Chem. B, 2001, 105, 25–35 CrossRef CAS.
- M. Busby, C. Blum, M. Tibben, S. Fibikar, G. Calzaferri, V. Subramaniam and L. De Cola, J. Am. Chem. Soc., 2008, 130, 10970–10976 CrossRef CAS.
- C. Blum, Y. Cesa, M. Escalante and V. Subramaniam, J. R. Soc. Interface, 2009, 6, S35–S43 CrossRef CAS.
- A. Gasecka, L.-Q. Dieu, D. Brühwiler and S. Brasselet, J. Phys. Chem. B, 2010, 114, 4192–4198 Search PubMed.
- M. Busby, A. Devaux, C. Blum, V. Subramaniam, G. Calzaferri and L. De Cola, J. Phys. Chem. C, 2011, 115, 5974–5988 Search PubMed.
- K. F. Domke, J. P. R. Day, G. Rago, T. A. Riemer, M. H. F. Kox, B. M. Weckhuysen and M. Bonn, Angew. Chem., Int. Ed., 2012, 51, 1343–1347 Search PubMed.
- E. Fois, G. Tabacchi and G. Calzaferri, J. Phys. Chem. C, 2010, 114, 10572–10579 Search PubMed.
- A. Devaux, C. Minkowski and G. Calzaferri, Chem.–Eur. J., 2004, 10, 2391–2408 CrossRef CAS.
- E. Fois, G. Tabacchi and G. Calzaferri, J. Phys. Chem. C, 2012, 116, 16784–16799 Search PubMed.
- A. Kuboyama, Chem. Phys. Lett., 1976, 41, 544–546 CrossRef.
- T. A. Wesolowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050–8053 CrossRef.
- T. A. Wesolowski, One-electron equations for embedded electron density: challenge for theory and practical payoffs in multi-level modelling of soft condensed matter, World Scientific, 2006, vol. X, pp. 1–82 Search PubMed.
- T. A. Wesolowski, J. Am. Chem. Soc., 2004, 126, 11444–11445 CrossRef CAS.
- T. A. Wesolowski, Phys. Rev. A, 2008, 77, 012504-1–012504-9 Search PubMed.
- K. Pernal and T. A. Wesolowski, Int. J. Quantum Chem., 2009, 109, 2520–2525 CrossRef CAS.
- G. Fradelos, J. J. Lutz, T. A. Wesolowski, P. Piecuch and M. Woch, J. Chem. Theory Comput., 2011, 7, 1647–1666 Search PubMed.
- G. Fradelos, J. J. Lutz, T. A. Wesolowski, P. Piecuch and M. Wloch, Advances in the Theory of Quantum Systems in Chemistry and Physics, Springer Netherlands, 2012, vol. 22, pp. 219–248 Search PubMed.
- R. Improta, V. Barone and F. Santoro, Angew. Chem., 2007, 119, 409–412 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. M. Newsam, J. Phys. Chem., 1989, 93, 7689–7694 CrossRef.
- G. Bandoli, D. Barreca, A. Gasparotto, R. Seraglia, E. Tondello, A. Devi, R. A. Fischer, M. Winter, E. Fois, A. Gamba and G. Tabacchi, Phys. Chem. Chem. Phys., 2009, 11, 5998–6007 RSC.
- D. Barreca, E. Fois, A. Gasparotto, R. Seraglia, E. Tondello and G. Tabacchi, Chem.–Eur. J., 2011, 17, 10864–10870 CrossRef CAS.
- D. Barreca, G. Carraro, A. Devi, E. Fois, A. Gasparotto, R. Seraglia, C. Maccato, C. Sada, G. Tabacchi, E. Tondello, A. Venzo and M. Winter, Dalton Trans., 2012, 41, 149–155 RSC.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- E. Fois, A. Gamba, G. Tabacchi, S. Quartieri and G. Vezzalini, J. Phys. Chem. B, 2001, 105, 3012–3016 CrossRef CAS.
- E. Fois, A. Gamba, G. Tabacchi, S. Quartieri and G. Vezzalini, Phys. Chem. Chem. Phys., 2001, 3, 4158–4163 RSC.
- E. Fois, A. Gamba, G. Tabacchi, R. Arletti, S. Quartieri and G. Vezzalini, Am. Mineral., 2005, 90, 28–35 Search PubMed.
- E. Spano', G. Tabacchi, A. Gamba and E. Fois, J. Phys. Chem. B, 2006, 110, 21651–21661 CrossRef CAS.
- G. Tabacchi, E. Gianotti, E. Fois, G. Martra, L. Marchese, S. Coluccia and A. Gamba, J. Phys. Chem. C, 2007, 111, 4946–4955 CrossRef CAS.
- A. Gamba, G. Tabacchi and E. Fois, J. Phys. Chem. A, 2009, 113, 15006–15015 CrossRef CAS.
- A. Tilocca and E. Fois, J. Phys. Chem. C, 2009, 113, 8683–8687 CrossRef CAS.
- E. Fois, G. Tabacchi, D. Barreca, A. Gasparotto and E. Tondello, Angew. Chem., Int. Ed., 2010, 49, 1944–1948 CAS.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS.
- J. Marx and D. Hutter, Ab Initio Molecular Dynamics, Cambridge University Press, 2009 Search PubMed.
- CPMD code, MPI fur Festkorperforschung: Stuttgart, Germany; IBM Zurich Research Laboratory: Zurich, Switzerland, www.cpmd.org, 1990–2012.
- M. E. Casida and T. A. Wesolowski, Int. J. Quantum Chem., 2004, 96, 577–588 CrossRef CAS.
- C. R. Jacob, J. Neugebauer and L. Visscher, J. Comput. Chem., 2008, 29, 1011 CrossRef CAS.
- J. Neugebauer, C. R. Jacob, T. A. Wesolowski and E. J. Baerends, J. Phys. Chem. A, 2005, 109, 7805–7814 CrossRef CAS.
- ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
- J. Neugebauer, J. Chem. Phys., 2009, 131, 084104-1–084104-12 Search PubMed.
- O. Gritsenko, P. Schipper and E. Baerends, Chem. Phys. Lett., 1999, 302, 199–207 CrossRef CAS.
- P. R. T. Schipper, O. V. Gritsenko, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2000, 112, 1344–1352 CrossRef CAS.
- L. Bernasconi, J. Chem. Phys., 2010, 132, 184513 Search PubMed.
- T. A. Wesolowski and J. Weber, Chem. Phys. Lett., 1996, 248, 71–76 CrossRef CAS.
- J. M. G. Lastra, J. W. Kaminski and T. A. Wesolowski, J. Chem. Phys., 2008, 129, 074107-1–074107-15 Search PubMed.
- J. Neugebauer, M. J. Louwerse, E. J. Baerends and T. A. Wesolowski, J. Chem. Phys., 2005, 122, 094115-1–094115-13 Search PubMed.
- N. A. Besley, M. T. Oakley, A. J. Cowan and J. D. Hirst, J. Am. Chem. Soc., 2004, 126, 13502–13511 CrossRef CAS.
- L. Goerigk and S. Grimme, J. Chem. Phys., 2010, 132, 184103-1–184103-9 Search PubMed.
- D. P. Chong and Y. Takahata, Chem. Phys. Lett., 2006, 418, 286–291 Search PubMed.
- M. E. Casida, in Time-dependent density-functional response theory for molecules, ed. D. P. Chong, World Scientific, Singapore, 1995, p. 155 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp42750h |
| This journal is © the Owner Societies 2013 |