Does the real ReN₂ have the MoS₂ structure?

Abstract

Rhenium nitride (ReN₂) with the hexagonal MoS₂ structure was recently synthesized by metathesis reaction under high pressure. Here the calculated elastic and thermodynamic stabilities and chemical bonding show that the MoS₂ phase is unstable based on first-principles calculations. Meanwhile, the MoS₂-type ReN₂ compound may be stabilized by nitrogen-vacancies from X-ray diffraction and supercell calculations. Structure searches identify a monoclinic C2/m phase for ReN₂, which is energetically more stable than previous predictions and MoS₂ structure over a wide range of pressures. Above 130 GPa, a tetragonal P4/mbm phase becomes favorable from enthalpy calculations. Both phases have superior mechanical properties, and their syntheses would have important applications fundamentally and technologically.

---

Introduction

Binary transition metal (TM) nitrides have received increasing interest due to their fascinating properties, such as high thermal and chemical stability, electrical or thermal conductivity, catalytic activity, and superior hardness.^1–5 Most of the early TM nitrides (N : TM = 1) belong to the NaCl structure and can be synthesized at ambient conditions, but N-rich nitrides (N : TM > 1) are quite difficult to obtain due to the requirement of a relatively higher nitrogen pressure during synthesis.⁶ Taking advantage of high-pressure techniques, bulk M₃N₄ (M = Zr, Hf) with high elastic moduli and hardness has been obtained, opening new avenues for the synthesis of other TM nitrides.⁷ In 2004, the successful synthesis of platinum nitride (PtN₂), which could be used as an alternative to ruby in high pressure experiments due to its structural stability at extremes, stimulated considerable research enthusiasm for 5d TM nitrides.⁸ Subsequently, osmium and iridium nitrides (OsN₂ and IrN₂) were synthesized.^9,10 These nitrides exhibit intriguing electronic properties and remarkable bulk moduli (B), rendering them as potential hard materials. Recently, Re₃N, and Re₂N were produced under high pressure high temperature (HPHT) conditions.¹¹ Their bulk moduli (395 GPa for Re₃N, 401 GPa for Re₂N) are comparable to diamond, making them excellent ultra-incompressible materials, but no experimental evidence supports the existence of other nitrides (e.g. ReN₂). Very recently, ReN₂ was synthesized by metathesis reaction under high pressure.¹² The recovered product at ambient pressure was determined by X-ray Diffraction (XRD) to be ReN₂ with the MoS₂ structure (space group: P6₃/mmc, denoted as m-ReN₂). The obtained B of this m-ReN₂, 173 GPa, is much lower than that of ReB₂ (360 GPa) although both structures are so similar to each other. Such a low B value is unusual since the relatively strong covalent bonding between rhenium and nitrogen atoms may enhance the resistance against uniform compression. To address this issue, via first-principles calculations, in this paper we systematically investigated the elastic and thermodynamic stabilities, XRD spectra, and chemical bonding of m-ReN₂. The results show that m-ReN₂ is unstable. Moreover, calculated XRD and density of states (DOS) hint at the presence of nitrogen-vacancies in m-ReN₂. Further structural searching identifies a possible ground state structure and a high-pressure phase for ReN₂. Both phases are found to exhibit excellent mechanical properties. The present results could provide a theoretical guidance for the experimental structural redetermination and characterizations of the physical properties of ReN₂ for potential technological applications.

Computational method

The structural search for ReN₂ is performed using CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) code¹³ based on a global minimization of free energy surfaces merging ab initio total-energy calculations via PSO technique. The simulation cells for ReN₂ are examined at 0 and 50 GPa, within four formula cells (f.u.). Furthermore, the experimentally obtained MoS₂-type structure and competing phases based on neighboring and similar compounds, such as OsN₂, IrN₂, ReB₂, WP₂ and ReP₂, together with previous predictions for ReN₂ and WN₂ are considered by comparison of their relative stabilities.^9,10,14–20

The obtained candidates for ReN₂ phase are fully optimized within the framework of density functional theory (DFT) as implemented by the CASTEP package.²¹ The exchange and correlation functional was treated by the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE).²² A 10 × 10 × 10 k-point and cutoff energy of 400 eV were adopted to guarantee high accuracy for both total energy and physical properties calculations. The heat of formation (ΔH_f) for candidate ReN₂ phases was calculated by the equation of ΔH_f = E_total(ReN₂) – (E_total(Re) + 2E_total(N)), in which hexagonal Re and a-N₂ were adopted for the calculations. Previously synthesized marcasite OsN₂, arsenopyrite IrN₂, Re₂N, and Re₃N were also calculated for comparison. Crystal orbital Hamilton populations (COHP) for present nitrides were calculated by the tight-binding linear-muffin-tin orbital calculations with the atomic sphere approximation (TB-LMTO-ASA).²³

Results and discussion

The calculated equilibrium lattice parameters for m-ReN₂, together with previous experimental results obtained for OsN₂, IrN₂, Re₂N, and Re₃N, are presented in Table 1. It can be observed that the lattice parameters are reasonably well reproduced for OsN₂, IrN₂, Re₂N, and Re₃N within a maximum error of 1.1%.^11,24–28 While for m-ReN₂, relatively larger deviations from the experimental lattice parameters are found in both a and c directions (2.1% and 6.2%, respectively).¹² Meanwhile, the obtained N–N distance (2.416 Å) in m-ReN₂ is much greater than that of the neighboring nitrides (1.438 Å in OsN₂ and 1.422 Å in IrN₂). Moreover, from calculated elastic constants (C_ij), m-ReN₂, either unrelaxed or relaxed, is found to be mechanically unstable due to the negative C₄₄ value (−15 and −34 GPa, respectively) according to the Born–Huang criterion for hexagonal structure.²⁹ This conflicting fact between the current calculations and experimental results motivated us to explore its reason and search for a possible ground state structure for ReN₂.

Table 1 Calculated equilibrium lattice parameters, a (Å), b (Å), and c (Å), for m-ReN₂, OsN₂, IrN₂, Re₂N, and Re₃N, with available results for comparison

		a	b	c
a Ref. 12. b Ref. 24. c Ref. 25. d Ref. 26. e Ref. 27. f Ref. 11. g Ref. 28.
m-ReN2	GGA	2.866		10.076
	Exp^a	2.806		10.747
OsN2	GGA	2.694	4.940	4.140
	GGA^b	2.682	4.915	4.121
	GGA^c	2.70	4.93	4.13
IrN2	GGA	4.903	4.982	4.972
	GGA^d	4.884	4.939	4.846
	GGA^e	4.876	4.926	4.917
Re2N	GGA	2.854		9.854
	Exp^f	2.83		9.88
	GGA^g	2.837		9.799
Re3N	GGA	2.807		7.167
	Exp^f	2.78		7.15
	GGA^g	2.8065		7.112

---

We started the exploration firstly by investigating the effect of nitrogen (N) vacancy on the structural stability of m-ReN₂. The XRD spectra of stoichiometric and substoichiometric m-ReN₂ are simulated and compared with the obtained pattern in experiment (Fig. 1). Unexpectedly, the obtained diffraction peaks of N-deficient m-ReN₂ (ReN_1.75 (Re₈N₁₄)) match well with the experimental XRD. This substoichiometry might account for its structural instability. Meanwhile, the DOS of this m-ReN₂ is calculated to further explore its stability. Other types of impurities or defects, such as oxygen and platinum from capsule material, are also included. The calculated DOS for N-deficient Re₈N₁₅ (ReN_1.875), Re₈N₁₄ (ReN_1.75), oxygen-doped Re₈N₁₅O (ReN_2−xO_x, x = 0.125), and platinum-doped Re₇PtN₁₆ (Re_1−xPt_xN₂, x = 0.125) are plotted in Fig. 2 based on supercell calculations. All these phases exhibit metallic character because of the nonzero value at the Fermi level (E_F). Additionally, the values at Fermi level (N(E_F), eV state⁻¹ atom⁻¹) follow a sequence: Re₈N₁₄ (0.424) < Re₈N₁₅ (0.5076) < Re₇PtN₁₆ (0.5834) < Re₈N₁₅O (0.7755) < ReN₂ (0.8249). Considering the general correlation between stability and the value at the Fermi level in the same metallic system, the presence of vacancies and impurities tend to stabilize the m-ReN₂. Specifically, N-deficient m-ReN₂ is most stable because of its lowest N(E_F) value. Thus, the observed MoS₂-structured ReN₂ in the previous experiment could be stabilized by the presence of nitrogen vacancies.

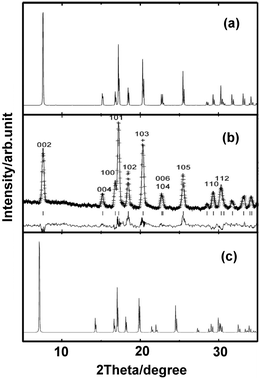Fig. 1 Simulated XRD curves for (a) ReN_1.75 (Re₈N₁₄), (b) experimental result reproduced from ref. 7, and (c) m-ReN₂.

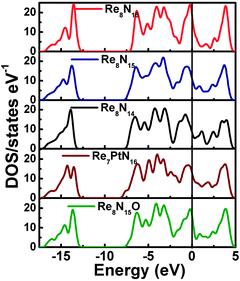Fig. 2 Calculated total density of states (DOS) for m-ReN₂ (Re₈N₁₆), N-deficient ReN_1.875 (Re₈N₁₅) and ReN_1.75 (Re₈N₁₄), platinum-doped Re_1−xPt_xN₂ (x = 0.125, Re₇PtN₁₆), and oxygen-doped ReN_2−xO_x (x = 0.125, Re₈N₁₅O).

We now turn our attention to explore the real structure for ReN₂. ΔH_f calculations (Fig. 3) uncover a monoclinic structure with space group C2/m for ReN₂ (C-ReN₂), whose total energy is lower than m-ReN₂ and other considered structures. Moreover, the positive ΔH_f value suggests that m-ReN₂ is thermodynamically instable towards dissociation into its constituent elements, although it may be stabilized kinetically. Also, the possibilities of P4₂/mnm¹⁷ and Pbcn¹⁸ phases as the ground state structure are rigorously ruled out in this study. In contrast to m-ReN₂, C-ReN₂ phase is found to be thermodynamically stable with a negative ΔH_f value, −0.148 eV per atom, close to previously obtained experimental values for Re₃N (−0.223 eV per atom) and Re₂N (−0.073 eV per atom),¹¹ indicating that this nitride could be obtained at moderate pressure. In C-ReN₂ phase, shown in Fig. 4, the Re atom is surrounded by seven nearest-neighbor nitrogen atoms with a distorted mono-capped-trigonal-prismatic geometry, different from the six-fold coordination of OsN₂ and IrN₂ that are composed of MN₆ polyhedra. Two types of nitrogen exist: one type forms an N₂ dimer located at the center of a trigonal-prism of six Re atoms, similar to OsN₂ and IrN₂;^25,26 the other type forming zigzag chains with Re atoms sitting at the center of a distorted tetrahedron formed by one N and three Re atoms. Furthermore, four denser phases, P4/mbm-, P4/mmm-, Cmc2₁-, and P2₁-type structures, are identified as potential high-pressure phases for C-ReN₂. The calculated enthalpy–pressure curve with respect to C-ReN₂ phase is given in Fig. 5. The C2/m phase is stable up to 130.2 GPa, and then transforms into the P4/mbm structure (P-ReN₂). The P4/mmm-type structure suggested in an earlier study¹⁹ was found to be unfavorable over a wide range of pressures. Also, P-ReN₂ is favored over Re + N₂, 1/3Re₃N + 5/6N₂, and 1/2Re₂N + 3/4N₂ above 11.5, 17.5, and 19.0 GPa, respectively, which may provide information for the synthesis of this high-pressure phase of ReN₂.

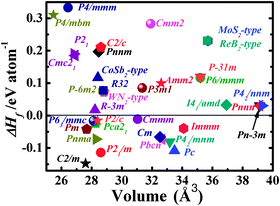Fig. 3 The calculated heat of formation (ΔH_f) and equilibrium volumes for searched ReN₂ phases (Detailed crystal information of the searched phases could be found in the ESI†).

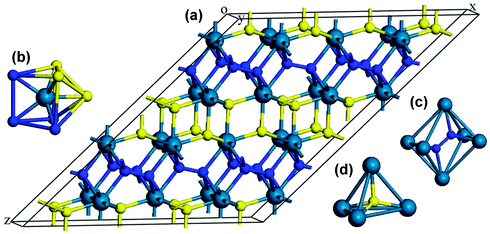Fig. 4 Crystal structure of C-ReN₂: 3D view (a), coordinative environment of Re atom (b) and two kinds of N atom ((c) and (d)). The predicted C-ReN₂ adopts a C2/m symmetry (No. 12), where Re atoms occupy the 4i (0.406, 0.5, 0.231), N atoms occupy 4i (0.009, 0.5, 0.136) and 4i (0.432, 0, 0.530) positions. The structural parameters are optimized to be a = 6.817 Å, b = 2.835 Å, c = 9.363 Å, and β = 142, 40°.

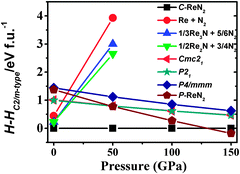Fig. 5 Calculated enthalpy differences of possible constituents (Re + N₂, 1/3Re₃N + 5/6N₂, and 1/2Re₂N + 3/4N₂) and four possible high-pressure phases (Cmc2₁-, P2₁-, P4/mmm-type, and P-ReN₂) with respect to C-ReN₂ phases as a function of pressure at zero temperature. The P-ReN₂ is predicted with a P4/mbm symmetry (No. 127), where Re atoms occupy 2b (0, 0, 0.5), N atoms occupy 4g (0.617, 0.117, 0) positions. The optimized structural parameters are a = 4.390 Å and c = 2.644 Å.

On the basis of C_ij calculations summarized in Table 2, we can check the local stability for C-ReN₂ and P-ReN₂. C-ReN₂ and P-ReN₂ exhibit not only mechanical stability, but also greater bulk moduli, against the experimentally obtained m-ReN₂. The obtained bulk modulus (B) of C-ReN₂ (369 GPa), is slightly greater than those of OsN₂ (353 GPa) and IrN₂ (333 GPa), but smaller than those of Re-rich nitrides (Re₂N (396 GPa) and Re₃N (392 GPa)). However, the shear moduli (G) of C-ReN₂ and Re-rich nitrides are quite close to each other. P-ReN₂ exhibits a quite high G (297 GPa), greater than OsN₂ (222 GPa) and IrN₂ (205 GPa) by 33.8% and 44.9%, respectively. In view of the greater B and G of P-ReN₂ (and C-ReN₂), ReN₂ could be a hard material for industrial coating applications. Furthermore, P-ReN₂ possesses a remarkable C₃₃, 967 GPa, comparable to diamond (1079 GPa),³⁰ revealing the extremely high stiffness along the c-direction. Moreover, the elastic anisotropy, highly correlated with the possibility of the appearance of microcracks and thus significantly affecting the application of a material, is also evaluated based on the universal elastic anisotropy index of A^U = 5G^V/G^R + B^V/B^R − 6,³¹ where B and G denote the bulk and shear moduli, and the superscripts V and R represent the Voight and Reuss approximations. The calculations demonstrate that the two predicted ReN₂ phases, especially for P-ReN₂, have superior elastic isotropic character as indicated by their smaller A^U values in comparison with neighboring OsN₂ and IrN₂.³¹

Table 2 Calculated single crystal elastic constants C_ij (GPa), bulk modulus B (GPa), shear modulus G (GPa), and universal elastic anisotropy (A^U) for m-ReN₂, OsN₂, IrN₂, Re₂N, and Re₃N

	C 11	C 22	C 33	C 44	C 55	C 66	C 12	C 13	C 23	B	G	A ^U
m-ReN2	530		9	−34			180	15		87
C-ReN2	843	546	652	201	252	210	209	211	256	369	217	0.333
P-ReN2	820		967	258		252	165	111		374	297	0.183
OsN2	772	869	821	167	167	153	72	140	146	353	222	0.770
IrN2	704	791	754	163	174	141	101	158	118	333	205	0.774
Re2N	660		813	182			207	261		396	210	0.101
Re3N	656		791	194			227	247		392	212	0.055

---

To further understand the underlying origin of the stability, mechanical properties and chemical bonding, DOS of the ‘isolated’ Re metal and ‘isolated’ N of different positions in the C-ReN₂-type structure, and C-ReN₂ were calculated as shown in Fig. 6. From Fig. 6(a), a striking feature of DOS is the totally different contributions of different isolated N and Re atoms, the N atom in the N₂ dimer (N1) opens a significant gap, whereas the N atom in zigzag Re–N chain (N2) and Re atom strongly localize at the Fermi level. But in real C-ReN₂, the presence of direct Re–N and N–N interactions in different coordination environments leads to a profound modification of the electronic structure (Fig. 6(b)). A tremendous shift of both Re and N orbitals to lower energy is discovered due to the orbital mixing. Around −15 eV, the lowest states in energy are dominated by N-2s states. Below the Fermi level, the states are mainly composed of the strong orbital mixing between Re-5d and N-2p states. Assuming the presence of N₂⁴⁻ in ReN_2,³² Re atom (oxidation state +4) with surplus three d-electrons would locate in the distorted trigonal-prismatic environment. According to crystal field theory, these three d-electrons may split into the fully occupied d_z²-orbital at lower energy and be partially occupied with d_x²−y² and d_xy orbitals at higher energy, and thus ReN₂ is metallic, as expected, consistent with the absence of an energy gap at the Fermi level in the DOS spectrum. Also, this bonding–antibonding splitting further increases the hybridization between Re-5d and N-2p states (Fig. 6(b)) to stabilize the distorted trigonal-prismatic arrangement in C-ReN₂. As evidenced by crystal orbital Hamilton populations (COHP) (Fig. 7(a)), a substantial Re–N bonding interaction is observed between −10 and −1.35 eV, and the antibonding state of the Re–N interaction appears from −1.35 eV to the Fermi level. Also, a covalent N–N bonding from the N₂ dimer in C-ReN₂ is also reflected by COHP. The presence of both Re–N and N–N interactions plays an important role in the exceptional mechanical properties of C-ReN₂. With the increase in valence electrons, from Re to Ir, the bonding states of metal and nitrogen gradually filled in the entire occupied region (Fig. 7(b) and (c)), which suggests the increasing stability. But N–N antibonding states start to increase from ReN₂ (0.80 eV per bond) to OsN₂ (0.87 eV per bond) to IrN₂ (0.92 eV per bond), making a negative contribution to B.³² However, for the obtained m-ReN₂ by experiment, the N–N antibonding interaction (Fig. 7(d)) is much stronger than the bonding interaction (from integral areas), this negligible N–N interaction in m-ReN₂ also supports the aforementioned instability.

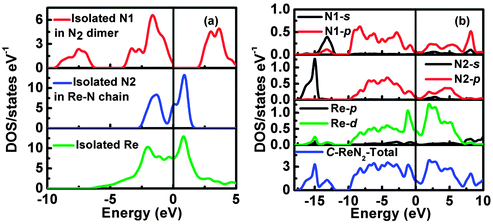Fig. 6 Calculated density of states (DOS) of the isolated Rhenium atom and Nirogen atom in different positions in C-ReN₂ (a), total and partial DOS of C-ReN₂ (b).

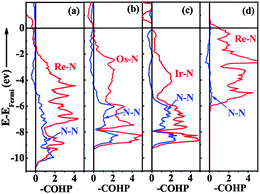Fig. 7 Crystal orbital Hamilton Populations (COHP, eV cell⁻¹) of Re–N and N–N interactions in C-ReN₂ (a), OsN₂ (b), IrN₂ (c), and m-ReN₂ (d) with the integrated N–N antibonding areas of 0.80, 0.87, 0.92, and 0.39 eV, respectively.

Conclusion

From first-principles calculations, we found MoS₂-structured ReN₂ is unstable as indicated by the negative C₄₄ value and positive heat of formation. Calculated XRD and DOS suggest that nitrogen vacancies may stabilize the MoS₂-type ReN₂. Furthermore, the structural searching based on CALYPSO code uncovers that a monoclinic C2/m phase for ReN₂ is more energetically stable than previous predictions and the experimental MoS₂ structure. Also, the C2/m phase will transform to a tetragonal P4/mbm phase above 130 GPa. Furthermore, both monoclinic and tetragonal ReN₂ have high bulk moduli and shear moduli, and thus are potential hard materials. The analysis of chemical bonding shows that the combined covalency from N₂ dimer and Re–N bonds results in the superior mechanical properties of ReN₂. Thus, further synthesis is urgent to understand this nitride.

References

1. L. E. Toth, Transitional Metal Carbides and Nitrides, Academic Press, New York, 1971.
2. S. T. Oyama, J. Solid State Chem., 1992, 96, 442.
3. S. T. Oyama, Catal. Today, 1992, 15, 179.
4. F. Lévy, P. Hones, P. E. Schmid, R. Sanjinés, M. Diserens and C. Wiemer, Surf. Coat. Technol., 1999, 120, 284.
5. A. L. Ivanovskii, Russ. Chem. Rev., 2009, 78, 303.
6. A. Friedrich, B. Winkler, E. A. Juarez-Arellano and L. Bayarjargal, Materials, 2011, 4, 1648.
7. A. Zerr, G. Miehe and R. Riedel, Nat. Mater., 2003, 2, 185.
8. E. Gregoryanz, C. Sanloup, M. Somayazulu, J. Badro, G. Fiquet, H. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 294.
9. A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. H. Hemley and H. K. Mao, Phys. Rev. Lett., 2006, 96, 155501.
10. J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275.
11. A. Friedrich, B. Winkler, L. Bayarjargal, W. Morgenroth, E. A. Juarez-Arellano, V. Milman, K. Refson, M. Kunz and K. Chen, Phys. Rev. Lett., 2010, 105, 085504.
12. F. Kawamura, H. Yusa and T. Taniguchi, Appl. Phys. Lett., 2012, 100, 251910.
13. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
14. H. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436.
15. F. Hulliger, Nature, 1964, 204, 775.
16. R. Rűhl and W. Jeitschko, Inorg. Chem., 1982, 21, 1886.
17. E. Zhao and Z. Wu, Comput. Mater. Sci., 2008, 44, 531.
18. Y. Li and Z. Zeng, Chem. Phys. Lett., 2009, 474, 93.
19. X. Du, Y. Wang and V. Lo, Phys. Lett. A, 2010, 374, 2569.
20. H. Wang, Q. Li, Y. Li, Y. Xu, T. Cui, A. R. Oganov and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 132109.
21. M. D. Segall, P. L. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
22. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. R. Dronskowski and P. E. Blőchl, J. Phys. Chem., 1993, 97, 8617.
24. Z. Chen, X. Guo, Z. Liu, M. Ma, Q. Jing, G. Li, X. Zhang, L. X. Li, Q. Wang, Y. Tian and R. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054103.
25. J. A. Montoya, A. D. Hernandez, C. Sanloup, E. Gregoryanz and S. Scandolo, Appl. Phys. Lett., 2007, 90, 011909.
26. Y. Wang, M. Arai, T. Sasaki and C. Fan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104110.
27. Z. Wu, E. Zhao, H. Xiang, X. Hao, X. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
28. R. Zhang, Z. Lin, H. Mao and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 060101.
29. M. Born and K. Huang, Dynamical Theory of Crystal Lattice, Oxford University Press, Oxford, 1954.
30. H. T. Mcskimin and P. Andreatch, J. Appl. Phys., 1972, 43, 985.
31. M. Segall, R. Shah, C. Pickard and M. Payne, Phys. Rev. B: Condens. Matter, 1996, 54, 16317.
32. W. Michael and R. Dronskowski, J. Am. Chem. Soc., 2010, 132, 2421.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cp43010j

---