 Open Access Article
Open Access ArticleComparing molecular photofragmentation dynamics in the gas and liquid phases†
Stephanie J.
Harris
a,
Daniel
Murdock
a,
Yuyuan
Zhang‡
b,
Thomas A. A.
Oliver§
a,
Michael P.
Grubb
a,
Andrew J.
Orr-Ewing
a,
Gregory M.
Greetham
c,
Ian P.
Clark
c,
Michael
Towrie
c,
Stephen E.
Bradforth
b and
Michael N. R.
Ashfold
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: mike.ashfold@bris.ac.uk
bDepartment of Chemistry, University of Southern California, Los Angeles, CA 90089, USA
cCentral Laser Facility, Research Complex at Harwell, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Didcot, Oxfordshire, OX11 0QX, UK
First published on 19th March 2013
Abstract
This article explores the extent to which insights gleaned from detailed studies of molecular photodissociations in the gas phase (i.e. under isolated molecule conditions) can inform our understanding of the corresponding photofragmentation processes in solution. Systems selected for comparison include a thiophenol (p-methylthiophenol), a thioanisole (p-methylthioanisole) and phenol, in vacuum and in cyclohexane solution. UV excitation in the gas phase results in RX–Y (X = O, S; Y = H, CH3) bond fission in all cases, but over timescales that vary by ∼4 orders of magnitude – all of which behaviours can be rationalised on the basis of the relevant bound and dissociative excited state potential energy surfaces (PESs) accessed by UV photoexcitation, and of the conical intersections that facilitate radiationless transfer between these PESs. Time-resolved UV pump-broadband UV/visible probe and/or UV pump-broadband IR probe studies of the corresponding systems in cyclohexane solution reveal additional processes that are unique to the condensed phase. Thus, for example, the data clearly reveal evidence of (i) vibrational relaxation of the photoexcited molecules prior to their dissociation and of the radical fragments formed upon X–Y bond fission, and (ii) geminate recombination of the RX and Y products (leading to reformation of the ground state parent and/or isomeric adducts). Nonetheless, the data also show that, in each case, the characteristics (and the timescale) of the initial bond fission process that occurs under isolated molecule conditions are barely changed by the presence of a weakly interacting solvent like cyclohexane. These condensed phase studies are then extended to an ether analogue of phenol (allyl phenyl ether), wherein UV photo-induced RO–allyl bond fission constitutes the first step of a photo-Claisen rearrangement.
Introduction
Photochemistry in solution is widely perceived to have been an essential element in the development of life on Earth, and most early scientific studies of molecular photochemistry were confined to the condensed phase.1–4 Illumination in these cases was continuous, incoherent and usually polychromatic, the progress of a reaction was typically monitored by detecting one or more of the stable end-products – through which the reaction ‘mechanism’ might be inferred; unravelling the detailed reaction dynamics necessarily remained the stuff of dreams.5 Technological advances in the latter half of the twentieth century – e.g. the availability and reliability of vacuum technology, of molecular beams and tuneable pulsed lasers, and in the power of computers and the theoretical progress that this encouraged – led to an explosion of interest in the study of molecular photofragmentation processes under collision-free conditions (i.e. at very low pressures, in the gas phase). Thus there now exists a huge database of detailed information relating to the primary photofragmentation of numerous (generally small) gas phase molecules, often as functions of excitation wavelength. Measured quantities typically include branching ratios into different sets of fragmentation products, or into different quantum (e.g. electronic, spin–orbit, vibrational, rotational, even the Λ-doublet) states of a given photoproduct, the velocity (speed and angular) distributions of these products, and subtle vector correlations between, for example, the velocity and rotational angular momentum vectors of a given product. Notwithstanding such spectacular experimental progress, and the equally impressive advances in the sophistication and accuracy of electronic structure theory, and in ways of calculating nuclear dynamics on (and between) the resulting potential energy surfaces (PESs), there remain numerous exciting challenges within the field of gas phase photodissociation (and in all areas of gas phase reaction dynamics). Obvious examples include extension to ever larger (and higher dimensionality) molecular systems (neutrals and charged species),6 to ever lower temperatures (ultracold chemistry),7 to ever shorter timescales (attochemistry)8,9 and to much higher high excitation energies (enabled by, for example, the emerging X-ray free electron laser systems).10,11Another area of fast-growing interest, and the focus of this perspective article, is the extent to which the exquisitely detailed dynamical insights gleaned from recent gas phase studies can inform our understanding of the dynamics of photo-induced reactions in solution. This is certainly not a new line of thought.12 Indeed, at first glance, it might not even appear to be a particularly fruitful approach. The solution environment is characterised by orders of magnitude higher densities and by extensive disorder.13 Solute–solvent interactions will inevitably introduce deactivation pathways for photofragments and excited molecules that are not available to their gas phase counterparts. Out-of-equilibrium rotational or translational energy distributions in the primary photoproducts are generally assumed to be thermalised by such interactions in a matter of picoseconds, though the much longer timescales deduced for the relaxation of the very highly rotationally excited CN fragments following UV photolysis of ICN in alcohols and water14 or predicted for the OH radicals from H2O2 photolysis in liquid argon15 should sound a cautionary note. The relaxation of non-equilibrium vibrational state population distributions has attracted much more attention, and is clearly system dependent. Intramolecular vibrational relaxation (IVR) mechanisms can be affected, as the constantly changing solvent environment induces fluctuations in the energy levels of the solute (and/or adds or removes small amounts of energy to/from the solute), thereby boosting IVR probabilities by bringing transitions that are non-resonant in the isolated molecule into resonance.13 Obviously, the presence of solvent also introduces opportunities for intermolecular energy flow, whereby energy in the excited solute species is transferred into individual modes of a solvent molecule or into low frequency modes of the entire solvent environment; this process is often termed intermolecular energy transfer (IET), also referred to as vibrational energy relaxation. Numerous studies have sought to explore the relative importance of IVR and IET in excited molecules in solution, and both processes are commonly encapsulated in the general term, vibrational energy transfer (VET).16,17
The timescales for VET are sensitively dependent on the mode of interest (isolated high frequency modes typically relax more slowly than low frequency vibrations) and on the strength of the solute–solvent interaction.16 In the case of strongly interacting systems (e.g. ions in a polar solvent), vibrational energy can be dissipated in less than a picosecond, whereas the analogous process in the case of a polyatomic species in a non-polar solvent may take hundreds of picoseconds. VET timescales can also be sensitively dependent on the extent of the initial vibrational excitation – a factor of particular relevance when considering the decay of photoexcited molecules. Consider, for example, the case of a photoexcited molecule that can fragment (to yield products with modest vibrational excitation) or undergo internal conversion (IC) to highly excited vibrational levels of the ground electronic state. The VET rate in the latter case will initially be much faster, on account of the higher density of states and small energy level separations, but will reduce as relaxation proceeds, the state density decreases and the inter-level energy spacings increase – leading to what is often viewed as a “bottleneck” for VET. Transfer out of these lowest few levels is generally recognised as the rate-limiting step in VET.18
Other processes can also arise. The adiabatic ionisation energy of a solute molecule is reduced in the presence of a polar solvent, enabling autoionisation at energies well below the (gas phase) ionisation potential.19–22 Recombination processes are even more common. Such processes are essentially non-existent in the gas phase (except at very high pressures) but are clearly pertinent to any discussion of photodissociation in the condensed phase.13 Recombination in the present context describes the encounter and subsequent reaction of two species, at least one of which is a product of the photodissociation. The re-encounter of two products from a single photodissociation event is termed geminate recombination. As shown in Fig. 1 and in the examples discussed later in this perspective article, the recombination product may differ from the original solute molecule. One can envisage at least two limiting classes of geminate recombination behaviour: caged recombination, occurring within the immediate solvation sphere formed by the solvent molecules that surround the molecule undergoing photodissociation, and a more convoluted process whereby the photo-products escape this cage, but re-encounter after a period of diffusional motion. Inevitably, most recombinations following photodissociation will involve a spectrum of such behaviours.23
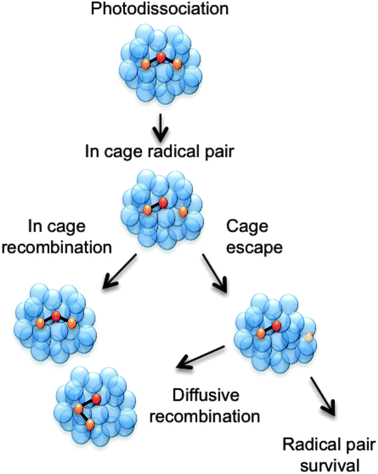 | ||
| Fig. 1 Cartoon showing three possible outcomes following a photodissociation event that produces a pair of radicals within a cage of solvent molecules. The pair can escape the solvent cage and persist separately in solution or diffusively recombine to form the starting molecule or an isomer. Alternatively, the radical pair could remain within the original solvent cage and recombine on a much faster timescale than that for diffusive recombination. | ||
The recent literature contains many studies of the UV photofragmentation of prototypical small molecules, e.g. I2,24–29 HgI2,30–37 I3−,19,38–42 ICN,11,43–47 ClNO,48–50 OClO,51–60 HOCl61,62 and CH3OCl,63 and haloalkanes like CF2I2,64–66 CH2I2,67–72 and CH2Br2,73,74 that seek more quantitative insights into VET and/or recombination mechanisms and, more generally, to explore the synergies and the obvious differences between molecular photofragmentations occurring in the gas and condensed phases.13,75 The present perspective article seeks to explore such issues by comparing and contrasting the UV photofragmentation behaviour of a limited family of molecules – phenols, thiophenols and selected ether/thioether analogues – in the gas phase and (at this time) in a limited range of weakly interacting solvents.
Gas phase photofragmentation dynamics – an overview
The potentials shown in Fig. 2 provide a good starting point for understanding the gas phase photochemistry of phenols, thiophenols, and of ethers and thioethers based on these aromatic chromophores. These displayed potentials are illustrative cuts along the S–H stretch coordinate (RS–H) through the multi-dimensional potential energy surfaces (PESs) for the ground and first two singlet excited states of a thiophenol, with all atoms constrained to lie in the ring plane. These provide a rationale for the UV absorption spectra of thiophenols. A π* ← π excitation, populating the 11ππ* state, provides the dominant absorption at long UV wavelengths, but this is progressively supplemented by contributions from a σ* ← π excitation (to the 11πσ* excited state) and then by a second (much stronger) π* ← π excitation (to the 21ππ* state, not shown in Fig. 2) as the excitation energy is increased. For compactness, it will prove convenient to label the 11ππ* and 11πσ* excited states S1 and S2, respectively.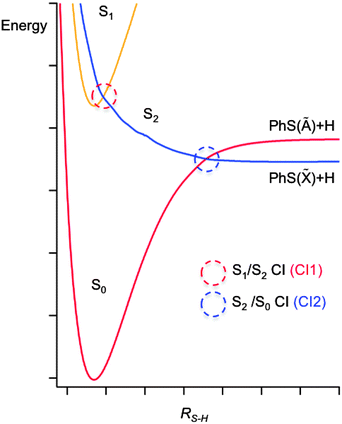 | ||
| Fig. 2 A cut through illustrative potential energy surfaces (along RS−H) for a thiophenol, with all atoms constrained to lie in the ring plane. | ||
These potential energy cuts (PECs) also illustrate two conical intersections (CIs), both of which can have a profound effect on the photofragmentation dynamics. CIs are regions of configuration space where two (or more) PESs are degenerate, and the non-adiabatic couplings between them consequently are greatest; CIs can provide a very efficient route for transfer of population between PESs.76 Thus the S2 state in thiophenol – population of which will result in S–H bond fission – can be accessed directly (by σ* ← π excitation) or indirectly, by photoexcitation to the S1 state and subsequent tunneling under CI1.77 Photofragment translational spectroscopy (PTS) studies of the UV photolysis of gas phase thiophenol and a range of substituted thiophenols show that the latter route is dominant at the very longest UV excitation wavelengths, but that direct photoexcitation to the S2 state becomes increasingly important as the excitation wavelength is reduced.77 The corresponding potentials for phenol are similar to those shown in Fig. 2,78 but the vertical energy separation between the S1 and S2 states in the vertical Franck Condon region is greater and the shape of the potentials different due to increased valence–Rydberg interactions. Thus the energy barrier under CI1 is much larger, but not sufficient to preclude some O–H bond fission on much longer timescales, by tunneling through the barrier.78–81
Fig. 2 reveals another CI, CI2, between the S2 and ground (henceforth S0) state PESs at much longer RS–H. This arises because, upon S–H bond fission in the planar limit, the S0 state correlates with the first excited electronic (Ã) state of the radical product (the singly occupied molecular orbital (SOMO) in which is a pσ orbital on the S atom), while the S2 state correlates with the ground electronic (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) state of the radical (for which the SOMO is a pπ orbital extending across the ring and the C–S bond). Nuclear motion in the vicinity of CI2 determines the electronic branching between the
) state of the radical (for which the SOMO is a pπ orbital extending across the ring and the C–S bond). Nuclear motion in the vicinity of CI2 determines the electronic branching between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à states of the radical. Molecules dissociating on the S2 PES that approach CI2 with non-planar geometries (i.e. with the S–H bond pointing out of the ring-plane) will typically follow the adiabatic path to à state products, whereas molecules sampling CI2 at planar geometries will tend to follow the diabatic route to ground state products.82–84 The recent PTS studies of thiophenols reveal formation of
and à states of the radical. Molecules dissociating on the S2 PES that approach CI2 with non-planar geometries (i.e. with the S–H bond pointing out of the ring-plane) will typically follow the adiabatic path to à state products, whereas molecules sampling CI2 at planar geometries will tend to follow the diabatic route to ground state products.82–84 The recent PTS studies of thiophenols reveal formation of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à state radical products at all excitation wavelengths, but also show that the branching between these states is dependent both on excitation wavelength and the nature of the substituent (in the para-position).77 The PECs for thioanisole (along the RS–Me coordinate, at planar geometries) are very similar to those shown in Fig. 2. The dissociation timescales are much longer85 as the process requires the molecule to access classically forbidden regions of the excited state PES (by torsional motion of the S–Me group out of the plane of the phenyl ring, where the barrier to dissociation is lower.) Nonetheless, velocity map imaging studies confirm that para-substitution can have a major influence on the electronic branching in the (substituted) thiophenoxyl radicals resulting from S–Me bond fission; in the case of p-methylthioanisole, near UV photolysis yields predominantly à state radicals (i.e. an inverted electronic state population distribution in the p-methylthiophenoxyl products).86,87 The energy separation between the
and à state radical products at all excitation wavelengths, but also show that the branching between these states is dependent both on excitation wavelength and the nature of the substituent (in the para-position).77 The PECs for thioanisole (along the RS–Me coordinate, at planar geometries) are very similar to those shown in Fig. 2. The dissociation timescales are much longer85 as the process requires the molecule to access classically forbidden regions of the excited state PES (by torsional motion of the S–Me group out of the plane of the phenyl ring, where the barrier to dissociation is lower.) Nonetheless, velocity map imaging studies confirm that para-substitution can have a major influence on the electronic branching in the (substituted) thiophenoxyl radicals resulting from S–Me bond fission; in the case of p-methylthioanisole, near UV photolysis yields predominantly à state radicals (i.e. an inverted electronic state population distribution in the p-methylthiophenoxyl products).86,87 The energy separation between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à states of the phenoxyl radical is much greater (ΔE PhO(à −
and à states of the phenoxyl radical is much greater (ΔE PhO(à − ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) = 7900 cm−1
) = 7900 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 88) cf. ΔE PhS(Ã −
(ref. 88) cf. ΔE PhS(Ã − ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) = 3000 cm−1
) = 3000 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 89)), and all studies to date (of phenol, and a range of substituted phenols) suggest that O–H bond fission (by tunneling through the barrier under the S1/S2 CI) results in dominant and, in most cases, exclusive formation of the
(ref. 89)), and all studies to date (of phenol, and a range of substituted phenols) suggest that O–H bond fission (by tunneling through the barrier under the S1/S2 CI) results in dominant and, in most cases, exclusive formation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state radicals.
state radicals.
UV photodissociation of thiophenols and thioanisoles in solution
We here focus here on recent studies of the UV photodissociation of p-methylthiophenol (p-MePhSH) and p-methylthioanisole (p-MePhSMe) using time-resolved ultrafast UV pump – and broadband UV/visible and infrared probe spectroscopy methods.21,90 For clarity, these are henceforth termed transient electronic absorption (TEA) and transient vibrational absorption (TVA) studies, though we (and others) have previously referred to these methods as TA and TRIR respectively. The sample concentrations (and thickness when experiments were carried out in a Harrick flow cell) in all cases were chosen so that the absorbance at 267 nm was 0.5 or less under the prevailing experimental conditions.
Fig. 3(a) shows representative TEA data following 267 nm photolysis of p-MePhSH in cyclohexane which is generally viewed as a weakly interacting solvent. An absorption feature centered at ∼480 nm, attributable to formation of p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals,91–93 is evident within the overall instrument response time (∼100 fs). This observation is indicative of prompt S–H bond fission, and is consistent with the reported gas phase photochemistry following population of the S2 state at this same wavelength.77 This TEA feature becomes narrower in data taken at later pump–probe time delays (Δt), reflecting the vibrational cooling of these photofragments through interaction with the solvent. The same radical absorption feature is evident in TEA data from 267 nm photolysis of p-MePhSH in ethanol but, at any given Δt, is notably less well resolved – reflecting the greater solute–solvent interaction, and thus inhomogeneous broadening, in a more polar solvent.93
) radicals,91–93 is evident within the overall instrument response time (∼100 fs). This observation is indicative of prompt S–H bond fission, and is consistent with the reported gas phase photochemistry following population of the S2 state at this same wavelength.77 This TEA feature becomes narrower in data taken at later pump–probe time delays (Δt), reflecting the vibrational cooling of these photofragments through interaction with the solvent. The same radical absorption feature is evident in TEA data from 267 nm photolysis of p-MePhSH in ethanol but, at any given Δt, is notably less well resolved – reflecting the greater solute–solvent interaction, and thus inhomogeneous broadening, in a more polar solvent.93
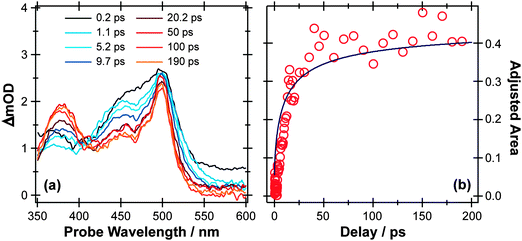 | ||
| Fig. 3 (a) TEA spectra measured at different Δt following 267 nm photoexcitation of a 90 mM solution of p-MePhSH in cyclohexane flowing through a wire guided liquid jet. (b) Numerical integration over the 360–390 nm region of these spectra allows extraction of a kinetic trace (open circles) for the formation of a MePh(H)S adduct. The solid blue line is a fit of the data using the survival probability model described in the text, eqn (1) and (2). | ||
267 nm photolysis of gas phase p-MePhSH yields both ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à state p-MePhS radical products with ∼40% of the radicals in the latter electronic state.77 This same photolysis in ethanol solution has recently been studied using TEA methods with sufficient time resolution to allow insight into the nascent
and à state p-MePhS radical products with ∼40% of the radicals in the latter electronic state.77 This same photolysis in ethanol solution has recently been studied using TEA methods with sufficient time resolution to allow insight into the nascent ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) /à state product branching ratio. These data show an additional absorption attributable to formation of MePhS(Ã) products93 at very short Δt, which is quenched in <200 fs (presumably via a frustrated dissociation and re-crossing through CI2). The influence of solvent on passage through regions of conical intersection between PESs94 for this reaction will be described in a future paper,95 but we will return briefly to the issue of the branching ratio later in this article.
/Ã state product branching ratio. These data show an additional absorption attributable to formation of MePhS(Ã) products93 at very short Δt, which is quenched in <200 fs (presumably via a frustrated dissociation and re-crossing through CI2). The influence of solvent on passage through regions of conical intersection between PESs94 for this reaction will be described in a future paper,95 but we will return briefly to the issue of the branching ratio later in this article.
Two further features in Fig. 3(a) are of note. The TEA spectra taken at short Δt reveal a fast decaying background absorption (most evident at long wavelengths). This is attributable to the formation (and subsequent rapid decay) of p-MePhSH(S1) molecules based on high-level calculations;96 as shown below, the corresponding parent excited state absorption (ESA) is much easier to observe in the thioanisole. The second feature of note is centered at ∼380 nm, and develops over a much longer timescale. This feature grows (Fig. 3(b)) with the same time constant as that for the decay of p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals. We conclude that the 380 nm feature is associated with an adduct formed via geminate recombination, similar to that proposed in pulsed radiolysis studies of PhSH in acidified aqueous solution.92 The p-MePhSH parent does not absorb at 380 nm but high-level electronic structure calculations suggest the sulfur analogue of 2,4- (or 2,5-) cyclohexadienone (i.e. structures formed by the returning H atom combining with the ring) as the most likely carrier for this absorption.95 These data highlight a limitation of many TEA studies; the available white light probe continuum does not extend to short enough wavelengths to allow simultaneous monitoring of the parent bleach signal (i.e. the instantaneous loss and gradual recovery of the ground state parent molecule). That is only a part of the problem, however, since in many cases the ESA at the relevant UV probe wavelength often has a larger cross-section than the excitation from S0. The parent bleach signal is thus buried within the parent molecule ESA. As we see later, TVA measurements can suffer from similar overlaps, but the IR features are typically narrower and thus easier to resolve. Returning to Fig. 3(a), one can estimate that ∼70% of the radical products formed in the 267 nm photolysis of p-MePhSH in cyclohexane survive but, with regard to the ∼30% that are lost by geminate recombination, TEA measurements cannot give the relative probabilities of adduct formation vs. parent reformation unless the respective absorption cross-sections are known, which in this particular case they are not.96
) radicals. We conclude that the 380 nm feature is associated with an adduct formed via geminate recombination, similar to that proposed in pulsed radiolysis studies of PhSH in acidified aqueous solution.92 The p-MePhSH parent does not absorb at 380 nm but high-level electronic structure calculations suggest the sulfur analogue of 2,4- (or 2,5-) cyclohexadienone (i.e. structures formed by the returning H atom combining with the ring) as the most likely carrier for this absorption.95 These data highlight a limitation of many TEA studies; the available white light probe continuum does not extend to short enough wavelengths to allow simultaneous monitoring of the parent bleach signal (i.e. the instantaneous loss and gradual recovery of the ground state parent molecule). That is only a part of the problem, however, since in many cases the ESA at the relevant UV probe wavelength often has a larger cross-section than the excitation from S0. The parent bleach signal is thus buried within the parent molecule ESA. As we see later, TVA measurements can suffer from similar overlaps, but the IR features are typically narrower and thus easier to resolve. Returning to Fig. 3(a), one can estimate that ∼70% of the radical products formed in the 267 nm photolysis of p-MePhSH in cyclohexane survive but, with regard to the ∼30% that are lost by geminate recombination, TEA measurements cannot give the relative probabilities of adduct formation vs. parent reformation unless the respective absorption cross-sections are known, which in this particular case they are not.96
Fig. 4 illustrates the complementary use of broad bandwidth IR probe radiation to follow the same process, viz. the 267 nm photolysis of p-MePhSH in cyclohexane. Solvent absorptions are an obvious potential complication in TVA studies, and cyclohexane shows a strong absorption band at 1455 cm−1 which will mask any solute or photoproduct related features that happen to fall near that wavenumber. This difficulty can be alleviated by using a different solvent (e.g. CD3CN)97 but, as Fig. 4(a) shows, the 1475–1650 cm−1 region provides sufficient insights to allow us to unravel much of the prevailing photophysics in cyclohexane solution. Two transient features are immediately evident – a bleach signal at ∼1495 cm−1 and a transient absorption signal at ∼1570 cm−1. These can be attributed to UV pump laser induced depletion of the parent ground state population and formation of p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) photoproducts, respectively. The latter feature narrows, and its centre shifts to higher wavenumber, with increasing Δt – consistent with initial formation of internally excited radicals which relax with a time constant τvib ∼ 8.5 ps – i.e. on the same timescale as that for the radical absorption feature to ‘sharpen’ in the TEA spectrum. As in the TEA studies, the radical signal maximises within the effective time resolution of the experiment (<1 ps in the TVA study) but in the TVA studies it is possible to see that the decay kinetics of this signal at later Δt match those determined by monitoring the bleach recovery – again pointing to geminate recombination of the photo-produced radical pair. Fitting the time-evolving p-MePhSH and p-MePhS(
) photoproducts, respectively. The latter feature narrows, and its centre shifts to higher wavenumber, with increasing Δt – consistent with initial formation of internally excited radicals which relax with a time constant τvib ∼ 8.5 ps – i.e. on the same timescale as that for the radical absorption feature to ‘sharpen’ in the TEA spectrum. As in the TEA studies, the radical signal maximises within the effective time resolution of the experiment (<1 ps in the TVA study) but in the TVA studies it is possible to see that the decay kinetics of this signal at later Δt match those determined by monitoring the bleach recovery – again pointing to geminate recombination of the photo-produced radical pair. Fitting the time-evolving p-MePhSH and p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) absorption signals (Fig. 4(b) and (c), respectively) with the survival probability expression:
) absorption signals (Fig. 4(b) and (c), respectively) with the survival probability expression:
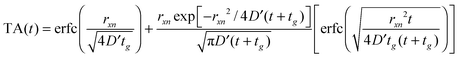 | (1) |
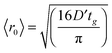 | (2) |
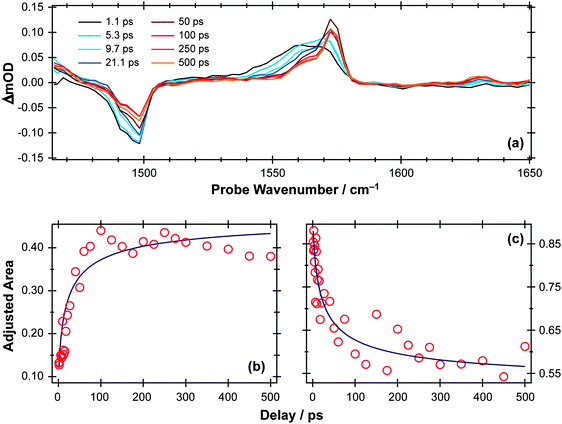 | ||
Fig. 4 (a) TVA spectra measured at different Δt following 267 nm photoexcitation of a 45 mM solution of p-MePhSH in cyclohexane flowing through a Harrick cell with a 100 μm spacer. Numerical integration over portions of the latter spectra allows extraction of kinetic traces (open circles) monitoring the (b) recovery of parent p-MePhSH(S0) population via the 1495 cm−1 feature and (c) decay of p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals (in the region 1535–1585 cm−1). The solid blue lines are fits to the data using the survival probability model described in the text, eqn (1) and (2). ) radicals (in the region 1535–1585 cm−1). The solid blue lines are fits to the data using the survival probability model described in the text, eqn (1) and (2). | ||
Fig. 5 and 6 show TEA and TVA data measured following 267 nm photolysis p-MePhSMe contained in a Harrick flow cell. The early time TEA spectra measured for p-MePhSMe in cyclohexane (Fig. 5(a)) are dominated by ESA, which contributes at all wavelengths and particularly in the red region of the spectrum. This signal decays slowly (cf. p-MePhSH) with a time constant τ ∼230 ps (Fig. 5(b)), during which time the characteristic p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radical absorption feature centered at ∼480 nm develops. TEA spectra recorded following 267 nm photolysis of p-MePhSMe in CH3CN evolve similarly, but the ESA signal decays even more slowly (with τ ∼500 ps). Extracting the radical kinetics from these data is complicated by the overlapping ESA signal, but the radical absorption is clearly contributing within a few ps.
) radical absorption feature centered at ∼480 nm develops. TEA spectra recorded following 267 nm photolysis of p-MePhSMe in CH3CN evolve similarly, but the ESA signal decays even more slowly (with τ ∼500 ps). Extracting the radical kinetics from these data is complicated by the overlapping ESA signal, but the radical absorption is clearly contributing within a few ps.
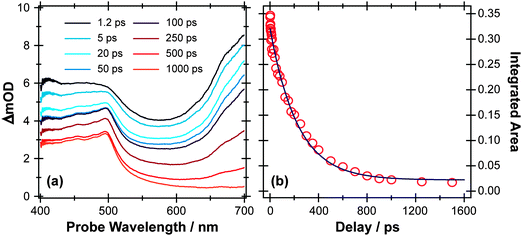 | ||
| Fig. 5 (a) TEA spectra measured at different Δt following 267 nm photoexcitation of a 45 mM solution of p-MePhSMe in cyclohexane flowing through a 100 μm Harrick cell. (b) Numerical integration between 650 and 700 nm allows monitoring of the time-dependent population of the p-MePhSMe(S1) state (open circles). The solid blue line is a least-squares fit of the kinetic data to a single exponential function. | ||
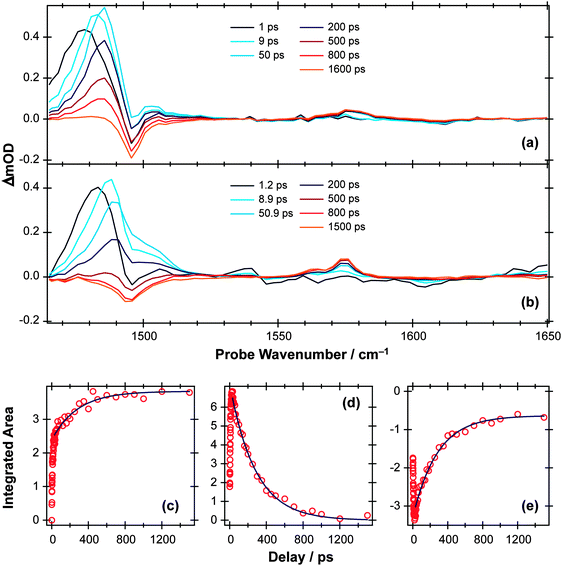 | ||
Fig. 6 TVA spectra measured at different Δt following 267 nm photoexcitation of a 11.25 mM solution of p-MePhSMe in (a) CD3CN and (b) cyclohexane flowing through 100 μm Harrick cells. (c) Time-dependent population of the p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radical photoproduct in cyclohexane obtained through numerical integration over the range 1570–1580 cm−1. Deconvolution of the 1465–1520 cm−1 region using Lorentzian functions enables extraction of kinetic traces for the (d) p-MePhSMe(S1; v = 0) and (e) p-MePhSMe(S0) populations. The solid blue lines are least squares fits of the long time (Δt > 30 ps) kinetic data to analytical functions obtained from the kinetic scheme described in the text. ) radical photoproduct in cyclohexane obtained through numerical integration over the range 1570–1580 cm−1. Deconvolution of the 1465–1520 cm−1 region using Lorentzian functions enables extraction of kinetic traces for the (d) p-MePhSMe(S1; v = 0) and (e) p-MePhSMe(S0) populations. The solid blue lines are least squares fits of the long time (Δt > 30 ps) kinetic data to analytical functions obtained from the kinetic scheme described in the text. | ||
Again, the TVA data provide complementary insights, which are rather simpler to picture in the case of p-MePhSMe in CD3CN (Fig. 6(a)) than in cyclohexane (Fig. 6(b)). The former spectra show an obvious bleach at ∼1495 cm−1 and transient absorptions at ∼1485 cm−1 and ∼1570 cm−1, whereas the corresponding bleach signal in Fig. 6(b) is masked by the overlapping absorption and only becomes apparent at longer Δt. The bleach in Fig. 6(a) is attributable to photoinduced depopulation of the S0 state, and the absorption feature at ∼1570 cm−1 is due to p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals – i.e. the same feature as in Fig. 4 but now arising as a result of S–CH3 bond fission. The more intense absorption at ∼1485 cm−1, which is clearly evident at the shortest time delays, is attributable to electronically excited p-MePhSMe(S1) molecules. This ESA feature blue-shifts with increasing Δt, consistent with initial formation of internally excited molecules, which then relax to the lowest vibrational level of the S1 state within a few picoseconds. Similar trends are also evident in the ESA signal following 267 nm photolysis of p-MePhSMe in cyclohexane (Fig. 6(b)), but disentangling the kinetics from those of the overlapping ground state bleach is more challenging.
) radicals – i.e. the same feature as in Fig. 4 but now arising as a result of S–CH3 bond fission. The more intense absorption at ∼1485 cm−1, which is clearly evident at the shortest time delays, is attributable to electronically excited p-MePhSMe(S1) molecules. This ESA feature blue-shifts with increasing Δt, consistent with initial formation of internally excited molecules, which then relax to the lowest vibrational level of the S1 state within a few picoseconds. Similar trends are also evident in the ESA signal following 267 nm photolysis of p-MePhSMe in cyclohexane (Fig. 6(b)), but disentangling the kinetics from those of the overlapping ground state bleach is more challenging.
The time-dependent population of the radical photoproduct arising from photolysis of p-MePhSMe in cyclohexane (Fig. 6(c)) is obtained through numerical integration over the 1570 cm−1 feature, and shows a fast initial rise followed by a continuing slower net production out to the longest delays investigated (Δt = 1.5 ns). The kinetics of the ground and excited state parent populations are derived by deconvoluting the ∼1480 cm−1 feature using a set of four model functions. The TVA spectrum at long Δt (i.e., when all electronically excited p-MePhSMe (S1) molecules have decayed) is used as a guide for the parent bleach signal, while the ESA was modelled as a sum of three Lorentzian functions representing molecules with v ≫ 0 (i.e. high levels of vibrational excitation), v > 0 (i.e. molecules that have undergone some vibrational relaxation) and v = 0 (i.e. fully vibrationally relaxed S1 molecules). The peak centers and widths of these various functions were held fixed through simultaneous fitting of all available data. The time dependence of the total area of the Lorentzian functions modelling the v ≫ 0 and v > 0 populations provides an estimate of the vibrational relaxation rate within the S1 manifold. The v = 0 population (Fig. 6(d)) increases at small Δt – as a result of relaxation from higher vibrational levels – but thereafter declines slowly as a result of IC (to the S0 state) and/or dissociation.
The bi- or multi-exponential radical formation kinetics observed in cyclohexane (Fig. 6(c)) and in CD3CN97 are consistent with a model in which the dissociation rate of p-MePhSMe(S1) molecules scales with their vibrational energy content. Such an assumption mirrors the findings of a recent femtosecond time-resolved velocity map ion imaging photolysis study of gas-phase thioanisole (PhSMe),100 which reported time constants τ = 1.4 ns when exciting at 289.8 nm (i.e. at the π* ← π origin), cf. 74 ps when exciting at 275 nm. Thus the TVA data following 267 nm photolysis of p-MePhSMe in cyclohexane were fitted using the following (limited) kinetic Scheme 1, where kIC denotes the IC rate from the S1(v = 0) level (vibrational relaxation within the S0 manifold is likely to be much faster than the IC rate and will thus have little impact on the derived rate constant), kVib describes the vibrational cooling at different levels within the S1 manifold, and kDiss(v>0) and kDiss(v=0) are dissociation rate constants for vibrationally excited and vibrationally relaxed p-MePhSMe(S1) molecules, respectively. This scheme neglects any re-population of p-MePhSMe(S0; v = 0) or loss of p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals by geminate recombination, though we recognise that this process must surely be significant. This kinetic scheme can be further simplified by recognising that there are two distinct time regimes – fast (10's of ps) dynamics attributable to the decay of p-MePhSMe(S1; v > 0) molecules, and slower (100's of ps) dynamics associated with decay of p-MePhSMe(S1; v = 0) population. The order of magnitude difference between kVib and kDiss(v>0)cf. kIC and kDiss(v=0) allows the long time (i.e., Δt > 30 ps) behaviour of the system to be modelled independently of the early time dynamics, thus reducing the kinetic scheme to that shown in the boxed region of Scheme 1 and where the decay of p-MePhSMe(S1; v = 0) population and subsequent formation of p-MePhSMe(S0; v = 0) and p-MePhS(
) radicals by geminate recombination, though we recognise that this process must surely be significant. This kinetic scheme can be further simplified by recognising that there are two distinct time regimes – fast (10's of ps) dynamics attributable to the decay of p-MePhSMe(S1; v > 0) molecules, and slower (100's of ps) dynamics associated with decay of p-MePhSMe(S1; v = 0) population. The order of magnitude difference between kVib and kDiss(v>0)cf. kIC and kDiss(v=0) allows the long time (i.e., Δt > 30 ps) behaviour of the system to be modelled independently of the early time dynamics, thus reducing the kinetic scheme to that shown in the boxed region of Scheme 1 and where the decay of p-MePhSMe(S1; v = 0) population and subsequent formation of p-MePhSMe(S0; v = 0) and p-MePhS(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) products occurs with an effective rate constant of kS1 = kIC + kDiss(v=0). The ∼80% recovery of the parent bleach signal gives a direct measure of the quantum yield for internal conversion, ϕIC, (in the limit of zero geminate recombination) which, in turn, enables estimation of the relative magnitudes of kIC and kDiss(v=0)via the relation ϕIC = kIC/(kIC + kDiss(v=0)).
) products occurs with an effective rate constant of kS1 = kIC + kDiss(v=0). The ∼80% recovery of the parent bleach signal gives a direct measure of the quantum yield for internal conversion, ϕIC, (in the limit of zero geminate recombination) which, in turn, enables estimation of the relative magnitudes of kIC and kDiss(v=0)via the relation ϕIC = kIC/(kIC + kDiss(v=0)).
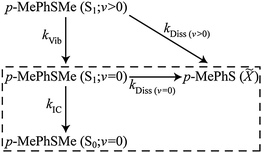 | ||
| Scheme 1 | ||
Analytical solutions101 for the time dependent populations (Δt > 30 ps) of the species included in the kinetic scheme yield best-fit rate constants: kDiss(v=0) = 0.69(5) ns−1 and kIC = 2.88(6) ns−1 (where the numbers in parentheses represent one standard deviation uncertainty in the last significant digit(s)). The solid lines in Fig. 6(c)–(e) illustrate the quality of the kinetic fits for the radical and for the S1; v = 0 and S0; v = 0 parent molecule populations. Whilst recognising the obvious limitations of this kinetic treatment (of which the neglect of any contribution from geminate recombination is arguably the most severe), it is instructive to compare these rate constants with those determined from the corresponding photolysis in CD3CN.97 The TEA data show that the total decay rate from the p-MePhSMe (S1; v = 0) level is ∼2-times faster in cyclohexane than in CH3CN/CD3CN, and the modelling of the TVA data suggests that this increase is wholly attributable to an increase in kIC. Comparing the static UV/Visible absorption spectra of p-MePhSMe in cyclohexane and in CH3CN (see ESI†), we note that the S1–S0 absorption in the former is slightly red-shifted. The slow (ns) timescale for dissociation from the S1; v = 0 level (τDiss(v=0) = 1.4(1) ns in cyclohexane, 560(20) ps in CD3CN) reflects its reliance on the very poor overlap between the extremities of the S1; v = 0 and S2 continuum wavefunctions; any small shift in the relative positions of these two PESs would have a profound effect on the efficiency of non-adiabatic coupling via CI1 and thus on the rate of S–Me bond scission. Thus the sensitivity of kDiss to change in solvent is not particularly surprising. The ∼4-fold change in IC rate is harder to rationalise, though we note that the trend in kIC with decreasing solvent polarity broadly mirrors that deduced from previous flash photolysis studies of a range of phenols.102
Notwithstanding the detailed solvent dependent differences, the principal findings regarding the UV photodissociation of p-MePhSMe(S1) molecules in solution are (i) that the dissociation rate constant scales with the degree of vibrational excitation and (ii) that kDiss(v=0) is several orders of magnitude smaller than from p-MePhSH(S1; v = 0). Both findings mirror the trends in excited state lifetime found in gas phase studies of thiophenols and thioanisoles, and are understandable given the potential barrier impeding transfer from S1 to the dissociative S2 state (Fig. 2) and the recognised importance of torsional motion in promoting non-adiabatic coupling between these states.77,100 One apparent difference as compared with the gas phase data is the non-observation of any signals attributable to à state radical products (which constitute >80% of the primary dissociation yield in the gas phase photolysis of p-MePhSMe), but this is unsurprising in light of the relative rates of their production (by dissociation) and quenching in solution. As noted above, capturing the initial branching ratio prior to electronic quenching may be possible in the case of a direct dissociation given sufficient (∼100 fs) experimental time resolution (as in the foregoing example of p-MePhSH) – but not in the case of a dissociation occurring on the nanosecond timescale.
UV photodissociation of phenol in solution
S–H bond fission following 267 nm photolysis of p-MePhSH is deduced to occur in tens of femtoseconds – in the gas phase and in cyclohexane solution (Fig. 3).93 O–H bond fission in gas phase phenol molecules, in contrast, occurs over a period of nanoseconds, by tunneling through the barrier under the S1/S2 CI in the RO–H stretch coordinate.78–80,103 Simply on lifetime grounds, therefore, one might anticipate that the photodissociation of phenol would be more susceptible to solvent interactions than in the case of thiophenol. Yet the TEA spectra recorded following 267 nm photolysis of a dilute solution of PhOH in cyclohexane solution using a wire guided jet (Fig. 7) show a structured feature in the 380–400 nm region – a signature of ground state PhO(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals21,104–106 – developing on a nanosecond timescale. The earlier time TEA spectra are dominated by a broadband feature that extends across the entire 350–650 nm observation window and decays with the same time constant (τ ∼2.1 ns) as the S1 fluorescence (τfl = 2.16 ns for 10 mM PhOH solution in cyclohexane,107 see ESI†). This is attributable to ESA (by the S1 state) in good agreement with the calculated S1 ESA spectrum.96
) radicals21,104–106 – developing on a nanosecond timescale. The earlier time TEA spectra are dominated by a broadband feature that extends across the entire 350–650 nm observation window and decays with the same time constant (τ ∼2.1 ns) as the S1 fluorescence (τfl = 2.16 ns for 10 mM PhOH solution in cyclohexane,107 see ESI†). This is attributable to ESA (by the S1 state) in good agreement with the calculated S1 ESA spectrum.96
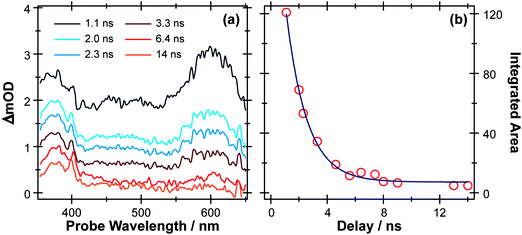 | ||
| Fig. 7 (a) TEA spectra measured for Δt values between 1–14 ns following 267 nm photoexcitation of a 10 mM solution of PhOH in cyclohexane flowed through a wire guided liquid jet. (b) Numerical integration between 575–625 nm allows extraction of kinetic traces (open circles). The solid blue line is a least-squares fit of the kinetic data to a single exponential function. | ||
TVA measurements again give complementary information. Spectra measured following 267 nm excitation of a dilute flowing solution of PhOH in cyclohexane in a Harrick cell are more congested than those obtained for p-MePhSH or p-MePhSMe, exhibiting no fewer than six bleach and seven absorption features in the 1250–1700 cm−1 range. Fig. 8(a) shows an illustrative part of the spectra in the range 1480–1700 cm−1 (a part of the fingerprint region that is free of overlapping solvent absorption features), recorded at several different Δt. All of the observed bleach features match with absorptions in the static FTIR spectrum, i.e. all indicate a depletion of S0 population upon UV photon absorption. Six of the seven absorption features show very similar kinetic behaviour, appearing within the experimental time resolution and decaying with time constants τ ∼ 2 ns as illustrated for the case of the 1552 cm−1 feature in Fig. 8(b). These features are assigned in terms of prompt population and subsequent decay of the S1 state of PhOH.
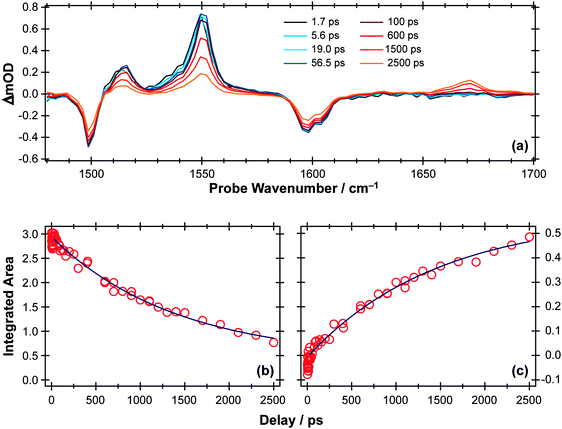 | ||
| Fig. 8 (a) TVA spectra in the range 1480–1700 cm−1 measured at different Δt following 267 nm photoexcitation of an 8 mM solution of PhOH in cyclohexane flowed through a Harrick cell with a 360 μm spacer. Numerical integration over portions of the latter spectra allows extraction of kinetic traces monitoring the (b) decay of the PhOH(S1) population (at 1552 cm−1) and (c) build-up of 2,4- and/or 2,5-cyclohexadienone adduct peak at 1670 cm−1. The solid blue lines are least-squares fits of the data to single exponential functions and intended as a visual guide. | ||
As Fig. 8(c) shows, the 1671 cm−1 absorption band exhibits different kinetics, growing in with a similar (τ ∼ 2 ns) time constant to that determined for the S1 population decay. There are no recorded or calculated normal modes of the phenoxyl radical near 1671 cm−1, however, and none of the features attributed to the phenoxyl radical in IR spectra taken following UV excitation of matrix-isolated PhOH (e.g. at 1481 cm−1, 1515 cm−1 and 1550 cm−1)108 are evident in the present data. The wavenumber of this unassigned absorption is more reminiscent of a carbonyl stretch vibration and, as in the previous matrix isolation studies,108 we assign this feature to 2,4- and/or 2,5-cyclohexadienone molecules formed by geminate recombination of the H + PhO products, i.e. analogous to the adduct identified in the UV photolysis of p-MePhSH. Note that this attribution says nothing about the relative yields of PhO(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals (which are clearly evident in the TEA spectra taken at long Δt but not in the TVA spectra) and adduct molecules (which are only identified in the TVA spectra). The strong showing of the adduct feature in the latter spectra is much more a reflection of the large cross-section of the C
) radicals (which are clearly evident in the TEA spectra taken at long Δt but not in the TVA spectra) and adduct molecules (which are only identified in the TVA spectra). The strong showing of the adduct feature in the latter spectra is much more a reflection of the large cross-section of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch fundamental (calculated to be at least one order of magnitude larger than the strongest phenoxyl band in the fingerprint region) rather than an indication that the adduct is a major recombination product.
O stretch fundamental (calculated to be at least one order of magnitude larger than the strongest phenoxyl band in the fingerprint region) rather than an indication that the adduct is a major recombination product.
TVA methods can be used to investigate the OH stretch region also, as illustrated in Fig. 9(a) for the case of 267 nm photolysis of a dilute solution of phenol in cyclohexane. The S0 bleach and an absorption due to PhOH(S1) molecules are apparent in this spectrum. The later time behaviour of both signals (Fig. 9(b) and (c), respectively) are both consistent with an S1 state lifetime τ ∼ 2 ns and (partial) bleach recovery by IC and/or geminate recombination.
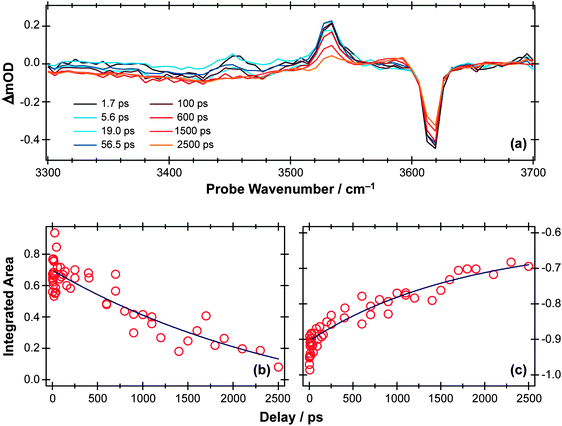 | ||
| Fig. 9 (a) TVA spectra in the range 3300–3700 cm−1 measured at different Δt following 267 nm photoexcitation of an 8 mM solution of PhOH in cyclohexane flowed through a 360 μm Harrick cell. Numerical integration over portions of these spectra enables extraction of kinetic traces monitoring (b) decay of the PhOH(S1) population and (c) recovery of the PhOH(S0) population (monitored at 3530 cm−1 and 3620 cm−1, respectively). The solid blue lines are least-squares fits of the data to single exponential functions and intended as a visual guide. | ||
The foregoing description glosses over a number of issues that merit further study. The PhO(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radical absorption in the TEA spectrum is sensitive to the flow conditions, and is generally more evident and repeatable in spectra recorded with the wire guided jet than in a flow cell. The present TVA measurements, which were all performed in a flow cell, consistently show that the extent of the parent bleach recovery is smaller than the fractional loss of S1 population. The ground state population is replenished by IC, geminate recombination and fluorescence decay. Thus the modest bleach recovery revealed by the TVA measurements could indicate that most photoexcited S1 molecules dissociate, and that (as in p-MePhSH) most of the dissociation products avoid geminate recombination. In apparent contradiction with this argument, however, we note the absence of signal unambiguously assignable to the phenoxyl radical in the TVA measurement at the longest time delay investigated, Δt = 2.5 ns. A previous IR study of the phenoxyl radical in a rare gas matrix108 identified absorptions within the spectral range covered in the present TVA study, with intensities comparable to those of ground state phenol. Thus it may seem surprising that no such radical features are observed in the TVA measurements reported here. However, we note that the TEA data contain insufficient points at long time to establish at what Δt the yield of PhO(
) radical absorption in the TEA spectrum is sensitive to the flow conditions, and is generally more evident and repeatable in spectra recorded with the wire guided jet than in a flow cell. The present TVA measurements, which were all performed in a flow cell, consistently show that the extent of the parent bleach recovery is smaller than the fractional loss of S1 population. The ground state population is replenished by IC, geminate recombination and fluorescence decay. Thus the modest bleach recovery revealed by the TVA measurements could indicate that most photoexcited S1 molecules dissociate, and that (as in p-MePhSH) most of the dissociation products avoid geminate recombination. In apparent contradiction with this argument, however, we note the absence of signal unambiguously assignable to the phenoxyl radical in the TVA measurement at the longest time delay investigated, Δt = 2.5 ns. A previous IR study of the phenoxyl radical in a rare gas matrix108 identified absorptions within the spectral range covered in the present TVA study, with intensities comparable to those of ground state phenol. Thus it may seem surprising that no such radical features are observed in the TVA measurements reported here. However, we note that the TEA data contain insufficient points at long time to establish at what Δt the yield of PhO(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radicals from PhOH photolysis in cyclohexane is maximal; it is likely to be at Δt > 2.5 ns. The observation of the cyclohexadienone product that we attribute to geminate recombination may also be deceptive. Its concentration is expected to be less than that of the PhO radical at the observation times of interest and, as noted earlier, its identification is primarily a reflection of the exceptional cross-section of the C
) radicals from PhOH photolysis in cyclohexane is maximal; it is likely to be at Δt > 2.5 ns. The observation of the cyclohexadienone product that we attribute to geminate recombination may also be deceptive. Its concentration is expected to be less than that of the PhO radical at the observation times of interest and, as noted earlier, its identification is primarily a reflection of the exceptional cross-section of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch fundamental. Thus a combination of small photodissociation quantum yield and the (relatively) modest IR transition strengths of the PhO radical might ensure that the radical signature is obscured by other features within the present TVA spectra, but further work is needed to fully reconcile the apparent differences between the TEA (jet) and TVA (cell) data.
O stretch fundamental. Thus a combination of small photodissociation quantum yield and the (relatively) modest IR transition strengths of the PhO radical might ensure that the radical signature is obscured by other features within the present TVA spectra, but further work is needed to fully reconcile the apparent differences between the TEA (jet) and TVA (cell) data.
UV photodissociation of allyl phenyl ether in solution
The foregoing examples have focussed on using ultrafast transient absorption spectroscopy methods to explore the UV photodissociation dynamics of molecules in solution, but the technique is equally applicable to studying the dynamics of photo-initiated bimolecular reactions109–113 and molecular rearrangements in solution. Our final example illustrates the latter facet, using a traditional photochemical reaction – the photo-Claisen rearrangement – as an exemplar.114 The thermal Claisen rearrangement, wherein aryl or allyl phenyl ethers rearrange to form 2-substituted products (Scheme 2), has been known for more than a century,115 while the photochemical version was first reported in 1952 for the specific cases of benzyl phenyl ether and allyl phenyl ether (APE).116 The various possible competing processes occurring during the photo-Claisen rearrangement are traditionally summarised as shown in Scheme 3.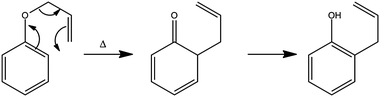 | ||
| Scheme 2 Thermal Claisen rearrangement of allyl phenyl ether. | ||
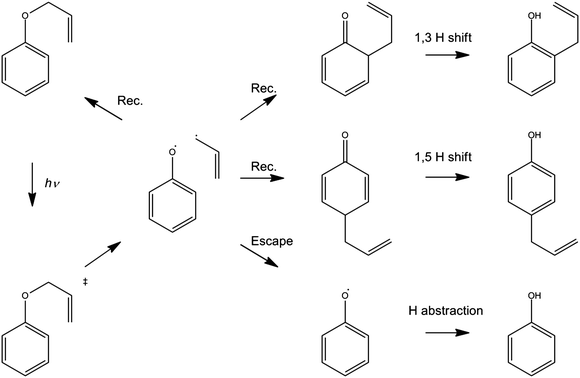 | ||
| Scheme 3 Photo-Claisen rearrangement of allyl phenyl ether. | ||
Ultrafast UV pump – broadband TEA or TVA probe methods offer a means of following the early stages of the various competing routes in the photo-Claisen rearrangement. Fig. 10(a) and (b) show representative TEA and TVA spectra following 267 nm photoexcitation of APE in solution in cyclohexane. As noted previously,117 cuts through the diabatic PESs for the first two excited singlet states along the RO–allyl stretch coordinates (at planar geometry) should be qualitatively similar to those shown in Fig. 2, with a bound S1(π* ← π) state and an S2(σ* ← π) potential. The S2 potential may support a shallow minimum at short range but, at long range, will be dissociative with respect to ground state radical products. The stability of the allyl radical will favour fission of the O−allyl rather than the O–phenyl bond.118 Support for these expectations comes from the measured UV absorption spectrum of APE in cyclohexane (which is very reminiscent of that of PhOH itself – see ESI†), and from previous LIF studies of APE in a supersonic molecular beam.119 The latter study identified the presence of more than one conformer in the jet-cooled sample, and an obvious drop in fluorescence quantum yield (attributed to competing predissociation) from S1 molecules with v > 0.
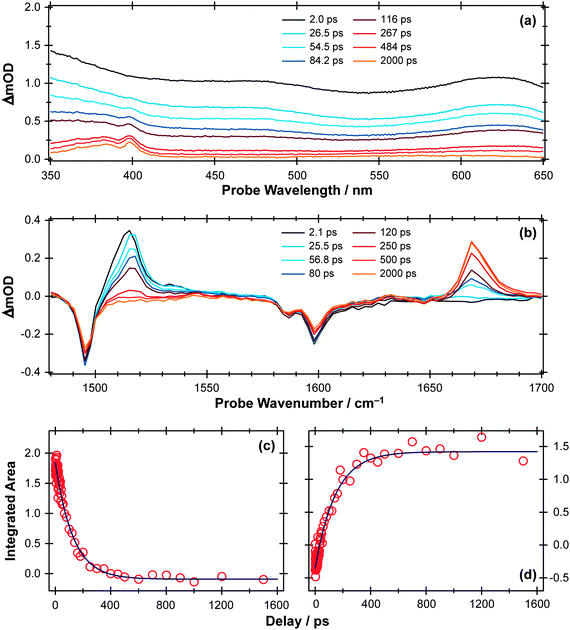 | ||
| Fig. 10 (a) TEA and (b) TVA spectra measured at different Δt following 267 nm photoexcitation of a 30 mM solution of APE in cyclohexane flowing through, respectively, a wire guided liquid jet and a 100 μm Harrick cell. Numerical integration over portions of these spectra allows extraction of kinetic traces (open circles) monitoring (c) APE (S1; 1516 cm−1) and (d) cyclohexadienone adduct (1669 cm−1). The solid blue lines are least-squares fits of the data to single exponential functions and intended as a visual guide. | ||
The TEA measured at Δt = 2 ps (the earliest pump–probe delay shown in Fig. 10a) spans the visible region and decays with a time constant τ ∼ 90 ps. Analogy with PhOH encourages assignment of this broad absorption to ESA from the S1 state of APE. As Fig. 10a shows, a structured absorption in the 380–400 nm region develops on a similar timescale. This is the signature of PhO(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) radical formation (recall Fig. 7). As with the earlier p-MePhSMe data, the overlapping ESA signal means that a global analysis is required for extraction of kinetic data for the production and/or subsequent vibrational cooling of these radical products. Nonetheless, the TEA experiment certainly confirms that the first step shown in Scheme 3 – O–allyl bond fission – occurs on a ∼90 ps timescale following excitation to the S1 state of APE (i.e. more than an order of magnitude faster than the analogous O–H bond fission in phenol).
) radical formation (recall Fig. 7). As with the earlier p-MePhSMe data, the overlapping ESA signal means that a global analysis is required for extraction of kinetic data for the production and/or subsequent vibrational cooling of these radical products. Nonetheless, the TEA experiment certainly confirms that the first step shown in Scheme 3 – O–allyl bond fission – occurs on a ∼90 ps timescale following excitation to the S1 state of APE (i.e. more than an order of magnitude faster than the analogous O–H bond fission in phenol).
The corresponding TVA spectra (Fig. 10b) display bleach signals at 1495, 1586 and 1598 cm−1. Three absorption features are also observed – at 1415, 1516 and 1669 cm−1 – the latter two of which are shown in Fig. 10(b). The 1415 and 1516 cm−1 features appear immediately. The band contours evolve in a manner consistent with vibrational cooling, then decay with a time constant, τ = 94(5) ps. Consistent with the TEA analysis, we attribute these absorptions to vibrational modes of the S1 state of APE. The 1669 cm−1 feature shows different kinetic behaviour, developing with a time constant τ = 150 (10) ps. The wavenumber of this feature is consistent with either (or both) of the allyl substituted 2,4- or 2,5-cyclohexadienones shown in Scheme 3, and its kinetic behaviour is broadly consistent with the proposed geminate recombination of the phenoxyl and allyl radicals formed in the initial photodissociation. Unfortunately the predicted wavenumbers of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch mode in these two cyclohexadienones would be indistinguishable with the available spectral resolution. Once again, we note the absence of any absorptions attributable to the phenoxyl radical in the TVA spectra, despite its clear showing in the TEA spectrum and the finding (from the time dependence of the parent bleach signal) that ∼80% of the photoexcited molecules do not reform as an APE(S0) molecule within the observation time window. The longer build-up time of the cyclohexadienone product (cf. the timescale of S1 decay) hints at a sequential formation mechanism (i.e.Scheme 3) rather than a concerted mechanism (Scheme 2), but we are not yet in a position to comment on the relative probabilities of allyl radical recombination at the 2- and/or 4-positions.
O stretch mode in these two cyclohexadienones would be indistinguishable with the available spectral resolution. Once again, we note the absence of any absorptions attributable to the phenoxyl radical in the TVA spectra, despite its clear showing in the TEA spectrum and the finding (from the time dependence of the parent bleach signal) that ∼80% of the photoexcited molecules do not reform as an APE(S0) molecule within the observation time window. The longer build-up time of the cyclohexadienone product (cf. the timescale of S1 decay) hints at a sequential formation mechanism (i.e.Scheme 3) rather than a concerted mechanism (Scheme 2), but we are not yet in a position to comment on the relative probabilities of allyl radical recombination at the 2- and/or 4-positions.
Another point to note is that Schemes 2 and 3 show the end product as o- or p-allyl phenol. Using the TVA experiment, it is possible to monitor the OH stretch region at >3 μm as described above for the case of bare PhOH. In the case of APE, however, we find no evidence for any OH stretch absorptions at any Δt investigated. Two possible explanations for this finding can be envisaged. One assumes that the 1,3- and 1,5-hydrogen shifts required to produce o- or p-allylphenol from the corresponding cyclohexadienone intermediate occur on a timescale longer than the 2 ns investigated in the present work. As an alternative, however, it is possible that the substituted phenols arise as a result of secondary photolysis of the cyclohexadienone product – a condition that we actively seek to avoid in the present pump–probe experiments by using a flowing sample. Further investigation is required to ascertain which of these possibilities is correct.
Conclusions and prospects
The introduction to this perspective article queried the extent to which insights gained from detailed studies of molecular photodissociations under isolated molecule conditions might usefully inform our understanding of photochemistry in solution. Our initial explorations of this question have been largely confined to detailed comparisons of the photofragmentation behaviour of a limited selection of molecules in vacuum and in a weakly interacting solvent like cyclohexane. Additional rigour is provided by monitoring the photoinduced chemistry in solution by both transient UV/visible and transient IR absorption spectroscopies.267 nm photoexcitation of p-MePhSH in the gas phase results in direct S–H bond fission. It is perhaps unsurprising that the same excitation of the same molecule in cyclohexane solution leads to the same outcome within the experimental time resolution of ∼50 fs. UV photoinduced S–Me bond fission in thioanisoles and O–H bond fission in PhOH have both also been studied extensively in the gas phase. Both are deduced to involve nuclear motions through classically forbidden regions of the PES, and both occur 4–5 orders of magnitude more slowly than S–H bond fission in thiophenols – i.e. on the timescale of many thousands of vibrational periods. Yet the time resolved studies of these two photodissociations in cyclohexane solution reveal kinetic behaviour that is again strikingly similar to that found in the gas phase. The presence of cyclohexane solvent appears to have minimal effect on the PhOH(S1) lifetime, for example, or on the possibility of O–H bond fission by tunnelling under the S1/S2 CI in the RO–H stretch coordinate. Thus, at least for the case of this weakly interacting solvent, we conclude that the fragmentation dynamics established from detailed gas phase studies really can provide useful insights into the early stages of photodissociation processes occurring in the condensed phase.
That said, the present studies also provide many illustrations of ways in which solvent interactions influence the photofragmentation dynamics. In all but the fastest dissociations, bond fission will be in competition with vibrational relaxation within the excited state parent molecule. 267 nm excitation of PhOH prepares S1(v > 0) molecules, which in solution will relax prior to dissociation. However, as noted previously, the FC active vibrations in PhOH are orthogonal to the dissociation coordinate and the loss of vibrational energy has no obvious effect on the dissociation rate.78,103,120 Similar FC arguments must apply in the 267 nm photolysis of p-MePhSMe but, in this case, the observed dissociation rate decreases as solvent interactions progressively drain vibrational energy from the photo-prepared S1 molecules. Such differences serve to illustrate the earlier assertion that VET processes can show quite striking molecule and mode dependencies. In the present case, the much higher vibrational state density in p-MePhSMe and, particularly, the low frequency CH3 torsional modes are assumed to facilitate rapid IVR, with the result that some of the initial vibrational excitation is available to promote dissociation at early times.16,17
Similar considerations apply to the photoproducts. Most contemporary studies of gas phase photodissociation processes measure the asymptotic velocities (kinetic energies) of the recoiling products and rely on energy conservation arguments to derive bond strengths, product branching ratios, etc. In terms of energy and angular momentum conservation, the evolution from parent to fragments can be viewed as a closed system. The situation in solution is very different: the solvent molecules provide an effective sink for product translational, rotational and (on longer timescales) vibrational excitation. The recoiling fragments will eventually be stopped by the friction exerted by the solvent, and the ensuing diffusion of the incompletely separated photo-products can lead to geminate recombination – reforming the original parent species, or an isomer. Isomer (adduct) formation is seen in the cases of p-MePhSH and PhOH, and is the raison d'ètre for the photo-Claisen rearrangement of APE. Nonetheless, continuing improvements in the wavelength tunability and the pump–probe time resolution mean that it is becoming increasingly possible to unravel nascent energy releases via determination of quantities like the ejection length, first pass branching ratios and, in appropriate cases, the rotational energy disposal in the products – as functions of photolysis wavelength.
We now reflect on the likely influence of solvent on nuclear motions in the vicinity of CIs. At one level, a weakly interacting solvent like cyclohexane appears to cause minimal perturbation of the potential energy landscape that determines the gas phase behaviour. Once on the S2 PES, therefore, it is difficult to see how the presence of solvent can have much influence on the ballistic inter-fragment separation out to CI2 in Fig. 2 (the region in which the electronic branching is determined in the gas phase photodissociation); the nuclear motion is just too fast. As noted above, however, solvent friction will slow and eventually stop the separating fragments, which are then well posed for geminate recombination. Recalling Fig. 2, one can envisage that such ‘frustrated’ dissociations will be more prevalent for molecules that attempt to follow the adiabatic potential – thus constituting an efficient means of ‘quenching’ the formation of electronically excited products.94
Finally, we re-emphasise aspects that have not been addressed in this article. The recent analyses of the gas phase photofragmentation dynamics of the chosen solute molecules assume no involvement of triplet excited states,117 and the necessity to invoke a role for such states when discussing the corresponding photodissociations in cyclohexane is debatable. Solute–solvent interactions become increasingly important with more polar solvents, and the extent to which a gas phase perspective can usefully inform our understanding of photofragmentation processes occurring in water, for example, is less clear. The appropriateness of gas phase PESs when considering photochemistry in a polar solvent is more questionable and, as noted previously, the attendant lowering of the adiabatic ionisation energy of the solute and the probability of forming solvated electrons all make like-for-like comparisons with the gas phase behaviour more difficult. Nonetheless, the increasing availability and diversity of ultrafast pump–probe methods for probing photo-induced dynamics in solution encourages the expectation of much further progress in this field of research.
Acknowledgements
The Bristol group are grateful to EPSRC for funding via a Programme Grant EP/G00224X and a Building Global Engagement award, to D. R. Glowacki, S. J. Greaves, J. N. Harvey, T. N. V. Karsili, T. J. Preston and A. M. Wenge for many useful discussions, and to STFC for programme access to the ULTRA laser facility (STFC Facility Grant ST/501784). MNRA and SJH are also grateful to, respectively, the Royal Society for the award of a Leverhulme Trust Senior Research Fellowship and the University of Bristol for a Postgraduate Research Scholarship. AJOE thanks the ERC for the award of Advanced Grant 290966 CAPRI. The work at USC is supported by the US National Science Foundation under CHE-0957869. The USC group acknowledge discussions and insights from Chris Rivera and Ilan Benjamin.References
- H. Urey, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 352–363 CrossRef.
- G. Joyce, Nature, 1989, 338, 217–224 CrossRef CAS.
- D. Mauzerall, Origins Life Evol. Biospheres, 1990, 293–302 CAS.
- R. E. Blankenship, Photosynth. Res., 1992, 33, 91–111 CrossRef CAS.
- H. D. Roth, Pure Appl. Chem., 2001, 73, 395–403 CrossRef CAS.
- M. S. de Vries and P. Hobza, Annu. Rev. Phys. Chem., 2007, 58, 585–612 CrossRef CAS.
- S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878 CrossRef CAS.
- P. H. Bucksbaum, Science, 2007, 317, 766–769 CrossRef CAS.
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- B. W. J. McNeil and N. R. Thompson, Nat. Photonics, 2010, 4, 814–821 CrossRef CAS.
- M. Vrakking and T. Elsaesser, Nat. Photonics, 2012, 6, 645–647 CrossRef CAS.
- J. Franck and E. Rabinowitch, Trans. Faraday Soc., 1934, 171, 120–130 RSC.
- C. G. Elles and F. F. Crim, Annu. Rev. Phys. Chem., 2006, 57, 273–302 CrossRef CAS.
- A. C. Moskun and S. E. Bradforth, J. Chem. Phys., 2003, 119, 4500 CrossRef CAS.
- B. Savitzky and R. Stratt, J. Phys. Chem. B, 2008, 112, 13326–13334 CrossRef CAS.
- J. Owrutsky, D. Raftery and R. M. Hochstrasser, Annu. Rev. Phys. Chem., 1994, 45, 519–555 CrossRef CAS.
- J. Assmann, M. Kling and B. Abel, Angew. Chem., Int. Ed., 2003, 42, 2226–2246 CrossRef CAS.
- N. Pugliano, S. Gnanakaran and R. M. Hochstrasser, J. Photochem. Photobiol., A, 1996, 102, 21–28 CrossRef CAS.
- L. Grossweiner, G. Swenson and E. Zwicker, Science, 1963, 141, 805–806 CAS.
- J. Peon, G. C. Hess, J. M. L. Pecourt, T. Yuzawa and B. Kohler, J. Phys. Chem. A, 1999, 103, 2460–2466 CrossRef CAS.
- X. Chen, D. S. Larsen, S. E. Bradforth and I. H. M. van Stokkum, J. Phys. Chem. A, 2011, 115, 3807–3819 CrossRef CAS.
- D. Ghosh, A. Roy, R. Seidel, B. Winter, S. Bradforth and A. I. Krylov, J. Phys. Chem. B, 2012, 116, 7269–7280 CrossRef CAS.
- E. Gershgoren, U. Banin and S. Ruhman, J. Phys. Chem. A, 1998, 102, 9–16 CrossRef CAS.
- T. Chuang, G. Hoffman and K. Eisenthal, Chem. Phys. Lett., 1974, 25, 201–205 CrossRef CAS.
- D. Kelley and P. Rentzepis, Chem. Phys. Lett., 1982, 85, 85–90 CrossRef CAS.
- M. E. Paige and C. B. Harris, Chem. Phys., 1990, 149, 37–62 CrossRef CAS.
- M. E. Paige, D. J. Russell and C. B. Harris, J. Chem. Phys., 1986, 85, 3699 CrossRef CAS.
- A. L. Harris, M. Berg and C. B. Harris, J. Chem. Phys., 1986, 84, 788–806 CrossRef CAS.
- D. E. Smith and C. B. Harris, J. Chem. Phys., 1987, 87, 2709–2715 CrossRef CAS.
- R. Bowman, M. Dantus and A. Zewail, Chem. Phys. Lett., 1989, 156, 131 CrossRef CAS.
- N. Pugliano, D. K. Palit, A. Z. Szarka and R. M. Hochstrasser, J. Chem. Phys., 1993, 99, 7273–7276 CrossRef CAS.
- S. Pedersen, T. Baumert and A. Zewail, J. Phys. Chem., 1993, 97, 12460–12465 CrossRef CAS.
- T. Baumert, S. Pedersen and A. Zewail, J. Phys. Chem., 1993, 97, 12447–12459 CrossRef CAS.
- J. S. Baskint and A. H. Zewail, J. Phys. Chem., 1994, 98, 3337–3351 CrossRef.
- N. Pugliano, A. Z. Szarka and R. M. Hochstrasser, J. Chem. Phys., 1996, 104, 5062–5079 CrossRef CAS.
- M. Volk and S. Gnanakaran, J. Phys. Chem. A, 1997, 2, 638–643 CrossRef.
- H. Bürsing and P. Vöhringer, Phys. Chem. Chem. Phys., 1999, 2, 73–82 RSC.
- U. Banin and S. Ruhman, J. Chem. Phys., 1993, 99, 9318–9321 CrossRef CAS.
- U. Banin and S. Ruhman, J. Chem. Phys., 1993, 98, 4391–4403 CrossRef CAS.
- U. Banin, A. Bartana, S. Ruhman and R. Kosloff, J. Chem. Phys., 1994, 101, 8461–8481 CrossRef CAS.
- T. Kühne and P. Vöhringer, J. Chem. Phys., 1996, 105, 10788 CrossRef.
- M. T. Zanni, B. J. Greenblatt, A. V. Davis and D. M. Neumark, J. Chem. Phys., 1999, 111, 2991–3003 CrossRef CAS.
- M. Dantus, M. J. Rosker and A. H. Zewail, J. Chem. Phys., 1988, 89, 6128–6140 CrossRef CAS.
- I. Benjamin and K. R. Wilson, J. Chem. Phys., 1989, 90, 4176–4197 CrossRef CAS.
- G. Roberts and A. Zewail, J. Phys. Chem., 1991, 95, 7973–7993 CrossRef CAS.
- N. F. Scherer, J. L. Knee, D. D. Smith and A. H. Zewail, J. Phys. Chem., 1985, 89, 5141–5143 CrossRef CAS.
- J. Larsen, D. Madsen, J. A. Poulsen, T. D. Poulsen, S. R. Keiding and J. Thøgersen, J. Chem. Phys., 2002, 116, 7997 CrossRef CAS.
- C. C. Cooksey, K. J. Johnson and P. J. Reid, J. Phys. Chem. A, 2006, 110, 8613–8622 CrossRef CAS.
- T. J. Bixby, J. D. Patterson and P. J. Reid, J. Phys. Chem. A, 2009, 113, 3886–3894 CrossRef CAS.
- J. D. Patterson and P. J. Reid, J. Phys. Chem. B, 2012, 116, 10437–10443 CrossRef CAS.
- H. F. Davis and Y. T. Lee, J. Chem. Phys., 1996, 105, 8142–8163 CrossRef CAS.
- J. Thøgersen and P. Jepsen, J. Phys. Chem. A, 1997, 101, 3317–3323 CrossRef.
- J. A. Poulsen, C. L. Thomsen, S. R. Keiding and J. Thøgersen, J. Chem. Phys., 1998, 108, 8461–8471 CrossRef.
- J. Poulsen, T. M. Nymand and S. R. Keiding, Chem. Phys. Lett., 2001, 343, 581–587 CrossRef CAS.
- S. C. Hayes, C. C. Cooksey, P. M. Wallace and P. J. Reid, J. Phys. Chem. A, 2001, 105, 9819–9826 CrossRef CAS.
- P. J. Reid, Acc. Chem. Res., 2001, 34, 691–698 CrossRef CAS.
- S. Hayes, P. Wallace, J. C. Bolinger and P. J. Reid, Int. Rev. Phys. Chem., 2002, 21, 405–432 CrossRef CAS.
- P. M. Wallace, J. C. Bolinger, S. C. Hayes and P. J. Reid, J. Chem. Phys., 2003, 118, 1883–1890 CrossRef CAS.
- I. Chorny, J. Vieceli and I. Benjamin, J. Phys. Chem. B, 2003, 107, 229–236 CrossRef CAS.
- J. C. Bolinger, S. C. Hayes and P. J. Reid, J. Chem. Phys., 2004, 121, 4795–4803 CrossRef CAS.
- C. L. Thomsen, D. Madsen, J. A. Poulsen, J. Thøgersen, S. J. K. Jensen and S. R. Keiding, J. Chem. Phys., 2001, 115, 9361–9369 CrossRef CAS.
- D. Madsen, C. L. Thomsen, J. A. Poulsen, S. J. Knak Jensen, J. Thøgersen, S. R. Keiding and E. B. Krissinel, J. Phys. Chem. A, 2003, 107, 3606–3611 CrossRef CAS.
- C. G. Elles, M. Cox, G. L. Barnes and F. F. Crim, J. Phys. Chem. A, 2004, 108, 10973–10979 CrossRef CAS.
- P. Z. El-Khoury, M. Olivucci and A. N. Tarnovsky, Chem. Phys. Lett., 2008, 462, 192–195 CrossRef CAS.
- P. Z. El-Khoury, A. N. Tarnovsky, I. Schapiro, M. N. Ryazantsev and M. Olivucci, J. Phys. Chem. A, 2009, 113, 10767–10771 CrossRef CAS.
- P. Z. El-Khoury, L. George, A. Kalume, S. A. Reid, B. S. Ault and A. N. Tarnovsky, J. Chem. Phys., 2010, 132, 124501 CrossRef.
- W. M. Kwok and D. L. Phillips, Chem. Phys. Lett., 1995, 235, 260–267 CrossRef CAS.
- A. Tarnovsky, J. Alvarez, A. Yartsev, V. Sundsstrom and E. Akesson, Chem. Phys. Lett., 1999, 312, 121–130 CrossRef CAS.
- D. Bingemann, A. M. King and F. F. Crim, J. Chem. Phys., 2000, 113, 5018–5025 CrossRef CAS.
- A. Charvat, J. Abmann and B. Abel, J. Phys. Chem. A, 2001, 105, 5071–5080 CrossRef CAS.
- C. M. Cheatum, M. M. Heckscher, D. Bingemann and F. F. Crim, J. Chem. Phys., 2001, 115, 7086–7093 CrossRef CAS.
- P. Z. El-Khoury, W. M. Kwok, X. Guan, C. Ma, D. L. Phillips and A. N. Tarnovsky, Chemphyschem, 2009, 10, 1895–1900 CrossRef CAS.
- P. Z. El-Khoury, S. K. Pal, A. S. Mereshchenko and A. N. Tarnovsky, Chem. Phys. Lett., 2010, 493, 61–66 CrossRef CAS.
- S. K. Pal, A. S. Mereshchenko, P. Z. El-Khoury and A. N. Tarnovsky, Chem. Phys. Lett., 2011, 507, 69–73 CrossRef CAS.
- F. F. Crim, Faraday Discuss., 2012, 157, 9–26 RSC.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS.
- T. A. A. Oliver, G. A. King, D. P. Tew, R. N. Dixon and M. N. R. Ashfold, J. Phys. Chem. A, 2012, 116, 12444–12459 CrossRef CAS.
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S.-I. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2010, 133, 124313 CrossRef CAS.
- T. N. V. Karsili, A. M. Wenge, S. J. Harris, D. Murdock, J. N. Harvey, R. N. Dixon and M. N. R. Ashfold, Chem. Sci., 2013 Search PubMed , accepted.
- J. S. Lim, I. S. Lim, K.-S. Lee, D.-S. Ahn, Y. S. Lee and S. K. Kim, Angew. Chem., Int. Ed., 2006, 45, 6290–6293 CrossRef CAS.
- I. S. Lim, J. S. Lim, Y. S. Lee and S. K. Kim, J. Chem. Phys., 2007, 126, 034306 CrossRef.
- A. L. Devine, M. G. D. Nix, R. N. Dixon and M. N. R. Ashfold, J. Phys. Chem. A, 2008, 112, 9563–9574 CrossRef CAS.
- M. Hoshino-Nagasaka, T. Suzuki, T. Ichimura, S. Kasahara, M. Baba and S. Kawauchi, Phys. Chem. Chem. Phys., 2010, 12, 13243–13247 RSC.
- J. S. Lim and S. K. Kim, Nat. Chem., 2010, 2, 627–632 CrossRef CAS.
- A. M. Wenge, T. N. V. Karsili, J. Rodriguez-Diaz, M. I. Cotterell, B. Marchetti and M. N. R. Ashfold, J. Phys. Chem. A, 2013 Search PubMed , awaiting submission.
- B. Ward, Spectrochim. Acta, Part A, 1968, 24, 813–818 CrossRef CAS.
- J. B. Kim, T. I. Yacovitch, C. Hock and D. M. Neumark, Phys. Chem. Chem. Phys., 2011, 13, 17378–17383 RSC.
- G. M. Greetham, P. Burgos, Q. Cao, I. P. Clark, P. S. Codd, R. C. Farrow, M. W. George, P. Matousek, A. W. Parker, M. R. Pollard, A. Robinson, Z. Xin and M. Towrie, Appl. Spectrosc., 2010, 64, 1311–1319 CrossRef CAS.
- R. Hermann, G. Dey, S. Naumov and O. Brede, Phys. Chem. Chem. Phys., 2000, 2, 1213–1220 RSC.
- Y. M. Riyad, S. Naumov, R. Hermann and O. Brede, Phys. Chem. Chem. Phys., 2006, 8, 1697–1706 RSC.
- T. A. A. Oliver, Y. Zhang, M. N. R. Ashfold and S. E. Bradforth, Faraday Discuss., 2011, 150, 439–458 RSC.
- C. Rivera, N. Winter, R. V Harper, I. Benjamin and S. E. Bradforth, Phys. Chem. Chem. Phys., 2011, 13, 8269–8283 RSC.
- Y. Zhang, T. A. A. Oliver, M. N. R. Ashfold and S. E. Bradforth, 2013, in preparation.
- Y. Zhang, T. A. A. Oliver, M. N. R. Ashfold and S. E. Bradforth, Faraday Discuss., 2012, 157, 141–163 RSC.
- D. Murdock, S. J. Harris, T. N. V. Karsili, G. M. Greetham, I. P. Clark, M. Towrie, A. J. Orr-Ewing and M. N. R. Ashfold, J. Phys. Chem. Lett., 2012, 3, 3715–3720 CrossRef CAS.
- J. A. Kloepfer, V. H. Vilchiz, V. A. Lenchenkov, A. C. Germaine and S. E. Bradforth, J. Chem. Phys., 2000, 113, 6288–6307 CrossRef CAS.
- Data reported in ref. 93 used this version of eqn (1) though it was type set incorrectly in that article.
- G. M. Roberts, D. J. Hadden, L. T. Bergendahl, A. M. Wenge, S. J. Harris, T. N. V. Karsili, M. N. R. Ashfold, M. J. Paterson and V. G. Stavros, Chem. Sci., 2013, 4, 993–1001 RSC.
- M. Berberan-Santos and J. Martinho, J. Chem. Educ., 1990, 67, 375–379 CrossRef CAS.
- R. Hermann and G. Mahalaxmi, J. Phys. Chem. A, 2002, 106, 2379–2389 CrossRef CAS.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS.
- K. Kesper, F. Diehl, J. G. G. Simon, H. Specht and A. Schweig, Chem. Phys., 1991, 153, 511–517 CrossRef CAS.
- D. Pullin and L. Andrews, J. Mol. Struct., 1982, 95, 181–185 CrossRef CAS.
- T. N. Das, J. Phys. Chem. A, 2005, 109, 3344–3351 CrossRef CAS.
- S. Das and S. E. Bradforth, unpublished result.
- B. M. Giuliano, I. Reva, L. Lapinski and R. Fausto, J. Chem. Phys., 2012, 136, 024505 CrossRef.
- S. J. Greaves, R. A. Rose, T. A. A. Oliver, D. R. Glowacki, M. N. R. Ashfold, J. N. Harvey, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, Science, 2011, 331, 1423–1426 CrossRef CAS.
- R. A. Rose, S. J. Greaves, T. A. A. Oliver, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, J. Chem. Phys., 2011, 134, 244503 CrossRef.
- D. R. Glowacki, R. A. Rose, S. J. Greaves, A. J. Orr-Ewing and J. N. Harvey, Nat. Chem., 2011, 3, 850–855 CrossRef CAS.
- R. A. Rose, S. J. Greaves, F. Abou-Chahine, D. R. Glowacki, T. A. A. Oliver, M. N. R. Ashfold, I. P. Clark, G. M. Greetham, M. Towrie and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2012, 14, 10424–10437 RSC.
- F. Abou-Chahine, S. J. Greaves, G. T. Dunning, A. J. Orr-Ewing, G. M. Greetham, I. P. Clark and M. Towrie, Chem. Sci., 2013, 4, 226–237 RSC.
- F. Galindo, J. Photochem. Photobiol., C, Photochem. Rev., 2005, 6, 123–138 CrossRef CAS.
- L. Claisen, Chem. Ber., 1912, 45, 3175 CrossRef.
- M. S. Kharesch, G. Stampa and W. Nudenberg, Science, 1952, 116, 309 Search PubMed.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238 RSC.
- T. J. Mach, R. A. King and T. D. Crawford, J. Phys. Chem. A, 2010, 114, 8852–8857 CrossRef CAS.
- T. Isozaki, T. Suzuki and T. Ichimura, Chem. Phys. Lett., 2007, 449, 63–66 CrossRef CAS.
- M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp50756d |
| ‡ Current address: Department of Chemistry and Biochemistry, Montana State University, Bozeman, Montana 59715, USA. |
| § Current address: Department of Chemistry, University of California, Berkeley, CA 94720, USA. |
| This journal is © the Owner Societies 2013 |
