 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Growth and oxidation of graphene on Rh(111)†
Karin Gotterbarm, Wei Zhao, Oliver Höfert, Christoph Gleichweit, Christian Papp* and Hans-Peter Steinrück
Lehrstuhl für Physikalische Chemie II, Universität Erlangen-Nürnberg, Egerlandstraße 3, 91058 Erlangen, Germany. E-mail: christian.papp@fau.de
First published on 3rd October 2013
Abstract
The growth and oxidation of graphene supported on Rh(111) was studied in situ by high-resolution X-ray photoelectron spectroscopy. By variation of propene pressure and surface temperature the optimum growth conditions were identified, yielding graphene with low defect density. Oxidation of graphene was studied at temperatures between 600 and 1000 K, at an oxygen pressure of ∼2 × 10−6 mbar. The oxidation follows sigmoidal reaction kinetics. In the beginning, the reaction rate is limited by the number of defects, which represent the active sites for oxygen dissociation. After an induction period, the reaction rate increases and graphene is rapidly removed from the surface by oxidation. For graphene with a high defect density we found that the oxidation is faster. In general, a reduction of the induction period and a faster oxidation occur at higher temperatures.
Introduction
Graphene is an intriguing 2D material1–3 with promising applications, e.g. in microelectronics,4–6 sensors,7–12 as spin-filtering materials,13,14 and as protective coatings.15,16 One versatile route to fabricate graphene is chemical vapor deposition (CVD) on metal surfaces.17,18 This method is particularly interesting, because the graphene–metal interface is important for many of the proposed applications. The morphology and the electronic structure of graphene on a metal substrate strongly depend on the lattice mismatch and on the specific chemical interactions.17–19 Graphene on Rh(111) is considered as an intermediate case, in between strong and weak coupling.19–22 On the Rh(111) single crystal surface, graphene forms a (12 × 11) Moiré superstructure with a periodicity of 2.9 nm due to a lattice mismatch of roughly 10%.20 In those regions of the supercell, where a carbon ring is centered over a bridge position relative to the Rh substrate atoms, hybridization between graphene and Rh 4d states occurs, leading to a carbon–Rh distance of less than 2.3 Å. For the atop position, the interaction between Rh and graphene is weak and the carbon–metal distance is more than 3 Å.22 The resulting complex corrugation pattern has been described in detail by scanning tunneling microscopy (STM) and atomic force microscopy (AFM) measurements.20,21While the structure of graphene on Rh(111) is well investigated,20–22 the growth mechanism during the CVD process on metals is still under investigation. Coraux et al.23 underlined the importance of step edges for the nucleation of graphene flakes on Ir(111), and showed that graphene growth even reshapes the step edges during CVD. Their STM study also indicates that incorporation of carbon adspecies at the graphene edges is the rate limiting step for graphene growth. This finding is supported by electron reflectivity measurements carried out by Loginova et al. on Ir(111) and also Ru(0001).24,25 Their results suggest the addition of five-atom carbon clusters rather than single adatoms to the graphene edges as the rate determining step. A rate model based on these data predicts that six of these five-atom clusters are needed to form a stable nucleus for further graphene growth.26 In contrast, on Rh(111) STM and density functional theory (DFT) studies indicate C21 and C24 clusters as likely precursors for CVD of graphene.27,28 It is suggested that minimizing the number of nucleation sites by controlling the C21 cluster concentration reduces the number of defects in graphene.27 Nevertheless, the growth mechanism of graphene on Rh(111) has not been studied in detail yet. However, the thorough understanding of this mechanism is crucial for the preparation of graphene layers with reproducible quality, i.e. low defect density and large single-crystalline domains. Important parameters to control the quality of graphene are precursor pressure and growth temperature.
Since graphene is also considered as a passivating layer,15,16 the stability of graphene in an oxygen atmosphere presents another important issue. The oxidation of graphene layers is also relevant for catalysis, because coke formation can lead to severe site blocking on heterogeneous catalysts.29 On Ru(0001)30–33 and Ir(111)33–35 etching and intercalation of O2 under the graphene layer were observed, depending on the temperature regime. While Cui et al.31 observed a linear time-dependence for the oxidation of graphene flakes on Ru(0001), Starodub et al.33 reported a more complex behavior: first the equilibrium between graphene and carbon adclusters is shifted by depleting the surface of carbon adatoms. Only thereafter, oxygen can intercalate under graphene and directly attack the layer from below. On Ir(111), the oxidation mechanism appears to be completely dominated by intercalation.33 Graphene on Rh(111) is considered as an intermediate system between Ru(0001) (strong graphene–metal interaction) and Ir(111) (weak graphene–metal interaction).21 One therefore could expect that oxidation of graphene on Rh(111) follows an intermediate mechanism between those two cases. It should also be noted that oxygen intercalation under graphene has only been observed for coverages below a full monolayer of graphene30,32–35 or oxygen pressures higher than 5 × 10−4 mbar.35
In this study, we present the in situ investigation of graphene growth on Rh(111) by high-resolution X-ray photoelectron spectroscopy (HRXPS). We systematically explore the influence of precursor pressure and growth temperature on the quality of graphene and derive optimized preparation parameters for graphene growth. As a subsequent step, HRXPS was also employed to monitor the oxidation of graphene monolayers on Rh(111) at different temperatures.
Experimental details
All measurements were carried out at beamline U49/2-PGM1 of Helmholtz-Zentrum Berlin in a transportable UHV apparatus, described in more detail elsewhere.36 The analyzer chamber is equipped with a three-stage supersonic molecular beam, enabling us to create pressures of up to 10−5 mbar on the sample while acquiring XP-spectra. The sample was a round Rh(111) single crystal with 10 mm diameter and 3 mm thickness (MaTeck). Temperatures between 80 and 1300 K are reached by liquid nitrogen cooling in combination with resistive heating. A type K thermocouple spotwelded to the Rh crystal is used to monitor the sample temperature. The sample was cleaned by Ar sputtering and subsequent annealing to 1100 K. Carbon contaminations (including graphene) were removed by oxidation with 2 × 10−6 mbar oxygen at 900 K and subsequent flashing to 1200 K to desorb oxygen. Final cleanliness was checked by XPS.Graphene layers were prepared by CVD of propene at temperatures between 700 and 1000 K using the molecular beam (to hit the sample directly) or using a background pressure of ∼2 × 10−8 mbar in the chamber. Note that when propene was dosed by backfilling the chamber the background pressure in the chamber slowly increased from 8 × 10−9 to 2 × 10−8 mbar during the experiment. C 1s spectra were collected during graphene growth until saturation of the C 1s signal was reached. The quality of the graphene layers was verified by low energy electron diffraction (LEED).19,21 Additionally we checked the electronic structure of the different graphene layers by measuring the valence band along the Γ-point (hν = 100 eV) and excellent agreement with earlier results was found for all cases.37 Oxygen was dosed directly with the molecular beam creating pressures between 1 × 10−6 and 2 × 10−6 mbar on the sample.
C 1s spectra were collected at a photon energy of 380 eV, with a total energy resolution of 170 meV. The acquisition time was 9 s per spectrum. All XP spectra were recorded at normal emission. The size of the photon beam on the sample was 125 μm. Binding energies are referenced to the Fermi level. For the background correction a straight line was subtracted from each spectrum. The components of the C 1s spectra were fitted with asymmetric Doniach–Sunjic functions convoluted with a Gaussian function.38 The Lorentzian width for both C 1s graphene components was kept constant at 0.1 eV. However, the Gaussian width varied from 0.23 to 0.68 eV depending on the defect density of the graphene layer and the temperature at which the spectra were recorded.
Results and discussion
Graphene was grown on the Rh(111) surface by CVD of propene at ∼2 × 10−8 mbar at elevated temperatures. Selected C 1s spectra recorded during the growth process at 920 K are shown in Fig. 1a. During propene exposure two signals at 285.2 and 284.5 eV arise simultaneously. This behavior is attributed to the corrugation of the graphene sheet on the Rh(111) surface, which results in carbon atoms with different bonding strengths to the surface.21,22 The different surface–graphene bonds lead to two separate signals in the C 1s region.19 The peak at 285.2 eV has a similar binding energy as found for graphene that is strongly coupled to a substrate (e.g. graphene on Ni(111)39). This contribution (referred to as C1) is therefore assigned to carbon atoms in the Moiré unit cell, which bond strongly to the surface, i.e. where a carbon ring is centered over a bridge position. The binding energy of 284.5 eV is close to the value found for weakly coupled or quasi-freestanding graphene.19 Hence this contribution (referred to as C2) is assigned to carbon atoms further away from the surface. A typical fit is shown in Fig. 1b. The Lorentzian width is 100 meV for both contributions and the Gaussian widths are 410 and 360 meV for C1 and C2, respectively. Fig. 1c shows the fit results for the data shown in Fig. 1a. The growth rate is constant in the beginning and slows down with increasing graphene coverage. This behavior is attributed to the decrease of uncovered Rh surface regions available for propene adsorption and subsequent dehydrogenation. At ∼30 Langmuir (L), the graphene coverage reaches saturation. The C1 signal is around 1.4 times higher than the C2 signal, which indicates (neglecting photoelectron diffraction effects) a larger fraction of strongly bound graphene atoms during the entire growth process. Rh 3d spectra recorded during the growth process are available in the ESI,† Fig. S1.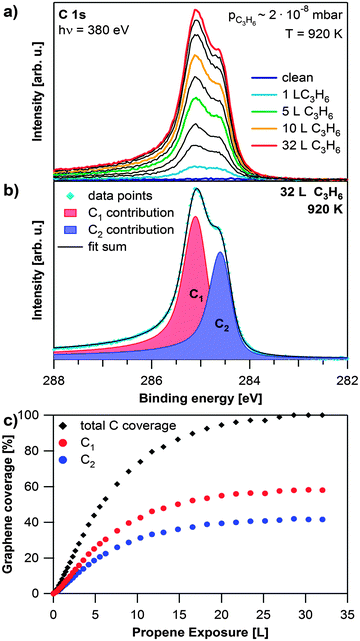 | ||
| Fig. 1 Growth of graphene on Rh(111). (a) Selected C 1s spectra during propene exposure at 920 K; the propene exposure of the coloured spectra is shown in the legend, black spectra are recorded at exposures in between the given values; during the experiment the pressure in the chamber slowly increased from 8 × 10−9 to 2 × 10−8 mbar. (b) Fit of saturated C 1s spectrum. (c) Quantitative analysis of the experiment shown in (a). | ||
After graphene growth the sample is cooled down and C 1s spectra are recorded during the cooling process. Selected spectra are shown in Fig. 2a. During cooling from 925 to 155 K, the peak at 284.5 eV increases in relative intensity. Additionally both contributions shift further apart by 50 meV and decrease in width. Fig. 2b shows that the Gaussian widths of both contributions decrease with temperature (by 58 meV for C1 and 97 meV for C2). We attribute this decrease to the fact that at lower temperatures less vibrations of the graphene layer are excited and thus the local environment is more defined, leading to a smaller linewidth. This effect is less pronounced for the more strongly bound carbon atoms, and thus the narrowing of the C1 signal is smaller than for the C2 signal. During cooling, the ratio between the two carbon species decreases from 1.4 to 1.2 indicating that at lower temperatures more carbon atoms are in the weakly coupled state with a larger distance from the Rh surface. In order to verify that we obtained a uniform graphene layer, we measured C 1s spectra at 155 K over the whole sample; except for regions close to the edge of the crystal, identical spectra were observed. This is in line with our LEED measurements (data not shown), which always showed a clear Moiré pattern.19,21
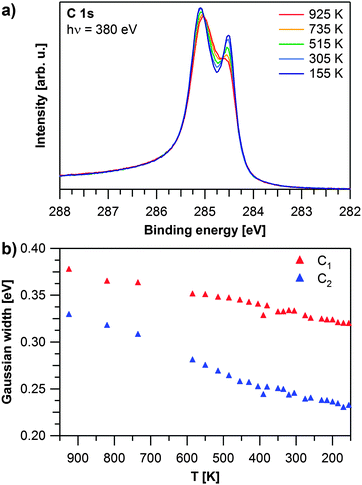 | ||
| Fig. 2 Temperature dependent evolution of graphene on Rh(111): (a) selected C 1s spectra recorded during cooling down. (b) Gaussian widths of the C 1s contributions as obtained by fitting the experiment shown in (a). | ||
To elucidate the influence of the growth parameters for graphene on Rh(111), both propene pressure and sample temperature were varied, yielding graphene layers of different quality. The spectra of graphene layers grown at temperatures from 700 to 1000 K, at propene pressures of 2 × 10−8 or 2 × 10−6 mbar are depicted in Fig. 3. They were recorded below 150 K to reduce the influence of vibrations in the graphene layer.
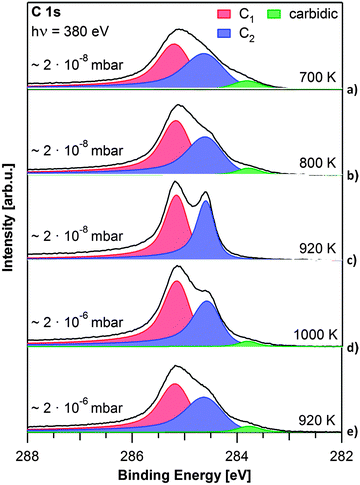 | ||
| Fig. 3 C 1s spectra of graphene layers grown at different pressures and temperatures, as denoted. All spectra were recorded at T < 150 K. | ||
First we discuss the influence of the precursor pressure on graphene growth. Fig. 3c shows the spectrum of a graphene layer grown at 920 K at 2 × 10−8 mbar. Graphene grows slowly and a closed layer is reached after 45 min (32 L) (see also Fig. 1). The layer shown in Fig. 3e was grown at the same temperature, but at a pressure of 2 × 10−6 mbar on the sample (achieved with the molecular beam hitting the sample directly), and is saturated already after 40 s (80 L). For the higher pressure and shorter preparation time, the C 1s graphene peaks are broad and not clearly separated. The Gaussian width is 0.54 eV for the C1 contribution at 285.2 eV and 0.66 eV for the C2 shoulder at 284.6 eV. A third carbon contribution from carbidic carbon forms at 283.8 eV. LEED measurements of this graphene layer showed a diffuse circle around the substrate spots instead of the clearly resolved Moiré pattern observed before, indicating multiple rotational graphene domains. From the comparison of the C 1s spectra of the two layers prepared at 920 K but with different precursor pressures, we conclude that the width of the C1 and C2 peaks is an indicator of the quality (i.e. defect density) of the graphene layers. The Gaussian widths and carbidic carbon content for all spectra displayed in Fig. 3 are listed in Table S2 in the ESI.† The higher defect density found for the higher precursor pressure can be explained as follows: at higher precursor pressure the carbon adatom concentration is well above the concentration necessary to nucleate graphene islands.24–26 Therefore nucleation simultaneously occurs at numerous sites, leading to a large number of small graphene domains and consequently domain boundaries, yielding a high defect density in the resulting layer. From our measurements we conclude that lower precursor pressures lead to graphene layers with a lower defect density.
Next, we discuss the influence of the substrate temperature: Fig. 3a–c show spectra of graphene layers prepared at the lower propene pressure of 2 × 10−8 mbar at 700, 800 and 920 K, respectively. The layer grown at 700 K exhibits broad C 1s signals (Gaussian widths: 0.59 and 0.68 eV for C1 and C2, respectively), and a carbidic carbon signal at 283.8 eV. With increasing temperature, the graphene signals become more distinct and the carbidic carbon contribution at 283.8 eV decreases (800 K) or vanishes completely (920 K) (see also Table S2, ESI†). This temperature dependence can be explained considering the results of Yuan et al.27 They found that the lifetime of C21 clusters, which are likely to be the nucleation sites for graphene growth, decreases with temperature. It is suggested that minimizing the number of nucleation sites will lead to less defects in the resulting graphene layer. At even higher temperatures carbon starts to dissolve into the bulk of the crystal and carbidic carbon from the subsurface can diffuse to the surface. From thermal stability experiments (see ESI,† Fig. S3) we conclude that the onset of carbon diffusion into the bulk of the crystal lies between 1000 and 1100 K. Therefore, we were not able to grow graphene at 1000 K using 2 × 10−8 mbar propene, but had to increase the propene pressure to 2 × 10−6 mbar. The corresponding C 1s spectrum in Fig. 3d shows significantly broader peaks than the one for growth at 920 K, along with a small carbidic carbon contribution at 283.8 eV. The Gaussian widths are 0.51 eV for the C1 peak and 0.53 eV for the C2 peak. Due to the higher propene pressure, saturation is again reached faster, leading to more domains and therefore a higher defect density (see discussion of Fig. 3e). To conclude this section, our pressure- and temperature-dependent measurements show that for graphene growth on Rh(111), a temperature of 920 K and a propene pressure of 2 × 10−8 mbar represent the best conditions to produce layers with extended domains and few defects.
As next topic, we discuss the oxidation of the saturated graphene layer, grown at 920 K and a propene pressure of 2 × 10−8 mbar, see also Fig. 3c. Selected spectra recorded during the oxidation of graphene with 1 × 10−6 mbar oxygen at 900 K are shown in Fig. 4a. After an induction period of ∼150 L (200 s), both carbon species start to vanish simultaneously. The carbon coverage continues to decrease, until no carbon is left on the surface after an exposure of 633 L of oxygen (red spectrum). Since we do not observe any other carbon species and carbon–oxygen groups we conclude that graphene is etched by exposure to oxygen and directly desorbed as CO or possibly CO2. The quantitative analysis of this experiment, shown in Fig. 4b, reveals S-shaped reaction kinetics. The first part of the reaction is an induction period, in which the carbon coverage stays almost constant. The induction period lasts until an exposure of approximately 150 L of oxygen. Thereafter, the carbon coverage decreases quickly until 450 L. The last part of the reaction resembles an exponential decay, which would be typical for a first or pseudo-first order reaction.
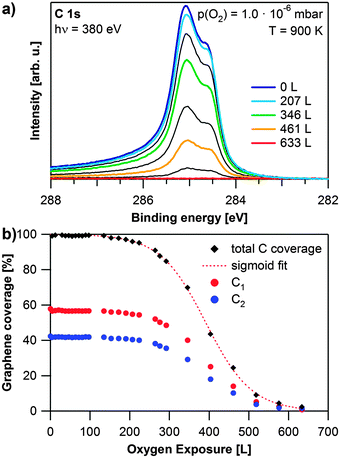 | ||
| Fig. 4 Oxidation of graphene on Rh(111): (a) selected spectra during oxidation with 1 × 10−6 mbar O2 at 900 K, the oxygen exposure of the coloured spectra is shown in the legend, black spectra are recorded at exposures in between the given values; (b) quantitative analysis of the experiment shown in (a) as obtained from fitting, red dotted line: sigmoidal fit of the total graphene coverage. | ||
The observed behavior can be explained, if we consider the relation between the number of free adsorption sites and the carbon coverage. Initially, the whole rhodium surface is covered with graphene. Therefore oxygen can only adsorb and dissociate at defects in the graphene layer. For Ir(111), graphene oxidation has, e.g. been reported to start at wrinkles of the graphene layer.33 In this initial regime, the reaction rate is limited by the oxygen coverage (i.e., the number of free adsorption sites). After the induction period, more and more adsorption sites on the Rh surface become available and the reaction rate increases. Subsequently, the (decreasing) carbon coverage becomes the rate-limiting factor causing the reaction rate to slow down again. Since oxygen is supplied in excess from the gas phase, the reaction rate depends only on the carbon coverage at this stage. Therefore the reaction can be considered as a pseudo first order reaction in this regime. The observed profile can be described by a sigmoidal curve as shown by the fit (dotted red line). At temperatures below 600 K (not shown), we observed no change in the C 1s signal, even after exposure to 1000 L of oxygen. This is in contrast to previous studies of graphene on Ru(0001) and Ir(111), which reported intercalation of oxygen below 600 K.30,34,35 Since we did not observe any signal in the O 1s region, intercalation of oxygen under the saturated graphene layer does not occur under the conditions applied in our study. Furthermore, even after exposure of a graphene layer to air for four hours we found no significant changes in the C 1s and Rh 3d core levels.
To elucidate the influence of defects, we studied the oxidation of two different saturated graphene layers on Rh(111), which were grown at 920 K at different propene pressures. Fast grown layers (2 × 10−6 mbar propene, Fig. 3e) are referred to as high defect density graphene, slowly grown layers (2 × 10−8 mbar propene, Fig. 3c) are referred to as low defect density graphene. For both layers, we investigated the oxidation at 2 × 10−6 mbar of oxygen in the temperature range from 600 to 1000 K. The corresponding results are shown in Fig. 5. The data points correspond to the total graphene coverage. All experiments show the same S-shaped time dependent behavior and can be fitted with sigmoidal curves (dotted lines).
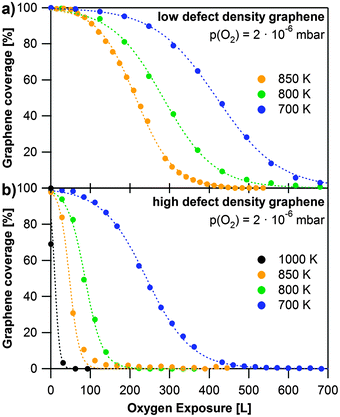 | ||
| Fig. 5 Oxidation of graphene at different temperatures with 2 × 10−6 mbar oxygen. The data points are the sum of both graphene C 1s contributions, dotted lines display sigmoidal fits of the data. (a) Oxidation of low defect density graphene; (b) oxidation of high defect density graphene. | ||
Fig. 5a shows a series of oxidation experiments with low defect density graphene, carried out at temperatures between 700 and 850 K. The length of the induction period decreases and the reaction rate increases with temperature. Note that the data in Fig. 4b at 900 K show a somewhat longer induction period than the data at 850 K in Fig. 5a (see also Fig. S4 in the ESI†). This behavior does not fit into the overall trend and seems to be a discrepancy at first glance. It can, however, be understood, if one considers that layers, which have been prepared independently under nominally the same conditions, can display different defect densities. While this influences the length of the induction period, it should not influence the slope of the subsequent decrease due to oxidation, which indeed occurs faster with increasing temperatures for all layers studied – see Fig. 5a (and Fig. S4 in the ESI†).
The series of oxidation experiments with high defect density graphene is displayed in Fig. 5b. In comparison to the data shown in Fig. 5a it is obvious that graphene sheets with a higher defect density are oxidized much faster than low defect density sheets under the same oxidation conditions. Especially the induction period is much shorter, since the oxidation starts at defects in the layer. The reaction rate again increases with temperature, as expected. It is interesting to note that for high defect density graphene we also observed etching at 600 K. However, at this temperature oxidation is very slow with an induction period of roughly 1000 L (1500 s). The layer was completely oxidized after exposure to 4000 L of oxygen.
Our data clearly show the great influence of the defect density on the oxidation rate. Ideally, one would aim at deriving the detailed reaction kinetics from the data in Fig. 5. We however, refrain from such an analysis due to the following reasons: XPS is a technique integrating over a large surface area as compared to the typical size of a graphene domain. Nevertheless regarding the high quality of the graphene layer the number of domain boundaries (and thus defects) and also the size of the domains probed will vary. The measured overall reaction rate, as deduced from Fig. 5, will be the sum of different induction periods and also different domain size-dependent oxidation rates. We thus have to conclude that while our measurements clearly allow demonstrating a dramatic decrease of the induction time and increase of the reaction rate, they do not permit us to determine detailed kinetic parameters such as the activation energy. Here, ideally local probes could be beneficial, which however face inherent problems in the in situ quantitative analysis at elevated temperatures.
Conclusions
We investigated the growth and oxidation of graphene on Rh(111) by in situ HRXPS. In agreement with previous studies, we find two C 1s species indicative of graphene regions exhibiting strong and weak interactions with the Rh substrate. The width of the C 1s signals is considerably temperature dependent due to vibrations of the graphene layer. By systematically exploring the preparation parameters we were able to optimize the graphene growth conditions. CVD of graphene on Rh(111) at 920 K and 2 × 10−8 mbar propene pressure leads to layers with low defect density and large, single crystalline domains. We present the first report of oxidation of graphene on Rh(111). Oxidation of graphene was observed at temperatures between 600 and 1000 K and at an oxygen pressure of ∼2 × 10−6 mbar. We find that the oxidation follows sigmoidal reaction kinetics. In the beginning the reaction rate is governed by the concentration of oxygen on the surface, which is determined by the number of free adsorption sites. After this induction period, the reaction rate accelerates and graphene is rapidly removed from the surface. The length of the induction period decreases and the rate constant increases with defect density in the graphene layers, and also with surface temperature. The reaction kinetics turned out to be very complex, which is attributed to the fact that both the length of the induction period and the reaction rate depend on the size of the graphene domains and defect density.Acknowledgements
The authors gratefully acknowledge the funding from SFB 953 “Synthetic Carbon Allotropes” and the German Research Council (DFG), which, within the framework of its “Excellence Initiative”, supports the Cluster of Excellence “Engineering of Advanced Materials” (www.eam.uni-erlangen.de) at the Universität Erlangen-Nürnberg. We thank HZB for the allocation of synchrotron radiation beamtime and the BESSY staff for support during beamtime. K. G. thanks the “Fonds der chemischen Industrie” for providing her a PhD grant. W. Z. thanks the China Scholarship Council for financing his PhD grant.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- K. S. Novoselov, Rev. Mod. Phys., 2011, 83, 837–849 CrossRef CAS.
- Y.-M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Farmer, H.-Y. Chiu, A. Grill and P. Avouris, Science, 2010, 327, 662 CrossRef CAS PubMed.
- Y.-M. Lin, A. Valdes-Garcia, S.-J. Han, D. B. Farmer, I. Meric, Y. Sun, Y. Wu, C. Dimitrakopoulos, A. Grill, P. Avouris and K. A. Jenkins, Science, 2011, 332, 1294–1297 CrossRef CAS PubMed.
- S. Bae, H. Kim, Y. Lee, X. Xu, J.-S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. Ri Kim, Y. I. Song, Y.-J. Kim, K. S. Kim, B. Ozyilmaz, J.-H. Ahn, B. H. Hong and S. Iijima, Nat. Nanotechnol., 2010, 5, 574–578 CrossRef CAS PubMed.
- S. Alwarappan, S. Boyapalle, A. Kumar, C.-Z. Li and S. Mohapatra, J. Phys. Chem. C, 2012, 116, 6556–6559 CAS.
- S. Alwarappan, K. Cissell, S. Dixit, C.-Z. Li and S. Mohapatra, J. Electroanal. Chem., 2012, 686, 69–72 CrossRef CAS PubMed.
- S. Alwarappan, A. Erdem, C. Liu and C.-Z. Li, J. Phys. Chem. C, 2009, 113, 8853–8857 CAS.
- S. Alwarappan, C. Liu, A. Kumar and C.-Z. Li, J. Phys. Chem. C, 2010, 114, 12920–12924 CAS.
- S. Alwarappan, S. R. Singh, S. Pillai, A. Kumar and S. Mohapatra, Anal. Lett., 2012, 45, 746–753 CrossRef CAS.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- V. M. Karpan, G. Giovannetti, P. A. Khomyakov, M. Talanana, A. A. Starikov, M. Zwierzycki, J. van den Brink, G. Brocks and P. J. Kelly, Phys. Rev. Lett., 2007, 99, 176602 CrossRef CAS.
- S. D. Yu and M. Fonin, New J. Phys., 2010, 12, 125004 CrossRef.
- E. Sutter, P. Albrecht, F. E. Camino and P. Sutter, Carbon, 2010, 48, 4414–4420 CrossRef CAS PubMed.
- S. Chen, L. Brown, M. Levendorf, W. Cai, S.-Y. Ju, J. Edgeworth, X. Li, C. W. Magnuson, A. Velamakanni, R. D. Piner, J. Kang, J. Park and R. S. Ruoff, ACS Nano, 2011, 5, 1321–1327 CrossRef CAS PubMed.
- J. Wintterlin and M.-L. Bocquet, Surf. Sci., 2009, 603, 1841–1852 CrossRef CAS PubMed.
- M. Batzill, Surf. Sci. Rep., 2012, 67, 83–115 CrossRef CAS PubMed.
- A. B. Preobrajenski, M. L. Ng, A. S. Vinogradov and N. Martensson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 073401 CrossRef.
- B. Wang, M. Caffio, C. Bromley, H. Früchtl and R. Schaub, ACS Nano, 2010, 4, 5773–5782 CrossRef CAS PubMed.
- E. N. Voloshina, Y. S. Dedkov, S. Torbrügge, A. Thissen and M. Fonin, Appl. Phys. Lett., 2012, 100, 241606 CrossRef.
- M. Iannuzzi and J. Hutter, Surf. Sci., 2011, 605, 1360–1368 CrossRef CAS PubMed.
- J. Coraux, A. T. N'Diaye, M. Engler, C. Busse, D. Wall, N. Buckanie, F. Meyer zu Heringdorf, R. van Gastel, B. Poelsema and T. Michely, New J. Phys., 2009, 11, 023006 CrossRef.
- E. Loginova, N. C. Bartelt, P. J. Feibelman and K. F. McCarty, New J. Phys., 2008, 10, 093026 CrossRef.
- E. Loginova, N. C. Bartelt, P. J. Feibelman and K. F. McCarty, New J. Phys., 2009, 11, 063046 CrossRef.
- A. Zangwill and D. D. Vvedensky, Nano Lett., 2011, 11, 2092–2095 CrossRef CAS PubMed.
- Q. Yuan, J. Gao, H. Shu, J. Zhao, X. Chen and F. Ding, J. Am. Chem. Soc., 2011, 134, 2970–2975 CrossRef PubMed.
- B. Wang, X. Ma, M. Caffio, R. Schaub and W.-X. Li, Nano Lett., 2011, 11, 424–430 CrossRef CAS PubMed.
- P. Forzatti and L. Lietti, Catal. Today, 1999, 52, 165–181 CrossRef CAS.
- P. Sutter, J. T. Sadowski and E. A. Sutter, J. Am. Chem. Soc., 2010, 132, 8175–8179 CrossRef CAS PubMed.
- Y. Cui, Q. Fu, H. Zhang, D. Tan and X. Bao, J. Phys. Chem. C, 2009, 113, 20365–20370 CAS.
- H. Zhang, Q. Fu, Y. Cui, D. Tan and X. Bao, J. Phys. Chem. C, 2009, 113, 8296–8301 CAS.
- E. Starodub, N. C. Bartelt and K. F. McCarty, J. Phys. Chem. C, 2010, 114, 5134–5140 CAS.
- E. Grånäs, J. Knudsen, U. A. Schröder, T. Gerber, C. Busse, M. A. Arman, K. Schulte, J. N. Andersen and T. Michely, ACS Nano, 2012, 6, 9951–9963 CrossRef PubMed.
- R. Larciprete, S. Ulstrup, P. Lacovig, M. Dalmiglio, M. Bianchi, F. Mazzola, L. Hornekær, F. Orlando, A. Baraldi, P. Hofmann and S. Lizzit, ACS Nano, 2012, 6, 9551–9558 CrossRef CAS PubMed.
- R. Denecke, M. Kinne, C. M. Whelan and H.-P. Steinrück, Surf. Rev. Lett., 2002, 9, 797–801 CrossRef CAS.
- M. Sicot, P. Leicht, A. Zusan, S. Bouvron, O. Zander, M. Weser, Y. S. Dedkov, K. Horn and M. Fonin, ACS Nano, 2012, 6, 151–158 CrossRef CAS PubMed.
- S. Doniach and M. Šunjić, J. Phys. C: Solid State Phys., 1970, 3, 285 CrossRef CAS.
- W. Zhao, S. M. Kozlov, O. Höfert, K. Gotterbarm, M. P. A. Lorenz, F. Vines, C. Papp, A. Görling and H.-P. Steinrück, J. Phys. Chem. Lett., 2011, 2, 759–764 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Rh 3d data of the CVD process, a table of the gaussian widths of the graphene signals and the area of the carbidic carbon signal of the discussed graphene layers, measurements of the thermal stability of graphene on Rh(111) and additional data regarding the oxidation of graphene. See DOI: 10.1039/c3cp53802h |
| This journal is © the Owner Societies 2013 |
