High energy X-rays and the frontiers of materials chemistry

In 2004, when I first joined the ESRF, and aside from a few vague notions about the X-rays one finds in hospitals, I had no awareness that very high energy X-rays existed or what they might be useful for. That I did eventually become aware at some point largely arose from the fact that I was working inside a big 3rd generation synchrotron and had the good fortune to meet a number of people who know far more than I do. It has been their willingness to rectify (in as much as one can) my own ignorance that has led to this themed issue.

Herein many of the real experts in a range of materials chemistry fields (e.g. solid state chemistry, catalysis, battery research, sensors, polymers, fuel cells, glassy materials, magnetic materials, materials for optical application, and so on), demonstrate why very high energy X-rays are a very important, though thus far relatively under-utilized, means to investigate a whole host of interesting and important systems and issues that are often intractable using other methods.

That very high energy X-rays have a great deal to offer all of these areas in many senses, is far from a new notion. However, it is the maturation of high energy, 3rd generation synchrotron sources – such as the ESRF (6 GeV), APS (7 GeV), Spring 8 (8 GeV), and Petra III (6 GeV) – along with other technological advances in detectors¹ and focusing optics,² that have radically and recently, changed the high energy X-ray landscape.

Instead of taking days, data may be collected in seconds or less and/or with extremely high spatial resolution. As such, a variety of experimental possibilities that may have been unthinkable only a few years ago, are now possible.

Some of this new potential simply complements the information that can be obtained at lower X-ray energies, or indeed from neutron studies. However, the nature of high energy X-rays means that techniques such as X-ray diffraction (energy dispersive – e.g. van der Voorde, DOI: 10.1039/c3cp44349c, and Williams, DOI: 10.1039/c3cp44339f, or monochromatic – e.g. Wallace, DOI: 10.1039/c2cp43732e, and Wragg, DOI: 10.1039/c3cp44343d) can be applied where otherwise they might not (for instance within restrictive sample environments, e.g. Ferri, DOI: 10.1039/c3cp44638g, Kubacka, DOI: 10.1039/c3cp44293d, Bounechada, DOI: 10.1039/c3cp44289f, Wragg, DOI: 10.1039/c3cp44343d, or for samples that are themselves extremely absorbing).

Other possibilities, such as total X-ray scattering/pair distribution function (PDF) analysis (where again there is an extremely attractive overlap with neutron scattering methods – see Bednarcik, DOI: 10.1039/c3cp44445g, Billinge, DOI: 10.1039/c3cp00111c, Bytchkov, DOI: 10.1039/c3cp50536g, Chapman, DOI: 10.1039/c3cp50590a, Coduri, DOI: 10.1039/c3cp44300k, Hannon, DOI: 10.1039/c3cp51348c, Hoppe, DOI: 10.1039/c2cp42772a, Cramer, DOI: 10.1039/c3cp44298e, Petkov, DOI: 10.1039/c2cp43378h, Sankar, DOI: 10.1039/c3cp50600b, Skinner, DOI: 10.1039/c3cp44347g, and White DOI: 10.1039/c3cp44342f), and EXAFS at heavy element K edges, are unique to the high energy X-ray arena (see Nagai et al., DOI: 10.1039/c3cp44316g, Korthout et al., DOI: 10.1039/c3cp44334e, D’Angelo et al., DOI: 10.1039/c3cp50842k).

Hopefully, the contents of this issue will exemplify all of these characteristics, overlaps, and possibilities, as applied to problems in materials chemistry, and possibly inspire those who have not yet done so to try something within whatever field of materials chemistry they operate.

What, therefore, are these basic characteristics of high energy X-rays that yield such experimental possibilities, and why are high energy synchrotrons in such a unique position to offer the highest potential of all in this area?

Fig. 1 shows the X-ray throughput obtained from bending magnet sources at a 3 GeV and 6 GeV source. It is more than evident that at high X-ray energies size does really matter. Moreover, this basic trend applies no matter what insertion device may be applied to further increase the basic X-ray throughput one can obtain.

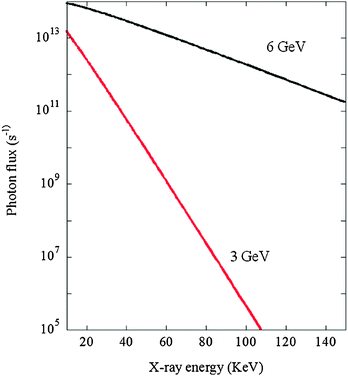Fig. 1 Photon flux from a bending magnet source (0.8 T, 200 mA source current) at a 6 GeV and 3 GeV synchrotrons in the range 10 to 150 keV. Calculated using the ESRF XOP software.³

Fig. 2 shows a representation of what physicists call the “flattening of the Ewald sphere”. What this means is that at high energies (short wavelengths, λ), reciprocal space (Q (Å⁻¹) or 2θ) is progressively compressed into smaller solid angles (λ α sin θ).

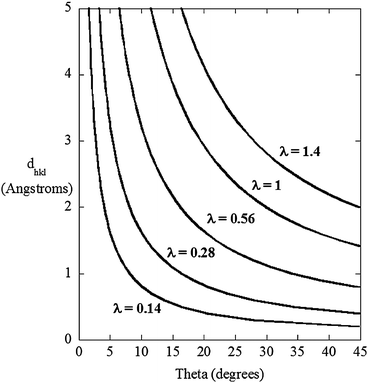Fig. 2 The angular compression of reciprocal space – in this case expressed in terms of real space – as a function of X-ray wavelength (λ). A wavelength of 0.14 Å corresponds to ca. 90 keV.

This very simple notion is extremely useful if one wishes to make X-ray scattering measurements in operando and within very restrictive sample environments. My own initial forays into this realm⁴ have been based almost entirely on this concept, and the contributions to this issue from Ferri (DOI: 10.1039/c3cp44638g), Kubacka (DOI: 10.1039/c3cp44293d) and Bounechada (DOI: 10.1039/c3cp44289f) rely upon this effect making a combination of time resolved diffuse reflectance infrared spectroscopy and high energy X-ray diffraction possible.

This basic idea also underpins the recent development of fast total X-ray scattering/PDF analysis.² At high energies the angular compression of reciprocal space is sufficient to make the large range of Q space required for PDF analysis obtainable using flat panel Si detectors.

Two other properties of high energy X-rays are also very worthy of note. Firstly, as the energy of the X-rays increases so does their ability to penetrate matter. Again this makes measurements within various environments, and with certain materials, possible, whereas they are either very difficult or not possible at all lower energies: for example, within a range of elements the ability to access a high energy K edge to obtain structural information using EXAFS is significantly preferred to interrogating the much lower energy L edges wherein the proximity of the L2 edge to the L3, or indeed overlap between L edges (or K edges of lighter elements) rules out the obtaining of EXAFS (e.g. Korthout, DOI: 10.1039/c3cp44334e, Nagai, DOI: 10.1039/c3cp44316g, and D’Angelo, DOI: 10.1039/c3cp50842k).

Secondly, and of particular importance when dealing with soft and/or intrinsically labile materials, the potential for adventitious damage caused by illumination by the X-rays themselves is often massively reduced at higher energies: both photo-excitation cross-sections, and the net absorption of X-ray energy, are far, far lower than at more conventional wavelengths.

As a final note, and returning to the continuing evolution of third generation synchrotrons: within the reworking of synchrotron sources themselves – to be undertaken in the near future at the ESRF, and possibly elsewhere as well – the provision of high energy X-rays should benefit enormously. Gains of the order of (at least) 30 in terms of flux can be foreseen.

A further step jump in the intrinsic potential of insertion device-based high energy experimentation is, therefore, seemingly just around the corner. As such, for the diverse collection of researchers in materials chemistry that this themed issue hopes to address, the future could be about to get much brighter: this assuming that the larger synchrotrons, all of which are currently in various stages of upgrading, ensure that sufficient resources are indeed committed to an area of X-ray provision within which they are, and will remain for the foreseeable future, peerless.

By way of acknowledgement I should very much like to thank all those authors whose research and hard work makes this issue what it is. PCCP and the RSC editorial office are gratefully thanked for taking on this idea in the first place, and for making the whole experience as smooth and pleasurable as I could have imagined. The Royal Society of Chemistry are also a thanked for the Journals grant (09 01 639) that permitted me to make my first foray into the world of high energy total X-ray scattering, as is the APS for a subsequent visiting scientist position to continue and develop that collaboration; the ESRF are thanked for permitting me the time away to follow this line of enquiry. Paul Thompson (XMAS – UK CRG beamline at the ESRF) is also gratefully thanked for calculating the X-ray flux curves shown in Fig. 1.

Finally I should very much like to thank Peter Chupas, Karena Chapman and all at sector 11 at the APS, as well as Marco Di Michiel and the team at ID15 at the ESRF, for reminding me that doing (hopefully) interesting new things and having a thoroughly good time are not mutually exclusive concepts.

References

1. For instance, (a) P. J. Chupas, X. Y. Qiu, J. C. Hanson, P. L. Lee, C. P. Grey and S. J. L. Billinge, J. Appl. Crystallogr., 2003, 36, 1342; (b) P. J. Chupas, K. W. Chapman and P. L. Lee, J. Appl. Crystallogr., 2007, 40, 463.
2. G. B. M. Vaughan, J. P. Wright, A. Bytchkov, M. Rossat, H. Gleyzolle, I. Snigireva and A. Snigirev, J. Synchrotron Radiat., 2011, 18, 125.
3. M. S. del Rio and R. J. Dejus, in Materials, manufacturing, and measurement for synchrotron radiation mirrors, Proc. SPIE–Int. Soc. Opt. Eng., 1997, 3152, 148.
4. M. A. Newton, M. Di Michiel, A. Kubacka and M. Fernández-García, J. Am. Chem. Soc., 2010, 132, 4540.

---