 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-stoichiometry in “CaCu3Ti4O12” (CCTO) ceramics†
Rainer
Schmidt
*a,
Shubhra
Pandey
bc,
Patrick
Fiorenza
d and
Derek C.
Sinclair
b
aUniversidad Complutense de Madrid, Departamento Física Aplicada III, GFMC, Facultad de Ciencias Físicas, 28040 Madrid, Spain. E-mail: rainerxschmidt@googlemail.com
bThe University of Sheffield, Materials Science and Engineering, Mappin Street, Sheffield, S1 3JD, United Kingdom
cIndian Institute of Technology Kanpur, Department of Materials Science and Engineering, Kalyanpur, Kanpur - 208 016, India
dCNR-IMM, Strada VIII n.5, Zona Industriale, 95121 Catania, Italy
First published on 24th May 2013
Abstract
A combined powder X-ray lattice parameter and ceramic impedance spectroscopy study is presented on materials within the CaO–CuO–TiO2 ternary phase diagram. Several compositions containing CaCu3Ti4O12 (CCTO) and small amounts of secondary phases such as TiO2, CaTiO3 and CuO are analysed and two different defect mechanisms are identified as the cause of the non-stoichiometry in CCTO. The first mechanism involves a variation in the Cu content, which explains the large differences in the intrinsic bulk and extrinsic grain boundary (GB) resistance, and the formation of the ceramic internal barrier layer capacitor (IBLC) structure. The second mechanism is associated with Ca–Cu anti-site disorder causing an unusually high intrinsic bulk permittivity above that predicted from Clausius–Mossotti calculations.
I. Introduction
The ternary oxide compound CaCu3Ti4O12 (CCTO) is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 A-site ordered perovskite (A′A′′3B4O12) where the oxygen octahedra are strongly tilted and the A′′ site Cu cations adapt a fourfold square–planar coordination. The CCTO unit cell is a doubled simple perovskite cell and is commonly indexed as cubic Im
3 A-site ordered perovskite (A′A′′3B4O12) where the oxygen octahedra are strongly tilted and the A′′ site Cu cations adapt a fourfold square–planar coordination. The CCTO unit cell is a doubled simple perovskite cell and is commonly indexed as cubic Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) .1,2 The octahedral tilting can be described as a+a+a+ in the Glazer notation.3–5
.1,2 The octahedral tilting can be described as a+a+a+ in the Glazer notation.3–5
CCTO has attracted considerable interest due to its giant dielectric permittivity values;6–11 in polycrystalline ceramics the highest values reported are ≈ 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.12 It is now well established that such high permittivity values have an extrinsic origin.13,14 In ceramics, an internal barrier layer capacitor (IBLC) structure has been proposed that is made up of semiconducting grains and insulating grain boundaries (GBs), where the extrinsic giant permittivity εGB would be called a GB effect.15 In single crystals and epitaxial thin films, giant permittivity can be associated with an extrinsic electrode–sample interface effect,16,17 which can also contribute to the giant permittivity in ceramics.18 The intrinsic relative dielectric permittivity, εb, of bulk CCTO was reported to be around 100.14 While this is considerably lower than the giant extrinsic values, it is still higher than would be expected in a non-ferroelectric material based on the polarizabilities of the constituent atoms19 as predicted by the Clausius–Mossotti equation (i.e., εb in CCTO is expected to be ≈ 48). The difference in electrical conductivity between the GB and bulk areas in CCTO is large: the GB charge transport activation energy EA is about 0.5–0.8 eV, while the bulk EA is about 10–100 meV,15,20 additionally, the nominal resistance of the GB and bulk areas vary by a factor of up to ≈ 105. Considering that the GB areas are expected to be thin layers the actual difference in resistivity may be even more dramatic. It was shown previously that this distinct ceramic IBLC structure becomes more pronounced during the ceramic sintering process and is associated with segregation of Cu towards the GB areas.21 More recently it was shown that the interior conducting grain phase of CCTO in fact grows out of an insulating matrix during sintering, most likely by segregation of Cu out of the conducting areas.22 Here, in this work, such Cu segregation is explicitly associated with a defect mechanism, which offers a plausible explanation for the large differences in conductivity between the bulk and GB regions. A second defect mechanism is associated with the Ca–Cu anti-site defects and the increased εb bulk permittivity.
000.12 It is now well established that such high permittivity values have an extrinsic origin.13,14 In ceramics, an internal barrier layer capacitor (IBLC) structure has been proposed that is made up of semiconducting grains and insulating grain boundaries (GBs), where the extrinsic giant permittivity εGB would be called a GB effect.15 In single crystals and epitaxial thin films, giant permittivity can be associated with an extrinsic electrode–sample interface effect,16,17 which can also contribute to the giant permittivity in ceramics.18 The intrinsic relative dielectric permittivity, εb, of bulk CCTO was reported to be around 100.14 While this is considerably lower than the giant extrinsic values, it is still higher than would be expected in a non-ferroelectric material based on the polarizabilities of the constituent atoms19 as predicted by the Clausius–Mossotti equation (i.e., εb in CCTO is expected to be ≈ 48). The difference in electrical conductivity between the GB and bulk areas in CCTO is large: the GB charge transport activation energy EA is about 0.5–0.8 eV, while the bulk EA is about 10–100 meV,15,20 additionally, the nominal resistance of the GB and bulk areas vary by a factor of up to ≈ 105. Considering that the GB areas are expected to be thin layers the actual difference in resistivity may be even more dramatic. It was shown previously that this distinct ceramic IBLC structure becomes more pronounced during the ceramic sintering process and is associated with segregation of Cu towards the GB areas.21 More recently it was shown that the interior conducting grain phase of CCTO in fact grows out of an insulating matrix during sintering, most likely by segregation of Cu out of the conducting areas.22 Here, in this work, such Cu segregation is explicitly associated with a defect mechanism, which offers a plausible explanation for the large differences in conductivity between the bulk and GB regions. A second defect mechanism is associated with the Ca–Cu anti-site defects and the increased εb bulk permittivity.
In the literature the CCTO bulk semiconductivity has been associated with quite different and often contradictory defect mechanisms for this nominally insulating compound. It is generally agreed that deviations from the nominal CaCu3Ti4O12 stoichiometry must exist in bulk areas to explain their semiconductivity, and that the insulating GBs would exhibit smaller or no deviations.23–25 Several defect mechanisms suggested in the literature are contradictions because they imply that different types of bulk semiconductivity are occurring, i.e. n-type electron or p-type hole conduction. Semiconductivity in bulk CCTO could potentially rely on mixed valence Ti3+/Ti4+ or Cu1+/Cu2+ (n-type), or Cu2+/Cu3+ (p-type) conduction. All defect mechanisms, solid solutions and possible compensation mechanisms reported in the literature23–25 are summarised below in eqn (A–D). A further mechanism appears to be plausible from the work presented here, shown in eqn (E). Brackets (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) are used to indicate the A′′ Cu sites.
) are used to indicate the A′′ Cu sites.
| O2−o + 2Ti4+ → V˙˙0 + 2Ti3+ 1/2O2↑ : Ca(Cu3)Ti4+4−uTi3+uO12−u/2 | (A) |
| 3Cu2+ → 2Cu1+ + Ti4+Cu + Cu↑ : Ca(Cu2+3−3vCu1+2vTi4+v)Ti4O12 | (B) |
| Cu+ + Ti4+ → Cu2+ + Ti3+ : Ca(Cu2+3−vTi4+v) Ti4+4−2vTi3+2vO12 | (C) |
| 3 Cu2+ → V′′Cu + 2Cu3+ + Cu↑ : Ca(Cu2+3−3vCu3+2vV′′v)Ti4O12 | (D) |
| O2−o + Ti4+ → V˙˙0 + Cu2+Ti + 1/2O2↑ : Ca(Cu2+3)Ti4+4−wCu2+wO12−w | (E) |
Eqn (A) represents oxygen loss and the formation of oxygen vacancies, which is a common phenomenon in perovskite and related structures.26,27 Compensation occurs by Ti4+ → Ti3+ reduction. Eqn (B) represents loss or deficiency of Cu, which is compensated for by the partial reduction of Cu2+ to Cu+ and partial occupation of the Cu sites by Ti4+. Processes in (A) and (B) would most likely take place during heat treatment at elevated temperatures under inert or reducing conditions. In eqn (C) the Cu2+ reduction at elevated temperatures described in eqn (B) is now assumed to be fully reversible upon cooling via reoxidation, whereas the Cu deficiency persists. The reoxidation of Cu+ → Cu2+ in turn is compensated for by the partial reduction of Ti4+ → Ti3+i.e., an internal redox process takes place. Only the redox process is displayed in eqn (C) as the high temperature Cu reduction is identical to eqn (B). Eqn (D) represents the loss of Cu due to Cu segregation or volatilisation and the formation of Cu vacancies. Compensation occurs via the partial oxidation of Cu2+ to Cu3+. Eqn (E) corresponds to excess Cu and compensation occurs by Cu2+ occupying Ti sites and the formation of oxygen vacancies. Alternatively, compensation in eqn (E) could also occur via oxidation of Cu2+ to Cu3+ and fewer oxygen vacancies would form. Models (A), (B) and (C) are supported by the propositions of n-type conduction.24,28 Processes (B) and (C) are consistent with the detection of Cu+ (ref. 29) and Ti3+ (ref. 29 and 30), respectively, both from XPS studies, whereas model (D) is supported by findings of (i) Cu loss;25,31 (ii) the presence of Cu3+ seen in XPS studies,25 and (iii) p-type bulk semiconductivity determined from Hall effect measurements.17Eqn (E) has not been mentioned in the literature, but may be applicable in Cu-rich GB areas. Furthermore, Ca2+ and Cu2+ anti-site defects have been proposed to be the origin of the high dielectric permittivity in CCTO,32 despite the considerable mismatch between the ionic radius of Ca2+ (XII coordination: 1.35 Å) and Cu2+ (IV square planar coordination: 0.62 Å). Another possible anti-site defect mechanism may be Cu–Ti disorder, where the ionic radii are more similar i.e., Cu2+ (VI: 0.73 Å)33 and Ti4+ (VI: 0.605 Å), and both cations are known to exist in a IV square–planar coordination. For the unusual square planar IV coordination of Ti4+ in CCTO34 the ionic radius may be assumed to be similar to that for the Ti4+ tetrahedral IV coordination (0.42 Å),35 because two such ionic radii are reported the same for IV Cu2+ as well.35
It is clear that the issue of non-stoichiometry in bulk CCTO is not resolved yet and clear experimental evidence for any of the above mentioned defect mechanisms [eqn (A–E)] is missing despite considerable research efforts in recent years. The work presented here is therefore intended to shed light on the defect chemistry and non-stoichiometry of CCTO by conducting a phase diagram study. Evidence is presented for two different defect mechanisms, and their corresponding solid solutions, which cause non-stoichiometry in CCTO. Powder and ceramic samples of different composition within the ternary CaO–CuO–TiO2 phase diagram are analysed, where the CCTO lattice parameter a and dielectric properties, such as intrinsic bulk resistivity (ρb) and permittivity (εb), of the ceramics were determined using X-ray diffraction (XRD) and impedance spectroscopy (IS), respectively. It is demonstrated herein, that only by relating such lattice and intrinsic dielectric parameters to each other can exceptionally small levels of CCTO non-stoichiometry be revealed. Data from the individual phase diagram study, lattice parameter determination from XRD and IS experiments alone show no or only inconclusive trends, and a combined study relating the results of all three techniques to each other is required to understand the defect mechanisms, non-stoichiometry and electrical properties of CCTO ceramics. Although evidence for small scale non-stoichiometry in CCTO is presented, the stoichiometric nomenclature of CaCu3Ti4O12 (CCTO) will be used throughout this work.
II. Experimental
Powders of various compositions within the ternary CaO–CuO–TiO2 phase diagram were synthesised from different amounts of dried high purity reagents of CaCO3 (Aldrich, 99.995% purity), CuO (Aldrich, 99.99%) and TiO2 (Sigma-Aldrich, 99.99%). Starting reagents of lower purity were found to be inappropriate for revealing the small intrinsic defect mechanisms in CCTO. Mixing and grinding of the precursor oxides was performed using an agate pestle and mortar. At least 3 successive mixing/grinding and heat treatment cycles were required to fully react and homogenise each composition. The powder reaction was achieved at 1000 °C in a Lenton muffle furnace on Pt foil in successive cycles of 12 and 8 h, until the phase compositions observed by XRD did not change any further. All powders were synthesised simultaneously to exclude differences in the processing conditions. A small portion of each powder was heated again at 1100 °C for 12 h to enable investigation of the phase diagram for both 1100 and 1000 °C fired materials. The former is the most frequently used densification–sintering temperature for CCTO ceramics, whereas CCTO synthesis is most commonly achieved at ≈ 1000 °C. Rapid cooling was performed for all powders by swiftly removing the Pt foils, on which the powders were placed, from the furnace and exposing them to ambient conditions on a brass block. Phase analysis of each composition was performed by XRD using a high-resolution STOE STADI-P diffractometer (STOE & Cie GmbH, Darmstadt) with an image plate detector and Cu-Kα1 radiation in transmission mode, operated at 40 kV and 40 mA. Data were collected using WinXPow® software. Small amounts from all of the 1000 and 1100 °C fired powders were mixed with an internal Si standard, and high angle XRD patterns were collected using the STOE STADI-P diffractometer with a position sensitive detector (PSD). The CCTO lattice parameters were refined from three or more high angle CCTO reflections using a linear least squares fitting routine provided within the WinXPow® software package. For each composition, pellets were pressed from freshly crushed and ground powders using a uni-axial hydraulic press (1 ton) and all were simultaneously sintered at 1100 °C on Pt foil for 12 h. This is the same holding time used for the 1100 °C phase diagram and the lattice parameter study on the powders. This renders comparable the CCTO 1100 °C powder lattice parameter a and the ceramic dielectric parameters such as intrinsic bulk resistivity (ρb) and permittivity (εb). As shown below, this is a viable approach to reveal the clear dependencies between a–ρb and a–εb.For dielectric characterisation, pellets were covered on both sides with Au electrodes using a dc sputtering technique. Alternating current IS was carried out at 10–500 K between 1 Hz–2 MHz using an Agilent E4980A LCR meter, a Solartron 1296/1255 impedance analyzer, both with 100 mV amplitude ac voltage signal, an Oxford Instruments closed-cycle He refrigerator and a custom built tube furnace equipped with a Eurotherm 2216 temperature controller. The real and imaginary parts of the complex impedance (Z*) were measured and converted into the complex capacitance (C*) and electric modulus (M*) formats using the standard conversion.36 Scanning electron microscopy (SEM) images were collected with a JEOL JSM 6400 microscope, which was equipped with a facility for quantitative energy dispersive analysis of X-rays (EDAX). Scanning tunnelling microscopy (STM) micrographs of the ceramic surfaces were collected using a Digital Instrument D3100 atomic force microscope (AFM) with a nanoscope V controller operating in air and equipped with a Conductive Atomic Force Microscopy (C-AFM) module.37,38
III. Results
A. Phase analysis in the CaO–CuO–TiO2 ternary phase diagram
The CaO–CuO–TiO2 ternary phase diagram for the heat treated powders at 1100 °C is presented in Fig. 1, where the filled black symbols within the main triangle represent the specific Ca–Cu–Ti cation ratios (at%) of all of the samples investigated. All numbered compositions (1–8) were investigated in more detail by determination of the lattice parameter using XRD and by IS on pellets sintered at 1100 °C.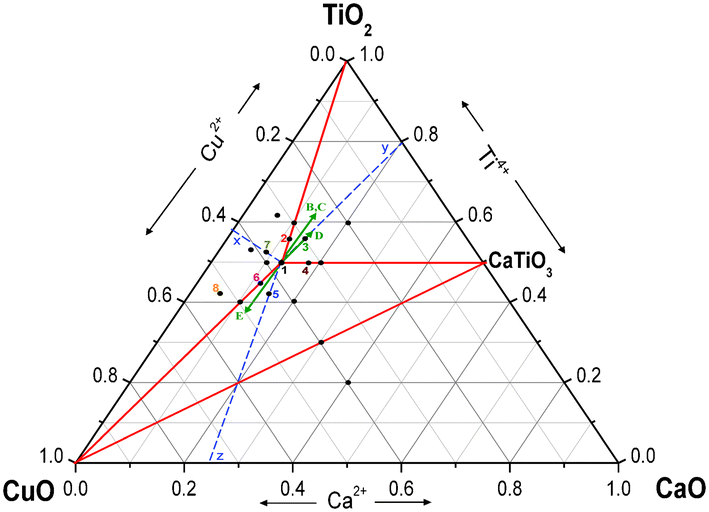 | ||
| Fig. 1 Ternary CaO–CuO–TiO2 phase diagram. Filled black symbols represent all of the compositions investigated. Numbered symbols represent the compositions analyzed by the determination of their lattice parameter and IS. On the full red lines two phases are present. Dashed blue lines represent CCTO compositions with potential Ca, Cu or Ti loss: Ca1−xCu3Ti4O12, CaCu3−yTi4O12 and CaCu3Ti4−zO12. Green arrows indicate the direction of the potential solid solutions, see eqn (B–E). Such arrows are much larger than any of the expected small solid solutions and may be regarded as a guide to the eye. | ||
The only single phase composition detected by XRD phase analysis within the main triangle was the CCTO phase, marked as composition 1. CaTiO3 (CTO) was the only significant single phase on the CaO–TiO2 binary join. On the solid (red) lines within the main triangle two phases are present, which are the two located at both ends of each line: e.g., CCTO and TiO2 are present on the line connecting CCTO (composition 1) and the TiO2 corner. The various smaller secondary triangular regions within the main triangle all contain the three phases located in the corners of these triangles: e.g., CCTO, CTO and TiO2 are present inside the triangle with corners CCTO, CTO and TiO2.
Compositions 1–8 were chosen so that the volume concentration of potential secondary phases like CuO, TiO2 and CaTiO3 would always be well below the percolation threshold for secondary phases randomly distributed within the primary CCTO matrix. This would ensure that the dielectric response in the sintered pellets of all of the labelled compositions would always be dominated by the CCTO phase. The theoretical percolation threshold for a secondary phase is known to be ≈ 16%,39 whereas experimental values are commonly reported to be up to ≈ 20%.40
No direct evidence for two different CCTO compositions is found in the phase diagram, i.e., for the GB and bulk CCTO phases. The phase relationships detected are consistent with the notion that no major defect mechanism and related solid solution are directly obvious and that CCTO and CTO are the only non-trivial single phase compositions in agreement with recently published work.41 Therefore, the solid solutions potentially causing the non-stoichiometry listed above in eqn (A–E) would be small and are indicated by the green arrows in Fig. 1. For demonstration purposes the length of the (green) arrows is depicted as being much larger than the small extent to which the solid solutions would be expected to be developed.
Unclear results were obtained within the triangle with corners CuO, CTO and CaO, where the phase relationships could not be determined unambiguously. No signs of CaO and Ca2CuO3 were detected, in contrast to previous reports on 950 °C heat treated powders.41 The compositions in this triangle were prone to extensive partial melting of CuO and possibly Ca containing phases other than CaO and Ca2CuO3 were formed. In fact, none of the compositions investigated showed any sign of CaO formation. The XRD patterns and SEM micrographs for all of the numbered compositions (Fig. 1) are displayed in the ESI, parts I(a) and (b).†
The phase diagrams for the heat treatments at 1000 and 1100 °C were found to be identical, with one exception: no crystalline CuO phase could be detected at 1100 °C in any composition by powder XRD, whereas at 1000 °C crystalline CuO was detected in all compositions, where it was expected [see ESI, part I(a)†]. It is suggested that CuO may partially melt at 1100 °C, which was confirmed in the CuO-rich pellets, where a Cu-rich phase precipitated out of the pellets during sintering at 1100 °C and remained on the Pt foil after cooling. No CuO phases could be detected in these pellets using XRD phase analysis, although some partially melted CuO may still be present in the GB areas and could remain amorphous or micro-crystalline after cooling and, therefore, cannot be detected by XRD.
The presence of a highly conductive Cu-rich phase was also confirmed on the surface of the pellet of composition 6 using C-AFM as presented in the ESI [part I(c)]†. It should be mentioned that the proposed partial melting and precipitation process of CuO may also occur, to a smaller extent, during synthesis of CCTO at 1000 °C. This may have prevented the full chemical reaction of CuO with the remaining precursors, which could serve as a plausible explanation for the unexpected finding of small amounts of CaTiO3 in certain compositions (Table 1). In the case of such Cu deficiency and concomitant unexpected CaTiO3 residues, some residual TiO2 would be expected as well for stoichiometric reasons. In composition 1 no TiO2 was detected, which may favour the mechanism in eqn (B) listed above or imply an unusual Ti-rich CaTiO3 phase. All phases detected for the 1100 °C powders and their expected phase compositions are summarised in Table 1, together with all of the powder CCTO lattice parameters a at 1100 and 1000 °C. It is evident that a is generally larger for the samples heat treated at 1100 °C, possibly due to the partial reduction of cations and concomitant increase in the cationic radii, e.g., Ti4+ → Ti3+, or Cu2+ → Cu+. This finding may favour defect mechanisms involving high temperature cationic reduction, i.e., those in eqn (A) and (B).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] or very small [[
] or very small [[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]] signs of an unexpected phase detected using EDAX; the CuO phase is written in italics for compositions where it was expected from the phase diagram, but missing from the XRD analysis; 5) lattice parameters after firing at 1100 °C and, 6) 1000 °C, where brackets (
]] signs of an unexpected phase detected using EDAX; the CuO phase is written in italics for compositions where it was expected from the phase diagram, but missing from the XRD analysis; 5) lattice parameters after firing at 1100 °C and, 6) 1000 °C, where brackets (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) contain the error in a for the last digit displayed from the linear least squares fitting routine
) contain the error in a for the last digit displayed from the linear least squares fitting routine
| Compos. number | Cation ratio (fractions) | Expected phases (wt) | Detected phases (1100 °C) | a /Å (1100 °C) | a /Å (1000 °C) |
|---|---|---|---|---|---|
| 1 | Ca 0.125, Cu 0.375, Ti 0.5 | CCTO (1) | CCTO, [CTO] | 7.3925 (1) | 7.3916 (4) |
| 2 | Ca 0.11, Cu 0.33, Ti 0.56 | CCTO (0.88), TiO2 (0.12) | CCTO, TiO2, [[CTO]] | 7.3928 (1) | 7.3917 (3) |
| 3 | Ca 0.14, Cu 0.3, Ti 0.56 | CCTO (0.84), CTO (0.07), TiO2 (0.09) | CCTO, CTO, TiO2 | 7.3924 (3) | 7.3905 (2) |
| 4 | Ca 0.175, Cu 0.325, Ti 0.5 | CCTO (0.88), CTO (0.12) | CCTO, CTO | 7.3931 (2) | 7.3925 (3) |
| 5 | Ca 0.145, Cu 0.435, Ti 0.42 | CCTO (0.74), CuO (0.17), CTO (0.09) | CCTO, CTO, CuO | 7.3922 (2) | 7.3929 (2) |
| 6 | Ca 0.1125, Cu 0.4375, Ti 0.45 | CCTO (0.9), CuO (0.1) | CCTO, [CTO], CuO | 7.3929 (4) | 7.3911 (2) |
| 7 | Ca 0.1025, Cu 0.385, Ti 0.5125 | CCTO (0.81), CuO (0.08), TiO2 (0.11) | CCTO, TiO2, [CTO], CuO | 7.3915 (1) | 7.3903 (2) |
| 8 | Ca 0.06, Cu 0.52, Ti 0.42 | CCTO (0.47), CuO (0.35), TiO2 (0.18) | CCTO, TiO2, [CTO], CuO, | 7.3912 (2) | 7.3905 (3) |
For the 1100 °C fired powders it can be seen that the Cu containing compositions, 7 and 8, show smaller lattice parameters than compositions 1–6. This was regarded as an initial indication that the bulk CCTO may indeed exhibit Cu non-stoichiometry. However, the changes in lattice parameter for the different compositions are rather small (the maximum difference in the 1100 °C powders is 0.026%) and no conclusive trend between all of the other compositions is evident from their lattice parameters alone.
B. Impedance spectroscopy (IS)
Fig. 2 shows the IS data obtained from the 1100 °C sintered pellets of composition 1–8 at 80 K using the formalism of the real part of the dielectric permittivity, ε′ vs. the frequency, f (Fig. 2a), and the imaginary part of the electric modulus, M′′ vs. f (Fig. 2b). The data have been fitted to the equivalent circuit model shown in Fig. 2a, which is discussed in more detail in section C. Fig. 2a displays two permittivity plateaus at high- and low-frequency as a result of the electronic heterogeneity of the pellets. This is well understood, for the single phase ceramic CCTO in terms of the typical IBLC structure.13 The low-frequency and high-permittivity plateau is interpreted as a GB effect and the high-frequency and low-permittivity plateau represents the intrinsic bulk.9 This interpretation requires that the brick-work layer model is valid and each relaxation can be described using a parallel resistor–capacitor element (RC element), and a possible equivalent circuit model would consist of a series of such RC elements.42,43 Fitting such a model to the data allows discrimination and separate analysis of the grain interior and GB dielectric response.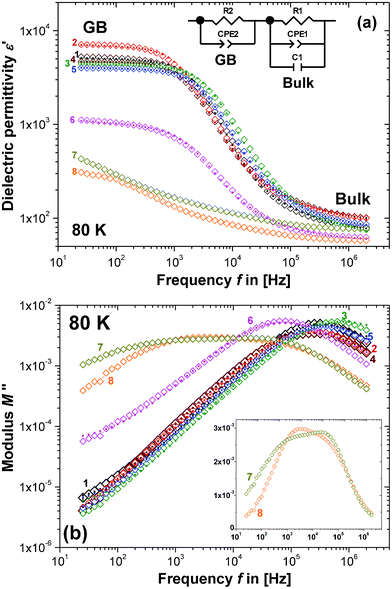 | ||
| Fig. 2 IS data for the 1100 °C sintered pellets of compositions 1–8 at 80 K, plotted on double-logarithmic axes of (a) the real part concerning the dielectric permittivity (ε′) vs. frequency (f), and (b) the imaginary part concerning the electric modulus (M′′) vs. f. Open diamonds (◊) represent experimental data, while the filled dots (•) represent the fit to the equivalent circuit model shown in the inset of part (a). The inset of part (b) shows M′′ vs. f for compositions 7 and 8 on semi-logarithmic axes. | ||
It is obvious from Fig. 2 that different secondary phases have a distinct influence on the dielectric behaviour and the IS data fall into two categories: Compositions 7 and 8 differ from 1–5, whereas 6 shows an intermediate dielectric response and may fall in between these two groups. According to the phase diagram in Fig. 1, compositions 7 and 8 belong to the same compositional triangle (CuO–CCTO–TiO2), which would be a plausible explanation for their dielectric distinction. Below in section III(D) it will be shown that this interpretation is incomplete: compositions 5 and 6 also differ from 1–4 when their dielectric response is related to the CCTO lattice parameter a. It appears that it is in fact the presence or absence of the CuO secondary phase that separates the investigated compositions, according to their dielectric response, into two categories: i) 1, 2, 3, 4 (no extra CuO); and ii) 5, 6, 7 and 8 (with extra CuO). From Fig. 2a it can be seen that the low-frequency and high-permittivity plateau, which is associated with the GB permittivity, varies strongly with the composition. Such a variation may express changes in the GB composition and/or variation in the GB thickness. Discrimination between these two explanations is not possible, but a major influence from the grain size can be excluded. It is demonstrated in the ESI [part I(b)]†, that the grain size only slightly varies with changes in the composition.
The variations in the IBLC structure demonstrated in Fig. 2a for the different compositions will be analysed in detail in the following section in order to obtain information on potential defect mechanisms and solid solutions that are present. In several previous studies, the effect of secondary phases on the CCTO giant dielectric permittivity had been analysed in detail, but the giant permittivity is extrinsic in nature. Those analyses therefore gave phenomenological information only and the investigation of the intrinsic bulk dielectric relaxation was carried out in this work to gain fundamental insight into the potential intrinsic changes of the CCTO phase induced by the presence of different secondary phases.
For the analysis of the intrinsic bulk dielectric relaxation it is advantageous to display IS data in terms of the electric modulus formalism as plots of M′′ vs. f (Fig. 2b). This is because each dielectric relaxation is shown as a relaxation peak in the M′′ vs. f plots, where the relaxation with the smallest capacitance (bulk) exhibits the largest peak.42 In contrast, for the conventional impedance −Z′′ vs. f plot the dielectric relaxation peak for the relaxation with the largest resistance in the sample (GB) is the most pronounced.42 The approximate peak frequencies for the GB and bulk relaxation peaks are given in eqn (1) for the respective plots of −Z′′ vs. f (GB) and M′′ vs. f (bulk), using two ideal RC elements connected in series. Eqn (1) implies that an extrinsic GB-type relaxation with large resistance and capacitance would appear at a lower f than the bulk, which is a common feature in the experimental impedance spectra of electroceramics. The different ordinates of the GB and bulk relaxation peaks are shown in eqn (2) for a typical CCTO scenario with distinct differences between the GB and bulk RC elements.
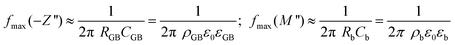 | (1) |
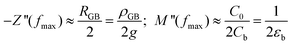 | (2) |
M′′ vs. f data are plotted on double-logarithmic axes in Fig. 2b. For compositions 1–5 only one high f relaxation peak is displayed, which is indicative of a conventional CCTO bulk dielectric relaxation process. Compositions 7 and 8 appear to display a flat peak response for M′′ vs. f, but it is in fact a double peak response (see Fig. 2b, inset) and the bulk dielectric response seems to be distinctly different, whereas composition 6 falls in between these two types of responses. Again, as mentioned above, this interpretation is incomplete and the categories are divided into i) 1–4; and ii) 5–8. Notably, the impedance spectra of 7 and 8, as well as all of the other compositions, display two additional relaxation processes, GB and electrode contributions, which are not visible in Fig. 2a and b, but are at higher temperatures [ESI, part II(a) and (b)†]. Therefore, neither of the double peaks in 7 and 8 are likely to represent a GB or electrode relaxation and may well be associated with two different bulk CCTO contributions or one CCTO contribution and a secondary phase. Since the typical high f bulk dielectric relaxation peak displayed in compositions 1–5 is missing from 7 and 8, it may be plausible that the peak with the higher f of the two double-peaks is more likely to represent the main bulk CCTO relaxation of composition 7 and 8. A complete absence of the CCTO bulk relaxation is unrealistic due to the XRD patterns clearly displaying the CCTO phase, which strongly dominates over all of the secondary phases.
Furthermore, it is important to consider that the double-peaks both occur at a significantly lower f compared to the bulk peaks for compositions 1–5. If it is assumed that each relaxation can be described by an RC element, the height of the relaxation peaks in Fig. 2b would be proportional to the reciprocal dielectric permittivity εb (eqn (2)), whereas the peak frequency is proportional to Rb × Cb, or εb × ρb (see eqn (1)). This implies that the two processes in composition 7 and 8, represented by the two M′′ vs. f double-peaks, both exhibit significantly increased ρb when compared to the single CCTO bulk relaxations for composition 1–5. The typical CCTO semiconducting bulk relaxation at high f is missing. Therefore, ρb must be strongly increased, because the typical low resistivity bulk CCTO relaxation process would be observable at high f, as in compositions 1–5, even in the presence of secondary phases, but no such observation was made. This was regarded as a further indication that the dielectric heterogeneity of CCTO is a result of the non-stoichiometry of Cu. The relaxation peak of composition 6 indicates an increased resistivity, as well as being consistent with the presence of secondary phase CuO.
Due to strong relaxation peak broadening and overlap, the double peaks in composition 7 and 8 cannot be modelled using two bulk-type RC elements connected in series.
C. Equivalent circuit fitting
The impedance data from the 1100 °C sintered pellets of compositions 1–5 were fitted to the equivalent circuit model shown in Fig. 2a, which had been successfully applied before.14,44 Bulk and GB relaxations were represented by RC elements. The intrinsic bulk dielectric relaxation process was fitted to a standard RC element, i.e., an ideal resistor (R1) and capacitor (C1) in parallel45 and an additional constant-phase element (CPE) in parallel (CPE1). The use of such a CPE has been shown previously to be appropriate to account for non-ideal bulk relaxations in electroceramics.46 The extrinsic GB relaxation was fitted with a non-ideal RC element (R2–CPE2) where the ideal capacitor was replaced with a CPE (CPE2). Non-ideal R–CPE or R–CPE–C circuits indicate a broadening of the respective dielectric relaxation peak as a reflection of the broadening of the distribution of relaxation times, τ.47 In an ideal RC element τ is derived from: τ = RC = ρε0ε.The two non-ideal RC elements were connected in series according to the brick-work layer model,43 and the data and model in Fig. 2a and b show good agreement. An equivalent circuit fit to composition 6 was also successfully carried out. The fitting errors were larger here, which may well be a reflection on the less ideal dielectric behaviour that was demonstrated in the M′′ vs. f plot (Fig. 2b).
The fitted bulk resistivity (ρb) and capacitance (εb) are plotted in Fig. 3a and b. The data could not be corrected for pellet porosity because the theoretical density was not accessible due to the mixed phase of the compositions and the potential Cu loss. Due to the high 1100 °C sintering temperature the pellet densities were assumed to be close to the theoretical value. In the case of composition 1, with a nominal single phase of CCTO, the experimental density was calculated to be 100%. In all other compositions CCTO is the major phase and CCTO grains were expected to sinter to a similarly high density. The ρb values are displayed as Arrhenius plots of logarithmic ρbvs. the reciprocal temperature 1000/T (Fig. 3a). All of the ln(ρb) vs. 1000/T curves show two distinct features: (1) a change in the general trend is evident near 80 K and conduction seems to undergo a transition; (2) differences between the various compositions are more distinct below 80 K.
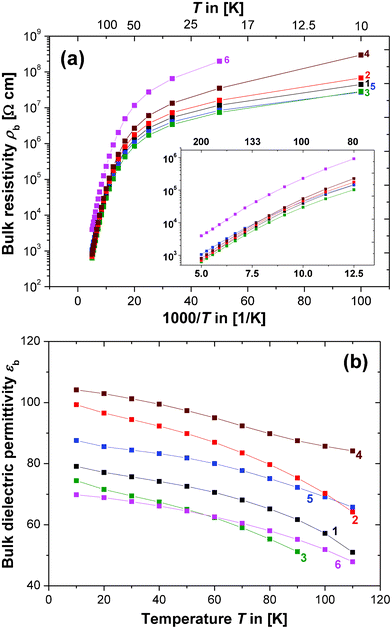 | ||
| Fig. 3 Plots showing the temperature trends of the equivalent circuit parameters R1 and C1: (a) logarithmic bulk resistivity ρb (in Ω cm) vs. reciprocal temperature 1000/T (in 1/Kelvin). Inset: Magnification of the high temperature data; axes and colour codes are identical to the main figure. (b) Bulk relative dielectric permittivity εbvs. T (in Kelvin). | ||
It has been shown that at low temperatures (T ≤ 100 K) the electrical conduction in semiconductors is often dominated by impurities.48 The change of slope in all of the ln(ρb) vs. 1000/T curves may be explained by a transition into an impurity conduction regime upon cooling to T ≤ 80 K. Since the pellets all have different compositions it is plausible that conduction varies more strongly at T ≤ 80 K in the impurity conduction regime where additional phases may have a stronger impact. Above 80 K electrical conduction may be dominated by the bulk CCTO phase and, therefore, the curves for compositions 1–5 are similar. The trends in the ln(ρb) vs. 1000/T curves show only small quantitative differences for T > 80 K, whereas composition 6 deviates. Additional Cu increases the CCTO bulk resistivity as mentioned previously.
The capacitance C1 is shown as the plot of dielectric permittivity εbvs. T in Fig. 3b. It should be noted that the equivalent circuit component C1 represents the high-frequency, low-permittivity plateau, but it is not equal to the intrinsic bulk permittivity. C1 contains a small contribution from the GB permittivity and can be corrected accordingly. This correction procedure has been carried out successfully on the IS data for Sr-doped CCTO,10 but it was found here that such a correction would change εb only marginally below the experimental error and equivalent circuit fitting errors. The sintering temperature (1100 °C) was higher here compared to the 1000 °C used in ref. 10, which led to a much more pronounced IBLC structure. As a consequence, we find larger differences between the GB and bulk permittivity and the GB permittivity has only a marginal effect on the bulk value. In Fig. 3b the uncorrected εb values are shown.
The apparent increase of εb (Fig. 3b) with reducing temperature can be explained either by incipient ferroelectricity or a charge–transfer mechanism.49 Such behaviour in CCTO has been reported previously,50 and is confirmed here. All of the trends in the εbvs. T curves are qualitatively similar and only quantitative variations are evident. Such quantitative differences are difficult to interpret from Fig. 3b alone. In the next section it will be demonstrated that such differences are correlated with the CCTO lattice parameter a.
D. Combined analysis of lattice and dielectric parameters
Summarising the results from the above section, indications have been found in the impedance spectra that the potential non-stoichiometry in CCTO may involve Cu. In this section clear trends between the bulk resistivity ρbvs. lattice parameter a and bulk dielectric permittivity εbvs. a are presented and at least two different defect mechanisms and associated solid solutions in CCTO are revealed.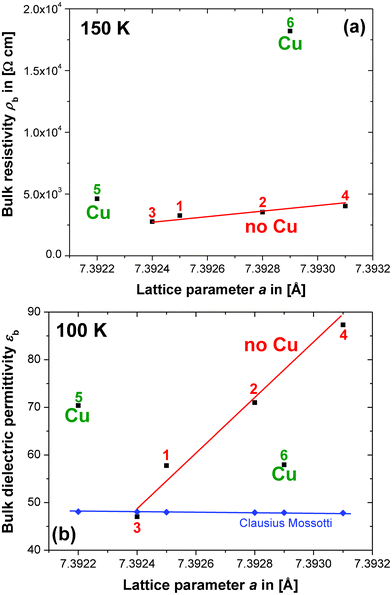 | ||
Fig. 4 Plots showing the trends in (a) the bulk resistivity ρb from the equivalent circuit fits vs. the lattice parameter a for compositions 1–6 (■), and (b) the bulk dielectric permittivity, εb, from the equivalent circuit fits vs. a (■). Estimations for εb in CCTO ( ) were obtained using the Clausius–Mossotti equation. ) were obtained using the Clausius–Mossotti equation. | ||
Compositions 5 and 6 do not follow the same trend and their ρb values seem to be elevated. The curves of ρbvs. a for compositions 1–6 at alternative temperatures of 20, 50 and 100 K all show equivalent features. This confirms that the presence of extra Cu in 5 and 6 leads to a higher bulk ρb compared to compositions 1–4. The highly resistive GB regions may contain a higher Cu content than the semiconducting Cu-deficient bulk.
The trend for the dielectric permittivity, εb, obtained from the equivalent circuit fits vs. a is presented in Fig. 4b, where the dielectric data have been collected at 100 K. The main feature of this data is the increase in dielectric permittivity εb with a for compositions 1–4, which cannot be explained by a simple lattice expansion. The Clausius–Mossotti equation predicts an approximately constant εb ≈ 48, taking into consideration the small changes in a observed and the atom polarizabilities obtained from ref. 19. The secondary phases in compositions 1–4, CaTiO3 and/or TiO2, both have a lower permittivity than CCTO and, therefore, cannot cause such an anomalous increase in εb directly, but may well influence the defect mechanism in the CCTO bulk phase responsible for the εb increase to ≈ 100. If it were the case that the secondary phase of CuO simply extends the existing defect mechanism for compositions 1–4 to higher Cu contents, compositions 5 and 6 would be expected to fall onto the same line as 1–4, which is clearly not the case, therefore, one or more additional defect mechanisms may well exist. The mechanism detected for compositions 1–4 may not involve large differences in Cu content because, in this case, a larger variation of ρb with a than that detected in Fig. 4a would be expected. Additionally, significant changes in the oxygen content are unlikely, because the concomitant changes in cationic valence would also be expected to lead to larger variations in ρb.
For the double-peaks in compositions 7 and 8 estimates were taken from the peak at a higher f in the M′′ vs. f plots, which was argued above to be more likely to represent the main CCTO bulk relaxation. The estimated ρb values obtained from the M′′ vs. f plots for compositions 5 and 6 were compared to the respective ρb values from the equivalent circuit fits [see section III(C)]. It was found that at 80 K the estimated ρb values were smaller by a factor of 3.23 (composition 5) and 3.72 (composition 6) than the values from the equivalent circuit fits. This can be explained by the non-ideality of the relaxation processes leading to a broadening of the relaxation peaks in M′′ vs. f. This, in turn, leads to a reduction in peak height and an overestimate of εb according to eqn (2). The error made in the estimation of ρb from the M′′ vs. f plots was approximated to be a uniform factor of ≈ 3.5. Thus, the estimated values (□ in Fig. 5) for compositions 7 and 8 were multiplied by a factor of 3.5 in order to account for the estimation error. Both, the uncorrected (□) and corrected (■)ρb values for compositions 7 and 8 at 80 K are plotted vs. a in Fig. 5 and approximately fall onto one line with composition 5 displaying a significant increase in ρ with decreasing a. Composition 6 is an exception to this trend, which is probably an experimental error or artefact. Still, the significant ρb increase with decreasing a detected in the Cu-rich samples 5, 7 and 8 strongly suggests the existence of a second defect mechanism and an associated solid solution. This mechanism may well relate the large differences between the GB and bulk resistivity to the Cu concentration: the GB regions would be Cu-rich and bulk regions Cu-deficient. Or, in other terms, the GB regions would exhibit compositions with a higher Cu-content, possibly quite close to the stoichiometric and nominally insulating CCTO phase, in contrast to the Cu-deficient bulk. The defect mechanisms mentioned above in eqn (B–D) involve Cu deficiency, but from the data presented here a clear discrimination is difficult. In agreement with the indications mentioned above, the mechanisms in eqn (B) and (C) may be favourable though, because the increase in a with decreasing ρb for the Cu-rich compositions (5–8), displayed in Fig. 5, may be inconsistent with the mechanism in eqn (D).
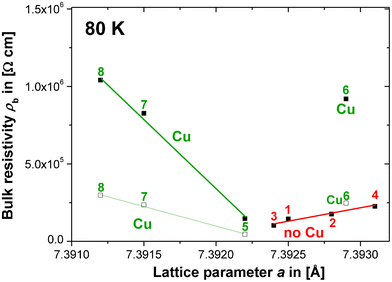 | ||
| Fig. 5 Trends of ρbvs. a for all compositions (1–8) derived from the equivalent circuit fits (■) and from estimates obtained from the M′′ vs. f relaxation peak analysis (□). For compositions 7 and 8 the ρb values (■) were multiplied by a constant correction factor (3.5), which was approximated from the difference in ρb for compositions 5 and 6 obtained from; (i) the M′′ method and (ii) the equivalent circuit fits. | ||
IV. Summary and discussion
Combined analysis of the XRD lattice parameter a and IS data revealed approximately linear relationships between the CCTO bulk resistivity ρbvs. a and the intrinsic bulk dielectric permittivity εbvs. a. For Cu-deficient compositions 1–4, an anomalous increase of the CCTO bulk dielectric permittivity εb with a was found, above that predicted using the Clausius–Mossotti equation, as a result of a distinct defect mechanism.Compositions 5–8 containing a CuO secondary phase did not follow the same trends. The presence of excess CuO led to an increased ρb and indications of a second defect mechanism were found, which may explain the large difference between the GB and bulk resistivity in terms of the difference in Cu content. This would most likely be associated with the defect mechanisms in eqn (B) and (C), mentioned in section I. For compositions 1–4 the source of their semiconductivity in the respective CCTO bulk phase may also be due to Cu deficiency, but it may be independent of the TiO2 and/or CaTiO3 secondary phases since no large differences in ρb were detected.
The rather small increase of ρb with a in compositions 1–4 (Fig. 5a) leads to some further important conclusions: the underlying defect mechanism causing high εb may not involve any large changes in the cationic valence of Cu and/or Ti, in which case larger differences in ρb would be likely. This would exclude major contributions from all of the mechanisms mentioned above in eqn (A–D), except for the mechanism shown in eqn (E), which concerns a Cu excess compensated for by the formation of oxygen vacancies. Since compositions 1–4 are all Cu-deficient, the mechanism in eqn (E) is unlikely. Instead, the formation of anti-site defects like Ca–Cu, Cu–Ti or Ca–Ti inter-site cation exchanges may be a more plausible explanation. Evidence for Ca–Cu anti-site disorder has indeed been reported in the literature,32,51 although it should be noted that, in this work, the Ca–Cu anti-site defects are proposed to serve as an explanation for the increased bulk permittivity εb and not for the extrinsic giant permittivity εGB.
The trends seen in ρbvs. a and εbvs. a are relatively uniform for all of the compositions investigated, which may be a result of the identical powder synthesis and pellet sintering conditions employed. The two distinct defect mechanisms detected were only obvious from combined analysis of a and the IS data, and cannot be clearly identified otherwise. From the difficulty of detection it is obvious that the extent to which the defect mechanisms in CCTO ceramics are developed may be small and difficult to control.
V. Conclusions
Compositions in the CaO–CuO–TiO2 phase triangle without a CuO secondary phase exhibit an anomalous increase of the CCTO bulk dielectric permittivity εb with a above the values predicted from the Clausius–Mossotti equation. This was associated with a defect mechanism based on Ca–Cu anti-site defects, which causes a high intrinsic bulk dielectric permittivity. Compositions containing a CuO secondary phase exhibit increased resistivity. A second mechanism is proposed to be responsible for the large difference between the GB and bulk resistivity in CCTO: GB areas may be Cu-rich, whereas bulk areas may be Cu-deficient. Such Cu gradients may well develop during the ceramic sintering processes.21Acknowledgements
The authors acknowledge funding from the European Union under the NUOTO project and grant agreement no. 226716 (FP7/2007-2013). DCS thanks the EPSRC (UK) for funding (EP/G005001/11). RS acknowledges a Ramón y Cajal fellowship from the MINECO (Spain).References
- M. A. Subramanian and A. W. Sleight, Solid State Sci., 2002, 4, 347 CrossRef CAS.
- A. P. Ramirez, M. A. Subramanian, M. Gardel, G. Blumberg, D. Li, T. Vogt and S. M. Shapiro, Solid State Commun., 2000, 115, 217 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384 CrossRef CAS.
- S. H. Byeon, S. S. Lee, J. B. Parise and P. M. Woodward, Chem. Mater., 2006, 18, 3873 CrossRef CAS.
- L. Wu, Y. Zhu, S. Park, S. Shapiro, G. Shirane and J. Tafto, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014118 CrossRef.
- M. A. Subramanian, D. Li, N. Duan, B. A. Reisner and A. W. Sleight, J. Solid State Chem., 2000, 151, 323 CrossRef CAS.
- C. C. Homes, T. Vogt, S. M. Shapiro, S. Wakimoto and A. P. Ramirez, Science, 2001, 293, 673 CrossRef CAS.
- S.-Y. Chung, I.-D. Kim and S.-J. L. Kang, Nat. Mater., 2004, 3, 774 CrossRef CAS.
- T. B. Adams, D. C. Sinclair and A. R. West, Adv. Mater., 2002, 14, 1321 CrossRef CAS.
- R. Schmidt and D. C. Sinclair, Chem. Mater., 2010, 22, 6 CrossRef CAS.
- V. Brizé, G. Gruener, J. Wolfman, K. Fatyeyeva, M. Tabellout, M. Gervais and F. Gervais, Mater. Sci. Eng., B, 2006, 129, 135 CrossRef.
- A. R. West, T. B. Adams, F. D. Morrison and D. C. Sinclair, J. Eur. Ceram. Soc., 2004, 24, 1439 CrossRef CAS.
- D. C. Sinclair, T. B. Adams, F. D. Morrison and A. R. West, Appl. Phys. Lett., 2002, 80, 2153 CrossRef CAS.
- P. Lunkenheimer, R. Fichtl, S. G. Ebbinghaus and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 172102 CrossRef.
- T. B. Adams, D. C. Sinclair and A. R. West, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094124 CrossRef.
- M. C. Ferrarelli, D. C. Sinclair, A. R. West, H. A. Dabkowska, A. Dabkowski and G. M. Luke, J. Mater. Chem., 2009, 19, 5916 RSC.
- G. Deng, T. Yamada and P. Muralt, Appl. Phys. Lett., 2007, 91, 202903 CrossRef.
- M. Li, Z. Shen, M. Nygren, A. Feteira, D. C. Sinclair and A. R. West, J. Appl. Phys., 2009, 106, 104106 CrossRef.
- R. D. Shannon, J. Appl. Phys., 1993, 73, 348 CrossRef CAS.
- D. Capsoni, M. Bini, V. Massarotti, G. Chiodelli, M. C. Mozzatic and C. B. Azzoni, J. Solid State Chem., 2004, 177, 4494 CrossRef CAS.
- R. Schmidt, M. C. Stennett, N. C. Hyatt, J. Pokorny, J. Prado-Gonjal, M. Li and D. C. Sinclair, J. Eur. Ceram. Soc., 2012, 32, 3313 CrossRef CAS.
- I. R. Costa, M. Li, J. R. Frade and D. C. Sinclair, RSC Adv., 2013, 3, 7030 RSC.
- M. Li, A. Feteira, D. C. Sinclair and A. R. West, Appl. Phys. Lett., 2006, 88, 232903 CrossRef.
- J. Li, A. W. Sleight and M. A. Subramanian, Solid State Commun., 2005, 135, 260 CrossRef CAS.
- T.-T. Fang, L.-T. Mei and H.-F. Ho, Acta Mater., 2006, 54, 2867 CrossRef CAS.
- R. A. De Souza, M. S. Saiful and E. Ivers-Tiffee, J. Mater. Chem., 1999, 9, 1621 RSC.
- A. R. West, Basic solid state chemistry, Wiley: New York, 1988 Search PubMed.
- P. Fiorenza, R. Lo Nigro, A. Sciuto, P. Delugas, V. Raineri, R. Toro, M. Catalano and G. Malandrino, J. Appl. Phys., 2009, 105, 061634 CrossRef.
- G. Deng, N. Xanthopoulos and P. Muralt, Appl. Phys. Lett., 2008, 92, 172909 CrossRef.
- L. Zhang and Z.-J. Tang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174306 CrossRef.
- T.-T. Fang and L.-T. Mei, J. Am. Ceram. Soc., 2007, 90, 638 CrossRef CAS.
- Y. Zhu, J. C. Zheng, L. Wu, A. I. Frenkel, J. Hanson, P. Northrup and W. Ku, Phys. Rev. Lett., 2007, 99, 037602 CrossRef CAS.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925 CrossRef CAS.
- M. Avdeev and V. B. Nalbandyan, Inorg. Chem., 2006, 45, 2217 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- Impedance Spectroscopy, ed. J. R. Macdonald, John Wiley & Sons, New York, 1987 Search PubMed.
- P. Fiorenza, R. L. Nigro, C. Bongiorno, V. Raineri, M. C. Ferarrelli, D. C. Sinclair and A. R. West, Appl. Phys. Lett., 2008, 92, 182907 CrossRef.
- P. Fiorenza, V. Raineri, M. C. Ferrarelli, D. C. Sinclair and R. Lo Nigro, Nanoscale, 2011, 3, 1171 RSC.
- H. Scher and R. Zallen, J. Chem. Phys., 1970, 53, 3759 CrossRef CAS.
- B. Vertruyen, R. Cloots, M. Ausloos, J.-J. Fagnard and P. Vanderbemden, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165112 CrossRef.
- M. Veith, S. Ren, M. Wittmar and H. Bolz, J. Solid State Chem., 2009, 182, 2930 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- R. Schmidt, Impedance Spectroscopy of Electroceramics, in Ceramic Materials Research Trends, ed. P. B. Lin, Novascience Publishers, Hauppauge, 2007, p. 321 Search PubMed.
- R. Schmidt, J. Ventura, E. Langenberg, N. M. Nemes, C. Munuera, M. Varela, M. Garcia-Hernandez, C. Leon and J. Santamaria, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035113 CrossRef.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- E. J. Abram, D. C. Sinclair and A. R. West, J. Electroceram., 2003, 10, 165 CrossRef CAS.
- R. Schmidt, W. Eerenstein, T. Winiecki, F. D. Morrison and P. A. Midgley, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245111 CrossRef.
- N. F. Mott and W. D. Twose, Adv. Phys., 1961, 10, 107 CrossRef CAS.
- C. Kant, T. Rudolf, F. Mayr, S. Krohns, P. Lunkenheimer, S. G. Ebbinghaus and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045131 CrossRef.
- Y. Liu, R. L. Withers and X. Y. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134104 CrossRef.
- P. Delugas, P. Alippi, V. Fiorentini and V. Raineri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra41319e |
| This journal is © The Royal Society of Chemistry 2013 |
