Cooperative and competitive effects associated with Fe(CO)3 binding to annelated benzenes†
Xiaoguang Bao, David A. Hrovat and Weston Thatcher Borden*
Department of Chemistry and the Center for Advanced, Scientific Computing and Modeling, University of North Texas, 1155 Union Circle, #305070, Denton, Texas 76203-5070, USA. E-mail: borden@unt.edu
First published on 26th September 2012
Abstract
Density functional theory (DFT) calculations have been carried out on the sequential transfer of Fe(CO)3 groups from the Fe(CO)3 complex of cyclobutadiene [CBD–Fe(CO)3, 5] to tris(etheno)-annelated benzene (3) and to 1,2;4,5-bis(etheno)-annelated benzene (9). The changes in the electronic structure of the central benzene ring in 3, brought about by each Fe(CO)3 transfer reaction, make the transfer of Fe(CO)3 groups to 3 from 1–3 molecules of 5 cooperative. Our calculations find that, as the number of Fe(CO)3 groups transferred to 3 increases, the bond lengths between the benzo carbons and each Fe atom decrease; and the energetic favorability of each Fe(CO)3 transfer reaction increases. In contrast, the transfer of Fe(CO)3 groups to 9 from two molecules of 5 is competitive. Transfer of a second Fe(CO)3 group from 5 to 9 increases the bond lengths between the benzo carbons and the Fe atoms and makes the second Fe(CO)3 transfer reaction more energetically unfavorable than the first. Our calculations also indicate that there is little, if any, π bonding between the three CBD–Fe(CO)3 rings in 8, the tris-Fe(CO)3 adduct of 3. Therefore, π bonding between the four-membered rings in 8 cannot explain the comparatively favorable energy for its formation.
Introduction
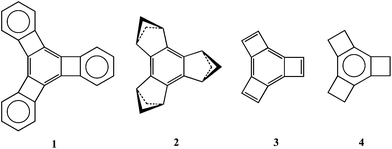
Alternation of the C–C bond lengths in benzene can be induced by annelation.1,2 Information about the causes of such C–C bond-length alternation has been gleaned from the bond lengths in benzene rings that are tris-annelated by benzo (1),3 1,3-cyclobutano (2),4 etheno (3),5 and ethano (4)6 groups.Molecule 1 was prepared by Diercks and Vollhardt in 1986 and characterized by X-ray crystallography.3 The bond lengths in the central benzene ring show strong alternation in a manner such that the C–C bonds that are exocyclic to the four-membered rings are shortened and the bonds that are endocyclic are lengthened. Subsequently, Siegel and coworkers synthesized 2 in which three 1,3-cyclobutano groups are fused to benzene.4a,b The X-ray structure of 2 indicates that the bond lengths in the benzene ring of 2 alternate in the same fashion as those in 1.4a Although 3 has not yet been prepared, calculations predict strong bond-length alternation, in which the double bonds in the six-membered ring are again localized exocyclic to the four-membered rings.2,5
In order to rationalize bond length alternation in the central benzene rings of 1–3, caused by the annelated small rings, two explanations have been proposed. The first argues that σ strain, induced by the fused small rings, results in C–C bond-length alternation in the central benzene rings.7 If this explanation were correct, it seems likely that strong C–C bond-length alternation would also be evident in the benzene ring of 4. Therefore, the very weak bond-length alternation found in the benzene ring of 4 (ref. 6d) makes it difficult, though not impossible,7a to attribute the origin of the bond-length alternation in 1–3 to σ strain.
The second explanation of the bond-length alternation in the central benzene rings of 1–3 focuses on π interactions between the annelating groups and the benzene ring.4c,5 The annelating groups in 1 and 3 contain π bonds, and the alternation of the C–C bond lengths in the central benzene rings in these two compounds may be attributed to minimization of antiaromaticity of the four-membered rings in 1 (ref. 3) and in 3.5
The second explanation can also rationalize the bond-length alternation found in 2,4 since the highest occupied (HO)MO of a 1,3-bridged cyclobutane ring consists of an in-phase combination of 2p AOs at C1 and C3, so that this MO behaves very much like a π bond.8 Hence, orbital interactions strongly prefer butadieno over etheno as a 1,3-cyclobutane bridging group.9 Thus, the interactions between the π-like HOMOs of the three 1,3-cyclobutano rings in 2 and the π bonds of the benzene ring can account nicely for the C–C bond length alternation found in the benzene ring of 2.10
It is convenient to attribute the C–C bond length alternation, found in the benzene rings of 1–3, to the avoidance of anti-aromatic π interactions between filled orbitals of the annelating groups and the filled π MOs of benzene. However, interactions between filled MOs do not change wave functions. Instead, the localization of the bonding π MOs of the benzene rings in 1–3, so that the π bonds are exocyclic to the rings formed by annelation, is actually due to the mixing between filled orbitals of the annelating groups and the π* orbitals of the benzene rings.2,5g
This type of orbital mixing, when combined with the mixing of the filled benzene π MOs with the π* orbitals of unsaturated annelating groups, leads to cooperative effects between the annelating groups in the energies for forming 1 and 3, even with the central benzene ring bond lengths fixed at R = 1.397 Å (the optimized C–C bond length in D6h benzene at the B3LYP/6-31G(d) level).2,5g However, due to the absence of a low-lying, unfilled MO in cyclobutane, this type of cooperativity is not found in 2.
On the other hand, cooperativity between the annelating groups was found, not only in 1 and 3, but also in 2, in the energy liberated on allowing the benzene bond lengths to alternate.2 As had been previously predicted,11 the stabilization energy associated with bond-length alternation was computed to vary as n2, the square of the number of annelating groups.2
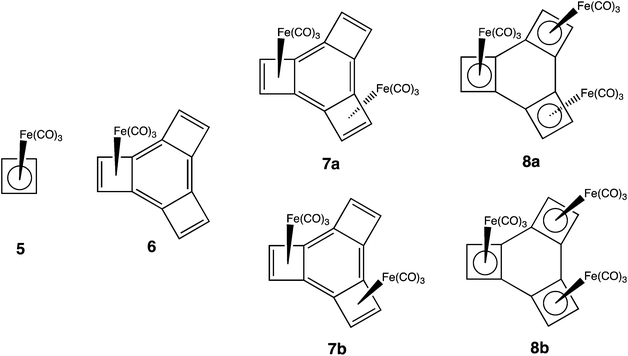
Although 3 has not been prepared, 8a, the tris-irontricarbonyl complex of 3 has been synthesized, and its X-ray structure was reported by Stanger and co-workers.12 Irontricarbonyl groups bind to conjugated dienes,13 and the binding of Fe(CO)3 to cyclobutadiene (CBD) in 5 (ref. 14a and b) is so strong that 5 can be regarded as “metalloaromatic”.14c Therefore, it would be expected that the presence of the three Fe(CO)3 groups in 8a should change the preference for localization of the benzene π bonds from exocyclic to the four-membered rings in 3 to endocyclic in 8a, resulting in the creation of three CBD–Fe(CO)3 rings.
The lengths of the C–C bonds, found in the central six-membered ring of 8a,12 are, in fact, quite different from those computed for 3.5 For instance, the average of the exocyclic C–C bond lengths in the X-ray structure of 8a is 1.444 Å, and the average of the endocyclic bond lengths is 1.469 Å.12 In contrast, the optimized bond lengths of the central six-membered ring of 3 at the B3LYP/6-31G(d) level are 1.338 Å for the exocyclic C–C bonds and 1.515 Å for the endocyclic C–C bonds.5g
Interestingly, the average length of the exocyclic C–C bonds in the six-membered ring of 8a is not longer, but 0.025 Å shorter than the average length of the endocyclic bonds. The lengths of the endocyclic bonds in 8a are similar to those found in the Fe(CO)3 complex of CBD (5);14b so it is the lengths of the exocyclic bonds in 8a that are surprisingly short. Although Stanger et al. have suggested that 8a can be regarded as containing three CBD–Fe(CO)3 rings, linked by C(sp2)–C(sp2) single bonds;12 the average exocyclic C–C bond length of 1.444 Å in 8a leaves open the possibility that there may be some π bonding between the CBD–Fe(CO)3 rings.
As already noted, we have previously shown that successive annelation of benzene by one, two, and three etheno groups, leading to 3, is cooperative.2,5g We wondered if structural and energetic evidence for cooperativity would also be found in a different type of reaction – the sequential complexation of the four-membered rings in 3 by three Fe(CO)3 groups, to form 8a. As the number of Fe(CO)3 groups increases, (3 < 6 < 7< 8), the benzene π bonds go from being localized exocyclic to the four-membered rings in 3 to becoming localized, or partially localized, within the four-membered rings of the three CBD–Fe(CO)3 groups in 8. Therefore, we wondered, as the number of Fe(CO)3 groups increases from 3 to 6 to 7, whether the addition of each subsequent Fe(CO)3 group becomes energetically more favorable?
In order to investigate whether sequential binding of Fe(CO)3 groups to 3 is, in fact, cooperative, we have carried out calculations on 3, 6, 7, and 8. We have also performed calculations to ascertain the degree to which there is π bonding between the three CBD–Fe(CO)3 rings in 8.
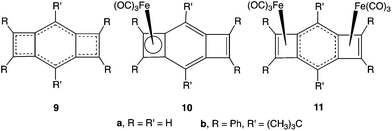
There is, in fact, already structural evidence from X-ray crystallography that interaction between two Fe(CO)3 groups, complexed to an etheno-annelated benzene, can be competitive, rather than cooperative. The X-ray structure of 10b,15 the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of Fe(CO)3 with 1,2;4,5-bis(etheno)benzene (9b),16a shows that 10b contains a nearly square CBD–Fe(CO)3 ring and that the bonds between Fe and the carbons of this four-membered ring all have similar lengths. The uncomplexed four-membered ring in 10b consists of a localized, endocyclic, double bond (R = 1.369 Å) and two, localized, exocyclic, double bonds (R = 1.354 Å) that are joined by two single bonds (R = 1.499 Å).
1 complex of Fe(CO)3 with 1,2;4,5-bis(etheno)benzene (9b),16a shows that 10b contains a nearly square CBD–Fe(CO)3 ring and that the bonds between Fe and the carbons of this four-membered ring all have similar lengths. The uncomplexed four-membered ring in 10b consists of a localized, endocyclic, double bond (R = 1.369 Å) and two, localized, exocyclic, double bonds (R = 1.354 Å) that are joined by two single bonds (R = 1.499 Å).
Upon reaction of 10b with a second equivalent of Fe(CO)3, the π bonding in the six-membered ring of the product (11b) becomes delocalized.15a The four, equivalent, C–C bonds of the six-membered ring in 11b all have lengths between 1.40 and 1.42 Å. The delocalized π bonding in the six-membered ring of 11b apparently weakens the Fe–C bonds to the benzo carbons, because these Fe–C bonds are 0.2 Å longer than the Fe–C bonds to the etheno carbons.15a
If competition between the two Fe(CO)3 groups in 11 for the π bonds in the benzene ring makes the bonding to each of these Fe(CO)3 groups weaker than the bonding to the Fe(CO)3 group in 10, this difference between 10 and 11 should show up in the relative energies of their formation by Fe(CO)3 addition reactions. Specifically, formation of 11 by addition of Fe(CO)3 to 10 should be much less favorable energetically than formation of 10 by addition of Fe(CO)3 to 9.
The apparent competition between the two Fe(CO)3 groups in 11 contrasts with the expected cooperativity between the Fe(CO)3 groups in the formation of 8 by sequential addition of Fe(CO)3 groups to 3. In order to explore the extent to which these contrasting expectations about additions of Fe(CO)3 groups to 3 and 9 are actually met, we performed calculations, the results of which are described in this paper.
Computational methodology
Electronic structure calculations were carried out using the B3LYP density functional method, which is a combination of Becke's 3-parameter hybrid functional17 with the electron correlation functional of Lee, Yang, and Parr (LYP).18 The 6-31G(d) basis set19 was used for carbon, oxygen, and hydrogen atoms. The LANL2DZ basis set, in conjunction with the LANL2DZ pseudopotential,20 was used for the iron atoms. Vibrational analyses were performed on all optimized geometries, in order to ensure that the optimized structures corresponded to local minima and to obtain zero-point energy (ZPE) corrections. The Gaussian 09 suite of programs21 was used for all of these calculations.Results and discussion
Evidence for cooperativity between Fe(CO)3 groups from the optimized geometries of 6–8
The optimized C–C and Fe–C bond lengths in 6–8, in which Fe(CO)3 group(s) are added successively to 3, are given in Fig. 1. For comparison, the optimized bond lengths of 3 and of 5 are also shown. The bond lengths in 5 (ref. 14b) and in 8a,12 determined by X-ray crystallography, are given in parentheses below or next to the calculated bond lengths. There is, in general, good agreement between the calculated and the experimental bond lengths in 5 and 8a, thus providing a measure of confidence that the calculated bond lengths in 6 and 7 are probably accurate too.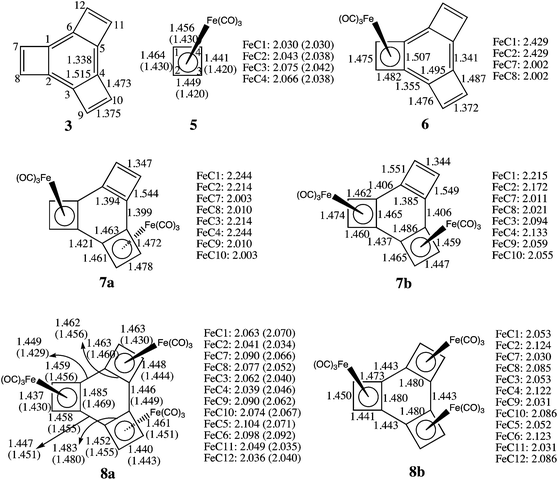 | ||
| Fig. 1 Optimized bond lengths of 3, 5, 6, 7a/7b, and 8a/8b (Å) at the B3LYP/6-31G(d)+LANL2DZ level. The available experimental results for 5 (ref. 14b) and 8a (ref. 12) are given in parentheses. The numbering of the carbons in 6–8 is the same as that shown for 3. | ||
As shown in Fig. 1, the single Fe(CO)3 group in 6 is computed to have two, significantly different, Fe–C bond lengths – R = 2.429 Å for the bond to the benzo carbons and R = 2.002 Å for the bond to the etheno carbons. The calculated Fe–C(benzo) bond length in 6 is 0.375 Å longer than the average of R = 2.054 Å for the calculated Fe–C bond lengths in CBD–Fe(CO)3 (5), whereas, the calculated Fe–C(etheno) bond length in 6 is actually 0.052 Å shorter than the average Fe–C bond length in 5. The Fe(CO)3 group in 6 is obviously bonded more strongly to the etheno than to the benzo carbons, suggesting the bonding of Fe(CO)3 to 6 may be better described as η2, rather than η4.
Fig. 1 shows that the addition of a Fe(CO)3 group to 3 has little effect on the calculated C–C bond lengths. The biggest change is the lengthening by 0.100 Å of the bond between the etheno carbons of the four-membered ring in 6, to which the Fe(CO)3 group is bonded. The lengths of the other C–C bonds in and to the carbons of this four-membered ring change by less than 0.02 Å on going from 3 to 6.
Adding a second Fe(CO)3 group to 6 in a trans manner produces 7a. The bonds between the iron atoms and the etheno carbons have about the same lengths in 7a as in 6, but the bonds between the iron atoms and the benzo carbons shorten. The average of the Fe–C(benzo) bond lengths in 7a (R = 2.229 Å) is 0.200 Å shorter than in 6.
The apparently stronger bonding between Fe and the benzo carbons in 7a, compared to 6, is achieved by localizing more π electron density in the three C–C bonds of the six-membered ring in 7a that are endocyclic in the four-membered rings (i.e., the bonds between C1–C2, C3–C4, and C5–C6, using the numbering shown for 3 in Fig. 1). The pair of these bonds that are endocyclic in the four-membered rings that are complexed to Fe(CO)3 are 0.044 Å shorter in 7a than in 6. However, a much larger change is the 0.101 Å shortening of the C(benzo)–C(benzo) bond that is endocyclic in the four-membered ring that remains uncomplexed to Fe(CO)3 in 7a.
The length of this bond (C5–C6) in 7a (R = 1.394 Å) is only 0.047 Å greater than that of the bond between the etheno carbons (R = 1.347 Å) in the uncomplexed four-membered ring. Consequently, the π bonding in this four-membered ring of 7a begins to resemble that in rectangular CBD. Indeed, on going from 6 to 7a, the C(benzo)–C(etheno) bonds in this ring lengthen by 0.057 Å, and the bond between the etheno carbons shortens by 0.025 Å, as the π bonding in the uncomplexed four-membered ring of 7a becomes more localized.
Another major change in bond length that occurs on going from 6 to 7a involves the C–C bonds that connect a complexed to an uncomplexed CBD ring. These bonds each lengthen by 0.058 Å as the C(benzo)–C(benzo) distance in the uncomplexed four-membered ring shortens by 0.101 Å. For comparison, in 3 the C(benzo)–C(benzo) bonds between the four-membered rings (C2–C3, C4–C5, and C6–C1) are 0.177 Å shorter than the C(benzo)–C(benzo) bonds that are endocyclic in the four-membered rings (C1–C2, C3–C4, and C5–C6). However, in 7a the bonds to the benzo carbons of the uncomplexed four-membered ring are actually slightly (0.005 Å) longer than the C(benzo)–C(benzo) bonds that are endocyclic in this four-membered ring.
Upon adding an Fe(CO)3 group to 7a, to form 8a, the major change in the Fe–C bond lengths is again in the bonds to the benzo carbons. In 6 the Fe–C(benzo) bonds are 0.427 Å longer than the Fe–C(etheno) bonds. In 7a the difference between these Fe–C bond lengths decreases to 0.222 Å; but, in 8a, the average length of the Fe–C bonds to the benzo carbons is actually 0.001 Å shorter than the average length of the Fe–C bonds to the etheno carbons.
The C–C bond lengths in the four-membered rings of 8a are about the same as those in 5. Therefore, the structure of 8a can best be described as consisting of three η4-CBD–Fe(CO)3 rings that are joined together by three C–C single bonds to form a six-membered ring.12
Is there π bonding between the CBD–Fe(CO)3 rings in 8?
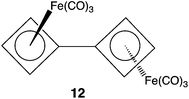
As already noted, the short bond lengths between the CBD–Fe(CO)3 rings in 8a, both calculated (Ravg = 1.447 Å) and found (Ravg = 1.443 Å), suggest that there might be some π bonding between the four-membered rings. Calculations on the bis-[CBD–Fe(CO)3] complex (12) afforded us the opportunity to investigate this question, because the computed length of the C–C bond between the four-membered rings in 12 is 1.440 Å, which is very close to the computed lengths of the corresponding bonds that are exocyclic to the four-membered rings in both 8a and 8b.The optimized anti geometry of 12 has a Fe–C–C–Fe dihedral angle of ϕ = 180.0°. There is also a mirror-image pair of local minima with a Fe–C–C–Fe dihedral angle of ϕ = 56.3°. Therefore, these minima are better described as gauche, rather than syn conformations. If there were significant delocalization of π electrons between the CBD rings, one would have expected the higher energy local minimum to occur closer to ϕ = 0° than to ϕ = 60°. Consequently, the finding that the higher energy conformation of 12 has a Fe–C–C–Fe dihedral angle of ϕ = 56.3° suggests that the interaction between the CBD–Fe(CO)3 rings in 12 is largely steric, rather than electronic in nature.
In order to investigate further if there is significant delocalization of π electrons between the two four-membered rings in 12, we located the transition state (TS) connecting the anti to the gauche conformer. The TS occurs at a Fe–C–C–Fe dihedral angle of ϕ = 113.2°, about halfway between the anti and gauche minima. As shown in Fig. 2, the TS has a C–C bond length of 1.458 Å, which is only 0.018 Å longer than that in the anti conformer and only 0.007 Å longer than that in the gauche conformer. The calculated energy of the TS is only 3.1 kcal mol−1 higher than that of the anti conformer and only 1.6 kcal mol−1 higher than that of the gauche conformer. Using Marcus theory,22 the intrinsic barrier to rotation in 12 is computed to be only 2.3 kcal mol−1.
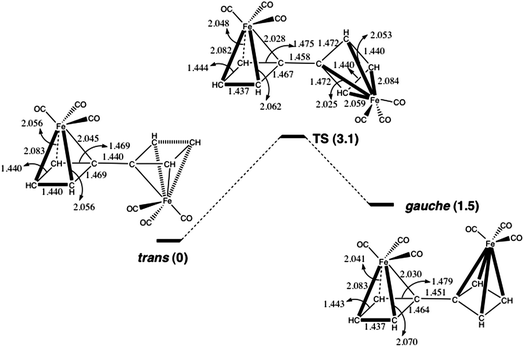 | ||
| Fig. 2 The changes in geometry (Å) and energy (kcal mol−1) on rotation about the C–C bond between the CBD–Fe(CO)3 groups in 12. | ||
The small size of the barrier and the small amount of lengthening of the C–C bond between the CBD–Fe(CO)3 rings in the TS indicates that there is very little, if any, π bonding between the CBD–Fe(CO)3 rings in 12. Therefore, the similarity between the calculated lengths of the C–C bonds between the CBD–Fe(CO)3 rings in 8 and 12 indicates that there is also very little π bonding between the CBD–Fe(CO)3 rings in 8. Thus, the results of our calculations on 12 strongly support the conjecture of Stanger et al. about the absence of π bonding between the CBD–Fe(CO)3 rings in 8a.12
If π bonding does not explain the short C–C bond between the CBD–Fe(CO)3 rings, calculated for 8 and 12 and found experimentally in 8a,12 what does? We believe that the origin of the short C–C bond length may be the hybridization of the carbons that form this bond. For example, in 12 the Fe–C–C and the two C–C–C bond angles at these carbons are 130.9 and 134.5°, respectively. These unusually large bond angles suggest that there is a large amount of 2s character in the C–C bond between the CBD–Fe(CO)3 rings in 12. We believe it is the large amount of 2s character in the C–C bonds between the CBD–Fe(CO)3 rings in 8, as well as in 12, that is responsible for the short length of these bonds, compared to the lengths of more normal C–C single bonds.23
Evidence for cooperativity between Fe(CO)3 groups from the energetics of formation of 6–8 from 3
The apparent absence of any significant π bonding between the CBD–Fe(CO)3 rings in 8 means that the energetics of the sequential transformation of 3 to 8 must be largely controlled by the relative strengths of Fe(CO)3 bonding to the π electrons within the four-membered rings in 6–8. Judging from the changes in the Fe–C(benzo) bond lengths, the strengths of the bonds to each of the Fe(CO)3 groups increases on going from 6 to 7a to 8a, indicating that Fe(CO)3 binding is cooperative in these three molecules. The origin of this cooperativity is that the preferred localization of the three π bonds of the six-membered ring changes from being exocyclic to the four-membered rings in 3 to being endocyclic in the four-membered rings in 8. Therefore, as more Fe(CO)3 groups are added to 3, the bonding to each Fe(CO)3 group increases, from being largely η2 in 6 to being η4 in 8.The apparent cooperativity between the Fe(CO)3 groups, seen in the decreases in the Fe–C(benzo) bond lengths as more Fe(CO)3 groups are added, should show up in the energetics of Fe(CO)3 bonding on going from 3 to 6 to 7 to 8. Therefore, we performed calculations of the relative strengths of the bonds to the Fe(CO)3 groups in 6–8 by computing the energies of the reactions in eqn (1)–(3). In these reactions an Fe(CO)3 group is transferred from CBD–Fe(CO)3 (5) to produce 6 from 3, 7 from 6, and 8 from 7. The calculated energies, ΔE, of these Fe(CO)3 transfer reactions are given in Table 1.24
| Eqn | Fe(CO)3 transfer reaction | ΔE |
|---|---|---|
| (1) | 3 + 5 → 6 + C4H4 | 63.3 (60.9) |
| (2a) | 6 + 5 → 7a + C4H4 | 42.9 (40.7) |
| (2b) | 6 + 5 → 7b + C4H4 | 45.6 (43.5) |
| (3a) | 7a + 5 → 8a + C4H4 | 14.3 (13.9) |
| (3b) | 7b + 5 → 8a + C4H4 | 11.6 (11.1) |
| (3c) | 7b + 5 → 8b + C4H4 | 14.0 (13.4) |
According to Table 1 the binding energy between CBD and Fe(CO)3 in 5 is 63.3 kcal mol−1 (60.9 kcal mol−1 after zero-point vibrational energy corrections) larger than that between 3 and the Fe(CO)3 group in 6. There are two, closely related, contributors to this large difference in Fe(CO)3 binding energies. One is that the bonding to Fe(CO)3 is stronger in 5 than in 6, as evidenced by the large difference between the lengths of the Fe–C bonds in 5 and the Fe–C(benzo) bonds in 6. The other is that CBD (C4H4) is destabilized by antiaromaticity;25 whereas, the localized, exocyclic π bonds in the 1,2-dimethylenecyclobutene rings of 3 keep 3 from being antiaromatic.2,5
Adding another Fe(CO)3 group to 6 can produce two stereoisomers, 7a and 7b. The relative energies of the reactions in eqn (2a) and (2b) show that trans isomer 7a is lower in energy than the cis isomer 7b by 2.7 (2.8) kcal mol−1.
Of greater significance is the difference between the energies of the reactions in eqn (2a) and (1). The energy difference of −20.4 (−20.2) kcal mol−1 between these two reactions is the energy of the disproportionation reaction,
| 2 6 → 3 + 7a ΔE = −20.4 (−20.2) kcal mol−1 | (4) |
Comparison of the Fe–C(benzo) bond lengths in 6 and 7a indicates that the exothermicity of this reaction is due to the bonds to the pair of Fe(CO)3 groups being much stronger in 7a than in two molecules of 6. Thus, the disproportionation reaction in eqn (4) provides an energetic measure of the cooperativity of Fe(CO)3 bonding in 7a.
What do differences between the π bonding in the uncomplexed four-membered rings in 3, 6, and 7a contribute to the energy of the reaction in eqn (4)? As noted above, the C–C bond lengths in the two uncomplexed four-membered rings of 6, are similar to those in 3, but the C–C bond lengths in the uncomplexed four-membered ring in 7a are much more like those in CBD than like those in an uncomplexed four-membered ring of 6. Consequently, the exothermicity of the reaction in eqn (4) is actually due to the stronger Fe(CO)3 bonding in 7a than in two molecules 6, minus the weaker π bonding in the uncomplexed four-membered ring in 7a, compared to that in an uncomplexed four-membered ring of 6.
The difference of 2.7 (2.8) kcal mol−1 between eqn (3a) and (3b) for forming 8a from, respectively, 7a and 7b represents, of course, the energy difference between the syn and anti isomers of 7. Similarly, the difference of 2.4 (2.3 kcal mol−1) between eqn (3b) and (3c) represents the difference between the energies of stereoisomers 8a and 8b.
According to eqn (3b), transfer of an Fe(CO)3 group from 5 to 7b, to form 8a, is only endothermic by 11.6 (11.1) kcal mol−1.26 This Fe(CO)3 transfer reaction is 51.7 (49.8) kcal mol−1 less endothermic than the transfer of an Fe(CO)3 group from 5 to 3, to form 6 (eqn (1)) and 34.0 (32.4) kcal mol−1 less endothermic than transfer of an Fe(CO)3 group from 5 to 6, to form 7b (eqn (2b)). As the number of Fe(CO)3 groups in the product increases, the energetic unfavorability of an Fe(CO)3 transfer reaction from 5 decreases dramatically. This is a clear indication of the cooperativity between the Fe(CO)3 groups in enhancing Fe(CO)3 bonding in these reactions.
The difference between eqn (3a) and (1), gives the reaction in eqn (5).
| 7a + 6 → 8a + 3 ΔE = −49.0 (−47.0) kcal mol−1 | (5) |
The energy change for this reaction is the energy associated with transferring an Fe(CO)3 group from 6 to 7a. The large exothermicity indicates that the bonding of the two Fe(CO)3 groups is highly cooperative.
The reaction in eqn (5) can be added to the reaction in eqn (4) to give
| 3 6 → 8a + 2 3 ΔE = −69.4 (−67.2) kcal mol−1 | (6) |
The extraordinarly large amount of energy liberated by the disproportionation reaction in eqn (6) is indicative of the large amount of cooperativity in the very strong binding of the three Fe(CO)3 groups in 8, compared to the very weak binding of the Fe(CO)3 groups in three molecules of 6.
The energy associated with the reaction in eqn (6) indicates, not surprisingly, that the η4 bonding to the three Fe(CO)3 groups in 8 really is much stronger than the largely η2 bonding to the Fe(CO)3 groups in three molecules of 6. The similarity between the C–C bond lengths in the uncomplexed four-membered rings of 6 and of 3 provides strong evidence that the exothermicity of the reaction in eqn (6) is, indeed, mostly due to the large difference between the strengths of the bonds to the Fe(CO)3 groups in 6 and in 8.
One might be concerned that the disproportionation reactions in eqn (4)–(6) all involve formation of 3; so perhaps it is the stability of 3 toward Fe(CO)3 addition that makes these three reactions exothermic. A simple test proves that this is not the case. The diproportionation reaction
| 2 7a → 8a + 6 ΔE = −28.6 (−28.8) kcal mol−1 | (7) |
The reactions in eqn (4) and (7) both involve transfer of one Fe(CO)3 group. Why is the reaction in eqn (7) 40% more exothermic than the reaction in eqn (4)?
Eqn (7) represents the difference between the Fe(CO)3 binding energies in forming 7a from 6 and in forming 8a from 7a. Cooperativity makes the latter Fe(CO)3 binding energy 28.6 (28.8) kcal mol−1 larger than the former. Eqn (4) represents the difference between the Fe(CO)3 binding energies in forming 6 from 3 and in forming 7a from 6. Cooperativity makes the latter Fe(CO)3 binding energy 20.4 (20.2) kcal mol−1 larger than the former.
Thus, the difference 8.2 (8.6) kcal mol−1 between eqn (7) and (4) represents the difference between the effects of cooperativity in the Fe(CO)3 binding energies of 8a and 7a and the effects of cooperativity in the Fe(CO)3 binding energies of 7a and 6. Not surprisingly, the effects of cooperativity increase with the number of Fe(CO)3 that are cooperating.
Evidence for competition between the Fe(CO)3 groups in 11a from the energies of the Fe(CO)3 complexation reactions of 9a and 10a
As discussed in the introduction, there is experimental evidence for competition between the two Fe(CO)3 groups in 11b from the X-ray crystal structures of 10b and 11b.15 Both of these complexes are formed by heating 9b (ref. 16a) with Fe2(CO)9.We have optimized the geometries of 9a–11a. As shown in Fig. 3, there is reasonably good agreement between the optimized geometries that we have computed for the unsubstituted complexes 9a–11a and those found experimentally for the substituted complexes 9b,16b10b,15a,b and 11b.15a
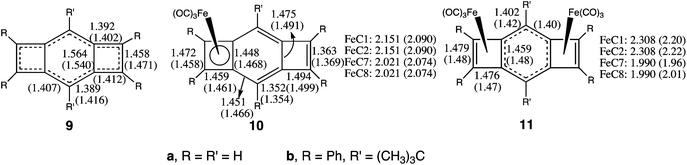 | ||
| Fig. 3 Optimized bond lengths (Å) of 9a, 10a, and 11a at the B3LYP/6-31G(d)+LANL2DZ level. The numbers in parentheses are from the X-ray crystal structures of 9b,16b10b,15a,b and 11b.15a | ||
There are two bond-shift isomers of 9,27 but the addition of a Fe(CO)3 group to either isomer leads to 10. In 10, as in 5, the half-filled frontier orbitals of both bond-shift isomers of 9 mix with the half-filled frontier orbitals of Fe(CO)3, creating a closed-shell of electrons in the complex between the four-membered ring in 10 and Fe(CO)3.
However, the localized 3,4-dimethylenecyclobutene ring in 10 is not well-suited to bonding to a second Fe(CO)3 group.28 This difference between 10 and 9 accounts for the much larger difference between the Fe–C(benzo) and Fe–C(etheno) bond lengths in 11 than in 10. Put another way, the competition between the two Fe(CO)3 groups in 11 makes the bonding to each of the largely η2-Fe(CO)3 groups much weaker than the bonding to the lone η4-Fe(CO)3 group in 10.
This analysis of the bonding to the Fe(CO)3 groups in 10 and 11 predicts that the transfer of the Fe(CO)3 group from 5 to 9, to form 10, should be much less unfavorable than the transfer of the Fe(CO)3 group from 5 to 10, to form 11. The results in Table 2 show that this prediction is correct.29
| Eqn | Fe(CO)3 transfer reaction | ΔE |
|---|---|---|
| (8) | 9a + 5 → 10a + C4H4 | 23.4 (22.7) |
| (9) | 10a + 5 → 11a + C4H4 | 46.2 (44.4) |
Subtraction of eqn (8) from eqn (9) gives
| 2 10a → 11a + 9a ΔE = 22.8 (21.7) kcal mol−1 | (10) |
In contrast to the disproportionation reaction of two molecules of 6 to 3 + 7a in eqn (4), ΔE = −20.4 (−20.2) kcal mol−1, the disproportionation reaction of two molecules of 10a to 11a + 9a in eqn (10) has ΔE = 22.8 (21.7) kcal mol−1. The magnitudes of the calculated energy changes in eqn (4) and (10) are similar, but the signs are opposite. The signs of the energy changes that are computed for these two disproportionation reactions are sufficient to establish that the interaction between the two Fe(CO)3 groups in 7a is cooperative; whereas the interaction between the two Fe(CO)3 groups in 11a is competitive.
Interestingly, the energy of binding a second Fe(CO)3 group is nearly the same in 6 → 7a as in 10a → 11a. Subtracting eqn (2a) from eqn (9) gives the difference in Fe(CO)3 binding energies as
| 10a + 7a → 11a + 6 ΔE = 3.3 (3.7) kcal mol−1 | (11) |
Consequently, subtracting eqn (11) from eqn (12) – the equation that gives the energy difference between the disproportionation reactions in eqn (10) and eqn (4),
| 2 10a + 3 + 7a → 2 6 + 11a + 9a ΔE = 43.2 (41.9) kcal mol−1 | (12) |
| 10a + 3 → 9a + 6 ΔE = 39.9 (38.2) kcal mol−1 | (13) |
Eqn (13) shows that the large energy difference of ΔE = 43.2 (41.9) kcal mol−1 between the disproportionation reactions in eqn (10) and (4) is almost entirely due to the binding energy of one Fe(CO)3 group being greater in 10a than in 6 by 39.9 (38.2) kcal mol−1.
Conclusions
The bond lengths in 6–8 in Fig. 1, as well as the relative energies in Table 1 for formation of these complexes by sequential addition of Fe(CO)3 groups to 3, show that the Fe(CO)3 groups in 6–8 act cooperatively to enhance their bonding to the benzo carbons of the four-membered rings. Increasing the number of complexed Fe(CO)3 groups favors the shift of the three double bonds of the benzene ring, which are exocyclic to the four-membered rings in 3, to being endocyclic in the four-membered rings in 8. The electronic structures and optimized geometries of 6 and 7 are compromises between (a) avoiding localization of two uncomplexed double bonds in the same four-membered ring, in order to minimize antiaromatic interactions between the double bonds, and (b) localization of two complexed double bonds within the same four-membered ring, in order to maximize Fe(CO)3 bonding to them.In contrast to the cooperativity between the Fe(CO)3 groups in 6–8, seen in both the bond lengths in Fig. 1 and in the Fe(CO)3 transfer energies in Table 1, successive coordination of Fe(CO)3 groups to 9 shows competition. This is apparent in both the bond lengths for 10 and 11 in Fig. 3 and in the Fe(CO)3 transfer energies in Table 2.
This study of the cooperative binding of the Fe(CO)3 groups in 6–8 and the competitive binding of the Fe(CO)3 groups in 10 and 11 adds additional examples of the cooperative and the competitive substituent effects that were previously found in the Cope rearrangement11,30 and in the annelation of benzene with etheno,5g benzo, and 1,3-cyclobutano groups.2,31
Acknowledgements
This research was supported by grant CHE-0910527 from the National Science Foundation and by grant B0027 from the Robert A. Welch Foundation.Notes and references
- For a brief review see: (a) S. M. Bachrach, Computational Organic Chemistry, John Wiley & Sons, Inc., Hoboken, New Jersey, 2007, pp. 97–103 Search PubMed; (b) F. Fabris, C. Zonta, G. Borsato and O. De Lucchi, Acc. Chem. Res., 2011, 44, 416 CrossRef CAS.
- X. Bao, D. A. Hrovat and W. T. Borden, Theor. Chem. Acc., 2011, 130, 261 Search PubMed.
- R. Diercks and K. P. C. Vollhardt, J. Am. Chem. Soc., 1986, 108, 3150 CrossRef CAS.
- (a) H.-B. Burgi, K. K. Baldridge, K. Hardcastle, N. L. Frank, P. Ganzel, J. S. Siegel and J. Ziller, Angew. Chem., Int. Ed. Engl., 1995, 34, 1454 CrossRef; (b) N. L. Frank, K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 1995, 117, 2102 CrossRef; (c) Prior to the experimental results, the localization of double bonds in the central benzene ring of 2 was computationally studied by K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 1992, 114, 9583 Search PubMed.
- (a) M. Eckert-Maksic, D. Kovacek, M. Hodoscek, D. Mitic, K. Poljanec and Z. B. Maksic, J. Mol. Struct., 1990, 206, 89 Search PubMed; (b) R. Faust, E. D. Glendening, A. Streitwieser and K. P. C. Vollhardt, J. Am. Chem. Soc., 1992, 114, 8263 CrossRef CAS; (c) Z. B. Maksic, M. Eckert-Maksic, D. Kovacek and D. Margetic, J. Mol. Struct., 1992, 260, 241 Search PubMed; (d) M. Eckert-Maksic, Z. B. Maksic, M. Hodoscek and K. Poljanec, J. Mol. Struct., 1993, 285, 187 Search PubMed; (e) M.-C. Ou and S.-Y. Chu, J. Phys. Chem., 1994, 98, 1087 CrossRef CAS; (f) S. Bachrach, J. Organomet. Chem., 2002, 643–644, 39 CrossRef CAS; (g) X. Bao, D. A. Hrovat and W. T. Borden, Collect. Czech. Chem. Commun., 2011, 76, 481 Search PubMed; (h) E. D. Jemmis and B. Kiran, J. Org. Chem., 1996, 61, 9006 CrossRef. The influence of the small, annelated rings in 3 on the diamagnetic ring currents was investigated by (i) P. W. Fowler, R. W. A. Havenith, L. W. Jenneskens, A. Soncini and E. Steiner, Chem. Commun., 2001, 2386 RSC; (j) A. Soncini, R. W. A. Havenith, P. W. Fowler, L. W. Jenneskens and E. Steiner, J. Org. Chem., 2002, 67, 4753 CrossRef CAS; (k) A. Stanger, J. Phys. Chem. A, 2008, 112, 12849 CrossRef CAS; The aromaticity of annelated benzene was investigated by (l) S. Sakai, J. Phys. Chem. A, 2002, 106, 11526 CrossRef CAS.
- The synthesis of 4 was reported by (a) W. Nutakul, R. P. Thummel and A. D. Taggart, J. Am. Chem. Soc., 1979, 101, 770 Search PubMed; (b) E. Heilbronner, B. Kovac, W. Nutakul, A. D. Taggart and R. P. Thummel, J. Org. Chem., 1981, 46, 5279 Search PubMed; (c) C. W. Doecke, P. J. Garratt, H. Shahriari-Zavareh and R. Zahler, J. Org. Chem., 1984, 49, 1412 CrossRef; The crystal structure of 4 was subsequently analyzed by (d) R. Boese, D. Blaerser, W. E. Billups, M. M. Haley, A. H. Maulitz, D. L. Mohler and K. P. C. Vollhardt, Angew. Chem., Int. Ed. Engl., 1994, 33, 313 CrossRef.
- (a) A. Stanger, J. Am. Chem. Soc., 1991, 113, 8277 CrossRef CAS; (b) A. Stanger, J. Am. Chem. Soc., 1998, 120, 12034 CrossRef CAS; (c) A. Stanger and E. Tkachenko, J. Comput. Chem., 2001, 22, 1377 CrossRef CAS; (d) I. V. Alabugin and M. Manoharan, J. Comput. Chem., 2007, 28, 373 CrossRef CAS.
- (a) R. Hoffmann and R. B. Davidson, J. Am. Chem. Soc., 1971, 93, 5699 CrossRef CAS; (b) R. Gleiter and T. Kobayashi, Helv. Chim. Acta, 1971, 54, 1081 Search PubMed.
- (a) W. L. Jorgensen and W. T. Borden, J. Am. Chem. Soc., 1973, 95, 6649 Search PubMed; (b) See also, W. L. Jorgensen and W. T. Borden, Tetrahedron Lett., 1975, 16, 223 Search PubMed; (c) W. L. Jorgensen, J. Am. Chem. Soc., 1975, 97, 3082 Search PubMed.
- (a) M. Nendel, K. N. Houk, L. M. Tolbert, E. Vogel, H. Jiao and P. V. R. Schleyer, Angew. Chem., Int. Ed. Engl., 1997, 36, 748 CrossRef; (b) S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, Chem. Rev., 2001, 101, 1501 CrossRef CAS; (c) For a dissenting view, see E. D. Jemmis and B. Kiran, J. Org. Chem., 1966, 61, 9006 Search PubMed.
- D. A. Hrovat and W. T. Borden, J. Chem. Theory Comput., 2005, 1, 87 Search PubMed.
- A. Stanger, N. Ashkenazi and R. Boese, J. Org. Chem., 1998, 63, 247 CrossRef CAS.
- Reviews: (a) A. J. Pearson, in Advances in Metal–Organic Chemistry, ed. L. S. Liebeskind, JAI Press, Greenwich, 1989, vol. 1, pp. 1–49 Search PubMed; (b) R. Gree and J. P. Lellouche, in Advances in Metal–Organic Chemistry, ed. L. S. Liebeskind, JAI Press, Greenwich, 1995, vol. 4, pp. 129–273 Search PubMed; (c) G. R. Stephenson, in Handbook of Functionalized Organometallics, ed. P. Knochel, Wiley-VCH, Weinheim, 2005, vol. 2, pp. 569–627 Search PubMed.
- (a) CBD–Fe(CO)3 (5) was synthesized by G. F. Emerson, L. Watts and R. Pettit, J. Am. Chem. Soc., 1965, 87, 131 Search PubMed; and its X-ray structure was determined by (b) P. D. Harvey, W. P. Schaefer, H. B. Gray, D. F. R. Gilson and I. S. Butler, Inorg. Chem., 1988, 27, 57 CrossRef CAS. An excellent review of the history of 5 and related molecules has been published by (c) D. Seyferth, Organometallics, 2003, 22, 2 CrossRef CAS.
- (a) T. Butters, F. Toda and W. Winter, Angew. Chem., Int. Ed. Engl., 1980, 19, 926 Search PubMed; (b) T. Butters, W. Winter and F. Toda, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 1532 Search PubMed.
- (a) F. Toda and M. Ohi, J. Chem. Soc., Chem. Commun., 1975, 506 RSC; (b) R. Boese, J. Benet-Buchholz, A. Stanger, K. Tanaka and F. Toda, Chem. Commun., 1999, 319 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- (a) R. A. Marcus, J. Phys. Chem., 1968, 72, 891 CrossRef CAS; (b) R. A. Marcus, J. Am. Chem. Soc., 1969, 91, 7224 CrossRef CAS.
- For other examples of this phenomenon, see: (a) R. Glilardi, M. Maggini and P. E. Eaton, J. Am. Chem. Soc., 1988, 110, 7230 CrossRef CAS; (b) R. Glilardi, M. Maggini and P. E. Eaton, J. Am. Chem. Soc., 1988, 110, 7232 CrossRef CAS; (c) O. Ermer, P. Bell, J. Schäfer and G. Szeimies, Angew. Chem., Int. Ed. Engl., 1989, 28, 473 CrossRef; (d) M. Tanaka and A. Sekiguchi, Angew. Chem., Int. Ed., 2005, 44, 5821 CrossRef CAS.
- In order to confirm that our qualitative results were not dependent on our use of the B3LYP functional,17,18 we performed geometry optimizations and energy calculations with the M06-L functional, which Truhlar has recommended for use in calculations on reactions that involve transition metals. ( Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 Search PubMed ). The M06-L energies for reactions (1), (2a), and (3a) in Table 1 are, respectively, 65.7, 42.3, and 11.3 kcal mol−1, in reasonable agreement with the B3LYP energies in Table 1.
- (a) Review: R. Breslow, Acc. Chem. Res., 1973, 6, 393 Search PubMed; (b) See however, J. I. Wu, Y. Mo, F. A. Evangelista and P. V. R. Schleyer, Chem. Commun., 2012, 48, 8437 Search PubMed.
- If the Fe(CO)3 bonding in 5 and 8a is assumed to be very similar, then the endothermicity of reaction (3b) is due to the greater antiaromaticity of CBD,24 relative to that of the uncomplexed ring of 7b.
- The isomer shown in Fig. 3, which has a [10]annulene perimeter, is calculated by B3LYP/6-31G(d) to be 2.3 kcal mol−1 lower in energy than the other bond-shift isomer, which has a central benzene ring and two, localized π bonds. For previous calculations on 9a see: (a) J. M. Schulman and R. L. Disch, J. Am. Chem. Soc., 1993, 115, 11153 CrossRef CAS; (b) I. Despotovic, M. Eckert-Maksic, Z. B. Maksic and D. M. Smith, J. Phys. Chem. A, 2003, 107, 10396 CrossRef CAS; (c) I. Antol, M. Eckert-Maksic, H. Lischka and Z. B. Maksic, ChemPhysChem, 2004, 5, 975 CrossRef CAS; (d) A. Stanger, J. Org. Chem., 2006, 71, 883 CrossRef CAS.
- We find that transfer of Fe(CO)3 from 5 to the four-membered ring of 3,4-dimethylenecyclobutene is computed to be energetically unfavorable by 66.1(63.7) kcal mol−1. This is only 2.8 kcal mol−1 more unfavorable than the transfer of Fe(CO)3 from 5 to 3 in reaction (1) of Table 1, emphasizing the similarity of the largely η2 bonding to Fe(CO)3 in the Cs, Fe(CO)3 complex of 3,4-dimethylene-cyclobutene and in 6. It should be noted, however, that the global minimum for the Fe(CO)3 complex of 3,4-dimethylenecyclobutene has only C1 symmetry, because one methylene group bends enough to complex weakly with the Fe(CO)3 group that is attached to the endocyclic double bond. The global C1 minimum is computed be 3.3 kcal mol−1 lower than the Cs structure. The geometries of both complexes are available in the ESI.† The incorporation of the exocyclic double bonds in 6 in the six-membered ring precludes 6 from achieving a geometry that is analogous to that of the C1 minimum for the Fe(CO)3 complex of 3,4-dimethylenecyclobutene, so that the optimized Cs geometry for 6 is the global energy minimum.
- One of the Referees of this manuscript suggested that a transition metal complex, which prefers η2 binding [e.g. Pt(PR3)2], might coordinate to the two unannelated carbons in the six-membered of 11 and thus strengthen the bonding to both Fe(CO)3 groups. A CH2 group also prefers η2 bonding, and we have no doubt the two CBD rings in 2,3;5,6-bis(etheno)norbornadiene – the hydrocarbon that results from CH2 bonding to the two unannelated carbons in the six-membered of 9 – would bind tightly to two moles of Fe(CO)3 in forming the methylene-bridged version of 11.
- (a) D. A. Hrovat, J. Chen, K. N. Houk and W. T. Borden, J. Am. Chem. Soc., 2000, 122, 7456 CrossRef CAS; (b) W. T. Borden, in Theory and Applications of Computational Chemistry: The First 40 Years, ed. C. Dykstra, G. Frenking, K. Kim and G. Scuseria, Elsevier, Oxford, 2005, pp. 859–872 Search PubMed.
- As we have done in our previous studies of cooperativity in the Cope rearrangement30 and benzene annelation reactions,2,5g we have determined the effect geometry relaxation in the product has on the energies of the Fe(CO)3 transfer reactions in Table 1. By computing the energies of the reactions in eqn (1), (2b) and (3b), with the C–C bonds in the six-membered rings of the products constrained to alternate between 1.338 and 1.515 Å (as these bonds do in 3), we determined that optimization of these bond lengths lowers the energy of 6 by 0.4 kcal mol−1, 7b by 6.8 kcal mol−1, and 8b by 15.0 kcal mol−1. A simple model predicts that the geometry relaxation energies should vary as n2, where n is the number of Fe(CO)3 groups transferred.11 Thus, based on the 15.0 kcal mol−1 relaxation energy for 8b, the predicted relaxation energies for 6b and 7b are, respectively, 15.0 × 1/9 = 1.7 kcal mol−1 and 15.0 × 4/9 = 6.7 kcal mol−1. The predicted geometry relaxation energy in 6 is about four times larger than the value of 0.4 kcal mol−1 that is computed; but the predicted and calculated geometry relaxation energies for 7b are nearly identical.
Footnote |
| † Electronic supplementary information (ESI) available: Fully optimized geometries and energies of 3, 5, 6, 7a/7b, 8a/8b, 9a, 10a, 11a, and 12 (trans, gauche, and TS). See DOI: 10.1039/c2sc20785k |
| This journal is © The Royal Society of Chemistry 2013 |