In search of colloidal hard spheres
C. Patrick
Royall
*abcd,
Wilson C. K.
Poon
e and
Eric R.
Weeks
f
aHH Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK. E-mail: paddy.royall@bristol.ac.uk
bSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK
cCentre for Nanoscience and Quantum Information, Tyndall Avenue, Bristol BS8 1FD, UK
dInternational Research Center for Materials Nanoarchitectonics (MANA), National Institute for Materials Science (NIMS), Tsukuba, Ibaraki 305-0044, Japan
eSUPA and School of Physics & Astronomy, University of Edinburgh, Kings Buildings, Mayfield Road, Edinburgh EH9 3JZ, UK
fDepartment of Physics, Emory University, Atlanta, GA 30322, USA
First published on 9th October 2012
Abstract
We recently reviewed the experimental determination of the volume fraction, ϕ, of hard-sphere colloids, and concluded that the absolute value of ϕ was unlikely to be known to better than ±3–6%. Here, in a second part to that review, we survey effects due to softness in the interparticle potential, which necessitates the use of an effective volume fraction. We review current experimental systems, and conclude that the one that most closely approximates hard spheres remains polymethylmethacrylate spheres sterically stabilised by polyhydroxystearic acid ‘hairs’. For these particles their effective hard sphere diameter is around 1–10% larger than the core diameter, depending on the particle size. We argue that for larger colloids suitable for confocal microscopy, the effect of electrostatic charge cannot be neglected, so that mapping to hard spheres must be treated with caution.
1 Introduction
A collection of hard spheres is one of the simplest examples of an interacting system. Hard-sphere packings have been important since the dawn of civilisation,1,2 while using hard spheres to model the liquid state dates back at least to Kirkwood and Boggs3 in the 1940s. The simplicity of hard spheres lends itself to analytical theory4–7 and computer simulation.8–10 While the absence of inter-particle attraction precludes a liquid phase, concentrated hard sphere fluids capture many properties of the liquid state.3,11,12 Due to its analytic tractability, and that it is described by just one parameter, volume fraction ϕ, the importance of the hard sphere system as a basic model in understanding condensed matter cannot be overstated.Early hard sphere experiments include Bernal's use of ball bearings to model liquid structure.13 However, ball bearings have negligible thermal motion. Suspensions of mesoscopic colloids exhibit Brownian motion and are thermodynamically equivalent to atoms and small molecules.14 In 1986, Pusey and van Megen15 showed that a suspension of sterically stabilised polymethylmethacrylate (PMMA) particles showed hard-sphere-like equilibrium phase behaviour. Their work led to many experimental studies of the statistical physics of hard spheres using colloids as models. Since Pusey and van Megen's work, the equation of state of hard-sphere colloids has been determined,16 crystal nucleation has been observed,17,18 and the glass transition has been studied.19
The body of experimental research just reviewed relied on light scattering as the structural and dynamical probe. The advent of single particle tracking in real space with confocal microscopy20,21 opened a new dimension in experiments on hard-sphere-like systems, yielding an unprecedented level of detailed information.22 Confocal microscopy of hard-sphere-like suspensions is thus ideal for studying generic processes where local events are important, such as crystal nucleation,23 melting24 and dynamical heterogeneity.25,26
In principle, the thermodynamics of a system of hard spheres is controlled solely by the state variable ϕ. We have recently reviewed the experimental determination of volume fraction27 and concluded that, although relative values of ϕ may be known with high precision, absolute values can only be determined to within 3–6% accuracy. This matters, especially when dealing with dynamical properties (e.g., phase transition kinetics and the glass transition), since these can be very strong functions of ϕ.
But the accurate determination of ϕ is only part of the experimental challenge. The other part of the challenge was hinted at by the title of Pusey and van Megen's 1986 paper, “Phase behaviour of concentrated suspensions of nearly hard colloidal spheres”,15 where we have added the italics to emphasise the point in question, namely, that true hard spheres do not exist in reality. In Pusey and van Megen's case, the lack of hardness is almost certainly due to the small but finite compressibility of the PHSA stabilising ‘hairs’. The same is generically true of other sterically stabilised particle systems.
In very-nearly-hard, sterically stabilised suspensions, a new sample has to be made for every state point ϕ. Apart from being cumbersome, this also restricts the accuracy with which the sole thermodynamic control parameter can be ‘tuned’. Thus, there has been a drive to use particles such as ‘microgels’, whose diameter is temperature dependent. Since temperature, T, can be tuned far more accurately than ϕ, this allows the scanning of a single sample very finely through ϕ space by varying T. But the price paid for the ‘tunability’ of particle diameter is that some softness is built in by design.
To understand a final reason why real model hard-sphere colloids may be somewhat soft, consider why in practice, not only ϕ but the particle diameter σ matters. Experimentally, colloids as synthesised are usually not matched in density to the dispersing medium. Significant sedimentation (or, less usually, creaming) during the timescale of an experiment therefore presents a problem. In light scattering studies, this is circumvented to a large extent by the use of small particles, say, σ ≲ 400 nm, so that for PMMA particles dispersed in cis-decalin, a single particle sediments ≲1 mm per day. The middle part of a bulk sample would therefore be little affected by sedimentation over a day. But if one wants to eliminate the effect all together (e.g. for long-time measurements), or when larger particles (say, σ ≳ 1000 nm) are needed for imaging purposes, then solvent mixtures for density matching are needed, which often introduces significant charging. The practical need for larger particles therefore inevitably brings softness.
In this second part of our review, we survey critically these three sources of softness in experimental systems of colloids that have been used to model hard spheres, Fig. 1. In the spirit of the first part of our review,27 we seek to provide a means by which the hardness may be assessed, and consider the consequences this may have on the behaviour of the system. Likewise, we argue for more clarity on the part of experimentalists, concerning the softness of the systems they use. We also suggest a number of criteria by which experimentalists (and theorists using experimental data) may judge whether a certain system of colloids may be considered ‘hard enough’ for answering particular physics questions.
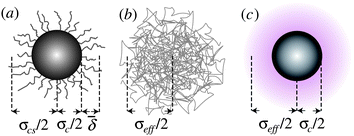 | ||
Fig. 1 Schematic representation of various models for hard-sphere colloids. (a) Sterically stabilized particle, with surface ‘hairs’ (not to scale), where the average thickness of the stabiliser layer ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) and the core–shell diameter σcs = σc + 2 and the core–shell diameter σcs = σc + 2![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) are needed for a full characterisation. (b) Microgel particle, which is a heavily cross-linked polymer. (c) Charged colloid, where the electrical double layer (shaded) gives rise to an effective diameter σeff. are needed for a full characterisation. (b) Microgel particle, which is a heavily cross-linked polymer. (c) Charged colloid, where the electrical double layer (shaded) gives rise to an effective diameter σeff. | ||
Below, we first discuss mapping experimental systems onto hard spheres via measuring the inter-particle potential in Section 2. We then treat softness of non-electrostatic origins in Section 3 and of electrostatic origins in Section 4; in general, both effects are present simultaneously. Finally we give a worked example in Section 5, illustrating many of the points raised throughout this review, before concluding in Section 6.
2 Mapping to effective hard spheres via the interaction potential
Given that real colloids inevitably display a degree of softness, it is important to be able to map their behaviour to that of hard spheres for the purpose of comparison with theories and simulations of perfect hard spheres. By mapping, we mean finding an effective hard-sphere diameter σeff so that one may map from the experimentally controllable particle number density ρ to an effective hard-sphere volume fraction ϕeff using ϕeff = πρσeff3/6. There are two conceptually distinct ways of determining σeff. First, one could map via some known hard-sphere property, such as the volume fraction at freezing (ϕHSf = 0.494), or the viscosity of the suspension as a function of ϕ. This class of methods have been reviewed in detail in the first part of our review.27 Here we concentrate on a second class of methods: determining σeff from the inter-particle potential, u(r). To do so, of course, requires means of measuring u(r), which is the main topic of this section.First, however, we briefly review how a knowledge of u(r) can be used to determine an effective hard-sphere diameter, σeff. Perhaps the simplest approach is to set an effective hard sphere diameter σkT such that the inter-particle repulsive energy at this centre-to-centre separation between two particles is equal to the thermal energy, i.e.
| βu(r = σkT) = 1, | (1) |
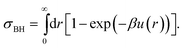 | (2) |
Other, yet more sophisticated mappings, exist, such as that due to Andersen et al.;29 this approximation is known to work well for mapping the static properties of liquids and more recently structural relaxation time near the glass transition.30 All of these approaches rely on knowing u(r). We now review methods for gaining this knowledge.
2.1 Direct measurement
A host of sophisticated techniques are now available for direct measurement of colloidal forces; integration of the measured force–distance relationship then gives u(r).In the case of PMMA particles sterically stabilised by poly-12-hydroxyl steric acid (PHSA) ‘hairs’, the interaction may be inferred via the direct measurement of the interaction potential between mica surfaces coated by PHSA using the surface-force apparatus. The results were well described by an inverse power law, suggesting a reasonably (but not absolutely) hard interaction;31 see Section 3 for more details.
Other methods for measuring colloidal interactions directly include total internal reflection microscopy, which measures the force between a colloid and a glass wall,32 and atomic force microscopy with a colloid on the tip of the cantilever.33 The interaction between two non-index-matched colloids confined to a line can be measured by optical tweezers.34
One attraction of such direct methods is that no a priori assumption need be made about u(r). However, their use requires care. Thus, e.g., in the case of optical tweezers, relatively small and subtle experimental errors can lead to the wrong sign of the interaction between charged colloids.35
2.2 Extraction from correlation functions
For a colloid at volume fraction ϕ, the inter-particle potential, u(r), uniquely determines the system's pair correlation function, g(r), or, equivalently, the structure factor S(q), which is essentially the Fourier transform of g(r). Determining g(r) or S(q) from a given u(r) is, of course, one of the classical problems of liquid state theory.36 In principle, it is also possible to reverse this procedure, and infer u(r) from measured correlation functions. The inversion of S(q) to obtain u(r) has a long history in liquid state physics, and has also been used for colloids.37,38 A fundamental difficulty with this approach is that, like many inverse problems, this one is ill-conditioned. Essentially, many different forms of interaction can give rise to indistinguishable S(q). For our purposes, it is instructive to bear in mind that the S(q) for the inert gases near their respective triple temperatures can be well fitted to the hard-sphere S(q) at an appropriate ϕ, even though the inter-particular potential under the same conditions is well approximated by a Lennard-Jones form: u(r) = Ar−12 + Br−6, which includes an attractive part, and a repulsive part that is very far from ‘hard’.Inverting the real-space pair correlation function, g(r), can also give the interaction potential,39,40 and is subject to the same ambiguities, especially when many-body effects are present.41 But if g(r) can be measured in the limit of vanishing ϕ, then the inversion to give u(r) reads:36
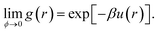 | (3) |
This approach has become possible with the advent of real-space techniques, which allows the determination of g(r) by direct counting of particles.21,40,42,43 In the limit represented by eqn (3), monodisperse hard spheres give a perfect step function form for g(r), but polydispersity and particle tracking errors would blur the sharpness of the edge at r = σ, as would a small degree of softness.43 In Fig. 2, we show the g(r) measured in this limit for a putative hard-sphere suspension.44 It is immediately clear that these particles cannot, in fact, be hard spheres. The peak in the dilute-limit g(r) is due to a short-range inter-particle attraction.† Computer simulations can be used to fit the measured dilute-limit g(r) using a square-well attraction for u(r); importantly, however, a distribution of particle sizes as well as random tracking errors (both modelled by Gaussians) are essential to obtain a good fit. Interestingly, it has been argued45 that eqn (3) remains a remarkably accurate approximation at finite but modest ϕ.
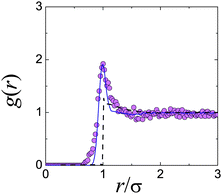 | ||
| Fig. 2 Attractions in “hard” spheres for confocal microscopy. Experimental data are from ref. 44. The dashed black line is from Percus Yevick theory for hard spheres at ϕ = 0.071.36 The solid line is computer simulation data with particle tracking errors and polydispersity added, for a square well attraction of depth kBT and range 0.09σ. | ||
2.3 Inference from second virial coefficient
Lastly, we mention a method for determining an effective hard-sphere diameter without directly measuring u(r). Instead, one measures using static light scattering46 what amounts to a functional of the interaction potential, namely, the second virial coefficient, which for an isotropic potential is given by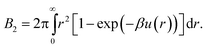 | (4) |
For hard spheres, BHS2 = 2πσ3/3. Thus, an effective hard-sphere diameter for a slightly soft system can be obtained by taking
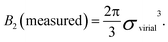 | (5) |
Note that even if the value of σvirial obtained in this way corresponds very closely to, say, a core radius determined from, e.g., electron microscopy, it does not follow that the system approximates closely to hard spheres: B2 is an integral quantity, so that a balance of repulsion and attraction can masquerade as a good fit to hard spheres on this level without u(r) being actually a hard potential.
2.4 Charged particles
The application of eqn (3) makes no a priori assumption about the form of u(r), and can therefore be applied to any system. For charged systems, if the inter-particle potential is modelled using, e.g. DLVO theory (for which see Section 4), then one could access u(r) via measuring the parameters of this theory, viz., an effective charge on the particles, Z, and the ionic strength of the solvent. The definition and therefore determination of Z is highly non-trivial,47 and the deduction of ionic strength from conductivity measurements in non-aqueous solvents depends on a number of assumptions.48 Nevertheless, reasonable results can be obtained.40,48,492.5 Accuracy
All of these methods have limitations. Those based on particle tracking methods (optical tweezers and extraction from real space) are limited by the accuracy with which the particle coordinates can be tracked, typically 30–100 nm, or up to 0.05σ for a 2 μm particle. Moreover, there is evidence that tracking errors on two closely approaching colloids may tend more to the point of contact, rather than being uniformly distributed.35,43 Furthermore, averaging over many particles in an inevitably polydisperse sample effectively adds an additional error to the measurements.43 Comparison with simulations can be used to compensate for some of these errors, though this avenue has been little explored to date. Finally, at higher concentrations,40 and in reciprocal space, one needs to make prior assumptions about the form of the inter-particle potential that one wants to determine in the first place.36–38 Accurate measurement of u(r) is therefore far from straightforward.3 Intrinsic softness
We now turn to review softness in model hard-sphere systems of non-electrostatic origin. There are two generic sources of such ‘intrinsic’ softness: steric stabilisation, and the use of particles with temperature-tuneable size.3.1 Steric stabilisation
A sterically stabilised particle is shown schematically in Fig. 1(a). We have previously27 reviewed ways to arrive at an effective hard sphere diameter for these particles via mapping to various hard-sphere properties. As already mentioned in Section 2.1, such mapping is also possible via direct measurement of colloidal forces. This has been done for PHSA-stabilised PMMA particles; these measurements, along with rheological data,64 are quite well described by an inverse power law potential with energy scale εs:31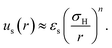 | (6) |
The relative range of us depends on the particle size, for example n = 170 for particles with a hydrodynamic diameter of σH = 200 nm, and increases with particle diameter. Likewise the strength of the interaction also depends on the particle size, with us(σH) = 146 kBT for σH = 200 nm. The results of Bryant et al.31 are replotted in Fig. 3. These quantify what is intuitively obvious, namely, that for a fixed length of stabilising ‘hairs’, larger particles are relatively harder.
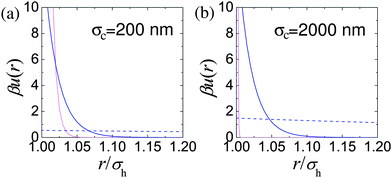 | ||
| Fig. 3 Estimation of effective colloid–colloid interactions in sterically stabilised PMMA particles: (a) σH = 200 nm, (b) σH = 2000 nm. In both parts, light pink lines denote us(r), the interaction due to the steric stabilisation. The dashed blue line in each case represents unscreened weak electrostatic interactions in low dielectric constant solvents (cis-decalin/TCE) calculated for effective charges Z = 2 and Z = 16 for (a) and (b) respectively and a Debye length of κ−1 = 5000 nm. The solid blue line represents typical screened electrostatic interactions: (a) in water (charge Z = 1700 and Debye length κ−1 = 4 nm), and (b) a density matching mixture of cis decalin and CXB (charge Z = 500 and Debye length κ−1 = 100 nm). | ||
Note that despite the steepness of the potential represented by eqn (6) with n ∼ 102, the effective volume fraction of PMMA colloids and other similarly sterically stabilised particles can nevertheless exceed the limit of random close packing, since the stabiliser layer can be compressed. Thus, for example, centrifuging PMMA colloids almost invariably generates sediments that are, at least initially before any relaxation, at volume fractions beyond random close packing. This illustrates well the point that whether certain particles are ‘hard enough’ depends on the experimental context.
3.2 Microgels
One main motivation to use soft particles to model hard spheres is that the diameter, and therefore the effective volume fraction, of these colloids may be temperature tuneable. The most popular systems here are microgel particles. As cross-linked polymer coils, their swelling is related to solvent quality, with the precise degree of swelling controlled by the cross-linking density. There are two varieties: ‘neutral’ microgels, in which a low amount of electrostatic charge is screened by added salt or is so small as to be negligible, and ionic microgels, which carry (much more) electrostatic charge, for which see Section 4.Few analytic expressions for microgel–microgel interactions exist. Expressions for polymer-covered flat surfaces have been suggested as a first approximation.50 The steric interactions between neutral microgels have been likened to crosslinked polymers, so that a form for the interaction can be obtained provided the density profile of the particle is known.51 Additional interactions in ionic microgels do have analytic forms,52 which can be added to the steric repulsion, for which an inverse power form is often assumed.
Irrespective of the absence of well-attested analytical forms for the inter-particle repulsion, swellable colloidal microgels are definitely not hard, and the degree of swelling depends sensitively on the experimental conditions, including possibly the concentration of microgel particles. If the latter is a significant effect, then any ϕeff would become state-dependent.
We now review a popular system, dispersions of poly(N-isopropylacrylamide) (PNiPAM) microgel particles,53 for which water is a poor solvent at T ≳ 33 °C, so that at and above this temperature, the diameter of the particles in an aqueous environment dramatically shrinks. Salt is usually added to screen electrostatic interactions, see Section 4. Changing the amount of the cross-linker N,N′-methylenbisacrylamide tunes how much shrinkage occurs.54 Sufficiently monodisperse samples crystallise at high volume fractions, giving crystals whose structure has been variously reported as face-centred cubic55 or as consisting of the more or less random stacking of hexagonally packed layers.56 Richtering and co-workers have examined the physical properties of PNiPAM microgel suspensions with a variety of probes and discussed their findings in terms of possible mapping onto hard spheres. We mention three aspects.
First, neutron scattering shows that an individual particle has a constant-density core, surrounded by a corona in which the density gradually decreases to zero over a distance that is approximately twice that of the core.57 From this finding alone, we expect the particles to be significantly soft.
Next, the structure factors of PNiPAM suspensions at progressively higher particle concentrations have been measured, and compared to those of hard spheres.58 Using two different methods of data analysis, it was concluded that the S(q) of these suspensions could be described adequately within a hard-sphere framework by assigning ϕeff (or, equivalently, σeff) to the particles at concentrations ϕeff ≲ 0.35. Above this concentration, increasingly large deviations from hard-sphere-like behaviour were observed. Interestingly, in a later paper,59 the same group points out that the mapping to hard-spheres at ϕeff was obtained by making one of two assumptions: either that a hard-sphere structure factor (from Percus–Yevick theory) in fact fitted the data, or that the form factor of a single particle57 determined in the low-concentration limit did not change when the microgel concentration was increased, which is not self-evidently true. Moreover, in the earlier paper, effective volume fractions determined from effective diameters obtained by fitting neutron scattering form factors do not match the volume fractions used for corresponding hard sphere structure factors in ref. 58.
Finally, Richtering and coworkers investigated the fluid-crystal coexistence gap.54,59 In one study of PNiPAM particles dispersed in water,54 a ϕeff was determined by requiring agreement with the hard-sphere expression for suspension viscosity at low concentrations, η/η0 = 1 + 2.5ϕeff + 5.9ϕeff2 (where η0 is the solvent viscosity). This procedure is problematic because of the aforementioned state-dependence of σeff (and therefore of ϕeff). Nevertheless, using this mapping, the fluid-solid coexistence gap was found to be ϕfeff = 0.59 ≤ ϕ ≤ 0.61 = ϕmeff, i.e. it occurs at significantly higher concentrations than that in hard spheres (0.494 = ϕfHS ≤ ϕHS ≤ ϕmHS = 0.545), and is substantially narrower (ϕmeff − ϕfeff = 0.02, ϕmHS − ϕfHS = 0.051).‡ Furthermore, the ϕeff obtained from the viscosity measurements does not match that obtained from fitting of the hard-sphere structure factors where by construction in the hard sphere fluid ϕHS ≤ 0.494. This shows nicely that softness effects influence static and dynamical properties in different ways. The discrepancy may be related to the fact that σeff for microgels is sensitive to the osmotic pressure, and thus can vary under shear, and also at different state points. Consequently, a mapping to hard spheres at a given state point under zero shear may not hold for other state points, or for the same state point under shear.
Comparison with simulations62 of the freezing of particles interacting via a power-law repulsion u(r) ∝ r−n gives n ≈ 13 for PNiPAM particles with 240 nm ≲ σH ≲ 300 nm. Comparable results have obtained from analysis of rheological data63 in oil-based microgel systems60 and the PNiPAM system.54,64 This is considerably softer than the inter-particle potential found31 for sterically stabilised particles of comparable size (σc = 200 nm), which can be characterised by a power law with exponent n = 170.
A different mapping was used in a second study of fluid-crystal coexistence,59 in which the PNiPAM microgel particles are now dispersed in dimethylformamide (DMF, a good solvent chosen for refractive index matching). The freezing concentration of the microgel particles expressed in mass fraction, μ = mmicrogel/(mmicrogel + msolvent), was converted to an effective hard-sphere volume fraction by a multiplicative factor, ϕeff = Sμ, where the ‘swelling ratio’ S was chosen to yield a freezing volume fraction of ϕfeff = 0.494. Interestingly, this procedure gave ϕmeff ≈ 0.55 for the point at which 100% crystallisation should occur, consistent with hard-sphere behaviour. This agrees with the findings by another group of a recent imaging study using larger PNiPAM particles dispersed in an aqueous medium,56 but contrasting strikingly with the previous finding by the same group of a significantly narrower coexistence gap.54 The same study found that the collective diffusion of these microgel particles dispersed in DMF and their hydrodynamic interactions could not be well described by any mapping to hard spheres.
These studies illustrate some of the difficulties associated with mapping microgels to hard spheres. An additional issue is that of polydispersity. Both softness in the inter-particle potential62,65,66 and polydispersity66,67 affect the width of the coexistence gap, so that the effect of these two quite distinct physical factors may be difficult to disentangle. Fortunately, microgels can be synthesised with polydispersities as low as ∼1% before swelling, so that perhaps the polydispersity effect can be neglected in the first approximation (cf. the very small effect 1% polydispersity on the miscibility gap of hard spheres67).
A variant of the ‘canonical’ microgel has been synthesised and characterised by Ballauff and co-workers68,69 consisting of a hard polystyrene core onto which is grafted a network of cross-linked PNiPAM, so that the swollen shell has approximately the same dimensions as the core radius (≈50 nm). To determine ϕeff, a core volume fraction ϕc was first measured by conversion from the particle mass fraction using the density of polystyrene. The hydrodynamic diameter of the particles, σH was then determined using dynamic light scattering; this was later confirmed to be very close to the diameter of the outer corona visible in cryo-transmission electron microscopy (cryo-TEM) images,69 which also gave the core diameter σc, and the polydispersity of the core–shell diameter distribution (≈9%). Finally, using ϕeff = ϕc(σH/σc)3, the fluid-crystal coexistence gap at 21 °C was found at 0.483 ± 0.007 < ϕeff < 0.546 ± 0.007, which is, within experimental uncertainties, very close to the hard-sphere interval of 0.494 to 0.545.§
It is interesting to analyse these fluid-crystal coexistence measurements further. As Ballauff and coworkers69 have pointed out, if ϕfeff is rescaled to exactly 0.494, then melting occurs at 0.556. This gives a coexistence gap wider than in perfect hard spheres. If this does not reflect experimental errors, then the situation is somewhat unusual – the most common ‘culprits’, polydispersity and softness in the repulsive potential, both narrow the coexistence gap [Fig. 4(a) and (b)].62,65,66 However, short-range attraction in the potential has the opposite effect of widening the coexistence gap if the polydispersity¶ is low enough.72–74 On the other hand, 9% polydisperse hard spheres should be at or beyond the experimental limit of crystallisation,75 probably due to the onset of multiple solid phase coexistence in the phase diagram,67,76 which requires long-range particle motion for fractionation. That crystallisation was still observed in these PNiPAM samples to give a coexistence gap wider than that of hard-spheres underlines the lack of complete understanding of microgel physics.
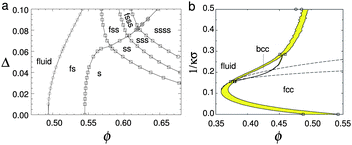 | ||
| Fig. 4 (a) The theoretical phase diagram of hard spheres at different polydispersities, σ. F = fluid, S = (crystalline) solid; thus FSS denotes fluid–solid–solid coexistence. Replotted from Wilding and Sollich.67 (b) Phase diagram of hard-core Yukawa particles, from ref. 65 in the absolute volume fraction – Debye length (1/κσ) plane. Here the contact potential εY = 8kBT. In the case of zero Debye length, the hard sphere limit is recovered. Replotted from Hynninen and Dijkstra.65 | ||
More recently, Ballauff and co-workers studied in detail the rheology of a 17% polydisperse suspension of their core–shell particles at and near the glass transition (found to occur at ϕeff = 0.640), and compared their data with mode-coupling theory (MCT) calculations for hard spheres.77 At this polydispersity crystallisation was inhibited, but this introduced an extra level of complexity into calculating ϕeff. The authors relied on the fact that the high-frequency viscosity had been found to be relatively insensitive to polydispersity,78 and mapped the high polydisperse system onto a less polydisperse system in which ϕeff had already been calibrated according to the procedure explained above. A large measurement of agreement with MCT predictions has been found. We note in this connection that the comparison with MCT mostly relies on a relative measure of the distance to the glass transition ϕg: ε = (ϕ − ϕg)/ϕg, so that the work is perhaps less vulnerable to systematic or statistical uncertainties in arriving at ϕeff, although the influence of softness on ε should certainly be investigated – to our knowledge, so far it has not been.
Very recently, the rheology of sterically stabilised, microgel and hard-core–microgel-shell particles has been compared.79 Qualitative differences have been found, with the yield strain exhibiting non-monotonic behaviour with respect to ϕ in the case of the sterically stabilised (solid) particles and monotonic behaviour otherwise. Furthermore, microgels have54,80 been studied at effective volume fractions above random close packing, which is impossible for true hard spheres.
3.3 Star polymers
In the spectrum of hard to soft colloids, microgels occupy a middle niche. Towards the soft end of this spectrum, we encounter star polymers; when the number of ‘arms’ (or ‘functionality’, f) is high enough, these can be considered soft colloids, with decreasing softness as f increases. Thus, for example, stars with f > 34 are predicted to crystallise above the overlap concentration (i.e. ϕeff ≃ 1),81 which has recently been observed experimentally.82 But the structures of the crystal phases differ from those formed from hard spheres (random stacking of hexagonal layers). Moreover, the effective potential between two particles at close approach is logarithmic,83 which is significantly softer than the power-law forms encountered in this review so far. Thus, although in a mixture of (large) hard colloids and (smaller) star polymers, 32-arm stars were found to behave almost hard-sphere like vis-à-vis the hard colloids,84 it is unlikely that pure star polymer suspensions can be used as models of hard spheres. A related class of materials is star-like micelles,85 which are similarly too soft to be considered as hard-sphere-like for our purposes.3.4 Emulsions
Another system of interest is emulsions. These have the attraction of having smooth surfaces by definition, and avoid any concerns with surface roughness of solid colloids and interdigitation in the case of sterically stabilised particles. While there is literature on using emulsions to form gels86–88 microemulsions are typically too polydisperse to crystallise. Although microfluidic methods which generate very monodiserse particles are straightforward to implement, these usually produce particles in the σ ≳ 20 μm size range.89 We are unaware of any studies directly comparing emulsions to hard spheres – the particles are usually too polydisperse to crystallise, and shearing may lead to coalescence. We further speculate that the surfactant molecules used to stabilise emulsions likely lead to electrostatic interactions. In short, emulsions are a potentially interesting system for hard-sphere like behaviour, but considerable development is called for before they can challenge sterically stabilised colloids.4 Electrostatics
It is now generally accepted that immersion of a colloid in a liquid medium always gives rise to some degree of charging of the particles. This is a potential source of softness that should always be considered in experiments. If charged groups are present on the surface of the particles, entropy inevitably favours at least a certain degree of dissociation; even when charged surface groups are absent, adsorption of charged species from the medium will give rise to charged particles.The treatment of electrostatic interactions on the mean-field, or linearised Poisson–Boltzmann (PB), level is largely adequate for our purposes. This is especially true for non-aqueous systems,48,90 in which the energetic penalty of ionisation is high, so that ion densities are low, and multivalent ions can be safely neglected.
The linearised PB theory is incorporated into the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory91 to describe the interaction between charged colloids. The original DLVO potential consists of van der Waals (vdW) and electrostatic components. We are primarily interested in situations in which sterically stabilised particles become charged, so we will assume that the steric repulsion is adequate to render the vdW component negligible. Instead, we will consider an inter-particle potential consisting of a steric repulsion, us(r), and an electrostatic interaction, which in linearised PB theory has an Yukawa form, uY(r):
| u(r) = us(r) + uY(r), | (7) |
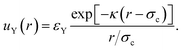 | (8) |
Here, the contact potential is given by
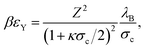 | (9) |
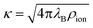 , where ρion is the number density of monovalent ions. The Bjerrum length
, where ρion is the number density of monovalent ions. The Bjerrum length| λB = βe2/(4πε0εr), | (10) |
4.1 Strong charging in aqueous solvents
Water has an unusually large zero-frequency dielectric constant, εr ≈ 80 around room temperature, giving a Bjerrum length of 0.7 nm. Since λB is comparable to the size of small ions, many ionic salts are readily soluble in water. This in turn means that the Debye length is easily controlled down to a few nanometres. For σ = 400 nm and Z = 1700 in water with a κ−1 = 4.0 nm, eqn (8), (9), (1) and (2) give σkT = 1.052σc and σBH = 1.062σc. Thus, screened charged colloids in water very often approximate hard spheres reasonably if they are either sterically stabilised or the short κ−1 is still large enough to render vdW attractions irrelevant. Nevertheless, some aspects of the behaviour of such colloids may still be non-hard-sphere-like. Thus, in their determination of the equation of state (EOS) Piazza et al.16 found that, although the EOS of their screened charged colloids approximated the hard sphere EOS at moderate to high ϕ, at low ϕ, the barometric distribution in the earth's gravitational field, ϕ(z) = ϕ(0)e−z/z0, was not observed, with the measured height distribution showing a more slowly decaying ‘tail’. This is related to a decoupling of ions and colloids, leading to a macroscopic electric field.93Very recently, it has been shown that in the case of ionic microgels, electrostatics can add a further level of complexity to the effective interactions. Changing concentration leads to a change in ionic strength which in turn couples to the particle size. This can lead to a significant change in effective hard sphere diameter as a function of particle concentration.94
4.2 Weakly charged small particles in non-aqueous media
In non-aqueous solvents, charging is profoundly altered. The reduced dielectric constant, ε ≲ 10, leads to λB ∼ 10–40 nm. With ionic sizes in the range of 1 nm, one expects strong coupling between oppositely charged ions and consequently little dissociation of surface groups. It was therefore a long-held assumption that electrostatics could be safely neglected. However, the work of the van Blaaderen and Yethiraj95 and others have shown that some electrostatic charging always occurs.It seems that the degree of charging in many systems40,49,92,96,97 can be described by the rule of thumb ZλB/σ ≈ 6. Thus, the system used by Pusey and van Megen,15 sterically stabilised PMMA (σ ≈ 700 nm) in a mixture of cis-decalin and carbon disulphide (εr = 2.64, λB ≈ 20 nm), can be expected to be charged to some extent, as later work on a similar suspension seems to confirm.97
Nevertheless, when the particles are small enough, such charging can often be ignored. Fig. 3(a) (dashed blue line) shows uY(r) for a charge of Z = 2 on the surface of σH = 200 nm particles (corresponding to ZλB/σ ≈ 6) in a dispersion medium with a Debye length of κ−1 = 5 μm. The measured steric repulsion for sterically stabilised PMMA particles of this size31 is also shown. It is clear that for all relevant length scales in this situation, uY(r) ≪ kBT. These particles can plausibly be considered hard spheres.
4.3 Particles for confocal imaging
The most popular hard-sphere model system to date for confocal microscopy is sterically stabilised PMMA, because of the possibility of using a solvent mixture for simultaneous refractive index and density matching. For accurate determination of coordinates, particles with σH ≳ 1 μm are required. The density-matching solvents used are typically halogenated hydrocarbons. The use of these solvents has a number of undesirable side effects. They tend to swell the particles much more aggressively than non-halogenated hydrocarbons, and they can damage the fluorescent dye molecules included in the particles for laser confocal microscopy. They also lead to significant levels of electrostatic charging.Four commonly used halogenated solvents are cycloheptyl bromide (CHB), cyclohexyl bromide (CXB), tetrachloroethylene (TCE), and carbon tetrachloride.|| In these low dielectric constant solvents (e.g., εr = 7.9 for CXB), colloids suitable for confocal microscopy (σH ∼ 2 μm) acquire a charge of Z ∼ 100–500. The Debye length in a density-matching CXB–cis decalin mixture can run to microns as the ionic strength (due predominantly to solvent self-dissociation) can be as low as 10−10 M,95 which is much lower than the ionic concentration in pure water (10−7 M).
The charge on the colloid, although much lower than what can be expected on similar sized particles in water, is now almost unscreened, which can lead to very long-ranged and strong interactions (εY ≳ 100 kBT). These interactions can and do vary from sample to sample, as the ionic strength in CXB and CHB varies from batch to batch, and as a function of time.40,48,49 Colloidal crystallization has been found in some cases23 at ϕ ≈ 0.4 (as compared to hard spheres at ϕfHS = 0.494), but at least one experiment saw crystallization at volume fractions as low as ϕ ∼ 0.01;95 often these crystals were body-centered-cubic (bcc) in contrast to hard-sphere crystals which are random-hexagonal-close-packed (rhcp) or fcc. Furthermore, for some batches of CXB, the colloid charge can change with particle concentration, leading to strongly ϕ-dependent interactions, and even to re-entrant melting.48 The use of PMMA particles in halogenated solvents for confocal microscopy is therefore problematic.
The situation can be improved somewhat by the use of salts to screen the charges. The problem with this approach is that salts soluble in these solvent mixtures such as tetrabutyl ammonium bromide (TBAB)95 are soluble only to around 260 nM.48,49 This results in a Debye length of κ−1 ≈ 100 nm. Although this is substantially less the diameter of imageable colloids (σH ≳ 1 μm), it is not negligible and a noticeable degree of softness will likely result, Fig. 3(b). On the other hand, since the majority of ions now come from the salt, the ionic strength and therefore the colloid–colloid effective interactions will likely be reasonably independent of ϕ.
Another possibility is to use lower dielectric constant solvents such as TCE and CCl4 (εr = 2.5 and 2.24 respectively). Lower εr increases λB, eqn (10). The rule of thumb for estimating the degree of charging, viz., ZλB/σc ≈ 6, therefore predicts a lower Z. However, both of these solvents are strongly absorbed by PMMA, and can lead to a volume swelling of ≳40%.44 Unless the swelling is very closely monitored and characterised, it becomes a source of potentially large systematic errors,27 because ϕ ∝ σ3. Solvent absorption also changes the density and refractive index of the particles. Thus, one of the initial attractions of using such halogenated solvents is lost – without swelling, adding one of these solvents can density match nearly exactly but also (fortuitously) nearly match the refractive index. With significant absorption, more TCE (say) than is needed for index matching has to be added to achieve density matching. Unless a third solvent is used to re-achieve index matching (which itself may lead to further swelling), a turbid sample results.
Such turbidity not only degrades image quality, but can also give rise to significant vdW attraction. For example, Fig. 2, which shows the measured g(r) of a ϕ = 0.071 suspension of sterically stabilised PMMA particles in a density-matching mixture of cis-decalin and TCE.44 The pronounced peak at touching immediately alerts us to the presence of inter-particle attraction, as simulations confirm.
5 A cautionary worked example
Since a well-attested analytical form for the interaction between charged colloids is available, eqn (7)–(10), we close by presenting an ‘exact’ comparison between the simulated phase behaviour of such particles, Fig. 4, and various ways of mapping their behaviour to hard spheres. This comparison illustrates how careful one must be in drawing conclusions from such mapping, even in the limit when inevitable experimental uncertainties (e.g. due to polydispersity or slightly soft steric-stabilising ‘hairs’) are negligible.Consider charged hard spheres, so that us(r) in eqn (7) is the perfect hard-sphere repulsion. We model scenarios that may reasonably represent sterically stabilised PMMA used in confocal imaging, and take σc = 2 μm, and a Debye screening length of κ−1 = 100 nm (so that κσc = 20). The latter is a round figure chosen to correspond roughly to a density-matching mixture of cis-decalin and CXB with the maximum possible amount of dissolved TBAB (260 nM). Consider two colloid charges Z = 500 and Z = 100. The former is consistent with the rule of thumb, ZλB/σ ≈ 6, while the latter is 5 times lower than predicted by this empirical relation. These charges have been reported in different studies40,48,98,99 for nominally identical PMMA particles used for confocal imaging dispersed in a density-matching mixture of cis-decalin and CXB. Eqn (9) gives εY ≈ 10kBT and ≈ 0.5kBT for these two charges respectively.
Taking these parameters, the simulation results65 replotted in Fig. 4(b) can be used to determine freezing and melting for our hypothetical systems. These are delimited by red lines in Fig. 5 for (a) Z = 500 and (b) Z = 100. Note first that these values of not-very-large surface charge, variously reported in the literature for nominally very similar PMMA colloids, in fact pertain to rather large differences in the freezing/melting transitions, both in terms of absolute values of the transitions points and in terms of width of the coexistence region. Thus, some kind of ‘mapping’ is clearly necessary if we are to use either system to model hard spheres meaningfully.
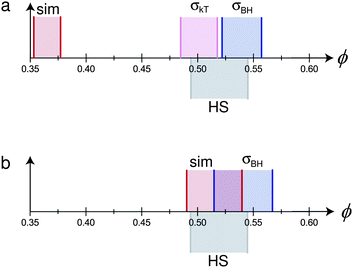 | ||
| Fig. 5 Mapping the phase behaviour of two hypothetical monodisperse charged hard sphere colloids (with parameters based on real systems – see text for details) to pure hard spheres. The hypothetical particles and solvent have the following properties: σc = 2 μm, κ−1 = 100 nm. The particles have two different charges (a) Z = 500, (b) Z = 100. In each case, differently shaded and delimited regions denote the fluid–solid coexistence gap of pure hard spheres (grey, ‘HS’), and from: simulations65 (red, ‘sim’), mapping using eqn (7) (lilac, ‘σkT’), and mapping using eqn (2) (blue, ‘σBH’). In (b), the result of mapping using eqn (7) does not change the coexistence region from that predicted by ‘sim’, and is not shown separately. | ||
We proceed to calculate σeff for the particles represented by these two parameter sets using either eqn (1) or eqn (2), and eqn (7)–(10). If mapping is to be helpful, we should expect that once we have transformed ϕ to ϕeff, freezing and melting of the two system should occur at approximately the hard-sphere values, viz., 0.494 and 0.545.
Fig. 5(a) shows that for the case Z = 500, eqn (1) predicts freezing at ϕfkT = 0.484, just 0.010 from the ‘correct’ value.** However, the width of the coexistence gap is reduced, which is the result of the softness of the screened electrostatic (Yukawa) repulsion. Since the mapping involves scaling ϕ by constant, ϕeff = (σeff/σ)3ϕ, it preserves the relative coexistence gap, so that the melting concentration, ϕfkT is significantly underestimated. Conversely, the Barker–Henderson treatment gives a relatively accurate estimate of ϕmkT, but rather significantly overestimates ϕfkT. In the case of Z = 100, since εY = kBT, σkT = σ, so that eqn (1) maps perfectly onto hard spheres. In this case, the Barker–Henderson approach does the worse job, even when compared to the raw (unmapped) coexistence gap given by simulations of the bare Yukawa interaction. We note that since the coexistence gap varies with the interaction, mapping to the true hard sphere volume fraction at freezing inevitably gives an erroneous melting volume fraction unless the colloids are absolutely hard.
Fig. 5 therefore shows that the different methods of mapping to hard spheres do not give the same result. In practice, of course, the inter-particle potential is not exactly known, and polydispersity is inevitable. What is clear from the worked example summarised in Fig. 5 is that even in the ‘ideal’ case of monodisperse spheres with an exactly known inter-particle interaction, mapping to hard spheres is system- and approach-specific. In practice, of course, polydispersity introduces significant uncertainties, and the Debye length is often not determinable to high accuracy. Moreover, we stress that the values of Z = 500 and Z = 100 are taken from experiments on nominally identical systems. Thus, conclusions derived from any ‘mapping to hard spheres’, e.g. comparison of nucleation rates at nominally equivalent state points in the coexistence gap, must be treated with significant caution.
6 Conclusions
We set out on a quest for colloids that mimic as closely as possible the ideal hard sphere. It seems that, to date, small (say σ ≲ 200 nm) sterically PMMA particles dispersed in index-matched hydrocarbons come about as close as possible to this ideal. Larger PMMA particles suitable for confocal microscopy require density matching to minimise sedimentation; but the solvents used inevitably induce a degree of charging that is difficult to screen out entirely using salts. The resulting soft, screened Coulomb inter-particle repulsion can be satisfactorily modelled on the mean-field level, however the interaction parameters vary hugely for nominally identical systems. The use of microgels such as PNiPAM, either on their own or as ‘shells’ on hard ‘cores’, has become popular, because their volume fraction can conveniently be tuned by temperature. Their inevitably soft mutual interaction has proven harder to model in a generic, analytical form. In both cases, the softness necessitates the use of a ϕeff to map onto hard spheres. We have reviewed various ways of performing this mapping, with or without the benefit of knowledge of the inter-particle potential u(r). None seem entirely satisfactory. Furthermore, the effective diameter of microgel particles is sensitive to osmotic pressure. Therefore, even for a given system, σeff can change as a function of volume fraction, and for a given sample, as a function of shear rate.We end by making two further observations. First, we widen the scope of our enquiry from charged particles and microgels to other kinds of non-hard inter-particle interaction, and ask what requirements should be satisfied before one may fruitfully embark on the exercise of ‘mapping’ to hard spheres. We suggest the minimum conditions to be satisfied are:
(1) the absence of any attractive interaction, so that the equilibrium physics is dominated by entropic effects;
(2) crystals in a sufficiently monodisperse dispersion at high concentrations consist of the stacking of hexagonal layers.
The first criterion highlights the importance of refractive index matching to minimise the ubiquitous vdW interaction. The second criterion explains why charged hard particles with κσ ≳ 6, Fig. 4, and microgels55,56 are suitable candidates for mapping to hard spheres, but star polymers are not.81
Secondly and finally, we point out that new developments in particle synthesis may yet produce μm-sized colloids that can be index and density matched using solvents or solvent mixtures that do not bring about charging and minimal swelling. Such development will be most welcome for the community of scientists wishing to use colloids to test fundamental theories of many-body physics via the hard-sphere model system.
Of course, soft particles, from microgels to star polymers and beyond, are fascinating systems in their own right.100 Furthermore, it is reasonable to enquire how much deviation from perfect hard spheres is acceptable, and the answer of course depends on what one wishes to study. Section 5 shows that the location of colloidal phase boundaries can vary in nontrivial and qualitative ways from hard spheres. However, it is plausible that slight softening may only have slight changes in, for example, the structural relaxation time.30
Our point, then, is that while particle interaction details may not matter in some cases (such as the pair structure of dense liquids), there are plenty of cases where the behaviour of the system depends strongly on both the volume fraction ϕ and the interparticle interactions, therefore accurate knowledge of the both is essential. Crucially, the interactions may well be known to even less precision that the absolute volume fraction ϕ, which we have already argued is knowable only to 3–6%.
Acknowledgements
We thank P. Bartlett, J. C. Crocker, R. Evans, D. Frenkel, M. Fuchs, A. A. Louis, P. N. Pusey, H. Tanaka and A. van Blaaderen for helpful discussions over many years, and P. Sollich and M. Dijkstra for the data in Fig. 4. CPR is funded by the Royal Society. WCKP held an EPSRC Senior Fellowship (EP/D071070/1), and thanks Universität Konstanz for hospitality, during which part of this work was done. ERW was supported by NSF grant NSF CHE-0910707.References
- T. C. Hales, Discrete Comput. Geom., 1997, 17, 1–51 Search PubMed.
- T. C. Hales, Discrete Comput. Geom., 1997, 18, 135–149 Search PubMed.
- J. G. Kirkwood and E. M. Boggs, J. Chem. Phys., 1942, 10, 394–402 CrossRef CAS.
- M. S. Werthiem, Phys. Rev., 1963, 10, 321–322 Search PubMed.
- E. Thiel, J. Chem. Phys., 1963, 39, 474–479 CrossRef.
- J. Lebowitz, Phys. Rev., 1964, 133, A895–A899 CrossRef.
- G. A. Mansoori, N. F. Carnahan, K. E. Starling and T. W. Leland, J. Chem. Phys., 1971, 54, 1523 CrossRef CAS.
- M. N. Rosenbluth and A. W. Rosenbluth, J. Chem. Phys., 1954, 22, 881–884 CrossRef CAS.
- B. Alder and T. Wainwright, J. Phys. Chem., 1957, 27, 1208–1209 Search PubMed.
- W. W. Wood and J. D. Jacobson, J. Chem. Phys., 1957, 27, 1207–1208 CrossRef CAS.
- B. Widom, Science, 1967, 157, 375–382 CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- J. D. Bernal, Nature, 1959, 183, 141–147.
- P. N. Pusey, in Liquids, Freezing and the Glass Transition, ed. J. P. Hansen, D. Levesque and J. Zinn-Justin, Elsevier, Amsterdam, 1991, pp. 765–942 Search PubMed.
- P. Pusey and W. van Megen, Nature, 1986, 320, 340 CrossRef CAS.
- R. Piazza, T. Bellini and V. Degiorgio, Phys. Rev. Lett., 1993, 25, 4267–4270 Search PubMed.
- D. W. Aastuen, N. A. Clark, L. K. Cotter and B. J. Ackerson, Phys. Rev. Lett., 1986, 57, 1733–1736 CrossRef CAS.
- K. Schätzel and B. J. Ackerson, Phys. Rev. Lett., 1992, 68, 337–340 Search PubMed.
- W. van Megen, T. C. Mortensen and S. R. Williams, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6073–6085 CrossRef CAS.
- A. van Blaaderen, A. Imhof, W. Hage and A. Vrij, Langmuir, 1992, 8, 1514–1517 CrossRef CAS.
- A. van Blaaderen and P. Wiltzius, Science, 1995, 270, 1177–1179 CrossRef CAS.
- V. Prasad, D. Semwogerere and E. R. Weeks, J. Phys.: Condens. Matter, 2007, 19, 113102 CrossRef.
- U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Science, 2001, 292, 258–262 CrossRef CAS.
- A. M. Alsayed, M. F. Islam, J. Zhang, C. P. J. Collings and A. Yodh, Science, 2005, 309, 1207–1210 CrossRef CAS.
- W. K. Kegel and A. van Blaaderen, Science, 2001, 287, 290–293 Search PubMed.
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2001, 287, 627–631.
- W. C. K. Poon, E. R. Weeks and C. P. Royall, Soft Matter, 2012, 8, 21–30 RSC.
- J. A. Barker and D. Henderson, Rev. Mod. Phys., 1976, 48, 587–671 CrossRef CAS.
- H. C. Andersen, J. D. Weeks and D. Chandler, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 1597–1607 CrossRef.
- M. Schmiedeberg, T. K. Haxton, S. R. Nagel and A. J. Liu, Europhys. Lett., 2011, 96, 36010 Search PubMed.
- G. Bryant, S. R. Williams, L. Qian, I. K. Snook, E. Perez and F. Pincet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 060501 CrossRef CAS.
- C. Bechinger, D. Rudhardt, P. R. R. Leiderer and S. Dietrich, Phys. Rev. Lett., 1999, 83, 3960–3963 CrossRef CAS.
- M. Piech and J. Walz, J. Colloid Interface Sci., 2002, 253, 117–129 CrossRef CAS.
- J. C. Crocker and D. G. Grier, Phys. Rev. Lett., 1994, 81, 352–355 Search PubMed.
- J. Baumgartl and C. Bechinger, Europhys. Lett., 2005, 487–493 Search PubMed.
- J.-P. Hansen and I. Macdonald, Theory of Simple Liquids, Academic press, London, 1976 Search PubMed.
- M. H. G. Duits, R. P. May, A. Vrij and C. G. De Kruif, Langmuir, 1991, 7, 62–68 CrossRef CAS.
- X. Ye, T. Narayanan, P. Tong and J. Huang, Phys. Rev. Lett., 1996, 76, 4640–4643 CrossRef CAS.
- M. Brunner, C. Bechinger, W. Strepp, V. Lobaskin and H. H. von Gruenberg, Europhys. Lett., 2002, 58, 926–965 CrossRef CAS.
- C. P. Royall, M. E. Leunissen and A. van Blaaderen, J. Phys.: Condens. Matter, 2003, 15, S3581–S3596 CrossRef CAS.
- A. Louis, J. Phys.: Condens. Matter, 2002, 14, 9187–9206 CrossRef CAS.
- S. H. Behrens and D. G. Grier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 050401(R).
- C. P. Royall, A. A. Louis and H. Tanaka, J. Chem. Phys., 2007, 127, 044507 CrossRef.
- T. Ohtsuka, C. P. Royall and H. Tanaka, Europhys. Lett., 2008, 84, 46002 CrossRef.
- A. Louis, Philos. Trans. R. Soc. London, Ser. A, 2001, 359, 939–960 Search PubMed.
- Neutron, X-rays and Light. Scattering Methods Applied to Soft Condensed Matter, ed. T. Zemb and P. Lindner, Elsevier BV, Amsterdam, North-Holland, 2002 Search PubMed.
- W. Russell, D. Saville and W. Schowalter, Colloidal Dispersions, Cambridge Univ. Press, Cambridge, 1989 Search PubMed.
- C. P. Royall, M. E. Leunissen, A.-P. Hyninnen, M. Dijkstra and A. van Blaaderen, J. Chem. Phys., 2006, 124, 244706 CrossRef.
- M. Leunissen, Ph.D. thesis, Utrecht Universiteit, 2006.
- C. L. Berli and D. Quemada, Langmuir, 2000, 16, 10509–10514 CrossRef CAS.
- D. Gottwald, C. N. Likos, G. Kahl and H. Lowen, J. Chem. Phys., 2005, 122, 074903 CrossRef CAS.
- A. R. Denton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011804 CrossRef CAS.
- H. G. Schild, Prog. Polym. Sci., 1992, 17, 163 CrossRef CAS.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- T. Hellweg, C. D. Dewhurst, E. Brückner, K. Kratz and W. Eimer, Colloid Polym. Sci., 2000, 278, 972–978 CrossRef CAS.
- V. D. Nguyen, M. T. Dang, B. Weber, Z. Hu and P. Schall, Adv. Mater., 2011, 2716–2720, 23 Search PubMed.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lidner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS.
- M. Stieger, J. S. Pedersen, P. Lindner and W. Richtering, Langmuir, 2004, 20, 7283–7292 CrossRef CAS.
- T. Eckert and W. Richtering, J. Chem. Phys., 2008, 129, 124902 CrossRef.
- S. E. Paulin, B. J. Ackerson and M. S. Wolfe, J. Colloid Interface Sci., 1996, 187, 251–262 Search PubMed.
- S. Iacopini, T. Palberg and H. J. Schope, J. Chem. Phys., 2008, 130, 084502 Search PubMed.
- R. Agrawal and D. A. Kofke, Mol. Phys., 1995, 85, 23 CAS.
- R. Buscall, J. W. Goodwin, M. W. Hawkins and R. H. Ottewill, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 2889–2899 RSC.
- A. Le Grand and G. Petekidis, Rheol. Acta, 2008, 47, 579–590 CrossRef CAS.
- A. P. Hynninen and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021407 CrossRef.
- M. Yiannourakou, I. G. Economou and I. A. Bitsanis, J. Chem. Phys., 2009, 130, 194902 Search PubMed.
- N. B. Wilding and P. Sollich, Soft Matter, 2011, 7, 4472–4484 RSC.
- J. J. Crassous, M. Siebenbürger, M. Ballauff, M. Drechsler, O. Henrich and M. Fuchs, J. Chem. Phys., 2006, 125, 204906 CrossRef CAS.
- J. J. Crassous, A. Wittemann, M. Siebenbürger, M. Schrinner, M. Dreschsler and M. Ballauff, Colloid Polym. Sci., 2008, 286, 2805–2812 Search PubMed.
- K. Ohno, T. Morinaga, S. Takeno, Y. Tsujii and T. Fukuda, Macromolecules, 2006, 39, 1245–1249 CrossRef CAS.
- S. M. Liddle, T. Narayanan and W. C. K. Poon, J. Phys.: Condens. Matter, 2011, 23, 194116 Search PubMed.
- A. P. Gast, C. K. Hall and W. B. Russel, J. Colloid Interface Sci., 1983, 96, 251–267 CrossRef CAS.
- H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564 CrossRef CAS.
- J. R. Elliot and L. Hu, J. Chem. Phys., 1999, 110, 3043–3048 CrossRef.
- P. N. Pusey, J. Phys., 1987, 48, 709–712 CAS.
- E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon, M. E. Cates and P. N. Pusey, Phys. Rev. Lett., 2009, 103, 135704 CrossRef CAS.
- M. Siebenbürger, M. Fuchs, H. Winter and M. Ballauff, J. Rheol., 2009, 53, 707–726 CrossRef CAS.
- Z. Cheng, J. Zhu, P. M. Chaikin, S.-E. Phan and W. B. Russel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041405 CrossRef.
- N. Koumakis, A. Panvouxoglou, A. S. Poulos and G. Petekidis, Soft Matter, 2012, 8, 4271–4284 RSC.
- V. Carrier and G. Petekidis, J. Rheol., 2009, 53, 245–274, DOI:10.1122/1.3045803.
- H. Löwen, M. Watzlawek, C. N. Likos, M. Schmidt, A. Jusufi and A. R. Denton, J. Phys.: Condens. Matter, 2000, 12, A465–A469 Search PubMed.
- E. Stiakakis, A. Wilk, J. Kohlbrecher, D. Vlassopoulos and G. Petekidis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020402(R).
- T. A. Witten and P. A. Pincus, Macromolecules, 1991, 24, 2509 Search PubMed.
- W. C. K. Poon, S. U. Egelhaaf, J. Stellbrink, J. Allgaier, A. B. Schofield and P. N. Pusey, Philos. Trans. R. Soc. London, Ser. A, 2001, 359, 897–907 Search PubMed.
- M. Laurati, J. Stellbrink, R. Lund, L. Willner and D. Richter, Phys. Rev. Lett., 2005, 94, 195504 CrossRef CAS.
- J. Bibette, T. G. Mason, H. Gang and D. A. Weitz, Phys. Rev. Lett., 1992, 69, 981–984 CrossRef CAS.
- J. N. Wilking, S. M. Graves, C. B. Chang, K. Meleson, M. Y. Lin and T. G. Mason, Phys. Rev. Lett., 2006, 96, 015501 CrossRef CAS.
- L. J. Teece, M. A. Faers and P. Bartlett, Soft Matter, 2011, 7, 1341–1351 RSC.
- S. Xu, Z. Nie, M. Seo, P. Lewis, E. Kumacheva, H. A. Stone, P. Garstecki, D. B. Weibel, I. Gitlin and G. M. Whitesides, Angew. Chem., 2005, 117, 734–738 CrossRef.
- C. P. Royall, R. van Roij and A. van Blaaderen, J. Phys.: Condens. Matter, 2005, 17, 2315–2326 CrossRef CAS.
- E. Verwey and J. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- S. Alexander, P. M. Chaikin, P. Grant, G. J. Morales, P. Pincus and D. Hone, J. Chem. Phys., 1984, 80, 5776–5781 CrossRef CAS.
- R. van Roij, J. Phys.: Condens. Matter, 2003, 15, S3569 CrossRef CAS.
- P. Holmqvist, P. S. Mohanty, G. Nagele, P. Schurtenberger and M. Heinen, Phys. Rev. Lett., 2012, 109, 048302 Search PubMed.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS.
- E. Trizac, L. Bocquet and M. Aubouy, Phys. Rev. Lett., 2002, 89, 248301 CrossRef.
- G. S. Roberts, T. A. Wood, W. J. Frith and P. Bartlett, J. Chem. Phys., 2007, 126, 194503 CrossRef.
- H. Sedgwick, S. U. Egelhaaf and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S4913–S4922 CrossRef CAS.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef.
- D. Vlassopoulos and M. Cloitre, Soft Matter, 2012, 8, 4010–4013 RSC.
Footnotes |
| † The step function form of g(r) for dilute hard spheres gives a featureless S(q) = 1. Residual attraction or softness therefore shows up much more obviously in real space. |
| ‡ The same narrowing of the fluid-crystal coexistence gap has been found in an oil-based systems of polystyrene microgels.60,61 |
| § We note that a similar system with silica cores and PMMA shells has been developed which has been density and index matched, and fluorescently labelled, making it suitable for confocal microscopy.70 |
| ¶ Experimentally, for hard spheres above a critical polydispersity, short-range attraction appears not to widen the coexistence gap.71 |
| || Note that carbon tetrachloride is a suspected carcinogen. |
| ** To put this difference in context, note that it is smaller than other sources of errors inherent in measuring ϕ.27 |
| This journal is © The Royal Society of Chemistry 2013 |
