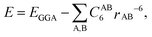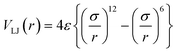Hierarchical simulations of hybrid polymer–solid materials

Abstract

Complex polymer–solid materials have gained a lot of attention during the last 2–3 decades due to the fundamental physical problems and the broad spectrum of technological applications in which they are involved. Therefore, significant progress concerning the simulations of such hybrid soft–hard nanostructured systems has been made in the last few years. Simulation techniques vary from quantum to microscopic (atomistic) up to mesoscopic (coarse-grained) level. Here we give a short overview of simulation approaches on model polymer–solid interfacial systems for all different levels of description. In addition, we also present a brief outlook concerning the open questions in this field, from the point of view of both physical problems and computational methodologies.

---

Karen Johnston

Karen Johnston obtained a PhD with Prof. Tony Paxton from the Department of Physics in Queen's University Belfast, UK in 2003. Her first postdoctoral position was in Rutgers University, New Jersey, USA, where she continued with density functional theory calculations of perovskite materials in the group of Prof. Karin Rabe. In 2005, she moved to Prof. Risto Nieminen's group in the Helsinki University of Technology (now Aalto University), Finland and became interested in polymer adhesion. Currently, she is a postdoctoral researcher in the Max Planck Institute for Polymer Research in Mainz, Germany and uses a hierarchical multiscale approach to model polymer–solid interfaces.

Vagelis Harmandaris

Vagelis Harmandaris is an Assistant Professor in the Department of Applied Mathematics at the University of Crete, Greece. Before he was a research associate in Max Planck Institute for Polymer Research (Mainz, Germany), working with Prof. K. Kremer on multi-scale modelling of polymer systems. He received his PhD in chemical engineering from the University of Patras (Greece) in 2002, under the direction of Prof. D. Theodorou and V. Mavrantzas on atomistic modelling of polymer viscoelasticity. His research interests focus on the development of hierarchical multi-scale simulation approaches and rigorous mathematical methods for modelling molecular and biomolecular complex systems, with particular emphasis on understanding the structure–property relationships of polymer–solid hybrid materials.

---

1 Introduction

Hybrid materials, which contain soft–hard matter interfaces, are becoming increasingly important in devices, such as solar cells, fuel cells, biosensors, etc. The properties of such devices should be tuned to provide optimal performance, and nanopatterning, such as nanoparticle arrays or nanopores, is a promising technique. The behaviour of soft matter close to an interface can differ drastically from its bulk behaviour and since these systems typically have a high interface density the behaviour of the materials at the nanoscale affects the properties of the system at the macroscale. For example, the strength of polymer adsorption at the interface may govern the properties of the nanostructured material. The key issues that must be addressed in hybrid multi-phase materials are the change in various properties (structural, dynamical, mechanical, electrical, etc.) at the interface compared to the bulk and the extent of these changes from the solid surface, which is of particular importance for nanostructured materials.^1–3

The study of hybrid polymer–solid systems is very challenging for both experiment and simulation due to the very broad range of length and time scales involved. This is a general characteristic of all macromolecular systems since there are different characteristic time scales associated with the motion of various parts (segments) of the chain.⁴ However, for hybrid multiphase polymer–solid systems the range of length and time scales may be even broader due to the presence of the interfaces. For example, concerning the length scales, the behavior of the polymer at the interface is related to the interaction of each atom with the solid surface and typically ranges from lengths of a few (1–2) Å, for strongly (chemically) adsorbed molecules, up to around 1 nm for weakly (physically) adsorbed molecules that interact with the surface via van der Waals (vdW) interactions. In contrast, the behaviour of the entire system is related to the dispersion (i.e. arrangement) of the solid phase (e.g. nanoparticles) in the polymer matrix, which might involve macroscopic dimensions of the order of a few mm. Therefore, at least 7–8 orders of magnitude in length scale are involved in hybrid multi-phase nanostructured materials. Things are even more complicated concerning the relevant time scales of hybrid materials. Atomic bond vibrations (within a molecule or between atoms in a molecule and atoms of a crystal) are typically characterized by times of a few fs (10⁻¹⁵ s), whereas conformational changes associated with dihedral transitions take place in times of the order of a few ps (10⁻¹² s) for temperatures well above the glass transition, T_g, and much longer times for temperatures close to T_g. Relaxation of the entire chain can be of the order of seconds even for temperatures far from T_g, whereas the dynamics of various segments along the chain is characterized by all intermediate time scales. In addition, the dynamics can be even slower for chains adsorbed on solid surfaces. Therefore, the dynamical behavior of collective phenomena related to the dynamics of the polymer matrix near a solid phase might span more than about 15 orders of magnitude.

Considering all of the above, various experimental approaches have been used to study different aspects of polymer–solid interfacial systems related to structure, conformations and dynamics.^5–8 For experiment, the challenge lies in characterization of the structural and dynamical properties near the interface, which is either too small to be resolved by the experimental technique or which is masked by the larger bulk region. For example, many experimental investigations have focused on the change in the glass transition temperature of polymer materials close to an interface, with conflicting results.^9–12 Recently, experimental work has focused on the properties near a solid surface; however, the results are inconclusive.^8,12

Furthermore, various experimental methods have been developed for studying a variety of potential applications of polymer nanocomposites.^13–16 For example, the dispersion of nanosized particles, or carbon nanotubes, into a polymer matrix has been shown to alter significantly the mechanical as well as rheological, electrical and barrier properties of pure polymers.^13,16 Clearly, there is a need for techniques probing the polymer–solid interfaces at the molecular level.

Simulations can complement experiments by providing the detailed structural, conformational and dynamical properties near the interface. However, for simulations the difficulty lies in treating the wide range of time and length scales simultaneously. To overcome such problems, different approaches have been used to model systems at various levels of description. To model the processing of polymeric materials, the traditional approach is to average out the details at the molecular level and simulate the system at the continuum level using, for example, fluid dynamics or finite-element methods. These methods rely on input parameters, such as viscosity, density and elastic moduli, which are usually assumed to be constant throughout the model system. Obtaining these parameters is a non-trivial issue even for bulk polymer systems. For hybrid polymer–solid systems the application of continuum simulations is even more difficult, since properties of the materials at the interface may be very different to the bulk properties. In addition, the continuum approximation breaks down at the nanoscale level. This is even more important for interfacial systems, in which the material parameters might vary as a function of distance from the interface.¹⁷

In contrast, particle-based simulation methods provide a more detailed description of soft matter and can be used to predict various properties, such as density, structure, and dynamics at the molecular level. These particle-based methods can be further subdivided into atomistic and coarse-grained (CG) models. CG models, which represent groups of atoms by single particles, can be used to describe systems in the mesoscopic regime. The choice of CG representation is a crucial factor in all CG simulation approaches, and depends crucially on the physical problem and the questions to be addressed. To obtain a more quantitative comparison between realistic model systems and experimental quantities, atomistic models can be used, which have the advantage of a detailed all-atom representation of the hybrid material. However, the accuracy of atomistic models depends on the classical force fields and standard classical force fields are usually not designed to describe the interaction with solid surfaces and changes in chemical bonding. Therefore, to understand the chemical bonding of a molecule with a solid surface and to develop accurate force fields one must use quantum mechanical methods.

It is clear from the above discussion that in order to build up an understanding of a complex hybrid multi-phase system and its properties, it is necessary to connect different levels of description by using a multiscale modelling approach. Hierarchical multiscale simulation methodologies are usually described via typical length-time pictures, such as the one shown in Fig. 1. The figure gives a qualitative picture of the various techniques, with the corresponding length and time scales, as well as representative snapshots from a polymer–solid interfacial system starting from the quantum level, through classical microscopic atomistic models, mesoscopic coarse-grained models and up to continuum methods. Of particular importance is the systematic procedure needed in order to link the different levels of description.

Fig. 1 Multiscale modelling of polymer–solid interfaces from the electronic structure level, through the atomistic level, to the mesoscopic coarse-grained level and beyond. Snapshots taken from ref. 18 and 19.

The purpose of this review is to discuss the main topics related to the application of modeling and simulation techniques to the polymer–solid interfacial system. This is a broad subject that covers different systems and simulation methodologies at various length and time scales. Here we will focus on quantum, microscopic and mesoscopic methods, with particular emphasis on particle-based simulation approaches. For a discussion of the continuum modeling of hybrid multi-phase materials see ref. 1 and 17 and references therein.

We organize the review as follows. In the next section we discuss molecule–surface studies at the quantum level and the development of accurate classical force fields based on quantum data. Atomistic molecular dynamics and Monte Carlo studies of polymer–solid interfaces are presented in Section 3. In Section 4 an overview of the mesoscopic simulation approaches and coarse-graining techniques is presented. Field theoretical approaches are discussed briefly in Section 5. Finally, the Outlook discusses open questions related to the physical problems, as well as technical aspects, in modeling soft–hard interfaces.

2 Quantum-based interface force field development

As stated in the Introduction, the properties of hybrid materials are strongly dependent on the surface interaction. To account properly for the chemical bonding and properties of adsorbed molecules quantum mechanical calculations are necessary. Post-Hartree–Fock ab initio approaches, such as Møller–Plesset perturbation theory or coupled-cluster (CCSD), directly solve the Schrödinger equation and are among the most accurate quantum mechanical methods available. However, they are computationally expensive and are limited to small system sizes of only a few atoms. Density functional theory (DFT) is an alternative quantum mechanical approach, which is computationally less expensive than quantum chemistry calculations. DFT is described in detail in textbooks²⁰ so this section focuses on recent efforts to include van der Waals forces in DFT and describes various schemes for the development of interface force fields based on DFT results.

In DFT, the total energy, E, can be written as a functional of the electronic charge density, ρ

E[ρ] = T_s[ρ] + E_H[ρ] + V_ext[ρ] + E_xc[ρ]. (1)

T _s is the kinetic energy of a system of non-interacting electrons with the same electronic density as the real system, E_H is the Hartree energy of the electrons, V_ext is the external energy, which in the simplest case is just the Coulomb energy of electrons in the potential of fixed nuclei, and E_xc[ρ] is the so-called exchange and correlation energy. The last term implicitly includes the difference in the kinetic energy of the real and fictitious systems as well as the many-body interactions in the electron–electron interaction energy. The analytical form of the exchange and correlation functional is unknown and it is the approximation of this term that limits the applicability of DFT.

The local density approximation (LDA) was successfully used for many solid materials where the electron density is fairly homogeneous. However, for soft matter systems, where the electron density varies considerably it does not work well and the generalised gradient approximation (GGA) is better. For chemisorbed molecules on solids the GGA often gives reasonable structural information but the adsorption energies can depend strongly on the particular GGA functional.²¹ Hybrid functionals, which combine GGA with Hartree–Fock exact exchange, give better results for covalently bonded systems and have been used for studies of biomolecules on surfaces.²²

A major limitation of the GGA and hybrid functionals is that they are local and, therefore, do not account for non-local effects such as van der Waals (vdW) forces. For systems containing soft matter, vdW forces can be significant and the GGA is inadequate. It is, therefore, necessary to add a non-local contribution to account for these interactions and various schemes have been proposed for this. A more detailed overview of these methods is given by Klimeš and Michaelides.²³ The simplest approach is to add empirical dispersion terms to the GGA energy, E_GGA; the methods are generally referred to as DFT-D methods.^24,25 The total energy is of the form

where the C^A,B₆ coefficients are treated as parameters and depend on the atomic species A and B. However, the C^A,B₆ coefficients are constant throughout the simulation and the values are not generally applicable to all bonding or chemical environments. The DFT-D methods can be improved by allowing the C^A,B₆ coefficients to vary according to the environment.^26–28 A more general first-principles approach is to calculate the vdW forces using the charge density of the system²⁹ so that the exchange and correlation functional is given by

E_xc = E_x,GGA + E_c,LDA + E_c,nl (2)

where the first term on the right is the exchange energy described by the revPBE³⁰ form of the GGA, the second term is the local correlation energy using the LDA and the third term is the non-local correlation energy, which is calculated from the electronic charge density. This method is known as vdW-DF and various modifications to the exchange and non-local correlation functionals have been proposed.^31,32 The accuracy of these methods is often compared using the S22 set of molecular complexes,^27,32,33 where the results of highly accurate CCSD methods are available. However, for extended systems, such as hard–soft matter interfaces, CCSD methods cannot be applied and it is less clear which method is the best choice.

In summary, the balance between accuracy and computational efficiency means that DFT (with vdW) is arguably the best approach for determining the adsorption behaviour of molecules on solid surfaces and enables one to perform DFT molecular dynamics studies of molecules on surfaces for a few tens of picoseconds.^22,34,35 However, despite the computational efficiency of DFT, it is not possible to calculate macromolecules on surfaces or small molecules for more than a few tens of picoseconds. For larger systems and longer times classical atomistic (usually molecular dynamics (MD) or Monte Carlo (MC)) simulations are necessary. The accuracy of the classical simulations relies on the quality of the atomistic force fields. Such simulations typically use simple pair potentials for the interaction between polymer atoms, where the shape of the potential can be controlled via several adjustable parameters. Standard force fields, such as GROMOS^36,37 or OPLS,^38,39 were fitted to reproduce properties of soft matter (e.g. homogeneous bulk systems) and are not designed to be used for soft–hard matter interfaces. To describe accurately the interactions of an atom with the surface, it might be necessary to reparameterise these potentials or use different types of functions.

For polymers it is convenient to divide the molecule into small subunits, typically a monomer or sub-monomer, and calculate the adsorption energies of these subunits separately. Potentials are developed based on the interactions of these subunits and it is assumed that the interactions of the different subunits are factorisable and uncorrelated. This technique is often referred to as the building-block approach and it has been used in studies of bisphenol-A–polycarbonate on nickel,⁴⁰ organic molecules on rutile,⁴¹ polypeptides on gold,^42,43 and polystyrene on gold.¹⁹ The polycarbonate and polystyrene examples will be described in more detail in the following sections.

There are several ways to parameterise force fields based on quantum mechanical calculations. One technique is to use a combined DFT-MD/classical-MD approach to parameterise analytical potentials via force matching.^44–46 However, since DFT-MD calculations are expensive an alternative approach is to use the results from static DFT calculations to optimise interatomic potentials. The cheapest way to fit pair potentials in molecule–surface systems is to take an existing parameter set and tweak the parameters so that they reproduce the properties of a single (usually ground state) adsorption structure. However, while this method may reproduce the energetics of the ground state adsorption structure it is unlikely to represent accurately the energetics of the variety of structures sampled during an MD simulation. In order to obtain a realistic sampling of the adsorption structures one must reproduce the potential energy surface that includes intermediate energy configurations. The issue of force field representability was investigated using a genetic algorithm to optimize Lennard-Jones parameters for a large variety of adsorption structures.^47,48 Other schemes use both the potential energy landscape and the atomic forces to optimize numerical potentials but they have only been applied to bulk solids.^49–51 More recently, an algorithm was developed to optimize accurate all-atom molecule–surface potentials that reproduce a large set of DFT data.^19,52 The method is based on simulated annealing and the parameters of the nonbonded interaction potential are chosen in order to minimize the target cost function. The cost function is defined as the difference between the quantum and classical molecule–surface interaction energies, for many different molecule–solid configurations, i.e. different distances from the surface, various adsorption sites as well as different molecule orientations. More details about the method can be found elsewhere.⁵²

The choice of the analytical form of the potential is also of importance. A commonly used potential in MD simulations is the 12–6 Lennard-Jones (LJ) pair potential,

where ε and σ are adjustable parameters, and it enables the use of combination rules in MD simulations.

The GolP force field was developed to describe the interaction between amino acids (proteins) and gold surfaces in explicit water⁵³ and contains four terms, namely image charge interaction, chemisorption, van der Waals and conjugated molecule interaction. The parameterisation of the chemisorption Lennard-Jones potential is based on DFT results and the vdW interactions used MP2 data to parameterize 12–6 Lennard-Jones potentials. The GolP force field has been applied to studies of ubiquitin on gold nanoparticles.⁴³

However, the Lennard-Jones potential may not be the optimal choice for describing the interaction with a surface so other potential forms may be more appropriate. For the interaction of benzene and ethane on a gold surface ^19,52 Lennard-Jones and Morse-type atomistic potentials were optimized to reproduce the DFT adsorption energies as a function of distance from the surface. The atomistic Morse potentials were of the form

V_M(r) = ε[exp(−2α(r − r₀)) − 2exp(−α(r − r₀))]

where α, ε and r₀ are all adjustable parameters for each type of atom pair combination. The potentials are shown in Fig. 2.

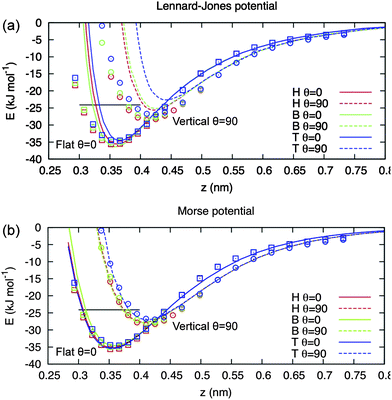Fig. 2 DFT adsorption energies for benzene on the Au(111) surface in various orientations and on various surface sites. z is the distance between the centre of the benzene molecule and the top of the surface; T, H and B denote top, hollow and bridge sites, respectively and θ = 0 (90) corresponds to a flat (vertical) orientation. Symbols are the DFT data and lines are the classical adsorption energies using optimized (a) Lennard-Jones and (b) Morse potentials. The figure is taken from ref. 52.

While both forms describe well the orientation dependence of benzene on the surface, it is clear that the Lennard-Jones potential overestimates the repulsion at close range whereas the Morse-type potential reproduces the adsorption energy over the entire range. Note also that a single set of Morse potential atom–atom pair parameters describe all different adsorption sites, conformations and molecule–surface distances. However, it should be noted that the dependence of the DFT adsorption energies on distance is also uncertain, since it depends on the choice of exchange and correlation and van der Waals functionals. Other schemes, in particular those used in solid state physics, avoid the use of analytical forms for potentials, for example the Gaussian Approximation Potential (GAP) approach.⁵¹

Other DFT-based interface force fields for polymers or large molecules on surfaces have not used interatomic potentials but instead have developed phenomenological potentials, such as a wall-type potential with only a z-dependence. This is typically the case for coarse-grained models, for example a study of bisphenol-A–polycarbonate on nickel⁴⁰ included 10–4 Lennard-Jones potentials between the beads and the surface, which correspond to integrated 12–6 Lennard-Jones interatomic potentials. A similar method was used in the atomistic studies of hydrated peptides on metal surfaces⁵⁴ and benzene and water on gold,⁵⁵ where the surface was represented by a z-dependent potential and repulsive or attractive potentials were added to virtual sites in the molecule. In a study of polycarbonate on silicon,⁵⁶ the adsorption of a polycarbonate monomer on the silicon surface was represented by attractive and repulsive potentials and a distance-dependent angular potential on the phenylene group. In addition surface site dependence was introduced by adding repulsive cosine potentials on various surface sites.

So far, the approaches described above are limited to rather well-defined systems, with smooth, ideal surfaces and no impurities and defects. Another important issue for classical force fields is reactivity, which is important for systems where molecules may become chemisorbed on the surface. For these systems it is important to use a force field that can describe the different bonding states of an atom. Several reactive force fields have been developed such as bond order potentials^57,58 and the ReaxFF force field.⁵⁹

In summary, interface force field development has largely been ignored in classical studies of soft–hard matter interfaces. However, as the demand for more quantitative and predictive capability increases the development of accurate interface force fields will become an important issue.

3 Classical atomistic simulations

As mentioned previously, atomistic simulations provide a detailed all-atom description, as well as a quantitative prediction of the properties of the hybrid multi-phase material. The most common classical atomistic simulation methods that are applied to hybrid polymer–solid systems are molecular dynamics (MD) and Monte Carlo (MC). At the heart of MD simulations is the numerical solution of Newton's classical equations of motion, whereas the MC method is a numerical scheme that involves random sampling of the high-dimensional configuration space of a complex system. The main limitation in the application of atomistic molecular dynamics simulations to complex macromolecular materials is that it is not possible to reach the long relaxation times of long-chain polymers and, therefore, equilibration of such systems is difficult. MC methods allow a more efficient sampling of the very complex phase space of macromolecular materials by using special MC moves that overcome strong energetic barriers. However, it is not possible to study dynamics using standard MC algorithms. More details about these methods can be found in classic textbooks.^60,61 We should also note here that in many atomistic simulation studies united atom (UA) models, in which hydrogens are lumped into carbons, are used. Such models, in principle, belong to the family of coarse-grained models. However, they are usually parameterized to reproduce the properties of systems over a broad range of conditions and used for quantitative studies. Therefore, we include them in the family of atomistic models, but distinguish them from all-atom (AA) models.

MD and MC simulations of polymer–solid interfacial systems began to appear in the literature 2–3 decades ago.^62–68 Most of the early work was concerned with very simple systems, such as alkane chains using UA models, polymethylene, etc., and was restricted to short polymer chains. Xia et al. used MD simulations to study 1 and 2 nm thick n-hexadecane films adsorbed on a crystalline substrate.⁶⁶ The alkane segmental density at the solid surface exhibited a regularly spaced oscillatory profile, with the amplitude of the density oscillations decreasing with increasing distance from the solid surface and extending about 2 nm into the film. Winkler and Hentschke studied the packing, orientation and local conformations of polymethylene chains near adsorbing surfaces through stochastic MD simulations.⁶⁷ Similarly, they observed an oscillating density profile, which returned to the bulk density around 1–2 nm from the surface. They also found that chains near the surface were oriented almost parallel to the interface. A combination of MC followed by energy minimisation was used to study glassy atactic polypropylene on graphite⁶⁵ and the flattening of chains was found to extend over a region of 1.5R_g from the surface, where R_g is the unperturbed root mean squared radius of gyration of bulk polypropylene. This flattening was due to reorientation of the chains rather than a change in chain conformation. Other studies have found that this flattened region extends from the solid surface by a distance of about the end-to-end chain length, R_e, for the specific model system.^67,69

A hybrid MC–MD approach was developed for bulk polymer systems, where MC algorithms are used to equilibrate rather long chain systems, followed by multiple time step MD simulations of the equilibrated structures.^70–72 The MC method involved special chain connectivity-altering moves that allowed a fast equilibration of long polymeric chains. This approach was later applied to the study of various polyethylene–graphite (PE–Gr) interfaces,^69,73 using a UA model, with molecular lengths below and (slightly) above the entanglement molecular length. The structure of the adsorbed layer on graphite was analyzed in terms of the distribution of adsorbed segments in trains, loops, and tails. The statistics of trains, loops and tails at the surface has been calculated and found to be in reasonable agreement with the predictions of Scheutjens–Fleer theory^74,75 for homopolymer adsorption from solution, in the limit of zero solvent concentration, in particular for the longer polymer chains.

The effect of the solid surface on the dynamics of the polymer has also been investigated. Diffusion constants can be calculated based on the mean-square displacements of the chain centers-of-mass or at the segmental level. For polymethylene it was observed that the mobility of the surface layer is anisotropic; it is reduced in the direction normal to the surface, due to the fact that particles are reflected by the surface, and it is increased, compared to bulk mobility, in the direction parallel to the surface.⁶⁷ The latter is a result of using a smooth, flat potential to represent the surface that results in a much smaller friction factor, instead of a more realistic corrugated surface.^56,76 More recent studies of model polymer–solid systems using an atomistic surface showed that the solid surface causes significantly slower dynamics compared to the bulk dynamics. ^19,73,77 This effect only extends to a few nm from the surface. Furthermore, a detailed atomistic MD study of a PE–Gr thick interfacial system,⁷³ of an unentangled chain (C₇₈), showed that segmental dynamics of the adsorbed molecules perpendicular to the surface is quantitatively and qualitatively different from that in the bulk and cannot be described by a constant diffusivity. It can, however, be accurately described using a macroscopic diffusion equation with a time-dependent diffusion coefficient, D(t). In more detail, it was found that local segmental diffusivities (calculated via the mean square displacement of atoms) normal to the surface depend strongly on the thickness, d, of the layer next to the surface on which they lie at the beginning of diffusion: the closer the layer to the graphite plane, the slower the segmental mobility. In order for the segmental dynamics, normal to the surface, in the interface to become bulklike at all time instances, very large values of d (equal to 6–7R_g for the C₇₈ chains) containing only a small number of adsorbed atoms should be considered. It still remains to be seen whether this length scale depends on the polymer–solid interactions and on the molecular length of the polymeric chains. This is particularly important if we consider that experimental studies with other polymer melt–solid surface systems have proposed totally different values for such a distance, ranging from 3–4 R_g⁷⁸ to 25R_g.⁷⁹

The glass-transition temperature, T_g, is also a very important issue, and can be directly compared to experimental measurements. The glass transition temperature can be calculated by measuring the change in density as a function of temperature. In a recent work Hudzinskyy et al.⁸⁰ calculated T_g for supported polystyrene (PS) films, using a UA model for PS, for the entire system as well as for three different layers (substrate, middle, and surface) according to the density profiles. They found that for the whole film the average density-based T_g value remains almost constant for films down to 2 nm thickness. For the middle layer itself T_g does not depend on the total film thickness, while an increase of up to 70 K was measured for the substrate layer depending on the strength of attraction to the actual substrate. However, statistical errors became rather important for the very thin films. The dynamics close to T_g is expected to be a non-universal phenomenon, governed by a complex interplay between adsorption, packing effects and intramolecular rotation barriers.⁸¹

In the above studies the surface was represented by either a simple phenomenological potential or by a standard Lennard-Jones potential for the pair molecule atom–surface atom interaction. However, as stated in the previous section, quantitative predictions of atomistic simulations depend on the accuracy of the classical polymer–solid interaction potentials, and properly designed interaction potentials that are parameterized based on quantum calculations are an important issue. Borodin et al.⁸² reported results from all-atom MD simulation studies of the interface between poly(ethylene oxide) and a TiO₂ surface using a quantum-based force field. Johnston and Harmandaris studied the structural and dynamical properties of polystyrene confined between gold surfaces using an interface force field that was developed using DFT calculations.^19,52 The orientation, as well as the short time segmental dynamics, for various vectors along the backbone and the side (phenyl) group of the polymer chains was examined. Data showed a strong tendency of both the backbone and phenyl groups to orient parallel to the surface plane mainly for monomers that belong to the first adsorption layer. In addition, the backbone dynamics was found to be slower than the dynamics of the phenyl groups, which are less constrained, whereas the dynamics of both backbone and side groups is much slower close to the Au surfaces.

Nowadays, with the large increase in computing power more complex polymer–solid materials, such as nanopores, carbon nanotubes (CNTs), polymer–graphene systems and nanoparticle composites, are being investigated using atomistic (AA or UA) models.^83–88 The effect of surface geometries on the adsorption of the polymer is another relevant issue. For instance, Barbier et al.⁸³ used fully atomistic MD simulations of a spherical silica nanoparticle of around 1.5 nm diameter in polyethylene oxide (PEO). The results revealed a dense packing of flattened PEO segments arranged in ordered shells around the silica nanoparticle and the dynamics at the nanoparticle surface was slower than the bulk dynamics, which is qualitatively similar behaviour to a planar surface. Pandey and Doxastakis⁸⁷ investigated in more detail the changes induced by curvature at length scales comparable to the polymer's Kuhn length using silica nanoparticles of diameters ranging from 0.5–3 nm in polyethylene as the model system and a new MC sampling scheme that accelerated the polymer equilibration close to the interface. It was shown that the surface concentration of polymer chains is directly affected by the increased free energy cost of extending long sections of polymer chains along the surface (trains), especially for small nanoparticles. This results in shorter trains from more polymer chains at the surface and a higher mass per unit area for highly curved surfaces. Typical snapshots of PE–silica nanoparticles are shown in Fig. 3. The MC results further support theoretical studies⁸⁹ based on geometrical criteria that promote a decrease of the polymer bound layer thickness. They also highlight the role of local rigidity on the scaling of the bound-layer with particle size.

Fig. 3 Snapshots of model polyethylene–silica planar surfaces and nanoparticles. Polymer molecules in contact with the surface are shown explicitly in black. Train segments belonging to different chains are depicted for a flat surface. The figure is taken from ref. 87.

Another issue that has received a lot of attention is grafting, where chain ends are chemically attached to the surface. At high grafting densities the polymer has a brush-like structure at the solid surface. Grafted polyethylene chains with various grafting densities on graphite were studied using MC simulations by Daoulas et al.⁹⁰ that resulted in slightly polydisperse systems. It was found that the local melt density in the region closest to the interface is systematically higher than in the bulk, exhibiting distinct local maxima due to polymer adsorption, which is in agreement with non-grafted polymer melts adsorbed on graphite. It was also seen that as the grafting density increases, free chains are progressively expelled from the surface region, in agreement with scaling arguments and the predictions of lattice-based self-consistent mean-field (SCF) theory.⁹¹

Furthermore, grafting is an important aspect in controlling the dispersion of nanoparticles in polymer matrices. Ndoro et al.⁹² presented a detailed atomistic study of hybrid systems of grafted and ungrafted spherical silica nanoparticles embedded in polystyrene. They showed that the expected modification of the polymer structure in the neighborhood of the particle is stronger for higher grafting densities and larger particle diameters. In addition, the infiltration of free PS chains into the grafted regime is reduced with increasing grafting density, thus making a NP with high grafting density a poor choice for a well-reinforced composite.

The study of polymers close to carbon nanotubes (CNTs) is also a subject that has received a lot of attention during the last few years.^93–96 For example, Wei⁹⁴ has demonstrated that PE melt chains around a single SWCNT show a strong dependence of the wrapping configurations on the radius and chirality of the SWCNT. Furthermore, non-equilibrium properties, such shear properties and thermal conductivity, have also been investigated. Alaghemandi et al. used non-equilibrium MD simulations to study the thermal conductivity of polyamide–CNT composites and found that the addition of CNTs to polyamide only increased the thermal conductivity moderately compared to the pure polymer.⁹⁷

4 Coarse-grained simulations

Despite the advances in computation, atomistic models of hybrid polymer–solid materials are still restricted to relatively small systems with a simple monomer structure, such as polyethylene and unentangled polymer chains and nanocomposites with a single, small nanoparticle in a short-chain polymer matrix. To model larger and more complex polymer–solid interfacial systems one must reduce the chemical detail or degrees of freedom and model the hybrid system at a mesoscopic coarse-grained (CG) level. These methods are expected to be accurate for distances larger than a characteristic length, which is usually of the order of the Kuhn length.

Coarse-grained simulation approaches can be divided into two main categories based on whether their goal is: (a) to describe only qualitatively some generic (e.g. universal) features of complex hybrid systems (generic CG models) or (b) to quantitatively predict properties of the specific system under study (systematic CG models). Mesoscopic modeling approaches can be further decomposed on particle-based simulations and field theoretical methods.

Generic coarse-grained models

This subsection begins with a short historical overview of simulation studies of hybrid polymer–solid materials using generic CG models. The first coarse-grained simulation works of hybrid interfacial systems involved simple bead–spring or lattice models. These models were found to be quite successful in predicting the generic behaviour of polymer-solid materials. Among the first coarse-grained simulation works of polymer–solid interfacial systems are those of Bitsanis and Hadziioannou who, through MD simulations of FENE chains,^98,99 investigated the structure and microscopic dynamics in thin films of homopolymer melts confined between structureless, planar solid walls. Yoon and co-workers⁶⁸ also studied the dynamics of short-chain systems near adsorbing surfaces through MD simulations using typical bead–spring models. Mansfield and Theodorou carried out dynamic CG MC simulations on freely jointed 20-bead model chain molecules in a cubic lattice in the vicinity of solid walls.¹⁰⁰ They evaluated the self-diffusion coefficient of chains and its spatial dependence. In addition, Aoyagi et al.¹⁰¹ carried out MD simulations of polymer melts confined between walls with a bead–spring model. The effect of the interface on the relaxation of polymer chains was studied by analyzing the time autocorrelation functions of the normal modes as a function of distance from the wall. The dynamics of polymeric chains confined between nonadsorbing solid surfaces has also been studied through MC calculations using the bond fluctuation model. MC data showed that for such systems segmental mobility is enhanced as the film thickness is decreased, but the overall chain dynamics remains unaltered.¹⁰²

In all the above cases polymer dynamics was qualitatively studied by calculating the mean-square center-of-mass displacement of polymer segments (beads) as a function of simulation time. The latter quantity showed a dramatic reduction in chain mobility near strongly adsorbing walls over several layers, but an enhancement near weakly adsorbing walls, mainly as a result of a decrease in polymer segmental density. Strong segment–wall attractive interactions were also seen to appreciably prolong relaxation times, in comparison to the bulk. These data are in general qualitative agreement with the behavior of more detailed atomistic simulation models, discussed in the previous section.

The dynamics of fluid polymers in confined geometries is also a topic studied extensively in the past through generic CG models.^103–107 The main questions in this topic are related to the dependence of the velocity profile, and the slip length (i.e. the proportionality coefficient between the slip velocity and the shear rate), on the boundary conditions at the liquid–solid interface. Most works in the literature concern atomically smooth, homogeneous surfaces and the slip length has been calculated for various systems.^107,108 More recently the slip in thin polymer films confined by either flat or periodically corrugated surfaces was investigated by simple FENE models.¹⁰⁹ It was shown that the effective slip length for corrugated surfaces depends on the wavelength of the corrugation: for wavelengths larger than the radius of gyration of polymer chains, the effective slip length decays monotonically with increasing corrugation amplitude, and the data can be described accurately by the numerical solution of the Stokes equation with constant and rate-dependent local slip length. In contrast, for corrugation wavelengths comparable to the radius of gyration, the continuum predictions overestimate the effective slip length obtained from molecular dynamics simulations.

From the above discussion it is clear that simple CG models can be successfully used in order to study and predict generic (e.g. universal) properties of polymer–solid hybrid systems. Their main advantages are related with their simplicity (i.e. simple form of CG bead–bead interactions) and their computational efficiency, compared to detailed atomistic models. Because of this such models are still used to predict the generic behavior of complex hybrid systems. For example, in a recent work De Virgilis et al.¹¹⁰ used a bead–spring model to study a polymer melt at a surface for various degrees of adhesion. They showed that the average length of trains and loops does not depend significantly on the adsorption strength, whereas the number of loops and trains slightly decreases with increasing adhesion. The dynamics of the adsorbed layer was found to follow a slightly non-Arrhenius behavior with the adsorption potential.

All the above works concerned polymer chains in contact with (or confined between) planar solid surfaces. Other topics in which generic CG models can be very useful is modeling the behavior of complex polymer-grafted surfaces and polymer nanocomposites that cannot be studied with all-atom models. The latter topic, in particular, is a subject in its own right that deserves an extended discussion; see for example the review by Zeng et al.¹⁷ Here we do not wish to discuss this issue in detail but we feel that it will be useful to include a few examples, since they are closely related to polymer–solid interfacial systems. For instance, a system of model polymer chains attached to a flat surface (polymer brush) was studied by the pioneering work of Grest¹¹¹ through MD and MC simulations using a simple bead–spring model. Both MD and MC studies showed layering of monomers close to the surface, in agreement with a system of polymer chains in contact with solid surfaces. In addition, the simulation data are in reasonable agreement with data from more detailed atomistic simulations discussed in the previous section.⁹⁰

During the last decade CG studies of more complex grafted polymer–solid systems were reported. Pakula and Klos^112,113 applied lattice MC simulations, with a cooperative motion algorithm to a system of linear chains end-grafted to a spherical surface. Good solvent conditions were considered and the monomer concentration profiles were found to change from concave to convex with increasing nanoparticle radius. For small surface coverage and for small nanoparticles with a high curvature, polymer conformations in which a chain can wrap around the nanoparticle were also observed. Kalb et al.¹¹⁴ further analyzed the effect of surface coverage and curvature of spherical grafted nanoparticles for an entangled system.

The computational efficiency of simple bead–spring models allows them to be used to study systems of high molecular weight, such as entangled polymer chains close to SWCNT that cannot be studied in full atomistic detail. In such a work Karatrantos et al.¹¹⁵ showed that in the presence of a SWCNT (with or without attractive interactions), the network of topological constraints (entanglements) is modified, i.e. the contour length of the primitive path increases indicating more entanglements. Moreover, concerning the dynamics of polymer chains, large heterogeneity was found due to the polymers in contact with the SWCNT. Furthermore, Smith and co-workers⁷⁶ used a simple bead–spring model to study viscoelastic properties of various polymer–nanoparticle systems with different nanoparticle–polymer interactions. They showed that viscoelastic properties of the polymer matrix were strongly perturbed by the NPs and depended upon the nature of the nanoparticle–polymer interactions. Standard bead–spring models can also be used to provide a qualitative picture about the nature of the direct, or mediated, effective interaction between nanoparticles embedded in a polymer matrix.¹¹⁶ More recently Cordeiro et al.¹¹⁷ investigated the interaction (mutual repulsion) between two grafted surfaces. They have shown that repulsive surfaces made chains to attain more extended conformations, than chains adsorbed onto attractive surfaces.

Furthermore, the glass transition of polymers near interfaces, and of polymer nanocomposites, has been studied using generic CG approaches based on percolation models. In such models the glass transition is explained as a dynamical procedure.^118–122 In more detail, Long and Lequeux first proposed that a material exhibits a macroscopic glass transition when small slowly relaxing regions percolate through the sample.¹¹⁸ They applied their model to general van der Waals liquids in bulk and in thin films. Later Kropka et al. used the percolation model to examine the changes in T_g for polymer nanocomposites and their equivalence for thin films.^120,121 More recently Lipson and Milner applied the percolation model for a polymer thin film. They show that, as predicted by the model, a free surface reduces the number of paths that connect a site, near to the surface, to percolating clusters, thus lowering the T_g of the polymer. However, the magnitude of this effect is not enough to account for the lowering of T_g observed experimentally, showing that other mechanisms may also contribute to the complex glass transition behavior.¹²²

Hybrid polymer–solid nanostructured systems have also been studied using a family of compressible free energy coarse-grained models based on traditional integral equation theories, such as the microscopic Polymer Reference Integration Site Model (PRISM).¹²³ In these models, chains are represented as bonded sites that interact via pair decomposable site–site potentials, composed of a repulsive branch (usually hard core) and longer range attractive interactions. The advantage of such models is that they allow a qualitative study of the structure and the phase diagram of more realistic model nanocomposite systems with many nanoparticles. In more detail, Schweizer and co-workers^124–126 extended the PRISM theory to study polymer nanocomposites, by incorporating specific polymer–nanoparticle and nanoparticle–nanoparticle contributions. Their work showed that depending on the range of intermolecular interactions, the particle–particle potential of mean force can show contact aggregation, steric stabilization, local and longer range (mediated by the environment) bridging attraction. These data could help to design fillers in polymer melts with specific thermodynamic stability and miscibility.

Following a similar methodology Frischknecht et al.¹²⁷ have studied the effect of well dispersed nanoparticles on the equilibrium chain configurations using a coarse-grained self-consistent polymer reference interaction site model (SC/PRISM). They observed an increase of polymer chain dimensions with increasing nanoparticle volume fraction for small nanoparticles with radius below the chain dimensions. This chain expansion effect was attributed to the attractive interaction between the monomers and the nanoparticles, as well as to the excluded volume taken up by the nanoparticles; both phenomena result in making the nanoparticles behave like a good solvent.

We should note here that all the above models offer a quite successful qualitative prediction of the structure and dynamics of generic polymer–solid interfacial systems, but lack a link to specific systems. In many cases a mapping of the model parameters onto data taken either from more detailed atomistic simulations or experiments provides also quantitative agreement with specific polymer–solid nanostructured systems.¹²⁴ However, a rigorous linking with microscopic all-atom model systems requires systematic CG models developed directly from the chemistry.

Systematic coarse-grained models

Systematic coarse-grained models are developed based on atomistic models and aim at retaining the essential chemistry of the system. The main idea behind coarse-graining is to lump groups of chemically connected atoms into “superatoms” and derive the effective CG interaction potential by taking into account the atomistic details of the particular polymer. CG models can differ in the degree of coarse-graining (the number of real atoms that correspond to one “superatom”) as well as in the way the effective CG potentials are derived. For structure-based CG models, a direct link to the chemistry is achieved through structurally defined bonded and nonbonded effective CG potentials derived from the atomistic model.^128–130 Such models have been applied with success to study quantitatively the structure, conformations and the thermodynamics of various bulk polymer systems. However, the direct usage of such CG models to describe the dynamics of complex systems is a more subtle issue. The reason is that due to the reduced degrees of freedom in the CG description, the friction between the CG beads is significantly reduced compared to what it would be if the monomers were represented in full atomistic detail. Therefore, the time scale in the CG description does not correspond to the one of the microscopic (underlying) chemical system. To overcome this limitation different methods are followed in the literature that are related either to an appropriate parameterization of the CG time scale^130–132 or to the involvement of the friction forces in the equations of motion.^133,134 Following these approaches quantitative information about the dynamics of bulk polymer systems can be also provided from the CG models. An additional advantage of systematic CG models, in which each CG “superatom” represents about O(10) atoms, is that detailed all-atom configurations of the model CG systems can be obtained through a back-mapping algorithm.^128,135

The extension of systematic CG models to polymer–solid interfacial systems is a challenging research area because of extra complexities due to the presence of interfaces. Therefore, only a few systematic CG studies have been applied to polymer–solid multi-phase systems. For example, the interaction of liquid polycarbonate near a nickel surface was studied by directly connecting ab initio density functional calculations to coarse-grained molecular dynamics simulations.^40,136 Density functional calculations of the adsorption of polymer fragments on the surface were used to parameterise the surface potentials. Based on the DFT calculations it was concluded that only the benzene subunits at the chain ends had the conformational freedom and a strong enough adsorption to adhere to the nickel surface, resulting in a polymer brush structure. They found that the surface only influenced the structural properties up to 2R_g from the surface, where R_g ≈ 1.9 nm for 10mer BPA-PC. These results are in agreement with the data from the more detailed atomistic simulations presented in the previous section. This model was used in subsequent investigations of chain end modification¹³⁷ and shear properties.^138,139 A similar approach was used to study BPA-PC on a Si(001)-(2 × 1) surface, which found similar structural properties at the surface.⁵⁶

It should be noted that the above methodology that parameterises the surface potentials using ground-state zero-temperature ab initio calculations does not properly describe entropy. Thus, this method is expected to be valid only for strong polymer–solid interaction energies, i.e. chemisorption, while it is not a good approximation for weakly interacting polymer–solid systems that are dominated by van der Waals interactions. In the latter case, entropy should be taken properly into account. This could be partially achieved by using DFT-MD simulations¹⁴⁰ to obtain an entropy-averaged adsorption energy for the polymer fragment. However, such methods can only be used for very small molecules; thus the entropic contribution is not really representative of a realistic polymer chain. Alternatively, entropy effects could be included by using atomistic MD simulations of the polymer chain on the surface to parameterize the CG interface potentials. Of course, to retain chemical accuracy the atomistic interface force field should itself be parameterized using DFT calculations.

Overall, the need for direct quantitative studies of complex realistic polymer–solid interfacial systems with high molecular weight makes the development of systematic CG models for polymer–solid hybrid systems a very intense research area. Through the above discussion it is also clear that this is also a very challenging area, since it directly involves linking between quantum, microscopic (atomistic) and mesoscopic (coarse-grained) simulations.

5 Field theoretical models

An alternative family of mesoscopic simulation approaches used to describe polymer–solid complex systems are field theoretical based methodologies.¹⁴¹ Field theoretical simulations for polymers on solid surfaces began with the seminal Scheutjens–Fleer self-consistent field theory (SCFT),^74,75 which analyzed the polymer chain conformations of a polymer solution close to a solid substrate and predicted the corresponding scaling laws. As described in the previous section, their predictions are in good agreement with particle-based molecular simulations of a polymer melt. These methods were extended to describe in more detail polymer–solid interfacial systems. For example, Daoulas et al.¹⁴² showed that self-consistent field calculations with the worm-like chain model that incorporates local stiffness provide a better description of the adsorption of PE molecules. Trombly and Ganesan¹⁴³ studied the curvature effects of polymer-grafted nanoparticles in a polymer melt. The interpenetration width between grafted and free chains was studied as a function of the curvature of the surface, the grafting density, and the relative molecular weights of the grafted and free chains. A greater tendency for interpenetration of free chains into the grafted chains regime with increasing surface coverage was found to be due to entropy.

During the last few years several different field theoretical approaches, using methods that go beyond the mean field approximation, have appeared in the literature.^144–149 These approaches are usually hybrid simulation methods such as (a) a scheme that combines SCFT for polymers with classical density functional theory for particles,¹⁴⁴ (b) particle-field simulations in which the coordinates and chemical potential field variables are updated simultaneously,¹⁴⁶ and (c) MC particle-based approaches within the quasi-instantaneous field approximation where the interaction of a monomer with its surroundings is expressed through a field that is frequently updated from the instantaneous positions of the particles.^145,150,151 All the above approaches are very promising for complex polymer–solid interfacial systems due to their strong computational efficiency. For instance, Theodorou and co-workers¹⁵² applied a Monte Carlo sampling formalism to investigate the structure of a polymer matrix filled with tightly cross-linked polymer nanoparticles. As expected both the density and the local structure of the polymer matrix in the vicinity of the nanoparticles are found to be different from those of the corresponding bulk, in accordance with the data of the more detailed atomistic and particle CG simulations. In addition, they found that the dispersion of many nanoparticles in the polymeric matrix leads to extension of the chains when their size is similar to the radius of the dispersed particles.

Overall, the above models provide efficient computational approaches for accessing the behaviour of complex polymer–solid hybrid systems, at least for length scales longer than the Kuhn segment. Their direct relation to the chemistry at the nanometer scale, which is particularly important for nanostructured materials, is a very challenging topic. We should also note that the studies discussed above are only a small portion of the field theoretical simulation approaches reported in the literature. A complete review of this field is far beyond the scope of the present article and we recommend some excellent reviews that have appeared in the literature in the last few years.^{123,153–156}

6 Outlook

The study of hybrid polymer–solid interfacial materials at the molecular level through simulation approaches is a very intense research area that has mainly addressed: (a) the deviation of various polymer melt properties from their bulk values (i.e. structural, conformational, dynamical, etc.), induced by the presence of the interface, and (b) the extent of these changes from the interface. The current level of fundamental knowledge shows clearly that the length of the interface depends on the actual property under consideration.

In particular the main findings for model polymer–solid interfaces, where the polymer chains are physisorbed onto the solid surfaces, are the following: (a) the segmental density of a polymer melt close to the interface shows an oscillating density profile with a clear maximum very close to the surface, which reaches the bulk density around 2–3 nm from the surface. This length scale appears to be independent of the monomer structure (chemistry) as well as the length of the polymer chains. (b) Conformations of polymer chains are clearly perturbed close to the surface, i.e. chains near the surface are oriented almost parallel to the interface. The polymer conformations are modified over a region up to around 2R_g from the surface. This length scale seems also to be independent of the polymer chemistry for the systems studied till now. (c) Orientational dynamics of the polymer chain at the segmental level, quantified usually by the decorrelation of a vector along the monomer, is slower near the solid substrate than in the bulk. The extent of the slower dynamics is up to a few (2–4) nm from the solid substrate. It further seems not to be strongly dependent on molecular length, as should be expected for segmental dynamics.

Despite the many advances that have been made in the modeling of polymer–solid hybrid systems, there are still many open questions and challenges, both from the view of fundamental physics and the development of simulation approaches. We have listed the following open issues that we believe are among the still important and relevant questions.

Glass transition temperature

Despite the large number of experimental studies in the literature, the effect of the substrate on T_g is still under debate. This is directly related to experimental difficulties in studying very thin films, and measuring T_g as a function of distance from the surface, rather than an average value over the whole film. Furthermore, there are additional complexities if someone compares the dynamic vs. calorimetric T_g and clear indications of dynamic heterogeneities close to the surface have been reported.¹⁵⁷ To understand this phenomenon further, detailed investigations of the distribution of segmental relaxation times at the solid surfaces compared to the bulk would be very useful.

Fluid dynamics at the interface

The effect of the surface on the polymer melt dynamics at the molecular level is also a very important issue. It is directly involved in studies related to slip phenomena and systems under non-equilibrium conditions. Even more, it has a strong influence on the rheological and linear viscoelastic properties of the hybrid material.^1,6 To clarify such issues, detailed studies of the chain, as well as the segmental, dynamics for various specific polymer–solid systems are needed.

Molecular weight dependence of properties

Several fundamental questions of polymer physics are related with the molecular weight dependence of the dynamics of polymer chains in contact with the surface.⁴ For instance, how well do the Rouse and the reptation exponents of the diffusion coefficient describe the dynamics of polymeric chains in contact with the surface? Are there universal power laws in accordance with the dynamics of bulk systems or do the exponents depend on the actual strength of the polymer–solid interaction? Is the network of entanglements at the interface very different to the bulk, unperturbed one? The answer to these questions will further help theoretical approaches aiming at the prediction of the dynamics and the rheology of hybrid polymer–solid systems.

Geometric effects

The detailed surface properties could have a pronounced effect on the structure and dynamics of the polymer near the surface. More studies are needed to address issues such as surface roughness and curvature. These will affect the ordering and the packing of the polymer as well as the friction at the surface. Such issues are further related to systems with more complex geometries of the solid phases, such as nanopores and nanoparticles with non-spherical geometry. Therefore, direct investigation, at the molecular level, of the influence of the degree, the specific type of corrugation, and of curvature on the properties of atoms at the interface is critical.

Fluctuations at the interface

Most of the current simulation approaches do not analyze in detail the thermal fluctuations at the interface. For example, the variability in the strength of adsorption for atoms/monomers in contact with a solid substrate is usually not discussed and average quantities are reported. However such issues might be important in the effective interaction between nanoparticles immersed in a polymer melt as well as the phase diagram of the hybrid material. Detailed investigation of the statistics of structural and dynamical quantities at the interface will be helpful to clarify the importance of such issues.

Collective phenomena in polymer-based nanocomposites

A major challenge in the simulations of polymer nanocomposites is to model more realistic systems with many nanoparticles. This will allow, at the molecular level, collective phenomena related to the effective interaction between nanoparticles to be studied, as a function of distance between them, and as a function of their concentration. This is particularly important if we consider that experimentally the dispersion of NPs is a rather problematic issue.¹⁵

Concerning the challenges related to the development of simulation methodologies we consider the required work in the following directions. First, there is a clear need to develop new and improved simulation algorithms in specific length-time scales. Second, it is even more important to develop systematic approaches to link methods over a wide range of length and time scales. In more detail, some of the major challenges in this field are the following:

1. Systematic hierarchical approaches that link quantum (DFT) to atomistic and atomistic to CG scale for polymer–solid systems are still in their infancy. To link DFT to atomistic simulations there are certain issues related to the rigorous matching of ab initio data (forces and energies) that allow the correct description of structure and entropy. The specific interactions close to the substrate might also involve the formation and breaking of chemical bonds, which would require reactive MD methods. For linking the atomistic to CG simulations an accurate estimation of the non-bonded CG bead–surface effective free energy and correct incorporation of the local polymer rigidity in the CG model are crucial. Of analogous importance is also the direct linking between atomistic (or CG) models to continuum ones.¹⁷ Furthermore, the quantitative prediction of dynamics of polymer–solid systems via simulation methodologies is an important issue for all approaches. In order to correctly predict the dynamics in the all-atom model the classical force fields should accurately describe the friction at the interface. In this case standard potentials based on the parameterization of DFT data (zero temperature) might not be enough. In order to correctly predict the dynamics with the CG models, the methods currently used to correct the CG time scale in bulk systems, based either on a post processing time rescaling step or via the inclusion of friction forces in the equations of motion, should be extended and/or new methodologies should be developed.

2. Clearly there is a need for simulation methodologies that span different levels of description simultaneously. The development of such methods is a very active field with several methods developed for bulk systems going from quantum mechanics to atomistic,^158,159 from atomistic to CG¹⁶⁰ and from atomistic or CG models to continuum ones.¹⁷ The extension of these approaches to hybrid systems could combine the advantages of all-atom models close to the interface and CG or continuum far away from it.

3. Equilibration issues are also an important topic in the modeling of complex polymer–solid systems with long polymeric chains. Indeed the equilibration of high molecular weight entangled chains close to the substrate or to nanoparticles might be a difficult task that requires more time than is computationally feasible. The combination of systematic CG techniques and advanced MC algorithms seems to be an attractive direction for overcoming such problems.

In summary, the development of hierarchical or simultaneous multiscale simulation methods for complex systems is a very challenging topic in computer simulation and modeling, with a major goal being the direct quantitative comparison between experiments and simulations. To achieve this, new mathematical and computational concepts will be required. These developments are crucial in order to accomplish the longstanding goal of material design and predict the structure–property relationships of complex materials at the molecular level.

Acknowledgements

We would like to thank Thomas Vilgis, Vakhtang Rostiashvili and Kostas Daoulas for valuable discussions. Funding for Karen Johnston was provided by the German research foundation grant SPP-1369.

References

1. J. Koo, Polymer Nanocomposites: Processing, Characterization, and Applications, McGraw-Hill, 2006.
2. A. J. Kinloch, Adhesion and adhesives: science and technology, Chapman and Hall, New York, 1987.
3. H. Kim, A. A. Abdala and C. W. Macosko, Macromolecules, 2010, 43, 65156530.
4. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, England, 1986.
5. H. Hu and S. Granick, Science, 1992, 258, 1339.
6. G. Tsagaropoulos and A. Eisenberg, Macromolecules, 1995, 28, 6067.
7. S. Granick, S. K. Kumar, E. J. Amis, M. Antonietti, A. C. Balazs, A. K. Chakraborty, G. S. Grest, C. Hawker, P. Janmey, E. J. Kramer, R. Nuzzo, T. P. Russell and C. R. Safinya, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2755.
8. R. D. Priestley, C. J. Ellison, L. J. Broadbelt and J. M. Torkelson, Science, 2005, 309, 456.
9. J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens and J. R. Dutcher, Phys. Rev. Lett., 1996, 77, 2002.
10. M. Y. Efremov, E. A. Olson, M. Zhang, Z. Zhang and L. H. Allen, Phys. Rev. Lett., 2003, 91, 085703.
11. A. Serghei, H. Huth, C. Schick and F. Kremer, Macromolecules, 2008, 41, 3636.
12. M. Tress, M. Erber, E. U. Mapesa, H. Huth, J. Mueller, A. Serghei, C. Schick, K.-J. Eichhorn, B. Voit and F. Kremer, Macromolecules, 2010, 43, 9937.
13. E. P. Giannelis, R. Krishnamoorti and E. Manias, Adv. Polym. Sci., 1999, 138, 107.
14. S. Anastasiadis, K. Karatasos, G. Vlachos, E. Manias and E. P. Giannelis, Phys. Rev. Lett., 2000, 84, 915.
15. S. S. Ray and M. Okamoto, Prog. Polym. Sci., 2003, 28, 1539–1641.
16. M. R. Bockstaller, R. A. Mickiewicz and E. Thomas, Adv. Mater., 2005, 17, 1331–1349.
17. Q. H. Zeng, A. B. Yua and G. Q. Lu, Prog. Polym. Sci., 2008, 33, 191–269.
18. R. Peköz, K. Johnston and D. Donadio, J. Phys. Chem. C, 2012, 116, 20409.
19. K. Johnston and V. Harmandaris, Soft Matter, 2012, 8, 6320–6332.
20. R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge University Press, 2004.
21. K. Johnston, A. Gulans, T. Verho and M. J. Puska, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235428.
22. A. Rimola, M. Aschi, R. Orlando and P. Ugliengo, J. Am. Chem. Soc., 2012, 134, 10899.
23. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
24. S. Grimme, J. Comput. Chem., 2004, 25, 1463.
25. K. Tonigold and A. Gross, J. Chem. Phys., 2010, 132, 224701.
26. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
27. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
28. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
29. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
30. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
31. K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101(R).
32. J. Klimes, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
33. A. Gulans, M. J. Puska and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 201105(R).
34. A. Calzolari, G. Cicero, C. Cavazzoni, R. D. Felice, A. Catellani and S. Corni, J. Am. Chem. Soc., 2010, 132, 4790.
35. T. D. Daff and N. H. de Leeuw, Chem. Mater., 2011, 23, 2718.
36. C. Oostenbrink, A. Villa, A. E. Mark and W. F. van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676.
37. N. Schmid, A. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. Mark and W. van Gunsteren, Eur. Biophys. J., 2011, 40, 843–856.
38. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657.
39. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225.
40. L. Delle Site, C. F. Abrams, A. Alavi and K. Kremer, Phys. Rev. Lett., 2002, 89, 156103.
41. M. L. Sushko, A. Y. Gal and A. L. Shluger, J. Phys. Chem. B, 2006, 110, 4853.
42. M. Hoefling, S. Monti, S. Corni and K. E. Gottschalk, PLoS One, 2011, 6, e20925.
43. G. Brancolini, D. B. Kokh, L. Calzolai, R. C. Wade and S. Corni, ACS Nano, 2012, 6, 9863.
44. G. Csányi, T. Albaret, M. C. Payne and A. DeVita, Phys. Rev. Lett., 2004, 93, 175503.
45. P. Maurer, A. Laio, H. W. Hugosson, M. C. Colombo and U. Rothlisberger, J. Chem. Theory Comput., 2007, 3, 628.
46. O. Akin-Ojo, Y. Song and F. Wang, J. Chem. Phys., 2008, 129, 064108.
47. C. R. Herbers, K. Johnston and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2011, 13, 10577.
48. K. Johnston, C. R. Herbers and N. F. A. van der Vegt, J. Phys. Chem. C, 2012, 116, 19781.
49. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
50. N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153101.
51. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403.
52. K. Johnston and V. Harmandaris, J. Phys. Chem. C, 2011, 115, 14707.
53. F. Iori, R. D. Felice, E. Molinari and S. Corni, J. Comput. Chem., 2009, 30, 1465.
54. L. M. Ghiringhelli, B. Hess, N. F. A. van der Vegt and L. Delle Site, J. Am. Chem. Soc., 2008, 130, 13460–13464.
55. P. Schravendijk, N. F. A. van der Vegt, L. Delle Site and K. Kremer, ChemPhysChem, 2005, 6, 1866.
56. K. Johnston, R. M. Nieminen and K. Kremer, Soft Matter, 2011, 7, 6457–6466.
57. D. G. Pettifor and I. I. Oleinik, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8487.
58. I. I. Oleinik and D. G. Pettifor, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8500.
59. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, J. Phys. Chem. A, 2001, 105, 9396.
60. D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, 2nd edn, 2001.
61. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1987.
62. G. C. J. P. Bareman and M. L. Klein, Phys. Rev. Lett., 1988, 60, 2152.
63. S. K. Kumar, M. Vacatello and D. Y. Yoon, J. Chem. Phys., 1988, 89, 5206.
64. S. K. Kumar, M. Vacatello and D. Y. Yoon, Macromolecules, 1990, 23, 2189.
65. K. F. Mansfield and D. N. Theodorou, Macromolecules, 1991, 24, 4295.
66. T. K. Xia, J. Ouyang, M. W. Ribarsky and U. Landman, Phys. Rev. Lett., 1992, 69, 1967.
67. R. G. Winkler, T. Matsuda and D. Y. Yoon, J. Chem. Phys., 1993, 98, 729.
68. T. Matsuda, G. D. Smith, R. G. Winkler and D. Y. Yoon, Macromolecules, 1995, 28, 165.
69. K. C. Daoulas, V. A. Harmandaris and V. G. Mavrantzas, Macromolecules, 2005, 38, 5780.
70. P. V. K. Pant and D. N. Theodorou, Macromolecules, 1995, 28, 7224.
71. V. G. Mavrantzas, T. D. Boone, E. Zervopoulou and D. N. Theodorou, Macromolecules, 1999, 32, 5072.
72. V. A. Harmandaris, V. G. Mavrantzas, D. Theodorou, M. Krger, J. Ramrez, H. C. Öttinger and D. Vlassopoulos, Macromolecules, 2003, 36, 1376–1387.
73. V. A. Harmandaris, K. C. Daoulas and V. G. Mavrantzas, Macromolecules, 2005, 38, 5796.
74. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619.
75. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1980, 84, 178.
76. G. D. Smith, D. Bedrov, L. Li and O. Byutner, J. Chem. Phys., 2002, 117, 9478.
77. L. Yelash, P. Virnau, K. Binder and W. Paul, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 050801.
78. E. Lin, W. Wu and S. Satija, Macromolecules, 1997, 30, 7224.
79. B. Frank, A. P. Cast, T. P. Rusell, H. R. Brown and C. Hawker, Macromolecules, 1996, 29, 6531.
80. D. Hudzinskyy, A. V. Lyulin, A. R. C. Baljon, N. K. B. K. Balabaev and M. A. J. Michels, Macromolecules, 2011, 44, 2299.
81. L. Yelash, P. Virnau, K. Binder and W. Paul, Europhys. Lett., 2012, 98, 28006.
82. O. Borodin, G. D. Smith, R. Bandyopadhyaya and O. Byutner, Macromolecules, 2003, 36, 7873.
83. D. Barbier, D. Brown, A.-C. Grillet and S. Neyertz, Macromolecules, 2004, 37, 4695.
84. A. P. Awasthi, D. C. Lagoudas and D. C. Hammerand, Modell. Simul. Mater. Sci. Eng., 2009, 17, 015002.
85. J.-S. Yang, C.-L. Yang, M.-S. Wang, B.-D. Chen and X.-G. Ma, Phys. Chem. Chem. Phys., 2011, 13, 15476–15482.
86. Y. Tatek and M. Tsige, J. Chem. Phys., 2011, 135, 174708.
87. Y. N. Pandey and M. Doxastakis, J. Chem. Phys., 2012, 136, 094901.
88. A. N. Rissanou and V. A. Harmandaris, J. Nanopart. Res., 2013, 15, 1589.
89. S. E. Harton, S. K. Kumar, H. Yang, T. Koga, K. Hicks, H. Lee, J. Mijovic, M. Liu, R. S. Vallery and D. W. Gidley, Macromolecules, 2010, 43, 3415.
90. K. C. Daoulas, A. F. Terzis and V. G. Mavrantzas, J. Chem. Phys., 2002, 116, 11028.
91. A. F. Terzis, D. N. Theodorou and A. Stroeks, Macromolecules, 2000, 33, 1385.
92. T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2011, 44, 2316.
93. C. R. Yang, P. Y. Chen, Y. C. Chiou and R. T. Lee, Sens. Actuators, A, 2005, 119, 263.
94. C. Wei, Nano Lett., 2006, 6, 1627–1631.
95. Q. Zheng, D. Xia, Q. Xue, K. Yan, X. Gao and Q. Li, Appl. Surf. Sci., 2009, 255, 3534–3543.
96. S. S. Tallury and M. A. Pasquinelli, J. Phys. Chem. B, 2010, 114, 4122–4129.
97. M. Alaghemandi, F. Müller-Plathe and M. C. Böhm, J. Chem. Phys., 2011, 135, 184905.
98. I. A. Bitsanis and G. Hatziioannou, J. Chem. Phys., 1990, 92, 3827.
99. A. N. Rissanou, S. H. Anastasiadis and I. A. Bitsanis, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 2462–2476.
100. K. F. Mansfield and D. N. Theodorou, Macromolecules, 1989, 22, 3143.
101. T. Aoyagi, J. Takimoto and M. Doi, J. Chem. Phys., 2001, 115, 552.
102. A. Milchev and K. Binder, J. Chem. Phys., 2001, 114, 8610.
103. P. A. Thompson and M. O. Robbins, Science, 1990, 250, 792.
104. P. Thompson and S. M. Troian, Nature, 1997, 389, 360.
105. A. Jabbarzadeh, J. D. Atkinson and R. I. Tanner, J. Chem. Phys., 1999, 110, 2612.
106. J.-L. Barrat and L. Bocquet, Phys. Rev. Lett., 1999, 82, 4671.
107. J. K. M. Cieplak and J. R. Banavar, Phys. Rev. Lett., 2001, 86, 803.
108. N. V. Priezjev and S. M. Troian, Phys. Rev. Lett., 2004, 92, 018302.
109. A. Niavarani and N. V. Priezjev, J. Chem. Phys., 2008, 129, 144902.
110. A. D. Virgilis, A. Milchev, V. G. Rostiashvili and T. A. Vilgis, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 97.
111. G. S. Grest, J. Chem. Phys., 1996, 105, 5532–5542.
112. J. Klos and T. Pakula, J. Chem. Phys., 2003, 118, 1507–1514.
113. J. Klos and T. Pakula, Macromolecules, 2004, 37, 8145–8151.
114. J. Kalb, D. Dukes, S. K. Kumar, R. S. Hoy and G. S. Grest, Soft Matter, 2011, 7, 1418.
115. A. Karatrantos, R. J. Composto, K. I. Winey, M. Kröger and N. Clarke, Macromolecules, 2012, 45, 7274.
116. F. W. Starr, J. F. Douglas and S. C. Glotzer, J. Chem. Phys., 2003, 119, 1777.
117. R. M. Cordeiro, F. Zschunke and F. Muller-Plathe, Macromolecules, 2010, 43, 1583–1591.
118. D. Long and F. Lequeux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 371–387.
119. J. Berriot, H. Montes, F. Lequeux, D. Long and P. Sotta, Macromolecules, 2002, 35, 9756–9762.
120. J. M. Kropka, K. W. Putz, V. Pryamitsyn, V. Ganesan and P. F. Green, Macromolecules, 2007, 40, 5424–5432.
121. J. M. Kropka, V. Pryamitsyn, V. Ganesan and P. F. Green, Phys. Rev. Lett., 2008, 101, 075702.
122. J. E. Lipson and S. T. Milner, Eur. Phys. J. B, 2009, 72, 133–137.
123. L. M. Hall, A. Jayaraman and K. S. Schweizer, Curr. Opin. Solid State Mater. Sci., 2010, 14, 38–48.
124. J. B. Hooper and K. F. Schweizer, Macromolecules, 2006, 39, 5133–5142.
125. R. Chakrabarti and K. S. Schweizer, J. Chem. Phys., 2010, 133, 144905.
126. U. Yamamoto and K. F. Schweizer, J. Chem. Phys., 2011, 135, 224902.
127. A. L. Frischknecht, E. S. McGarrity and M. E. Mackay, J. Chem. Phys., 2010, 132, 204901.
128. J. Baschnagel, K. Binder, P. Doruker, A. A. Gusev, O. Hahn, K. Kremer, W. L. Mattice, F. Müller-Plathe, M. Murat, W. Paul, S. Santos, U. W. Suter and V. Tries, Adv. Polym. Sci., 2000, 152, 41.
129. K. Kremer, in Computer simulations in condensed matter: from materials to chemical biology, ed. M. Ferrario, G. Ciccotti and K. Binder, Springer, Berlin, Heidelberg, 2006, ch. Polymer dynamics: long time simulations and topological constraints.
130. V. A. Harmandaris and K. Kremer, Macromolecules, 2009, 42, 791.
131. V. A. Harmandaris and K. Kremer, Soft Matter, 2009, 5, 3920.
132. D. Fritz, K. Koschke, V. A. Harmandaris, N. F. A. van der Vegt and K. Kremer, Phys. Chem. Chem. Phys., 2011, 13, 10412.
133. J. T. Padding and W. J. Briels, J. Chem. Phys., 2002, 117, 925.
134. I. Lyubimov and M. G. Guenza, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031801.
135. V. A. Harmandaris, N. P. Adhikari, N. F. A. van der Vegt and K. Kremer, Macromolecules, 2006, 39, 6708.
136. C. F. Abrams, L. Delle Site and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 21807.
137. L. Delle Site, S. Leon and K. Kremer, J. Am. Chem. Soc., 2004, 126, 2944–2955.
138. X. Zhou, D. Andrienko, L. Delle Site and K. Kremer, Europhys. Lett., 2005, 70, 264.
139. D. Andrienko, S. León, L. Delle Site and K. Kremer, Macromolecules, 2005, 38, 5810–5816.
140. R. Car and M. Parinello, Phys. Rev. Lett., 1985, 55, 2471.
141. G. H. Fredrickson, The equilibrium theory of inhomogeneous polymers, Clarendon Press, 2nd edn, 2006.
142. K. C. Daoulas, D. N. Theodorou, V. A. Harmandaris, N. C. Karayiannis and V. G. Mavrantzas, Macromolecules, 2005, 38, 7134.
143. D. M. Trombly and V. Ganesan, J. Chem. Phys., 2010, 133, 154904.
144. R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Science, 2001, 292, 2469.
145. M. Müller and G. D. Smith, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 934.
146. S. W. Sides, B. J. Kim, E. J. Kramer and G. H. Fredrickson, Phys. Rev. Lett., 2006, 96, 250601.
147. D. H. Kim, D. S. Choi, S. Hong and S. Kim, J. Phys. Chem. C, 2008, 112, 7412.
148. J. H. Kim and B. E. Park, Ferroelectrics, 2009, 379, 22.
149. B. Vorselaars, J. U. Kim, T. L. Chantawansri, G. H. Fredrickson and M. W. Matsen, Soft Matter, 2011, 7, 5128–5137.
150. F. A. Detcheverry, H. Kang, K. C. Daoulas, M. Müller, P. F. Nealey and J. J. de Pablo, Macromolecules, 2008, 41, 4989–5001.
151. K. C. Daoulas and M. Müller, J. Chem. Phys., 2006, 125, 184904.
152. G. G. Vogiatzis, E. Voyiatzis and D. N. Theodorou, Eur. Polym. J., 2011, 47, 699–712.
153. M. Müller and F. Schmid, Adv. Polym. Sci., 2005, 185, 1.
154. M. Müller, J. Stat. Phys., 2011, 145, 967.
155. M. Müller, in Polymer Science: A Comprehensive Reference, ed. K. Matyjaszewski and M. Möller, Elsevier, 2012, vol. 1, ch. 3. Polymers at interfaces and surfaces and in confined geometries, p. 387.
156. V. Ganesan, C. J. Ellison and V. Pryamitsyn, Soft Matter, 2010, 6, 4010–4025.
157. K. Paeng and M. D. Ediger, Macromolecules, 2011, 44, 7034.
158. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357.
159. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schafer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1.
160. M. Praprotnik, L. Delle Site and K. Kremer, Annu. Rev. Phys. Chem., 2008, 59, 545–571.

---