Optimization of solid phase extraction chromatography for the separation of Np from U and Pu using experimental design tools in complex matrices†
Pablo J.
Lebed
a,
Sabrina
Potvin
a,
Dominic
Larivière
*a and
Xiongxin
Dai
b
aDepartment of Chemistry, Université Laval, Centre de recherche sur les propriétés des interfaces et la catalyse (CERPIC), Québec G1V 0A6, QC, Canada. E-mail: dominic.lariviere@chm.ulaval.ca; Tel: +1-418-656-7250
bChalk River Laboratories, Atomic Energy of Canada Limited, Chalk River K0J 1J0, ON, Canada. E-mail: daix@aecl.ca; Tel: +1-613-584-3311 ext. 46128
First published on 25th October 2013
Abstract
Effective solid phase extraction separation methods of actinides and fission products are required in the control and evaluation of common or experimental nuclear spent fuel reprocessing strategies and environmental contaminated samples. In this study, we have developed a simpler sequential analytical separation scheme to isolate 237Np from U and Pu. Experimental design tools were used to achieve parameter optimization. We studied the contribution of critical factors such as the type of resin, acidity, sulfamic acid concentration and sample volume to actinide extraction with a multivariate approach. Following a sequential assembly approach, fractional factorial designs were used to select the best resin. Full factorial designs were used to evaluate the expected response for the chosen multifactorial space. After discarding a first order linear model, the designs were augmented and the response surface methodology was used to evaluate the response through the use of a quadratic model together with graphical and canonical analysis. Knowledge acquired from multiple actinide responses allowed us to find multi-criteria compromise solutions that were successfully applied for the separation of Np from Pu and U in complex matrices.
Introduction
A sustainable nuclear energy generation strategy should include effective fuel use and waste minimization through recycling the actinide fuel. The aqueous reprocessing of nuclear fuels through partitioning and transmutation is the most explored strategy followed by the majority of nuclear energy capable countries. This approach would allow the reduction of long-term radio-toxicity in nuclear repositories whereas most of the minor actinides and long-lived fission products would be separated in complement to the industrial separation of uranium and plutonium.1Neptunium-237, a long lived α-particle emitter (t1/2 = 2.14 × 106 years) by-product of the nuclear fuel cycle, originates from two main sources: in the short term from the neutron capture of uranium isotopes and in the long term as a decay product of 241Am. In the nuclear fuel reprocessing (NFR) of spent fuel 237Np can be completely recovered as a mixture with U/Pu in the first decontamination cycle of fuel solutions in the PUREX process adapted for Np recovery.2 Other innovative approaches involve the co-extraction of U/Pu/Np after a crystallization step to remove excess of U or, like in the ERIX process, the separation of a U/Pu/Np mixture after valence adjustment and ion exchange column extraction.3,4
To control aqueous reprocessing strategies, evaluate new experimental lab-scale actinide recovery approaches, or address potential environmental nuclear material discharge, the measurement of Np is usually performed by α counting and mass spectrometry detection techniques. Unfortunately both techniques have critical disadvantages that prevent direct sample measurement: 237Np and 242Pu α counting spectra overlap and 238U excess interferes with the detection of 237Np in mass spectrometry. Hence, a previous 237Np separation protocol must be applied.
This task is commonly performed using extraction chromatography resins (EXC).5 Typically, 237Np has been difficult to separate from actinide mixtures since it is present in the Pu elution fraction. Maxwell et al. have recently developed a new procedure that uses two stacked TEVA and DGA resins. First, Np(IV) and Pu(IV) are retained in the TEVA resin and then plutonium is transferred to the DGA resin as Pu(III) by a reduction step with a mixture of ascorbic acid and ferrous nitrate.6–8
Similarly, Larivière's group have introduced innovative approaches for the analysis of neptunium using a combination of TEVA and DGA resins to separate U(IV) and Np(III)9 and a second sequential approach using two UTEVA resins and Np(VI) as a final pre-concentration step.10 Traditionally, radiochemical separation methodologies are developed by monitoring the influence of one factor at a time (e.g., acidity level, type of column, redox agents, etc.) on an experimental response (e.g., yield, retention capacity, decontamination factor); while only one parameter is modified, others are kept at a constant value.
Although it is possible to obtain successful results, this approach presents some disadvantages such as the time-consuming nature of the optimization of each parameter, though each factor may not always be relevant to the separation, and the lack of inclusion of the interactive effects among the variables studied with the consequence of an incomplete effect description of the parameters on the response. Multivariate statistic techniques can overcome these disadvantages, and are valid tools in the pathway of simultaneous level parameter optimization to achieve the maximum system performance.11 Despite wide application of these tools in the analytical chemistry field, in radiochemistry, the only reported method so far has been performed applying the Doehlert design with the objective of pre-concentrate uranium from natural waters using the cloud point extraction methodology.12
The aim of the present work was to develop a simplified analytical separation scheme to compare the effectiveness of several commercial EXC resins and conditions in obtaining 237Np samples free from other potentially interfering actinides. The protocol optimization used a sequential assembly strategy13 by means of statistical experimental design tools, mainly factorial designs and the response surface methodology (RSM),14,15 where the measurements were done using ICP-MS. Finally, the optimized protocol was applied to samples with diverse matrix complexity.
Experimental section
Reagents and chemicals
Solutions of environmental-grade HNO3 (Anachemia, Montréal, QC, Canada), reagent grade ammonium oxalate ((NH4)2C2O4), and sulfamic acid (Fisher Scientific, Fair Lawn, NJ, USA) were prepared using high-purity water (18 MΩ cm) from a Milli-Q purification system (Milipore, Bedford, MA, USA). Such chemicals were used throughout this investigation unless stated otherwise. Neptunium-237 (2555 Bq L−1) and Pu-242 (1153 Bq L−1) were purchased from the National Institute of Standards and Technology (Gaithersburg, MD, USA) and thallium (1000 mg L−1), natural uranium (1000 mg L−1) and EU-H-1 waste water solution standards were obtained from SCP Science (Baie D'Urfé, QC, Canada). TEVA, UTEVA and DGA cartridges containing 2 mL of each resin (particle size: 50–100 μm, Eichrom Technologies, Darien, IL, USA) were used throughout this investigation.Sample preparation
Sediment samples taken upstream of the Gentilly-II nuclear power plant (Bécancour, QC, Canada) in the St. Lawrence River and certified waste water samples were used as reference matrices to determine the reliability of the developed method. Sediment samples were completely digested by fusion with lithium metaborate in a platinum crucible following the protocol reported elsewhere.10 The final solutions were split into equal volumes and spiked with a standard solution containing 237Np, 238U and 242Pu.Separation procedure
All extraction procedures were developed following the same scheme: (1) column pre-conditioning with the same matrix than the one of the sample analyzed, (2) sample loading (conditioned with the appropriate combination of factors and levels), (3) filtrate collection (since we used the elution chromatography mode the initial and final volumes are identical) and (4) column washing with 10 mL of 0.1 mol L−1 ammonium oxalate followed by 10 mL of H2O. The internal standard Tl was added to all collected fractions and then measured by mass spectrometry with the conditions described in the following section.Instrumentation
Mass spectrometric analyses of uranium, plutonium and neptunium were performed using a Varian 800MS ICP-MS (Mississauga, ON, Canada). Validation of instrumental parameters was performed once using a 1 μg L−1 multi-element standard (VAR-TS-MS, Varian) and the torch position parameter was re-optimized daily prior to analysis.Calculations and statistical analysis
Since the aim of the work is to retain Pu and U while Np is eluted, low response values for Np and high values for Pu and U are desired.Examples of how to calculate main and interaction effects of the half-fractional and full factorial experiments together with the calculation of standard errors of effects from replicates and center points and how to establish the significance of an effect are presented in the ESI.† The least squares procedures, analysis of variance, quadratic graphical and canonical analysis and the response profiling were performed using JMP 10 (SAS Institute Inc., Cary, NC, USA).
Results and discussion
To investigate the multicomponent yield response, the development of the sequential protocol was divided into two parallel processes. Though a single column strategy might have produced the desired separation, considering the experimental conditions needed to elute Np and retain U/Pu and the low number of theoretical plates typically offered by SPE resins, we choose a two-step approach. EXC commercial resins were used to remove plutonium and uranium (Step A) and then the remaining uranium from neptunium in the sample (Step B). Since the objective is to produce clean 237Np samples, the EXC resins were operated in elution mode for this actinide. All experimental designs used in this work are represented in Scheme 1.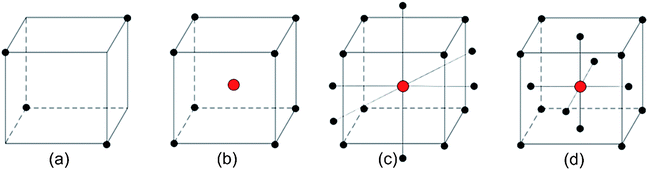 | ||
| Scheme 1 Experimental designs. (a) Half-fractional 23 factorial; (b) full 23 factorial with center point; (c) central composite design; (d) face-centered central composite design. | ||
Half-fractional 23 factorial designs
We used half-fractional factorial designs to determine the most suitable resin types for the two-step process and to allow for the elimination of a categorical variable. For Step A, the factors and levels (in parenthesis) used were resin (DGA–TEVA), HNO3 acidity (pH 0–2) and sulfamic acid (0–10 mM). For Step B, we tested resin (UTEVA–DGA), HNO3 acidity (pH 0–2) and sulfamic acid (10–30 mM). The experiment was replicated three times to increase the sensitivity to small response changes.The designed levels of combination and extraction results for Steps A and B are shown in Tables S1 and S2,† respectively, and the calculated main effects for both steps are presented in Table 1.
| Main effect | Step Ab | Step Bc | |||
|---|---|---|---|---|---|
| 237Np ± S.E. | 242Pu ± S.E. | 238U ± S.E. | 237Np ± S.E. | 238U ± S.E. | |
| a Standard errors of the effects were calculated with the estimate of σ2 from experimental cubic (triplicate) points. b s 2 Np = 2.2, s2Pu = 11.9 and s2U = 1.6. c s 2 Np = 3.0 and s2U = 41.0. d The significance of the effects was established considering the 95% confidence interval as ±(2.3 × S.E.), with Pr (|t8| > 2.3) = 0.05. | |||||
| Resin | −3.4 ± 0.9d | −48 ± 2d | −57.2 ± 0.8d | 0 ± 4 | −5 ± 1d |
| HNO3 | −3.2 ± 0.9d | −46 ± 2d | −39.5 ± 0.8d | −2 ± 4 | −64 ± 1d |
| Sulfamic acid | −6.3 ± 0.9d | 44 ± 2d | −7.0 ± 0.8d | −3 ± 4 | −6 ± 1d |
Results for Step A indicate that changing the EXC resin from DGA to TEVA produced a favourable situation from the retention of Np (−3.4 ± 0.9%) but a more serious non-favourable condition from the standpoint of Pu (−48 ± 2%) and U (−57.2 ± 0.2%). This means that while Np can be weakly retained on TEVA, Pu and U are not retained. Therefore, DGA resin should be used for the proposed application. The results for the HNO3 acidity level confirm what is usually observed in the literature; a lower HNO3 acidity value offers elution conditions in these systems. Finally, the presence of 10 mM sulfamic acid has the highest impact on Pu, greatly favouring its retention (44 ± 2%).
Table 1 shows that in Step B, the retention of Np is not significantly influenced by any of the factors and levels. In contrast, U extraction appears to be slightly enhanced using UTEVA (−5 ± 1%) but in this case it is a change in HNO3 acidity that produces the highest change in the extraction yield (−64 ± 1%). These results allow us to conclude that the resin combination Step A/DGA and Step B/UTEVA was the most suitable to achieve the proposed separation.
Full 23 factorial designs
Once the appropriate resin for each step (A: DGA, B: UTEVA) was selected and the importance of the chosen quantitative factors (HNO3 acidity and sulfamic acid) confirmed, we proceeded to investigate the response in more detail (extraction yield) using full 23 factorial experimental designs by replacing the categorical factor (resin) with a numerical one (sample volume). These experimental designs allowed us to evaluate the presence and magnitude of two-level interactions between the factors. Additionally, we included center points in the model to enable the quantification of the experimental error and more importantly, to test the presence of curvature in the response. The designed level combination and extraction yields for Steps A and B are presented in Tables S3 and S4,† respectively, while calculated averages and interaction effects can be seen in Table 2. As an illustration, cube effect plots are presented in Fig. 1.| Effects | Step Ab | Step Bc | ||||
|---|---|---|---|---|---|---|
| 237Np ± S.E. | 242Pu ± S.E. | 238U ± S.E. | 237Np ± S.E. | 238U ± S.E. | ||
| a Standard error of effects was calculated with the estimate of σ2 from experimental center points. b s 2 Np = 5.9, s2Pu = 0.1 and s2U = 143.7. c s 2 Np = 0.8 and s2U = 0.04. d The significance of the effects was established considering the 95% confidence interval as ±(2.353 × S.E.), with Pr (|t3| > 2.353) = 0.05. A: HNO3 acidity (pH); S: sulfamic acid (mM); V: volume. Three-factor interactions were not significant and are not presented. | ||||||
| Main | ||||||
| A | −1 ± 6 | −1.7 ± 0.3d | −72 ± 12d | 6.2 ± 0.9d | −52.7 ± 0.2d | |
| S | −1 ± 6 | 0.2 ± 0.3 | 3 ± 12 | −0.5 ± 0.9 | −2.3 ± 0.2d | |
| V | −5 ± 6 | −0.6 ± 0.3 | −9 ± 12 | −6.4 ± 0.9d | −52.5 ± 0.2d | |
| Interactions | ||||||
| A–S | −4 ± 6 | 0.1 ± 0.3 | −3 ± 12 | −1.4 ± 0.9 | −2.0 ± 0.2d | |
| A–V | 2 ± 6 | 0.1 ± 0.3 | 7 ± 12 | 4.8 ± 0.9d | −53.3 ± 0.2d | |
| S–V | 3 ± 6 | 0.4 ± 0.3 | 3 ± 12 | 0.6 ± 0.9 | −1.9 ± 0.2d | |
In Step B, where the experiment was performed using UTEVA resins, in general the extraction yields of Np and U were in line with the objectives of this step: a low retention of neptunium while the remaining uranium is being removed. The analysis of factors revealed a significant unfavourable contribution of a change in HNO3, from high to low acidity, for both actinides. The volume change, from 8 to 10 mL, also greatly affected the retention of both elements, especially U. The cube plots (Fig. 1b) offer a clear picture of the change in the responses with the UTEVA column enabling the selection of the best solution for a particular set of experimental conditions. This experimental design also allowed us to observe significant interactions between factors. The fact that HNO3 acidity and volume are the parameters that interact the most intensively indicates that it would be possible to achieve a certain desired extraction yield using more than one set of parameter combinations.
| Model | Step A | Step B | |||||
|---|---|---|---|---|---|---|---|
| 237Np | 242Pu | 238U | 237Np | 238U | |||
| a S M: model sum of squares; SR: residual sum of squares; SL: lack-of-fit sum of squares; SE: error sum of squares; FD points: * 5%, ** 1%, and *** 0.1%. | |||||||
| Linear | |||||||
| F S M/SR | 2.2494 | 2.1194 | 6.4070 | 39.8580 | 7.4940 | ||
| Significance | p-Value | 0.1958 | 0.2136 | 0.0300 | 0.0005 | 0.0215 | |
| F D % points | — | — | * | *** | * | ||
| F S L/SE | 0.2899 | 9.1284 | 3.3280 | 1.3380 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840.56 840.56 |
||
| Significance | p-Value | 0.2899 | 0.0530 | 0.173 | 0.3840 | <0.0001 | |
| F D % points | — | — | — | — | *** | ||
| Quadratic | |||||||
| F S M/SR | 4.1680 | 6.6196 | 11.8785 | 19.0940 | 87.1070 | ||
| Significance | p-Value | 0.0225 | 0.0048 | 0.0005 | 0.0002 | <0.0001 | |
| F D % points | * | ** | *** | *** | *** | ||
| F S L/SE | 1.6136 | 0.6401 | 0.3314 | 2.1420 | 1765.70 | ||
| Significance | p-Value | 0.3032 | 0.6568 | 0.8465 | 0.2135 | <0.0001 | |
| F D % points | — | — | — | — | *** | ||
The significance of the model sum of squares/residual sum of squares and lack-of-fit sum of squares/error sum of squares were evaluated through the p-value and F-distribution score points. A complete version of the ANOVA tables can be found in Tables S5 to S9.†
In Step A, the analysis of variance of the experimental models for the response of Np and Pu did not show a significant fit to the extraction yield data. In the case of Pu, an evident lack of fit (p = 0.0530) was observed, which indicated that the linear first order model was not the appropriate one and some degree of curvature was present. However, a significant fit to the experimental data (p-value = 0.030) and the absence of lack of fit (p-value = 0.173) showed no evidence to reject the proposed hypothesis for the extraction yield of U. In Step B, a linear first order model seems to correctly describe the response of Np and U. However, in the case of U, the model proposed showed a strong lack of fit (p-value < 0.0001). It is possible that these fitted responses were located in a tridimensional factorial space where the response could be represented by a minimax and quadratic coefficients are cancelled (a minimax is the point in the tridimensional factorial space where the response reaches a steady state value and a change from this point in the direction of one of the factor levels produces a response in the opposite sense than a change in the direction of another factor).
Design augmentation: response surface methodology
The results obtained in the previous analysis do not provide enough evidence to accurately describe the responses by a linear first-order model; the extraction yield responses of Np, Pu and U in both EXC resins are complex possibly due to closeness of the stationary point. To address this hypothesis, we tried to explain the response through a quadratic second order model using one of the possibilities offered by the sequential assembly strategy augmenting the full factorial experimental data of A and B into a central composite design (Scheme 1c and d, respectively) through the addition of six axial and two central experimental points and orthogonal blocking ensuring that a potential shift in the response between experimental parts has no effect on the estimated model coefficients. The designed level combination and extraction yields for A and B are presented in Tables S10 and S11,† respectively.| Step | Actinide | Stationary point location | Canonical form | Shape | |||
|---|---|---|---|---|---|---|---|
| A | S | V | R,a% | A: X12; S: X22; V: X32 | |||
| a Response value at the stationary point. A stationary point is the point in the tridimensional factorial space where the response reaches a steady state value. This point could belong to a minimum-, maximum- or saddle-type response surface. | |||||||
| A | 237Np | 0.3 | 11.2 | 9.6 | 8.4 | y Np = 8.39 + 1.54X12 + 1.26X22 − 0.90X32 | Saddle |
| 242Pu | 1.9 | 5.5 | 11.7 | 91.6 | y Pu = 91.60 + 0.53X12 + 0.34X22 + 0.08X32 | Minimum | |
| 238U | 2.4 | 4.1 | 11.3 | 9.0 | y U = 9.02 + 15.65X12 + 4.25X22 + 2.23X32 | Minimum | |
| B | 237Np | 3.7 | 11.9 | 2.1 | 13.0 | y Np = 13.04 + 1.78X12 − 0.53X22 − 0.1.85X32 | Saddle |
| 238U | 0.6 | 20.0 | 7.1 | 108.8 | y U = 108.77 + 6.20X12 − 2.30X22 − 28.73X32 | Saddle | |
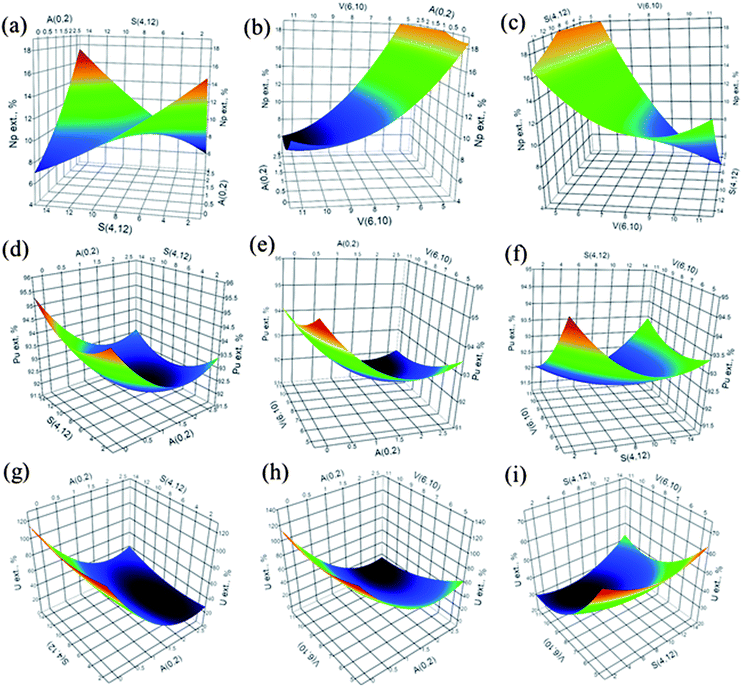
Beginning with the responses obtained in A with DGA resins, Np represents a classic saddle-shaped surface, as can be seen in Fig. 2a (factors: HNO3 acidity and sulfamic acid). Also, an incipient indication of this shape can be seen at higher values of volume and sulfamic acid in Fig. 2b and c, respectively. The canonical equations confirmed the assignment of a saddle-shaped response, as indicated by the positive and negative signs of the coefficients.
The coefficients show that the response increases in the direction of the HNO3 acidity and sulfamic acid and decreases in the volume direction; since the retention of neptunium is not desired at higher acidity, small redox agent concentrations and higher sample volumes would favour the achievement of this particular objective.
On the other hand, both of the Pu and U responses present a classic minimum-shaped surface (Fig. 2d–f for Pu and 2g–i for U) with response values of 91.6% and 9.0% at the stationary point for Pu and U, respectively (Table 4). Considering the coefficients calculated in the canonical equations, Pu appears to have slow growth in the response with almost no influence of volume in its extraction.
The case of U could be considered problematic at first, considering the minimum value. But, if we carefully look at the position of the stationary point outside the tridimensional factorial space (HNO3 acidity, pH: 2.4; sulfamic acid: 4.1 mM; volume: 11.3 mL), we can assume that a better extraction condition could only be achieved once inside the factorial space.
The canonical equation indicates that a strong response increment would be obtained with small changes in the acidity level. The response surfaces modelled in the second step (ESI, Fig. S1†) using UTEVA resins showed no definitive minimum- or maximum-shaped responses that could be a sign of saddle-type responses.
These observations are confirmed by the coefficients of the responding canonical forms, clearly indicating the presence of a stationary saddle point for Np and U. For neptunium, the response extraction value at this region is high (13.0%); but according to the canonical equations two of the three factors, sulfamic acid and volume, could shift the response to better values. Finally, the response of uranium presents an ideal situation, since complete extraction is predicted at the stationary point.
A snapshot of the solutions found for Steps A and B is presented in Fig. S2 and S3,† respectively. We used a fixed 10 mL volume value, considering a hypothetical sample of whose acidity level and redox state should be adjusted in both steps. The compromise solution for Step A (DGA resin) appears to be a sample solution of 10 mL at HNO3 acidity of pH 0.35 with 12 mM of sulfamic acid in nitric acid medium. For Step B (UTEVA resin), the optimized conditions are 10 mL, HNO3 acidity pH 0 and 10 mM of sulfamic acid in nitric acid medium. The estimated extraction values are 9 ± 4%, 93.5 ± 0.8% and 72 ± 18% for Np, Pu and U, respectively, with DGA resin and −6 ± 3% and 100 ± 11% for Np and U, respectively, with UTEVA resin.
Complex matrix samples
The optimized separation method was applied to waste water and soil solution samples spiked with 237Np, 242Pu, and 238U. After processing (see Separation procedure), the samples were analyzed by ICP-MS. The results are shown in Table 5.| Step | Waste water | Soil solution | ||||
|---|---|---|---|---|---|---|
| 237Np (ng L−1) | 242Pu (ng L−1) | 238U (μg L−1) | 237Np (ng L−1) | 242Pu (ng L−1) | 238U (μg L−1) | |
| a Optimal conditions: Step A – DGA: HNO3 acidity, pH 0.35; sulfamic acid: 12 mM; volume: 10 mL. Step B – UTEVA: HNO3 acidity, pH 0; sulfamic acid: 10 mM, volume: 10 mL. 238U CLOD = 0.049 ± 0.002 μg L−1; 242Pu CLOD = 6 ± 1 ng L−1. Ci: concentration before extraction, in duplicate; Cf: concentration after extraction, in triplicate. Extraction percentages were calculated averaging triplicate values. | ||||||
| A – DGA | ||||||
| C i ± S.E. | 634 ± 8 | 254 ± 2 | 140.0 ± 0.1 | 103 ± 5 | 43 ± 2 | 3.0 ± 0.1 |
| C f ± S.E. | 592 ± 6 | 14 ± 1 | 3.9 ± 0.8 | 107 ± 4 | 0.6 ± 0.4 | 0.067 ± 0.008 |
| Ext. % ± S.E. | 7 ± 1 | 94.2 ± 0.4 | 97.3 ± 0.8 | −4 ± 4 | 99 ± 1 | 98.3 ± 0.7 |
| A + B – DGA + UTEVA | ||||||
| C i ± S.E. | 630 ± 1 | 262 ± 1 | 137.9 ± 0.3 | 104 ± 11 | 43 ± 4 | 3.1 ± 0.4 |
| C f ± S.E. | 601 ± 1 | 13 ± 5 | 0.07 ± 0.06 | 99 ± 5 | 0.2 ± 0.2 | 0.007 ± 0.004 |
| Ext. % ± S.E. | 4.7 ± 0.2 | 95 ± 2 | 99.96 ± 0.03 | 5 ± 5 | 99.5 ± 0.6 | 99.8 ± 0.1 |
The experiment used replicate sets of samples to separately evaluate the contribution of each part of the method to the final outcome. For waste water, there is a similar residual Np retention (4.7 to 7%) with both steps, implying that the experimental conditions used in the second EXC column do not contribute to the extraction of this actinide. A similar analysis in retention mode can be done for Pu, while U was removed to a concentration (0.07 ± 0.06 μg L−1) close to the instrumental detection limit emphasising the success of the column tandem used DGA–UTEVA. The DGA resin used with the chosen conditions enabled the removal of almost 1.36 μg of U (almost completely removing it from the sample).
The method applied to soil solution samples also offered interesting results: the quantity of Np remains unchanged throughout the procedure. Also, reducing the total actinide mass that was loaded into the column by a factor of nearly fifty did not influence the extraction though higher removal of Np could be expected. The removal of U was excellent (>99%) even at μg L−1 levels.
Finally, despite the fact that the separation method was developed with DGA followed by an UTEVA resin step, it is possible to alter this order; it would be more efficient, for example in soil samples processed with the fusion method, to begin with the UTEVA resins since the acidity level used (HNO3, 1 M) would be the same as the sample would have after soil dissolution, and just a small redox adjustment would need to be done.
Conclusions
The main conclusions drawn from the results are as follows:We demonstrated that experimental design tools with a multifactorial approach can be applied for the resolution of radiochemical separation problems. An experimental sequential assembly strategy allowed us to use a minimum of experiments to quickly arrive at a modelling analysis stage.
We proposed a 237Np separation strategy with an optimization process where all optimal value and actinide response changes in the selected experimental space are presented, whether they have useful applications or not. This information is likely to be valuable for extrapolation to other target actinides (Pu or U) or sample constraints (e.g. different sample volumes).
The separation of 237Np performed in elution mode avoids extra retention–elution steps and could be considered as an alternative for 237Np recovery from U/Pu mixtures in the continuous flow process as part of an aqueous partitioning nuclear reprocessing strategy. For ultra-trace 237Np environmental analysis the methodology could be easily adapted to include a pre-concentration step.
Notes and references
- T. Fanghänel, J.-P. Glatz, R. J. Konings, V. V. Rondinella and J. Somers, in Handbook of Nuclear Engineering, Springer, 2010 Search PubMed.
- R. Taylor, C. Gregson, M. Carrott, C. Mason and M. Sarsfield, Solvent Extr. Ion Exch., 2013, 31, 442–462 CrossRef CAS.
- Y. Koma, M. Watanabe, S. Nemoto and Y. Tanaka, J. Nucl. Sci. Technol., 1998, 35, 130–136 CrossRef CAS.
- H. Hoshi, Y.-Z. Wei, M. Kumagai, T. Asakura and Y. Morita, J. Alloys Compd., 2004, 374, 451–455 CrossRef CAS PubMed.
- P. Thakur and G. Mulholland, Appl. Radiat. Isot., 2012, 70, 1747–1778 CrossRef CAS PubMed.
- S. L. Maxwell, B. A. Culligan, V. D. Jones, S. T. Nichols and G. W. Noyes, J. Radioanal. Nucl. Chem., 2010, 287, 223–230 CrossRef.
- S. L. Maxwell, B. K. Culligan, V. D. Jones, S. T. Nichols, M. A. Bernard and G. W. Noyes, Anal. Chim. Acta, 2010, 682, 130–136 CrossRef CAS PubMed.
- S. L. Maxwell, B. K. Culligan, V. D. Jones, S. T. Nichols, G. W. Noyes and M. A. Bernard, Health Phys., 2011, 101, 180–186 CrossRef CAS PubMed.
- N. Guérin, K. Nadeau and D. Larivière, Talanta, 2011, 87, 8–14 CrossRef PubMed.
- N. Guérin, M. A. Langevin, K. Nadeau, C. Labrecque, A. Gagné and D. Lariviere, Appl. Radiat. Isot., 2010, 68, 2132–2139 CrossRef PubMed.
- M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. A. Escaleira, Talanta, 2008, 76, 965–977 CrossRef CAS PubMed.
- H. S. Ferreira, M. A. Bezerra and S. L. C. Ferreira, Microchim. Acta, 2006, 154, 163–167 CrossRef CAS.
- G. E. Box, Qual. Eng., 1993, 5, 321–330 CrossRef.
- G. E. Box, J. S. Hunter and W. G. Hunter, Statistics for experimenters: design, innovation, and discovery, Wiley, 2005 Search PubMed.
- D. C. Montgomery, Design and analysis of experiments, Wiley, 2008 Search PubMed.
- G. E. Box, Biometrics, 1954, 10, 16–60 CrossRef.
- G. E. Box and P. Youle, Biometrics, 1955, 11, 287–323 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Factor and level combinations and extraction yield data, ANOVA tables, surface plots, surface response profiles and tutorial for effects and error calculation. See DOI: 10.1039/c3ay41352g |
| This journal is © The Royal Society of Chemistry 2014 |