Retracted Article: Determination of silk fibroin secondary structure by terahertz time domain spectroscopy
Chao
Yan
a,
Bin
Yang
*a and
Zhicheng
Yu
ab
aKey Laboratory of Advanced Textile Materials and Manufacturing Technology, Zhejiang Sci-Tech University, Hangzhou, Zhejiang, China. E-mail: yangbin665959@gmail.com
bEcological Engineering Research Center of Dyeing and Finishing Technology, Hangzhou, Zhejiang, China
First published on 10th October 2013
Abstract
Silk fibroin membranes with different secondary structures were fabricated, and subsequently employed as an ideal system model for the investigation into the conformational transition of native proteins by terahertz time domain spectroscopy (THz-TDS). In comparison to conventional Fourier Transform Infrared (FTIR) Spectroscopy, THz spectroscopy presents distinct features for each kind of secondary structure with narrower bandwidths. Based on the theoretical calculation, absorption features observed in the range of 2.0–2.6 THz may be attributed to intramolecular modes of peptide chain. Three bands centered at 1.84 THz, 1.68 THz, and 1.55 THz are attributed to random coil, α-helix, and antiparallel β-pleated sheet, respectively. The results indicate that THz-TDS presents great potential as a complementary method to FTIR in determining the secondary structure of silk fibroin.
1 Introduction
Silk has recently emerged as a highly promising biopolymer owing to its excellent mechanical1 and optical properties,2 biocompatibility3 and implant ability.4 These significant properties are deemed to be associated with their corresponding protein secondary structure,5 which refers to the organization of amino acid residues in a polypeptide chain and are predominantly composed of α-helical and β-sheet conformations. Understanding the conformational structure of proteins is a fundamental problem for studies on their function. In addition, the fact that silk filaments are formed naturally under physiological conditions at ambient temperatures, without high pressure and using water as a solvent has motivated us to investigate the conformational transition involved in this remarkable process. Therefore, seeking effective approaches to determine protein conformation is of significance for developing novel fibroin biomaterials and interpreting the spinning mechanism of Bombyx mori, and further providing guidance to bionic-spinning.Currently, several experimental methods exist for protein secondary structure determination such as circular dichroism (CD),6–8 FTIR spectroscopy,9–14 nuclear magnetic resonance (NMR),15–19 Raman spectroscopy,14,19,20 and X-ray diffraction (XRD).16 Among these methods, although XRD and NMR spectroscopy have been employed to elucidate the conformation of a protein at high resolution, the two methods are restricted to a few proteins with low molecular weight and are not applicable to native proteins. Therefore, CD, Raman spectroscopy, and FTIR spectroscopy are routinely used to study the secondary structure of a protein. In particular, FTIR spectroscopy is considered as a powerful and well-established approach for estimating the secondary structure content of proteins. For the analysis of the secondary structure of proteins from FTIR spectra, the amide I region (1720–1600 cm−1) is normally utilized. Different conformational types, such as random coil, helix, sheet, etc., result in different discrete bands in the amide I region. Therefore, the secondary structure content of proteins can be predicted quantitatively using the curve fitting technique.10,12 However, the spectral features observed in the amide I region of proteins is slightly perturbed by the characteristic bands originating from water. As an alternative, THz-TDS is carried out for the estimation of the secondary structure of the protein.
The THz (1 THz = 1012 Hz ∼ 300 μm ∼ 33.3 cm−1) wave, which lies in the frequency gap between the infrared and microwave, typically covers from 0.1 THz to 10 THz. Remarkable progress in low scale semiconductor and ultrafast optoelectronic techniques, THz-TDS presents great potential as a powerful tool for structural identification based on the unique resonant properties that materials exhibit in the THz frequency range.21–30 THz spectra offer structural information that results from intramolecular interaction, intermolecular interaction or coupling of these interactions that are not accessible at other wavelengths. Therefore, THz-TDS is advantageous over other methods in probing low frequency collective modes associated with non-local vibrations and conformation, giving the opportunity to study the secondary structure of a protein where a number of atoms move in a concerted fashion. Previous investigations have confirmed that some amino acids with definite structures exhibit “fingerprint” characteristics in the THz regime corresponding to functionally relevant, collective modes with periods on the picosecond timescale.31,32 Therefore we try to investigate the conformation of native silk proteins using THz-TDS.
In this work, fibroin membrane obtained from Bombyx mori cocoons is employed as an ideal system model for the investigation on conformational transition of native protein. Both FTIR and THz-TDS measurements were performed on the prepared fibroin membranes. In addition, theoretical simulation based on density function theory (DFT) was also carried out on three dominant dipeptides to attempt to partially interpret the absorption features arising from intramolecular modes.
2 Experimental
2.1 Chemicals and materials
All chemicals used in this study were purchased from Aladdin, which were of analytical grade and used without any further purification. Cocoons were kindly provided by the Bombyx mori breeding base located in Zhejiang province.2.2 Sample preparation
Bombyx mori cocoons were cut into pieces and then boiled in a 0.02 M aqueous solution of sodium carbonate for 60 min to remove sericin. It is necessary to go on with this process until the sericin is completed degummed. The remaining fibroin fibers were then rinsed three times in distilled water, dried in an oven, and dissolved in an mixed solution system of CaCl2–CH3CH2OH–H2O (mole ratio: 1/2/8) at 70 °C for 0.5 h. Subsequent dialysis in distilled water extracted the salt from the solution, and centrifugation followed by filtration eliminated particles to yield 8–10% w/v silk fibroin solution with minimal contaminants. Typical pH values range from 6.5–7.5. Casting the resulting fibroin solution onto flat piece of polyethylene substrate yielded uniform membranes of approximately 0.9 mm thickness, and this was left to dry overnight in ambient conditions. As in the method reported by M. Tsukada,33 three representative kinds of fibroin membranes with different conformational ratios were prepared by the process of immersion in different methanol–water systems. All samples were dried and used for experimentation within a 24 h period after both casting and processing.2.3 FTIR and THz measurements
As the prepared samples were membranes of a certain thickness, that can meet the requirements of FTIR and THz, measurements were easily performed on them without further processing.For FTIR measurements, as a conventional method, the absorption features were recorded using a Nicolet 5700 FTIR spectrometer over the range of 1800–1200 cm−1, with a resolution of 4 cm−1, and averaged over 32 scans.
For THz measurements, the THz-TDS used in this paper is described elsewhere,34 THz spectra were measured under a nitrogen atmosphere with a spectral resolution of 40 GHz and bandwidth between 0.5 and 2.6 THz. All the measurements were operated at room temperature, the whole testing system was located in an airtight enclosure to mitigate the effects of water vapor on the THz beams, and the relative humidity was kept lower than 0.1%. In this paper, three repeated measurements were performed on each sample, we confirm that three spectra for one sample present the same peak location although the peak intensity varies slightly. So, each THz spectrum presented in this work is the average of three individual THz spectra, each representing a complete set of samples.
2.4 Data processing
In aiming to extract optical information from the time-domain data, the theory put forward by T. D. Dorney and L. Duvillaret is employed to calculate the absorption spectra.35,36 During the analysis of transmission spectrum, measurement through pure nitrogen is employed as a reference, samples information can be subsequently calculated by the complex transmission function “T(ω)” which is from the comparison between signal spectrum and reference spectrum. “T(ω)” is the function of complex refractive index N = n + ik, where “n” is the factual refractive index and “k” is the extinction coefficient, which stands for chromatic dispersion and absorption characteristics, respectively. The complex transmission function presents as the following equation: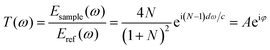 | (1) |
In view of the weak absorption for biomaterials, the refractive index “n(ω)” and absorption coefficient “α(ω)” can be approximately calculated as the following equations:
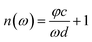 | (2) |
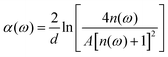 | (3) |
2.5 Theoretical calculation
The rapid development of computer power and efficient quantum-chemical theory has allowed for the assignment of observed THz absorption peaks to be increasingly reliable. In this present paper, the aim to partially interpret the spectral features originating from intramolecular modes, calculations on three dominant dipeptides of silk fibroin were performed by the Linearity Combination of Atomic Orbital (LCAO) method. Density Functional Theory was used to determine the ground-state structures and harmonic vibrational frequencies of the samples. The B3LYP was carried out with the 6-311+G(d, p) Gaussian type basis set and program option “tight” convergence criteria. Quantum chemical calculations with full geometry optimization and frequency analysis of the optimized structures were performed using the GAUSSIAN 03 program package.3 Results and discussion
3.1 FTIR spectra
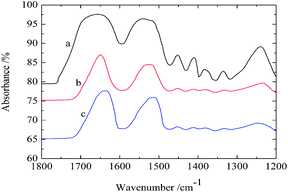
Three kinds of representative fibroin membranes with different conformational proportions obtained from Bombyx mori cocoons are employed as an ideal system model for the investigation of the conformational transition of native proteins. Prior to THz measurements, FTIR determinations were performed as a conventional method to predict the conformational proportion of prepared samples. Fig. 1 shows that the amide I bands present significantly different spectral features corresponding to different processing conditions, which can also be verified in band II and band III. The deconvolving method was introduced in this paper to quantitatively estimate the conformational ratio in the amide I region.10 This method can provide an approximate percentage for each kind of conformation, although this brings some subjective influence to the results. The calculated results (Fig. 2) show that fibroin membrane processed by 60% methanol solution presents the highest percentage of antiparallel β-pleated sheet. The reason is that hydrogen bonds between peptide chains are broken and reconstructed while water and methanol molecules are introduced into the fibroin membrane, which leads to conformational transition from random coil or α-helix to antiparallel β-pleated sheet. In addition, the synergistic effect of water and methanol on the reconstruction is stronger than that of pure methanol.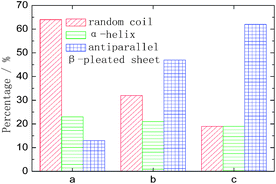 | ||
| Fig. 2 The amount of conformation that derived from amide I band by the deconvolving method. The meanings of a, b and c are identical to those used in Fig. 1. | ||
3.2 Theoretical analysis
As there is no available crystal structure for native fibroin, it is tremendously difficult to reproduce the intermolecular modes of this complex biomolecule through normal theoretical simulation.37–39 However, in silk fibroin, most of combination modes of amino acids exist in the following three forms, glycine-alanine, glycine-serine, glycine-tyrosine. Therefore, DFT performance on these dipeptides can be employed as an effective way to partially interpret the intramolecular modes.It can be seen from Fig. 3 that three dipeptides present distinct features arising from intramolecular resonances, which are primarily located in the range above 2.0 THz except 1.12 THz for glycine-serine. Besides, representations of the corresponding resonant modes with displacement vectors are given in Fig. 4. These intramolecular modes are delocalized and involve most of the atoms as a whole, unlike the mid-IR vibration modes involving localized pendant group motions of the molecule. Although the intermolecular modes are not taken into account in this calculation, simulation on the basic units of native fibroin do provide the opportunity to understand partial vibrations arising from intramolecular modes.
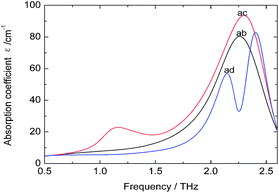 | ||
| Fig. 3 Theoretical spectra of dipeptides at THz region. Dipeptides: glycine-alanine (ab), glycine-serine (ac) and glycine-tyrosine (ad). | ||
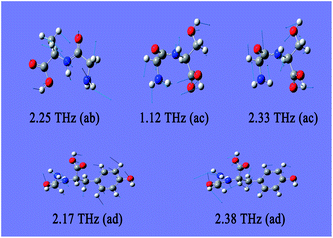 | ||
| Fig. 4 Resonant modes of dipeptides in the THz region. The meanings of ab, ac and ad are identical to those used in Fig. 3. | ||
3.3 THz spectra
The characteristic absorption features of fibroin membranes in the range of 0.5–2.6 THz were obtained by THz-TDS, with THz signal transmitting through the nitrogen as the reference waveform for the samples. It can be clearly seen from Fig. 5 that three samples present significantly different absorption features in the range of 1.3–2.0 THz, while the same characteristics are shared in the frequency region beyond 2.0 THz. According to the theoretical calculation for the basic units of native fibroin (Fig. 3), the experimental absorption features in the region of 2.0–2.6 THz may be associated with the intramolecular resonant modes of dipeptides, which means that the calculated results do interpret partial features though it can not completely reproduce the whole spectra. It can be further inferred that conformational responses to the THz wave originate from intermolecular modes that are not observed in the theoretical simulation on dipeptides. According to the conformational percentage estimated in Fig. 2, it can be found that the intensity change of absorption peaks ranging from 1.3 to 2.0 THz is coincident with conformational transition. Specifically, the band centered at 1.84 THz is associated with random coil, another band located around 1.55 THz corresponds to antiparallel β-pleated sheet, and the band between them is attributed to α-helix. In addition, a weak peak emerges at 1.44 THz with the increase of antiparallel β-pleated sheet. This aims to further verify the assignment of the three dominant spectral features, quantitative analysis based on peak fitting is shown in Fig. 6. The ratio of amounts of random coil, α-helix, antiparallel β-pleated sheet obtained from THz spectra agree well with that from FTIR. Therefore, THz spectra present great potential as a powerful tool in studying the conformational structure of silk fibroin.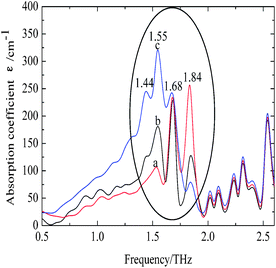 | ||
| Fig. 5 THz spectra of silk fibroin membranes. The samples of a, b and c are identical to those used in Fig. 1. | ||
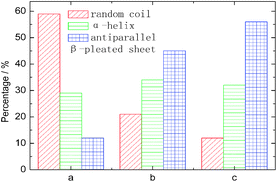 | ||
| Fig. 6 The amount of conformation derived from THz spectra by deconvolved method. The meanings of a, b and c are identical to those used in Fig. 5. | ||
4 Conclusion
In conclusion, coupled with conventional FTIR, THz-TDS has been demonstrated to be an effective method to study the conformational transition of native silk fibroin. Compared to conventional FTIR, THz spectra can directly provide distinct features for each kind of conformation with narrower bandwidth. In terms of the origin of THz spectra for silk fibroin, three bands located at 1.84 THz, 1.68 THz, 1.55 THz are attributed to random coil, α-helix, antiparallel β-pleated sheet, respectively, while the features above 2.0 THz may be associated with the intramolecular resonant modes of the peptide chain. Owing to the outstanding sensitivity obtained, THz-TDS can be employed as a powerful tool for various studies involving conformational transition of native proteins.Acknowledgements
The authors would like to acknowledge the financial support provided by the Scientific Research Innovation Fund in Zhejiang Province (YK2011055), the Science and Technology Plan Projects of AQSIQ (2011IK092), as well as an open project of the Key Laboratory of Terahertz Optoelectronics at Capital Normal University.References
- Z. Z. Shao and F. Vollrath, Nature, 2002, 418, 741 CrossRef CAS PubMed.
- T. Hu, J. J. Amsden, A. C. Strikwerda, K. Fan, D. L. Kaplan, X. Zhang, R. D. Averitt and F. G. Omenetto, Adv. Mater., 2010, 22, 3527–3531 CrossRef PubMed.
- H. J. Jin, J. S. Chen, V. Karageorgiou, G. H. Altman and D. L. Kaplan, Biomaterials, 2004, 24, 1039–1047 CrossRef.
- B. Panilaitis, G. H. Altman, J. Chen, H. J. Jin, V. Karageorgiou and D. L. Kaplan, Biomaterials, 2003, 24, 3079–3085 CrossRef CAS.
- Y. Liu, Z. Z. Shao and F. Vollrath, Nat. Mater., 2005, 4, 901–905 CrossRef CAS PubMed.
- N. J. Greenfield, Nat. Protoc., 2006, 1, 2876–2890 CrossRef CAS PubMed.
- W. C. Johnson, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 145–166 CrossRef CAS PubMed.
- L. Whitmore and B. A. Wallace, Biopolymers, 2007, 89, 392–400 CrossRef PubMed.
- K. Eckert, R. Grosse, J. Malur and K. R. H. Repke, Biopolymers, 1977, 16, 2549–2563 CrossRef CAS PubMed.
- D. M. Byler and H. Susi, Biopolymers, 1986, 25(2), 469–487 CrossRef CAS PubMed.
- A. Dong, L. S. Jones, B. A. Kerwin, S. Krishnan and J. F. Carpenter, Anal. Biochem., 2006, 351, 282–289 CrossRef CAS PubMed.
- W. K. Surewicz, H. H. Mantsch and D. Chapman, Biochemistry, 1993, 32, 389–394 CrossRef CAS.
- X. Chen, Z. Z. Shao, N. S. Marinkovic, L. M. Miller, P. Zhou and M. R. Chance, Biophys. Chem., 2001, 89, 25–34 CrossRef CAS.
- X. X. Feng, Y. H. Guo and J. Y. Chen, J. Biomater. Sci., Polym. Ed., 2007, 18, 1443–1456 CrossRef CAS PubMed.
- H. Saito, R. Tabeta, T. Asakura, Y. Iwanaga, A. Shoji, T. Ozaki and I. Ando, Macromolecules, 1984, 17, 1405–1412 CrossRef CAS.
- T. Asakura, K. Ohgo and K. Komatsu, Macromolecules, 2005, 38, 7397–7403 CrossRef CAS.
- T. Asakura, H. Suzuki and Y. Watanabe, Macromolecules, 1983, 16, 1024–1026 CrossRef CAS.
- T. Asakura, T. Watanabe, A. Uchida and H. Minagawa, Macromolecules, 1984, 17, 1075–1081 CrossRef CAS.
- P. Zhou, X. Xie, D. P. Knight, X. H. Zong, F. Deng and W. H. Yao, Biochemistry, 2004, 43, 11302–11311 CrossRef CAS PubMed.
- M. E. Rousseau, L. Beaulieu, T. Lefevre, J. Paradis, T. Asakura and M. Pezolet, Biomacromolecules, 2006, 7, 2512–2521 CrossRef CAS PubMed.
- O. Esenturk, A. Evans and E. J. Heilweil, Chem. Phys. Lett., 2007, 442, 71–77 CrossRef CAS PubMed.
- J. Xu, K. W. Plaxco, S. J. Allen, J. E. Bjarnason and E. R. Brown, Appl. Phys. Lett., 2007, 90, 031908 CrossRef.
- Z. Yan, D. Hou, P. Huang, B. Cao, G. Zhang and Z. Zhou, Meas. Sci. Technol., 2008, 19, 015602 CrossRef.
- C. T. Konek, B. P. Mason, J. P. Hooper, C. A. Stoltz and J. Wilkinson, Chem. Phys. Lett., 2010, 489, 48–53 CrossRef CAS PubMed.
- A. Arora, T. Q. Luong, M. Kruger, Y. J. Kim, C. H. Nam, A. Manz and M. Havenith, Analyst, 2012, 137, 575–579 RSC.
- J. E. Bjarnason, T. L. J. Chan, A. W. M. Lee, M. A. Celis and E. R. Brown, Appl. Phys. Lett., 2004, 85, 519–521 CrossRef CAS.
- A. D. Burnett, W. Fan, P. C. Upadhya, J. E. Cunningham, M. D. Hargreaves, T. Munshi, H. M. Edwards, E. H. Linfield and A. G. Davies, Analyst, 2009, 134, 1658–1668 RSC.
- A. R. Sanchez, G. Salvatella, R. Galceran, E. Roldos, J. G. Reguero, M. Castellari and J. Tejada, Analyst, 2011, 136, 1733–1738 RSC.
- Q. L. Zhou, C. L. Zhang, K. J. Mu, B. Jin, L. L. Zhang, W. W. Li and R. S. Feng, Appl. Phys. Lett., 2008, 93, 101106 CrossRef.
- C. J. Strachan, T. Rades, D. A. Newnham, K. C. Gordon, M. Pepper and P. F. Taday, Chem. Phys. Lett., 2004, 390, 20–24 CrossRef CAS PubMed.
- I. Dunayevskiy, B. Bortnik, K. Geary, R. Lombardo, M. Jack and H. Fetterman, Appl. Opt., 2007, 46, 6161–6165 CrossRef CAS.
- K. Yamamoto, K. Tominaga, H. Sasakawa, A. Tamura, H. Murakami, H. Ohtake and N. Sarukura, Biophys. J., 2005, 89, 22–24 CrossRef PubMed.
- M. Tsukada, Y. Gotoh, M. Nagura, N. Minoura and G. Freddi, J. Polym. Sci., Part B: Polym. Phys., 1994, 32, 961–968 CrossRef CAS.
- C. Yan, B. Yang and Z. C. Yu, Anal. Lett., 2013, 46, 946–958 CrossRef CAS.
- T. D. Dorney, R. G. Baraniuk and D. M. Mittleman, J. Opt. Soc. Am. A, 2001, 18, 1562–1571 CrossRef CAS.
- L. Duvillaret, F. Garet and J. L. Coutaz, Appl. Opt., 1999, 38, 409–415 CrossRef CAS.
- M. D. King, W. D. Buchanan and T. M. Korter, Anal. Chem., 2011, 83, 3786–3792 CrossRef CAS PubMed.
- S. P. Delaney, D. Pan, M. Galella, S. X. Yin and T. M. Korter, Cryst. Growth Des., 2012, 12, 5017–5024 CAS.
- M. D. King, W. Ouellette and T. M. Korter, J. Phys. Chem. A, 2011, 115, 9467–9478 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |