Estimating sampling uncertainty – how many duplicate samples are needed?

Abstract

A knowledge of the measurement uncertainty arising from sampling is crucial for the rational design of sampling programmes and the interpretation of their outputs (AMC Technical Briefs No 16, 2008). Usually the principal source of uncertainty is the lack of homogeneity (either spatial or temporal) in the object of sampling – the sampling target. Other sources of variation—the analytical and sampling processes—are also important.

---

This Technical Brief concentrates on these sources of variation, the estimation of the corresponding uncertainties, and the reliability of these estimates. An evaluation of the magnitude of heterogeneity of the sampling target is valuable because it facilitates the design of a sampling strategy of appropriate power and leads to the best use of sampling and analytical resources. Lack of such knowledge could lead to effort wasted in addressing minor sources of variation whilst more important ones are neglected.

How target heterogeneity and sample size interact

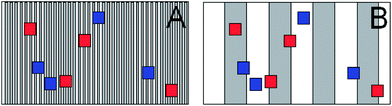
Fig. 1 below illustrates schematically the variation in targets and samples, in space (for static targets) or in time (for flowing targets). It shows how the coarseness of the heterogeneity influences the way that variation might be observed within and between individual samples. The striped rectangles represent areas to be assessed for contamination, i.e., different sampling targets. The dark and light stripes in each rectangle indicate regions of high and low contamination respectively. Superimposed on each sampling target are duplicated samples each comprising four increments, which are portions of the target taken at random positions within the sampling target to make up the composite sample. These increments are indicated by the coloured squares, the size of which suggests the relative size of the increment.

Fig. 1 Schematic effect of target heterogeneity on sampling uncertainty. Target A has fine structure, while Target B has coarser structure. Grey and white bars indicate regions of high and low concentration of contaminant. Duplicate samples each comprising four randomly-placed increments are shown as squares, coloured red (first sample) and blue (second sample). A greater between-sample (within target) variation with the same pattern would be evident in the coarser target.

Next consider the level of agreement between duplicate samples from the same target. Case A indicates target heterogeneity on a fine scale – in this situation the differences between duplicate composite samples are (on average) small, because the increments tend towards an average contamination. In Case B—heterogeneity on a coarser scale—there is a greater potential for duplicate samples to encompass areas of either high or low contamination, tending towards larger within-sampling uncertainty. Differences between duplicate samples would here range from small to potentially large, but greater on average than in Case A. Note also that the sample size—indicated on the diagram by the size of increments—influences the perception of local heterogeneity. As the size of sampling footprint increases in relation to the true scale of variation, the effect of local heterogeneity will tend to decrease.

Perception and estimation of uncertainty

The main issues emerge in a concrete form in the following example. Suppose that the aim of a particular investigation is to determine the concentration of zinc in an effluent discharge over a period of a year. The interest is in both the average value and the variability of zinc concentration. We can focus on variability, since monitoring programmes that are adequate to determine variability automatically provide a sound assessment of average value. We can identify three sources of variation, arising from (a) the imprecision of analysis, (b) uncertainty from sampling (UfS) and (c) the variation in the effluent composition itself. Imprecision of analysis is expressed as the dispersion of the results when identical test portions are analysed. UfS is expressed as variation in the composition of samples taken at nominally the same place and time (i.e., within a single target), but with due regard to randomisation. Variation in the results from separate sampling events (e.g., on different days) is simply the target-to-target variation. All of these can be estimated together in a single experiment as part of the study of UfS simply by duplication of both sampling and analysis on a succession of targets, followed by analysis of variance (ANOVA).

Estimating the uncertainty components

This leads us to the question of how best to design the experiment, how to evaluate the overall measurement uncertainty associated with different possible monitoring strategies and to interpret their outcomes. Such preliminary estimates are of great value in determining the optimum approach to sampling, for instance whether to visit the effluent discharge many times during the year, or to visit less frequently and take more samples on each occasion.

In our example, the measurand is the average zinc concentration of the sampling target (in this example, the ‘target’ is the total quantity of effluent considered during a particular sampling event). The best approach to the evaluation of UfS—in the absence of prior knowledge about the underlying heterogeneity of the effluent—is to take a number (N) of duplicate effluent samples, say one pair of samples on each of N days spread out though the year (note that it is assumed for the sake of this example that there are no systematic changes in the measurand or the quality of sampling and measurement over the period of the investigation). Duplicate effluent samples are taken on the same day: practicality in visiting the sampling site means that the sampling procedure is effectively assigned this timescale. The aim then would be to analyse each sample in duplicate.¹ This number N of sampling events, in this example visits to the effluent discharge point, is critical in determining the confidence interval around the uncertainty estimates and the overall cost of the operation; the higher the value of N, the better the estimate of UfS, but also the greater the effort and the higher the cost.

Once the data are assembled, nested analysis of variance can then be used to separate the effects of the three variable factors—analytical, sampling, and day-to-day changes in the effluent—expressed as standard deviations s_a, s_s, s_d respectively. These estimates can then be combined to give the uncertainty of the chosen sampling programme.

Reliability of estimates of components of variability

The question that remains involves the choice of the number N and the consequent reliability of each standard deviation value. Table 1 shows the 5th and 95th percentiles for estimates of each standard deviation in simulations in which the true values of s_a, s_s and s_d were known. It was assumed that analytical and sampling variations were normally distributed and day-to-day variation was lognormal (of course, different situations might justify alternative assumptions). A single estimate of each level of variability using N samples (as indicated in the tables) could be expected to lie in the corresponding confidence interval with a probability of 0.9. The main points to emerge from evaluations of the power of tests of this type to determine variability are:

Table 1 Ranges (5–95%) of estimates of relative standard deviation (RSD) – the standard deviation expressed as a percentage of the mean

Example 1	RSD (percent)
True RSD	Analytical	Sampling	Between-target
%	5%	10%	15%
Number of samples N	Observed range	Observed range	Observed range
2	2.1–7.6	0.0–18.0	0.0–31.6
4	2.9–6.9	2.9–15.9	0.0–26.3
8	3.5–6.4	5.1–14.3	4.9–23.0
12	3.8–6.2	6.0–13.7	7.2–21.5
24	4.1–5.8	7.3–12.6	7.2–21.5
48	4.4–5.6	8.1–11.8	7.3–21.5

---

Example 2	RSD (percent)
True RSD	Analytical	Sampling	Between-target
%	1%	10%	10%
Number of samples N	Observed range	Observed range	Observed range
2	0.4–1.5	2.2–17.6	0.0–23.0
4	0.6–1.4	4.2–15.5	0.0–18.7
8	0.7–1.3	5.8–14.0	0.0–16.1
12	0.8–1.2	6.6–13.4	1.2–14.9
24	0.8–1.2	7.6–12.3	2.7–14.8

---

• the confidence interval associated with estimates of uncertainty can be wide, even for a relatively large number of targets (N).

• The three sources of variation interact to affect the range of estimated values. The smaller the variance low in the hierarchy (from analytical upwards), the more precise the estimate of the next higher variance. Specifically, excellent analytical precision gives a smaller confidence interval in s_s. Good precision in analysis and relatively low s_s are both needed for precise determination of s_d. This makes it clear that to determine the components of sampling uncertainty it is important to use as precise a measurement technique as might be available—even if it is not intended to use this technique for routine analysis. Also, the estimation of sampling uncertainty using a measurement technique that has a high relative standard deviation (say >10%, a value which is not uncommon for some trace analytical techniques), may produce measured values of uncertainty from sampling that themselves have an unacceptably large confidence interval.

• A value of N less than 8 gives fairly imprecise estimates of uncertainty. Given the fact that 4N analyses are required, a value of N larger than about 12 not only leads to escalating costs of testing, but also yields diminishing returns with respect to the precision of the estimates of uncertainty that are obtained. This suggests that N in the range 8 to 12 is likely to be a reasonable choice, in the absence of data to the contrary.²

Caution : Valid interpretation of this type of experiment depends on assuming a reasonably uniform analytical precision and between-sampling precision, from target to target. If successive targets vary widely in composition this assumption may not be justifiable, in which case a more complex statistical approach would be required, and expert advice should be sought.

Conclusions

Randomly duplicated experiments in sampling provide the information needed for the optimal design of a monitoring programme. The optimal number of successive targets to be sampled in such a study probably lies in the range 8 to 12. However, it is essential that the distinctions between (a) the sampling target, (b) the random sample, and (c) the increments that comprise the sample, are clear from the outset.

M J Gardner [Atkins Limited]

This Technical Brief was written on behalf of the Subcommittee for Uncertainty from Sampling (Chair M H Ramsey) and approved by the Analytical Methods Committee on 23.10.13.

References

1. M. H. Ramsey and A. Argyraki, Estimating measurement uncertainty from field sampling: implications for the classification of contaminated land, Sci. Total Environ., 1997, 198, 243–257.
2. J. A. Lyn, M. H. Ramsey, S. Coad, A. P. Damant, R. Wood and K. A. Boon, The duplicate method of uncertainty estimation: are eight targets enough?, Analyst, 2007, 132, 1147–1152.

---