Random samples

Abstract

Chemical analysis is undertaken to help us make decisions about particular masses of a test material. Does this shipment of peanuts fall within the permitted limit for the concentration of aflatoxins? What should I pay for this batch of tin ore? How much phosphate fertiliser should I apply to this field? Can we release today's effluent stream into the river? Is the iridium content of this geological layer higher than that of the adjacent beds? In instances like these we need information about a large amount of test material (the target), but we can only remove for analysis a much smaller amount, the sample.

---

Analysts stress that this sample must be ‘representative’ of the target, but what does that really mean? When we are sampling a discrete amount of finely-divided, well-mixed, single-phase powder, representation does not pose a problem. But many targets, especially raw materials, are multi-phase, coarsely grained and heterogeneous at many scales. How do we approach getting a representative sample in such an instance? There are two key requirements. The sampling should be as far as possible unbiased, and the between-sample precision should be sufficiently good.

The meaning of sampling bias

Bias is the systematic aspect of a sampling procedure. It is the difference between the mean of the compositions of a large number of samples from a target and the composition of the target itself. Of course we don't know the true composition of the target—that's why we take a sample—but we do know how to reduce bias to an acceptable level: either the sampling procedure or the target itself must be randomised. Think of the target as being partitioned into a very large number of very small cells by imaginary walls. To take an unbiased sample, each cell must have an equal probability of being selected to be part of the sample. Real-life sampling inevitably falls short of this ideal, but randomness is the key to getting an unbiased sample.

Random and systematic sampling patterns

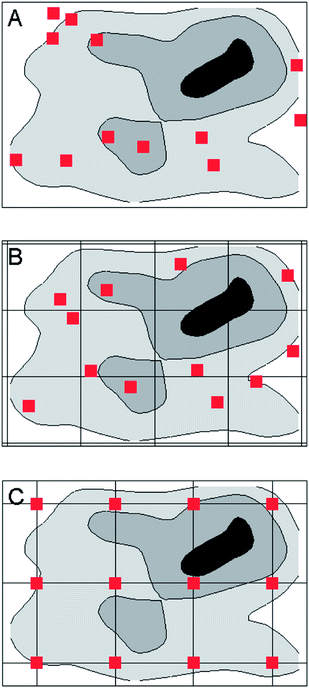
Target types are legion and varied in nature, so it is always difficult to generalise about sampling practice. We have to fall back on specific examples to establish the principles. But for important types of material there are established sampling protocols that are widely regarded as acceptable practice. Most protocols aiming for a representative sample require the collection of a number of increments, small portions of the test material taken from different parts of the target and then combined to make the primary sample, in such instances called a composite or aggregate sample. We can illustrate the notion by considering increments disposed in two dimensions, as might be used for sampling say topsoil in a field or a product in a flattened heap. Let's look at the possible arrangement of the increments.

A randomised scheme for a roughly rectangular target might look something like Fig. 1A. The distances of the increments from a fixed point, in two perpendicular directions, are taken at random. In contrast a completely systematic plan can be seen in Fig. 1C, where the increments are collected at the intersections of a rectangular grid. A compromise scheme is stratified random sampling, in which the increments are placed at random within regular segments (strata) of the target (Fig. 1B). The strata could be purely notional, as when created by the imaginary partitioning of the surface of a large field, or real, as when a product is delivered in a number of discrete containers. Targets that are flowing, such as material on a conveyor belt or water in a culvert, are essentially one dimensional and are handled by taking increments at regular, randomly spaced, or stratified time intervals as appropriate.

Fig. 1 Schematic of possible arrangements of increments in sampling a target showing an underlying pattern of heterogeneity (shades of grey). Increments are taken at points (red squares) within the target: (A) at random locations; (B) at stratified random points, with the lines defining the strata; (C) at the intersections of a rectangular grid.

The pros and cons of randomisation

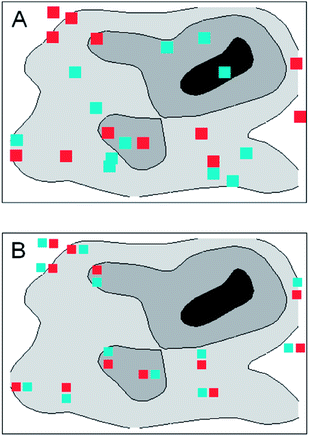
Do randomly placed increments have any real advantage over systematic patterns? It depends on the nature of the target. In Fig. 1A the random placing shown has by chance no increment in the ‘hotspot’ (the black area on the map) and is therefore likely to provide a sample with a lower-than-average result. But if the random sampling were replicated, some samples would have increments in the hotspot (one such can be seen in Fig. 2A). The results from successive samples will clearly vary, some higher and some lower than the mean composition of the target, but the randomised procedure produces an unbiased sample, meaning that on average the samples have the same composition as the target.

Fig. 2 Schematic of duplicate sampling of a target, showing increment points for the first sample (red squares) and second sample (cyan squares). (A) The increments of both samples are at random locations. (B) The increments of the second sample are located systematically close to those of the first sample.

If the target itself can be randomised, say by grinding and mixing, a systematic pattern will produce an effectively random sample. This is sometimes an acceptable expedient in practice, and is often simpler to execute than sampling on a random basis. If the target is systematically structured, however, perhaps through a peculiarity of the production process, and further, that the target structure is fortuitously correlated with the pattern of increments, the sample would be biased. In the systematic sampling shown in Fig. 3 the sample would provide a biased result whereas a random scheme would not. Sometimes a systematic pattern will meet our needs, but that cannot be taken on trust—if used it should be regularly tested. Only a randomised scheme is guaranteed to provide an unbiased sample.

Fig. 3 Schematic diagram of one-dimensional sampling of a moving target with periodically-variable contamination (black dots). The increments (red rectangles) are systematically-spaced but collected in the areas of low contamination. In such an instance the sample would be biased and underestimate the mean level of contamination.

But an unbiased sample is not automatically representative. We have seen that, in replicated randomised sampling of a single target, successive samples will have different compositions. This leads to a modern concept of representative, namely that the between-sample variation from random samplings has to be sufficiently small in relation to an appropriate fitness-for-purpose criterion.

Sampling precision

How do we address between-sample precision? Such studies, either in method validation or in quality control, call for properly randomised duplicated sampling (and indeed duplicated analysis) on a number of typical targets. This can be addressed simply by collecting a second set of increments at new random positions within each target (Fig. 2A). If the increments for the second sample were collected systematically very close to those of the first sample (Fig. 2B) the duplicate samples would be very similar and, as a consequence, the between-sample precision would be seriously underestimated. For random duplication in a stratified scheme, the second increment is collected at a new random position within each stratum. Oddly enough, a systematic way of placing increments may be duplicated randomly: with grids, for example, a second grid could be set up with a new origin and orientation, both selected at random.

(Note. In the examples used here, all sampling points refer to increments. In other instances, intersections of sampling grids may define the centres of separate targets within a larger study area. In the latter case, duplicated targets might legitimately be closely spaced so that within-target uncertainty would be forced to reflect surveying inaccuracy.)

Conclusions

Randomness (either of the sampling or of the target) is an essential ingredient of sampling if a representative sample is the aim. But randomness is not enough: representation is a matter of degree, as no sample has the exact average composition of the target. It's simply a question of whether the discrepancy is acceptably small. The degree to which an unbiased sample represents a target is quantified as between-sample precision and largely determined by the size and number of the increments and the heterogeneity of the target. We need to know this precision to check that our sampling is fit for purpose, and we need randomness to estimate it.

This Technical Brief was written on behalf of the Subcommittee for Uncertainty from Sampling (Chair Prof M. H. Ramsey) and approved by the Analytical Methods Committee on 21/02/14.

---