Biophysical properties of nucleic acids at surfaces relevant to microarray performance
Archana N.
Rao
a and
David W.
Grainger
*ab
aDepartment of Pharmaceutics and Pharmaceutical Chemistry, University of Utah, Salt Lake City, UT 84112, USA
bDepartment of Bioengineering, University of Utah, Salt Lake City, UT 84112, USA. E-mail: david.grainger@utah.edu
First published on 14th February 2014
Abstract
Both clinical and analytical metrics produced by microarray-based assay technology have recognized problems in reproducibility, reliability and analytical sensitivity. These issues are often attributed to poor understanding and control of nucleic acid behaviors and properties at solid–liquid interfaces. Nucleic acid hybridization, central to DNA and RNA microarray formats, depends on the properties and behaviors of single strand (ss) nucleic acids (e.g., probe oligomeric DNA) bound to surfaces. ssDNA's persistence length, radius of gyration, electrostatics, conformations on different surfaces and under various assay conditions, its chain flexibility and curvature, charging effects in ionic solutions, and fluorescent labeling all influence its physical chemistry and hybridization under assay conditions. Nucleic acid (e.g., both RNA and DNA) target interactions with immobilized ssDNA strands are highly impacted by these biophysical states. Furthermore, the kinetics, thermodynamics, and enthalpic and entropic contributions to DNA hybridization reflect global probe/target structures and interaction dynamics. Here we review several biophysical issues relevant to oligomeric nucleic acid molecular behaviors at surfaces and their influences on duplex formation that influence microarray assay performance. Correlation of biophysical aspects of single and double-stranded nucleic acids with their complexes in bulk solution is common. Such analysis at surfaces is not commonly reported, despite its importance to microarray assays. We seek to provide further insight into nucleic acid-surface challenges facing microarray diagnostic formats that have hindered their clinical adoption and compromise their research quality and value as genomics tools.
1. Introduction
Nucleic acid microarray technology enables gene expression profiling for thousands of genes in parallel in a single assay.1 Information from DNA microarray-based assays is used in genotyping,2 DNA–protein interactions,3 genome sequencing,4 pharmacogenomics and drug discovery,5 infectious and genetic disease,6 cancer diagnostics,7 forensic and genetic identification,8 toxicology9 and many other applications. Though a powerful high-throughput tool with assorted applications, microarray analytical accuracy and assay reliability in assessing clinical samples, producing analyte quantitation and in clinical decision-making is questionable.10 Data analysis and interpretation have provided unique challenges and “the transition from bedside to bench to bedside” has been slower than expected due to various pitfalls in using its diagnostic and prognostic insights.11 Despite common perceptions otherwise, only four FDA-approved microarray based diagnostics are currently marketed for clinical decision guidance.12 Requirements for assay standardization and validation for each microarray experimental step, emphasizing quality control protocols in array fabrication, scanner calibration and data verification, have proven difficult to surmount. The USA FDA's initiative of Microarray Quality Control I, II and III (MAQC) consortia are charged with identifying and assessing critical factors affecting array data quality, and to optimize and standardize microarray assay and analytical procedures.13 This effort has focused on resolving procedural discrepancies and improving assay and data repeatability and reproducibility among various array platforms, but has not yet effectively addressed several fundamental root causes of assay variability issues.14,15Despite the various dimensions to this assay problem, at their basis commonly lies the understanding of biophysical aspects of short single-strand nucleic acids as surface-immobilized probes, and their resulting behavior at surfaces in producing hybridization with target analytes. Certainly improved bioinformatics and biostatistics for assessing target capture data and accurate signal interpretation remain critical to yielding meaningful, relevant medical outcomes.16–18 Nonetheless, a first-principles perspective of DNA properties at surfaces and its central control of the molecular interactions controlling these data is important to guide array fabrication and assay design. Table 1 summarizes some major obstacles facing the successful design of improved DNA microarrays. Many of these challenges rely on a basic understanding and ability to exert some control over the molecular “disposition” of single ssDNA strands immobilized on assay surfaces to promote target binding – on various commercial surfaces, different printing milieus, drying conditions, hybridization buffers and assay compositions.
| Microarray methods | Major challenges | References |
|---|---|---|
| Microarray design | Addressing the biological question with selection of proper controls, fiduciary markers, internal calibrations, quality controls | 26, 264, 265 |
| Experimental processing | Probe immobilization, target preparation from complex milieu and reliable hybridization, sample-to-answer time efficiencies, signal: noise challenges | 1, 17, 21 |
| Data extraction | Assay (e.g., fluorescence) signal translation for quantification of gene of interest, absolute abundance correlations, reliable quantitation, platform-platform correlation | 266–269 |
| Data analysis and modeling | Standardized, validated bioinformatics and biostatistics algorithms | 270–272 |
| Data repeatability and reproducibility | MAQC-I, -II and -III-identified optimization, reliability, intra- and inter-platform reproducibility issues | 13, 273, 274 |
| Limited database access | Access to web-based data-mining platforms aimed at facilitating discovery from genome-wide expression analyses | 10, 275, 276 |
Recent technological advances, new analytical methods and sophisticated experimental tools such as optical (e.g., fluorescence methods), surface analytical and molecular force approaches have yielded new information on the dynamic behaviors and properties of nucleic acids, both in bulk states and on surfaces. Parameters regarding ssDNA molecular conformations, structural transitions and dynamics at nanometer scales and in short (i.e., millisecond) time frames, provide data for ssDNA relevant to understanding certain behaviors on microchips and array surfaces. Additionally, new in silico computational models, molecular dynamics simulations, and software tools have produced correlations with experimental data as well as accuracy in predicting certain ssDNA structural phenomena. While simulations and modeling are recognized to have some discrepancies with experimental data, they should now be more capable of providing valuable insight into understanding certain, relevant biophysical properties.19
2. Microarray design and fabrication
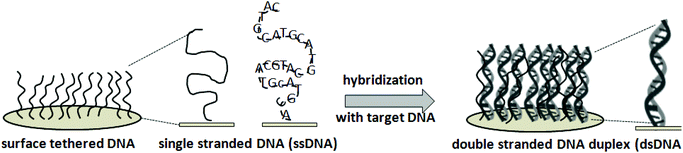
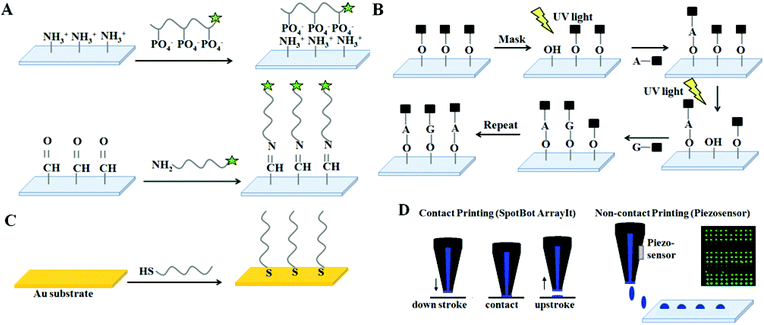
The nucleic acid microarray strategy exploits surface-tethered complementary oligonucleotides on solid supports – often dense-packed, surface-grafted, immobilized, adsorbed or printed short nucleotide ensembles – to capture targeted complementary nucleotides from a sample via hybridization. Fig. 1 shows general schematics for the working principles behind the DNA microarray design. Synthetic ssDNA assay probes are typically short (i.e., usually 20–70, up to 200 bases). Probe immobilization at a solid–liquid interface, typically involving droplet printing and subsequent rapid evaporation at a solid–air interface, produces a unique dried tethered state for ssDNA not found naturally. These unconventional immobilization and processing steps with an unusual synthetic ssDNA construct, and resulting ssDNA surface microenvironments, all profoundly influence subsequent ssDNA–surface interactions and dsDNA hybridization responses with incoming ssDNA or RNA targets. Therefore, understanding both ss- and dsDNA interfacial behavior during this processing is critical to asserting control over assay performance and in designing rational steps for improvements that address the certain needs described in Table 1.Various strategies are used for realizing DNA microarray constructions shown in Fig. 2, with several ssDNA–surface immobilization methods on a wide range of solid (and often poorly defined) substrate chemistries and forms.20,21 ssDNA probe immobilization on a surface has three fundamental approaches broadly characterized as: (1) ssDNA “grafting to”; (2) ssDNA “grafting from”; and (3) ssDNA nanodroplet printing/drying. In the first approach, anionic polyphosphate ssDNA probe oligomers are either adsorbed to cationic surfaces electrostatically, or by combinations of polar and hydrophobic interfacial interactions to other surfaces (i.e., nitrocellulose, silicon oxide, or polypropylene). In the second “grafting from” approach, fluidics, photolithography and photochemistry are combined with automated microprocessing to sequentially add and spatially direct each individual DNA nucleotide to grow ssDNA probe chains directly from chemical primer sites, pre-immobilized across patterned surfaces. In the third strategy, automated dispensing equipment places ssDNA probe solution droplets in specified surface locations and allows rapid drying by evaporation, effectively adsorbing the dried ssDNA probes to specific locations as disorganized ssDNA surface films. These approaches are summarized in Fig. 2. Importantly, each method yields different, physically distinct endpoints for resulting DNA probes on the surface. These fundamental DNA-substrate fabrication differences then result in distinct capabilities for probe–target interactions and assay hybridization yields and signals.
Commercially popular amine-terminated organosilane-coated and poly(L-lysine)-modified glass slides provide cationic surfaces for electrostatically binding anionic ssDNA probes, the basis for several popular microarray products using the “grafting to” approach (see Fig. 2A).22,23 Alternatively, covalent “grafting to” approaches for DNA probes are diverse, but many use terminally amine-modified ssDNA and amine-reactive surface chemistries, including aldehyde, isothiocyanate, isocyanate chemistry and also reactive esters including p-nitro- and perfluoro-phenyl and N-hydroxysuccinimide (NHS) terminal groups on coated slides.24 “Grafting from” strategies are also commercially used in ssDNA array fabrication. For example, Affymetrix combines masked-based automated photolithography and combinatorial chemistry to synthesize very high density DNA chips.25 Hydroxylated, silanized fused silica wafers are derivatized with a linker molecule and a light-sensitive protecting group. Photolithographic masks then illuminate specific locations on the silanized wafer, with UV exposure causing chemical site deprotection to activate surface chemistry that then couples free nucleotides onto the silica wafer only where irradiated (Fig. 2B).26 Additional capping steps then prevent unattached molecules from becoming probes. Nucleotide side chains are also protected to prevent branched-chain formation. Photo-induced deprotection, coupling and capping steps are sequentially at multiple sites under computer-controlled mask pattern changes, and continued until full-length immobilized probes of diverse sequence variation are fabricated on chip at known sites, controlled at high density.27 In an alternative commercial approach, NimbleGen (Roche) builds arrays using photo-deposition chemistry based on a mask-less array synthesizer (MAS), specifically a mask-less light projector acting as a ‘virtual mask’ instead of the physical photomasks used by Affymetrix.28 In each case, the stepwise photo-controlled on-chip synthesis yield is approximately 85–95% hence oligonucleotide probes longer than 25 bases are not reliably synthesized with high fidelity. Alternatively, patterned metal films facilitate patterned DNA islands as chemisorbed DNA adlayers from solution.29Fig. 2C shows thiolated DNA probes that react spontaneously with clean, patterned gold, copper, platinum, and silver metallic surfaces via metal–thiolate bond formation from aqueous solution to yield immobilized DNA probes with patterned array fidelity corresponding to metal patterns. This popular solution-based metal–thiolate coupling chemistry has been widely studied as a fundamental method for accessing DNA single-point attached monolayer films as well as commercialized for array and assay uses.30,31
Fig. 2D depicts more common DNA microarray fabrication using direct droplet printing and evaporation based on high definition spatial deposition of nanoliter probe solution volumes. Dispensing of these droplets can exploit contact precision pins, inkjets, bubble jets or piezo-actuated technologies capable of reliably dispensing 100 pL to 2 mL volumes per array area. Contact pin printing usually results in spot densities of 2000–4000 spots cm−2 of ∼100 micron spot diameters, while non-contact (i.e., piezo) printing yields slightly higher spot density with smaller spot diameters. Reliable fabrication of printed probe microspotted arrays is a multi-parameter optimization challenge. Spot performance in hybridization assay is a function of final probe spot morphology and probe density, and probe lateral distribution within the spots affects target hybridized density and resulting target signal distribution.32–34 Little methods standardization is currently present, meaning that each spotting recipe, instrument, surface and print protocol produces different DNA probe spot properties with different final dried densities and resulting distinct probe/target hybridization capabilities, therefore different assay signals. This issue is central to the variable metrics challenges behind current DNA array-based assay answers.
3. Immobilized DNA-surface models
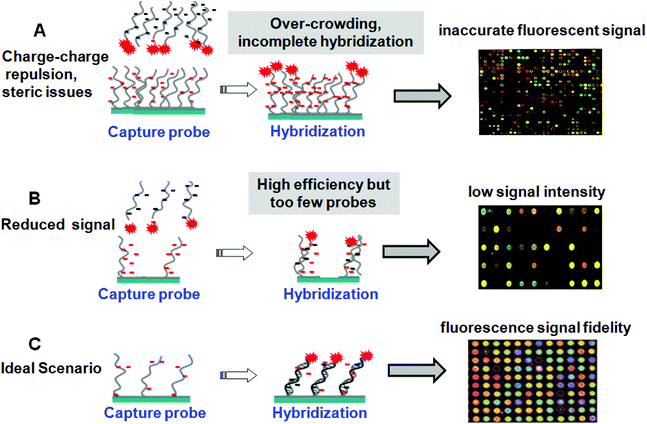
Given these diverse DNA array fabrication methods, all but droplet spotting methods are expected to yield immobilized monolayers of probe nucleic acids on supports. Droplets dry rapidly in situ, leaving behind a thick dried residue of ssDNA and buffer salts that may or may not be rinsed away in subsequent washing steps to yield reliable DNA immobilized thin films. This leads to high density and random orienting ssDNA probes on surfaces. Additionally, microarray “grafting to” immobilization methods (e.g., Fig. 2A, C and D) all use pre-synthesized oligonucleotide probes purified by capillary electrophoresis or high-performance liquid chromatography prior to array deposition of nearly homogeneous probe samples, increasing assay specificity. By contrast, in situ probe synthesis (Fig. 2B) is not 100% accurate, and ready validation of the fidelity of the final ssDNA probe composition on the array surface is difficult.35 These photo-generated “grafting from” microarrays therefore contain significant nucleotide chain defects distinct from the desired sequence.36 A consequence of high probe density is slow hybridization kinetics that produces incomplete duplexing in practical assay timelines, resulting in low hybridization efficiencies and reduced hybridized target analyte capture and sensitivity. In contrast, low surface probe densities lead to relatively fast kinetics but with absolute hybridized target signal limited by the reduced surface probe amounts.37 This trade-off between signal yield and assay speed is also a central issue for such printed array formats. Table 2 summarizes array spot areas and probe densities for the various immobilization methods.29,38,39 A “Goldilocks principle” might be appropriately assigned to the current state of ssDNA tethering and density at surfaces in search of the optimal signal generation by target capture. This is depicted in Fig. 3. High density of immobilized probe presents steric and electrostatic barriers (detailed below) that preclude accurate target capture and alter hybridization kinetics (Fig. 3A). Low probe densities capture target at high efficiency but the end result is insufficient signal and high background noise from non-specific capture (Fig. 3B). Optimal probe density, while such optimization is case dependent on probe sequence and length and surface assay conditions, might be described as a condition between these two extremes where sufficient signal is produced at reasonable time scales and with fidelity to target abundance and sequence (Fig. 3C). Only thorough understanding of both ssDNA and resulting dsDNA chain duplexing behavior and properties at surfaces will permit rational designs for such optimization.| Surface | Area | Probe density/cm2 |
|---|---|---|
| Gold | 100 μm diameter spot | 5 × 1012 |
| Amine-modified surface | 4.5 mm diameter spot | 2.5 × 1012 |
| Photolithography | 5–10 μm | 106 |
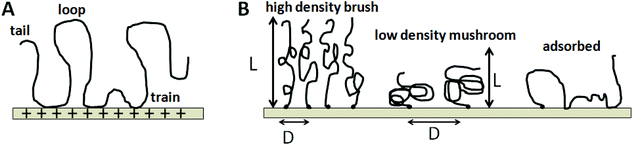
Knowledge and control of ssDNA probe density and its physical state are fundamentally important to interpreting differences in assay signal from both label-free and labeled microarray assays, and to design more highly efficient, reproducible assay formats. Importantly, each ssDNA probe immobilization approach yields distinctly different probe molecular fates that determine the resulting dsDNA duplex events on surfaces. For example, physi- or chemi-sorption of oligo-ssDNA probe chains to surfaces in the “grafting to” approach (Fig. 2A) provide little control over immobilized ssDNA chain densities and probe chain segmental conformations. In these cases, relative amounts of surface ssDNA probe chain loops, trains, and tails (see Fig. 4)40,41 are stochastic endpoints of the adsorption process and drying, with distances between adsorbed chains unknown, uncontrolled and perhaps entangled, affecting pairing with incoming targets. A critical physicochemical distinction from other ssDNA probe immobilization methods is the largely unproven presumption that such adsorbed ssDNA chains (i.e., not single point attached) lie largely horizontal on the surface due to the multiplicity of chain–surface adsorption sites and polyvalent DNA chain segments.
By contrast, end-point ssDNA immobilization resulting from both photochemical in situ patterning/reaction approaches, as well as metal–thiolate probe chemisorption and covalent chain-end reaction chemistry (Fig. 4B and C), is presumed to produce brush-like chain conformations oriented largely orthogonal to the surface.42–44 These important differences in immobilized probe ssDNA chain orientations as a function of fabrication method should be reflected in their resulting kinetics, thermodynamics and efficiencies of target capture during duplex formation under assay conditions.
These influences can be appreciated by inspection of idealized DNA chain physical states on surfaces, shown in Fig. 4. Uncontrolled ssDNA–surface interactions yield adsorbed DNA chains with multiple surface-binding states, leading to the classic surface-immobilized polymer “loop-trains-tails” surface configurational scenario (Fig. 4A).45 How DNA–DNA duplexes form from this random surface-adsorbed state in microarray assays, given that short ssDNA probe oligomers of 20–30 bases require substantial complementary pairing to form stable duplexes with targets, is not known. Yet, many long-standing nucleotide array platforms utilize this ssDNA probe (physi-)adsorption approach (e.g., FAST™ slides) to create arrays.46,47 End-point grafted probes (Fig. 4B, e.g., Affymetrix or Nimblegen arrays) produce distinctly different immobilized probe states where ssDNA chain lateral density in brush-like formats is a function of the chain's size and other physical conditions. How this chain physical state is understood for ssDNA immobilized on array surfaces determines how we understand its interactions with complementary and non-complementary ssDNA targets it encounters, how it can select perfect duplex partners to achieve reliable assay and how microarray assays might be better designed to reliably achieve this endpoint.
4. Idealized tethered polymer chain models
Fortunately, immobilized chain polymer physics has experienced considerable theoretical model development and validation using several experimental immobilized chain models. These tethered chain systems exploit polymer statistical conformational and configurational properties derived from their bulk solution states. In bulk dilute solution, generic polymer size is idealized by the Flory radius, RF, the end-to-end distance for an ideal but expanded chain where self-avoiding random walks and excluded volume effects from chain expansion dominate. This condition is distinct from ideal chains defined as having freely jointed chains and conformational random walks, comprising monomers as rigid rods of fixed length and chain orientation completely independent of the orientations and positions of neighboring monomers, to the extent that two monomers can co-exist at the same place (i.e., phantom chain). Polymer RF scales with the square root of the polymer's end-to-end distance, <R> (i.e., RF = <R2>0.5). By contrast, the chain's radius of gyration, Rg, is substantially smaller than the polymer's end–end distance in the freely jointed chain model, so that Rg2 = RF2/6. Additionally, Flory's mean-field model polymer size yields a well-known scaling law for Rg as Rg ∼ Nν, where N is the number of bonded polymer segments (i.e., degree of polymerization). Chains in good solvents yield values for the Flory exponent ν as ν = 3/5 (expanded), and for bad solvents as ν = 1/3 (condensed).48 In so-called theta conditions, ν = 1/2, the result consistent with the simple random walk model, so that this chain behaves ideally.49 Generally, then the Flory expression for Rg is:Rg ∝ Nν![[b with combining low line]](https://www.rsc.org/images/entities/i_char_0062_0332.gif) | (1) |
In 1977, Alexander extended polymer scaling concepts to strongly stretched, densely grafted polymer chains on impenetrable surfaces (termed polymer brushes). This was then further improved by de Gennes using a blob modification to the tethered idealized chain scaling model. The resulting Alexander-de Gennes scaling model for polymers end-grafted to surfaces, and resulting properties and possible applications is widely accepted due to its simplicity and usually good “real chain” approximations of ideal “bulk” solvent-swollen brush properties such as brush height and brush modulus.50 Schematic depictions for idealized tethered “mushroom” and “brush” polymer structures on substrates are idealized in Fig. 4B. In the “mushroom” regime, immobilized chains are considered to occupy hemispherical volumes separated by distances precluding lateral chain–chain overlap. de Gennes demonstrated that the mushroom regime reflects the lower limit of chain immobilized density (σ) where chains do not overlap at a lateral surface spacing distance, D. Ideal chain separations of Rg < D lead to a tethered polymer surface density, σ < N−6/5, meaning that surface chain density is nearly inversely proportional to polymer length. When σ increases to σ > N−6/5, grafted chains begin to crowd each other, with conformational extensions away normal from the surface to reduce segment crowding and repulsive entropic, enthalpic and possible polar or electrostatic issues, yielding a “brush” of extended chains.51 The basic enduring relationship for ideal polymer brushes is the power scaling law relation between swollen brush thickness, H, and polymer grafting density, σ, where H ∼ σν.52 The Flory scaling exponent abruptly changes from ν = 0 to ν = 1/3 when grafted, ideal polymer chain spacing becomes less than Rg (i.e., the so-called mushroom-to-brush density transition).
A critical primary assumption in the Alexander-de Gennes polymer brush model is that monomer density is assumed to be constant throughout the brush. This implies that the tethered polymers are uniformly stretched, all chain ends are located at the outer edge of the brush.53 This oversimplification underestimates the conformational entropy of the grafted chains. More than 30 years of efforts have sought to describe the polymer brush theory experimentally and theoretically with the model by incorporating different grafting scenarios such as graft density, chain length, good or bad solvents (i.e., differential chain swelling), charged polymer chains, aqueous solvents of varying ionic strengths, presence of bulk surfactants and colloids, and many other variables. Experimental alignment, given these experimental complexities, with the original Alexander-de Gennes theory has been difficult. This has prompted evolution of newer scaling theories, analytical self-consistent-field (aSCF) models and other numerical models to improve theoretical accuracy.50,54,55
The aSCF model assumes that grafting density is sufficiently high for the brush to be laterally homogeneous, implying that both monomer and chain end density are solely functions of distance from the impenetrable grafting surface. A parabolic density distribution profile is predicted in the brush compared to the constant “box-model” of Alexender-de Gennes model. The numerical self-consistent-field (nSCF) models overcomes the limitations of aSCF,56 modeling monomer density in the brush at a given distance from the grafting plane as the combined sum of the density “σ” at the given distance “H” of all possible conformations, weighted by the probability of each conformation.57 The equilibrium density distribution, self-consistent with the distribution of polymer conformations it generates, is determined numerically for a given grafting density, chain length, adsorption properties and solvent conditions. This nSCF model accommodates long chains at relatively high grafting densities under good solvent conditions. Also, a segment depletion region close to the surface is predicted, as the grafting plane impermeability is entropically unfavored.58 The most important limitation is the assumption of most probable chain conformation and fluctuations around this conformation are not considered. This is especially limiting for low grafting densities or short chains. aSCF and nSCF are applicable to long chains grafted at either a low grafting density (mushrooms) or at a high grafting density (brushes).
Nonetheless, very recent work59 does show that single-strand tethered DNA of ∼1000 bases does follow brush scaling predictions for polyelectrolyte brush height60 as a function of both chain density and ionic strength. So, to a certain extent, intermediate length polyelectrolyte brush behaviors in high ionic strength milieu can be predicted. A large number of experimental tethered chain systems (i.e., most DNA brush systems among them) will not meet these criteria, however, either due to far shorter chains (e.g., 20–80 bases) or an insufficient grafting density to obtain a polymer brush, and hence termed as quasi-static or pseudo-static regimes.61 Additionally, it is important to note that the exact chain conformation for grafted layers depends on the grafting density and solvent conditions. The above models are limited to good solvent; the Scheutjens–Fleer self-consistent field lattice model (SF-SCF) is used for chain grafts in bad solvents.62
4.1 Scaling theories and DNA brushes
Polymer scaling models have been applied to tethered polyelectrolyte DNA at surfaces using many theoretical and experimental approaches. ssDNA is often described as a random polymer coil with long-range interactions expected to induce swollen polyelectrolyte configurations characterized by a Flory radius. Distinguishing features of polyelectrolyte brushes result from Coulombic interactions between charged monomers within the chains. These interactions are partially screened, also in salt-free solution, by the presence of mobile counterions, ensuring system electroneutrality. In electrolyte solutions, both co- and counter-ions contribute significantly to this screening. Additionally, immobilized charges present on the tethering surface also elicit long-range attractive or repulsive forces between the surface and grafted chains. Charges exist on experimental surfaces from ions adsorbed from solution, surfactants adsorbed to hydrophobic surfaces, or solid-state functional groups dissociated on the surface. Repulsion of charged polymer segments both from this charged surface and from other charged polymer chain segments results in the extension of grafted polyions in the direction perpendicular to the surface. Magnitudes of these two repulsive forces determine the brush conformational dynamics in polyelectrolyte brushes. Electro-neutrality overall is derived from the presence of a compensating amount of mobile counterions in the solution. A critical length scale in the system is the Gouy–Chapman double layer thickness (i.e., Debye screening length) determined by the media ionic strength and valencies.Several models have been proposed to understand the effects of added salt (increased ionic strength) on polyelectrolyte brush height.63 Zhulina's group64,65 adapted theoretical brush models to ssDNA “brushes” at surfaces and the important crossover to the mushroom regime of non-overlapping tethered polyelectrolyte tails, and compared DNA hybridization constants on surfaces versus the bulk.66 They used a Flory version of the Alexander model for ssDNA brushes as applied to terminally anchored polyelectrolytes in aqueous solutions of high ionic strength, modifying it to incorporate the influence of an impenetrable grafting surface.51 Dense, strongly ionized polymer brushes produce the so-called “osmotic” regime where the majority of the mobile counterions are trapped within the polyelectrolyte brush to compensate the immobilized polyanion brush charge density. The resulting osmotic pressure from these entrapped counterions swells this strongly charged brush with solvent (water), and the equilibrium balance between this osmotic pressure and chain entropic elastic forces produce a scaling expression for the equilibrium thickness of this “osmotic brush”, H:
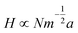 | (2) |
By contrast, weak polyelectrolyte brushes comprising anchored polymer chains establish a local equilibrium between neutral, undissociated and charged, dissociated polymer moieties. In such systems, the degree of dissociation depends on the local pH value and local charge density, also considering added salt. A weaker polyanion (less completely charged) brush exhibits brush height increase with increasing salt concentration, described by a scaling function more weakly dependent on grafting density and ionic strength:68–70
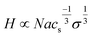 | (3) |
4.2 DNA brushes, hybridization models and intrinsic limitations
Gong and Levicky applied the Halperin, Buhot and Zhulina polymer brush theory (HBZ)51 to understand DNA hybridization isotherms, and the cooperative relationship between probe coverage and ionic strength for the initial hybridization reaction onset and the more complex regimes with increased target binding.73 Hagan and Chakraborthy predicted hybridization kinetic regimes for surface-tethered ssDNA oligomers with solubilized targets with both theoretical and experimental approach.74 Their theoretical approach included modifying the Alexander-de Gennes theory combined with the Zimms model of penetrating diffusion for duplexing target. Both experimental and theoretical evidence revealed that nucleation sites near the grafted ends of the polyanion probes are the least accessible; thus, ssDNA targets that preferentially bind to this region show more drastic rate reductions than those that bind near probe free ends. Brush regimes in ssDNA and dsDNA layers were distinguished by Halperin et al. by specifying unique molecular length scales for ssDNA versus dsDNA across a range of parameters: in contrast to the ssDNA random coil, dsDNA is a stiffer rod-like molecule with each base-pair contributing 0.34 nm to its length.51 The radius of a dsDNA helix is 0.95 nm and its cross-sectional area is 28.4 nm2, given the typical nucleotide monomer size of 0.6 nm.However, two important physicochemical distinctions characteristic of ssDNA immobilized in the various array formats limit applicability of classic polymer chain scaling theories to its analysis. Critically, DNA is a polyanion with high chain charge density and, in array states, often immobilized as short chain single-strand oligomers (20–60 bases long). Immobilized chain physics models do not frequently address these two conditions (i.e., incompatible with accommodating both high charges and short stiff chain lengths) and at an impenetrable interface. The commonly invoked Gaussian chain elasticity model cannot detail the local structure of the immobilized chain and therefore is mostly applicable to study flexible chains on large length scales where the local chain correlations are negligible. Typical tethered ssDNA array probes of 20–200 bases in water or low ionic strength conditions are often considered short, stiff, rod-like molecules with few degrees of freedom. Persistence length arguments (vide infra) support this. However, high ionic strength conditions for hybridization can seemingly allow longer ssDNA molecules to obey scaling relationships.
For example, the Flory and Alexander-de Gennes models for other tethered polymers are compromised for polyelectrolytes: each ssDNA immobilized layer is characterized by distinct ssDNA segmental density distributions normal to the surface (using Gaussian statistics), with the resulting ssDNA layer thickness, H, that produces significant steric and electrostatic barriers to target hybridization.51 These distributions and thicknesses are highly dependent on chain–chain, chain–surface and chain–solvent electrostatic interactions, without a unifying theory that accurately accounts for all of these factors. The worm-like chain (WLC) model (also called the Kratky–Porod model) is a special case of the freely rotating chain model for very small values of bond angles. This is a good model for stiff polymers, (e.g., dsDNA) for which the flexibility is due to fluctuation of the contour of the chain from a straight line. Recent work has shown as well that for 1000 bases long ssDNA grafted in the mushroom regime59 the observed sub-linear dependence of height with contour length at high salt (i.e., 250 mM) fits well with the end-to-end distance of a semiflexible polymer in solution (WLC model, i.e., H ∝ RWLC), showing stiff rod-like behavior for short ssDNA polymers and ideal chain behavior for long ssDNA polymers. Low-density ssDNA probe immobilization (i.e., sometimes below the limit where the ionic double layer Debye length is smaller than the brush thickness, H, and therefore the screening length extends beyond the brush thickness in low salt concentrations) can also facilitate ssDNA probe–surface adsorptive interference. In these cases, sufficient ssDNA surface access is available for probe–surface binding that this interaction hinders subsequent hybridization.38,42 ssDNA chain–surface adsorption makes the probe unavailable for target duplex formation, compromising assay performance in a graft density-dependent way. This is reversible in some cases when competing surface-adsorbing and space-filling surface-active diluents are used to displace weak ssDNA–surface physisorption, prompting grafted chain reorientation and improved accessibility to target.42,75
The ssDNA probe brush thus formed on surfaces affects both the hybridization isotherm and the duplex rate conditions, depending on its density, thickness and media. In particular, the brush lowers both the hybridization rate and the attainable hybridization efficiency (yield) for a given concentration of ssDNA targets.51 Therefore, DNA microarray design should carefully consider probe density influences on target uptake in formulating protocols for array preparation and hybridization as well as in the analysis of assay results. Specifically, surface chemistries are sought for ssDNA probe binding that improve ssDNA surface coupling efficiency and lateral homogeneity, and minimize non-specific binding from undesired cross-reactive groups intrinsic to many ssDNA combinations with surfaces.76 Importantly, various surface modifications to improve ssDNA–surface binding have evolved from original affinity reagent printing and desiccation on intrinsically ssDNA-adhesive surface chemistries (i.e., nitrocellulose, glass), thicker, three-dimensional chemically reactive films (i.e., immobilized hydrogels, sol–gels) coated over solid glass supports, and array-patterned photochemical and electrochemical immobilization methods.25 Detailed descriptions for strategies for microarray and design fabrication, as well as array detection methods, are available.24,77
5. Microarray assay signal detection
Despite the diversity and mature development of ssDNA array immobilization methods and substrate chemistries, the conventional detection method for screening duplexed array signals has remained primarily the conventional fluorescent scanner. This signal typically derives from dye-labeled ssDNA targets derived from PCR-amplified samples prepared with dye-labeled nucleotides that produce surface-bound fluorescent signals complementary to probes placed in different spatial locations. Importantly, integrated fluorescent intensity within each spot becomes the assay “answer”, ostensibly reflecting gene presence and abundance in such assays. Nonetheless, microarray fluorescence data generally do not reliably quantify each gene's absolute abundance. This is attributed to the effects of different hybridization rates and efficiencies for different target strand sequences and base contents, as well as both variable steric and electrostatic influences of densely printed probes at surfaces. Assay fluorescent signal from a given array microspot is generally arbitrarily judged to be significantly different from baseline (i.e., normal expression) if different than two log orders in spot intensity (increase or decrease in relative fluorescent units, S, i.e., 2log S).78 Assay detection limits and relative noise levels vary, depending on substrate, probe length, target length, detection milieu and spotting method. Routine conventional fluorescence scanner images provide information for integrated spot pixel intensity, shape and morphology, but lack important details for incorporating intra-spot ssDNA immobilized heterogeneity and intra-spot structural issues known to affect both target capture signals and duplex hybridization kinetics critical to this assay's answer development and diagnostic reliability.34 Additionally, signal quantitation is affected by numerous, known surface issues and background noise sources that confound reliable, quantitative correlations of spot-to-spot fluorescent assay signals and experiment-to-experiment comparisons.17,79 Significantly, integration of spot fluorescent intensity to report assay signal with commonly used fluorescence scanners demonstrates that the typical fluorescence scanner cannot discern microspot optical heterogeneity and fluorescence intensity variations within single printed spots to yield a reliable metric.80 High resolution chemical state imaging surface mass spectrometry (TOF-SIMS) studies of printed ssDNA microspots confirm that fluorescence scanning analysis fails to reliably report absolute quantitation of immobilized ssDNA probe amounts. Inaccuracy in this fluorescent metric is attributed to fluorescent dye–dye and dye–surface interactions, leading to quenching of surface fluorescence signal.346. DNA chain states on surfaces as a key feature for performance
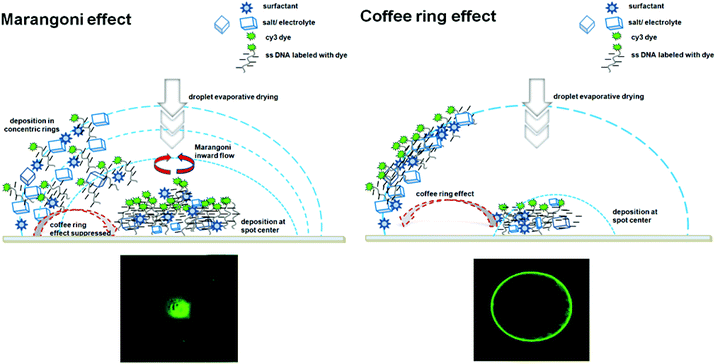
Many factors affect DNA microarray performance quality (Table 1) aside from the stringency that affects analytical figures of merit (i.e., sensitivity, specificity) through probe design, sequence selection, and target affinity (shown in Fig. 2 and 3). A major influence comes from ssDNA immobilized chain “states” that directly affect probe “availability” to target binding at surfaces. Hybridization processes and DNA duplex formation (i.e., duplex kinetics, thermodynamics, and efficiency) are directly affected by ssDNA chain physical states on surfaces. Factors such as ssDNA length, sequence, grafted probe density, electrostatic interactions, segment conformational states and steric hindrance are critically important to assay signal generation.34,80,81 These intrinsic properties of ssDNA chains at surfaces are reflected in physical manifestations of ssDNA chain persistence length and radius of gyration. ssDNA conformations both hydrated and dessicated on surfaces, in solutions with various ionic strengths, with printed surfactants in print buffers and with dye labels further dictate the biophysical properties of tethered ssDNA on surfaces and resulting interactions with targets. Additionally, target fluorescent labels necessary for fluorescent DNA assay can produce dye–dye, dye–surface, and dye–DNA aggregation non-idealities that also influence fluorescent signal generation.82,83A last consideration in this regard is that non-equilibrium drying of printed DNA solution spots during ssDNA droplet-based immobilization (Fig. 4D) often leads to coffee ring and Marangoni convection flow drying effects that alter dried ssDNA immobilized density and distributions within final probe spots.33,84 As probe lateral distribution affects target capture to these spots, kinetically, spatially, and spot-to-spot, these spot-drying artifacts represent a source of DNA assay variability within spots and spot-to-spot with a fundamental and well-studied history.85,86
In summary, inherent variables in the chemistry and physics of ssDNA immobilization and its resulting properties at surfaces are correlated to currently observed limitations in the information content and reliability of DNA microarray assays. Understanding of and control over ssDNA–surface interactions are therefore key for improving microarray assay reliability, quantitative capability and detection limits as well as for developing new microarray surfaces more effective in performing in complex media. Nonetheless, careful analysis linking known bulk ssDNA biophysical properties to ssDNA–surface behavior is rarely reported. This review seeks to describe the current knowledge base in this theme to help identify the fundamental issues affecting DNA–DNA recognition and binding at surfaces. Such knowledge will move more of these technologies to diagnostic applications. A further benefit is a more general extension of this critical review process and analytical rationale to emerging, analogous opportunities in saccharide, cell-based, high-throughput drug screening arrays, and protein-based capture assays.
7. DNA biophysics – a primer
Because ssDNA oligomer probes are densely immobilized at surfaces in microarray formats, their chain–chain interactions, chain–surface interactions, hydration, response to changing ionic strength, drying and other hybridization conditions all impose forces that alter ssDNA chain conformations and segmental densities at surfaces differently from ssDNA chains in bulk solution.7.1 ssDNA chain structure and conformational forms
ssDNA oligomers of 20–70 nucleotides are routinely used in arrays and bead-based assays.26 Immobilized ssDNA probes up to 200 bases long can be purchased commercially (Agilent). As surface-tethered systems, immobilized ssDNA chains will assume an array-dependent equilibrium conformational state at surfaces responding to their immobilization state and local thermodynamic stimuli. ssDNA chains are either described as highly negatively charged, long, semi-flexible or short, rigid polymers based on their length. As a polyphosphate with regular anionic group repeats bridging each nucleotide monomer, they have some properties characteristic of a typical polyanion with fractional, incomplete charging. While longer ssDNA chains can be considered to be semi-flexible polyelectrolytes, shorter ssDNA chains are charged, rigid rod-like structures. For ssDNA lengths > 150 bases, the ssDNA chain is generally recognized to exist as a flexible polymer and for lengths < 150 bases, it is considered as rod-like (based on the persistence length for DNA in physiological conditions: LP = 50 nm or ∼150 bases). As a strongly charged polyelectrolyte, DNA's electrostatic interactions are screened by counterion condensation.87–89 The charge dependence of DNA persistence length and the role of electrostatics in mediating ssDNA stiffness can be altered by varying surface chemistries and components in assay buffers.The worm-like chain (WLC) model is often used to describe the intermediate behavior between a rigid rod and a random coil to account for the striking local stiffness but long-range flexibility of ssDNA.90,91 The WLC model describes ssDNA molecules at low applied forces as an entropic spring and an inextensible worm-like chain, and at higher applied forces (i.e., 6 pN to ∼70 pN) as behaving like an elastic rod.92,93 Development of this model for ssDNA and other semi-flexible (or semi-stiff) polymer chains has been an important contribution of polymer theory. It can be modified in various forms to account for other theoretical and experimental variables. ssDNA's flexible chains form diffuse adsorbed layers extending from the surface into bulk solution in contrast to typical semi-flexible or rigid chains forming dense and compact surface-adsorbed layers. ssDNA chain coiling (chain flexibility based on the Kuhn length, i.e., 2 times the chain persistence length), conformational degrees of freedom based on solvent conditions (Flory theory of polymer–solvent interactions, excluded volume effects), repulsive interactions between ssDNA electrostatic components, and the chain spring constant reflecting the chain elasticity all describe the ssDNA chain conformation states when tethered at the liquid–solid interface.
7.2 Parameters used to describe DNA physical properties
Physical properties of ssDNA and dsDNA are primarily a function of their chain lengths and solution conditions. Flexibility of both ssDNA and dsDNA chains depends on chain persistence length (Lp), radius of gyration (Rg), and chain flexibility angle (θ), as shown in Fig. 5. Persistence length provides a measure of the rigidity of a linear polymer and is evaluated by determining how quickly the orientation of a polymer backbone changes as its chain contour is traversed. Shorter persistence lengths reflect greater chain conformational freedom. Polymer radius of gyration (Rg) is a measure of the volume occupied by the linear polymer under equilibrium conformational conditions and is evaluated by calculating the time average of the root-mean-square distance of the polymer components from its centroid. The chain flexibility angle (θ) is a fixed bond angle constraining the rotational flexibility around the chain backbone, resulting in chain stiffness. As the bond angle is reduced, the persistence length increases dramatically. Fig. 5 schematically correlates chain contour length (L) and persistence length (Lp), radius of gyration (Rg) and the angle of flexibility (θ) for ssDNA and dsDNA tethered to a substrate. The relationship between Rg for ssDNA considered as a semi-flexible chain and persistence length Lp is given by: where Lp/b is the number of monomers in a persistent segment.37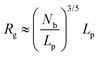 | (4) |
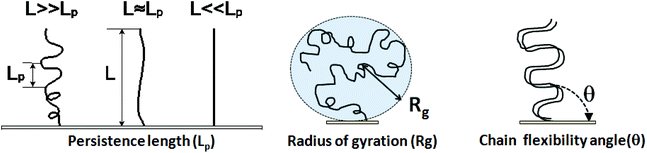 | ||
| Fig. 5 Persistence length, radius of gyration and chain flexibility angle for immobilized ssDNA and dsDNA tethered ideally on surfaces. | ||
The Flory scaling exponent for a solvent-swollen chain with excluded volume interactions (3/5) in good solvent is retained. Chain persistence length for ssDNA (10 ≤ N ≤ 70 nucleotides) ranges from 1.5 nm in 2 M NaCl to 3 nm in 25 mM NaCl, demonstrating the effect of charge screening on ssDNA chain flexibility.94
7.3 ssDNA persistence length
Persistence length is used to characterize the flexibility of linear macromolecules and their conformations in the absence of excluded volume interactions. The persistence length can be considered as the length scale above which chains behave ideally (vide supra) but below which they are rigid. Persistence length provides an estimate for the typical curvature radius of the polymer chain under thermal fluctuations.95 Various models (i.e., WLC, Monte Carlo simulations) and experimental methods have been used to report persistence length for ssDNA and dsDNA. The WLC model characterizes the bending length scale of a semi-flexible polymer as persistence length, (Lp), mathematically defined by the decay length of tangent–tangent angular orientational correlations along the chain. The energy required to bend a semi-flexible polymer over an angle (θ) over length (L) depends on chain chemistry, the temperature and persistence length, Lp, of the polymer.96 The rod's local direction de-correlates at distance(s) along the curve according to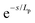 . For contour lengths L ≥ Lp, ssDNA can be described as a flexible polymer (essentially a self-avoiding freely jointed chain) whose entropic component of free energy is dominant. In contrast, for contour lengths L ≤ Lp, ssDNA is asserted to be more rod-like, with an elastic-dominated energy (see Fig. 5); the stiffer the chain, the longer the persistence length.
. For contour lengths L ≥ Lp, ssDNA can be described as a flexible polymer (essentially a self-avoiding freely jointed chain) whose entropic component of free energy is dominant. In contrast, for contour lengths L ≤ Lp, ssDNA is asserted to be more rod-like, with an elastic-dominated energy (see Fig. 5); the stiffer the chain, the longer the persistence length.
Both dsDNA and ssDNA bending rigidities are also described by the WLC model for a polyelectrolyte.97 dsDNA shows a reduced persistence length when DNA-binding proteins reduce the normal DNA bond angle of 120° to 114 ± 21° in 50 mM Na+ ion salt solution.98 The dsDNA contour length increases from 0.34 to 0.397 nm per base, independent of salt concentration.99 The electrostatic influence on persistence length originally expressed in Odijk–Skolnick–Fixman (OSF) theory is the sum of bare persistence length (LPi) resulting from the intrinsic chain rigidity, and an electrostatic contribution (LPe) depending on media ionic strength (where LP = LPi + LPe).100 Electrostatic persistence length (LPe) for polyelectrolytes like DNA is proportional to the Debye screening length (κ−1) and inversely proportional to the Bjerrum length (lB) (0.7 nm in water/monovalent ions) as LPe = κ−1/4lB. OSF theory estimates for the energy required to bend a straight charged chain show that screened Coulombic interactions led to very high induced chain stiffness.101
Single molecule experiments such as optical93 and laser102 tweezers in various buffer conditions have been used to study DNA rigidity. In monovalent salt (e.g., Na+(aq)), the measured ssDNA persistence length is consistent with an electrostatic contribution that varies inversely with the ionic strength.103,104 The persistence length for ssDNA (e.g., oligo-dT in the range between 10 and 70 nucleotides) decreases from 3 nm at low salt (25 mM NaCl) to 1.5 nm at high salt (2 M NaCl).94 Using FRET and SAXS measurement of ssDNA, Chen et al.105 showed that Mg2+ cation is approximately 20–40 times more efficient at charge screening than Na+ ion in terms of ionic strength (60–120 times in terms of cation concentration). The persistence length of ssDNA (dT40) in NaCl (monovalent 0.1 M) is ∼1.6 nm and for MgCl2 (divalent, 0.1 M) is ∼0.9 nm. In a range of moderate-to-high ionic concentrations (∼0.1 to 1 M salt) dsDNA persistence length drops noticeably by ∼25%.106 Persistence length shortens with increasing ionic strength due to the complex interplay of both chain conformation and ionic strength. OSF theory fails with multivalent cations like Co(NH3)63+(aq) and spermidine3+(aq). Measurements with these ions gave apparent LPe values some 25–30 nm lower than the Lpi (intrinsic) persistence length, as the dsDNA locally bends towards the transiently bound multivalent ions, shortening the intrinsic persistence length.102
7.4 Radius of gyration (Rg) and ssDNA conformation
Free ssDNA in aqueous solution is generally considered a relatively well-behaved polymer based on conventional polymer physics models.93 Early experiments deducing ssDNA's radius of gyration (Rg) in buffered aqueous solutions showed Rg to be a function of weight-average molecular weight (Mw),107 consistent with both Flory and blob models (vide infra). This relationship between Rg and Mw was derived from experimental data and Monte Carlo simulations incorporating the Kratky–Porod persistence chain model, and is schematically shown in Fig. 6A. As one example, ssDNA of 5000 bases in solution has an Rg of 30 nm.108 Long ssDNA under high salt conditions also behaves as a flexible coil-like polymer,109 however, these values reflect bulk solution properties in dilute DNA solutions where DNA–DNA intermolecular interactions are not involved and where chain–solvent and intra-chain energetics determine chain conformations in isotropic milieu. ssDNA surface immobilization or adsorption relevant to array formats alters the chain Rg due to new interactions with the impenetrable surface and lateral chain–chain surface crowding where chain–chain interactions appreciably affect chain morphologies, brush-mushroom regimes and resulting layer thickness, H (Fig. 6B and 6C).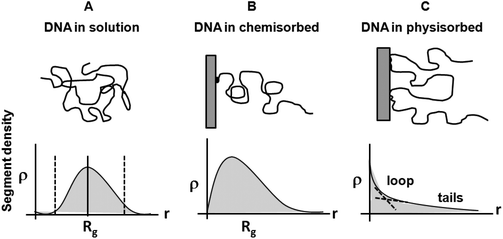 | ||
| Fig. 6 Schematics of DNA segment distribution as a function of distance from the surface. (A) DNA in solution. (B) DNA chemisorbed (end-tethered) on a surface, and (C) DNA physisorbed on a surface, forming tails, loops and trains (see Fig. 3). | ||
The presence of an impenetrable array substrate profoundly affects immobilized ssDNA chain conformation and segment distribution with N segments attached ideally by one end at a tethered surface density, σ (see Fig. 4). Surface forces resulting in enthalpic interactions dictate this adsorbed-state chain conformation in each case, balancing long-range electrostatic, medium range dipolar and hydration forces, and short-range dispersion and hydrophobic forces between ssDNA and substrate chemistry versus those for ssDNA and solution in more ideal terms. However, this analysis does not consider the unusual history of ssDNA–surface interactions during array fabrication. This arraying treatment often includes ssDNA nanodroplet solution deposition onto a substrate, non-equilibrium spot drying onto the solid substrate under increasing ionic strength, desiccation, subsequent aqueous rinsing in high ionic strength media, and desiccation again, then final exposure to sample where rapid rehydration and hybridization must occur. This atypical wet-dry processing of immobilized ssDNA produces considerable opportunities for unusual, even irreversible, ssDNA–surface interactions and adsorbed states beyond consideration in classical 2-body treatments. When interactions between ssDNA segments and the substrate are repulsive, scaling theory for isolated end-tethered polymers predicts a depletion zone of ssDNA segments near the surface in the absence of ssDNA–surface adsorption enthalpy. This is characterized by chain segment distribution, ρ(z), increasing as ρ(z) ∼ z1−ν/ν with the distance z from the substrate110 (shown in Fig. 6) and ν is the Flory scaling exponent. At larger z distances, the influence of the surface weakens and the chain segment distribution approaches a maximum value ρ(Rg) ≅ σ(n)Rg – the average segment density within the polymer layer whose height, H, is approximately given by Rg of the free, unperturbed chain, where n is the number of segments attached to it by one of its ends at a tether surface density of σ.51,111,112 Beyond this z ∼ Rg, the segment distribution falls off normal to the surface. Hence the ssDNA tethered chain for lengths of at least 1000 bases exhibits a maximum chain density at a distance well-away from the surface, not at the surface.59
The reduced chain segment distribution close to the substrate, together with its faster decay for distances z ≥ Rg suggests that the chain segment distribution of an end-tethered polymer in the low-density limit (i.e., σRg2 ≤ 1) is distinct from its bulk solution form (Fig. 6A) and is strongly asymmetric, resembling the shape of a mushroom (compare Fig. 6A with Fig. 4B and 5B).113 Lehner et al.112 measured segment distributions of end-tethered polymers with uniform chain length in a good solvent using confocal fluorescence microscopy on isolated ssDNA labeled with dye to evaluate the chain conformations. The segment distribution ρ(z) as a function of distance from the substrate, z, measured for chains with contour lengths of 15.4 μm ≤ L ≤ 59.4 μm showed persistence length as Rg ∼ Lp0.57±0.05 supporting the presence of excluded-volume interactions between charged ssDNA segments.
ssDNA chains have been shown to adsorb laterally on surfaces with no chain–chain interpenetration, with Rg estimated as 0.38N1/2 nm, where N is the number of ssDNA nucleotide bases.108 At high ionic strength (0.1 M salt), ssDNA probe surface density is proportional to the reciprocal of the effective cross-section of a DNA probe coil, 1/Rg2, corresponding to an inverse dependence on its length, N, i.e., probe surface density ∼1/N.34,81,108 Longer ssDNA probes exhibit flexible coil behavior (i.e., Rg ∼ N1/2) in high ionic strength solution (measured for ssDNA 280 to 5380 nucleotides long where the Debye length is sub-nanometer).108 This provides two insights; (1) that ssDNA dimensions on surfaces are different than that of their respective bulk states at high ionic strengths, and (2) this distinct difference in bulk (i.e., target) versus surface (i.e., probe) ssDNA chain dimensionality affects their ability to hybridize.114,115 Another profound outcome is that ssDNA surface coverage decreases with N over the entire ssDNA size range investigated, dropping by nearly an order of magnitude from ∼6 × 1012 probes cm−2 for 8-mer ssDNA probes to ∼7 × 1011 probes cm−2 for 48-mers.81 At low ionic strength, temperature-dependent stiffening of ssDNA is rationalized by combining counterion condensation theory with the OSF description of the electrostatic persistence length and the unstacking of bases at elevated temperatures.87,116 Steel et al.81 showed that surface coverage of DNA probe strands longer than 24 bases begins to decrease notably with increased probe length, consistent with less ordered surface arrangement of DNA chains, reflecting increasingly polymeric behavior.
7.5 Electrostatic effects on ssDNA chain properties
Manning's counterion condensation concept for highly charged polyelectrolytes, including ssDNA, essentially condenses counterions near charged polymer surfaces.88 The approach was proposed for rod-like polyions with large persistence lengths as a conceptual framework, not as a predictive theory. The condensed counterion layer is sufficient to neutralize ∼76% of DNA formal charge, reducing the anionic charge of each phosphate to −0.24e; divalent and trivalent counterions reduce residual phosphate charges to −0.12e and −0.08e, respectively88 but these cations also induce altered DNA bending states (vide supra). In doing so, the electrostatic contribution to DNA stiffness is reduced by phosphate backbone charge screening under counterion condensation.71,87 Cation binding to DNA is an ion-exchange reaction, releasing other counterions into bulk solvent and providing favorable entropic sources of binding energy. Schurr et al.89 complemented this theory using experimental data comparisons with theoretical models with polyelectrolytes, showing the effects of counterion condensation on ssDNA configuration at surfaces. Other experiments show that supercoiled dsDNAs in solution deform farther from their minimum energy configuration than corresponding surface-confined dsDNAs, with the number of configurations available in solution dsDNA vastly greater than surface-confined DNA.89,117,118 Optical tweezers experiments showed decreasing dsDNA persistence length for increasing counterion valence102 meaning that dsDNA is more flexible with increased counter-cation valency. Manning also proposed contributions of DNA's phosphate anion charge to DNA stiffness; dsDNA helical configuration represents an equilibrium between stretching forces caused by inter-phosphate repulsion and compressive forces caused by attractive interactions between Hoogsten or Watson–Crick base-paired nucleotides.119 Thus, the strong dependence of both ss- and ds-DNAs’ persistence lengths on salt concentration and resulting chain condensation is manifest through double layer screening interactions. Recent observation of major conformational changes for a ssDNA brush (968 bases) confirmed the universal scaling of polyelectrolyte brush height as a power of 1/3 with density-to-salt ratio. However, the actual effects of DNA charge on the molecular rigidity of DNA are debated.120 Theoretical and experimental results have shown that DNA conformation depends on the local molecular-level charge balance.121 X-ray crystallography experiments involving tethering of cations in the major groove of dsDNA (directed radially outward) suggested that these cations mediate chain bending and dsDNA collapse through electrostatics without disrupting base stacking.19 Thus, both phosphate neutralization and adduction (cations bound to major grove) induce spontaneous dsDNA bending,121,122 with influences on persistence length and layer thickness as described (vide infra).Dramatic reductions often observed in immobilized ssDNA hybridization efficiency and thermal denaturation curve broadening as immobilized probe surface density increases are attributed to the so-called Coulomb blockage.123 Intra-chain Coulombic repulsion between like-charged ssDNA nucleotides in immobilized probes in crowded surface packing results in a more extended and swollen chain conformation. Inter-chain charge-charge repulsion is a natural consequence of laterally immobilized ssDNA, adding to steric forces in compelling immobilized ssDNA to stretch away from the surface, subject to local chain rigidity and conformational limitations. High local field strengths are expected from these high charge densities fixed on surfaces via DNA arraying. On metal surfaces (e.g., thiolated ssDNA on gold) this also generates image charges.121 This considerable negative electrostatic barrier leads to surface repulsion of incoming ssDNA target as well. These local opposing surface potentials must be mitigated to enable duplex formation with incoming targets of like charge density, and also limit lateral probe–probe interactions that would interfere with hybridization. This necessitates use of high ionic strength printing and hybridization buffers and wash solutions to screen charge density and enable shorter-range duplex hydrogen bonding through short ssDNA oligomer base complementarity. Additionally, steric barriers to duplex formation are introduced by the short, rigid, dense ssDNA chain densities arrayed on surfaces. Electrostatic contributions to ssDNA stiffness are reduced by phosphate screening (i.e., counterion condensation).71,124 Local ssDNA deformability (softness) with respect to chain bending due to excess cation–ssDNA binding121 both help induce spontaneous DNA bending and twisting to alter chain conformations in a ssDNA sequence-dependent manner.125,126 These are proposed to facilitate statistical sampling of multiple chain states between surface and bulk ssDNA pairs to produce duplexes. Probe ssDNA–surface interactions that produce multiple ssDNA surface-adsorbed states (i.e., loops, trains, and tails)127 or induction of ssDNA secondary structures confound this ideal duplexing situation: entire probe strand sequences may not be available to bind target if adsorbed to surfaces or too stiff to accommodate incoming target encounters required for duplexes.80 Control of probe conformation and orientation is therefore essential to ensure high pairwise reactivity, orientation, accessibility, and stability of the surface-confined probe, and to avoid nonspecific binding.25 Conformation and orientation of ssDNA probes on gold surfaces have been extensively studied by varying ionic strength, temperature,116 length of probes and their linkers/spacers, and monitoring of these probes with magnetic and fluorescent labels128 indicating that all these factors play a major role in duplex formation.
Substantial differences in hybridization thermodynamics and hybridization efficiency have been reported for ssDNA free in solution versus surface-tethered DNA (i.e., for both glass and gold surfaces) due to transport, steric (i.e., probe density) and predominant electrostatics effects.80,111 Comparison of data obtained from commercial microarrays suggests that solid-phase hybridization is less thermodynamically favored than hybridization of the same sequences in solution.129 At lower ionic strengths, an electrostatic balance between the concentration of immobilized oligonucleotide charge and solution ionic strength governs the onset of hybridization. The electrostatic repulsion of the target nucleic acids from the probe array dominates the binding thermodynamics, causing the Coulombic blockage of the hybridization, leading to dramatically decrease of both hybridization efficiency and thermal denaturation curve broadening as probe surface density increases.123 With increasing ionic strength, the electrostatic dominance diminishes and hybridization behavior becomes more complex.73 Suppression of hybridization affinity constants relative to solution values, and their weakened dependence on the concentration of DNA counterions have indicated that the immobilized strands form complexes that compete with hybridization with analyte target strands.
For a typical hybridization assay on ssDNA-immobilized glass surfaces under conditions near pH 7 in salt content of 1 and 0.1 M, the surface potential is −35 and −80 mV, respectively.130 At a high probe density of 3 × 1013 per cm2 in an ionic concentration of 0.3 M salt, the maximum electrostatic potential in the ssDNA probe layer is ∼130 mV.131 This repulsion increases further as DNA duplexes are formed with the probe layer (i.e., charge density increases), accompanied by crowding and steric issues, and suppresses further hybridization with Columbic blockage and reduced microarray efficiency and sensitivity.123 Hence, Coulombic screening using high ionic strength hybridization buffers and multivalent counterion enhancement can mitigate some of these adverse effects by reducing Debye lengths.132 Nonetheless, their effects on DNA probe and target molecular conformations are frequently not considered in influencing how probe and target must interact to duplex.133 Use of three-dimensional arrays using probe immobilization in gels, mimicking aspects of solution hybridization, can also reduce these effects on DNA duplex formation.134 Alternatively, reduced DNA chain–chain repulsion and enhanced hybridization kinetics at surfaces have been achieved by applying a positive electrostatic potential to ssDNA-immobilized surfaces, leading to claims for increasing assay sensitivity and stringency by reversing the field once hybridization is achieved to repel all mis-matched pairs with reduced binding affinities.135,136
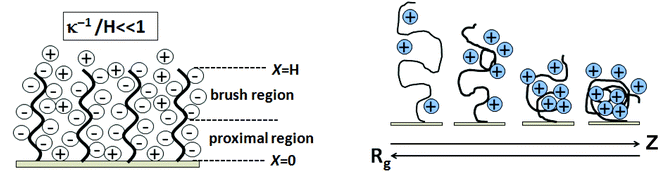
Schematics showing Coulombic blockage by ssDNA on surfaces and the dependence of Rg on ionic strength (ion valence of Z) are shown in Fig. 7. Two different scenarios emerge in the charged brush regime characterized by two length scales: the average vertical ssDNA extension from the surface, H, and the typical extent of the counterion cloud thickness, denoted by x shown in Fig. 7. Counterions can either extend outside the brush, x > H, as shown, or be confined inside the brush, x ≈ H. In the weak-charge limit, the counterion cloud has a thickness x larger than the thickness of the brush layer, H. For the strong-charge limit, where all counterions are contained inside the layer, the brush and cloud have a single length scale, x ≈ H.137 As shown in Fig. 7 (left), ions pass freely between the layers and the external electrolyte for case (x > H). The ssDNA chains provide a constant negative charge density inside the brush, producing a local electric field interacting with salt ions referred to as the proximal region. In a brush regime, the surface field decays and is zero. The Debye length (electrostatic screening) with the ssDNA layer is sufficiently less than the layer thickness, H. Neutron reflectivity measurement indicated that for 25-mer oligonucleotides at coverage of 3 × 1012 cm−2 in 1 M NaCl, the Debye length (κ−1) is below 0.2 nm.132 The influence of ionic strength on the flexible chain of Rg is depicted in Fig. 7. The ionic strength (Z) and Rg have inverse relations due to chain condensation with added salt, affecting the probe and target chain conformations, and probe Rg influencing duplex formation. Different buffer salts influence probe immobilization efficiencies and kinetics. Petrovykh et al.138 showed that buffers with divalent salts dramatically increase the efficiency of immobilization and result in high immobilized surface densities.
7.6 ssDNA bending and elasticity
ssDNA chain stiffness opposes interaction processes in duplex formation requiring bending, twisting, and looping typical for conformationally induced hybridization.139,140 As both ssDNA probe accessibility and target binding affinity are key parameters affecting hybridization efficiency in surface-based biosensor technologies, improved chain accessibility and flexibility result in higher hybridization efficiency.141 The classic framework for understanding long-range ssDNA shape and resistance to bending is explained fairly well by the WLC for ssDNA flexibility.19 Marko and Sigga142 described the free energy required to deform a stiff helical, symmetrical DNA molecule to explain the bending and twisting of ssDNA with elastic theory. Cluzel et al.143 measured ssDNA bending by the movement of the micropipette tip causing the tethered ssDNA molecule to be stretched between the optical fiber of known stiffness and the bead with the applied force proportional to the measured bending for a known stiffness of the optical fiber. Willam and Maher121 explained DNA bending using electrostatic theory for chain phosphate neutralization and excess cation binding to the major grove of DNA, inducing spontaneous molecular bending. Local ssDNA bending and chain twisting is also sequence-dependent.125,126 Both kinked WLC (KWLC) and single-stranded bubble models propose local distortions that could strongly enhance DNA bending and bidirectional molecular torsional flexibility.144 ssDNA solution conformation is often described using statistical approaches such as flexibly jointed or WLC models.94 However, dsDNA distortion such as formation of circles smaller than ∼85 bp which include sharp dsDNA bending or kinking cannot be explained with the WLC model.145,146 Thus, while models and simulations for both ss and ds DNA chain dynamics and conformations can be used to explain certain experimental data, they are often limited in accuracy, case-specific and not universal. This is particularly true for short ssDNA tethered chains at surfaces. Similarly, the forces (or, more likely, balance of forces) responsible for ssDNA's unique bending stiffness remains unresolved,19 also for immobilized strands at surfaces. The fundamental forces responsible for the remarkable resistance of DNA to bending and twisting remains controversial.19Zhang et al.147 studied ssDNA elasticity through Monte Carlo-based implementation of a modified freely jointed chain (FJC) model with electrostatic, base-pairing, and base-pair stacking interactions. In low-salt solution, electrostatic interactions dominate while at low forces, the molecule can be more easily aligned than an unmodified FJC. In high-salt solution, secondary hairpin structures appear in ssDNA by self-complementarily while external stretching induces a hairpin-coil structural transition that is continuous for ssDNA made of random sequences. Their modeling calculations along with experimental data indicated that base pairing of ssDNA tends to form a nested, independent planar hairpin structure rather than a coiled in solution. These results demonstrate that increased ssDNA accessibility increased dsDNA hybridization efficiency using pH- and salt-driven bending of ssDNA probes.
7.7 Factors influencing DNA persistence length
Chain persistence length varies depending on whether chains are bound to surfaces or in bulk solution, with various surface interactions, temperature, type of buffer, divalent or multivalent ions present, and also based on the method of measurement.148 For example, the apparent persistence length (Lpa) of dsDNA assessed using AFM is much shorter on 3-aminopropylsilane layers over mica (AP-mica) (zeta potential > 0 mV) than on bare mica (zeta potential < 0 mV). The same surface effect has also been shown qualitatively for plasmid DNA with Lpa of dsDNA varying from 55 to 100 nm on bare mica and from 20 to 40 nm on AP-mica surfaces.149 Persistence lengths measured by different methods vary considerably: the dsDNA Lpa value measured by electron microscopy is 150 nm in 30 mM ammonium acetate150 in minimum salt concentration, whereas it is 35–50 nm in solutions with Mg2+ cation concentrations above 0.1 mM.151 Additionally, the experimental persistence length does not correlate well with simulations (consistently less than experimental values) since the persistence length is highly sensitive to factors such as base sequence, hairpin loops, and differences in experimental methods (typically fluorescence spectroscopy, laser tweezers, and gel electrophoresis). Under physiological conditions, conventional ssDNA values for Lp are near 50 nm or ∼150 bases. Evidence also suggests that sequence-dependent differences in base stacking forces can measurably influence ssDNA persistence length. However, the scale of these stacking effects has never been experimentally compared with electrostatic effects.152,1537.8 Persistence length of ssDNA tethered to surfaces
Understanding the structure of ssDNA tethered to surfaces is critical for optimizing its accessibility and binding to target ssDNA, influencing hybridization rates and efficiencies, and ultimately assay signal quality and reliability. While a substantial literature exists on ssDNA Lpa in solution, relatively few measurements of ssDNA persistence lengths tethered to surfaces are reported, despite the implications of chain conformational dynamics, mobilities and mechanics on duplex formation. Calculations of ssDNA persistence length based on a coarse-grained model is dependent on chain length.154 For a small, identical number of bases, ssDNA has a longer end-to-end distance (0.64 nm distance between bases) compared to dsDNA (i.e., 0.34 nm inter-base distance for coiled base-paired duplexes). However, adding more bases, ssDNA yields shorter end-to-end distances than dsDNA because it curls over on itself much more on average, reflecting its shorter persistence length (≈1.48 nm).155 Some experimental and simulation approaches have evaluated DNA persistence length as a function of temperature, salt concentration, base sequence, interaction potential strength, and local position along the chain. ssDNA persistence length tethered to a modified graphite surface using atomic force microscopy at very low ionic strength was Lp = 9.1 nm and this decreases with increasing ionic strength to 6.7 nm and 4.6 nm at 1 mM and 10 mM NaCl, respectively.108,156 Murphy et al.94 used FRET to deduce persistence lengths for ssDNA (oligodeoxythymidylates, dTN) of chain lengths (10 ≤ N ≤ 70 nucleotides) over a wide range of salt concentrations. Persistence length varied from 1.5 nm in 2 M NaCl to 3 nm in 25 mM NaCl. The ssDNA in this case was not bound to a surface directly but attached to dsDNA immobilized on a streptavidin-coated quartz surface. Chen et al.105 measured persistence length of dT40 tethered to a glass surface at the same ionic strengths as Murphy et al. They however used X-ray and fluorescence methods and found that persistence lengths were 50% less for tethered ssDNA, possibly due to glass surface interaction influences on immobilized chain conformations. Crozier et al.157 reported the persistence length of ssDNA with molecular dynamics (MD) simulations using a coarse-grained model for single polyelectrolyte chains grafted to a solid surface. This study revealed a small intrinsic persistence length that is highly extended in zero salt simulations. Added salt does shrink the chain as salt ions enter the volume near the chain. Persistence lengths predicted for ssDNA using the coarse-grained DNA model (with bases modeled as rigid-body ellipsoids to capture their anisotropic stereochemistry) initially decreases with increasing temperature in accord with the WLC model; however, at higher temperatures where nonlocal interactions become important, the persistence length shows an increasing trend over a broad range of temperature. Below the crossover temperature (i.e., the transition between expanded and collapsed chain globules), base stacking interactions stiffen the ssDNA chains and increase its persistence length, while above this temperature, nonlocal base–base van der Waals interactions soften the chain and decrease the persistence length.154The persistence length for a homogeneous ssDNA comprising homo-adenine as long as ∼50 bases is more than the corresponding homogenous strand of thymine bases (LP ≈ 2 bases) at low temperature due to the large enthalpic costs for hairpin formation in poly(A) over poly(T) nucleotides.125 However, at higher temperatures due to non-local interactions between bases, poly(A) forms a collapsed globule with shorter persistence length while poly(T) forms an expanded globule.154 Temperature has a drastic influence on persistence length and Rg for both ss-poly(A) and ss-poly(T). Thus ssDNA persistence length tethered to surfaces varies considerably with many factors (temperature, ionic strength, sequence and type of surface immobilization), influencing accessibility and properties for further binding target DNA and important for considering probe accessibility and mobility in the microarray chip design.
7.9 Persistence length of dsDNA at surfaces
Hybridization of ssDNA to form dsDNA is a necessary event required of two complementary DNA strands (probe and target) in a microarray assay. The physical properties of each DNA partner change upon hybridization: dsDNA is much more rigid than its ssDNA precursors.158 This difference in chain rigidity can be described in terms of altered persistence length.159 Persistence length of dsDNA has been shown to be ∼50 nm in environments containing salt concentrations greater than 10 mM, while that of ssDNA has been shown to be only about 1 nm.151 As discussed (vide supra), ssDNA molecules of lengths less than 50 nm have very different chain rigidities compared to dsDNA molecules of the same lengths, and each as distinct persistence lengths in solutions versus bound states. This several disparate properties must converge in their hybridization at a surface. Stretching persistence length of dsDNA has also been measured using single-molecule techniques.97,160 Abels et al. measured individual dsDNA molecules attached at one end to a glass cover slip and at the other end to a magnetic bead, yielding values of 54 nm, in agreement with other values reported.95,97,161 Brinkers et al.96 measured persistence length for a lone dsDNA using dark field microscopy by capturing the projected positions of attached nanoparticles undergoing constrained Brownian motion. With Monte Carlo simulation and experimental evidence, the authors evaluated persistence lengths of 45 single molecules of four different lengths of dsDNA measured under high salt concentrations. These had a mean value of 35 nm (standard error of ±2.8 nm). In contrast, Mastroianni et al. measured short dsDNA persistence lengths in solutions with dsDNA-linked dimers of gold nanoparticles using small-angle X-ray scattering without requiring any external forces or binding to a substrate. These results for dsDNA comprising 42–94 bases were consistent with a simple WLC model of dsDNA elasticity and comparable to results from Monte Carlo simulations. A persistence length of 50 nm (∼150 bases) is consistent with results from single-molecule force-extension experiments on much longer dsDNA chains. These results contrasted recent suggestions of enhanced DNA flexibility at these length scales.162 dsDNA persistence length also depends on media ionic strength, similar to ssDNA.The persistence lengths of both ssDNA and dsDNA have the same functional dependence on ionic concentration. Notably, dsDNA is roughly 55 times stiffer at 0.02 M, 25 times stiffer at 0.04 M and 52 times stiffer at 0.13 M than ssDNA.108 Extra stability is provided by hybridization since weakening base–base interactions with increasing ionic strength only modestly reduces chain stiffness due to stacking.154 Decreased DNA persistence length was also observed for increasing counterion valency.9
7.10 ssDNA chain elasticity
DNA chain mechanical properties include force extension (stretching), elasticity, torque as a function of twist for stretched ssDNA and torsional strain.163 ssDNA chain flexibility and conformational adaptation are important factors for duplex formation. Various theories are proposed to understand ssDNA elasticity. The classic framework for understanding long-range ssDNA chain shape and resistance to bending is embodied in the WLC model of ssDNA flexibility in a Kratky–Porod chain (i.e., simple polymer chain with no torsional stress).164 The elasticity of longer DNA chains including looping, distance-dependent flexibility165 and J-factor (ring-closure probability for a given DNA length, an experimentally accessible measure of polymer stiffness) are consistently explained by the WLC model.166AFM and optical tweezers have been used to successfully measure DNA stretching under applied forces.100 Measuring DNA elasticity by tethering DNA to a surface and applying various loads to determine chain elongation and yield points are also well known.167 Various experimental methods and instruments with newer technologies have aimed at determining DNA's molecular elasticity. However, dsDNA elasticity is highly influenced by factors such as the type of surface anchor, a duplexed terminal anchored to the material, type of substrate material (e.g., hydrophilic or hydrophobic) and media ionic strength.168,169 Changes in ionic strength predict DNA elasticity based on persistence length and elastic modulus determinations. Lowering ionic strength increases persistence length and reduces DNA elastic stretch modulus.100
The finite WLC (FWLC) model modifies the classical WLC model by including finite chain length, chain-end boundary conditions and bead rotational fluctuations (inherent in optical trapping assays where beads are used to apply forces).170 The FWLC solution provides a significant improvement to the theoretical framework used to analyze single-molecule experiments over a broad range of experimentally accessible DNA lengths, including both short contour length (a few hundred nanometers) and very long (microns in contour length) molecules.170 The freely jointed chain (FJC) model reliably predicts properties for a polymer chain whose segments are unrestricted in their orientation, corresponding to freely rotating segments of the Kuhn length (i.e., 2Lp). However, the FJC model is not a good approximation for the elastic behavior of DNA molecules at large extensions (i.e., H > Rg).139 The WLC model is much better for describing the behavior of oligo-DNA particularly at large extensions (i.e., for DNA fragments 105–130 bases in length, H > Rg). However, dsDNA cyclization studies have revealed the non-applicability of the WLC model to DNA bending on biologically relevant length scales (∼85 bases in length). The WLC model cannot describe the force of extension, solution scattering, and long contour-length cyclization experiments, and therefore alteration of the WLC model is required to include sharp bending or kinking of dsDNA.171
The elastic properties of both short and long ssDNA and dsDNA tethered to charged and uncharged supports under aqueous conditions are important in defining probe interfacial properties affecting the kinetics, thermodynamics and binding efficiency of DNA target in microarrays. Electrical manipulation studies by Rant et al. of ssDNA and dsDNA end-tethered to gold surfaces in electrolyte solutions showed dissimilar dynamic behavior attributed to elasticity of the bound DNA (flexibility of ssDNA and rod like stiff behavior of dsDNA).172 Stiff polymers undergo rotation around their anchoring pivot point on a surface (i.e., a cone of polymer occupancy); flexible polymers, by contrast, are pulled onto the attracting surface, segment by segment, leading to ssDNA loops, trains and tails. These features are important determinants of ssDNA accessibility and the ability of self-assembled probes to bind complementary target sequences.
Studies of DNA mechanical properties indicate that DNA's elasticity is similar to that of synthetic polyamide, nylon.173 Recently, Eijck et al.174 used neutron scattering through aligned fibers of dsDNA to gauge the speed of sound waves vibrating along DNA helices, yielding a chain force constant (modulus) of 83 N m−1. Using a computer simulation model of DNA's vibrations, the authors explained the large variation in previously reported dsDNA elasticities ranging from 0.3 to 133 N m−1. Studies of mechanical properties as early as 1995 by Marko and Siggia analyzing stretching of dsDNA tethered at one end and stretched by a force applied directly to the free end by an electric field or by hydrodynamic flow have been compared with a statistical mechanical treatment of the WLC model. All experiments display a strong stretching regime where end-to-end distance approaches the DNA contour length as 1/(force)1/2, consistent with WLC elasticity.142,175
Experiments with torsionally constrained single molecules provided the first direct measurements for coupling twists and stretches in dsDNA.176 A constrained twist of a DNA strand manifests itself as a link, twist or writhe due to DNA's elastic entropy.176 Experiments using torsionally constrained DNA have permitted determination of coupling between DNA twist and stretch.91,177,178 Results are consistent with fundamental principles predicted from classical WLC elasticity theory. Single-molecule stretch experiments indicate that dsDNA deviates from the inextensible WLC model up to forces of 10 pN. Beyond 65 pN, dsDNA suddenly changes its form from B to S, stretching up to 70% beyond its canonical B-form contour length. dsDNA's “S form” is stable in high salt up to forces of approximately 150 pN (for random sequences). Some 300 pN above this force, S-DNA melts into single strands that exhibit the characteristic force/extension behavior of ssDNA.177 The simplest extensible WLC with twist rigidity is considered a model for DNA under tension. However, dsDNA is chiral; demanding that helix stretching coupled with twisting must lead to a structural transition.97,84 Force–extension occurs when single DNA molecules are twisted in either direction and pulled to high force179 and the phase boundaries correspond to the structural states of DNA in coexistence with adjacent pure phases.180 Stretching of helical dsDNA twists molecule, perturbing its twist degree of freedom and leading to its supercoiling as it relaxes – a distinct phenomenon occurring in DNA compared to other polymers.
When dsDNA is stretched beyond its contour length, a highly cooperative overstretching transition is observed, dependent on ionic strength. Wenner et al.181 performed measurements of DNA elasticity and overstretching transition by stretching single dsDNA molecules as a function of monovalent salt concentration using optical tweezers. DNA persistence length with sodium chloride concentration change from 1000 to 2.57 mM increased from 46 to 59 nm, with the elastic stretch modulus remaining constant. However, as this salt concentration was further decreased, the overstretching transition force decreased from 68 to 52 pN, attributed to reduced dsDNA double helix stability. Although Watson–Crick hydrogen bonds break as helical DNA is overstretched, these data indicate that both DNA strands remain close together during the transition. Punkkinen et al.182 theoretically described the salt-dependent over-stretching transition of DNA by coupling the two-state model and the elasticity theory proposed for monovalent salt effects on elastic modulus during the transition. In dsDNA, the effective chain length per unit charge varies with salt in agreement with both the Manning71 and Poisson–Boltzmann models for thin polyelectrolyte rods,183 whereas the other model parameters describing structural features exhibit little salt dependence.71 Thus, electrostatic components of force-induced DNA overstretching might be apparently mediated mesoscopically via elasticity.182 This is an important factor since DNA microarray duplexing assays are conducted typically in high ionic strength buffer and salt systems to minimize electrostatic repulsions while maximizing ssDNA elasticity, extension and accessibility that impact the efficiency of target binding and the stability of resulting dsDNA at surfaces.
DNA solution pH also affects chain extension, efficient hybridization and the stability of the resulting DNA duplex via influences on DNA conformation and duplex stability. Single molecule dsDNA exhibits a highly cooperative overstretching transition under varying pH at high ionic strength.121 Williams et al.184 showed that as solution pH was increased from pH 6.0 to 10.6 in 250 mM NaCl, overstretching transition forces decreased from 67.0 ± 0.8 pN to 56.2 ± 0.8 pN, while the transition force width remained nearly constant. As the pH was lowered from pH 6.0 to 3.1, the overstretching force decreased from 67.0 ± 0.8 pN to 47.0 ± 1.0 pN, but the transition width increased from 3.0 ± 0.6 pN to 16.0 ± 3 pN. These results quantitatively support that DNA strand dissociation, or melting, occurs during the overstretching transition.184 However, other data suggest that dsDNA should unwind under tension as it is pulled towards its denatured structure.91,143,177,185 Gore et al.186 used rotor bead tracking to directly measure twist–stretch coupling in single dsDNA molecules. dsDNA overwinds under tension, reaching a maximum twist at a tension of ∼30 pN, and when increased above this critical value, the dsDNA begins to unwind. The observed twist–stretch coupling predicts that dsDNA should also lengthen when overwound under constant tension. This property would possibly explain the anomalously large torsional rigidity of dsDNA186 and might also have implications for surface-tethered DNA since ssDNA must stretch and twist to form dsDNA when duplexing new target to compensate for variability in chain dimensionalities at encounter, and to align bases for optimal hydrogen bonding in duplexes. dsDNA is well-described as a worm-like chain at concentrations of di- and trivalent cations capable of inducing condensation but such condensation is prevented by keeping the dsDNA molecule stretched. A retractile force appears in the presence of multivalent cations at molecular extensions that allows intramolecular contacts, suggesting that condensation in stretched DNA occurs by a “thermal ratchet” mechanism.102 Using designed sequences of DNA with nearly identical DNA curvatures (based on same length, e.g., 132 bases) with different elasticities and varied AT base pair (i.e., duplex melting point) contents, Raghunath et al.187 showed that dsDNA persistence length varies by almost 30% between sequences containing 61% AT and 45% AT nucleotides.
DNA, like other biopolymers, differs from classical polymers in its intrinsic torsional stiffness. The force of extension, torque, and angle of DNA for structural and elastic parameters of torsionally melted dsDNA single molecules was measured by Sheinin et al.188 using an angular optical trap. Under moderate forces, melted DNA assumes a left-handed structure and is highly torsionally compliant. For lower forces, melted DNA properties are highly dependent on DNA sequence.188 Moroz and Nelson140 studied DNA force extension as a function of over-twist over a wide range of applied force with a theoretical model. The statistical character of DNA conformations under tension changes from a classical random walk to “torsional random walk” whose random variables are the direction of each step relative to its predecessor, together with a relative axial twist. The similarity between Metropolis Monte Carlo simulation189 and experimental measurement of torsionally stretched DNA by Strick et al.91 strongly suggests that correlations observed between base stacking and permanent hydrogen bond constraints play an important role in understanding this supercoiled DNA elasticity. Bryant et al.163 measured torque as a function of twist for stretched dsDNA: that is, torsional strain in over- or under-wound molecules to power the rotation of sub-micrometer beads serving as calibrated loads. With dsDNA's twist elasticity, the torsional modulus shows an over- or under-wound dsDNA molecule behaving as a constant-torque wind-up motor capable of repeatedly producing thousands of rotations, and that an overstretched molecule acts as a force–torque converter. These results reflect the importance of external forces on dsDNA. However, dsDNA elasticity and mechanics influences occurring at the microarray surface are not directly comparable to these results since most of these molecular mechanics exercises impose applied forces, extensions and rate-dependent transitional behaviors not relevant to array duplex formation. Therefore, these effects should be evaluated further for specific effects on target capture, especially the hybridization transitions of ssDNA to dsDNA tethered to surfaces influenced by external factors such as ionic strength and pH.
In summary, absent the application of external extensional forces, short ssDNA maintains a compact conformation consistent with a short polyelectrolyte; its chain extension per base pair is shorter than that of dsDNA for forces smaller than ∼6 pN. At higher applied forces, however, the situation is reversed. As the ssDNA single strand is not constrained to follow a helical path in extension, it becomes nearly twice as long as dsDNA as it is pulled in tension, forming brush-like conformations on the surface under applied forces (i.e., shear, tensile, electrical).97 These chain tensile properties seem to be affected by their surface environment when tethered.190 However, without external forces, ssDNA chain conformational adaptations in a tethered-state must adapt to accommodate DNA target binding on surfaces by overcoming these local higher chain energies, extending spontaneously from a surface to form an accessible chain capable of rapid target encounter and dsDNA duplex formation that is then much stiffer. dsDNA chains are generally helical with twisted conformations that contain complex torsional and elastic energies exhibiting non-linear chain extension responses to external forces. Rather than extending fully to a brush-like state with forced extension, dsDNA is separated into ssDNA unimers by stretching forces strong enough to cleave chain–chain base-paired hydrogen bonds after torsional and helical elastically stabilized conformational changes are completed.191
The longer the DNA chain, the higher the chain polyphosphate negative charge density at assay pH, affecting chain conformational mobility as seen through persistence length and chain mechanical changes that change assay hybridization efficiency.141 Importantly, longer ssDNA and dsDNA chains respond to ionic strengths and applied electrical forces differently than shorter ssDNA typically used in probe tethering at surfaces (i.e., ssDNA, but also dsDNA).131 Longer ssDNA chains forms secondary structures that alter strand accessibility and hybridization while shorter chains reduce the sensitivity of detection. Additionally, longer ssDNA probes have Coulombic repulsion and chain–chain steric issues that scale depending on their immobilized density much differently than shorter probes.51 Since target chain conformations in bulk solution are also distinct from those of ssDNA probes at surfaces, hybridization must change both probe and target chain dimensions and conformations upon encounter, and within the complex double-layer and steric environment of the array surface-immobilized probe, in order to produce a successful assay event. How these molecular properties are discriminated for duplex specificity, or controlled or optimized in current array formats is not understood, at least at the level of fabrication and experimental use.
8. Extending ssDNA and dsDNA tethered chains biophysical behaviors to microarray applications
Determination of tethered ssDNA probe and dsDNA duplex conformations on surfaces and correlated hybridization properties with incoming ssDNA targets provides empirical information required to understand barriers to DNA duplex formation in arrays. This information is difficult to collect but is necessary to rationally move DNA interfacial applications forward using known surface designs and described behaviors to improve their reliability, and clinical and biotechnological utility in many surface-bound formats. Immobilized ssDNA monolayers are widely used in both fundamental and applied genomics and are also versatile experimental models for elucidating fundamental behaviors of charged polymers at interfaces. The physical behavior of these assay systems is to a large extent governed by internal microenvironments within adsorbed or tethered layers of polyanion ssDNA oligonucleotides, external influences from salts, pH, and temperature, and resulting fundamental intermolecular forces that yield dsDNA duplexes within complex surface states.ssDNA molecular conformations tethered to a microarray surface significantly affect the rates and efficiencies of hybridization. Many diverse methods have been applied to determine structural features of the immobilized ssDNA layer, such optical or contact methods as ellipsometry,192 optical reflectivity,193 neutron reflectivity,194 X-ray photoelectron spectroscopy,195 FRET,94 SPR,196 and AFM.197 Many are spatially or time-averaged measurements and intrinsically not very sensitive to variations in ssDNA chain conformations or surface chain densities shown to influence ssDNA molecular behavior (vide supra). The ssDNA immobilized adlayer response to alternating repulsive and attractive electric surface fields studied by time-resolved fluorescence measurements of ssDNA and dsDNA end-tethered to gold surfaces in electrolyte solutions shows distinct dynamics for flexible single-stranded oligoDNA probes versus stiff dsDNA. Hydrodynamic simulations rationalize this finding to disclose two different kinetic mechanisms: stiff polymers undergo rotation around the anchoring pivot point while flexible ssDNA polymers are pulled onto the attracting surface segment by segment.198
To assess conformations of surface-bound ssDNA, Moiseev et al. used an optical interferometric technique (spectral self-interference fluorescence microscopy) for precise polymer extension measurements.128 This method estimated the shape of coiled ssDNA, the average tilt of dsDNA of different lengths, and the amount of hybridization by evaluating the average location of a fluorescently labeled nucleotide in a ssDNA layer relative to the surface. The ssDNA conformation varied on surfaces based on differences in ssDNA length, whether dye labeling was at the proximal or distal end of the probe and with the dye labeling position on the ssDNA target.128 Interestingly, unlabeled 50-bases ssDNA probe strands hybridized with 21-bases ssDNA targets dye-labeled at their distal ends and complementary to either the probe's top or bottom part changed conformations differently. The surface distance of the duplex distal end increased from 5.5 to 6.5 nm for the duplex target complementary to the probe's distal end, different from the proximal duplex conformation relative to the surface.
The local electrostatic environment within a dense, tethered polyanion ssDNA surface layer differs strikingly from ssDNA in solution and affects DNA array behavior (vide supra) and that of related surface-focused technologies. Electrochemical techniques have been used to probe the ionic microenvironment within end-attached ssDNA oligonucleotide monolayers (i.e., as ssDNA brushes). Local electrostatic field strengths within these immobilized layers are estimated to be −35 and −80 mV for salt contents of 1 and 0.1 M, respectively) for a probe density of 5 × 1012 per cm2, reflecting the expected substantial local surface potential from highly phosphorylated nucleotides.131 Vainrub and Pettitt predicted strong electrostatic destabilization effects for ssDNA immobilized in electric double layers.136 Retention of counterions by the ssDNA brushes manifests as lowered susceptibility of the interfacial capacitance to external salt conditions. The charging response exhibits signatures of structural reorganization whereby DNA strands stretch or relax with changes in solution ionic strength, consistent with expected physical behavior of charged polymer layers. The quantity of bound ssDNA and strand coverage can be evaluated based on shifts in reduction potentials for redox counterions associated with the ssDNA monolayer.132 The resulting electrostatic potential for immobilized ssDNA probes is significantly influenced by surface properties. For example, the silica surface charge density in 1 M sodium nitrate aqueous solution increases from zero at pH 4 to 0.24 per cm2 at pH 9.5, corresponding to surface potential ranges from 0 to −100 mV, with the glass/silica surface being prone to static charging.130 Extensive studies of ssDNA surface potential with change in probe density and hybridization on various surfaces with buffers, pH and sequences have been proven to decrease the electrostatic charging.73,199,200 Further, Shen et al.,132 Fritz et al.,201 and Heaton et al.,202 showed that an externally applied electric field can improve hybridization rates without loss of efficiency, discriminating against mismatched dsDNA duplex formation and also improving electronic control of DNA hybridization and facilitating design of chips avoiding the ssDNA folding problem.
9. Microarray surface-capture assay kinetics
Kinetics of DNA hybridization is well studied in bulk solution, however solid-phase probe–target hybridization kinetics is more complicated.80 Achieving duplex equilibrium is an important endpoint often assumed for microarray assay analysis. Understanding the actual difference in equilibrium constant (KE = kf/kr) between bulk vs. surface hybridization is a key to understanding hybridization kinetics and this assay endpoint. Equilibrium binding constants for solid-phase hybridization differ by many orders of magnitude relative to solution values.203 Microarray DNA assays use competitive surface reactions between many different immobilized probe sequences with highly varying concentrations of matched and unmatched target strands, influencing the assay equilibrium.204 Additionally, when the surface density of ssDNA oligonucleotide probes increases, DNA hybridization rates and efficiencies decrease,51,203 making true equilibrium endpoints often impractical (i.e., too long) for convenient assay use. Henry et al.205 reported that rate of forward reaction (kf) for hybridization of end-tethered 22-mers in 0.11 M salt was five times slower than in solution when ssDNA probe coverage was 1.4 × 1012 per cm2, and ten times slower when probe coverage increased to 2.8 × 1012 per cm2. The free energy penalty associated with inserted charged targets into dense probe layers modifies both the hybridization isotherms and the duplex rate equations: the attainable ssDNA hybridization fractional completion and rate of DNA hybridization are both reduced.51 Probe design (sequence, length, immobilization chemistry) and hybridization (target designs), the array design and its resulting interfacial characteristics are important parameters for improved performance of the microarray. Hybridization kinetics and equilibrium are influenced by (1) concentration- and sequence-dependent competition between diverse strand–strand interactions, both in target solutions as well as at surface between matched and mismatched duplexes, and (2) aspects of the array fabrication process (probe printing or deposition and resulting density, conformational states). Possible design parameters include the nature of the surface (i.e., the treatment used to minimize nonspecific adsorption and maximize ssDNA tethering and accessibility), and ssDNA probe design (i.e., length, charge, lack of secondary structure, hydrophobicity and the chemical design/length of spacer chains joining the probe to the surface).Langmuir isotherm surface treatments for thermodynamic approaches to attaining duplex binding equilibrium and their corresponding duplex kinetic equations for hybridization represent a common starting model for non-interactive probes (i.e., no competing nearest neighbor interactions) when ssDNA probe density is sufficiently low; at higher probe densities, the Langmuir model requires modification.80 However, this treatment has traditionally been based on ideal DNA–DNA duplex binding analyses and strand–strand affinities based on complementarity of isolated matched pairings in equimolar concentrations compared to that for isolated mis-matched pairings at similar equimolar concentrations, without complications of multi-component strand mixing or competition (so-called strand multiplexing). Real assays have complex competition from targets of different sequences and mis-match affinities in varying concentrations.
Longer targets lead to reduced duplex equilibrium binding constants on surfaces due to incomplete or partial overlap of target strands, incurring an entropic penalty for penetrating the dense probe surface (steric issues), and an enthalpic penalty for polyanion–polyanion electrostatic repulsion.51 ssDNA probe chain crowding can lead to a brush-like regime,59 modifying the Langmuir isotherm and kinetics due to free energy penalty associated with brush capture of target compared to less dense, conformationally mobile probe mushroom-type layer densities. Some controversies remain in this regard: while Guo et al.206 observed that the maximum attainable hybridization fraction increases at higher probe density when the number of bases in the target increases, Su et al. reported slower hybridization as the number of bases in the ssDNA target increases at fixed probe density.207 Surface diluents and probe spacer/linkers are used to overcome these complications by providing space between or flexibility/mobility within crowded ssDNA chains. For example, surface diluents reactive to gold (e.g., thiolated surfactants) are mixed into thiolated DNA ssDNA probes, or used to displace ssDNA after gold assembly (e.g., mercaptohexanol,159 11-mercapto-1-undecanol,42 thiol-terminated oligoethylene glycols42) to increase the average spacing between probe chains.
Additionally, probe surface area (Σ0) and the number of bases per ssDNA probe chain become important features in electrostatic field and steric contributions to crowded array spots. Probe densities in typical array spots varies from 1.2 × 1010 (low density) to 4 × 1013 (high density) probes per cm2, corresponding to molecular probe surface area between 25 nm2 ≤ Σ0 ≤ 830 nm2.37 With a dsDNA duplex radius of 2 nm and a probe lateral spacing, d, of ∼0.6 nm, sufficient space should accommodate polyanion reactivity at this density. Labeling of probe and target with signal molecules (e.g., Cy3 or Cy5 dyes, or redox reporters) can also affect hybridization behavior and signal intensity (discussed in detail in a section below). Repeated drying and solution wetting steps in common arraying procedures further complicate immobilized chain interactions with each other within the adlayer and with the solid support. Hybridization condition variables include the composition of the hybridization solution (ionic strength, salt composition, use of surfactants and pH, all of which practically deviate from conditions used in theoretical DNA brush models, vide supra), hybridization temperature and hybridization time (incubation time).208 Typical hybridization temperatures vary over the range 30–60 °C depending on the GC base fractions (i.e., duplex chain melt point). The assay incubation time (i.e., time to hybridization endpoint stabilization) can be very long and variable (i.e., from 2 to 16 hours reported)30,209,210 depending on assay signal sensitivity, duplex bulk composition, target concentration, ionic strength and probe grafting density. Importantly, whether this assay time reflects an equilibrium endpoint or not is critical to the assay answer. The real problem lies in assays of heterogeneous ssDNA targets where diverse sequences, lengths, mixed target and non-target concentrations and possible mis-match duplex co-equilibria confound approaches to a single equilibrium assay endpoint.203,211,212 Incubation times often vary, different even for similar concentrations of probe and target, but depending on assay conditions and largely influenced by ssDNA probe density distributions and ssDNA sequence and length.37,133,213
Sensitivity and specificity of hybridization isotherms on ssDNA arrays depend on the important assumption that “perfect match” duplexes form exclusively, and with the same affinity, thermodynamic and kinetic behavior that they exhibit in bulk solution as isolated pairs, and significantly, without any influence from the presence of other ssDNA strands and possible duplexes. However, “real” microarrays operate in “multiplex” mode, where many other ssDNA strands and their possible duplex pairings, even as mismatches with finite metastability, are present and competitively operative.211,214 Few studies report deviations for perfect match probabilities or kinetics in the presence of strand multiplex bias where different ssDNA concentrations and relative ranges of strand–strand affinities for a multitude of various duplex reactions compete simultaneously, either in bulk or at surfaces. Several additional essential features of multiplex hybridization must be considered. These considerations are associated with the significant probability of formation of mismatch hybrids (cross-hybridization) brought about by sequence homology with other strands and sequence-dependent stability of mismatch basepairs, especially at non-equilibrium endpoints.203 Competitive hybridization, both at the surface and in bulk ssDNA solutions containing many sample ssDNA strands, lowers the array sensitivity.133 Assay noise, represented as non-equilibrium “mis-matched” cross-hybridization from competing ssDNA multiplexed reactions, depends on relative competing strand concentrations, strand sequences and the sensitivity of all mis-matches to temperature, and surface probe conditions. These variables are not controlled in common “real life” arrays (as opposed to lab bench model concoctions), given their multiplex design. Hence, the actual fidelity of capture signals produced from such arrays are questionable unless equilibrium binding conditions and algorithms for predicting confounding multiplexing are implemented.204
The DNA–DNA surface hybridization model often assumes a Langmuir form modified for electrostatic interactions within the probe layer. Vainrub and Pettitt's modeling of molecules immobilized in an electrostatic double layer (at high 1 M NaCl and low 0.01 M NaCl ionic strengths) for both dielectric and metallic substrates136 predicted strong electrostatic effects on duplex kinetics. These studies suggested the feasibility of electrostatic control for DNA hybridization and design of assays to avoid DNA secondary structure folding problems (i.e., self complementarity).212 They used linear Poisson–Boltzmann theory for double-layer interactions between an ion-penetrable sphere and a hard plate with variables including binding enthalpy, entropy and equilibrium reaction constants for the immobilized complex. They also developed a mean field model for Coulombic effects in two-dimensional DNA arrays to understand the binding isotherms and thermal denaturation of the double helix.123 These studies on dsDNA duplex models reveal substantial differences in hybridization thermodynamics between ssDNA in solution and that surface-tethered. Electrostatic repulsion of targets from immobilized ssDNA probes dominates the binding thermodynamics, causing the Coulomb blockage of the hybridization and explaining the observed dramatic reduction in hybridization efficiency and the thermal denaturation curve broadening as probe surface density grows in DNA microarrays.
Chen et al.215 investigated substrate–ssDNA interaction influences on both thermodynamics and kinetics of DNA hybridization of ssDNA-modified gold nanoparticles (GNPs). They proposed that during hybridization, the target ssDNA in solution does not directly react with the immobilized probe, but rather it is first adsorbed onto the GNP surface, followed by two-dimensional diffusion until it finally hybridizes with an immobilized probe ssDNA. Different duplex melting properties observed between hairpin and random-coil sequence ssDNA strands were proposed to arise from sequence- and structure-influenced interactions between ssDNA and GNPs. Steric hindrance induced by the compact configuration in a DNA hairpin probe prevented interactions with the gold surface, facilitating higher stability of hairpin-formed duplexes on the GNPs.
Deviations or extensions of the Langmuir model for DNA–DNA interactions on surfaces reflect the surface environment encountered by multiple targets at different concentrations multiplexing as cross-hybrid duplexes with different affinities, including mismatches. This leads to widely different approaches to equilibrium for assay endpoints. Predictions of real-time DNA hybridization kinetics in microarrays have been performed by various researchers. Halperin et al.51,133 and Bhanot et al.203 both analyzed effects of competitive surface hybridization for hybridization at a number of spots contacted with multicomponent solutions of targets with no bulk hybridization. Importantly, the result demonstrated that array performance is best when equilibrium is attained. Halperin et al.37 also analyzed the impact of the brush regime on kinetics of hybridization, indicating that slower kinetics can affect the attained hybridization even after long hybridization periods. Forman et al.216 analyzed observable selectivity in hybridization and the ability to distinguish perfectly matched and mismatched target sequences that are affected by surface interactions. Hagan and Chakraborty74 developed a theory describing kinetics of solid-phase hybridization based on polymer theory. Also the effect of bulky fluorescent labels on the hybridization was first considered theoretically by Naef and Magnasco217 and recognized the difference in hybridization between DNA duplexes on the surface versus those in solution. However, duplex kinetics on ssDNA chips are heterogeneous hybridization consisting of many kinetic coefficients of reversible nonspecific adsorption and desorption of the targets with the probes in various random conformations. These different approaches individually and collectively have provided new insight of the complexity in DNA hybridization kinetics on surfaces. However, the actual kinetics of DNA duplex formation in complex milieu has only been considered conceptually by a combination of various approaches addressed individually, without a global method to accurately and reliably predict in such complex multi-equilibria systems.218 Experimental data to validate duplex models for short, well-controlled ssDNA immobilized layers as a function of controlled media and controlled densities are not yet available.
Additionally, both Moiseev et al.128 and Unruh et al.219 reported the influence of dye–DNA interactions, using fluorescence methods to study biomolecular dynamics under fluorescent dye influences on chain mobility and conformation with labeled ssDNA. Dye-labeled ssDNA influences the chain conformation and length both before and after hybridization with dye-labeled and unlabeled targets, thereby affecting hybridization kinetics and efficiency.219 As DNA hybridization is a complex 3D scenario that must consider various factors including non-specific binding, transport of target from bulk to crowded, charged probe surfaces, variable probe densities, competitive binding, and secondary structural issues, the time to attain equilibrium in such complex situations is not readily predictable. The result is that most actual assays cannot readily know when an equilibrium endpoint is achieved for each assay. Assays that terminate before equilibrium is reached could produce an inaccurate answer.203,204,212 Experimental designs including microfluidic, statistical modeling and simulation approaches should be considered to understand the kinetics of real time hybridization in microarrays in complex milieu for efficient endpoint analysis.
10. Use of probe linker chemistry as spacers in ssDNA probe surface immobilization
Surface immobilization technologies have long exploited spacer chemistries to enhance bio-affinity interactions at surfaces.220 Flexible spacer chemistries (e.g., oligoethylene glycols, reactive alkanes, oligo(dT) tails), are frequently utilized on probe termini as an alternative anchoring chemistry to direct ssDNA probe surface coupling (typically a hexamethylene anchoring spacer with functional coupling group) in order to improve DNA probe immobilization quality and enhance their hybridization capabilities in microarrays.221 These immobilizing spacers are highly diverse both chemically and physically, and can include various nucleotide or hydrophilic synthetic oligomers with diverse claims to their effects on hybridization yields. Low ssDNA probe grafting densities allow probes to lie flat on the solid surface, reducing accessible ssDNA probe chain configurations. Higher grafting densities yield different ssDNA brush regimes (see Fig. 4) that introduce hybridization penalties in both steric and electrostatic forms (vide supra). Hence, long flexible spacers weaken probe–surface effects, and their hybridization behavior can approach more bulk-like characteristics, depending on media effects (ionic strength) that affect ssDNA mobility and mechanics (vide supra).111 Probe brush or mushroom regimes can be formed on surfaces when ssDNA is tethered with spacers, depending on the number of bases in the probe and the spacer length. However, this effect also depends strongly on ssDNA target length.37 A unique probe brush regime was reported for long neutral spacers (e.g., ethylene glycol oligomers) and short targets at intermediate media ionic strengths where ssDNA chain stretching in response to local electrostatic interactions between immobilized probes is facilitated.111 In contrast to the advantages of relieving steric issues at the grafting site, a non-monotonic effect of spacer length is observed when targets are short. At higher grafting densities, probe chains crowd each other, producing a polymer brush, higher ssDNA surface charge density, possible Coulombic blockage, steric hindrance to approaching targets and resulting poor duplex efficiency.11111. Hairpin and secondary structured probes in arrays
Assessing control of probe density on substrates to optimize further probe–target binding kinetics in microarray applications is important in conventional linear oligomer ssDNA arrays. However, with the advent of deliberately structured next-generation probe sensors, such as those incorporating designer secondary structures such as hairpins as in molecular beacons or aptamers,222,223 it becomes more important to understand these surface-mediated structural effects on array polymer layer properties, assay kinetics and answers. These looped immobilized probes are deliberately designed with meta-stable folded immobilized states triggered to change conformation in the presence of complementary target.221 Intramolecular base pairs involved in secondary structure that stabilize single-stranded self-conformations create a higher energy barrier to intermolecular hybridization, altering hybridization kinetics. Additionally, the more dramatic conformational changes required to open a hairpin loop require different surface spatial characteristics than linear probes to permit accessibility to incoming target required to trigger the transformation. Comparative studies of DNA hybridization kinetics both in solution and on the surface with SPR, UV absorbance, QCM indicate that both probe and target secondary structure affect hybridization kinetics.222 Although planar gold surfaces and conventional ssDNA probe layer environments suppress the measured duplex rates 20- to 40-fold compared to their bulk behaviors, the effects of secondary structure produce similar duplex behaviors in solution versus surface environments.222ssDNA probes deliberately designed to contain secondary structures such as hairpin loops (e.g., molecular beacons) alter their spatial requirements, probe immobilization densities and chain physics on surfaces with subsequent effects on hybridization in microarray assays.224–226 The role of the surface in ssDNA folding is more complicated than simply restricting conformations available to the random coil state.227 Some molecular beacon probe designs enable separation from the surface to minimize surface influences.228 Several known molecular motifs alter ssDNA secondary structures thereby influencing the thermodynamics and kinetics of hybridization reactions.229 Both ssDNA probe and stem lengths impact hairpin probe binding specificity and hybridization rates.230 Their stem-loop structure provides a competing reaction for probe–target hybridization that serves to increase probe specificity, and is particularly useful when single-base discrimination is desired.231 Probe hairpin stem base composition and overall loop length significantly affect their sensitivity and selectivity: surface-immobilized hairpins discriminated between two sequences differing by a single base-pair mismatch with high sensitivity (>order of magnitude difference in signal).232 Thermodynamic analysis of the transitions between open–closed hairpin loop states justifies their improved specificity. Structural constraints on probe loop conformations lead to enhanced specificity with increasing stem length, increasing the difference between melting temperatures of perfectly complementary duplexes and mismatched duplexes.233 Rates of spontaneous hairpin self-duplex formation may be reduced by decreasing loop length and increasing stem length.234 Aalberts et al.235 showed that the persistence length for beacon-type hairpin loops depends on their base stacking enthalpy, stacking entropy and temperature. Stacking also plays an important role in the kinetic behavior and folding conformations of these hairpins in solution. As temperature decreases, stacked regions become longer and loop closing times increase. Open/closed hairpin transition rates are reported in microsecond range.236
Gao et al.222 showed that hairpins with longer stem lengths have improved abilities to discriminate between targets over broader ranges of temperatures. However, this is accompanied by decreased hybridization rates. Longer hairpin probe lengths tend to have lower dissociation constants, increased kinetic rate constants, and reduced specificity. Consistently, very short stems exhibit lower signal-to-background ratios than longer stems. Yao et al.234 studied the hybridization kinetics of surface-immobilized single-molecule hairpin beacon-type probes. Hybridization produces a spontaneous conformational reorganization with the stem opening, leading to fluorescence restoration. Du et al.232 found that hybridization efficiency is sensitive both to hairpin secondary structure immobilized on gold surfaces, as well as to DNA hairpin immobilized density. Kastantin et al.237 found that ssDNA hairpins exhibit faster kinetics on hydrophobic TMS (trimethylsilane) versus hydrophilic oligo(ethylene glycol) (OEG) surfaces: TMS is claimed to favor hairpin states both by slowing ssDNA unfolding and speeding up folding relative to OEG. Yao et al.234 investigated biotinylated ssDNA hairpin probes immobilized on avidin surfaces. A 25-base linker was found optimal for hybridization.
12. DNA probe printing and drying produces immobilized DNA heterogeneity
ssDNA probes on many commercial and home-brew arrays are deposited on substrates (e.g., reactive, coated glass substrates) by spatially controlled deposition of nanoliter drops of complex ssDNA solutions using robotic spotters, followed by evaporation of deposited liquid droplets within seconds.86,238 Non-contact inkjet printing and contact (pin) spotting of DNA generally all yield sub-microliter droplet volumes on surfaces as the basis for ssDNA microspot formation in arraying. Unfortunately, droplet drying at this size scale and with typical arraying conditions most frequently results in inhomogeneous solute deposition upon droplet drying.39,238 For assay purposes, this resulting ssDNA dried spot heterogeneity is undesired, but is difficult to control from the combined phenomena of droplet solution composition, deposition wetting, spreading, evaporation, and subsequent ssDNA drying patterns. Evaporation from sessile droplets induces radial convection within the drop, producing the well-known “coffee ring” drying effect.239,240 Deegan et al.241 pointed out that the physical origin of the coffee stain effect is due to a combination of pinning of the three-phase contact line and a convective flux driven by the evaporation. The occurrence of “coffee stain like” droplets is caused by a combination of solvent evaporation and contact line pinning: whenever the contact line of an evaporating drop is prevented from receding, a convective flux is generated from the center towards the edge of the drop in order to sustain the solvent evaporation.242 This flux carries solute from the bulk of the drop towards the contact line, leading to a local increase in concentration and eventually to precipitation of the solute at the drying droplet edges.Droplet evaporation also induces a gradient in temperature across the droplet and consequently a gradient in surface tension, generating Marangoni flow.86 In a sessile evaporating drop, Marangoni stress (i.e., a surface tension gradient over the droplet during evaporation) can be induced by local temperature variation near the fluid interface or by change in concentration caused by solvent evaporation.239 The circulating convective flows lead to intensive mixing of the solutes during evaporation, helping to overcome mass transport limitations due to the coffee ring effect. Marangoni droplet drying patterns with high concentration of the ssDNA at the dried droplet center are the result.243,244 Drying conditions for printed ssDNA droplets on a surface are proposed to result from competition between the dominant effects of coffee ring versus Marangoni droplet drying patterns.34 Dugas et al.86 studied the effect of ssDNA droplet drying on hydrophobic flat surfaces and proposed that droplets flatten with a constant contact area, and then the droplet shrinks at a constant contact angle. These results produce variations in diameters and morphologies for thousands of spots deposited on microarray surfaces that are not uniform since their local wetting/spreading and resulting drying behaviors are non-uniform from sub-micron variabilities in solid support chemistry. If surfaces exhibit sufficiently uniform chemistry, then control of some physicochemical properties (wetting, evaporation rate) of the droplet allows formation of well-controlled spots compatible with ssDNA grafting.
Overall, the rapid evaporative process produces increased solution ionic strength and solute concentrations in the drying ssDNA film, resulting in distinct differences in immobilized ssDNA structure, density and chemistry compared to bulk solution coupling reactions between ssDNA and surfaces.245 Probe spot drying thus commonly leads to “halo” or “doughnut” shaped spots which provide variable integrated intensities and target capture with conventional fluorescence scanner readings. Extensive high-resolution imaging techniques such as confocal and epifluorescence can be combined with other more exotic surface analytical tools (e.g., TOF-SIMS and XPS compositional surface imaging) to evaluate the chemical distribution of ssDNA within dried spots and probe effects due to drying artifacts.34,86,246 The major significance of probe spot drying is that each probe ssDNA is deposited in highly heterogeneous densities across any given spot, and none reproducibly. Since ssDNA probe density is a primary determinant of target capture (vide supra), arrays then capture targets with different kinetics and efficiencies depending on local probe densities that remain uncontrolled by printing methods. This produces substantial variations in signals from spots, both spatially within spots and spot–spot. Integrated signal intensities, representing common spot assay “answers” then depend on local drying phenomena and not necessarily on the ideal strand duplex characteristics based on complementarity.
Pappaert et al.247 reported hybridization processes as a primary cause of doughnut-shaped ssDNA spot images used to determine assay signals. Studies by Dandy et al. with a combination of computer simulation, theoretical calculation and optical technique measurements have shown that the ring-shaped hybridization pattern results from diffusion-limited conditions present during hybridization process.29 Near spot centers, ssDNA target is delivered to the probe surface solely through linear normal diffusion, whereas toward the outer edge, a lateral (radial) component of diffusive flux augments the normal linear transport component, producing hemispherical diffusion. This results in spot outer edges accumulating more target through greater proximate fluid volume transport versus spot centers.33 Since equilibrium binding depends on many factors in multiplexed arrays (vide supra), determining equilibrium duplex binding for each spot when many probe and target strand sequences are present is difficult. These authors therefore hypothesized that these spot patterns occur during hybridization, especially with short oligonucleotides that have a very high binding probability and fast hybridization kinetics. Longer target ssDNA molecules and long assay times lead to a more evenly distributed intensity signals. These effects result collectively in the outer spot edges accumulating more ssDNA targets through sampling greater proximate fluid volume transport versus spot centers. This was further verified by real-time hybridization kinetics studies using imaging with confocal fluorescence microscopy.33
Assay signal answer is therefore a multi-factorial result of the influence of high probe density heterogeneity upon droplet drying33,34 on duplex formation, combined with intrinsic target mass transport effects from target concentrations and other known kinetic influences of various probe–target combinations that produce both cross-hybridized mismatches and perfect matches in competition at surfaces.29,218 Improving the uniformity of probe coverage across each spot feature could improve assay signal consistency at any given assay endpoint, even prior to target saturation at the unique equilibrium point for any given spot probe–target pairing.
Further details of dried intra-spot and spot-to-spot heterogeneity seen with different concentrations of both total DNA and fraction of dye-labeled ssDNA can be explained from spot drying behavior in the presence of ssDNA-bound signal dyes, surfactants and dissolved salts.86,143 Evaporation kinetics and behaviors for droplets containing ssDNA varied as a function of ssDNA concentration: drops containing very low ssDNA concentrations dried by maintaining a constant base area (pinning),85 whereas those with high concentration dried with a constant contact angle. Fang et al.85 showed with confocal and rheological studies that high concentration ssDNA droplets formed a shell while low ssDNA concentrations resulted in isolated island formation. Various efforts to improve inter-spot ssDNA dried spot such as increased relative humidity from 40% to 80% during drying and also use of surfactants such as betaine and co-solvents like DMSO. McQuain et al.248 optimized surfactant concentration to 1.5 M betaine and maintained relative humidity at 60%, reducing inter-spot and intra-spot variations. Addition of anionic surfactant (e.g., SDS) initially facilitates uniform droplet spreading and stabilizes the drop evaporation, drastically altering the “coffee ring effect”.249 Surfactant-driven Marangoni flows arise when the local surfactant concentration at the pinned contact line increases due to the coffee ring effect, thereby decreasing the local surface tension and inducing Marangoni flow towards the spot center.239 The extent of circular Marangoni flow is influenced by variation of SDS concentration along the air–water interface.249 Spot evaporation modes can also be influenced by salts, with DNA probe deposition patterns following the salting trace.86 Schematics of ssDNA droplet drying in the presence of solutes, salts and buffers, leading to either coffee-ring or Marangoni droplet drying phenomena, are shown in Fig. 8.
Phase separation upon drying, producing salt crystallization in evaporating droplets of ssDNA solutions containing salts, occurs as well.250,251 Exceeding the local solubility limit for different salts in evaporating droplets leads to rich morphologies of deposited salt crystals and ssDNA. Formation of radially varying salt concentration yields deposited rings with spacing between the concentric rings that depends on the ssDNA concentration and ion species concentration.251 Marangoni inward flow of solution produces various salt patterns with deposition of the ssDNA–dye in concentric patterns within spots.252 The physicochemical properties of the evaporating ssDNA solution are influenced by the dynamic changes in ssDNA concentration, changing ionic strength and surfactant concentrations, influencing final dried ssDNA patterns.86 Theoretical and experimental results conclude that at low concentrations of salt, the deposit becomes more uniform, covering the entire surface beneath the droplet, whereas at higher concentration, salt deposits appear predominantly along the outer rim of the spot.251 At lower ssDNA concentration, ssDNA at the liquid–vapor interface is deposited at the droplet edge during initial evaporation stages, and eventually under developing Marangoni flow, transitions to deposition of ssDNA aggregates at the spot centers. Hence, periodic patterning is less dominant at very low concentrations due to reduced spreading. Nonetheless, drying of many ssDNA droplets containing mixtures of ssDNA, surfactants and dissolved salts undergo phase separation. Despite the use of non-ionic/zwitterionic surfactants to limit ssDNA probe interactions, ssDNA segregation86 into two phases can occur upon drying: one enriched in ssDNA and another in surfactant, leading to another form of phase segregation upon drying and formation of a ssDNA precipitate with increasing electrolyte and surfactant concentration upon evaporation.252–254 Furthermore, supersaturated salt conditions also promote ssDNA phase separation.86,251 Precipitation occurs at very low concentrations of both ssDNA and surfactant, and is further enhanced in the presence of electrolytes.246,254–256 Similar aggregation is predominant at higher ssDNA concentrations (i.e., micromolar to molar)82 and with dye labeled ssDNA oligomers.83 It is likely that such concentrations are achieved within the droplets within a few seconds of printing due to rapid drying.
Furthermore, cyanine dyes analogous to commonly used ssDNA labeled Cy3 are known to readily form molecular aggregates in aqueous media.257 Cyanine dyes are also known to interact with dsDNA in aqueous media through various interactions, either by intercalation, minor groove binding between base pairs or dye–dye aggregation.82,257,258 Cyanine dye aggregation is also reported in Langmuir-Blodgett monolayer of amphiphilic nucleic acids during evaporation rates controlled by mass transfer across the aqueous-film–air interface.259 In cyanine dye-labeled single-strand probe ssDNA, dye–dye interactions and dye–nucleotide aggregations in the presence of increasing ionic strength and surfactant concentrations reduce probe stability and quench fluorescence.83,124,219 Singly labeled fluorescent ssDNA probes exhibit dye–ssDNA interactions as studied by fluorescence anisotropy and lifetime assays. As Cy3-ssDNA content increases in print solutions up to 100% ssDNA mass fraction, ssDNA aggregation is seen to be much more predominant leading to increasing dye quenching and reducing fluorescence intensity.34
As these various factors affect droplet drying morphology, including ssDNA concentration, temperature, humidity, buffer, salts and dye-labels, in complex ways, efforts to alter microdroplet footprint shapes on surfaces have recently gained attention. Yunker et al.242 and Weon et al.243 altered droplet shapes to obtain uniform droplet drying. Additionally, polymer “lift-off” arrays combine the hydrophobic surface properties of di-p-xylylene (Parylene) with photolithographically etched hydrophilic openings within the polymer substrate to control spot morphology260 and resulting uniformity of deposition.261 Manipulating surface wetting properties, mixing of the droplet with frequency dependent oscillating flow262 to alter flow pattern of the evaporating droplet, and electrowetting263-driven microfluidic flows are shown to suppress coffee ring effects for variable concentrations. The global objective of these strategies is to modify and perhaps control DNA probe deposition physics on surfaces, specifically to affect probe immobilization density and lateral distributions within dried DNA spots that affect assay equilibrium and reliable assay ‘answers’.
13. Conclusions
DNA microarrays have been used extensively for more than a decade in numerous forms. However, high variabilities in the designs and applications of probes, surfaces, targets and types of immobilization (different platforms) has led to challenges in obtaining reproducible and reliable assay results. This is particularly challenging in those that produce assay answers directly from complex samples without PCR amplification, or whose signals seek to reflect target absolute abundance (i.e., quantitative output). The coordinated probe and substrate design techniques for “grafting to”, and “grafting from” ssDNA probes, challenges in overcoming kinetic limitations of assay in multiplex mode and in dense probe states, and variations caused by spot deposition methods have compelling limitations in attaining uniform ssDNA probe grafting efficiency and probe density, and reliable target capture. These result in microarrays with deficiencies in the resulting assay metrics, reproducibility and reliability as a diagnostic format.The biophysical aspects of ssDNA molecular mechanics, conformations, electrostatics, control and stability of surface-tethered states, interactions with the surface, with neighboring probes, with matched and mis-matched targets in competition, and within high ionic strength environments in duplex formation all impact the array behavior and assay answer. These factors have been subject to some study in simplified formats. However, none have been studied in relevant combinations present in real nucleic acid-based assays.
To improve these assays, these variables need to be more thoroughly evaluated in surface-immobilized formats since there is no direct translation of bulk ssDNA characteristics to surface-tethered ssDNA properties. Common polymer physical parameters such as radius of gyration, persistence length, ssDNA elasticity, flexibility and chain conformational mechanics have not been investigated in detail for either surface-tethered ssDNA or dsDNA. ssDNA probe chain accessibility on surfaces that determines target binding and ultimately array performance is determined by local tethered flexibility and conformations based on ssDNA sequence, electrostatic interactions, media influences, substrate chemistry and surface immobilization techniques. Though various theoretical and experimental approaches seek to explain DNA surface behavior with optical, fluorescent, and force spectroscopies, several discrepancies persist for explaining ssDNA flexibility vs. stiffness at surfaces. ssDNA chain conformations effects due to phosphate backbone charges and base stacking are still unresolved. WLC remains the widely accepted classic model for understanding ssDNA molecular mechanics despite its several shortcomings. Extensive improvements have been made to the WLC model to accommodate ssDNA bending angles and chain flexibility. Various molecular dynamics simulations and other models have been developed to attempt to correlate and supplement the shortcomings of WLC. The newly developed coarse-grained approach is widely accepted for treating ssDNA as an inextensible elastic rod and despite lacking atomic details, is accurate for thousands of base pairs down to few hundred. However, its applicability remains controversial for short DNA molecules with persistence lengths of less than 1 nm, and remains unvalidated as a function of the many variables used in experimental array assays.
Studies of physical structure and biophysical properties of ssDNA as well as mechanistic extensions to short immobilized ssDNA probes at surfaces have proven useful in initial understanding of some fundamental issues relevant to nucleic acid capture at surfaces. Modeling and simulations contribute to explaining these data but are limited when dealing with short, rigid polyelectrolyte DNA probe chains at surfaces in complex ionic milieu. The process of DNA hybridization at surfaces is a critical part of nucleic acid-based array technology; fundamental understanding of this process under relevant conditions for actual assays is very challenging currently. Future improvements in the development and fabrication of microarrays, designing new nucleic acid applications, will require better knowledge of ssDNA as tethered chains and how strand–strand duplexation behavior is controlled kinetically and thermodynamically under assay conditions that approach equilibrium slowly in complex media. Comparisons of actual assay conditions experienced by tethered DNA probes on array surfaces versus current capabilities to model DNA brushes using scaling theories are summarized in Table 3.
| ssDNA properties at surfaces | ssDNA tethered in microarrays | ssDNA brush modeling |
|---|---|---|
| ssDNA grafting density | Uncontrolled grafting density, spanning sparse, mushroom and brush in the same surface locale | Controlled, uniform grafting density of mushroom or brush across an impenetrable surface |
| Tethered ssDNA chain orientations | Uncontrolled immobilized chain orientations and conformations | Uniform controlled brush heights and chain orientations |
| ssDNA chain lengths | 20–200 bases (short) probes | >1000 bases (long) brushes |
| ssDNA chain flexibility | ssDNA is short, rigid, rod-like | ssDNA is longer, flexible |
| ssDNA solvent/media exposure | High ionic strength but complex mixed salt solutions, surfactants and other solutes in drying cycles | Wide range of salt concentrations (monovalent) |
| Interactive conditions at the surface | Repeated surface solvation/drying steps in assay that modulate ionic strength and solvation dramatically | Equilibrium models or constrained simulations, with little dynamic interactive changes in polymer/solvent/surface conditions |
| ssDNA chain dynamics under a given analysis | Persistence lengths, radius of gyration, brush heights and chain condensation vary widely | Persistence lengths, radius of gyration, brush heights and chain condensation vary little |
The complexity of this task is compounded by the large number of reported protocols for preparing and functionalizing surfaces for DNA microarray use in practical assay deployment and in the various milieu these assays are conducted. Polyelectrolyte media and interfacial brush as well as aqueous droplet drying theories help to elucidate some basic properties of ssDNA target–probe interactions, media and substrate effects. These provide additional information to analyze the effects of immobilized ssDNA probe density on the thermodynamics and kinetics of DNA hybridization on array surfaces in simple binary and even multiplex assay modes. As the kinetics and thermodynamics of immobilized probe molecules tethered farther away from the solid support can approach those in solution states, the utility of introducing spacer chains for ssDNA immobilization is currently exploited but largely from an empirical approach. The beneficial role of spacers is generally recognized, but a coherent view of their optimal design and underlying physics has not been presented. Accurate measurement of probe surface coverage, a parameter crucial for determination of efficiencies of immobilization and hybridization protocols, is extremely difficult. More careful evaluation of probe lateral density and its heterogeneity for understanding this influence on target hybridization isotherms and rate constants for different platforms are required to understand DNA microarray performance. Clear elucidation of molecular mechanisms surrounding DNA duplex formation on tethered probe surfaces and sources of its variability will move the nucleic acid microarray approach to standardization, and even towards rigorous quantitative answers required for their more successful clinical translation to inform medical decision-making.
Abbreviations
| L p | Persistence length |
| κ −1 | Debye length |
| l B | Bjerrum length |
| R g | Radius of gyration |
| N av | Avogadro's number |
| R F | Flory radius of the free chain |
| N | Number of DNA nucleotide/base (length of DNA/polymer chain) |
| L | DNA chain length |
| D | Lateral chain spacing |
| b | Nucleotide size |
| Z | Ionic strength |
| K | Boltzmann constant |
| T | Temperature |
| c s | Salt concentration |
| m | The number of neutral (uncharged) monomer units in the chain between two neighboring charged monomers |
| a | The monomer unit length (0.3–0.6 nm) |
| H | Osmotic brush thickness/DNA probe brush thickness |
| L Pi | Bare persistence length |
| L Pe | Electrostatic persistence length |
| L pa | Apparent persistence length |
| θ | Angle of semiflexible polymer |
| σ | Probe surface density or chain grafting density |
| ρ(z) | Chain segment distribution |
| n | The number of segments attached to it by one of its ends at a tethered surface density of σ |
| z | Distance from the substrate |
| ν | Flory scaling exponent |
| ξ | Neutralization length (Gouy–Chapman length) |
| x | Counterion cloud thickness |
| Σ 0 | Surface area of probe |
| K E | Equilibrium constant |
| k f | Rate of forward reaction |
| k r | Rate of reverse reaction |
Acknowledgements
This work was supported by NIH grant R01 EB001473.References
- M. J. Heller, DNA microarray technology: Devices, systems, and applications, 2002, pp. 129–153 Search PubMed.
- J. D. Hoheisel, Microarray technology: Beyond transcript profiling and genotype analysis, Nat. Rev. Genet., 2006, 7, 200–210 CAS.
- M. L. Bulyk, DNA microarray technologies for measuring protein-DNA interactions, Curr. Opin. Biotechnol., 2006, 17, 422–430 CrossRef CAS PubMed.
- D. Gresham, M. J. Dunham and D. Botstein, Comparing whole genomes using DNA microarrays, Nat. Rev. Genet., 2008, 9, 291–302 CrossRef CAS PubMed.
- W. E. Evans and M. V. Relling, Moving towards individualized medicine with pharmacogenomics, Nature, 2004, 429, 464–468 CrossRef CAS PubMed.
- P. A. Bryant, D. Venter, R. Robins-Browne and N. Curtis, Chips with everything: DNA microarrays in infectious diseases, Lancet Infect. Dis., 2004, 4, 100–111 CrossRef CAS.
- J. Kononen, L. Bubendorf, A. Kallioniemi, M. Bärlund, P. Schraml and S. Leighton, et al., Tissue microarrays for high-throughput molecular profiling of tumor specimens, Nat. Med., 1998, 4, 844–847 CrossRef CAS PubMed.
- B. Sobrino, M. Brión and A. Carracedo, SNPs in forensic genetics: A review on SNP typing methodologies, Forensic Sci. Int., 2005, 154, 181–194 CrossRef CAS PubMed.
- E. K. Lobenhofer, P. R. Bushel, C. A. Afshari and H. K. Hamadeh, Progress in the application of DNA microarrays, Environ. Health Perspect., 2001, 109, 881–892 CrossRef CAS.
- R. L. Stears, T. Martinsky and M. Schena, Trends in microarray analysis, Nat. Med., 2003, 9, 140–145 CrossRef CAS PubMed.
- L. Pusztai, Chips to bedside: Incorporation of microarray data into clinical practice, Clin. Cancer Res., 2006, 12, 7209–7214 CrossRef CAS PubMed.
- X. Li, R. J. Quigg, J. Zhou, W. Gu, P. Nagesh Rao and E. F. Reed, Clinical utility of microarrays: Current status, existing challenges and future outlook, Curr. Genomics, 2008, 9, 466–474 CrossRef CAS PubMed.
- L. Shi, The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements, Nat. Biotechnol., 2006, 24, 1151–1161 CrossRef CAS PubMed.
- H. Ji and R. W. Davis, Data quality in genomics and microarrays, Nat. Biotechnol., 2006, 24, 1112–1113 CrossRef CAS PubMed.
- J. Lundeberg, D. Klevebring, M. Gry, J. Lindberg and A. Eidefors, Automation of cDNA synthesis and labelling improves reproducibility, J. Biomed. Biotechnol., 2009, 2009 Search PubMed.
- R. Šášik, C. H. Woelk and J. Corbeil, Microarray truths and consequences, J. Mol. Endocrinol., 2004, 33, 1–9 CrossRef.
- G. C. Tseng, M. K. Oh, L. Rohlin, J. C. Liao and W. H. Wong, Issues in cDNA microarray analysis: Quality filtering, channel normalization, models of variations and assessment of gene effects, Nucleic Acids Res., 2001, 29, 2549–2557 CrossRef CAS PubMed.
- K. R. Hess, W. Zhang, K. A. Baggerly, D. N. Stivers, K. R. Coombes and W. Zhang, Microarrays: Handling the deluge of data and extracting reliable information, Trends Biotechnol., 2001, 19, 463–468 CrossRef CAS.
- J. P. Peters and L. J. Maher, DNA curvature and flexibility in vitro and in vivo, Q. Rev. Biophys., 2010, 43, 23–63 CrossRef CAS PubMed.
- M. Schena, Microarray analysis, Wiley-Liss, Hoboken, NJ, 2003 Search PubMed.
- I. Barbulovic-Nad, M. Lucente, Y. Sun, M. Zhang, A. R. Wheeler and M. Bussmann, Bio-microarray fabrication techniques – A review, Crit. Rev. Biotechnol., 2006, 26, 237–259 CrossRef CAS PubMed.
- P. Gong and D. W. Grainger, Microarrays: Methods in Molecular Biology-Methods and Protocols, 2007 Search PubMed.
- D. J. Duggan, M. Bittner, Y. Chen, P. Meltzer and J. M. Trent, Expression profiling using cDNA microarrays, Nat. Genet., 1999, 21, 10–14 CrossRef CAS PubMed.
- P. Wu, D. G. Castner and D. W. Grainger, Diagnostic devices as biomaterials: A review of nucleic acid and protein microarray surface performance issues, J. Biomater. Sci., Polym. Ed., 2008, 19, 725–753 Search PubMed.
- A. Sassolas, B. D. Leca-Bouvier and L. J. Blum, DNA biosensors and microarrays, Chem. Rev., 2008, 108, 109–139 CrossRef CAS PubMed.
- M. Schena, R. A. Heller, T. P. Theriault, K. Konrad, E. Lachenmeier and R. W. Davis, Microarrays: Biotechnology's discovery platform for functional genomics, Trends Biotechnol., 1998, 16, 301–306 CrossRef CAS.
- E. H. Chowdhury and T. Akaike, Case studies-Development of oligonucleotides, Wiley-Interscience, Cary, North Carolina, 2007 Search PubMed.
- C. Lausted, T. Dahl, C. Warren, K. King, K. Smith and M. Johnson, et al., POSaM: a fast, flexible, open-source, inkjet oligonucleotide synthesizer and microarrayer, Genome Biol., 2004, 5, R58-R CrossRef PubMed.
- D. S. Dandy, P. Wu and D. W. Grainger, Array feature size influences nucleic acid surface capture in DNA microarrays, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8223–8228 CrossRef CAS PubMed.
- A. W. Peterson, R. J. Heaton and R. M. Georgiadis, The effect of surface probe density on DNA hybridization, Nucleic Acids Res., 2001, 29, 5163–5168 CrossRef CAS PubMed.
- R. H. Liu, J. Yang, R. Lenigk, J. Bonanno and P. Grodzinski, Self-Contained, Fully Integrated Biochip for Sample Preparation, Polymerase Chain Reaction Amplification, and DNA Microarray Detection, Anal. Chem., 2004, 76, 1824–1831 CrossRef CAS PubMed.
- P. Gong and D. W. Grainger, Comparison of DNA immobilization efficiency on new and regenerated commercial amine-reactive polymer microarray surfaces, Surf. Sci., 2004, 570, 67–77 CrossRef CAS PubMed.
- A. N. Rao, C. K. Rodesch and D. W. Grainger, Real-Time Fluorescent Image Analysis of DNA Spot Hybridization Kinetics To Assess Microarray Spot Heterogeneity, Anal. Chem., 2012, 84, 9379–9387 CrossRef CAS PubMed.
- A. N. Rao, N. Vandencasteele, L. J. Gamble and D. W. Grainger, High-resolution epifluorescence and time-of-flight secondary ion mass spectrometry chemical imaging comparisons of single DNA microarray spots, Anal. Chem., 2012, 84, 10628–10636 CrossRef CAS PubMed.
- R. Ramakrishnan, D. Dorris, A. Lublinsky, A. Nguyen, M. Domanus and A. Prokhorova, et al., An assessment of Motorola CodeLink microarray performance for gene expression profiling applications, Nucleic Acids Res., 2002, 30 CrossRef PubMed.
- H. Dai, M. Meyer, S. Stepaniants, M. Ziman and R. Stoughton, Use of hybridization kinetics for differentiating specific from non-specific binding to oligonucleotide microarrays, Nucleic Acids Res., 2002, 30 Search PubMed.
- A. Halperin, A. Buhot and E. B. Zhulina, On the hybridization isotherms of DNA microarrays: The Langmuir model and its extensions, J. Phys.: Condens. Matter, 2006, 18, S463–SS90 CrossRef CAS.
- P. Gong, C. Y. Lee, L. J. Gamble, D. G. Castner and D. W. Grainger, Hybridization behavior of mixed DNA/alkylthiol monolayers on gold: Characterization by surface plasmon resonance and 32P radiometric assay, Anal. Chem., 2006, 78, 3326–3334 CrossRef CAS PubMed.
- S. Venkatasubbarao, Microarrays–status and prospects, Trends Biotechnol., 2004, 22, 630–637 CrossRef CAS PubMed.
- M. Conti, Y. Bustanji, G. Falini, P. Ferruti, S. Stefoni and B. Samorì, The desorption process of macromolecules adsorbed on interfaces: The force spectroscopy approach, ChemPhysChem, 2001, 2, 610–613 CrossRef CAS.
- E. Paleček, Electrochemical behaviour of biological macromolecules, Bioelectrochem. Bioenerg., 1986, 15, 275–295 CrossRef.
- C. Y. Lee, P. Gong, G. M. Harbers, D. W. Grainger, D. G. Castner and L. J. Gamble, Surface coverage and structure of mixed DNA/Alkylthiol monolayers on gold: Characterization by XPS, NEXAFS, and fluorescence intensity measurements, Anal. Chem., 2006, 78, 3316–3325 CrossRef CAS PubMed.
- C.-Y. Lee, L. J. Gamble, D. W. Grainger and D. G. Castner, Mixed DNA/oligo (ethylene glycol) functionalized gold surfaces improve DNA hybridization in complex media, Biointerphases, 2006, 1, 82–92 CrossRef CAS PubMed.
- C.-Y. Lee, P.-C. T. Nguyen, D. W. Grainger, L. J. Gamble and D. G. Castner, Structure and DNA hybridization properties of mixed nucleic acid/maleimide-ethylene glycol monolayers, Anal. Chem., 2007, 79, 4390–4400 CrossRef CAS PubMed.
- R. S. Dias, A. A. C. C. Pais, P. Linse, M. G. Miguel and B. Lindman, Polyion adsorption onto catanionic surfaces. A Monte Carlo study, J. Phys. Chem. B, 2005, 109, 11781–11788 CrossRef CAS PubMed.
- B. A. Stillman and J. L. Tonkinson, FAST(TM) slides: A novel surface for microarrays, BioTechniques, 2000, 29, 630–635 CAS.
- D. W. Grainger, C. H. Greef, P. Gong and M. J. Lochhead, Current Microarray Surface chemistry, in Microarrays Volume-1 Synthesis Methods, ed. J. B. Rampal, Humana Press, 2007, pp. 37–58 Search PubMed.
- S. Araki, T. Nakai, K. Hizume, K. Takeyasu and K. Yoshikawa, Hydrodynamic radius of circular DNA is larger than that of linear DNA, Chem. Phys. Lett., 2006, 418, 255–259 CrossRef CAS PubMed.
- J. P. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- E. Currie, W. Norde and M. Cohen Stuart, Tethered polymer chains: surface chemistry and their impact on colloidal and surface properties, Adv. Colloid Interface Sci., 2003, 100, 205–265 CrossRef.
- A. Halperin, A. Buhot and E. B. Zhulina, Brush effects on DNA chips: Thermodynamics, kinetics, and design guidelines, Biophys. J., 2005, 89, 796–811 CrossRef CAS PubMed.
- L. C. Moh, M. D. Losego and P. V. Braun, Solvent Quality Effects on Scaling Behavior of Poly (methyl methacrylate) Brushes in the Moderate-and High-Density Regimes, Langmuir, 2011, 27, 3698–3702 CrossRef CAS PubMed.
- P.-Gd. Gennes, P. Pincus, R. Velasco and F. Brochard, Remarks on polyelectrolyte conformation, J. Phys., 1976, 37, 1461–1473 Search PubMed.
- E. B. Zhulina, O. V. Borisov and V. A. Priamitsyn, Theory of steric stabilization of colloid dispersions by grafted polymers, J. Colloid Interface Sci., 1990, 137, 495–511 CrossRef CAS.
- T. Birshtein, Y. V. Liatskaya and E. Zhulina, Theory of supermolecular structures of polydisperse block copolymers: 1. Planar layers of grafted chains, Polymer, 1990, 31, 2185–2196 CrossRef CAS.
- C. Wijmans, J. Scheutjens and E. Zhulina, Self-consistent field theories for polymer brushes: lattice calculations and an asymptotic analytical description, Macromolecules, 1992, 25, 2657–2665 CrossRef CAS.
- S. T. Milner, Strong-stretching and Scheutjens–Fleer descriptions of grafted polymer brushes, J. Chem. Soc., Faraday Trans., 1990, 86, 1349–1353 RSC.
- E. Currie, F. Leermakers, M. Cohen Stuart and G. Fleer, Grafted adsorbing polymers: scaling behavior and phase transitions, Macromolecules, 1999, 32, 487–498 CrossRef CAS.
- D. Bracha, E. Karzbrun, G. Shemer, P. A. Pincus and R. H. Bar-Ziv, Entropy-driven collective interactions in DNA brushes on a biochip, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4534–4538 CrossRef CAS PubMed.
- E. B. Zhulina and M. Rubinstein, Ionic strength dependence of polyelectrolyte brush thickness, Soft Matter, 2012, 8, 9376–9383 RSC.
- H. Bijsterbosch, V. De Haan, A. De Graaf, M. Mellema, F. Leermakers and M. C. Stuart, et al.: Tethered adsorbing chains: neutron reflectivity and surface pressure of spread diblock copolymer monolayers, Langmuir, 1995, 11, 4467–4473 CrossRef CAS.
- G. J. Fleer, Polymers at interfaces, Springer, 1993 Search PubMed.
- N. A. Kumar and C. Seidel, Polyelectrolyte brushes with added salt, Macromolecules, 2005, 38, 9341–9350 CrossRef CAS.
- R. Hariharan, C. Biver, J. Mays and W. Russel, Ionic strength and curvature effects in flat and highly curved polyelectrolyte brushes, Macromolecules, 1998, 31, 7506–7513 CrossRef CAS.
- R. Hariharan, C. Biver and W. Russel, Ionic strength effects in polyelectrolyte brushes: The counterion correction, Macromolecules, 1998, 31, 7514–7518 CrossRef CAS.
- V. Pryamitsyn, F. Leermakers and E. Zhulina, Brush theory of tethered chains with a charged group at the free end, Macromolecules, 1997, 30, 584–589 CrossRef CAS.
- O. Borisov, F. Leermakers, G. Fleer and E. Zhulina, Polyelectrolytes tethered to a similarly charged surface, J. Chem. Phys., 2001, 114, 7700 CrossRef CAS PubMed.
- E. Zhulina, J. Klein Wolterink and O. Borisov, Screening effects in a polyelectrolyte brush: self-consistent-field theory, Macromolecules, 2000, 33, 4945–4953 CrossRef CAS.
- R. Israels, F. Leermakers and G. Fleer, On the theory of grafted weak polyacids, Macromolecules, 1994, 27, 3087–3093 CrossRef CAS.
- Y. V. Lyatskaya, F. Leermakers, G. Fleer, E. Zhulina and T. Birshtein, Analytical self-consistent-field model of weak polyacid brushes, Macromolecules, 1995, 28, 3562–3569 CrossRef CAS.
- G. S. Manning, Limiting laws and counterion condensation in polyelectrolyte solutions I. Colligative properties, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS PubMed.
- E. Zhulina, T. Birshtein and O. Borisov, Theory of ionizable polymer brushes, Macromolecules, 1995, 28, 1491–1499 CrossRef CAS.
- P. Gong and R. Levicky, DNA surface hybridization regimes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5301–5306 CrossRef CAS PubMed.
- M. F. Hagan and A. K. Chakraborty, Hybridization dynamics of surface immobilized DNA, J. Chem. Phys., 2004, 120, 4958–4968 CrossRef CAS PubMed.
- F. Cheng, L. J. Gamble and D. G. Castner, XPS, TOF-SIMS, NEXAFS, and SPR characterization of nitrilotriacetic acid-terminated self-assembled monolayers for controllable immobilization of proteins, Anal. Chem., 2008, 80, 2564–2573 CrossRef CAS PubMed.
- W. Steven, M. J. L. Metzger and D. W. Grainger, Surface chemistries enable application of protein microarray technologies to diagnostics, 2002 Search PubMed.
- M. Dufva, Fabrication of high quality microarrays, Biomol. Eng., 2005, 22, 173–184 CrossRef CAS PubMed.
- M. R. Fielden, R. G. Halgren, E. Dere and T. R. Zacharewski, GP3: GenePix post-processing program for automated analysis of raw microarray data, Bioinformatics, 2002, 18, 771–773 CrossRef CAS PubMed.
- A. M. Dudley, J. Aach, M. A. Steffen and G. M. Church, Measuring absolute expression with microarrays with a calibrated reference sample and an extended signal intensity range, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7554–7559 CrossRef CAS PubMed.
- R. Levicky and A. Horgan, Physicochemical perspectives on DNA microarray and biosensor technologies, Trends Biotechnol., 2005, 23, 143–149 CrossRef CAS PubMed.
- A. B. Steel, R. L. Levicky, T. M. Herne and M. J. Tarlov, Immobilization of nucleic acids at solid surfaces: Effect of oligonucleotide length on layer assembly, Biophys. J., 2000, 79, 975–981 CrossRef CAS.
- J. L. Seifert, R. E. Connor, S. A. Kushon, M. Wang and B. A. Armitage, Spontaneous assembly of helical cyanine dye aggregates on DNA nanotemplates, J. Am. Chem. Soc., 1999, 121, 2987–2995 CrossRef CAS.
- J. B. Randolph and A. S. Waggoner, Stability, specificity and fluorescence brightness of multiply-labeled fluorescent DNA probes, Nucleic Acids Res., 1997, 25, 2923–2929 CrossRef CAS PubMed.
- J. F. Allemand, D. Bensimon, R. Lavery and V. Croquette, Stretched and overwound DNA forms a Pauling-like structure with exposed bases, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 14152–14157 CrossRef CAS.
- X. Fang, B. Li, E. Petersen, Y. S. Seo, V. A. Samuilov and Y. Chen, et al., Drying of DNA droplets, Langmuir, 2006, 22, 6308–6312 CrossRef CAS PubMed.
- V. Dugas, J. Broutin and E. Souteyrand, Droplet evaporation study applied to DNA chip manufacturing, Langmuir, 2005, 21, 9130–9136 CrossRef CAS PubMed.
- H. Schiessel and P. Pincus, Counterion-condensation-induced collapse of highly charged polyelectrolytes, Macromolecules, 1998, 31, 7953–7959 CrossRef CAS.
- G. S. Manning, The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides, Q. Rev. Biophys., 1978, 11, 179–246 CrossRef CAS.
- J. M. Schurr and B. S. Fujimoto, Extensions of counterion condensation theory. I. Alternative geometries and finite salt concentration, Biophys. Chem., 2002, 101–102, 425–445 CrossRef CAS.
- T. R. Strick, J. F. Allemand, D. Bensimon and V. Croquette, Behavior of supercoiled DNA, Biophys. J., 1998, 74, 2016–2028 CrossRef CAS.
- T. R. Strick, J. F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, The elasticity of a single supercoiled DNA molecule, Science, 1996, 271, 1835–1837 CAS.
- S. B. Smith, Y. Cui and C. Bustamante, Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules, Science, 1996, 271, 795–799 CrossRef CAS.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Stretching DNA with optical tweezers, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS.
- M. C. Murphy, I. Rasnik, W. Cheng, T. M. Lohman and T. Ha, Probing Single-Stranded DNA Conformational Flexibility Using Fluorescence Spectroscopy, Biophys. J., 2004, 86, 2530–2537 CrossRef CAS.
- C. Bouchiat, M. D. Wang, J. F. Allemand, T. Strick, S. M. Block and V. Croquette, Estimating the persistence length of a worm-like chain molecule from force-extension measurements, Biophys. J., 1999, 76, 409–413 CrossRef CAS.
- S. Brinkers, H. R. C. Dietrich, F. H. De Groote, I. T. Young and B. Rieger, The persistence length of double stranded DNA determined using dark field tethered particle motion, J. Chem. Phys., 2009, 130 Search PubMed.
- C. Bustamante, Z. Bryant and S. B. Smith, Ten years of tension: Single-molecule DNA mechanics, Nature, 2003, 421, 423–427 CrossRef PubMed.
- A. Pardi, D. R. Hare and C. Wang, Determination of DNA structures by NMR and distance geometry techniques: a computer simulation, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 8785–8789 CrossRef CAS.
- M. C. Williams and L. J. Maher, Biophysics of DNA-protein interactions: from single molecules to biological systems, Springer, New York, 2011 Search PubMed.
- C. Bustamante, S. B. Smith, J. Liphardt and D. Smith, Single-molecule studies of DNA mechanics, Curr. Opin. Struct. Biol., 2000, 10, 279–285 CrossRef CAS.
- A. V. Dobrynin, R. H. Colby and M. Rubinstein, Scaling theory of polyelectrolyte solutions, Macromolecules, 1995, 28, 1859–1871 CrossRef CAS.
- C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Ionic effects on the elasticity of single DNA molecules, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190 CrossRef CAS.
- T. Odijk, Polyelectrolytes near the rod limit, J. Polym. Sci., Part B: Polym. Phys., 1977, 15, 477–483 CrossRef CAS.
- J. Skolnick and M. Fixman, Electrostatic persistence length of a wormlike polyelectrolyte, Macromolecules, 1977, 10, 944–948 CrossRef CAS.
- H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Ionic strength-dependent persistence lengths of single-stranded RNA and DNA, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 799–804 CrossRef CAS PubMed.
- A. Savelyev, Do monovalent mobile ions affect DNA's flexibility at high salt content?, Phys. Chem. Chem. Phys., 2012, 14, 2250–2254 RSC.
- R. G. Kirste, Radius of gyration of stiff chain molecules as a function of the chain length and the interactions with the solvent, Discuss. Faraday Soc., 1970, 49, 51–59 RSC.
- B. Tinland, A. Pluen, J. Sturm and G. Weill, Persistence length of single-stranded DNA, Macromolecules, 1997, 30, 5763–5765 CrossRef CAS.
- S. V. Kuznetsov, Y. Shen, A. S. Benight and A. Ansari, A semiflexible polymer model applied to loop formation in DNA hairpins, Biophys. J., 2001, 81, 2864–2875 CrossRef CAS.
- P. G. De Gennes, Conformations of polymers attached to an interface, Macromolecules, 1980, 13, 1069–1075 CrossRef CAS.
- A. Halperin, A. Buhot and E. B. Zhulina, Hybridization at a surface: The role of spacers in DNA microarrays, Langmuir, 2006, 22, 11290–11304 CrossRef CAS PubMed.
- R. Lehner, J. Koota, G. Maret and T. Gisler, Segment distributions of end-tethered polymers in a good solvent, Phys. Rev. Lett., 2006, 96, 107801 CrossRef CAS.
- M. Adamuti-Trache, W. E. McMullen and J. F. Douglas, Segmental concentration profiles of end-tethered polymers with excluded-volume and surface interactions, J. Chem. Phys., 1996, 105, 4798–4811 CrossRef CAS PubMed.
- D. Rekesh, Y. Lyubchenko, L. S. Shlyakhtenko and S. M. Lindsay, Scanning tunneling microscopy of mercapto-hexyl-oligonucleotides attached to gold, Biophys. J., 1996, 71, 1079–1086 CrossRef CAS.
- R. C. Mucic, M. K. Herrlein, C. A. Mirkin and R. L. Letsinger, Synthesis and characterization of DNA with ferrocenyl groups attached to their 5′-termini: Electrochemical characterization of a redox-active nucleotide monolayer, Chem. Commun., 1996, 555–557 RSC.
- W. Kaiser and U. Rant, Conformations of end-tethered DNA molecules on gold surfaces: influences of applied electric potential, electrolyte screening, and temperature, J. Am. Chem. Soc., 2010, 132, 7935–7945 CrossRef CAS PubMed.
- J. M. Schurr and S. A. Allison, Polyelectrolyte contribution to the persistence length of DNA, Biopolymers, 1981, 20, 251–268 CrossRef CAS PubMed.
- J. M. Schurr, Polyanion Models of Nucleic Acid-Metal Ion Interactions, RSC Biomol. Sci., 2009, 307–349 CAS.
- G. S. Manning, K. K. Ebralidse, A. D. Mirzabekov and A. Rich, An estimate of the extent of folding of nucleosomal DNA by laterally asymmetric neutralization of phosphate groups, J. Biomol. Struct. Dyn., 1989, 6, 877–889 CAS.
- A. Savelyev, C. K. Materese and G. A. Papoian, Is DNA's rigidity dominated by electrostatic or nonelectrostatic interactions?, J. Am. Chem. Soc., 2011, 133, 19290–19293 CrossRef CAS PubMed.
- L. D. Williams and L. J. Maher Iii, Electrostatic mechanisms of DNA deformation, 2000, pp. 497–521.
- T. Moulaei, T. Maehigashi, G. T. Lountos, S. Komeda, D. Watkins and M. P. Stone, et al., Structure of B-DNA with cations tethered in the major groove, Biochemistry, 2005, 44, 7458–7468 CrossRef CAS PubMed.
- A. Vainrub and B. M. Pettitt, Coulomb blockage of hybridization in two-dimensional DNA arrays, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 041905/1–041905/4 CrossRef CAS.
- I. Nazarenko, R. Pires, B. Lowe, M. Obaidy and A. Rashtchian, Effect of primary and secondary structure of oligodeoxyribonucleotides on the fluorescent properties of conjugated dyes, Nucleic Acids Res., 2002, 30, 2089–2095 CrossRef CAS PubMed.
- N. L. Goddard, G. Bonnet, O. Krichevsky and A. Libchaber, Sequence dependent rigidity of single stranded DNA, Phys. Rev. Lett., 2000, 85, 2400–2403 CrossRef CAS.
- B. D. Coleman, W. K. Olson and D. Swigon, Theory of sequence-dependent DNA elasticity, J. Chem. Phys., 2003, 118, 7127–7140 CrossRef CAS PubMed.
- K. D. Dorfman, S. B. King, D. W. Olson, J. D. P. Thomas and D. R. Tree, Beyond gel electrophoresis: Microfluidic separations, fluorescence burst analysis, and DNA stretching, Chem. Rev., 2012, 113, 2584–2667 CrossRef PubMed.
- L. Moiseev, M. S. Ünlü, A. K. Swan, B. B. Goldberg and C. R. Cantor, DNA conformation on surfaces measured by fluorescence self-interference, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 2623–2628 CrossRef CAS PubMed.
- G. Held, G. Grinstein and Y. Tu, Modeling of DNA microarray data by using physical properties of hybridization, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7575–7580 CrossRef CAS PubMed.
- A. Vainrub and B. Montgomery Pettitt, Surface electrostatic effects in oligonucleotide microarrays: control and optimization of binding thermodynamics, Biopolymers, 2003, 68, 265–270 CrossRef CAS PubMed.
- I. Y. Wong and N. A. Melosh, An electrostatic model for DNA surface hybridization, Biophys. J., 2010, 98, 2954–2963 CrossRef CAS PubMed.
- G. Shen, N. Tercero, M. A. Gaspard, B. Varughese, K. Shepard and R. Levicky, Charging behavior of single-stranded DNA polyelectrolyte brushes, J. Am. Chem. Soc., 2006, 128, 8427–8433 CrossRef CAS PubMed.
- A. Halperin, A. Buhot and E. B. Zhulina, Sensitivity, Specificity, and the Hybridization Isotherms of DNA Chips, Biophys. J., 2004, 86, 718–730 CrossRef CAS.
- V. A. Vasiliskov, D. V. Prokopenko and A. D. Mirzabekov, Parallel multiplex thermodynamic analysis of coaxial base stacking in DNA duplexes by oligodeoxyribonucleotide microchips, Nucleic Acids Res., 2001, 29, 2303–2313 CrossRef CAS PubMed.
- T. T. Nguyen, A. Y. Grosberg and B. I. Shklovskii, Screening of a charged particle by multivalent counterions in salty water: strong charge inversion, J. Chem. Phys., 2000, 113, 1110–1125 CrossRef CAS PubMed.
- A. Vainrub and B. M. Pettitt, Thermodynamics of association to a molecule immobilized in an electric double layer, Chem. Phys. Lett., 2000, 323, 160–166 CrossRef CAS.
- R. R. Netz and D. Andelman, Neutral and charged polymers at interfaces, Phys. Rep., 2003, 380, 1–95 CrossRef CAS.
- D. Y. Petrovykh, H. Kimura-Suda, L. J. Whitman and M. J. Tarlov, Quantitative analysis and characterization of DNA immobilized on gold, J. Am. Chem. Soc., 2003, 125, 5219–5226 CrossRef CAS PubMed.
- T. Strick, J. F. Allemand, V. Croquette and D. Bensimon, Twisting and stretching single DNA molecules, Prog. Biophys. Mol. Biol., 2000, 74, 115–140 CrossRef CAS.
- J. D. Moroz and P. Nelson, Torsional directed walks, entropic elasticity, and DNA twist stiffness, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14418–14422 CrossRef CAS.
- J. Zhang, H. P. Lang, G. Yoshikawa and C. Gerber, Optimization of DNA hybridization efficiency by pH-driven nanomechanical bending, Langmuir, 2012, 28, 6494–6501 CrossRef CAS PubMed.
- J. F. Marko and E. D. Siggia, Stretching DNA, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J. L. Viovy and D. Chatenay, et al., DNA: an extensible molecule, Science, 1996, 271, 792–794 CAS.
- T. E. Cloutier and J. Widom, DNA twisting flexibility and the formation of sharply looped protein-DNA complexes, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3645–3650 CrossRef CAS PubMed.
- R. A. Forties, R. Bundschuh and M. G. Poirier, The flexibility of locally melted DNA, Nucleic Acids Res., 2009, 37, 4580–4586 CrossRef CAS PubMed.
- T. Cloutier and J. Widom, DNA twisting flexibility and the formation of sharply looped protein–DNA complexes, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3645–3650 CrossRef CAS PubMed.
- Y. Zhang, H. Zhou and Z. C. Ou-Yang, Stretching single-stranded DNA: Interplay of electrostatic, base-pairing, and base-pair stacking interactions, Biophys. J., 2001, 81, 1133–1143 CrossRef CAS.
- H. G. Hansma, K. J. Kim, D. E. Laney, R. A. Garcia, M. Argaman and M. J. Allen, et al., Properties of biomolecules measured from atomic force microscope images: A review, J. Struct. Biol., 1997, 119, 99–108 CrossRef CAS PubMed.
- M. Bezanilla, S. Manne, D. E. Laney, Y. L. Lyubchenko and H. G. Hansma, Adsorption of DNA to mica, silylated mica, and minerals: Characterization by atomic force microscopy, Langmuir, 1995, 11, 655–659 CrossRef CAS.
- C. Frontali, E. Dore, A. Ferrauto, E. Gratton, A. Bettini and M. R. Pozzan, et al., An absolute method for the determination of the persistence length of native DNA from electron micrographs, Biopolymers, 1979, 18, 1353–1373 CrossRef CAS PubMed.
- P. J. Hagerman, Flexibility of DNA, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 265–286 CrossRef CAS PubMed.
- E. Protozanova, P. Yakovchuk and M. D. Frank-Kamenetskii, Stacked-unstacked equilibrium at the nick site of DNA, J. Mol. Biol., 2004, 342, 775–785 CrossRef CAS PubMed.
- M. Caserta, E. Agricola, M. Churcher, E. Hiriart, L. Verdone and E. Di mauro, et al., A translational signature for nucleosome positioning in vivo, Nucleic Acids Res., 2009, 37, 5309–5321 CrossRef CAS PubMed.
- A. Morriss-Andrews, J. Rottler and S. S. Plotkin, A systematically coarse-grained model for DNA and its predictions for persistence length, stacking, twist, and chirality, J. Chem. Phys., 2010, 132 Search PubMed.
- J. Ambia-Garrido, A. Vainrub and B. M. Pettitt, A model for structure and thermodynamics of ssDNA and dsDNA near a surface: A coarse grained approach, Comput. Phys. Commun., 2010, 181, 2001–2007 CrossRef CAS PubMed.
- K. Rechendorff, G. Witz, J. Adamcik and G. Dietler, Persistence length and scaling properties of single-stranded DNA adsorbed on modified graphite, J. Chem. Phys., 2009, 131 Search PubMed.
- P. S. Crozier and M. J. Stevens, Simulations of single grafted polyelectrolyte chains: ssDNA and dsDNA, J. Chem. Phys., 2003, 118, 3855–3860 CrossRef CAS PubMed.
- D. Erts, B. Polyakov, H. Olin and E. Tuite, Spatial and mechanical properties of dilute DNA monolayers on gold imaged by AFM, J. Phys. Chem. B, 2003, 107, 3591–3597 CrossRef CAS.
- R. Levicky, T. M. Herne, M. J. Tarlov and S. K. Satija, Using self-assembly to control the structure of DNA monolayers on gold: A neutron reflectivity study, J. Am. Chem. Soc., 1998, 120, 9787–9792 CrossRef CAS.
- J. Wang, G. Rivas, X. Cai, M. Chicharro, C. Parrado and N. Dontha, et al., Detection of point mutation in the p53 gene using peptide nucleic acid biosensor, Anal. Chim. Acta, 1997, 344, 111–118 CrossRef CAS.
- J. A. Abels, F. Moreno-Herrero, T. Van Der Heijden, C. Dekker and N. H. Dekker, Single-molecule measurements of the persistence length of double-stranded RNA, Biophys. J., 2005, 88, 2737–2744 CrossRef CAS PubMed.
- A. J. Mastroianni, D. A. Sivak, P. L. Geissler and A. P. Alivisatos, Probing the conformational distributions of subpersistence length DNA, Biophys. J., 2009, 97, 1408–1417 CrossRef CAS PubMed.
- Z. Bryant, M. D. Stone, J. Gore, S. B. Smith, N. R. Cozzarelli and C. Bustamante, Structural transitions and elasticity from torque measurements on DNA, Nature, 2003, 424, 338–341 CrossRef CAS PubMed.
- O. Kratky and G. Porod, Diffuse small-angle scattering of X-rays in colloid systems, J. Colloid Sci., 1949, 4, 35–70 CrossRef CAS.
- K. Rippe, P. H. Von Hippel and J. Langowski, Action at a distance: DNA-looping and initiation of transcription, Trends Biochem. Sci., 1995, 20, 500–506 CrossRef CAS.
- J. Shimada and H. Yamakawa, Ring-closure probabilities for twisted wormlike chains, Application to DNA, Macromolecules, 1984, 17, 689–698 CrossRef CAS.
- J. Maddox, The case for a great many journals, Nature, 1995, 375, 11 CrossRef CAS PubMed.
- D. Bensimon, A. J. Simon, V. V. Croquette and A. Bensimon, Stretching DNA with a receding meniscus: Experiments and models, Phys. Rev. Lett., 1995, 74, 4754–4757 CrossRef CAS.
- J. Van mameren, E. J. G. Peterman and G. J. L. Wuite, See me, feel me: Methods to concurrently visualize and manipulate single DNA molecules and associated proteins, Nucleic Acids Res., 2008, 36, 4381–4389 CrossRef CAS PubMed.
- Y. Seol, J. Li, P. C. Nelson, T. T. Perkins and M. D. Betterton, Elasticity of short DNA molecules: Theory and experiment for contour lengths of 0.6–7 μm, Biophys. J., 2007, 93, 4360–4373 CrossRef CAS PubMed.
- P. A. Wiggins and P. C. Nelson, Generalized theory of semiflexible polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73 Search PubMed.
- U. Rant, K. Arinaga, S. Scherer, E. Pringsheim, S. Fujita and N. Yokoyama, et al. Switchable DNA interfaces for the highly sensitive detection of label-free DNA targets, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17364–17369 CrossRef CAS PubMed.
- L. Van Eijck, F. Merzel, S. Rols, J. Ollivier, V. T. Forsyth and M. R. Johnson, Biophysics: DNA is as elastic as nylon, Nature, 2011, 477, 372 Search PubMed.
- L. Van Eijck, F. Merzel, S. Rols, J. Ollivier, V. T. Forsyth and M. R. Johnson, Direct determination of the base-pair force constant of DNA from the acoustic phonon dispersion of the double helix, Phys. Rev. Lett., 2011, 107 Search PubMed.
- T. Morii, R. Mizuno, H. Haruta and T. Okada, An AFM study of the elasticity of DNA molecules, Thin Solid Films, 2004, 464–465, 456–458 CrossRef CAS PubMed.
- P. Nelson, New measurements of DNA twist elasticity, Biophys. J., 1998, 74, 2501–2503 CrossRef CAS.
- J. F. Marko, Stretching must twist DNA, Europhys. Lett., 1997, 38, 183–188 CrossRef CAS.
- A. Stasiak and E. Di Capua, The helicity of DNA in complexes with RecA protein, Nature, 1982, 299, 185–186 CrossRef CAS.
- J. F. Léger, G. Romano, A. Sarkar, J. Robert, L. Bourdieu and D. Chatenay, et al., Structural transitions of a twisted and stretched DNA molecule, Phys. Rev. Lett., 1999, 83, 1066–1069 CrossRef.
- A. Sarkar, J. F. Léger, D. Chatenay and J. F. Marko, Structural transitions in DNA driven by external force and torque, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 519031–5190310 CrossRef.
- J. R. Wenner, M. C. Williams, I. Rouzina and V. A. Bloomfield, Salt dependence of the elasticity and overstretching transition of single DNA molecules, Biophys. J., 2002, 82, 3160–3169 CrossRef CAS.
- O. Punkkinen, P. L. Hansen, L. Miao and I. Vattulainen, DNA overstretching transition: Ionic strength effects, Biophys. J., 2005, 89, 967–978 CrossRef CAS PubMed.
- M. Le Bret and B. H. Zimm, Monte Carlo determination of the distribution of ions about a cylindrical polyelectrolyte, Biopolymers, 1984, 23, 271–285 CrossRef CAS PubMed.
- M. C. Williams, J. R. Wenner, I. Rouzina and V. A. Bloomfield, Effect of pH on the overstretching transition of double-stranded DNA: Evidence of force-induced DNA melting, Biophys. J., 2001, 80, 874–881 CrossRef CAS.
- R. D. Kamien, T. C. Lubensky, P. Nelson and C. S. O'Hern, Direct determination of DNA twist-stretch coupling, Europhys. Lett., 1997, 38, 237–242 CrossRef CAS.
- J. Gore, Z. Bryant, M. Nöllmann, M. U. Le, N. R. Cozzarelli and C. Bustamante, DNA overwinds when stretched, Nature, 2006, 442, 836–839 CrossRef CAS PubMed.
- K. Raghunathan, Y. F. Chenc, J. Blaty, B. A. Juliar, J. Milstein and J. C. Meiners, Mechanics of DNA: Sequence dependent elasticity. San Diego, CA, 2011 Search PubMed.
- M. Y. Sheinin, S. Forth, J. F. Marko and M. D. Wang, Underwound DNA under tension: Structure, elasticity, and sequence-dependent behaviors, Phys. Rev. Lett., 2011, 107 Search PubMed.
- Z. Yang, Z. Haijun and O. Y. Zhong-Can, Monte Carlo implementation of supercoiled double-stranded DNA, Biophys. J., 2000, 78, 1979–1987 CrossRef CAS.
- H. G. Hansma, D. E. Laney, M. Bezanilla, R. L. Sinsheimer and P. K. Hansma, Applications for atomic force microscopy of DNA, Biophys. J., 1995, 68, 1672–1677 CrossRef CAS.
- L. Gao, J. Wu, D. Gao and J. Wu, Separation of long DNA molecules through cleavage of hydrogen bonds under a stretching force, Appl. Phys. Lett., 2007, 91 CAS.
- D. E. Gray, S. C. Case-Green, T. S. Fell, P. J. Dobson and E. M. Southern, Ellipsometric and interferometric characterization of DNA probes immobilized on a combinatorial array, Langmuir, 1997, 13, 2833–2842 CrossRef CAS.
- L. A. Chrisey, C. E. O'Ferrall, B. J. Spargo, C. S. Dulcey and J. M. Calvert, Fabrication of patterned DNA surfaces, Nucleic Acids Res., 1996, 24, 3040–3047 CrossRef CAS PubMed.
- R. Levicky, N. Koneripalli, M. Tirrell and S. K. Satija, Stratification in bidisperse polymer brushes from neutron reflectivity, Macromolecules, 1998, 31, 2616–2621 CrossRef CAS.
- T. M. Herne and M. J. Tarlov, Characterization of DNA probes immobilized on gold surfaces, J. Am. Chem. Soc., 1997, 119, 8916–8920 CrossRef CAS.
- K. A. Peterlinz, R. M. Georgiadis, T. M. Herne and M. J. Tarlov, Observation of hybridization and dehybridization of thiol-tethered DNA using two-color surface plasmon resonance spectroscopy, J. Am. Chem. Soc., 1997, 119, 3401–3402 CrossRef CAS.
- S. O. Kelley, J. K. Barton, N. M. Jackson, L. D. McPherson, A. B. Potter and E. M. Spain, et al., Orienting DNA helices on gold using applied electric fields, Langmuir, 1998, 14, 6781–6784 CrossRef CAS.
- U. Rant, K. Arinaga, M. Tornow, W. K. Yong, R. R. Netz and S. Fujita, et al., Dissimilar kinetic behavior of electrically manipulated single- and double-stranded DNA tethered to a gold surface, Biophys. J., 2006, 90, 3666–3671 CrossRef CAS PubMed.
- C. F. Edman, D. E. Raymond, D. J. Wu, E. Tu, R. G. Sosnowski and W. F. Butler, et al., Electric field directed nucleic acid hybridization on microchips, Nucleic Acids Res., 1997, 25, 4907–4914 CrossRef CAS PubMed.
- A. B. Steel, T. M. Herne and M. J. Tarlov, Electrochemical quantitation of DNA immobilized on gold, Anal. Chem., 1998, 70, 4670–4677 CrossRef CAS.
- J. Fritz, E. B. Cooper, S. Gaudet, P. K. Sorger and S. R. Manalis, Electronic detection of DNA by its intrinsic molecular charge, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 14142–14146 CrossRef CAS PubMed.
- R. J. Heaton, A. W. Peterson and R. M. Georgiadis, Electrostatic surface plasmon resonance: direct electric field-induced hybridization and denaturation in monolayer nucleic acid films and label-free discrimination of base mismatches, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 3701–3704 CrossRef CAS PubMed.
- G. Bhanot, Y. Louzoun, J. Zhu and C. DeLisi, The importance of thermodynamic equilibrium for high throughput gene expression arrays, Biophys. J., 2003, 84, 124–135 CrossRef CAS.
- J. Bishop, A. Chagovetz and S. Blair, Kinetics of multiplex hybridization: mechanisms and implications, Biophys. J., 2008, 94, 1726–1734 CrossRef CAS PubMed.
- M. R. Henry, P. Wilkins Stevens, J. Sun and D. M. Kelso, Real-time measurements of DNA hybridization on microparticles with fluorescence resonance energy transfer, Anal. Biochem., 1999, 276, 204–214 CrossRef CAS PubMed.
- Z. Guo, R. A. Guilfoyle, A. J. Thiel, R. Wang and L. M. Smith, Direct fluorescence analysis of genetic polymorphisms by hybridization with oligonucleotide arrays on glass supports, Nucleic Acids Res., 1994, 22, 5456–5465 CrossRef CAS PubMed.
- H. J. Su, S. Surrey, S. E. McKenzie, P. Fortina and D. J. Graves, Kinetics of heterogeneous hybridization on indium tin oxide surfaces with and without an applied potential, Electrophoresis, 2002, 23, 1551–1557 CrossRef CAS.
- R. A. Dimitrov and M. Zuker, Prediction of hybridization and melting for double-stranded nucleic acids, Biophys. J., 2004, 87, 215–226 CrossRef CAS PubMed.
- A. Hassibi, H. Vikalo, J. L. Riechmann and B. Hassibi, Real-time DNA microarray analysis, Nucleic Acids Res., 2009, 37 Search PubMed.
- A. Toegl, R. Kirchner, C. Gauer and A. Wixforth, Enhancing results of microarray hybridizations through microagitation, J. Biomol. Tech., 2003, 14, 197–204 Search PubMed.
- A. Chagovetz and S. Blair, Real-time DNA microarrays: reality check, Biochem. Soc. Trans., 2009, 37, 471 CrossRef CAS PubMed.
- J.-C. Walter, K. M. Kroll, J. Hooyberghs and E. Carlon, Nonequilibrium effects in DNA microarrays: a multiplatform study, J. Phys. Chem. B, 2011, 115, 6732–6739 CrossRef CAS PubMed.
- E. Carletti, E. Guerra and S. Alberti, The forgotten variables of DNA array hybridization, Trends Biotechnol., 2006, 24, 443–448 CrossRef CAS PubMed.
- M. Horne, D. Fish and A. Benight, Statistical thermodynamics and kinetics of DNA multiplex hybridization reactions, Biophys. J., 2006, 91, 4133–4153 CrossRef CAS PubMed.
- C. Chen, W. Wang, J. Ge and X. S. Zhao, Kinetics and thermodynamics of DNA hybridization on gold nanoparticles, Nucleic Acids Res., 2009, 37, 3756–3765 CrossRef CAS PubMed.
- J. E. Forman, I. D. Walton, D. Stern, R. P. Rava and M. O. Trulson, Thermodynamics of Duplex Formation and Mismatch Discrimination on Photolithographically Synthesized Oligonucleotide Arrays, 1998, pp. 206–228 Search PubMed.
- F. Naef and M. O. Magnasco, Solving the riddle of the bright mismatches: Labeling and effective binding in oligonucleotide arrays, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 119061–119064 CrossRef.
- D. Erickson, X. Liu, U. Krull and D. Li, Electrokinetically controlled DNA hybridization microfluidic chip enabling rapid target analysis, Anal. Chem., 2004, 76, 7269–7277 CrossRef CAS PubMed.
- J. R. Unruh, G. Gokulrangan, G. H. Lushington, C. K. Johnson and G. S. Wilson, Orientational dynamics and dye-DNA interactions in a dye-labeled DNA aptamer, Biophys. J., 2005, 88, 3455–3465 CrossRef CAS PubMed.
- G. T. Hermanson, Bioconjugate Techniques, Academic Press, Elsevier, 2008 Search PubMed.
- S. L. Beaucage, Strategies in the preparation of DNA oligonucleotide arrays for diagnostic applications, Curr. Med. Chem., 2001, 8, 1213–1244 CrossRef CAS.
- Y. Gao, L. K. Wolf and R. M. Georgiadis, Secondary structure effects on DNA hybridization kinetics: A solution versus surface comparison, Nucleic Acids Res., 2006, 34, 3370–3377 CrossRef CAS PubMed.
- T. H. Nguyen, J. P. Hilton and Q. Lin, Emerging applications of aptamers to micro- and nanoscale biosensing, Microfluid. Nanofluid., 2009, 6, 347–362 CrossRef CAS.
- T. J. Drake and W. Tan, Molecular Beacon DNA Probes and their Bioanalytical Applications, Appl. Spectrosc., 2004, 58, 269A–280A CrossRef CAS PubMed.
- D. A. Di Giusto, W. A. Wlassoff, J. J. Gooding, B. A. Messerle and G. C. King, Proximity extension of circular DNA aptamers with real-time protein detection, Nucleic Acids Res., 2005, 33, e64-e CrossRef PubMed.
- K. Wang, Z. Tang, C. J. Yang, Y. Kim, X. Fang and W. Li, et al., Molecular engineering of DNA: molecular beacons, Angew. Chem., Int. Ed., 2009, 48, 856–870 CrossRef CAS PubMed.
- X. Fang, X. Liu, S. Schuster and W. Tan, Designing a novel molecular beacon for surface-immobilized DNA hybridization studies, J. Am. Chem. Soc., 1999, 121, 2921–2922 CrossRef CAS.
- W. Tan, K. Wang and T. J. Drake, Molecular beacons, Curr. Opin. Chem. Biol., 2004, 8, 547–553 CrossRef CAS PubMed.
- J. SantaLucia Jr. and D. Hicks, The thermodynamics of DNA structural motifs, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef PubMed.
- H. Wang, J. Li, H. Liu, Q. Liu, Q. Mei and Y. Wang, et al., Label-free hybridization detection of a single nucleotide mismatch by immobilization of molecular beacons on an agarose film, Nucleic Acids Res., 2002, 30, e61-e CrossRef PubMed.
- S. A. Marras, S. Tyagi and F. R. Kramer, Real-time assays with molecular beacons and other fluorescent nucleic acid hybridization probes, Clin. Chim. Acta, 2006, 363, 48–60 CrossRef CAS PubMed.
- H. Du, C. M. Strohsahl, J. Camera, B. L. Miller and T. D. Krauss, Sensitivity and specificity of metal surface-immobilized “molecular beacon” biosensors, J. Am. Chem. Soc., 2005, 127, 7932–7940 CrossRef CAS PubMed.
- G. Bonnet, S. Tyagi, A. Libchaber and F. R. Kramer, Thermodynamic basis of the enhanced specificity of structured DNA probes, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6171–6176 CrossRef CAS.
- G. Yao, X. Fang, H. Yokota, T. Yanagida and W. Tan, Monitoring molecular beacon DNA probe hybridization at the single-molecule level, Chem.–Eur. J., 2003, 9, 5686–5692 CrossRef CAS PubMed.
- D. P. Aalberts, J. M. Parman and N. L. Goddard, Single-strand stacking free energy from DNA beacon kinetics, Biophys. J., 2003, 84, 3212–3217 CrossRef CAS.
- J. Jung and A. Van Orden, Folding and unfolding kinetics of DNA hairpins in flowing solution by multiparameter fluorescence correlation spectroscopy, J. Phys. Chem. B, 2005, 109, 3648–3657 CrossRef CAS PubMed.
- M. Kastantin and D. K. Schwartz, DNA Hairpin Stabilization on a Hydrophobic Surface, Small, 2013, 9, 933–941 CrossRef CAS PubMed.
- J. Perelaer, P. J. Smith, M. M. P. Wijnen, E. Van Den Bosch, R. Eckardt and P. H. J. M. Ketelaars, et al., Droplet tailoring using evaporative inkjet printing, Macromol. Chem. Phys., 2009, 210, 387–393 CrossRef CAS.
- H. Hu and R. G. Larson, Marangoni effect reverses coffee-ring depositions, J. Phys. Chem. B, 2006, 110, 7090–7094 CrossRef CAS PubMed.
- A. Bietsch, M. Hegner, H. P. Lang and C. Gerber, Inkjet deposition of alkanethiolate monolayers and DNA oligonucleotides on gold: Evaluation of spot uniformity by wet etching, Langmuir, 2004, 20, 5119–5122 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature, 1997, 389, 827–829 CrossRef CAS PubMed.
- P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Suppression of the coffee-ring effect by shape-dependent capillary interactions, Nature, 2011, 476, 308–311 CrossRef CAS PubMed.
- B. M. Weon and J. H. Je, Capillary force repels coffee-ring effect, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82 Search PubMed.
- C. Poulard and P. Damman, Control of spreading and drying of a polymer solution from Marangoni flows, Europhys. Lett., 2007, 80, 64001 CrossRef.
- P. Gong, G. M. Harbers and D. W. Grainger, Multi-technique comparison of immobilized and hybridized oligonucleotide surface density on commercial amine-reactive microarray slides, Anal. Chem., 2006, 78, 2342–2351 CrossRef CAS PubMed.
- C. Y. Lee, G. M. Harbers, D. W. Grainger, L. J. Gamble and D. G. Castner, Fluorescence, XPS, and TOF-SIMS surface chemical state image analysis of DNA microarrays, J. Am. Chem. Soc., 2007, 129, 9429–9438 CrossRef CAS PubMed.
- K. Pappaert, H. Ottevaere, H. Thienpont, P. Van Hummelen and G. Desmet, Diffusion limitation: A possible source for the occurrence of doughnut patterns on DNA microarrays, BioTechniques, 2006, 41, 609–616 CrossRef CAS PubMed.
- M. K. McQuain, K. Seale, J. Peek, S. Levy and F. R. Haselton, Effects of relative humidity and buffer additives on the contact printing of microarrays by quill pins, Anal. Biochem., 2003, 320, 281–291 CrossRef CAS.
- T. Still, P. J. Yunker and A. G. Yodh, Surfactant-induced Marangoni eddies alter the coffee-rings of evaporating colloidal drops, Langmuir, 2012, 28, 4984–4988 CrossRef CAS PubMed.
- I. I. Smalyukh, O. V. Zribi, J. C. Butler, O. D. Lavrentovich and G. C. L. Wong, Structure and dynamics of liquid crystalline pattern formation in drying droplets of DNA, Phys. Rev. Lett., 2006, 96, 177801 CrossRef.
- D. Kaya, V. Belyi and M. Muthukumar, Pattern formation in drying droplets of polyelectrolyte and salt, J. Chem. Phys., 2010, 133, 114905 CrossRef CAS PubMed.
- V. N. Truskett and K. J. Stebe, Influence of surfactants on an evaporating drop: Fluorescence images and particle deposition patterns, Langmuir, 2003, 19, 8271–8279 CrossRef CAS.
- K. Lee, N. Ivanova, V. Starov, N. Hilal and V. Dutschk, Kinetics of wetting and spreading by aqueous surfactant solutions, Adv. Colloid Interface Sci., 2008, 144, 54–65 CrossRef CAS PubMed.
- R. Dias, M. Rosa, A. C. Pais, M. Miguel and B. Lindman, DNA-surfactant interactions. Compaction, condensation, decompaction and phase separation, J. Chin. Chem. Soc., 2004, 51, 447–470 CAS.
- G. Zanchetta, M. Nakata, M. Buscaglia, T. Bellini and N. A. Clark, Phase separation and liquid crystallization of complementary sequences in mixtures of nanoDNA oligomers, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1111 CrossRef CAS PubMed.
- F. Liu, J. Yang, L. Huang and D. Liu, Effect of Non-Ionic Surfactants on the Formation of DNA/Emulsion Complexes and Emulsion-Mediated Gene Transfer, Pharm. Res., 1996, 13, 1642–1646 CrossRef CAS.
- B. A. Armitage, Cyanine dye–DNA interactions: intercalation, groove binding, and aggregation, DNA Binders and Related Subjects, 2005, 55–76 CAS.
- T. Y. Ogul'chansky, M. Y. Losytskyy, V. Kovalska, V. Yashchuk and S. Yarmoluk, Interactions of cyanine dyes with nucleic acids. XXIV. Aggregation of monomethine cyanine dyes in presence of DNA and its manifestation in absorption and fluorescence spectra, Spectrochim. Acta, Part A, 2001, 57, 1525–1532 CrossRef.
- U. Lehmann, Aggregation of cyanine dyes at Langmuir-Blodgett monolayers, Thin Solid Films, 1988, 160, 257–269 CrossRef CAS.
- H. B. Eral, D. M. Augustine, M. H. G. Duits and F. Mugele, Suppressing the coffee stain effect: How to control colloidal self-assembly in evaporating drops using electrowetting, Soft Matter, 2011, 7, 4954–4958 RSC.
- J. M. Moran-Mirabal, C. P. Tan, R. N. Orth, E. O. Williams, H. G. Craighead and D. M. Lin, Controlling microarray spot morphology with polymer liftoff arrays, Anal. Chem., 2007, 79, 1109–1114 CrossRef CAS PubMed.
- J. M. Oh, D. Legendre and F. Mugele, Shaken not stirred – On internal flow patterns in oscillating sessile drops, Europhys. Lett., 2012, 98 Search PubMed.
- R. G. Larson, Re-shaping the coffee ring, Angew. Chem., Int. Ed., 2012, 51, 2546–2548 CrossRef CAS PubMed.
- S. Tomiuk and K. Hofmann, Microarray probe selection strategies, Briefings Bioinf., 2001, 2, 329–340 CrossRef CAS PubMed.
- E. F. Petricoin Iii, J. L. Hackett, L. J. Lesko, R. K. Puri, S. I. Gutman and K. Chumakov, et al., Medical applications of microarray technologies: a regulatory science perspective, Nat. Genet., 2002, 32, 474–479 CrossRef PubMed.
- J. Quackenbush, Computational analysis of microarray data, Nat. Rev. Genet., 2001, 2, 418–427 CrossRef CAS PubMed.
- A. Brazma, P. Hingamp, J. Quackenbush, G. Sherlock, P. Spellman and C. Stoeckert, et al., Minimum information about a microarray experiment (MIAME) – toward standards for microarray data, Nat. Genet., 2001, 29, 365–371 CrossRef CAS PubMed.
- D. M. Rocke and B. Durbin, A model for measurement error for gene expression arrays, J. Comput. Biol., 2001, 8, 557–569 CrossRef CAS PubMed.
- R. D. Canales, Y. Luo, J. C. Willey, B. Austermiller, C. C. Barbacioru and C. Boysen, et al., Evaluation of DNA microarray results with quantitative gene expression platforms, Nat. Biotechnol., 2006, 24, 1115–1122 CrossRef CAS PubMed.
- Y. F. Leung and D. Cavalieri, Fundamentals of cDNA microarray data analysis, Trends Genet., 2003, 19, 649–659 CrossRef CAS PubMed.
- R. Simon, M. D. Radmacher, K. Dobbin and L. M. McShane, Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification, J. Natl. Cancer Inst., 2003, 95, 14–18 CrossRef CAS.
- D. B. Allison, X. Cui, G. P. Page and M. Sabripour, Microarray data analysis: from disarray to consolidation and consensus, Nat. Rev. Genet., 2006, 7, 55–65 CrossRef CAS PubMed.
- R. F. Chuaqui, R. F. Bonner, C. J. M. Best, J. W. Gillespie, M. J. Flaig and S. M. Hewitt, et al., Post-analysis follow-up and validation of microarray experiments, Nat. Genet., 2002, 32, 509–514 CrossRef CAS PubMed.
- S. Draghici, P. Khatri, A. C. Eklund and Z. Szallasi, Reliability and reproducibility issues in DNA microarray measurements, Trends Genet., 2006, 22, 101–109 CrossRef CAS PubMed.
- D. R. Rhodes, J. Yu, K. Shanker, N. Deshpande, R. Varambally and D. Ghosh, et al., ONCOMINE: a cancer microarray database and integrated data-mining platform, Neoplasia, 2004, 6, 1–6 CAS.
- A. J. Holloway, R. K. Van Laar, R. W. Tothill and D. D. L. Bowtell, Options available – from start to finish – for obtaining data from DNA microarrays II, Nat. Genet., 2002, 32, 481–489 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |