Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational modelling of oxygenation processes in enzymes and biomimetic model complexes
Sam P.
de Visser
*a,
Matthew G.
Quesne
a,
Bodo
Martin
b,
Peter
Comba
*b and
Ulf
Ryde
*c
aManchester Institute of Biotechnology and School of Chemical Engineering and Analytical Science, the University of Manchester, 131 Princess Street, Manchester M1 7DN, UK. E-mail: sam.devisser@manchester.ac.uk; Fax: +44 (0)1613065201; Tel: +44 (0)1613064882
bAnorganisch-Chemisches Institut, Universität Heidelberg, Im Neuenheimer Feld 270, 69120 Heidelberg, Germany. E-mail: Peter.Comba@aci.uni-heidelberg.de; Fax: +49 6221 546617; Tel: +49 6221 548453
cDepartment of Theoretical Chemistry, Lund University, Chemical Centre, P. O. Box 124, SE-221 00 Lund, Sweden. E-mail: Ulf.Ryde@teokem.lu.se; Fax: +46 46 2228648; Tel: +46 462224502
First published on 29th October 2013
Abstract
With computational resources becoming more efficient and more powerful and at the same time cheaper, computational methods have become more and more popular for studies on biochemical and biomimetic systems. Although large efforts from the scientific community have gone into exploring the possibilities of computational methods for studies on large biochemical systems, such studies are not without pitfalls and often cannot be routinely done but require expert execution. In this review we summarize and highlight advances in computational methodology and its application to enzymatic and biomimetic model complexes. In particular, we emphasize on topical and state-of-the-art methodologies that are able to either reproduce experimental findings, e.g., spectroscopic parameters and rate constants, accurately or make predictions of short-lived intermediates and fast reaction processes in nature. Moreover, we give examples of processes where certain computational methods dramatically fail.
Introduction
Nature has a large arsenal of efficient catalysts that are able to perform regioselective as well as stereospecific substrate conversions. These chemical systems, i.e. enzymes, work at ambient temperature and pressure and have specific functions such as biodegradation, bioconversion or biosynthesis of compounds. Enzymatic reactions influence the general health and well-being of the organism and as such are important. Often the enzymes contain a transition metal active site, where the catalysis takes place. As iron is abundant relative to other metals on planet Earth, many enzymes utilize iron in their active site,1,2 but there are also numerous examples of copper-,3 vanadium-,4 molybdenum-,5 and other transition metal-containing enzymes as well as non-transition metal containing enzymes. In addition, enzymes sometimes use clusters of two or more transition metal atoms as catalytic centres, as is, for instance, the case in the diiron enzyme ribonucleotide reductase6 or the multi-metal cluster in photosystem II.7The mononuclear iron-containing enzymes can be split into heme1 and nonheme2 categories of which we show the active site structure of two typical examples in Fig. 1: namely for the heme enzyme cytochrome P450 and the nonheme iron enzyme taurine/α-ketoglutarate dioxygenase.8,9 The crystal structure coordinates of the former were taken from the human enzyme cytochrome P450 2A13, which is a liver enzyme involved in the detoxification of endogenous compounds. The heme group is linked to the protein via a direct bond of the metal with the thiolate group of Cys439, the axial ligand. It has been proposed that this axial ligand fine-tunes the electronic properties of the oxidant and gives it the functional properties to act as a monooxygenase.10 In contrast, other heme enzymes, such as peroxidases, typically have a histidine group as the axial ligand,11 while catalases use a tyrosinate group.12 As usual, key intermediates of the catalytic cycles of enzymes are short-lived, and consequently, difficult to detect and characterize. This means that experimental work in the field often needs to be complemented by theoretical studies. Computational modelling has been instrumental in assisting experiment into establishing the fundamental properties and changes upon ligand substitution in heme enzymes and their catalytic features.13 For instance, more than 10 years before the first characterization of the active species of P450 enzymes, theory proposed a high-valent iron(IV)–oxo heme cation radical (Compound I) that was found to react with substrates via radical mechanisms with low barriers.14 Only a few years ago, Rittle and Green characterized Compound I using electron paramagnetic resonance (EPR), absorption and Mössbauer spectroscopy.15
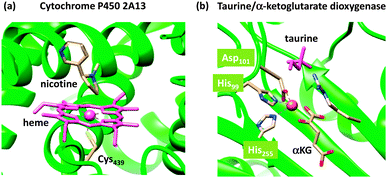 | ||
| Fig. 1 Active site structures of two typical mononuclear iron enzymes: (a) cytochrome P450 from 4EJG pdb file and (b) taurine/α-ketoglutarate dioxygenase from 1OS7 pdb file. | ||
As a comparison, we also show in Fig. 1(b) the crystal structure of a nonheme iron enzyme, where the metal is bound via a characteristic facial triad represented by two histidine and an aspartate amino acid. This enzyme is involved in the biodegradation of taurine and functions as a sulphur source. Also here, computational modelling assisted in establishing differences in the properties between heme and nonheme iron enzymes and the origin of the efficiency of hydrogen-atom abstraction.16 However, axial and equatorial ligand effects in substrate oxidation by heme and nonheme iron complexes have been extensively reviewed previously and will not be covered here.17
It is clear from these examples that theory can assist experimental studies related to biocatalysis and biotransformations and give insight into reaction mechanisms and pathways. Unfortunately, these studies are not routinely done, but may involve caveats and pitfalls. To fully appreciate and understand the computational decisions on method and model selection, we review here computational approaches with relevance to transition metal catalysis. We will start with a brief overview of the basic methods in the field and their general accuracy and reproducibility and then give some recent examples on how theory guided and assisted experimental work.
Methods
Quantum mechanics and density functional theory
According to quantum mechanics (QM), all properties of a molecular system can be obtained from the wave function (Ψ), which is the solution of the Schrödinger equation,18eqn (1), and expresses the total energy of the molecule (E) as an eigenfunction of the Hamilton operator (H).| H Ψ = E Ψ | (1) |
The Hamilton operator includes the kinetic and potential energy contributions of all the electrons and nuclei within a molecule as described in eqn (2) and (3).19 Here, ℏ is Planck's constant divided by 2π, me is the electron mass, e is the elementary charge, ε0 represents the permittivity in vacuum, and rIj are the distances between nuclei and electrons, whereas the distances between two electrons and two nuclei are described by rij and RIJ, respectively. The Hamiltonian in eqn (2) is split into four components that represent the kinetic energy of the electrons, the electron–nucleus attractions, the electron–electron repulsions and the nucleus–nucleus repulsions, respectively. Within the Born–Oppenheimer approximation the nucleus–nucleus interactions are constant and the electronic energy E is calculated for a rigid molecular geometry.
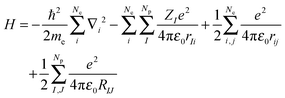 | (2) |
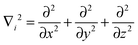 | (3) |
The solutions to the Schrödinger equation clearly depend on the number of electrons (Ne) and the number of nuclei (Np) in the chemical system and will increase dramatically in complexity as the size of the system expands. Because of its complexity, the Schrödinger equation can only be solved exactly for the hydrogen atom and the H2+˙ ion, while for any larger chemical system approximations need to be used. This has led to the development of a large range of computational chemistry methods that all have different features and accuracies. For accurate results, thorough benchmarking and calibration is required, especially for systems that contain transition metals whereby the consistency and reproducibility of methods is tested by comparison to higher-level methods or against experimental data, as shown in several examples below.
The most basic solution to the Schrödinger equation comes from Hartree–Fock (HF) theory, in which it is assumed that each electron moves in the average field of all the other electrons and the one-electron wave functions are expanded into a set of known (hydrogen-like) orbitals: the basis set. The solution of the Schrödinger equation is not the end of the calculation as shown schematically in Fig. 2. Thus, after one has created a starting geometry and selected a method, i.e. a Hamilton operator description, and basis set, or wave function model, one can solve the Schrödinger equation and obtain the energy associated with the starting structure. Subsequently, the geometry is modified and a new energy is calculated. Thereafter, the energy is minimized with respect to all geometric coordinates in the chemical system and when the first derivatives of the energy with respect to the degrees of freedom reach a certain threshold value, the structure is considered converged, i.e. an optimized geometry is found. A frequency calculation, vide supra, will then establish whether a structure is a local minimum or a higher-order saddle point.
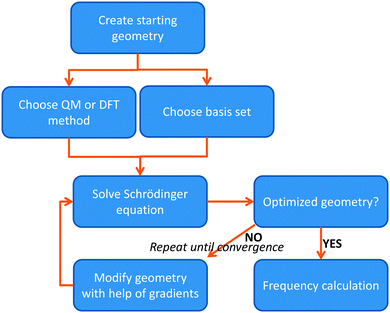 | ||
| Fig. 2 Flow chart displaying the procedure of calculating a structure using either QM or DFT methods. | ||
The HF method gives reasonable geometries but its energies are not good enough to reproduce chemical reaction mechanisms and experimental barrier heights. Improved results are generally obtained with Møller–Plesset second-order perturbation theory (MP2)20 that gives much more accurate energies and chemical structures as compared to HF.20 Even better results are obtained with coupled-cluster calculations using singles, doubles and perturbatively treated triples (CCSD(T)),21 which is currently considered as the gold-standard method in QM.22 Unfortunately, MP2 and especially CCSD(T) are computationally demanding and even with current resources they can only be applied to chemical systems with less than about 50 and 20 atoms, respectively.23 For biosystems and biomimetic complexes with often well over 100 atoms, computationally cheaper methods are needed.
As an alternative to the wave function methods, DFT was developed by Kohn and co-workers in the 1960s.24 They showed that there is a one-to-one correspondence between the wave function and the electron density, ρ(r). The latter is a functional of the three Cartesian coordinates (r), whereas the wave function is a function of the coordinates of every electron in the chemical system; therefore, this was a major simplification. In DFT, the electronic energy (Eel) is calculated from a functional of the electron density, which unfortunately is not known. However, a typical expression is given by the sum of the integrals in eqn (4). The first term contains an integral over the Laplacian over the atomic orbitals and represents the kinetic energy of the electrons. The second and third terms involve the electron–nucleus attractions and the electron–electron repulsions, respectively. The final exchange-correlation term (Exc) has the largest uncertainty as no exact equations are known for this component; it is normally split into individual exchange and correlation components, Ex and Ec, where the exchange energy results from ferromagnetic interactions of two electrons with the same spin (α or β) in different orbitals, while the correlation energy is determined by the electron pairing energies of two electrons in the same molecular orbital.
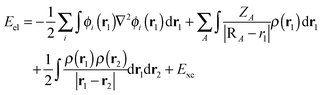 | (4) |
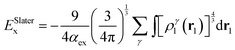 | (5) |
| EVWNc = ∫ρ1(r1)εc[ρα1(r1), ρβ1(r1)]dr1 | (6) |
| EB3LYPxc = AESlaterx + (1 − A)EHFx + BΔEBeckex + EVMNc + CΔELYPc | (7) |
In recent years it has been found that the B3LYP method has weaknesses, especially for transition metal containing systems, and alternative DFT methods have been suggested. Unfortunately, no universal and consistent method has been developed yet, so that a range of different methods are in current use. For example, it has been shown that a modified hybrid DFT method with 15% EHFx (rather than the standard 20%), termed B3LYP*, gives better energetics for some transition metal complexes,30 but as will be discussed below for other properties higher amounts of EHFx may be needed. In addition, neither HF nor standard DFT methods can describe dispersion interactions. Recent work by the Grimme group has shown that a simple empirical dispersion correction significantly improves calculated energies: B3LYP-D.31
Typically, the results of DFT calculations show only limited dependence on the functionals used. However, for transition metal complexes with close-lying spin states the ordering and spin-state energy splitting often strongly depend on the functional chosen, and particularly on the amount of EHFx. It is of paramount importance, therefore, to calibrate DFT calculations on transition metal complexes to either experimental data or to do test calculations with alternative methods.
Geometries, frequencies and free energies
The solution of the Schrödinger equation is not the end of the calculation as shown schematically in Fig. 2. Thus, after one has created a starting geometry and selected a method and basis set, the QM method gives the energy associated with the starting structure. Thereafter, the energy can be minimized with respect to the geometric coordinates of the chemical system using the first derivatives of the energy with respect to the coordinates. A frequency calculation can establish whether a structure is a local minimum or a higher-order saddle point.A QM calculation gives the electronic energy of the studied system. In order to convert these energies into values that can be compared to experiments, one needs to add vibrational, entropic and often also solvent effects. The former two can be obtained from a frequency calculation on the optimized geometry, which establishes the second derivatives of the energy with respect to the coordinates, i.e. the degrees of freedom. These derivatives are used to calculate the vibrational energy levels of a molecule and give the zero-point energy (ZPE) (see Fig. 3). ZPE is the lowest vibrational energy level (ν0) in which the system will reside at 0 K temperature. Fig. 3 shows the potential energy profile along one degree of freedom (e.g., a reaction coordinate) between two local minima S1 and S2 with electronic energies ES1 and ES2, respectively. These two local minima are separated from each other by a transition state (TS). Higher energy vibrational levels of the local minimum S1 are given as ν1, ν2 and ν3 in Fig. 3. A Boltzmann distribution at a specific temperature will determine the degree of occupation of each individual vibrational energy level.
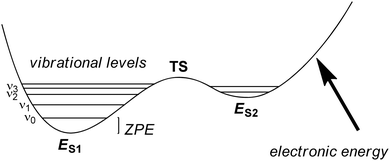 | ||
| Fig. 3 Potential energy profile between two local minima S1 and S2 each with their own vibrational energy levels (ν) and ZPE. | ||
In addition, using the information of the geometry and the vibrational energy levels the entropy can be calculated from the individual partition functions (Q) for the translational, rotational and vibrational entropy components. Generally, the entropy of a molecule is calculated from the partial derivative of the free energy (G) to the temperature (T) at constant pressure (p), eqn (8). In this equation R is the gas constant and N is the total number of particles.
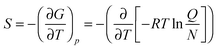 | (8) |
The partition function is the product of all molecular variables and includes the translational (Qtr), rotational (Qrot) and vibrational (Qvib) contributions of the molecule as well as those arising from internal rotations (Qint) and electronic spin (Qes), eqn (9). For a molecule obeying the harmonic oscillator, rigid-rotor and Ideal Gas Law conditions, equations have been derived for these partition function components, eqn (10)–(12).32 In these equations kB is Boltzmann's constant, h is Planck's constant, m is the molecular mass, T is the temperature and σ is the symmetry number. The moments of inertia A, B and C in eqn (11) are dependent on the Cartesian coordinates of the molecule with respect to its centre of mass.
| Q = Qtr × Qrot × Qvib × Qint × Qes | (9) |
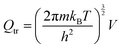 | (10) |
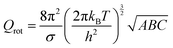 | (11) |
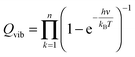 | (12) |
Quantum chemical software packages usually include these entropy derivations in order to approximate the free energy of a molecule. The obtained free energies of activation can then be compared with experimentally determined values or rate constants. We did that on several occasions and found that free energies of activation agree to within 3 kcal mol−1 from experiment using B3LYP with a triple-ζ basis set and solvent corrections.33
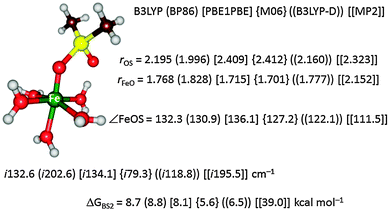
To further test the method dependence on the calculated free energy of activation we did a set of test calculations as shown in Fig. 4. Thus, Pestovsky and Bakac34 reported experimental studies on the reactivity of [FeIV(O)(H2O)5]2+ with dimethylsulfoxide and measured a free energy of activation of 10.5 kcal mol−1 at 298 K. To find out how well computations can reproduce this, we studied the catalytic mechanism with the B3LYP, BP86, PBE1PBE, M06 and B3LYP-D DFT methods as well as with MP2. Fig. 4 displays the optimized geometries of the sulfoxidation transition states and the corresponding free energies of activation. In this particular example the DFT methods are within a couple of kcal mol−1 from the experimental value and B3LYP and BP86 are closest. Interestingly, the computationally expensive MP2 method performs very poorly and gives a much higher barrier of 39.0 kcal mol−1. Clearly, computational time in this example does not correlate with higher accuracy.
Environmental (solvent) effects
Calculated energies using computational chemistry methods refer to gas-phase data. In order to compare computational results with experimental data, the solvent needs to be implemented into the calculations. This can be done by simply adding explicit solvent molecules to the chemical model and reoptimizing the structures. However, calculations with a large number of atoms require more resources and are not always practical, especially since solvent molecules can exist in many possible conformations.35 Therefore, a more common approach is to add solvent corrections to the energetics using an implicit solvent model.36 This can either be done at the single point level, whereby the energy is recalculated with a solvent model on the gas-phase optimized geometry, or by reoptimizing the structure using a solvent model.Most QM software packages include implicit solvent models like the polarizable continuum model (PCM), the conductor-like screening method (COSMO) or the density solvation model (SMD).37 In these calculations, the molecule is placed in a cavity that is surrounded by the dielectric continuum, characterized by a dielectric constant, and a reaction fluid builds up at the cavity surface, described by a number of surface charges, perturbing the wave function. The cavity is normally defined by a set of atomic radii. The electrostatic part of the solvation energy is supplemented by non-polar terms, which typically include dispersion, repulsion and cavitation terms.
A common approach to investigate enzyme reactions is to cut out a small model of the active site from the protein (50–200 atoms) and study it with QM methods, called the QM-cluster approach.38 In order to ensure that the geometry of the model does not change too much from that in the protein, one or several atoms are fixed at the positions where the protein is truncated to form the QM model. Moreover, a continuum-solvation method is commonly employed to model the surrounding protein in an approximate manner. A dielectric constant of ∼4 is typically used,39 a quite arbitrary choice, but fortunately it has been shown that as the size of the QM system is increased to 150–200 atoms, the results obtained with different values of the dielectric constant typically converge.38a,40
Quantum mechanics/molecular mechanics (QM/MM)
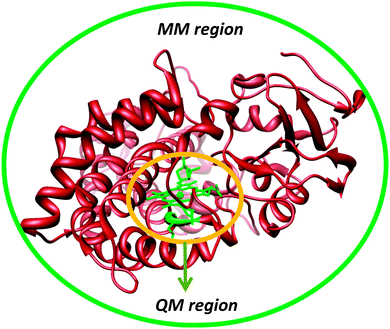
Another approach to include the effect of the surrounding into QM calculations is to use the quantum mechanics/molecular mechanics (QM/MM) approach.41 The philosophy of the QM/MM technique is to divide the chemical system, such as an enzyme, into two or more regions (shells), Fig. 5: the inner core, which is calculated with accurate QM or DFT methods, and the outer region, which contains the remaining protein and solvent, is calculated with computationally cheap methods, like molecular mechanics (MM).42 The inner core is the region of interest and contains the basic features of the enzyme active site and the substrate, but is held in position by interactions with the rest of the protein. These chemical constraints ensure that the active site remains in a conformation that is relevant for the enzyme. Ideally, this would combine the accuracy of QM methods with the speed of MM methods.In practice, the QM/MM approach is implemented by an energy function of the type
| Etot(r1, r2) = EQM(r1) + EMM(r2) + EQM/MM(r1, r2) | (13) |
| Etot(r1, r2) = EQM(r1) + EMM(r1, r2) − EMM(r1) | (14) |
A complication arises when the QM and MM systems are connected by covalent bonds (so-called junctions).41 Then, the QM system needs to be capped in some way to fulfil the valences of the dangling bond. This can be done either by adding extra atoms (the link-atom approach), usually hydrogen atoms, although halogen-like pseudoatoms have also been tried, or by using localised orbitals that place frozen hybrid orbitals at the boundary. With a careful calibration, both approaches can give results of a similar quality,43 and therefore, the hydrogen link-atom approach is most common, because it is simple and can be used without any modifications of the QM software. However, it should be kept in mind that the junction problem is one of the largest sources of errors for the QM/MM approach, the influence of which can be reduced by moving the junctions away from the site of interest (making the QM system larger).
Another important issue is how to treat the interactions between the QM and MM systems.41 Van der Waals interactions are normally properly treated by MM, e.g. by the simple energy function in eqn (14). However, electrostatic interactions are more complicated to describe. The simplest solution is to treat these at the MM level (as in eqn (14)), giving what is called mechanical embedding. It requires a MM representation of the QM system, typically a point-charge model obtained by a fit to the QM electrostatic potential. However, this ignores the polarisation of the QM system by the MM system and vice versa. Therefore, it is more common that a point-charge model of the MM system is included in the QM calculations and the charges of the QM system are zeroed in into the MM calculations, which is called electrostatic (or electronic) embedding. Then, the QM system is polarised by the MM system, whereas the MM system is still not polarised. It has been argued that this may lead to an overpolarisation of the QM system44 and it has been much discussed which charges (especially around junctions) to include in the point-charge model.41 It should also be noted that mechanical embedding reduces the link-atom problem, because the full MM calculation (and therefore the electrostatic interactions) is performed without any link atoms. With electrostatic embedding, the link-atom problem is severe, because charges are positioned close to the artificial link-atoms. Corrections to this have been suggested,45 but it has been shown that they often do more harm than good.44 In fact, a carefully designed molecular-embedding method typically gives better results than electronic embedding. However, the ideal procedure would be to use polarised embedding, i.e. employing a polarisable MM method and including both point charges and polarisabilities (and possibly also higher-order multipoles) in the QM calculations. Only a few applications have been performed along those lines so far.41,46
QM/MM codes are available in most common QM and MM software packages (e.g. Gaussian, ADF, Amber, CHARMM, Schrödinger), as well as in some independent interfaces (e.g. ChemShell and COMQUM).47 A promising approach is to combine QM/MM methods with experimental data (X-ray reflections, NMR, EXAFS) to obtain an ideal compromise between theory and experiments.48
The advantage of QM/MM methods compared to QM-cluster calculations is that the surroundings are explicitly accounted for, avoiding a bias caused by the selection of the modelled system or any need of fixing atoms at the periphery of the QM model. The disadvantage of QM/MM is that the modelled system is so large that it is hard to ensure that all structures along a reaction pathway reside in the same local minimum (a change in the hydrogen-bond pattern of a single water molecule far from the active site can change the total energy by ∼7 kcal mol−1, although it is probably not relevant for the reaction). Many solutions have been suggested to such problems, e.g. by keeping the surroundings fixed at the starting (crystal) structure, by running reactions back and forth until the energy stabilises, or by calculating reactions for many different structures, taken from snapshots from molecular dynamics simulations.41 However, the preferred solution is to calculate free energies, rather than pure energies (from minimised structures).41,45a,49 This can be done at the MM and semi-empirical QM/MM level with free-energy perturbation methods. Unfortunately, it is a challenge for high-level (including DFT-type) QM/MM methods, owing to the cost of these calculations and differences in the MM and QM potential energy surfaces.
Finally, it should be mentioned that both QM and QM/MM methods have problems with convergence of the calculations with respect to the size of the QM system. Convergence studies of QM-cluster calculations have shown that reaction energies can change by 3–14 kcal mol−1 as the QM system is enlarged from 27–83 to 161–220 atoms.40 Other studies have shown that a difference of 14 kcal mol−1 can remain even for systems of ∼400 atoms and that the energy may differ by 11 kcal mol−1 between QM systems of 300 and 1600 atoms.40c The convergence is not improved by geometry optimisations.50 However, QM/MM methods also have similar problems, due to the limited accuracy of the MM methods and the link-atom problem: electrostatic-embedded QM/MM calculations gave a mean absolute deviation similar to QM-cluster calculations over 40 sizes of the QM system (40–446 atoms), of 4 and 5 kcal mol−1, respectively.44 Only a carefully designed mechanical-embedding QM/MM method could bring this difference down to 1.7 kcal mol−1. Therefore, we currently recommend the use of QM/MM geometry optimisations with a quite small QM system, followed by a single-point QM calculation with a very big QM system, involving all groups within ∼4.5 Å of the minimal QM system and all buried charged groups in the protein, and moving all junctions three residues away from the minimal QM system, typically 600–1000 atoms.50,51
The QM/MM methodology starts off from experimentally determined crystal structure coordinates available from the internet.52 Often these pdb files refer to a resting state structure of the enzyme rather than its catalytically active species. Therefore, the structure often needs to be converted to a later structure in the catalytic cycle. In addition, the pdb files typically do not contain hydrogen atoms, so that they need to be added, as well as a number of explicit solvent molecules. Generally, this is done in the set-up where the user carefully checks protonation states of residues, salt and disulphide bridges and ions. Histidine groups in proteins can exist in three possible protonation states: deprotonated, singly protonated (with two different tautomers) or doubly protonated. Therefore, all His residues need to be manually and visually investigated for likely hydrogen bonding donor and acceptor groups, as well as their solvent accessibility. Counterions can be added to the surface to balance the overall charge of the system. After this initial set up the system is equilibrated, and heated to room temperature with molecular dynamics (MD) simulations in a stepwise protocol.41,53
Examples
In this section we will give examples of several computational studies that either supported experiment or had predictive value and guided experimental work in the field. In addition, we discuss bioinorganic examples where computation was calibrated against experimental rate constants, crystal structures and spectroscopic parameters. Thus, from the ground state electronic wave function, it is, in principle, possible to calculate many molecular properties besides geometries, by calculating derivatives of the energy (such as e.g. the electric dipole moment as a first derivative of the external field). For properties involving electronic transitions, however, at least a reasonable approximation to the excited state electronic wave functions is needed, which often requires the application of more involved computational methods, as detailed below. These examples highlight the challenges that computational work needs to overcome. We will start, however, with a section on the enzymatic reaction mechanism, and in particular, focus on topics that are hard to study experimentally. In the second part of this section, we will discuss several biomimetic studies that were aimed at establishing a suitable method and technology to address the chemical systems.Part 1: enzymatic models
Computational studies were performed using both QM-cluster model and QM/MM approaches,53,55 and because CDO has a tight substrate-binding pocket with a large number of stabilizing hydrogen bonds and salt bridges linked to the substrate that keep the substrate in a rigid orientation, a large QM region was chosen to include this hydrogen-bonding network. The QM-cluster model and the QM region in the QM/MM calculations included iron(III)–superoxo with substrate cysteinate and the amino acid side chains of His86, His88, His140, Arg60, His155, Tyr157 and Cys93. The computational studies initially investigated the iron(III)–superoxo complex that was calculated in the lowest lying singlet, triplet, quintet and septet spin states using QM-cluster models and QM/MM. The work tested a range of DFT methods of which we show the B3LYP,28,29 BP86,27,56 OPBE57 and B3LYP-D31 results in Fig. 6. All methods gave an open-shell singlet spin state as the ground state with orbital occupation π*xy2 π*xz2 π*yz1 π*OO1 that represents a superoxo radical antiferromagnetically coupled to a metal-oxo π*-type unpaired electron. With most QM/MM methods the nearest excited spin state is the triplet state, which is 3.0–6.0 kcal mol−1 higher in energy, and the quintet spin state is more than 10 kcal mol−1 above the ground state. These studies are well reproduced with QM-cluster models55 that give the same spin-state ordering and minor differences in relative energies. In addition, the QM-cluster calculations also located a septet spin state at 5.2 kcal mol−1 above the singlet spin ground state. Clearly there are a number of close-lying spin-state structures within 5 kcal mol−1 from the electronic ground state, which may result in a Boltzmann distribution and a mixture of low-lying geometries and spin-states at room temperature. Indeed for a biomimetic nonheme iron(III)–superoxo complex 12 different close-lying spin-state structures were calculated,58 which highlights the complications in the description of iron(III)–superoxo complexes. Nevertheless, all computational studies on CDO agree that the iron(III)–superoxo has an open-shell singlet configuration. Addition of O2−˙ to the substrate-bound resting state of the CDO enzyme led to a stable structure that was characterized spectroscopically and identified as the most likely septet spin state of a ferromagnetically coupled iron(III), S = ![[/]](https://www.rsc.org/images/entities/char_e11f.gif) , coupled to an S = ½ radical.59 Currently, it is not clear whether this intermediate is a catalytic cycle intermediate and why it has a significant lifetime for spectroscopic detection. It may very well be that the other spin states are more reactive and do not let the iron(III)–superoxo accumulate over time.
, coupled to an S = ½ radical.59 Currently, it is not clear whether this intermediate is a catalytic cycle intermediate and why it has a significant lifetime for spectroscopic detection. It may very well be that the other spin states are more reactive and do not let the iron(III)–superoxo accumulate over time.
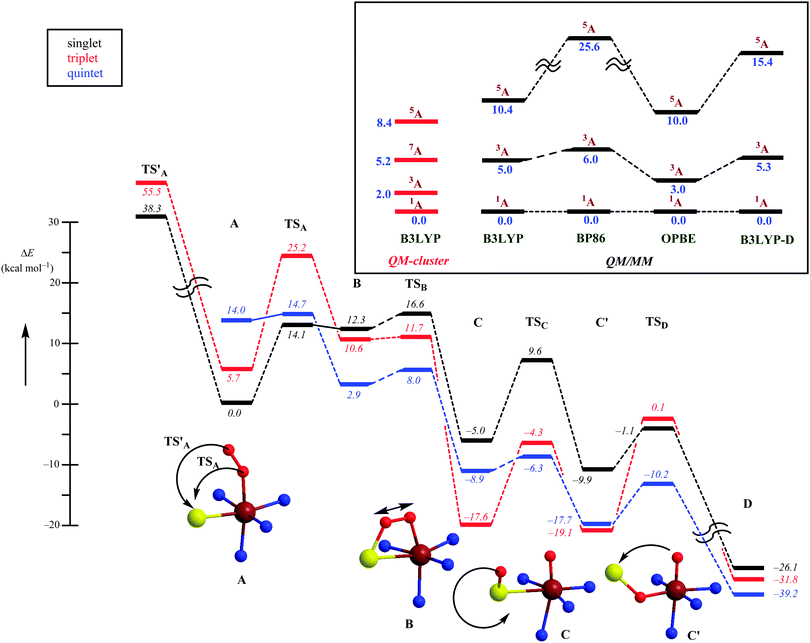
Subsequently, the catalytic mechanism leading to cysteine sulfinic acid products was studied with QM-cluster and QM/MM methods. The lowest energy mechanism starts off from an open-shell singlet iron(III)–superoxo (A) with the formation of an S–O bond via a transition state TSA to give the ring-structure B. Past the transition state, the system will cross over to the triplet spin state 3B, which is slightly lower in energy than 1B. The ring-structure has a weakened O–O bond and splits into an iron(IV)–oxo state with a bound sulfoxide. Similar to biomimetic nonheme iron(IV)–oxo complexes with hexacoordination the triplet spin state is lower in energy than the quintet spin state.60 The final stages of the mechanism include a sulfoxide isomerization to form C′ followed by oxygen-atom transfer to give cysteine sulfinic acid products D.
An alternative mechanism was recently suggested, based on a crystal structure that appeared to give a stable persulfenate intermediate.61 Therefore, it was also tested whether the distal oxygen atom of the iron(III)–superoxo could attack the sulphur atom of cysteinate to form a persulfenate structure via transition state TS′A. However, this pathway was found to be substantially higher in energy with barriers >30 kcal mol−1 as well as highly endothermic. Consequently, the persulfenate structure is a high-energy structure that cannot take part in the catalytic mechanism. The fact that it was observed experimentally implicates that it arises from a dead-end side reaction.
Thus, theory has predicted a most likely mechanism for CDO enzymes and predicted a multistate reactivity pattern on several close-lying spin state surfaces and a rate-determining O–S bond formation step.
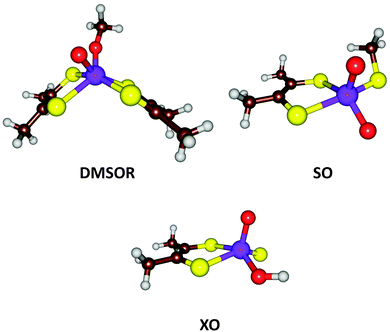 | ||
| Fig. 7 Active site structures of three families of Mo-containing oxo-transfer enzymes: DMSOR, SO, and XO. | ||
From the description above, it can be derived that the active sites of the three families can be represented by MoVIO(MPT)XY, where X and Y are varying ligands, being MPT and Ser/Cys/SeCys for the DMSOR family, O2− and Cys for the SO family, and S2− and OH− for the XO family. Thus, the X ligand has a double negative charge and the Y ligand a single negative charge. With QM-cluster calculations, the intrinsic properties and reactivities of the three enzyme families can be studied, as well as intermediate sites with other combinations of X and Y ligands. For example, the driving force of a general oxo-transfer reaction can be studied:
| MoVIO(MPT)XY + Z → MoIV(MPT)XY + ZO | (15) |
Second, the reoxidation of the active site was studied, i.e.
| MoIV(MPT)XY + H2O → MoVIO(MPT)XY + 2H+ + 2e− | (16) |
Finally, the actual reaction mechanisms (and therefore the activation barriers) for the typical reactions of each of the three families were studied. It turns out that the active sites of all three families can catalyse the DMSOR reaction with reasonable barriers. In fact, the native DMSOR ligands give the highest barrier, owing to the less favourable reaction energy discussed above (Fig. 8). Likewise, all three active sites can catalyse the SO reaction with similar barriers, although the native ligands give the lowest activation barrier (by 3–5 kcal mol−1). However, for the more complicated XO reaction, only the native model was active. In particular, the S2− ligand seems to be essential as a hydride acceptor.
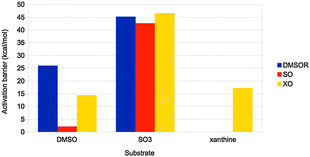 | ||
| Fig. 8 Activation barriers (in kcal mol−1) for substrate activation by the active sites of the three families in Fig. 7. The substrates used were DMSO, SO32− and xanthine, respectively. | ||
Thus, we can conclude that the ligands seem to have been selected to give exothermic reactions (but typically by a minimal amount of energy), both for the main reaction and for the regeneration of the active site, as well as reasonable activation barriers. This illustrates how QM-cluster calculations can give insight into the evolutionary design of active sites of different enzyme families.
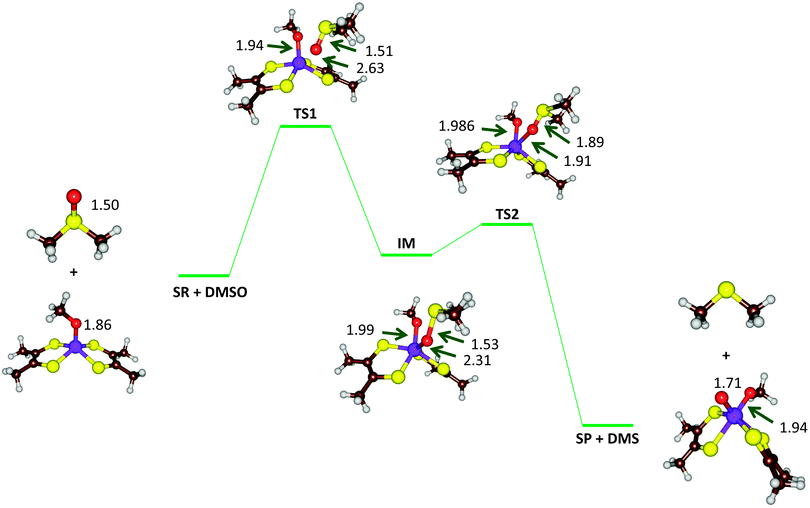 | ||
| Fig. 9 Optimized geometries (B3LYP-D3/def2-TZVPP+ZORA+COSMO, ε = 4, level of theory) of critical points along the reaction mechanism of DMSOR with bond lengths in angstroms. | ||
Different dispersion corrected DFT methods give varying results for the activation barrier of this reaction (and also for the reaction energy), ranging from 5.5 to 33 kcal mol−1 (Fig. 10).67 The barrier height follows quite closely the amount of exact exchange in the functional, e.g. 5.5–7.9, 11, 18, 21, and 33 kcal mol−1 for pure functionals, TPSSH-D3, B3LYP-D3, PBE0-D3, and BHLYP-D3 with 0, 10, 20, 25, and 50% exact exchange, respectively. In order to determine which of these results is most accurate, local CCSD(T) calculations were performed with extrapolations to complete basis sets and to canonical methods. These gave a barrier of 16 kcal mol−1, i.e. closest to B3LYP-D3. However, other states in the reaction were more accurately predicted by the pure functionals. Thus, there is not a single DFT method that gives good results for all states. Instead, it is better to use the LCCSD(T) energies and add corrections for solvation, entropy, and thermal effects from the DFT calculations. In fact, the time seems to be ripe to start to use LCCSD(T) (which currently can be used for complexes with up to 70–90 atoms) calculations also for metal-containing systems, provided that the multiconfigurational character is not too large.
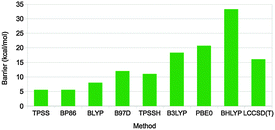 | ||
| Fig. 10 Rate-limiting activation barriers (in kcal mol−1) for the DMSOR reaction as calculated with various DFT methods (all including the DFT-D3 dispersion correction) and LCCSD(T).67 | ||
With such an approach, a barrier of 15 kcal mol−1 was obtained67 in perfect agreement with the experimental estimate68 (which of course is fortuitous). There are several previous theoretical studies of the same enzyme, which all have reported similar barriers, 8.8–19 kcal mol−1.69 This is unexpected, because none of them included dispersion effects, which are pronounced for this barrier, 17 kcal mol−1, and they employ both pure and hybrid density functionals. However, looking closer at the earlier studies, it can be seen that they used either a too small basis set (that gives a too low barrier by ∼17 kcal mol−1) or the pure BP86 functional (that gives an ∼10 kcal mol−1 too low barrier), in both cases compensating for the missing dispersion. Thus, the previous studies obtained the correct answer for the wrong reason.
The take-home message is that the seemingly simple Mo oxy-transfer reactions are quite complicated to treat with QM methods. Large basis sets must be used (at least triple-ζ quality), dispersion and solvation effects need to be included (also the non-polar solvation terms), and the DFT methods should ideally be calibrated against more accurate coupled-cluster or multiconfigurational methods.
The MCOs catalyse oxidation of various substrates at the T1 site, coupled to the reduction of O2 to H2O at the T23 site. By spectroscopic methods, two intermediates in the catalytic cycle have been characterized, the peroxy and native intermediates.70 The former arises when O2 binds to the fully reduced (CuI3) state, leading to an immediate reduction of O2 to the peroxide level. However, it was originally not known how O2 bound to the T23 cluster – the experiments could not decide whether it binds inside the cluster, coordinating to all three Cu ions, or on its periphery, coordinating only to two of the ions.71 In the native intermediate, all three copper ions are fully oxidised (CuII3), the O–O bond is cleaved, and both O atoms are fully reduced. However, again it could not be decided whether it contained a central O2− ion coordinated to all three Cu ions or three OH− ions, bridging each pair of Cu ions.72
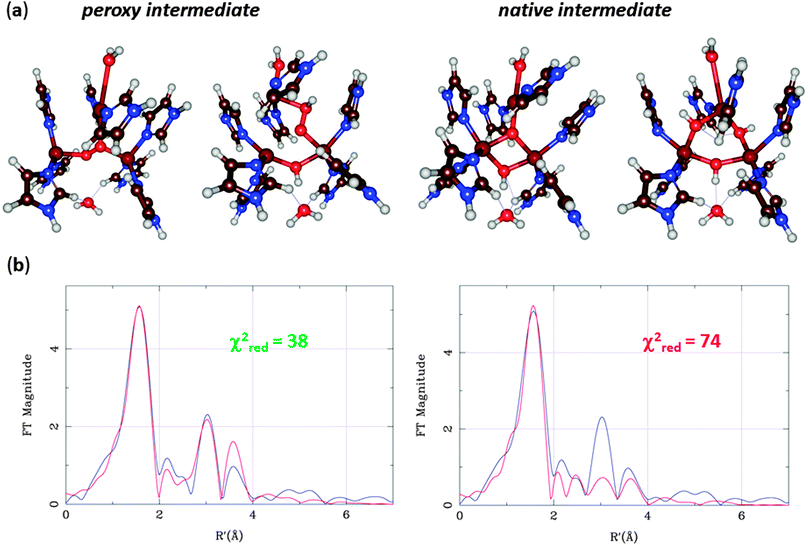
At this point, Rulíšek et al.73 performed a QM/MM study of the MCO reaction. They could obtain geometries of both the suggested structures of the peroxy and native intermediates, as can be seen in Fig. 11a. The structures were similar to what was suggested by experiments, although the peroxide ion bound in a diagonal manner inside the T23 site, and no other structural interpretations of these states could be found even if many other starting configurations were tried. Already from Fig. 11, it can be seen that the peripheral binding of both intermediates seems to be more strained than the central ones. Moreover, approximate energy considerations (the complexes do not contain the same number of atoms, so the energies are not directly comparable, but by removing or adding atoms, an approximate comparison can be made) indicate that the central binding is favoured by 11–34 and 28–34 kcal mol−1. Thus, the QM/MM calculations indicated that the central structures (first and third structures in Fig. 11a) were the correct interpretation of these intermediates. The only problem was that the preferred peroxy-intermediate structure had an incorrect ground state (ferromagnetically, rather than antiferromagnetically coupled).
This problem was later solved by advanced calculations using multiconfigurational perturbation theory (CASPT2), which showed that all intermediates are antiferromagnetically coupled.74 These calculations also gave further support to the central structures by giving better excitation energies for low-lying excited states. Additional support for these structures were also obtained by calculating EPR tensors.75
EXAFS data for the Cu–Cu distances in the two intermediates were also available,67,68 but both structures agreed equally well. However, the EXAFS data contain much more information than only Cu–Cu distances. A combined QM/MM and EXAFS refinement gave structures that are an ideal compromise between QM and EXAFS data and showed that the central structure fits the EXAFS data appreciably better than that with peripheral binding of HO2− (Fig. 11b).76 Subsequently, spectroscopic and inorganic modelling studies have confirmed that the central binding is the correct mode of both the peroxy and native intermediates of the MCOs.70,77 Altogether, these studies show the predictive power of the QM calculations and the strength of combining various spectroscopic and theoretical investigations.
Part 2: biomimetic systems
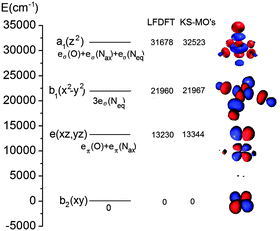
In the case of [trans-Fe(O)(NCCH3)TMC]2+, the structure was first carefully optimized with BP8685a and then studied with LF-DFT, ΔSCF and time-dependent DFT (TD-DFT). The ΔSCF method is similar to a normal DFT calculation, but one or more valence electrons are placed into higher-lying Kohn–Sham orbitals. As a comparison, the optimized geometries of [trans-Fe(O)(NCCH3)TMC]2+ at the BP86 and B3LYP levels of theory are shown in Fig. 12 and the MO diagram is given in Fig. 13.85a,88
 | ||
| Fig. 12 Geometry-optimized structure of [trans-Fe(O)(NCCH3)TMC]2+ from a BP86 (B3LYP) optimization,85a,88 for the electronic ground state S = 1. | ||
As can be seen from Table 1, both LF-DFT and TD-DFT produce acceptable results, whereas SORCI gives an incorrect ground state. For the ground state to 3A1 transition, the TD-DFT value is closer to experiment than the LF-DFT value, but on the other hand the TD-DFT calculation fails to predict the ground state to 3A2 transition.89 As the size of the complex is already challenging for a SORCI treatment, not all transitions could be obtained; on the other hand, some transitions, such as the 1A1 and 1A spin-flip transitions, cannot be explained by the LF-DFT method.
| Electronic state | LF-DFTg | SORCI | ΔSCF | TD-DFT (SAOP) | Assignment | Exp (polarization) |
|---|---|---|---|---|---|---|
| a Ground state configuration. b Spin-change within the ground state configuration. c Spin-change within the ground state configuration with significant contributions from excited state configurations. d Substantial multiconfigurational character. e Two-electron transition. f Not found in the energy range below the ligand-to-metal charge-transfer excitations. g Calculated using the reported S = 1 DFT geometry optimized structure89 showing negligible deviation from the D4h symmetry. | ||||||
| 3A2 | 0 | 3226 | 0 | 0 |
xy
2
xz
1
yz
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
— |
| 5A1 | 911 | 0 | 6488 | 8146 | xy → x2 − y2 | — |
| 1B2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 036 036 |
— | 6170 | Spin-flip![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | |
| 5B1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
— | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 759 759 |
xy → z2 | — | |
| 1B1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979 979 |
— | 6314 | Spin-flip![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
— | |
| 3E | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 968 |
— | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
9472 | xy → xz, yz | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500(xy) 500(xy) |
| 3E | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 680 |
— | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 726 726 |
xz, yz → z2, x2 − y2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000(xy) 000(xy) |
| 1A1 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
Spin-flip![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
— | |
| 3A1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 347 347 |
— | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
xy → x2 − y2 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000(z) 000(z) |
| 5E | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359 359 |
— | — |
xy(xz, yz) → z2, x2 − y2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
— | |
| 1E | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
9436 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
xy → xz, yz, x2 − y2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
— | |
| 3B2 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012 012 |
— | xy → x2 − y2 | — | ||
| 3E | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 184 |
— | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 848 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739 739 |
xz, yz → z2, x2 − y2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
— |
| 3B1 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599 |
— | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 662 |
xy → x2 − y2 | — | |
| 3A1 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 799 |
— | — | xy → x2 − y2 | — | |
| 3A2 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 525 |
— | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 948 948 |
— |
xy → z2, x2 − y2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000(z) 000(z) |
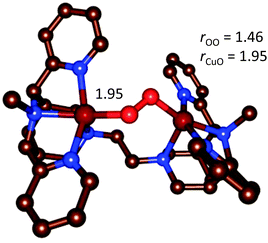 | ||
| Fig. 14 Optimized geometry of the end-on [{(bispidine)Cu}2(O2)]2+ complex.90 | ||
The d–d spectrum for [{(bispidine)Cu}2(O2)]2+ was determined experimentally and subsequent TD-DFT computations led to the spectrum shown in Fig. 15. As expected the spectra match only qualitatively, and among the three mentioned methods for the prediction of d–d transitions, i.e. the LF-DFT, SORCI and TD-DFT methods, probably the latter is the least accurate. TD-DFT also has fundamental problems.95 In the case of the dinuclear complex above, however, the semi-quantitative picture still allows one to assign the experimentally observed transitions to the computed ones.
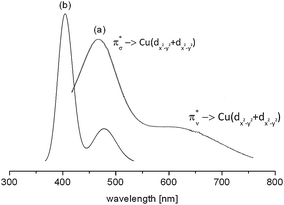 | ||
| Fig. 15 Experimental (a) and TD-DFT calculated (b) absorption spectrum of end-on [{(bispidine)Cu}2(O2)]2+. The transitions reflect π*σ → Cu(dx2−y2 + dx2−y2) [(a) 486 nm and (b) 405 nm] and π*ν → Cu(dx2−y2 + dx2−y2) [(a) 650 nm and (b) 486 nm].90 Reprinted with permission from the American Chemical Society (ref. 90b). | ||
| HHDvV = 2 J12S1S2 | (17) |
The broken-symmetry approach, eqn (18), can be used for a DFT-based calculation of the exchange coupling constants.96 In this equation, EHS and EBS represent the energies of the high-spin (HS) and low-spin broken-symmetry (BS) states, whereas 〈S2〉HS and 〈S2〉BS are their spin-expectation values, respectively. The broken symmetry state refers to a symmetry lowering due to a spin-flip of an otherwise identical electronic configuration.
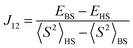 | (18) |
Accurate predictions of J values depend strongly on the method and basis set used, as follows from calculations on the bisphenolate-bridged dicopper(II) complex, shown in Table 2. Thus, the hybrid DFT methods B3LYP,28,29 B3P86,28,57 and B3PW9128,98 reproduce the experimental value within reasonable accuracy, which contrasts the results obtained from pure DFT methods that due to their poor description of the broken-symmetry state do not give accurate results. The basis set should be of triple-ζ quality on the metal and its first coordination sphere, but can be much smaller for the atoms not involved in the electronic coupling, which should speed up the calculation.99
| Method | J G09 | J Orca | J Jaguar |
|---|---|---|---|
| a In cm−1. b J exp = −298 cm−1. c Initial guess obtained with Jaguar.47a d Basis set: TZVP for CuII and the donor atoms, 6-31G* for the remaining atoms. | |||
| B3LYP/TZV | −229 | −231 | −231 |
| B3P86/TZV | −238 | −227 | −241 |
| B3PW91/TZV | −228 | −230 | −227 |
| BLYP/TZV | −838 | −838 | −854 |
| BP86/TZV | −861 | −834 | −880 |
| BPW91/TZV | −831 | −832 | −848 |
| PBE/TZV | −841 | −841 | −854 |
| SVWN/TZV | −1156 | −1178 | −1181 |
| B3LYP/3-21G | −103 | −99 | −114 |
| B3LYP/TZVP | −215 | −214 | −231 |
| B3LYP/6-31G*/TZVPd | −237 | −216 | −239 |
For the prediction of coupling constants, it is important to do an initial geometry optimization of the structures with DFT, rather than a single-point calculation on an available X-ray structure. This procedure avoids possible errors with the DFT method – as, strictly speaking, properties derived from the Kohn–Sham (KS) wave function are only valid at stationary points on the PES. On the other hand, correlating properties derived from DFT-relaxed geometries to experimentally determined ones also may have problems as the environment (e.g. solvent) used in the DFT calculation may be imperfectly modelled. Nonetheless, one can show that J coupling constants for a number of oligonuclear transition metal complexes containing Cu, Mn, Fe, V, Ni, and Cr can be obtained with similar accuracy from DFT-optimized structures.99
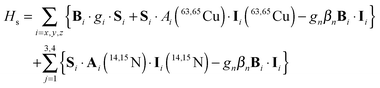 | (19) |
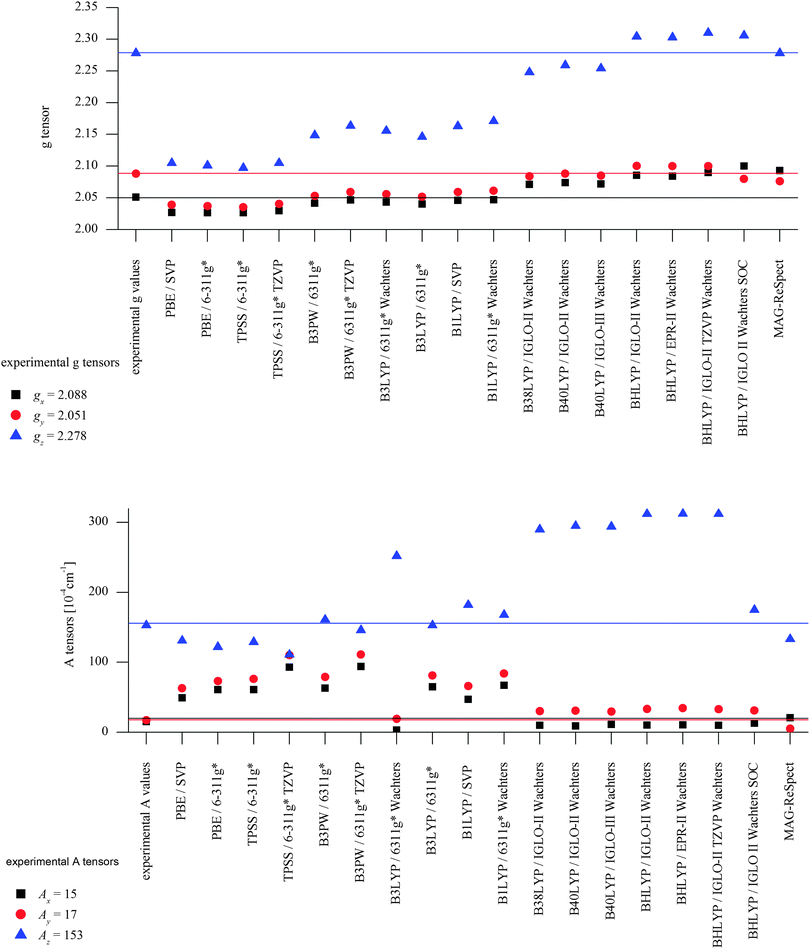
DFT calculations using a number of different functionals and basis sets have been tested for three complexes with different cyclic peptide ligands with the program packages ORCA 2.697 and Mag-ReSpect.102 The results are given in graphical form in Fig. 17 for the g-tensor (part a) and the A-tensor (part b) components. Usually, the x and y components of the g-tensor are obtained accurately with a hybrid DFT method with double to triple-ζ quality basis set, but difficulties in the correct description of the gz component arise in this case. The calculated gz value depends partly on the chosen basis set and, for instance, improves in quality upon changing the basis set from a split-valence basis set (SVP) to a much larger Wachters-type basis set103 for copper and the first ligand sphere. In order to obtain values that are close to experiment, though, the amount of exact exchange in the DFT method needs to be modified (often arbitrarily, to a value of 38 or 40%, or alternatively through the use of a functional such as BHLYP which contains 50% exact exchange). Even with these modifications, all components of the g-tensor cannot be accurately reproduced with “standard” DFT methods. The MAG-ReSpect program gives values very close to experiment, employing the spin Hamiltonian as given in eqn (19), but unfortunately is computationally very demanding.100 A similar situation occurs for calculations of the A-tensor, but as can be expected for the hyperfine coupling, accurate predictions critically depend on a very good basis set (even for the Ax and Ay components). Also here, improvement of the results is obtained by changing the total amount of exact exchange in the DFT method, whereby values beyond the 20% EHF in B3LYP are needed, although in this case the Az values are overestimated by a factor of 2. Only with spin–orbit coupling (SOC) treatments one can expect to obtain accurate predictions for the A-tensor.
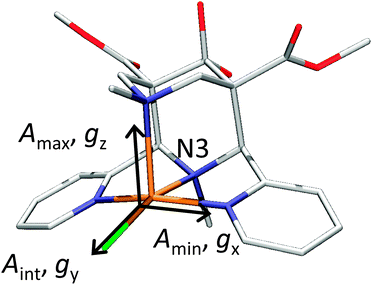 | ||
| Fig. 18 X-ray structures of [Cu(L1)(Cl)]+ with Cl trans to N3. Reprinted with permission from Wiley VCH (ref. 105). | ||
To summarize, there does not appear to be a straightforward method to calculate electronic properties such as d–d transitions, EPR parameters or spin distributions from the existing DFT functionals without using more specialized methods such as LF-DFT, Mag-ReSpect or SORCI for EPR values and d–d transitions, or to carefully tune the functional to reproduce a given property. The size of many model systems prohibits the use of a more computationally demanding method, and one has to resort to trial and error for picking the right combination of DFT method and basis set to compensate effects such as too covalent metal-to-ligand interactions in pure DFT methods. Still, the choice of an established functional can often be advantageous, because the weaknesses and strengths of a well-known functional such as B3LYP or BP86 are relatively well understood, especially for geometry optimizations, which often give the right trends for a given property, if not the experimentally observed values. If accurate predictions of experimental observables are needed, though, no single DFT method will give satisfactory results without careful tuning to experimental and/or high level ab initio reference data.
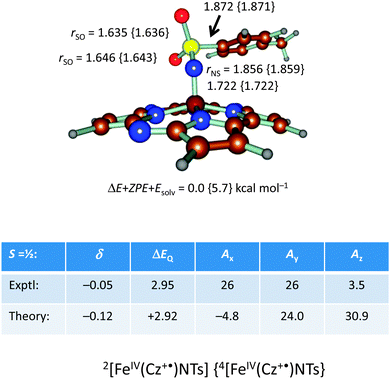
In addition, we calculated the Mössbauer and EPR parameters of 2[FeIV(Cz+˙)NTs] in Orca,97 which we report at the bottom of Fig. 19 alongside the experimentally determined values. Spectroscopic parameters were calculated at the B3LYP28,29 level of theory on the optimized geometries reported in Fig. 19 in combination with the CP(PPP) basis set on Fe coupled to a TZVP basis set on the rest of the atoms.108 The quadrupole splitting (ΔEQ) was calculated from the electric field gradients Vi (i = x, y, and z), the elementary charge of a proton–electron (e), the nuclear quadrupole moment Q(57Fe) of 0.16 barn, and the asymmetry parameter of the nuclear quadrupole tensor (η) using eqn (20) and (21).
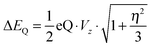 | (20) |
| η = (Vx − Vy)/Vz | (21) |
The isomer shift δ was calculated from the spin density at the iron nucleus ρ0(Fe) using fit-parameters as implemented in Orca,97 whereas the magnetic hyperfine parameters Ai (i = x, y, and z) were obtained using the scalar relativistic zero-order regular approximation (ZORA) at the B3LYP level of theory. These calculated variables were then used to fit the experimental Mössbauer spectrum, taking into account that the Euler angles had to be rotated due to differences in the principal axis between the experimental and computational studies. Nevertheless, as follows from Fig. 19, the computational methods reproduced the experimentally determined Mössbauer and EPR parameters excellently. Calculated values of δ and ΔEQ are within 0.10 mm s−1 from experiment, although it should be noted that this type of agreement cannot be expected for all transition metal complexes at this level of theory. Therefore, precaution should be used to predict experimental Mössbauer and EPR spectroscopic parameters from DFT calculations.
Conclusions
Since the formulation of the Schrödinger equation and the development of computational quantum chemistry almost a century ago, theory has come a long way. Major advances in the field have been made, in particular in the area of methods development. Especially, computational resources have become more efficient and powerful enabling computational studies of relatively large (bio)chemical systems. Some of these techniques are highly accurate and are able to reproduce experimentally measured variables well. However, for challenging chemical systems such as biomimetic transition metal complexes as well as biochemical systems, some major challenges remain. Currently, there is not a single universal method that is applicable to transition metal chemistry. Therefore, considerable testing and benchmarking alongside experiment is still needed. However, it appears that theory has established a strong foothold in biochemistry and biomimetic chemistry and more and more computational studies are done alongside experiment. As such theory can make predictions and guide experiment in the field and address reaction mechanisms and spectroscopic parameters of short-lived intermediates.Acknowledgements
This investigation has been supported by grants from the Swedish research council (UR, project 2010-5025). It has also been supported by computational resources provided by the National Service of Computational Chemistry Software (NSCCS) to SdV and the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University (UR). MGQ thanks the BBSRC for a studentship. The EU-COST Network is thanked for funding for a short-term-scientific-mission to Heidelberg of SdV. PC and BM are grateful for financial support from the German Science Foundation (DFG) and the University of Heidelberg.Notes and references
- (a) M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841 CrossRef CAS PubMed; (b) J. T. Groves, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3569 CrossRef CAS PubMed; (c) Cytochrome P450: Structure, Mechanism and Biochemistry, ed. P. R. Ortiz de Montellano, Kluwer Academic/Plenum Publishers, New York, 3rd edn, 2004 Search PubMed; (d) B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947 CrossRef CAS PubMed; (e) A. W. Munro, H. M. Girvan and K. J. McLean, Nat. Prod. Rep., 2007, 24, 585 RSC; (f) Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific Publishing Co., New Jersey, 2010 Search PubMed; (g) P. R. Ortiz de Montellano, Chem. Rev., 2010, 104, 932 CrossRef PubMed; (h) Iron-containing enzymes: Versatile catalysts of hydroxylation reaction in nature, ed. S. P. de Visser and D. Kumar, RSC Publishing, Cambridge (UK), 2011 Search PubMed.
- (a) E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S.-K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y.-S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235 CrossRef CAS PubMed; (b) T. D. H. Bugg, Curr. Opin. Chem. Biol., 2001, 5, 550 CrossRef CAS; (c) M. J. Ryle and R. P. Hausinger, Curr. Opin. Chem. Biol., 2002, 6, 193 CrossRef CAS; (d) M. Costas, M. P. Mehn, M. P. Jensen and L. Que Jr, Chem. Rev., 2004, 104, 939 CrossRef CAS PubMed; (e) S. V. Kryatov, E. V. Rybak-Akimova and S. Schindler, Chem. Rev., 2005, 105, 2175 CrossRef CAS PubMed; (f) M. M. Abu-Omar, A. Loaiza and N. Hontzeas, Chem. Rev., 2005, 105, 2227 CrossRef CAS PubMed; (g) A. R. McDonald and L. Que Jr., Coord. Chem. Rev., 2013, 257, 414 CrossRef CAS PubMed; (h) D. Buongiorno and G. D. Straganz, Coord. Chem. Rev., 2013, 257, 541 CrossRef CAS PubMed; (i) S. Al-Attar and S. de Vries, Coord. Chem. Rev., 2013, 257, 64 CrossRef CAS PubMed.
- See, e.g., (a) L. Quintanar, L. Rivillas-Acevedo, R. Grande-Aztatzi, C. Z. Gómez-Castro, T. Arcos-López and A. Vela, Coord. Chem. Rev., 2013, 257, 42 CrossRef PubMed; (b) S. Fukuzumi and K. D. Karlin, Coord. Chem. Rev., 2013, 257, 187 CrossRef CAS PubMed; (c) L. Rulíšek and U. Ryde, Coord. Chem. Rev., 2013, 257, 445 CrossRef PubMed.
- See, e.g., (a) V. Conte, A. Coletti, B. Floris, G. Licini and C. Zonta, Coord. Chem. Rev., 2011, 255, 2165 CrossRef CAS PubMed; (b) G. Licini, V. Conte, A. Coletti, M. Mba and C. Zonta, Coord. Chem. Rev., 2011, 255, 2345 CrossRef CAS PubMed.
- See, e.g., (a) P. J. Gonzalez, M. G. Rivas, C. S. Mota, C. D. Brondino, I. Moura and J. J. G. Moura, Coord. Chem. Rev., 2013, 257, 315 CrossRef CAS PubMed; (b) H. Broda, S. Hinrichsen and F. Tuczek, Coord. Chem. Rev., 2013, 257, 587 CrossRef CAS PubMed.
- See, e.g., (a) A. B. Tomter, G. Zoppellaro, N. H. Andersen, H.-P. Hersleth, M. Hammerstad, Å. K. Røhr, G. K. Sandvik, K. R. Strand, G. E. Nilsson, C. B. Bell III, A.-L. Barra, E. Blasco, L. Le Pape, E. I. Solomon and K. K. Andersson, Coord. Chem. Rev., 2013, 257, 3 CrossRef CAS PubMed; (b) P. Nordlund and P. Reichard, Annu. Rev. Biochem., 2006, 75, 681 CrossRef CAS PubMed; (c) J. Herrick and B. Sclavi, Mol. Microbiol., 2007, 63, 22 CrossRef CAS PubMed.
- See, e.g., (a) N. Nelson and C. F. Yokum, Annu. Rev. Biochem., 2006, 57, 521 CAS; (b) C. W. Cady, R. H. Crabtree and G. W. Brudvig, Coord. Chem. Rev., 2008, 252, 444 CrossRef CAS PubMed; (c) D. J. Vinyard, G. M. Ananyev and G. C. Dismukes, Annu. Rev. Biochem., 2013, 82, 577 CrossRef CAS PubMed; (d) P. E. M. Siegbahn, Chem.–Eur. J., 2008, 14, 8290 CrossRef CAS PubMed.
- N. M. DeVore and E. E. Scott, J. Biol. Chem., 2012, 287, 26576 CrossRef CAS PubMed.
- J. R. O'Brien, D. J. Schuller, V. S. Yang, B. D. Dillard and W. N. Lanzilotta, Biochemistry, 2003, 42, 5547 CrossRef CAS PubMed.
- J. H. Dawson, R. H. Holm, J. R. Trudell, G. Barth, R. E. Linder, E. Bunnenberg, C. Djerassi and S. C. Tang, J. Am. Chem. Soc., 1976, 98, 3707 CrossRef CAS.
- (a) P. R. Ortiz de Montellano, Annu. Rev. Pharmacol. Toxicol., 1992, 32, 89 CrossRef CAS PubMed; (b) M. Hofrichter, Enzyme Microb. Technol., 2002, 30, 454 CrossRef CAS; (c) E. L. Raven, Nat. Prod. Rep., 2003, 20, 367 RSC; (d) T. L. Poulos, Arch. Biochem. Biophys., 2010, 500, 3 CrossRef CAS PubMed; (e) F. Hollmann, I. W. C. E. Arends, K. Buehler, A. Schallmey and B. Bühler, Green Chem., 2011, 13, 226 RSC.
- (a) P. Nicholls, I. Fita and P. C. Loewen, Adv. Inorg. Chem., 2000, 51, 51 CrossRef; (b) N. G. Veitch and A. T. Smith, Adv. Inorg. Chem., 2000, 51, 107 CrossRef; (c) H.-P. Hersleth, U. Ryde, P. Rydberg, C. H. Görbitz and K. K. Andersson, J. Inorg. Biochem., 2006, 100, 460 CrossRef CAS PubMed.
- (a) F. Ogliaro, S. P. de Visser and S. Shaik, J. Inorg. Biochem., 2002, 91, 554 CrossRef CAS; (b) P. Rydberg, E. Sigfridsson and U. Ryde, JBIC, J. Biol. Inorg. Chem., 2004, 9, 203 CrossRef CAS PubMed; (c) D. Kumar, B. Karamzadeh, G. N. Sastry and S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 7656 CrossRef CAS PubMed; (d) D. Kumar, R. Latifi, S. Kumar, E. V. Rybak-Akimova, M. A. Sainna and S. P. de Visser, Inorg. Chem., 2013, 52, 7968 CrossRef CAS PubMed.
- (a) M. T. Green, J. Am. Chem. Soc., 1999, 121, 7939 CrossRef CAS; (b) S. P. de Visser, S. Shaik, P. K. Sharma, D. Kumar and W. Thiel, J. Am. Chem. Soc., 2003, 125, 15779 CrossRef CAS PubMed; (c) K. Yoshizawa, Y. Shiota and T. Yamabe, J. Am. Chem. Soc., 1999, 121, 147 CrossRef CAS.
- J. Rittle and M. T. Green, Science, 2010, 330, 933 CrossRef CAS PubMed.
- (a) S. P. de Visser, Angew. Chem., Int. Ed., 2006, 45, 1790 CrossRef CAS PubMed; (b) S. P. de Visser, J. Am. Chem. Soc., 2006, 128, 9813 CrossRef CAS PubMed; (c) A. Decker, M. D. Clay and E. I. Solomon, J. Inorg. Biochem., 2006, 100, 697 CrossRef CAS PubMed; (d) R. Latifi, M. Bagherzadeh and S. P. de Visser, Chem.–Eur. J., 2009, 15, 6651 CrossRef CAS PubMed.
- (a) S. P. de Visser, J.-U. Rohde, Y.-M. Lee, J. Cho and W. Nam, Coord. Chem. Rev., 2013, 257, 381 CrossRef CAS PubMed; (b) K. P. Jensen, P. Rydberg, J. Heimdal and U. Ryde, A comparison of the tetrapyrrole cofactors in nature and their tuning by axial ligands, in Computational modeling for homogeneous and enzymatic catalysis, ed. K. Morokuma and J. Musaev, Wiley-VCH, Weinheim, 2008, pp. 27–56 Search PubMed.
- E. Schrödinger, Phys. Rev., 1926, 28, 1049 CrossRef.
- (a) P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, 3rd edn, 1997 Search PubMed; (b) F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Ltd., Chichester, 2nd edn, 2007 Search PubMed; (c) S. P. de Visser, Introduction to quantum behaviour – a primer, in Quantum Tunnelling in Enzyme-Catalysed Reactions, ed. R. K. Alleman and N. S. Scrutton, RSC Publishing, Cambridge, 2009, ch. 2, p. 18 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 0618 CrossRef.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968 CrossRef CAS.
- Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, ed. S. R. Langhoff, Kluwer, Dordrecht, 1995 Search PubMed.
- J. W. W. McDouall, Computational Quantum Chemistry, RSC Publishing, Cambridge, 2013 Search PubMed.
- (a) P. Hohenberg and W. Kohn, Phys. Rev. B: Solid State, 1964, 136, 864 Search PubMed; (b) W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133 Search PubMed.
- J. C. Slater, The self-consistent field for molecular and solids. In Quantum Theory of Molecular and Solids, McGraw-Hill, New York, vol. 4, 1974 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48 CrossRef CAS PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397 RSC.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, Chapman & Hall, London, 1954 Search PubMed.
- (a) D. Kumar, S. P. de Visser and S. Shaik, Chem.–Eur. J., 2005, 11, 2825 CrossRef CAS PubMed; (b) S. P. de Visser, K. Oh, A.-R. Han and W. Nam, Inorg. Chem., 2007, 46, 4632 CrossRef CAS PubMed; (c) A. K. Vardhaman, C. V. Sastri, D. Kumar and S. P. de Visser, Chem. Commun., 2011, 47, 11044 RSC; (d) A. K. Vardhaman, P. Barman, S. Kumar, C. V. Sastri, D. Kumar and S. P. de Visser, Angew. Chem., Int. Ed., 2013, 52, 12288 CrossRef CAS PubMed.
- O. Pestovsky and A. Bakac, Inorg. Chem., 2006, 45, 814 CrossRef CAS PubMed.
- J. H. Jensen, Molecular Modeling Basics, CRC Press, Boca Raton, 2010 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- (a) C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361 CrossRef CAS; (b) M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669 CrossRef CAS PubMed; (c) A. Klamt and J. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 5, 799 RSC; (d) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- (a) M. J. Ramos and P. A. Fernades, Acc. Chem. Res., 2008, 41, 689 CrossRef CAS PubMed; (b) P. E. M. Siegbahn and F. Himo, WIREs Comput. Mol. Sci., 2011, 1, 323 CrossRef CAS.
- (a) T. Borowski, A. Bassan and P. E. M. Siegbahn, Biochemistry, 2004, 43, 12331 CrossRef CAS PubMed; (b) S. P. de Visser, Chem.–Eur. J., 2006, 12, 8168 CrossRef CAS PubMed; (c) S. P. de Visser, Chem. Commun., 2007, 171 RSC.
- (a) R. Sevastik and F. Himo, Bioorg. Chem., 2007, 35, 444 CrossRef CAS PubMed; (b) P. Georgieva and F. Himo, J. Comput. Chem., 2010, 31, 1707 CAS; (c) L. Hu, J. Eliasson, J. Heimdal and U. Ryde, J. Phys. Chem. A, 2009, 113, 11793 CrossRef CAS PubMed.
- (a) A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227 CrossRef CAS; (b) H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198 CrossRef CAS PubMed; (c) R. Lonsdale, K. E. Ranaghan and A. J. Mulholland, Chem. Commun., 2010, 46, 2354 RSC.
- H. M. Senn and W. Thiel, Top. Curr. Chem., 2007, 268, 173 CrossRef CAS.
- N. I. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem., 2000, 104, 1720 CrossRef CAS.
- L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2011, 7, 761 CrossRef CAS.
- (a) T. H. Rod and U. Ryde, J. Chem. Theory Comput., 2005, 1, 1240 CrossRef CAS; (b) T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815 CrossRef CAS.
- (a) P. Söderhjelm, C. Husberg, A. Strambi, M. Olivucci and U. Ryde, J. Chem. Theory Comput., 2009, 5, 649 CrossRef; (b) C. Steinmann, D. G. Fedorov and J. H. Jensen, J. Phys. Chem. A, 2010, 114, 8705 CrossRef CAS PubMed.
- (a) Jaguar 7.6, Schrödinger LLC, New York NY, 2007 Search PubMed; (b) M. J. Frisch, et al., Gaussian-09, Revision A.02, Wallingford, CT, 2009 Search PubMed; (c) A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024 CrossRef; (d) W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz Jr., D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179 CrossRef CAS; (e) A. D. MacKerell, D. Bashford, J. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586 CrossRef CAS; (f) G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E.-J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS; (g) M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357 CrossRef CAS; (h) U. Ryde, J. Comput. Aided Mol. Des., 1996, 10, 153 CrossRef CAS; (i) P. Sherwood, et al. , J. Mol. Struct., 2003, 632, 1 CrossRef CAS.
- U. Ryde, Dalton Trans., 2007, 607 Search PubMed.
- H. Hu and W. Yang, Annu. Rev. Phys. Chem., 2008, 59, 573 Search PubMed.
- S. Sumner, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205 Search PubMed.
- (a) L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 640 Search PubMed; (b) R. Z. Liao and W. Thiel, J. Comput. Chem., 2013, 34, 2389 Search PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235 Search PubMed.
- D. Kumar, W. Thiel and S. P. de Visser, J. Am. Chem. Soc., 2011, 133, 386 Search PubMed.
- (a) M. H. Stipanuk, Annu. Rev. Nutr., 2004, 24, 539 Search PubMed; (b) G. D. Straganz and B. Nidetzky, ChemBioChem, 2006, 7, 1536 Search PubMed; (c) C. A. Joseph and M. J. Maroney, Chem. Commun., 2007, 3338 Search PubMed.
- (a) S. Aluri and S. P. de Visser, J. Am. Chem. Soc., 2007, 129, 14846 Search PubMed; (b) S. P. de Visser and G. D. Straganz, J. Phys. Chem. A, 2009, 113, 1835 Search PubMed; (c) S. P. de Visser, Coord. Chem. Rev., 2009, 253, 754 Search PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 Search PubMed.
- (a) N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403 Search PubMed; (b) W.-M. Hoe, A. Cohen and N. C. Handy, Chem. Phys. Lett., 2001, 341, 319 Search PubMed; (c) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 Search PubMed.
- K.-B. Cho, H. Chen, D. Janardanan, S. P. de Visser, S. Shaik and W. Nam, Chem. Commun., 2012, 48, 2189 Search PubMed.
- J. A. Crawford, W. Li and B. S. Pierce, Biochemistry, 2011, 50, 10241 Search PubMed.
- (a) H. Hirao, D. Kumar, L. Que Jr and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590 Search PubMed; (b) S. P. de Visser, J. Am. Chem. Soc., 2006, 128, 15809 Search PubMed; (c) R. Latifi, M. A. Sainna, E. V. Rybak-Akimova and S. P. de Visser, Chem.–Eur. J., 2013, 19, 4058 Search PubMed.
- C. R. Simmons, K. Krishnamoorthy, S. L. Granett, D. J. Schuller, J. E. Dominy Jr., T. P. Begley, M. H. Stipanuk and P. A. Karplus, Biochemistry, 2008, 47, 11390 Search PubMed.
- S. M. Pratter, C. Konstantinovics, C. L. M. DiGiuro, E. Leitner, D. Kumar, S. P. de Visser, G. Grogan and G. D. Straganz, Angew. Chem., Int. Ed., 2013, 52, 9677 Search PubMed.
- R. H. Holm, E. I. Solomon, A. Majumdar and A. Tenderholt, Coord. Chem. Rev., 2011, 255, 99 Search PubMed.
- J.-L. Li and U. Ryde, JBIC, J. Biol. Inorg. Chem. Search PubMed , submitted.
- S. Metz and W. Thiel, J. Am. Chem. Soc., 2009, 131, 14885 Search PubMed.
- J. Heimdal, M. Kaukonen, M. Srnec, L. Rulíšek and U. Ryde, ChemPhysChem, 2011, 12, 3337 Search PubMed.
- J.-L. Li, R. A. Mata and U. Ryde, J. Chem. Theory Comput., 2013, 9, 1799 Search PubMed.
- N. Cobb, T. Conrads and R. Hille, J. Biol. Chem., 2005, 280, 11007 Search PubMed.
- (a) C. E. Webster and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 5820 Search PubMed; (b) A. Thapper, R. J. Deeth and E. Nordlander, Inorg. Chem., 2002, 41, 6695 Search PubMed; (c) J. P. McNamara, I. H. Hillier, T. S. Bhachu and C. D. Garner, Dalton Trans., 2005, 3572 Search PubMed; (d) M. Hofmann, J. Mol. Struct., 2006, 773, 59 Search PubMed; (e) M. Hofmann, Inorg. Chem., 2008, 47, 5546 Search PubMed; (f) E. Hernandez-Marin and T. Ziegler, Can. J. Chem., 2010, 88, 683 Search PubMed; (g) A. L. Tenderholt, J. J. Wang, R. K. Szilagyi, R. H. Holm, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2010, 132, 8359 Search PubMed.
- (a) E. I. Solomon, A. J. Augustine and J. Yoon, Dalton Trans., 2008, 3921 Search PubMed; (b) E. I. Solomon, J. W. Ginsbach, D. E. Heppner, M. T. Kieber-Emmons, C. H. Kjaergaard, P. J. Smeets, L. Tian and J. S. Woertink, Faraday Discuss., 2011, 148, 11 Search PubMed.
- W. Shin, U. M. Sundaram, J. L. Cole, H. H. Zhang, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1996, 118, 3202 Search PubMed.
- S.-K. Lee, S. DeBeer George, W. E. Antholine, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2002, 124, 6180 Search PubMed.
- L. Rulíšek, E. I. Solomon and U. Ryde, Inorg. Chem., 2005, 44, 5612 Search PubMed.
- J. Chalupský, F. Neese, E. I. Solomon, U. Ryde and L. Rulíšek, Inorg. Chem., 2006, 45, 11051 Search PubMed.
- S. Vancoillie, J. Chalupský, U. Ryde, E. I. Solomon, K. Pierloot, F. Neese and L. Rulíšek, J. Phys. Chem. B, 2010, 114, 7692 Search PubMed.
- U. Ryde, Y.-W. Hsiao, L. Rulíšek and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 726 Search PubMed.
- J. Yoon, L. M. Mirica, T. D. P. Stack and E. I. Solomon, J. Am. Chem. Soc., 2005, 127, 13680 Search PubMed.
- (a) F. Neese, D. G. Liakos and S. Ye, JBIC, J. Biol. Inorg. Chem., 2011, 16, 821 Search PubMed; (b) M. Güell, J. M. Luis, M. Solá and M. Swart, J. Phys. Chem. A, 2008, 112, 6384 Search PubMed; (c) M. Swart, M. Güell and M. Solá, Phys. Chem. Chem. Phys., 2011, 13, 10449 Search PubMed.
- H. B. Schlegel and M. A. Robb, Chem. Phys. Lett., 1982, 93, 43 Search PubMed.
- (a) B. O. Roos, K. Andersson, M. P. Fulscher, L. Serrano-Andres, K. Pierloot, M. Merchan and V. Molina, THEOCHEM, 1996, 338, 257 Search PubMed; (b) B. O. Roos, Acc. Chem. Res., 1999, 32, 137 Search PubMed.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138 Search PubMed.
- (a) C. Hampel and H. J. Werner, J. Chem. Phys., 1996, 104, 6286 Search PubMed; (b) F. Neese, A. Ansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 15 Search PubMed.
- F. Neese, J. Chem. Phys., 2003, 119, 9428 Search PubMed.
- (a) E. K. U. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255 Search PubMed; (b) M. E. Casida, Time Dependent Density Functional Response Theory for Molecules, in Recent advances in density functional methods, ed. D. P. Chong, World Scientific, Singapore, 1995, vol. 1, p. 155 Search PubMed; (c) E. K. U. Gross, J. F. Dobson and M. Petersilka, Density functional theory of time-dependent phenomena, in Density Functional Theory, Springer Series: Topics in Current Chemistry, ed. R. F. Nalewajski, Springer, Berlin, Germany, 1996 Search PubMed; (d) S. J. A. Van Gisbergen, J. G. Snijders and E.-J. Baerends, J. Chem. Phys., 1995, 103, 9347 Search PubMed; (e) R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454 Search PubMed; (f) A. Rosa, G. Ricciardi, O. Gritsenko and E.-J. Baerends, Struct. Bonding, 2004, 112, 49 Search PubMed; (g) F. Wang and T. Ziegler, Mol. Phys., 2004, 102, 2585 Search PubMed; (h) A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 Search PubMed; (i) F. Wang, T. Ziegler, E. van Lenthe, S. J. A. Van Gisbergen and E.-J. Baerends, J. Chem. Phys., 2005, 122, 204103 Search PubMed; (j) M. Seth and T. Ziegler, J. Chem. Phys., 2005, 23, 144105 Search PubMed.
- (a) M. Atanasov, P. Comba, C. A. Daul and F. Neese, The Ligand Field Paradigm and New Insights into the Electronic Properties of Transition Metal Complexes Based on Modern Electronic Structure Calculations, in Models, Mysteries and Magic of Molecules, ed. J. C. A. Boeyens and J. F. Ogilviee, Springer, Dordrecht, the Netherlands, 2008 Search PubMed; (b) M. Atanasov, C. A. Daul and C. Rauzy, Chem. Phys. Lett., 2003, 367, 737 Search PubMed; (c) M. Atanasov, C. Daul and C. Rauzy, Struct. Bonding, 2004, 106, 97 Search PubMed; (d) C. Daul, C. Rauzy, M. Zbiri, P. Bättig, R. Bruyndonckx, E.-J. Baerends and M. Atanasov, Chem. Phys. Lett., 2004, 399, 433 Search PubMed; (e) M. Atanasov, C. Rauzy, P. Bättig and C. Daul, Int. J. Quantum Chem., 2005, 102, 119 Search PubMed.
- (a) M. Atanasov, P. Comba and C. A. Daul, Inorg. Chem., 2008, 47, 2449 Search PubMed; (b) M. Atanasov, P. Comba, G. R. Hanson, S. Hausberg, S. Helmle and H. Wadepohl, Inorg. Chem., 2011, 50, 6890 Search PubMed; (c) M. Atanasov, P. Comba and S. Helmle, Inorg. Chem., 2012, 51, 9357 Search PubMed.
- M. Atanasov, P. Comba, S. Helmle, D. Müller and F. Neese, Inorg. Chem., 2012, 51, 12324 Search PubMed.
- S. P. de Visser, R. Latifi, L. Tahsini and W. Nam, Chem.–Asian J., 2011, 6, 493 Search PubMed.
- A. Decker, J.-U. Rohde, L. Que Jr and E. I. Solomon, J. Am. Chem. Soc., 2004, 126, 5378 Search PubMed.
- (a) H. Börzel, P. Comba, C. Katsichtis, W. Kiefer, A. Lienke, V. Nagel and H. Pritzkow, Chem.–Eur. J., 1999, 5, 1716 Search PubMed; (b) P. Comba, B. Martin, A. Muruganantham and J. Straub, Inorg. Chem., 2012, 51, 9214 Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 Search PubMed.
- (a) S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 Search PubMed; (b) J. L. Pascual-Ahuir, E. Silla and I. Tunon, J. Comput. Chem., 1994, 15, 117 Search PubMed.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 Search PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 Search PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 Search PubMed.
- J. Schirmer and A. Dreuw, Phys. Rev. A, 2007, 122513 Search PubMed.
- (a) A. Aizman and D. A. Case, J. Am. Chem. Soc., 1982, 104, 3269 Search PubMed; (b) K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed. V. H. Smith, Reidel Inc., Dordrecht, 1986 Search PubMed; (c) R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2003, 42, 268 Search PubMed; (d) J. R. Long, in Molecular Cluster Magnets in Chemistry of Nanostructured Materials, ed. P. Yang, World Scientific, Hong Kong, 2003, p. 291 Search PubMed; (e) I. Rudra, Q. Wu and T. van Voorhis, J. Chem. Phys., 2006, 124, 024103 Search PubMed; (f) M. Atanasov, P. Comba, S. Hausberg and B. Martin, Coord. Chem. Rev., 2009, 253, 2306 Search PubMed.
- F. Neese, ORCA – an ab initio, DFT and semiempirical SCF-MO package, version 2.7-00, Bonn, Germany, 2009 Search PubMed.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533 Search PubMed.
- P. Comba, S. Hausberg and B. Martin, J. Phys. Chem A, 2009, 113, 6751 Search PubMed.
- (a) P. Comba, L. R. Gahan, G. Haberhauer, G. A. Hanson, C. J. Noble, B. Seibold and A. L. van den Brenk, Chem.–Eur. J., 2008, 14, 4393 Search PubMed; (b) N. Dovail, PhD Dissertation, University of Heidelberg, Germany, 2010; (c) P. Comba, N. Dovalil, G. Haberhauer, G. R. Hanson, J. Harmer, C. J. Noble, M. J. Riley and B. Seibold, Manuscript in preparation.
- F. Neese, J. Chem. Phys., 2001, 115, 11080 Search PubMed.
- V. G. Malkin, O. L. Malkina, R. Reviakine, A. F. Arbouznikov, M. Kaupp, B. Schimmelpfennig, I. Malkin, T. Helgakerand H. Ruud, MAG-ReSpect 1.2.
- A. Wachters, J. Chem. Phys., 1969, 52, 1033 Search PubMed.
- M. Güell, J. L. Luis, L. Rodríguez-Santiago, M. Sodupe and M. Solá, J. Phys. Chem. A, 2009, 113, 1308 Search PubMed.
- M. Atanasov, P. Comba, B. Martin, V. Müller, G. Rajaraman, H. Rohwer and S. Wunderlich, J. Comput. Chem., 2006, 27, 1263 Search PubMed.
- P. Leeladee, G. N. L. Jameson, M. A. Siegler, D. Kumar, S. P. de Visser and D. P. Goldberg, Inorg. Chem., 2013, 52, 4668 Search PubMed.
- (a) Y. Hu and M. W. Ribbe, Acc. Chem. Res., 2010, 43, 475 Search PubMed; (b) B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2013, 46, 587 Search PubMed.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |