Coupled-cluster calculations of the lowest 0–0 bands of the electronic excitation spectrum of naphthalene

Abstract

Approximate singles and doubles coupled-cluster (CC2) calculations have been carried out for the 0–0 bands of the 1A_g → 1B_3u and 1A_g → 1B_2u transitions of naphthalene. The vertical excitation energies calculated for the 16 lowest excited singlet states have also been calculated using a sequence of large basis sets. The CC2 excitation energies extrapolated to the basis-set limit are in rather good agreement with values recently calculated at the multiconfiguration second-order perturbation theory (CASPT2) and at the singles, doubles and approximate triples (CC3) levels. Best values for the vertical excitation energies and the 0–0 transition energies have been obtained by adding higher-order correlation contributions to the basis-set extrapolated CC2 energies. For some of the states, the best estimated vertical excitation energies in this work deviate up to 0.3 eV from the previously best estimated energies, because larger basis sets have been employed in this study. The calculations of the 0–0 transitions show the importance of considering vibrational effects when aiming at reliable comparisons of calculated and measured excitation energies for assessing the accuracy of employed computational methods. Calculations at the density functional theory (DFT) level using Becke's three-parameter functional (B3LYP) yield less accurate excitation energies. At the B3LYP level, the two lowest states appear in reverse order with a deviation of 0.50 eV from experiment for the 0–0 transition energy of the 1B_3u state.

---

1 Introduction

Comparisons of calculated electronic excitation energies with vertical excitation energies deduced from measured ultraviolet-visible (UV-Vis) spectra are difficult, because the exact positions of the vertical transitions are obscured in the vibrationally broadened absorption bands of recorded UV-Vis spectra. The main obstacles from the computational point of view are that the calculated excitation energies strongly depend on the employed computational level including the basis-set size. A more reliable approach for assessing the accuracy of the employed computational method is to compare vibrationally corrected transition energies with excitation energies from high-resolution vibrationally resolved spectra. However, calculations of vibrationally resolved excitation energies such as the 0–0 transition energies are though more involved than the calculation of vertical excitation energies, because the calculation of vibrational contributions to excitation energies requires computation of the vibrational frequencies for the upper and the lower states, which presupposes optimization of the molecular structures for both the ground and the excited state.^1,2

The aim of this study is to assess the accuracy of the approximative second-order coupled-cluster (CC2) calculations by studying the 0–0 transition energy of the electronic excitation spectrum of naphthalene at the linear response CC2 level using basis sets that yield values in the complete basis-set limit. Best estimated values for the vertical excitation energies are reported. The excitation energies are also calculated at the linear-response time-dependent density functional theory (TDDFT) level using Becke's three-parameter functional (B3LYP). Comparisons of the calculated and measured transition energies for the 0–0 band yield error bars for the CC2 and TDDFT excitation energies. The vertical excitation energies calculated at the CC2 and TDDFT levels can then be used to estimate the accuracy of other computational levels that are used for calculating the electronic excitation energies. The CC2 vertical excitation energies for the lowest states are also compared to values obtained in recent multiconfiguration second-order perturbation theory (CASPT2) calculations.

The article is outlined as follows: after the description of our computational methodology in Section 2, a basis-set study is presented in Section 3. The basis-set extrapolated vertical excitation energies are compared to previously calculated and measured values in Section 4. In Section 5, the 0–0 transition energies for the two lowest excited states of naphthalene calculated at the CC2 and B3LYP levels are compared to experimental data. The main results of the study are summarized in Section 6.

2 Computational details

The molecular structure of the ground state of naphthalene used in the basis set study was taken from ref. 3, where they optimized the naphthalene structure at the B3LYP level using double-ζ polarization (DZP) basis sets.^4,5 The molecular structure belongs to the D_2h point group. The molecule is oriented in the xy plane with the x axis along the long axis of the molecule. The molecular structure was also optimized at the B3LYP and second-order Møller–Plesset perturbation theory (MP2)⁶ levels using the Karlsruhe triple-ζ basis sets augmented with double sets of polarization functions (TZVPP). The molecular structure of naphthalene is shown in Fig. 1.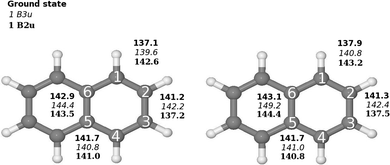

Fig. 1 Comparison of the molecular structure of the ground and excited states of naphthalene (D_2h) calculated at (left) B3LYP/def2-TZVP and (right) CC2/def2-TZVPP levels of theory. The Cartesian coordinates of the optimized structures are given as ESI.†

The vertical excitation energies were calculated at the linear response CC2 level^7–12 using Turbomole¹³ and the Karlsruhe aug-TZVPP, daug-TZVPP, aug-QZVPP, TZVPD, and QZVPD basis set.^14–17 The CC2 calculations were performed with the RI-CC2 module using the frozen core and the resolution of the identity (RI) approximations.^10,12,18 The aug-TZVPP and aug-QZVPP basis sets were constructed by adding the diffuse functions of the Dunning aug-cc-pVTZ^19,20 basis set to the TZVPP and QZVPP ones. The daug-TZVPP basis sets were analogously constructed by adding the diffuse functions of the doubly augmented daug-cc-pVTZ basis to the Karlsruhe TZVPP basis sets.^19,20 The extrapolated CC2 excitation energies were obtained by adding the difference between the energies obtained with the aug-TZVPP and daug-TZVPP basis sets to the ones obtained using aug-QZVPP basis sets.

Single point calculations of vertical excitation energies using the long range corrected CAM-B3LYP functional²¹ were performed with Gaussian 09, Revision D.01²² and the def2-TZVP basis set, while the single point calculations with the BH-LYP functional²³ were done with Turbomole.¹³ The Cartesian coordinates of the optimized structures are given as ESI.†

The excitation energies for the 0–0 transitions were calculated at the linear response CC2^9–12 and time-dependent density functional theory (TDDFT)^24–26 levels using split-valence polarization and triple-ζ polarization basis sets.^27,28 The B3LYP functional was employed in the TDDFT calculations of the 0–0 transition energies.

In the CC2 and DFT calculations of the vibrational energy contributions to the excited energies, the ground state structure was optimized at the CC2 and B3LYP levels, respectively, whereas the excited state structures were optimized at the CC2 and TDDFT/B3LYP levels. The vibrational frequencies were calculated numerically using the NumForce script of the Turbomole code. At the B3LYP level, the frequencies were calculated analytically using the AOFORCE module of Turbomole.^29,30

3 Basis-set studies

The vertical excitation energies were calculated at the CC2 level using a variety of rather large basis sets ranging from TZVPP to aug-QZVPP. The obtained excitation energies are given in Table 1. The basis-set study shows that the CC2 calculations using the TZVPP basis sets yield excitation energies of the valence states that deviate less than 0.35 eV from the basis-set limit, whereas diffuse functions are very crucial for the Rydberg states to obtain accurate excitation energies. For the Rydberg states, the contribution from diffuse basis functions varies between 1 eV to 2 eV. However, for most of the Rydberg states only one set of diffuse functions is enough for obtaining converged excitation energies with a contribution of less than 0.05 eV from the second set of diffuse functions. The exceptions are the 3A_g, 2B_1u, and 2A_u Rydberg states as well as the 2B_1g state, which is characterized as a valence state. For them, the second set of diffuse functions lowers the excitation energies by 0.07–0.21 eV.

Table 1 Vertical excitation energies (in eV) calculated at the CC2 level for the lowest singlet states using different basis sets. The valence and Rydberg states are marked with (V) and (R), respectively

State		TZVPP	TZVPD	aug-TZVPP	daug-TZVPP	QZVPD	aug-QZVPP
1B3u	(V)	4.37	4.36	4.35	4.35	4.35	4.34
1B2u	(V)	4.79	4.76	4.75	4.74	4.75	4.74
1B1g	(V)	6.03	5.94	5.81	5.77	5.90	5.82
2Ag	(V)	6.10	6.06	6.01	6.01	6.03	6.01
2B3u	(V)	6.10	6.04	5.99	5.98	6.02	5.99
2B2u	(V)	6.37	6.34	6.30	6.30	6.31	6.30
2B1g	(V)	6.63	6.57	6.42	6.23	6.52	6.41
3Ag	(V)	7.17	7.12	7.06	6.85	7.10	7.05
1B2g	(R)	7.07	6.31	5.94	5.91	6.23	5.97
1B3g	(R)	7.19	6.39	5.97	5.93	6.29	6.00
1Au	(R)	7.26	5.88	5.56	5.53	5.80	5.59
2B2g	(R)	7.65	7.06	6.63	6.60	6.96	6.66
2B3g	(R)	7.67	7.09	6.69	6.65	7.00	6.72
1B1u	(R)	7.97	6.59	6.26	6.23	6.50	6.29
2B1u	(R)	8.17	7.08	6.51	6.44	6.90	6.54
2Au	(R)	8.53	6.93	6.48	6.35	6.80	6.50

---

For the valence states, the excitation energies obtained using the TZVPD basis set lie roughly halfway between the TZVPP and aug-TZVPP values. However, the energy contributions from the first set of diffuse functions of 0.02–0.22 eV are also small. For the Rydberg states, the diffuse functions of the TZVPD basis set significantly improve the excitation energies. The discrepancy in the daug-TZVPP excitation energies of 0.3–0.6 eV are though much larger for the Rydberg states, because the TZVPD basis sets have much fewer diffuse basis functions than the aug-TZVPP basis set.

The uncertainty introduced by using molecular ground-state structures optimized at other levels of theory is less than 0.10 eV, whereas optimization of the molecular structure of the excited states leads to significant changes in the excitation energies. The CC2/TZVPP excitation energies for the 1B_3u and 1B_2u states using the molecular structure optimized at the B3LYP/TZVP level are 4.46 eV and 4.86 eV, respectively. For the MP2/TZVP structure, they are 4.43 eV and 4.81 eV, respectively.

The transition from the 1A_g ground state to the excited 1B_3u and 1B_2u states are dipole allowed with a very small oscillator strength of 0.00001 for the 1B_3u state. The oscillator strength of 0.081 for the 1B_2u state calculated at the CC2/TZVPP level is much larger. The transition to the 1B_3u state is along the long axis and can based on simple particle in the box arguments be expected to be the lowest excited state. However, calculations of the two lowest states at the TDDFT level using the B3LYP functional yielded surprisingly the two lowest excited states in the reverse order with 1B_2u as the lowest excited state as also found in a recent TDDFT study.³¹ The excitation energies of the 1B_2u and 1B_3u states calculated at the B3LYP/TZVPD level are 4.28 eV and 4.38 eV, respectively.

Calculations of the vertical excitation energies at the CAM-B3LYP/TZVP level yield excitation energies of 4.62 eV and 4.66 eV for the 1B_2u and 1B_3u states. Thus, the CAM-B3LYP energies are 0.25 eV and 0.20 eV larger than the energies calculated at the B3LYP/TZVP level obtained at the same geometry. Calculations at the BH-LYP/TZVP level yielded excitation energies of 4.66 eV and 4.73 eV for the 1B_2u and 1B_3u states, which are in close agreement with the CAM-B3LYP excitation energies. The CAM-B3LYP and BH-LYP excitation energies for the 1B_2u state are 0.17 eV and 0.13 eV smaller than the excitation energy calculated at the CC2 level, whereas for 1B_3u the excitation energies calculated at the CAM-B3LYP and BH-LYP levels are 0.32 eV and 0.39 eV larger than the CC2 excitation energies. The 1B_2u and 1B_3u states appear in reverse order also at the CAM-B3LYP and BH-LYP levels.

Optimization of the molecular structure of the ground and two lowest excited states at the B3LYP and CC2 levels yielded very similar structures with the largest deviation in the C–C distances of 1.14 pm. The excitation to the 1B_2u state changes the bond-length alternation of the C1–C2 and C2–C3 bonds. In the ground state, the C1–C2 and C2–C2 distances are 137.9 pm and 141.3 pm, respectively as compared to 143.2 pm and 137.5 pm for the 1B_2u state. In the molecular structure of the 1B_3u state, the bond-length alternation around the molecule is significantly smaller than for the two other states and the C5–C6 bond is 6.1 pm longer than for the ground state. The bond distances are shown in Fig. 1.

4 Comparison to literature values

The CC2 excitation energies extrapolated to the basis-set limit are in rather good agreement with values calculated at the coupled-cluster singles and doubles (CCSD), coupled-cluster singles, doubles and approximate triples (CC3)³² levels as well as with excitation energies recently obtained in complete active space second-order perturbation theory (CASPT2) calculations.³³ Comparisons of the CC2 and CCSD excitation energies calculated using TZVP basis sets show that CC2 calculations yield more accurate excitation energies than obtained at the CCSD level. Best estimates for the vertical excitation energies are obtained by adding the difference between the CC2 and CC3 excitation energies reported by Schreiber et al.³² to the extrapolated basis-set limit of the CC2 calculations of this work. The small difference between the excitation energies calculated at the CC2 and CC3 levels shows that a multireference treatment is not necessary for obtaining accurate excitation energies of the lowest excited states of naphthalene. However, the multiconfiguration character of the wavefunction is important when optimizing the molecular structure of higher excited states as well as when calculating excitation energies of larger acenes as shown in a comprehensive study by Hachmann et al. who employed density matrix renormalization group calculations.³⁴

For most states, the best estimated values of this work agree well with the best estimated values reported by Schreiber et al.³² However, for the 1B_1g, 2B_1g, and 3A_g states, the discrepancies are 0.36 eV, 0.29 eV, and 0.31 eV, respectively, because diffuse basis functions significantly lower the excitation energies even though they are valence states. The best estimated excitation energies of this work are in most cases lower than the previous estimated values, because larger basis sets were employed in this work. The basis-set extrapolated CC2 excitation energies and the best estimated excitation energies are compared to previously calculated values in Table 2.

Table 2 Comparison of basis-set extrapolated vertical CC2 excitation energies (in eV) for naphthalene with previously calculated values. The best estimated values are obtained by adding the triples contribution to the CC2 basis-set limit

State	CC2	Best estimate	CC2	CCSD	CC3	CASPT2
	Extrap.	PW (ref. 32)	Ref. 32	Ref. 32	Ref. 32	Ref. 32	Ref. 33	Ref. 36
1B3u	4.34	4.16 (4.24)	4.45	4.41	4.27	4.24	4.26	4.03
1B2u	4.73	4.80 (4.77)	4.96	5.21	5.03	4.77	4.62	4.56
1B1g	5.78	5.64 (6.00)	6.21	6.53	6.07	6.00	5.94	5.53
2Ag	6.01	5.77 (5.90)	6.22	6.23	5.98	5.90	6.05	5.39
2B3u	5.98	6.06 (6.07)	6.25	6.55	6.33	6.07	6.05	5.54
2B2u	6.30	6.30 (6.33)	6.57	6.77	6.57	6.33	6.13	5.93
2B1g	6.22	6.19 (6.48)	6.82	6.97	6.79	6.48	6.34	5.87
3Ag	6.84	6.40 (6.71)	7.34	7.77	6.90	6.71	6.72	6.04
1B2g	5.94							5.94
1B3g	5.96							5.98
1Au	5.56							5.54
2B2g	6.63							6.45
2B3g	6.68							6.48
1B1u	6.26							6.03
2B1u	6.47							6.50
2Au	6.37

---

The CASPT2 values deviate by −0.17–0.16 eV from the extrapolated CC2 values, whereas the agreement between the CASPT2 energies and the best estimated values of −0.18–0.32 eV is worse, because too small basis sets were employed in the CASPT2 study. Comparisons of the CASPT2 excitation energies with the best estimated values show that the largest deviations of 0.30 eV, 0.28 eV and 0.32 eV appear for the 1B_1g, 2A_g and 3A_g states, respectively. The comparison of the CC2 and CASPT2 excitation energies suggests that the studied states can be accurately described by single excitations from the Hartree–Fock reference when the molecular structure of the ground state is used.

Knippenberg et al.³⁵ have studied excitation energies of naphthalene at the CCSD and the algebraic diagrammatic construction (ADC) levels using split-valence polarization (SVP) basis sets, which leads to CCSD excitation energies that are 0.17–0.75 eV above the here estimated CCSD limit. Adding the basis-set corrections to the ADC(2)-x excitation energies shows that the ADC(2)-x model underestimates the excitation energies with 0.72–1.34 eV for the 1B_3u, 1B_2u, 1B_1g, and 2A_g states.

The excitation energies obtained in the older CASPT2 study are 0.06–0.68 eV smaller that the CASPT2 values of the more recent study.^33,36 The main reason for the deviation between the two sets of CASPT2 excitation energies is the use of different zeroth-order Hamiltonians (H₀) in the CASPT2 calculations. The good agreement between the CC2 and the newer CASPT2 excitation energies indicates that the newer H₀ yields more accurate excitation energies than the old one.³⁷

The CC2 calculations yield eight Rydberg states between 5.56 eV and 6.68 eV, because diffuse functions were included in the basis set. States with Rydberg character can be identified from the change in the energy when adding diffuse basis functions to the basis set or from expectation values of the x̂, ŷ, and ẑ operators that indicate the extent of the molecule. The excitation energy of the Rydberg states are significantly lower when diffuse basis functions are included in the basis set. The classification into valence and Rydberg states in Table 1 agrees with the experimental characterization of the excited states, which is collected in the computational study of Rubio et al.³⁶

Among the experimental studies, we mention the study of George and Morris, who reported 0–0 transitions energies for naphthalene measured in the gas phase.³⁸ Dick and Hohlneicher measured the electronic excitation spectra of naphthalene in ethanol solution with high resolution.³⁹ Accurate transition energies for the lowest dipole forbidden states were deduced from two-photon spectroscopy measurements by Mikami and Ito.⁴⁰ Rumi et al. have recently published a review of two-photon spectroscopy studies on organic molecules.⁴¹ The electronic excitation spectrum of naphthalene has been obtained in a few other experimental studies using different experimental techniques.^42–47 For a more comprehensive list of older references to experimental spectroscopy studies on naphthalene, see e.g. Rubio et al.³⁶

In the basis-set limit, the lowest Rydberg state has an energy of 5.56 eV at the CC2 level, which is in good agreement with the experimental value of 5.60 eV⁴⁸ and with the value of 5.54 eV obtained in the CASPT2 calculation using the older H₀.³⁶ Huebner et al. were not completely confident that their experimental assignment of the 1A_u state at 5.60 eV was correct. However, the present calculations as well as the CASPT2 calculations of Rubio et al.³⁶ support the experimental assignment even though the vibrational contributions have not been taken into account in the calculations. Thus, the 1A_u Rydberg state is the third excited state of naphthalene.

The best estimated values for the excitation energies of the valence states deviate by 0.16–0.39 eV from the corresponding experimental values for the 0–0 transitions, whereas a much better agreement was obtained for the first Rydberg state (1A_u). The discrepancies between calculated and measured excitation energies can be assigned to vibrational effects. The best estimated vertical excitation energies are compared to experimental values in Table 3.

Table 3 The best estimated values for the vertical excitation energies of the lowest valence states obtained in this work are compared to experimental values obtained in high-resolution spectroscopy measurements. The excitation energy of the lowest Rydberg state (A_u) is also compared to the experimental value

State	Best	Exp.	Exp.	Ref.	Comment
a 5.63 eV is obtained using optical spectroscopy in solution and gas phase. Ref. 43. b 5.55 eV is obtained from solid state measurements. Ref. 44. c 5.8 eV is obtained from measurement in solution. Ref. 45.
1B3u	4.16	3.97	4.0	38 and 39	0–0
1B2u	4.80	4.45	4.7	38 and 48	0–0, energy loss in vapor
1B1g	5.64	5.28	5.22	39 and 40	0–0
2Ag	5.77	5.50	5.52	39 and 40	0–0
2B3u	6.06	5.89^a^,^b		38, 42 and 48	0–0, energy loss in vapor, gas phase
2B2u	6.30	6.14	6.0	38 and 48	0–0, energy loss in vapor
2B1g	6.19	6.01	6.05^c	39 and 40	0–0
3Ag	6.40	6.01	6.05	39 and 40	0–0
1Au	5.56	5.60		48	Energy loss in vapor

---

5 Calculation of 0–0 transition energies

The molecular structure of the 1B_3u and 1B_2u states, which are the two lowest excited states of naphthalene, were optimized at the CC2/TZVPD level, using Dunnings aug-cc-pVTZ basis set as auxiliary basis. The calculated vibrational frequencies show that the obtained structures of the two excited states are minima on the potential energy surface. The lowest vertical excitation energies calculated at the CC2/TZVPD level for the optimized molecular structures of the 1B_3u and 1B_2u states are 4.13 eV and 4.18 eV, respectively. Thus, the relaxation of the molecular structure of the excited states red shifts the excitation energies by 0.23 eV and 0.18 eV, respectively.

Optimization of the molecular structures of the 1B_3u and 1B_2u states at the B3LYP/TZVPD level did not change the order of the two lowest states. For the optimized structures of the corresponding excited states, the lowest vertical B3LYP excitation energies are 3.78 eV and 4.16 eV, respectively, which correspond to red shifts of 0.50 eV and 0.12 eV as compared to the excitation energies calculated using the ground state structure.

The 0–0 transition energies from the ground state of the two excited states were obtained by adding the difference between the zero-point vibrational energies (ZPVE) of the ground and excited states to the corresponding adiabatic excitation energy. The zero-point vibrational energies (ZPVE) are given in the ESI.† The calculated 0–0 transition energies of the two lowest excited states are compared to experimental data in Table 4.

Table 4 The energies of the two lowest 0–0 transitions calculated at the CC2 and B3LYP levels are compared to experimental values. Extrapolated CC3 values are also reported

State	CC2				B3LYP	CC3^a	Exp.	Ref.
	SVP	TZVPD	TZVPP	Limit	TZVP
a The estimated CC3 energies are obtained by adding the difference between the CC2 and CC3 energies of −0.18 eV and 0.07 eV^32 for the 1B3u and 1B2u states to the CC2 basis-set limit values, respectively.
1B3u	4.14	4.13	4.13	4.10	4.20	3.92	3.97	38
1B2u	4.58	4.38	4.42	4.36	3.95	4.43	4.45	38

---

The vibrationally corrected transition energy for the 1B_3u state calculated at the CC2/SVP and CC2/TZVPP levels are 4.14 eV and 4.13 eV, respectively. Assuming that the basis-set correction is the same as for the vertical excitation using the ground-state structure yields a transition energy of 4.10 eV in the basis-set limit. By analogously considering the difference between the vertical CC2 and CC3 excitation energies calculated by Schreiber et al.,³² the extrapolated CC3 energy for the 0–0 transition to the 1B_3u state is 3.92 eV, which can be compared to the experimental value of 3.97 eV.³⁸ The same procedure for the 1B_2u state yields a CC2 basis-set limit of 4.36 eV and a CC3 extrapolated value of 4.43 eV for the 0–0 transition to the 1B_2u state.

The main reason for the deviation between the estimated CC3 energies and the experimental values is most likely the employed molecular structure, as the use of the more accurate MP2/TZVP structures leads to CC2 excitation energies for the 1B_3u and 1B_2u states that are 0.06 eV and 0.02 eV larger than obtained using the B3LYP/DZP structure, respectively, which is practically the same as the difference between the experimental and the CC3 extrapolated values.

Calculations at the B3LYP level yield 0–0 transition energies in the reverse order for the 1B_3u and 1B_2u states. The excitation energy of the 1B_3u state of 4.20 eV is 0.23 eV larger than the experimental value of 3.97 eV, whereas for 1B_2u, the B3LYP excitation energy of 3.95 eV is 0.5 eV smaller than the experimental value of 4.45 eV.

6 Summary and conclusions

The vertical excitation energies of the lowest valence and Rydberg states of naphthalene have been calculated at the CC2 level using large basis sets. Vertical excitation energies at the CC2 level have been estimated in the limit of complete basis sets by extrapolation. The present best estimated values for the vertical excitation energies of the lowest valence states have been obtained by adding electron correlation corrections to the basis-set limit values. The electron correlation corrections have been estimated as the difference in the excitation energies calculated at the CC2 and CC3 levels by Schreiber et al.³²

The 0–0 transition energies from the ground state to the two lowest excited states were obtained by adding the difference in the zero-point energy corrections of the two involved states to the corresponding adiabatic excitation energy calculated at the CC2 level. The comparison of the estimated 0–0 transition energies including basis-set extrapolation contributions and higher-order correlation effects shows that the largest deviation between calculated and measured values is most likely due to the employed molecular structure in the calculation of the vertical excitation energies. The use of larger basis sets and a more accurate computational level in the optimization of the molecular structure of the ground state yields structural corrections of the CC2 excitation energies that are of the same size and sign as the deviation between the calculated and measured 0–0 transition energies. The extrapolated CC3 excitation energies of the ground-state 0–0 transitions to the 1B_3u and 1B_2u states are in excellent agreement with experiment.

Calculations at the B3LYP level yield the two lowest excited state in the reverse order with errors of 0.5 eV in the excitation energy of the 1B_3u state.

The present study shows that CC2 calculations using large basis sets might be a good starting point for obtaining accurate excitation energies when neither the ground state nor the excited state requires multiconfigurational treatment, as the deviations between the vibrationally corrected, structurally corrected, and basis-set extrapolated CC2 energies and the experimental values are 0.19 eV and 0.07 eV for the 1B_3u and 1B_2u, respectively. By considering higher-order correlation effects, an excellent agreement with experiment is obtained.

Acknowledgements

This research has been supported by the Academy of Finland through its Computational Science Research Programme (LASTU/258258) and projects 137460 and 266227. We also acknowledge the Magnus Ehrnrooth Foundation for financial support. CSC – the Finnish IT Center for Science – is acknowledged for computer time. H.F. is thankful for support from the Norwegian Research Council through the CoE Centre for Theoretical and Computational Chemistry (Grant No. 179568/V30). This work has received support from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K).

References

1. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630.
2. M. Dierksen and S. Grimme, J. Phys. Chem. A, 2004, 108, 10225–10237.
3. C.-P. Hsu, Z.-Q. You and H.-C. Chen, J. Phys. Chem. C, 2008, 112, 1204–1212.
4. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
5. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
6. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
7. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
8. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
9. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
10. C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951.
11. A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036.
12. C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60.
13. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
14. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
15. A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597.
16. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
17. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
18. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5461.
19. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
20. D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975–2988.
21. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013, see www.gaussian.com.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
24. M. E. Casida, THEOCHEM, 2009, 914, 3–18.
25. R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Chem. Phys. Lett., 1997, 264, 573–578.
26. D. Rappoport and F. Furche, J. Chem. Phys., 2005, 122, 064105.
27. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
28. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
29. P. Deglmann and F. Furche, Chem. Phys. Lett., 2002, 362, 511–518.
30. P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518.
31. M. Krykunov, S. Grimme and T. Ziegler, J. Chem. Theory Comput., 2012, 8, 4434–4440.
32. M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110.
33. V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168.
34. J. Hachmann, J. J. Dorando, M. Avils and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309.
35. S. Knippenberg, J. H. Starcke, M. Wormit and A. Dreuw, Mol. Phys., 2010, 108, 2801–2813.
36. M. Rubio, M. Merchán, E. Ortí and B. O. Roos, Chem. Phys., 1994, 179, 395–409.
37. G. Ghigo, B. O. Roos and P. Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
38. G. A. George and G. C. Morris, J. Mol. Spectrosc., 1968, 26, 67–71.
39. B. Dick and G. Hohlneicher, Chem. Phys. Lett., 1981, 84, 471–478.
40. N. Mikami and M. Ito, Chem. Phys. Lett., 1975, 31, 472–478.
41. M. C. Rumi, S. Barlow, J. Wang, J. W. Perry and S. R. Marder, Photoresponsive Polymers I, Springer, Berlin, Heidelberg, 2008, vol. 213, pp. 1–95.
42. T. Kitagawa, J. Mol. Spectrosc., 1968, 26, 1–23.
43. H. B. Klevens and J. R. Platt, J. Chem. Phys., 1949, 17, 470–481.
44. A. Bree and T. Thirunamachandran, Mol. Phys., 1962, 5, 397–405.
45. D. Bebelaar, Chem. Phys., 1974, 3, 205–216.
46. T. Vondrk, S. Sato and K. Kimura, Chem. Phys. Lett., 1996, 261, 481–485.
47. M. C. R. Cockett, H. Ozeki, K. Okuyama and K. Kimura, J. Chem. Phys., 1993, 98, 7763–7772.
48. R. H. Huebner, S. R. Mielczarek and C. E. Kuyait, Chem. Phys. Lett., 1972, 16, 464–469.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized Cartesian coordinates of naphthalene. See DOI: 10.1039/c3cp54421d

---