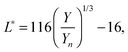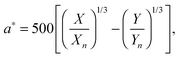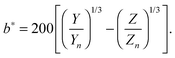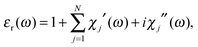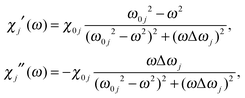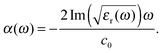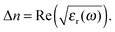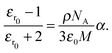Optical spectrum, perceived color, refractive index, and non-adiabatic dynamics of the photochromic diarylethene CMTE†
Received
28th December 2013
, Accepted 11th March 2014
First published on 12th March 2014
Abstract
Photochromism allows for reversible light-induced conversion of a molecular species into a different form with significantly altered optical properties. One promising compound that excels with high fatigue resistance and shows its photochromic functionality both in solution and in molecular solid films is the diarylethene derivative CMTE. Here we present a comprehensive study of its photophysical properties with density-functional theory based methods and benchmark the results against higher-level quantum-chemical approaches and experiments. In addition to static properties such as optical absorption, perceived color, and refractive index, we also investigate reaction dynamics based on non-adiabatic ab initio molecular dynamics. This gives detailed insight into the molecules' ultrafast reaction dynamics and enables us to extract reaction time scales and quantum yields for the observed electrocyclic reaction following photoexcitation.
I. Introduction
Functionalization with molecular materials poses a promising route towards the design of novel optoelectronic and photonic devices.1,2 Light-controlled, reversible molecular mechanisms add to the list of properties typically available in materials used in optical systems. One such molecular mechanism is photochromism, which is defined as a reversible transformation of a single chemical species between two forms with different absorption spectra. This transformation is induced in one or two directions via light irradiation.3,4 Among the different photochromic materials that can reversibly and optically be switched between both of their forms, diarylethenes excel with high fatigue resistance, thermal stability, and relatively high quantum yields.5–7 One particular diarylethene derivative that shows its photochromic functionality even in solid films is cis-l,2-dicyano-l,2-bis(2,4,5-trimethyl-3-thienyl)ethene (CMTE) (cf.Scheme 1).5,8 This makes it a promising candidate to be used in future solid-state/molecular photonic hybrid structures.9,10
 |
| | Scheme 1 Diarylethene derivative CMTE. Shown are open (left) and closed (right) ring form. The essential part for a normal-type diarylethene is shown in black, the side groups of CMTE in blue. Cyclization and cycloreversion by illumination with light are indicated. | |
Using diarylethenes as the active component in a light controlled dielectric environment, both absorptive and dispersive parts of the dielectric function play an important role.11 Most studies, however, focus on the optical absorption; only little information is available on the dispersive behavior of the dielectric response. Experimental studies also include investigations of the reaction dynamics of certain diarylethene derivatives with ultrafast spectroscopic techniques and determination of reaction quantum yields.12–14 Theoretical work is mostly focused on the fundamental understanding of the chemical reaction mechanism underlying the photochromism.15–17 Detailed ab initio calculations of the reaction dynamics of diarylethenes were not reported.
In this article we present a comprehensive study of the photophysics of the diarylethene derivative CMTE. This includes the optical absorption spectra, perceived color, frequency dependent refractive index, and the reaction dynamics following photoexcitation. The latter gives us direct access to reaction timescales and quantum yields, which are typically difficult to access theoretically. We benchmark our results against higher-level quantum chemical methods and experiments. The convincing agreement we find highlights the potential of density-functional theory (DFT) based non-adiabatic ab initio molecular dynamics for the future design of more efficient photochromic compounds.
II. Methods
A. Experiment
For the absorption measurements CMTE (TCI, Japan) was dissolved in acetonitrile and stirred at room temperature for 24 h by weight percentage of 0.02 wt%, corresponding to a concentration of 0.0005 M. To minimize the solvent effect in determination of the refractive index, toluene was used with the same concentration. The measurements were performed using a quartz cuvette with a width of 1 cm. All data were normalized to a spectrum of the empty cuvette as a reference. The photochromic reaction was induced by continuous wavelength irradiation with Xe lamp light (150 W). Interference filters with central wavelengths of 546 nm and 405 nm and bandwidths of 10 nm were used. The setup for measurements of the extinction spectra consisted of a Xe light source, four off-axis parabolic mirrors, a grating monochromator (600 grooves per mm, blaze wavelength 400 nm), and a charge coupled device as a detector.
B. Theory
Geometry optimization and spectra.
The ground state structures of the two isomers were optimized using density-functional theory (DFT)18 with the PBE019,20 functional and the def2-SVP basis set.21 The structures found are stable minima as proven by vibrational frequency analysis. The excitation energies were calculated with time-dependent DFT (TDDFT)22 using the same functional and basis set. These were compared with calculations of excitation energies using the Tamm–Dancoff approximation (TDA)23 and simplified Tamm–Dancoff approximation (sTDA).24 To further assess the accuracy of TDDFT, TDA, and sTDA, respectively, excitation energies were also calculated using a wavefunction-based method. To this end, open and closed ring structures were optimized with CC225 using the resolution-of-the-identity implementation (RI-CC2)26–29 in Turbomole30 in combination with the def-TZVPP basis set31 and the corresponding auxiliary basis set. The vertical excitation energies were then calculated with RI-CC2 using the def2-TZVPPD basis set32 with the corresponding auxiliary basis set. All these calculations were done with Turbomole 6.5.30 Basis set convergence and influence of solvent on the electronic excitation spectra for the DFT calculations were checked with a larger basis set and the polarizable continuum model with acetonitrile as solvent using the Gaussian 09 software package33 and PBE0 functional. The deviations were found to be small, so the smaller basis set was used and no solvent was included in all production runs using Turbomole. Molecular structures were visualized using GaussView.34
Potential energy surfaces.
Potential energy surfaces were calculated using the Gaussian09 suite33 following the ideas of Masunov and co-workers.35,36 The def-SVP basis set was used with the PBE0 functional. To account for the diradical character near the transition state, the PES for the ground state was calculated using unrestricted DFT with broken symmetry guess, i.e., keyword guess = (mix, always) was used in Gaussian. The scan was performed varying the distance between the two reactive carbon atoms. The vertical excitation energies were then calculated with restricted TDDFT using TDA, starting from the structures of the relaxed ground state scan.
Non-adiabatic ab initio molecular dynamics.
The non-adiabatic ab initio molecular dynamics for the cycloreversion, i.e., ring opening reaction, was calculated along the lines given in ref. 37. The basis set and functional used were the same as for the static calculations, def2-SVP and PBE0, respectively. To generate a swarm of trajectories for the dynamical calculations with different initial conditions, the ground state of the rather rigid closed ring isomer was sampled using Born–Oppenheimer molecular dynamics. A timestep size of 50 a.u. was used and the ground state trajectory was calculated for a total of 4000 steps (∼4.84 ps). To ensure thermal equilibration, a Nosé–Hoover thermostat with a temperature of 300 K and a response time of 500 a.u. was used. Finally, 100 structures with corresponding nuclear velocities were randomly chosen to calculate the non-adiabatic ab initio molecular dynamics starting in the first excited singlet state based on Trajectory Surface Hopping.38 TDDFT in Tamm–Dancoff approximation was used with a timestep of 40 a.u. and a total of 1000 timesteps (corresponding to ∼0.97 ps). The initial conditions sampled from a canonical ensemble are then evolved in a microcanonical ensemble for the non-adiabatic dynamics – no thermostat was used. The implementation of the non-adiabatic dynamics calculations is based on linear response time-dependent density-functional theory.39 Further details are given in ref. 37 and 40. Only the non-adiabatic coupling between the first excited state and the ground state is included which can be easily justified here with the significant energy separation to higher-lying excited states as long as the system is found in the first excited state (cf.Fig. 7 and 8; Fig. S4 and S5, ESI†). Methodological problems using TDDFT in the vicinity of the conical intersection41 of ground and first excited states are alleviated using TDA.42 Finally, we note that in order to perform the calculations with the SMP-version of Turbomole 6.5, the parallelization described in ref. 43 needs to be used.
III. Results and Discussion
A. Spectra of open and closed ring forms
Absorption spectra of CMTE measured in solution of open and closed ring forms are shown in Fig. 1 and 2, respectively. Conversion between the two forms is achieved by illumination with light in the visible or the UV spectral range, respectively, cf.Scheme 1. We compare the measured spectra with spectra for the two forms computed with a number of different theoretical methods. For proper calculation of the spectrum of the open ring form, two stable conformers have to be considered.8 It is to be expected (very similar total energies are found for the two conformers) that the concentration for both conformers is about the same such that their contributions are equally weighted in the calculated spectra. This way, a convincing agreement with the measured data is obtained with the wavefunction based RI-CC2 calculations. We note that the corresponding values of the D1 diagnostics44 are sufficiently small (0.0658 and 0.0652 for the antiparallel and the parallel conformer, respectively) such that reliable results are obtained. We note that the spectra of antiparallel and parallel conformer individually do not agree as well with experiment as the averaged spectrum (cf. the sticks in Fig. 1 showing the contributions of both conformers separately and Fig. S1 and S2 of the ESI†). For the DFT-based calculations, we use the same approach. Inclusion of the two conformers still improves the overall result, however, in TDDFT the spectra are more similar for the two conformers such that the experimentally observed double-peak structure of the spectrum at shorter wavelength is not quite as well reproduced. The closed ring form of CMTE is rather rigid and only one stable ground state conformer exists. The spectra are shown in Fig. 2. Characteristic of the closed ring form of diarylethenes is the absorption at higher wavelength compared to the open ring form. This is found in all calculations and the excitation energies are in good agreement with the measurement. The high-energy peak found in experiment at approximately 350 nm is modeled less accurately. The D1 diagnostics here yields a value of 0.0948. Overall, we can conclude that the results of RI-CC2 and DFT-based methods are very similar for the closed ring form, but the (computationally much more expensive) wavefunction-based method yields a slightly improved absorption spectrum for the open ring form. This improvement is mostly found in the UV region, whereas the absorption in the visible region is rather similar.
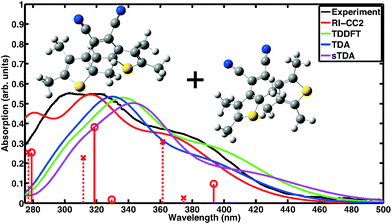 |
| | Fig. 1 Absorption spectrum of the open ring form of CMTE. The spectrum was measured in acetonitrile. Computed spectra are shown for different theoretical methods. These include both stable conformers in equal proportion. For RI-CC2 the transitions belonging to the antiparallel and parallel conformers are included as solid sticks with circles and dashed sticks with crosses, respectively. Due to the broken electronic conjugation of the inner ring in the open ring form, there is only negligible absorption in the visible range. Each spectrum is normalized to the corresponding maximum for the closed ring isomer in Fig. 2. | |
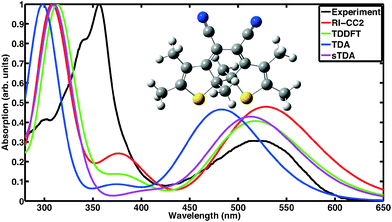 |
| | Fig. 2 Absorption spectrum of the closed ring form. Shown are the absorption measured in acetonitrile and theoretical data obtained with different methods. In contrast to the open ring form in Fig. 1, the lowest absorption feature lies here well within the visible range. Each spectrum is normalized to its maximum value. | |
B. Estimation of perceived color
A significant difference in the optical absorption of open and closed ring forms of CMTE in the visible spectral range is found above. This difference also determines the physiologically perceived difference in color of the two forms. To estimate the color from the optical absorption, this has to be translated into wavelength-dependent transmission or reflectance. To this end, we normalize the calculated absorption, α(λ), in the interval 380–780 nm. As successfully used in previous work,45 from this the “inverse spectrum” can be calculated as a measure of the reflectance following the idea of Beck:46Now normalized values for the CIE Tristimulus values can be calculated as:47| | 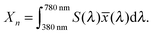 | (2) |
In this equation S(λ) is the spectral power distribution of the illuminant. To simulate daylight conditions, the D65 standard illuminant is used. ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (λ) is one of the three color matching functions (CMF) for which the CIE 1931 standard is used. Analogous equations are defined for Yn and Zn with the corresponding CMF, ỹ and
(λ) is one of the three color matching functions (CMF) for which the CIE 1931 standard is used. Analogous equations are defined for Yn and Zn with the corresponding CMF, ỹ and ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) . Data for these quantities are for example tabulated online48 and can be found in ref. 47. The tristimulus values are now obtained as:
. Data for these quantities are for example tabulated online48 and can be found in ref. 47. The tristimulus values are now obtained as:| | 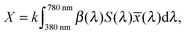 | (3) |
with k = 100/Yn. The other two values, Y and Z, are calculated analogously. If needed, the tristimulus values obtained can be transformed into other color spaces, e.g., chromaticity coordinates or CIE (L*a*b*)-space (cf. Table S1 of the ESI†). For the latter, the following equations can be used as long as 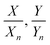 , and
, and 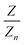 are larger than 0.01:47
are larger than 0.01:47| | 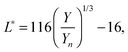 | (4) |
| | 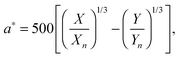 | (5) |
| | 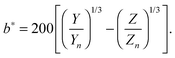 | (6) |
The colors that we determined as described above are shown in Fig. 3 for experiment and the different theoretical methods used. Pictures of CMTE in solution in open and closed ring form are shown in Fig. 4. The difference in color compared to the colors estimated in Fig. 3 is partly due to the different ambient illumination under laboratory conditions. We note that according to the ΔE-values given in the ESI,† for the open ring form CC2 yields the best results and for the closed ring form sTDA and TDDFT. This is consistent with the absorption spectra of open and closed ring form in the visible range.
 |
| | Fig. 3 Perceived colors of open and closed ring isomers as determined from the absorption spectra under daylight conditions. Colors are obtained from experiment and the different theoretical methods used. | |
 |
| | Fig. 4 Pictures of CMTE in solution in open (left) and closed (right) ring forms. The difference in color perception compared with Fig. 3 is partly due to the different ambient light laboratory conditions under which the pictures were taken. | |
C. Dielectric function and refractive index
The absorption spectra discussed thus far (Fig. 1 and 2) only contain direct information about the imaginary part of the molecules' dielectric response. However, a thorough analysis of the optical properties and changes thereof in the different forms of the photochromic molecules should also include the dispersive part of the dielectric function. For the system under study, the spectral range of interest is in the visible region, where the biggest change of optical properties is found with the photochromic conversion process. As this spectral range contains resonances related to electronic excitations, care has to be taken in constructing the dielectric response. The resonant contribution to the dielectric response can be given as:| | 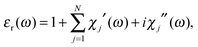 | (7) |
with the real and imaginary parts:| | 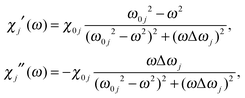 | (8) |
of the dielectric response. From the measured extinction data, we determine the absorption coefficient taking into account the cuvette thickness and the molecular concentration used. Then we fit the absorption data using a Lorentz oscillator model for εr(ω) with multiple oscillators:| | 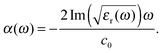 | (9) |
Using the resulting fitting parameters (widths, amplitudes, and spectral position) of each Lorentzian the resonant contribution to the (real) refractive index Δn(ω) is computed:| | 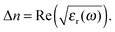 | (10) |
For the open form, good agreement between the fit and the experimental data was obtained using four model oscillators. For the closed form of the molecule, five oscillators were required. From the theoretical side, the resonant part of the dielectric function can be constructed directly based on eqn (8) using the computed oscillator strengths χ0j and resonance energies ω0j. Here, all the computed 20 transitions are included with a common broadening to reproduce the experimental absorption spectrum. A common prefactor was included to obtain the correct absolute values for the concentration used in the experiment. In addition to the resonant contribution discussed above, the refractive index also contains a contribution from the static polarizability of the system, both from the solvent and from the molecules of interest. In a first approximation, here we add a constant offset to the dielectric function such that n(ω → 0) ≈ 1.54 for the closed ring form is obtained, which is in good agreement with previous work.49 Results are shown in Fig. 5. A significant change of the refractive index is found in the visible spectral range upon photo-induced isomerization between open and closed ring forms. Comparing the experimental data with the computed results, the main difference lies in the slight offset for the open ring form. We note that this is consistent with the difference in the absorption spectra in the UV spectral range comparing experiment and theory in Fig. 1. In a more sophisticated approach, computed data can also be used for the static part of the dielectric function using the Lorentz–Lorenz equation| | 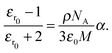 | (11) |
Here, εr0 denotes the static relative electric permittivity. On the right-hand side, ρ is the density of the substance, NA Avogadro's number, ε0 the vacuum permittivity, and M the molar mass. To be applicable to molecules in a solvent, also the solvent contribution has to be taken into account and the Lorentz–Lorenz equation for a two-component system has to be used.50 In the ESI,† we have tabulated our computed values for the diarylethenes' contribution to the static polarizability α and give a brief discussion of the accuracy of different quantum chemical methods for obtaining this quantity.
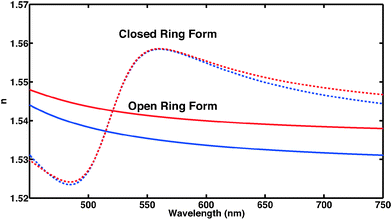 |
| | Fig. 5 Frequency-dependent refractive index of CMTE in the visible spectral range. Clearly visible is the significant difference of open and closed ring form in the spectral range shown both for experiment (blue) and theory (red). | |
D. Reaction mechanism and non-adiabatic ab initio molecular dynamics
Apart from the molecular equilibrium properties discussed above, insight on an entirely different level can be obtained from an investigation of the actual reaction mechanism leading to photochromic conversion upon light irradiation. In addition to the equilibrium properties, important quantities that characterize the reaction are for example the reaction quantum yield and reaction timescales. Both are typically difficult to access, experimentally and theoretically.
Here we focus on a detailed analysis of the cycloreversion reaction, leading from the closed ring form to the open ring form. A qualitative feeling for the reaction can be obtained from the potential energy surfaces along a reactive coordinate, i.e., the inter-atomic distance of the two reactive carbon atoms of the central conjugated ring of CMTE. The computed result is shown in Fig. 6 and the different reaction pathways after illumination of the closed-ring form with visible light are indicated. After vertical excitation into the first excited state S1, the system arrives in a pronounced minimum in energy on the S1 surface. In order for the cycloreversion reaction to occur, the system now has to reach the conical intersection between S0 and S1 at about 2.1 Å. For this, the potential energy barrier of about 0.8 eV has to be overcome. Otherwise, the molecule relaxes back to the former ground state through a different non-radiative relaxation channel (in experiment also radiative decay can occur), preventing a successful cycloreversion. We note that for methodological reasons (cf. Methods section above), the data in Fig. 6 in the vicinity of the conical intersection (grey-shaded area) have to be treated with care.
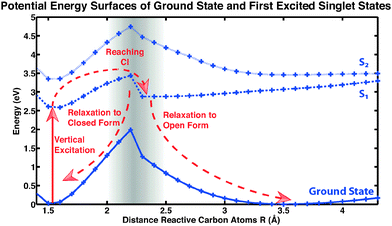 |
| | Fig. 6 Potential energy surfaces of CMTE. Shown are ground state and excited states S1 (dashed) and S2 (dotted). The lines are included as a guide to the eye. For a successful cycloreversion after vertical excitation (photoexcitation) a potential barrier has to be overcome in the S1 state to reach the conical intersection (CI). For more details see discussion in the text. | |
In the following we present a detailed analysis of the cycloreversion reaction based on non-adiabatic ab initio molecular dynamics calculations. We note that in contrast to the largely simplified one-dimensional picture of the potential energy surface in Fig. 6, which gives only a rough picture of the expected reaction, in these calculations the reaction takes place on the very complex and high-dimensional potential energy surface including all the dynamical degrees of freedom. We have computed 100 trajectories starting from slightly different initial conditions in the S1 state (see details in the Methods section above). The trajectories we find can be grouped into four different categories.
The first category consists of eleven trajectories that underwent a successful cycloreversion. A representative example of such a trajectory is shown in Fig. 7. The minimum in the first excitation energy from the ground state is found in each trajectory at a distance between the two reactive carbon atoms at about 2 Å. This is consistent with the PES shown in Fig. 6. This minimum was reached in the calculations within 150–500 fs, followed by successful ring opening.
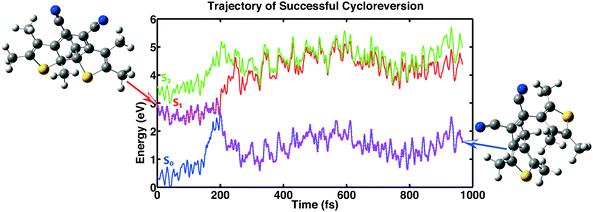 |
| | Fig. 7 Example showing a successful cycloreversion reaction. The trajectory shown is representative of 11 of the computed 100 trajectories. | |
Ten trajectories belong to the second category. These reached the conical intersection at about 2 Å but subsequently relaxed back to the closed ring form in the ground state (see Fig. S4 of the ESI†). The time needed to reach the conical intersection in these cases is about the same as in the first category. The distance for the minimum energy of the first excitation tends to be about 0.03 Å lower than in the first category. The minimum of the first excitation energy we find is about 0.2 eV or smaller.
The third category consists of 26 trajectories. For these the system “hopped” back into the ground state even though the conical intersection was still far away. This process is mediated by vibronic coupling.40 Analyzing the data of these trajectories it is found that apart from one exception, the minimal value of the first excitation energy is bigger than 0.8 eV. The distance between the reactive carbon atoms does not exceed 1.87 Å for all trajectories except the trajectory with an energy separation lower than 0.8 eV. So for this category, the trajectories seem to be trapped in a minimum of the first excited state that prevents the molecules from reaching the conical intersection and consequently does not lead to ring opening. In Fig. 8 we show one of the trajectories of this third category as an example of the reaction dynamics.
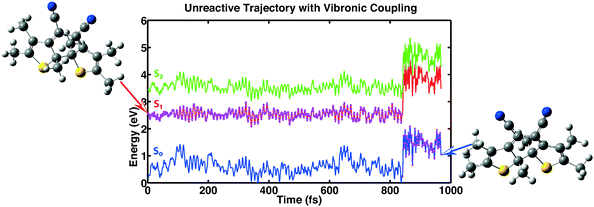 |
| | Fig. 8 Example showing one out of 26 trajectories for which the molecule relaxed back into the ground state without actually reaching the conical intersection. This process is mediated by vibronic coupling. | |
Finally, the fourth category consists of 53 trajectories that did not reach the ground state within the time of simulation (see Fig. S5 of the ESI†). Only seven trajectories reach a distance between the reactive carbon atoms of 1.9 Å or larger, and the minimum in the first excitation energy is bigger than 0.5 eV. So it is to be expected that these trajectories do not reach the conical intersection but are trapped in a minimum of the first excited state similar to the third category. Continuation of these trajectories for another 2000 time steps in the dynamics led to 24 trajectories that jumped back into the ground state, but none of these underwent successful cycloreversion.
Videos showing the computed time-evolution of the molecular geometries for the four types of different trajectories discussed are available online in the ESI.†
After analysis of all the data, it appears to be plausible to assume that the trajectories of the third and fourth category will not undergo successful cycloreversion. So the quantum yield for cycloreversion we determine by our simulations is 0.11. This is in good agreement with previous values found experimentally, i.e. 0.07 ± 0.02 and 0.12 ± 0.02 respectively.8
We note that in contrast to the non-adiabatic ab initio molecular dynamics of the cycloreversion, for the dynamics of the cyclization process, more than just the first excited singlet state may have to be included. In the spectrum of the open form, Fig. 1, it is clearly visible that the lowest excitation energy is only a shoulder on a higher-lying excitation. Therefore, irradiation with UV light will result in population of multiple excited singlet states. However, in the current implementation of the trajectory surface hopping in Turbomole as employed here, analytic non-adiabatic coupling (NAC) vectors are only available between the ground and the first excited state. The calculation of analytic NAC-vectors between excited states has already been described theoretically51 and an extension of the present approach to also include these is to be expected in the future. We further note that Newton-X52 interfaced with Turbomole already offers the possibility to calculate non-adiabatic dynamics on any excited state using TDDFT. However, to the best of our knowledge the combination with TDA we used here to improve the description of the potential energy surfaces of ground and first excited singlet states near the conical intersection53 is currently not supported. We further note that in our calculations each single trajectory requires 1000 ground state DFT calculations with subsequent calculation of excitation energies using TDA. To reduce computational cost in future studies of larger systems usage of sTDA instead of TDA may also be a viable option.
IV. Conclusion
We have investigated different facets of the photochromic diarylethene derivative CMTE. We have shown that optical absorption related to electronic excitations, perceived color, frequency dependent refractive index, and reaction quantum yields and time scales can be successfully computed (and predicted) using density-functional theory based quantum-chemical approaches. The computed results compare well with experimental data. For example, from our non-adiabatic ab initio molecular dynamics calculations, we confirm that the cycloreversion quantum yield of CMTE is about 11%. For the future it would be worthwhile to build upon these first results and theoretically study the influence of different substituents to improve on the quantum yield without the need to actually synthesize all the molecules studied. Furthermore, with its proven photochromic capabilities also in solid films, CMTE would be a promising compound to be used in future solid-state/molecular hybrid structures utilizing the light-induced change in the molecular material's dielectric response for optical applications.11
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
We are grateful for fruitful discussions with Prof. Martin J. Paterson, Heriot-Watt University, Edinburgh, UK. We acknowledge financial support from the DFG (GRK 1464) and a grant for computing time at PC2 Paderborn Center for Parallel Computing. C.W. is grateful for his PhD-scholarship from the Friedrich-Ebert-Stiftung. We thank the Turbomole Support team for providing helpful information on the implementation of the TSH-algorithm.
References
- A. Bianco, S. Perissinotto, M. Garbugli, G. Lanzani and C. Bertarelli, Laser Photonics Rev., 2011, 5, 711–736 CrossRef CAS.
- D. Nau, R. P. Bertram, K. Buse, T. Zentgraf, J. Kuhl, S. G. Tikhodeev, N. A. Gippius and H. Giessen, Appl. Phys. B: Lasers Opt., 2006, 82, 543–547 CrossRef CAS.
-
Photochromism, ed. G. H. Brown, John Wiley & Sons, 1971, vol. III Search PubMed.
-
Photochromism: Molecules and Systems, ed. H. Dürr and H. Bouas-Laurent, Elsevier, 2003 Search PubMed.
-
New Frontiers in Photochromism, ed. M. Irie, Y. Yokoyama and T. Seki, Springer, Japan, 2013 Search PubMed.
- M. Irie, Proc. Jpn. Acad., Ser. B, 2010, 86, 472–483 CrossRef CAS PubMed.
- M. Irie, Chem. Rev., 2000, 100, 1685–1716 CrossRef CAS PubMed.
- A. Spangenberg, J. A. P. Perez, A. Patra, J. Piard, A. Brosseau, R. Métivier and K. Nakatani, Photochem. Photobiol. Sci., 2010, 9, 188–193 CAS.
- H. Jean-Ruel, R. R. Cooney, M. Gao, C. Lu, M. A. Kochman, C. A. Morrison and R. J. D. Miller, J. Phys. Chem. A, 2011, 115, 13158–13168 CrossRef CAS PubMed.
- S. Kobatake, H. Hasegawa and K. Miyamura, Cryst. Growth Des., 2011, 11, 1223–1229 CAS.
- K. A. Piegdon, M. Lexow, G. Grundmeier, H.-S. Kitzerow, K. Pärschke, D. Mergel, D. Reuter, A. D. Wieck and C. Meier, Opt. Express, 2012, 20, 6060–6067 CrossRef CAS PubMed.
- Y. Tatsumi, J. Kita, W. Uchida, K. Ogata, S. Nakamura and K. Uchida, J. Phys. Chem. A, 2012, 116, 10973–10979 CrossRef CAS PubMed.
- Y. Ishibashi, T. Umesato, S. Kobatake, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2012, 116, 4862–4869 CAS.
- H. Jean-Ruel, M. Gao, M. A. Kochman, C. Lu, L. C. Liu, R. R. Cooney, C. A. Morrison and R. J. D. Miller, J. Phys. Chem. B, 2013, 117, 15894–15902 CrossRef CAS PubMed.
- M. Boggio-Pasqua, M. Ravaglia, M. J. Bearpark, M. Garavelli and M. A. Robb, J. Phys. Chem. A, 2003, 107, 11139–11152 CrossRef CAS.
- S. Nakamura, K. Uchida and M. Hatakeyama, Molecules, 2013, 18, 5091–5103 CrossRef CAS PubMed.
- A. Perrier, S. Aloïse, M. Olivucci and D. Jacquemin, J. Phys. Chem. Lett., 2013, 4, 2190–2196 CrossRef CAS.
- M. Häser and R. Ahlrichs, J. Comput. Chem., 1989, 10, 104–111 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2013, 138, 244104 CrossRef PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951 CrossRef.
- C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef.
- C. Hättig, A. Hellweg and A. Köhn, Phys. Chem. Chem. Phys., 2006, 8, 1159–1169 RSC.
-
TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available fromhttp://www.turbomole.com.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
-
R. Dennington, T. Keith and J. Millam, GaussView Version 5.0.9, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
-
I. Mikhailov and A. E. Masunov, Theoretical Photochemistry of the Photochromic Molecules Based on Density Functional Theory Methodsin Computational Science – ICCS 2009, ed. G. Allen, J. Nabrzyski, E. Seidel, G. D. van Albada, J. Dongarra and P. M. A. Sloot, Springer-Verlag, Berlin, Heidelberg, 2009, vol. 5545, pp. 169–178 Search PubMed.
- P. D. Patel and A. E. Masunov, J. Phys. Chem. C, 2011, 115, 10292–10297 CAS.
- E. Tapavicza, A. M. Meyer and F. Furche, Phys. Chem. Chem. Phys., 2011, 13, 20986–20998 RSC.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- E. Tapavicza, I. Tavernelli and U. Röthlisberger, Phys. Rev. Lett., 2007, 98, 023001 CrossRef PubMed.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348 RSC.
- B. G. Levine, C. Ko, J. Quenneville and T. J. Martnez, Mol. Phys., 2006, 104, 1039–1051 CrossRef CAS.
- E. Tapavicza, I. Tavernelli, U. Röthlisberger, C. Filippi and M. E. Casida, J. Chem. Phys., 2008, 129, 124108 CrossRef PubMed.
- C. Van Wüllen, J. Comput. Chem., 2011, 32, 1195–1201 CrossRef PubMed.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- M. E. Beck, Int. J. Quantum Chem., 2005, 101, 683–689 CrossRef CAS.
-
G. Wyszecki and W. S. Stiles, Color Science: Concepts and Methods, Quantitative Data and Formulae, John Wiley & Sons, 2000 Search PubMed.
-
www.cie.co.at
.
- A. Spangenberg, R. Métivier, R. Yasukuni, K. Shibata, A. Brosseau, J. Grand, J. Aubard, P. Yu, T. Asahi and K. Nakatani, Phys. Chem. Chem. Phys., 2013, 15, 9670–9678 RSC.
- G. Callierotti, A. Bianco, C. Castiglioni, C. Bertarelli and G. Zerbi, J. Phys. Chem. A, 2008, 112, 7473–7480 CrossRef CAS PubMed.
- I. Tavernelli, B. F. E. Curchod, A. Laktionov and U. Röthlisberger, J. Chem. Phys., 2010, 133, 194104 CrossRef PubMed.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, WIREs: Comput. Mol. Sci., 2014, 4, 26–33 CrossRef CAS.
- S. L. Li, A. V. Marenich, X. Xu and D. G. Truhlar, J. Phys. Chem. Lett., 2014, 5, 322–328 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated spectra of the parallel and antiparallel conformers of the open ring form and of the closed ring form, tabulated values for the determination of color, tabulated values for static polarizability, trajectories of categories 2 and 4, and videos of the molecular dynamics. DOI: 10.1039/c3cp55490b |
|
| This journal is © the Owner Societies 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

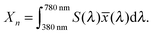
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) (λ) is one of the three color matching functions (CMF) for which the CIE 1931 standard is used. Analogous equations are defined for Yn and Zn with the corresponding CMF, ỹ and
(λ) is one of the three color matching functions (CMF) for which the CIE 1931 standard is used. Analogous equations are defined for Yn and Zn with the corresponding CMF, ỹ and ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) . Data for these quantities are for example tabulated online48 and can be found in ref. 47. The tristimulus values are now obtained as:
. Data for these quantities are for example tabulated online48 and can be found in ref. 47. The tristimulus values are now obtained as: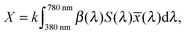
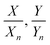 , and
, and 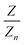 are larger than 0.01:47
are larger than 0.01:47