 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revisiting the density scaling of the non-interacting kinetic energy
Alex
Borgoo
*a,
Andrew M.
Teale
*ab and
David J.
Tozer
c
aDepartment of Chemistry, Centre for Theoretical and Computational Chemistry, University of Oslo, P.O. Box 1033, Blindern, Oslo N-0315, Norway. E-mail: ajborgoo@gmail.com; andrew.teale@nottingham.ac.uk
bSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
First published on 21st March 2014
Abstract
Scaling relations play an important role in the understanding and development of approximate functionals in density functional theory. Recently, a number of these relationships have been redefined in terms of the Kohn–Sham orbitals [Calderín, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 86, 032510]. For density scaling the author proposed a procedure involving a multiplicative scaling of the Kohn–Sham orbitals whilst keeping their occupation numbers fixed. In the present work, the differences between this scaling with fixed occupation numbers and that of previous studies, where the particle number change implied by the scaling was accommodated through the use of the grand canonical ensemble, are examined. We introduce the terms orbital and ensemble density scaling for these approaches, respectively. The natural ambiguity of the density scaling of the non-interacting kinetic energy functional is examined and the ancillary definitions implicit in each approach are highlighted and compared. As a consequence of these differences, Calderín recovered a homogeneity of degree 1 for the non-interacting kinetic energy functional under orbital scaling, contrasting recent work by the present authors [J. Chem. Phys., 2012, 136, 034101] where the functional was found to be inhomogeneous under ensemble density scaling. Furthermore, we show that the orbital scaling result follows directly from the linearity and the single-particle nature of the kinetic energy operator. The inhomogeneity of the non-interacting kinetic energy functional under ensemble density scaling can be quantified by defining an effective homogeneity. This quantity is shown to recover the homogeneity values for important approximate forms that are exact for limiting cases such as the uniform electron gas and one-electron systems. We argue that the ensemble density scaling provides more insight into the development of new functional forms.
1 Introduction and background
In density functional theory (DFT), significant insight has been gained by studying the behaviour of functionals using scaling procedures. The derived properties have played a key role as exact conditions in the development of new approximations, which are now commonly used in the Kohn–Sham (KS) scheme. Recently, Calderín has suggested that many of these scaling relations can be unified by considering the scaling of quantities entering the Kohn–Sham equations.1 However, for the case of scalings which do not preserve the particle number, the generalization proposed in ref. 1 is different from those used in earlier studies.2–7In the present article we compare and contrast these different definitions and, in particular, their implications for the behaviour of the non-interacting kinetic energy functional of central importance in DFT. In the remainder of this section we briefly review the commonly used scaling relations and their unification in terms of Kohn–Sham orbital scalings as put forth in ref. 1. We compare this with previously used interpretations and discuss the concept of homogeneity. In Section 2 we focus on the implications of each approach for examining the properties of their associated non-interacting kinetic energy functionals. Finally, in Section 3 we make some concluding remarks.
1.1 Scaling relations
The most commonly used scaling is uniform coordinate scaling| ρη(r) = η3ρ(ηr), | (1) |
| ∫ρη(r)dr = ∫ρ(r)dr = N, | (2) |
A number of alternative scaling relations that do change the normalization of the electronic density, have been proposed. Liu and Parr introduced the concept of density scaling,2,3
| ργ(r) = γρ(r), | (3) |
| ρζ(r) = ζ2ρ(ζ1/3r). | (4) |
This scaling has been utilized to understand the behaviour of density-functional approximations in the nuclear charge Z → ∞ limit.
1.2 Homogeneity of density functionals
The concept of homogeneity has turned out to be a useful concept in the context of scaling procedures.3 A functional, X[ρ], is said to be homogenous of degree m in coordinate scaling if it satisfies the relationship| X[ρη] = ηmX[ρ], | (5) |
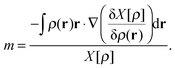 | (6) |
Similarly, a functional is said to be homogenous of degree k in density scaling if it satisfies the relationship
| X[ργ] = γkX[ρ], | (7) |
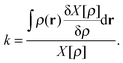 | (8) |
For local density functionals such as the Dirac exchange functional or the Thomas–Fermi kinetic energy functional the notions of density and coordinate scaling are connected via the homogeneity.4 If a local functional is homogeneous of degree m under coordinate scaling then it is also homogenous of degree k = (m + 3)/3 under density scaling. However, beyond these purely local functionals this relation breaks down, meaning that a functional may be homogeneous under one type of scaling and not the other. Therefore, at the generalized gradient approximation level and beyond, density scaling relations can offer useful additional constraints in the development of practical approximations. For a recent example utilizing this information for developing approximate non-interacting kinetic energy density functionals see ref. 11. Recently, Laricchia et al. have also assessed new functionals using scaling relations.12 Finally, we note that for local and semi-local density-functional approximations the functional derivatives in eqn (6) and (8) are well defined. However, this may not be the case for the exact quantities. We discuss this issue in more detail for the non-interacting kinetic energy functional in Section 2.2.
1.3 Kohn–Sham orbital based scaling relations
Recently, the scaling relations in eqn (1), (3) and (4) were generalised,1 and expressed in terms of scaled KS orbitals (see eqn (7) in ref. 1.),| φ(i)γηmp(r) = γm/2φi(ηpr), | (9) |
As a case in point consider, for example, that in ref. 1 the Kohn–Sham orbitals were scaled whilst keeping the orbital occupation numbers fixed. Alternatively, in ref. 6 we considered expressions based on the ensemble Kohn–Sham approach, in which the occupation numbers change to accommodate the density scaling. Both of these definitions go beyond the scope of the original definition in eqn (3), which was defined without further reference to the Kohn–Sham system. To distinguish the approaches we will refer to eqn (3) as density scaling, eqn (9) as orbital scaling and the scaling of ref. 6 based on the ensemble Kohn–Sham approach as ensemble density scaling.
The functionals within each approach are intrinsically different. This is clear if one considers their domains; in the ensemble approach the domains of the non-interacting kinetic energy and exchange–correlation functionals are the ensemble-v-representable densities, whereas in the orbital scaling approach the domain of the associated functionals is that of densities which can be associated with the ground state of a renormalized pure state Kohn–Sham system.
2 Non-interacting kinetic energy
The non-interacting kinetic energy functional plays a key role in KS-DFT where it is expressed as an implicit functional of the density via the Kohn–Sham orbitals. It is also of key importance for orbital-free density-functional methods where explicit density-functional approximations for this quantity are required. The properties of this functional have, however, proved controversial in the literature.In their initial work Liu and Parr3 concluded that the non-interacting kinetic energy Ts[ρ], as a functional of the density, is homogeneous of degree k = 1 under density scaling. However, later the proof was shown not to hold.13 Chan and Handy7 also showed that a functional, homogeneous of degree k = 1 under density scaling, does not satisfy the Lieb–Thirring bound14 and they further established that Ts[ρ] is inhomogeneous under density scaling, i.e. there does not exist a unique k that satisfies eqn (8). The authors anticipated this result by highlighting that although the scaling procedure is defined by a simple scaling relation, the relation that maps the eigenstates to the density is highly non-linear. Another strong indication of the inhomogeneity of Ts[ρ] is given by the Thomas–Fermi and von Weizsäcker functionals. Both are exact for certain limits15,16 and both satisfy eqn (7) for different values of k: 5/3 for the former and 1 for the latter.
Recently, the debate over the homogeneity of a non-interacting kinetic energy functional has been re-opened with a new orbital scaling based derivation, leading to the conclusion that the functional is homogeneous of degree 1 in density scaling.1 This conclusion is in sharp contrast to our own work in the context of ensemble density scaling,6 which leads to the conclusion that the non-interacting kinetic energy functional is inhomogenous. We now consider how these two approaches lead to such different conclusions.
2.1 Orbital scaling
First we consider the homogeneity properties under orbital scaling with constrained orbital occupation numbers as envisaged in ref. 1. The scaling in eqn (9) for p = 0 and m = 0| φ(i)γ(r) = γ1/2φi(r), | (10) |
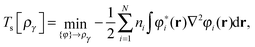 | (11) |
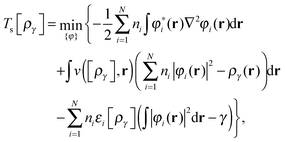 | (12) |
In ref. 1 it was observed that scaling the orbitals in eqn (12) yields
| Ts[ργ] = γTs[ρ], | (13) |
Alternatively the same result (k = 1) can be understood by evaluating the right-hand side of eqn (11) at the minimising orbitals. Then
Ts[ρ] = 〈Φ|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ〉, |Φ〉, | (14) |
Ts[ργ] = 〈Φγ|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φγ〉 = γ〈Φ| |Φγ〉 = γ〈Φ|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ〉 = γTs[ρ], |Φ〉 = γTs[ρ], | (15) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the kinetic energy operator and where we have used the fact that this is a linear one-electron operator. To the best of our knowledge the orbital scaling with constrained occupation number is unlike the procedure originally envisaged by Liu and Parr.
is the kinetic energy operator and where we have used the fact that this is a linear one-electron operator. To the best of our knowledge the orbital scaling with constrained occupation number is unlike the procedure originally envisaged by Liu and Parr.
While the scaling in eqn (10) is interesting in its own way, we have to bear in mind that the constraint on the orbital occupation numbers goes beyond the original density scaling and that it requires the generalised definition of the non-interacting kinetic energy eqn (12). It is worth pointing out that although eqn (12) affects the Levy–Lieb (LL) definition only at densities when γ ≠ 1, where the LL functional assumes the value +∞, it has not been shown that the generalisation procedure itself (the introduction of Lagrangian multipliers) does not affect the homogeneity.
2.2 Ensemble density scaling
Now we turn our attention to the homogeneity of Ts[ρ] under the ensemble density scaling of ref. 6 (where we do not constrain the occupation numbers). This procedure remains within the usual LL definition of the non-interacting kinetic energy. To evaluate the functional derivative in eqn (8) at integer particle numbers we consider the grand canonical ensemble picture.17 This is the most natural way to include the change in the particle number implied by the changing normalisation under density scaling. Similar to Chan and Handy,7 we consider the definition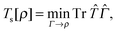 | (16) |
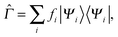 | (17) |
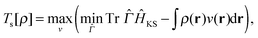 | (18) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the non-interacting effective Kohn–Sham Hamiltonian with
is the non-interacting effective Kohn–Sham Hamiltonian with ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and
and 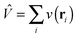 are the kinetic and potential energy operators forming the non-interacting Hamiltonian with external potential v(r), respectively. At the maximising potential vs(r) this becomes
are the kinetic and potential energy operators forming the non-interacting Hamiltonian with external potential v(r), respectively. At the maximising potential vs(r) this becomes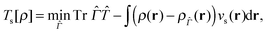 | (19) |
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) (r) is the density of the density matrix
(r) is the density of the density matrix ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) and ρ(r) the input density, at which the functional is evaluated. The minimising density matrix
and ρ(r) the input density, at which the functional is evaluated. The minimising density matrix ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) 0 yields the KS orbitals and the input density, corresponding to the effective potential vs(r).
0 yields the KS orbitals and the input density, corresponding to the effective potential vs(r).
We note that for a fractional number of electrons between the integer particle numbers N and N + 1 the non-interacting kinetic energy may be expressed in terms of the resulting one-electron KS orbitals and occupation numbers. See, for example, ref. 19 and 20 for further discussion and examples of practical calculations that utilize this mapping in the context of unrestricted KS theory.
At integer particle numbers the ensemble reduces to a pure state and the optimisation problem in eqn (19) can be solved by using the Wu–Yang approach.21 The KS orbitals and energies obtained from this procedure can then be used to evaluate Ts[ρ] and its functional derivative using the King–Handy expression22
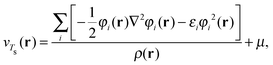 | (20) |
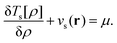 | (21) |
Note that the King–Handy expression does not require further generalization to account for fractional occupations when employed at the integer. However, the ensemble density-functional context of the approach becomes relevant when one considers the possible values for μ. The literature on the choice of μ is abundant, the consensus however is (and has now been for many years) to relate it to the chemical potential.15,17,23,24 With superscripts added to indicate the electron deficient and electron abundant side of the integer, this means μ− = −I and μ+ = −A, respectively.17 These limiting values arise naturally from the fact that the ensemble ground state energy is piecewise linear as a function of the number of electrons.17
There does however remain a further subtle issue; the identification of the function vTs(r) using the functional derivative of the non-interacting kinetic energy relies on the Euler equation, which assumes the differentiability of Ts[ρ] as defined by eqn (19). This functional is equivalent to the Lieb functional, FL, at zero electronic interaction strength.16 Lammert has shown25 that unfortunately it is certainly not differentiable in the normal Gâteaux sense and its convexity and lower semi-continuity are not sufficient to ensure this property. The possibility that the functional behaved well on dom FL does however remain open. Very recently Kvaal et al. have presented a solution to this long standing issue using the Moreau envelope,26 a concept from the convex analysis. Within this framework differentiability is restored for a regularized functional for a finite but arbitrarily small regularization parameter, for further detailed discussion see ref. 26.
Here we have followed the arguments of King and Handy22 in identifying the function of eqn (20) using the functional derivative of Ts, this may be valid only in some (as yet to be determined) restricted sense – however, a Moreau-Yosida regularized version of this functional can be defined as prescribed in ref. 26 and its derivative coincides with the function of eqn (20) for all practical purposes as the regularization parameter is taken to be very small. Furthermore, even in the absence of regularization, we have verified numerically for standard density-functional approximations that when the function in the first term of eqn (20) is evaluated it has the same shape as −vs, which would be expected based on the Euler eqn (21). Throughout this work we have therefore made the usual assumption that this function can be identified using the functional derivative, and it is justified to write an Euler equation as given in eqn (21).
Since the value of μ (and similarly the function vTs(r)) is not uniquely defined at integer numbers of particles we must consider how this affects our definition of the homogeneity of a functional. On the electron deficient side of the integer we define the effective homogeneity under density scaling as
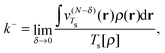 | (22) |
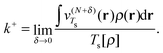 | (23) |
From a functional development perspective it is interesting to consider the average 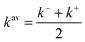 because whilst the exact functional is not differentiable at the integer commonly utilized approximations are, and so it has been argued that an averaging quantity may be the most appropriate reference.6,11 For a recent assessment of how well similar averaging effects hold for an approximate exchange–correlation functional see ref. 19, 20 and 27.
because whilst the exact functional is not differentiable at the integer commonly utilized approximations are, and so it has been argued that an averaging quantity may be the most appropriate reference.6,11 For a recent assessment of how well similar averaging effects hold for an approximate exchange–correlation functional see ref. 19, 20 and 27.
In Fig. 1 we present the effective homogeneities under density scaling for a range of atomic systems, calculated in ref. 6. The quantities k− (red), k+ (black), and kav (blue) are plotted for systems with increasing Z. For the H atom (Z = 1) the three effective homogeneities coincide and all yield a value of 1. This is consistent with the homogeneity of the von Weizsäcker functional,28 which yields the exact non-interacting kinetic energy for one orbital systems. For Z = 2 the effective homogeneity k− remains at 1; however, the value of k+ is substantially higher as a result of the change from μ− to μ+ in the associated definition of vTs. Interestingly, the value of kav is substantially closer to, but below, 5/3.
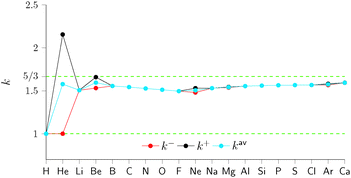 | ||
| Fig. 1 Effective homogeneities under the ensemble density scaling, for atoms in the first two rows in the periodic table and Ca. The results for open-shell atoms are based on the data in ref. 29. To highlight the exact asymptotic values, minor changes have been made to the figure previously published in ref. 6. | ||
As Z increases we see that the differences between the effective homogeneities k−, k+ and kav decrease markedly for the closed shell systems (compare He, Be, Ne, Mg, Ar and Ca). In addition, the values appear to approach 5/3. This value is significant because in the high Z limit the zeroth order term in the gradient expansion (the Thomas–Fermi functional) becomes exact.15 The homogeneity of the Thomas–Fermi functional is 5/3 and the trend towards this value is clearly shown in Fig. 1. The effective homogeneities therefore appear to be a useful quantity for examining the properties of the non-interacting kinetic energy functional. In particular the limiting case Z = 1 where k = 1 and the approach to the asymptotic limit Z → ∞ where k = 5/3 are well captured.
The results indicate that no unique value of k can be obtained, consistent with the inhomogeneity of the non-interacting kinetic energy functional. However, for an approximation consistent with an exactly averaging vTs the values of kav are remarkably consistent, being close to but just below the limiting value of 5/3 for Z > 1. Recently, we have exploited this observation11 in the development of new GGA functionals for Ts[ρ].
2.3 Comparing orbital and ensemble density scaling
We interpret the density scaling of eqn (3) as applied to the physical density of this system, a choice must then be made as to how to map this density to an appropriate non-interacting system. In the ensemble approach, the associated non-interacting density is then composed of completely filled KS orbitals except for a, possibly degenerate, highest occupied molecular orbital with fractional occupation numbers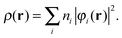 | (24) |
Each orbital is normalized in the conventional manner such that ∫|φi|2dr = 1. Given these constraints on the occupation numbers in the ensemble approach, extra orbitals are introduced into the summation in eqn (24) to accommodate the overall particle number change and their occupation numbers may be mapped directly to the ensemble weights in eqn (17).
The orbital scaling approach of ref. 1 can be understood as choosing a different mapping from the physical to non-interacting KS density. In that case the occupation numbers are fixed to values of 1 but the orbitals are scaled by a factor of 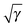 allowing their normalization to change to ∫|φi|2dr = γ. This leads to the required change in the normalization of the electronic density, whilst remaining within a pure-state framework. The resulting non-interacting density expression is then the same as would be achieved by naive application of eqn (3) to the standard pure-state KS-DFT expression.
allowing their normalization to change to ∫|φi|2dr = γ. This leads to the required change in the normalization of the electronic density, whilst remaining within a pure-state framework. The resulting non-interacting density expression is then the same as would be achieved by naive application of eqn (3) to the standard pure-state KS-DFT expression.
We note that in ref. 1 it was observed that choosing k = 1 in eqn (33) of ref. 6,
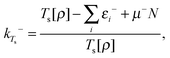 | (25) |
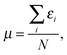 | (26) |
3 Conclusion
In this work we have highlighted the inherent ambiguity associated with scaling relations based purely on the electronic density. When employing these relations, which do not preserve the particle number normalization, in the context of Kohn–Sham theory, ancillary definitions are required to specify the type of Kohn–Sham approach considered. We have examined two different choices, which we referred to as orbital scaling and ensemble density scaling.The implications of these choices for examining the properties of the non-interacting kinetic energy functional were reviewed. In particular, the different definitions of Ts[ρ] within each approach were highlighted and their associated homogeneity properties discussed in detail. The homogeneity of degree 1 under the orbital scaling approach was shown to arise from the fact that the kinetic energy operator is a linear operator. Whilst interesting this property provides little information that may be applied in the construction of new density-functional approximations for Ts[ρ].
In contrast, the ensemble density scaling approach can be associated directly with the ensemble Levy–Lieb definition of the universal density functional. The ensemble approach has long been used to give insight into the properties of the exchange–correlation functional in DFT, particularly with respect to its derivative discontinuity associated with a change in the particle number. The relations used in the present work are consistent with this view of KS-DFT, but instead focus on the behaviour of the non-interacting kinetic energy contribution. As such the derived relations may be of use in developing approximate functional forms, just as those derived for the exchange–correlation energy have proven. A GGA type functional based on the observed inhomogeneity of the Ts[ρ] functional has already been constructed in ref. 11 and shown to have favourable properties when describing molecular systems. There are of course many avenues for incorporating this new information in addition to important existing constraints and investigation of further improved Ts[ρ] functionals is underway.
Acknowledgements
A.B. acknowledges the support from the European Community Seventh Framework Programme (FP7, 2007-2013), Marie Curie Intra-European Fellowship, under the Grant Agreement No. FP7-254150 (OF-DFT/MCHF project). A.M.T. and A.B. are grateful for the support from the European Research Council advanced grant FP7 project ABACUS (grant number 267683). A.M.T. is also grateful for the support from the Royal Society university research fellowship scheme. We thank Dr Simen Kvaal for useful discussions.References
- L. Calderín, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 032510 CrossRef.
- R. G. Parr and S. Liu, Chem. Phys. Lett., 1997, 276, 164–166 CrossRef CAS.
- S. Liu and R. G. Parr, Chem. Phys. Lett., 1997, 278, 341–344 CrossRef CAS.
- S. Liu and R. G. Parr, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 2211–2219 CrossRef CAS.
- M. Levy and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2010–2021 CrossRef CAS.
- A. Borgoo, A. M. Teale and D. J. Tozer, J. Chem. Phys., 2012, 136, 034101 CrossRef PubMed.
- G. K.-L. Chan and N. C. Handy, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 2670–2679 CrossRef CAS.
- M. Levy and H. Ou-Yang, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 651–652 CrossRef CAS.
- J. P. Perdew, L. A. Constantin, E. Sagvolden and K. Burke, Phys. Rev. Lett., 2006, 97, 223002 CrossRef.
- S. K. Ghosh and R. G. Parr, J. Chem. Phys., 1985, 82, 3307–3315 CrossRef CAS PubMed.
- A. Borgoo and D. J. Tozer, J. Chem. Theory Comput., 2013, 9, 2250–2255 CrossRef CAS.
- S. Laricchia, L. A. Constantin, E. Fabiano and F. Della Sala, J. Chem. Theory Comput., 2014, 10, 164–179 CrossRef CAS.
- T. Gál, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 044501 CrossRef.
- E. H. Lieb and W. E. Thirring, Phys. Rev. Lett., 1975, 35, 687–689 CrossRef CAS.
- R. M. Dreizler and E. K. Gross, Density Functional Theory An Approach to the Quantum Many Body Problem, Springer-Verlag, 1990 Search PubMed.
- E. H. Lieb, Int. J. Quantum Chem., 1983, 24, 243–277 CrossRef CAS PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- E. H. Lieb, in Density Functionals for Coulomb Systems, ed. R. Dreizler and J. da Providencia, Plenum Nato ASI Series, 1985, vol. 123, pp. 31–80 Search PubMed.
- G. K.-L. Chan, J. Chem. Phys., 1999, 110, 4710 CrossRef CAS PubMed.
- A. M. Teale, F. De Proft, P. Geerlings and D. J. Tozer, Phys. Chem. Chem. Phys., 2014 10.1039/c3cp54528h.
- Q. Wu and W. T. Yang, J. Chem. Phys., 2003, 118, 2498–2509 CrossRef CAS PubMed.
- R. A. King and N. C. Handy, Phys. Chem. Chem. Phys., 2000, 2, 5049–5056 RSC.
- R. G. Parr and W. T. Yang, Density Functional Theory of Atoms and Molecules, Oxford University, New York, 1989 Search PubMed.
- F. E. Zahariev and Y. A. Wang, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 042503 CrossRef.
- P. E. Lammert, Int. J. Quantum Chem., 2007, 107, 1943 CrossRef CAS PubMed.
- S. Kvaal, U. Ekström, A. M. Teale and T. U. Helgaker, J. Chem. Phys., 2014, 140, 18A518 CrossRef PubMed.
- D. J. Tozer, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 3524 CrossRef CAS.
- C. von Weizsäcker, Z. Phys., 1935, 96, 431–458 CrossRef.
- R. C. Morrison and Q. Zhao, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 1980–1984 CrossRef CAS.
| This journal is © the Owner Societies 2014 |
