Open Access Article
Open Access ArticleAn isomeric reaction benchmark set to test if the performance of state-of-the-art density functionals can be regarded as independent of the external potential†
Tobias
Schwabe
Center for Bioinformatics and Institute of Physical Chemistry, University of Hamburg, Bundesstraße 43, 20146 Hamburg, Germany. E-mail: schwabe@zbh.uni-hamburg.de
First published on 18th March 2014
Abstract
Some representative density functionals are assessed for isomerization reactions in which heteroatoms are systematically substituted with heavier members of the same element group. By this, it is investigated if the functional performance depends on the elements involved, i.e. on the external potential imposed by the atomic nuclei. Special emphasis is placed on reliable theoretical reference data and the attempt to minimize basis set effects. Both issues are challenging for molecules including heavy elements. The data suggest that no general bias can be identified for the functionals under investigation except for one case – M11-L. Nevertheless, large deviations from the reference data can be found for all functional approximations in some cases. The average error range for the nine functionals in this test is 17.6 kcal mol−1. These outliers depreciate the general reliability of density functional approximations.
1 Introduction
Nowadays, density functional theory (DFT) is the most often applied quantum chemical method to treat a variety of problems. Its computational efficiency and its broad applicability explain the success of DFT. Nevertheless, as the true functional is unknown, approximate density functionals have to be used.1,2 While the amount of empiricism varies in the development of such functionals, they are all known to have some shortcomings of one or the other kind. The most severe and most often discussed ones are the self-interaction (or delocalization) error3–5 as well as the insufficient description of London dispersion interactions.6,7 Many other failures observed for density functional methods can be traced back to these two fundamental issues. They are even coupled to some extent.8,9 Another problem could arise from the way the functionals have been constructed, i.e. the way they have been parametrized (if applicable). Therefore, the approximate form of density functionals demands for a regular assessment of functional capabilities and a deepening of our knowledge in density functional development.Most often, assessing and analyzing functionals is approached by studying their performance for various benchmark sets. These sets are either compiled to evaluate the broad applicability of a given functional10–13 or to evaluate its performance for a specific problem.14–16 Even mindless benchmarks have been advertised.17 While in the beginning the main goal was to reproduce experimental values nowadays the focus lies on the comparison with more sophisticated quantum chemical methods because this allows for a better judgment of the quality. In any case, the choice and compilation of a given benchmark set (can) bias the result.
Benchmark sets or subsets of them are naturally also involved in the parametrization of empirically trained functionals. Of course, the number of fitting points for the parametrization has to be limited and their choice is influenced by a number of considerations among which efficiency and the existence of reliable reference data are the most important. Another important aspect is the desired purpose of a functional. Sometimes they are trained for special problems although there is a general agreement that a good functional should perform equally well for as many problems as possible. Because of resource limitations during the development process it cannot be excluded that the composition of its parametrization set corrupts an empirically trained functional.
For example, molecules containing atoms of higher rows of the periodic table are less often part of parametrization or benchmark sets. The reason for this is just that molecules with heavy atoms are all but what they should be like. It takes more time to compute results for them because of the larger number of electrons, it is more difficult to obtain reliable reference results and the heavier elements are less frequently found in experimental chemistry and thereby are less of general interest. Although these molecules often show similar chemical behavior as their cousins containing lighter atoms of the same group the electronic structure is of course not identical. Especially the influence of inner (d-) shell electrons can be significant. This effect might be important not only for transition metal elements but also for main group elements. And of course, going to larger and larger atoms, relativistic effects would become more and more important and can have a significant influence depending on what molecular property is investigated.18 All this led to the present study where a set of representative functionals is tested for their dependency on the involved atoms. It is a fundamental statement of the Hohenberg–Kohn theorems that the exact functional is independent of the external potential which is imposed by the atomic nuclei.1,2 Here, it is tested if this requirement is fulfilled for a representative set of recent density functional approximations.
To assess the functionals a set of isomerization reactions has been compiled. Isomerization reactions have been found to be quite sensitive to the electronic structure method used for computing reaction energies.19–23 For each reaction the atom of interest is systematically exchanged with a heavier atom of the same group in the periodic table. To be independent of experimental data sophisticated reference data based on post-Hartree–Fock approaches are computed and serve to evaluate the performance of the functionals. Only main group elements are considered because for these elements the reference data are the most reliable. Relativistic effects have been investigated but for the problems at hand, i.e. the assessment of density functional approximations, they can be ignored as long as the treatment is consistent for the reference and evaluated methods. The chosen functional approximations represent state–of-the-art functionals which are known to be suitable for the problem at hand, especially because for the more recent ones, isomerization reactions are normally part of the training set in the development process. The assessment is presented as follows. First, computational details are given, followed by a detailed presentation of the test set. Next, the computed reference data are discussed before the actual evaluation of the functionals is given. Finally, some concluding remarks are drawn.
2 Computational details
All geometries are optimized with PBE0-D324,25/def2-TZVPP.26 Energies in the SCF and geometry optimization steps have been converged to 10−7 a.u. The density integration has been carried out with the multiple grid m4.27 Based on these geometries, single point energies have been computed with SCS-MP2,28 B2GP-PLYP-D3,29 PBE0-D3, B3LYP-D3,30,31 PW6B95-D3,32 M06-2X,33,34 oTPSS-D3,35ωB97X-D,36 M11,37 and M11-L38 all in combination with a cc-p(wC)V5Z basis set. The latter labels a basis set where the cc-pV5Z basis set39,40 is used for all atoms except for those of the second and third rows (here, Si, P, S, Cl, Ge, As, Se, and Br) for which the cc-pwCV5Z basis set41,42 is applied. The empirical dispersion correction is Grimme's 2010 version (D3)43 as implemented in the applied program packages.Finally, single point energies have also been computed with CCSD(T)44/cc-p(wC)VTZ and SCS-MP2/cc-p(wC)VTZ to obtain energy corrections for higher correlation effects. For some reactions, even more sophisticated computations based on the cc-p(wC)VQZ basis set have been carried out (see ESI†).
For all wavefunction based correlation methods, the resolution-of-the-identity approximation in combination with the corresponding auxiliary basis sets has been used for the correlation treatment.45–49 Further, a partial frozen core treatment has been applied. That is, only valence electrons are considered except for the heavier elements (here, Si, P, S, Cl, Ge, As, Se, and Br) where the n −1 shell is also taken into account. Following a recent suggestion,50 this scheme has also been applied to the double-hybrid functional. To estimate the effect of core–electron correlation, CCSD(T)/cc-pVTZ results with a full frozen core approximation have also been computed.
Single point energies for PW6B95-D3 are obtained using ORCA, version 2.9,51 for ωB97X-D using version 3.0. Both versions make use of the Libint2 Library.52 For an estimation of relativistic effects, PW6B95-D3/def2-QZVPP26 results with and without the ZORA approximation53 (using a corresponding decontracted basis set54) are also computed. The standard integration grid is always used.
Computations for M06-2X are carried out using NWChem 6.0, M11 and M11-L with version 6.3.55 To avoid problems with the meta(hybrid) functionals, the integration grid xfine, the largest standard grid, was chosen.
All other computations are done using a locally modified version of TURBOMOLE 6.4.56
3 Composition of the test set
The test set consists of several isomerization reactions which are listed in Fig. 1. They are arranged by the element group of the heteroatom. In all reactions the chemical environment for the heteroatom changes considerably, i.e. the atom is not just part of a (conserved) functional group, such that error compensation is less likely with respect to the treatment of that atom. Further, the first seven reactions for elements of groups 14, 15, and 16 are chosen to represent similar isomerizations which allow for some comparison between groups. Because of their monovalency, the set of reactions for group 17 elements contains different and less isomerizations. Reactions 10 for group 15 and 16 is only considered for second and third row atoms because they include molecules which are sometimes labeled hypervalent. Regardless whether these molecules feature a special kind of bonding the electronic structure can be seen as an extreme case because of large polarization effects at the heteroatom nucleus. Therefore, these molecules are taken into account. Finally, for carbon reaction 3 is trivial because it yields the identical molecule and reaction 2 is identical to reaction 1. The latter is also true for reactions 8 and 9 in the case of carbon. These reactions are not considered therefore. In total, the test set consists of 94 isomerization reactions. For the ease of reference, reactions are labeled by the element of interest and the reaction entry, like for example Se.07, which is the seventh reaction for group 16 with selenium as a heteroatom.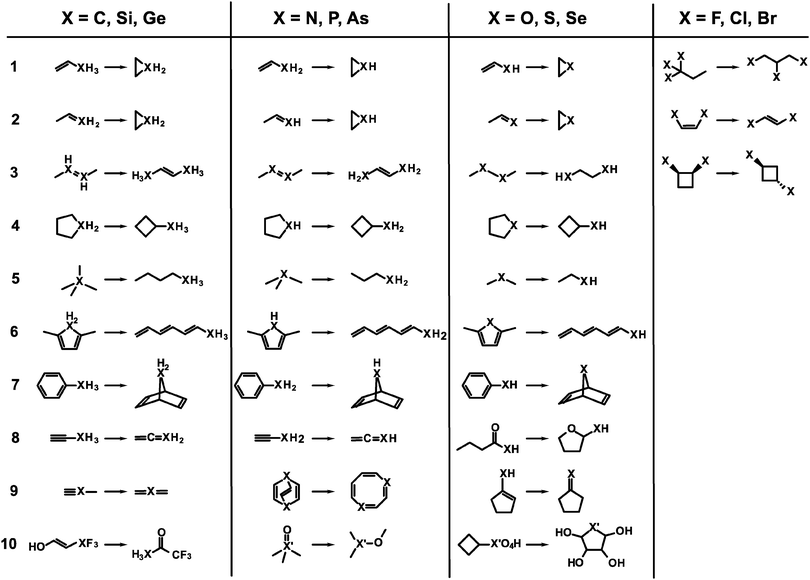 | ||
| Fig. 1 Scheme for all isomerization reactions included in the test set. Primes on generic heavy atoms X indicate that onlythe 2nd and 3rd row elements are considered. | ||
4 Results and discussion
4.1 Reference data
To obtain reliable reference data, the following strategy has been chosen. First, SCS-MP2/cc-p(wC)V5Z results are obtained. These results are then corrected for higher correlation effects based on CCSD(T) computations to yield the final ΔE(ref):| ΔE(ref) = ΔE(SCS-MP2/cc-p(wC)V5Z) + (ΔE(CCSD(T)/cc-p(wC)VTZ) − ΔE(SCS-MP2/cc-p(wC)VTZ)) | (1) |
The reference data for the isomerization reactions under consideration are collected in Table 1. They span the range from 0.0 to 153.7 kcal mol−1 (absolute values) which indicates the challenging character of the test set because very different changes in the electronic structure occur for the individual reactions.
| Rct | Group 14 | Group 15 | Group 16 | Group 17 |
|---|---|---|---|---|
| First row | ||||
| 1 | 5.9 | 16.6 | 15.8 | 26.9 |
| 2 | — | 17.9 | 25.2 | 1.0 |
| 3 | — | −20.9 | −63.7 | −2.7 |
| 4 | 17.7 | 12.3 | 9.9 | |
| 5 | 3.8 | −12.0 | −12.4 | |
| 6 | 18.9 | 32.0 | 27.4 | |
| 7 | 45.1 | 57.1 | 58.8 | |
| 8 | 1.3 | −14.2 | 19.6 | |
| 9 | — | −31.8 | −11.5 | |
| 10 | −9.1 | — | — | |
| Second row | ||||
| 1 | 6.4 | −4.9 | −2.6 | −3.3 |
| 2 | −10.1 | −1.7 | −0.9 | 0.6 |
| 3 | −3.9 | 23.0 | 6.6 | −1.6 |
| 4 | 28.2 | 26.1 | 19.8 | |
| 5 | 33.4 | 10.8 | −1.2 | |
| 6 | 21.5 | 6.6 | 35.5 | |
| 7 | 28.9 | 35.3 | 47.1 | |
| 8 | 22.0 | −3.9 | 11.9 | |
| 9 | −4.5 | 17.9 | −3.0 | |
| 10 | 153.7 | 33.2 | −15.2 | |
| Third row | ||||
| 1 | 8.0 | −7.9 | −6.8 | −6.3 |
| 2 | −7.4 | −5.7 | −5.1 | 0.1 |
| 3 | 14.2 | 38.7 | 16.0 | −1.6 |
| 4 | 26.7 | 27.2 | 20.8 | |
| 5 | 24.6 | 9.8 | 0.0 | |
| 6 | 19.7 | −4.8 | 32.8 | |
| 7 | 30.7 | 33.0 | 43.4 | |
| 8 | 19.1 | −4.2 | 10.7 | |
| 9 | −2.3 | −3.1 | −2.9 | |
| 10 | 93.5 | −2.9 | −68.9 | |
On average, the correction for higher correlation effects amounts to 0.6 kcal mol−1 with a minimum of −4.6 and a maximum of 2.4 kcal mol−1 (see ESI† for SCS-MP2 results). The difference between the CCSD(T)(FC)/cc-pVTZ and CCSD(T) (partial FC)/cc-p(wC)VTZ treatments is 1.0 kcal mol−1 on average (only considering the second and third row results). The largest deviation in that case is −18.4 kcal mol−1 for reaction S.10 but note that already the HF results differ by −17.0 kcal mol−1. Obviously, additional core-polarization functions are needed already at the SCF level to treat the electronic structure in a balanced way. On the other hand, for reaction Ge.03, the difference is only 0.4 kcal mol−1 on the SCF level, but −5.0 between the two CCSD(T) treatments.
To show that this way of approximating higher correlation effects is not very sensitive to the choice of the lower correlation method, the corrected SCS-MP2 results are compared to the corrected MP2 results (see ESI†). On average, both sets deviate by less than 0.1 kcal mol−1 in absolute numbers with a maximum deviation of 0.3 kcal mol−1.
It is known that even the quintuple-ζ basis set might not yield results at the complete basis set limit although only relative energies are considered. To estimate this effect SCS-MP2 results extrapolated to the complete basis set limit have been computed (see ESI† for details). On average, the results change by 0.2 kcal mol−1 for absolute deviations with a maximum of 1.0 kcal mol−1 for reaction Ge.10. In addition, for the first three reactions with all heteroatoms under consideration (34 data points in total) CCSD(T)/cc-p(wC)VQZ results are also obtained and are extrapolated to the complete basis set limit (see ESI† for details). This allows us to test the correction for higher correlation effects.
To compute results for heavier elements which can be compared to experimental data relativistic effects have to be taken into account. To estimate these effects for the present test set, corrections from PW6B95-D3/def-QZVPP with and without the ZORA approximation have been computed. These corrections are small, 0.4 kcal mol−1 on average for absolute values and even only 0.5 when only 2nd and 3rd row results are considered. Nevertheless, for single cases the correction can be up to 7.6 kcal mol−1 (for Se.10) even for closed shell systems (see ESI† for all results). This effect cannot be neglected when chemical accuracy is aimed for. On the other hand, for the present study only relative performances between electronic structure methods are of interest. Therefore, the effect can safely be ignored as long as every method is treated on equal footing. Even if relativistic corrections would be computed based on the different approaches, the actual variation between methods should be below 1.0 kcal mol−1.
Based on these numbers, a conservative estimate is a maximum deviation of 1.0 kcal mol−1 from the reference results and the true CCSD(T) results at the quintuple-ζ level – presumably even for an all electron treatment (although that would require a basis set which is trained for such a treatment). For those reaction energies for which CCSD(T) results have been computed with a larger basis set (see ESI†), estimating CCSD(T) values or actually compute them yields virtually the same results. The mean absolute deviation is 0.1 kcal mol−1 with a maximum deviation of 0.4 kcal mol−1. A direct judgment of the results' quality with respect to the true electronic structure is not possible. Based on the present data, no estimate can be given for what the effect of even higher correlation terms would be. But as none of the calculations shows a significant multi-reference character and given the general belief that such higher correlation terms are only significant for results beyond the chemical accuracy, it might be safe to assume no larger effect than an additional deviation of 1.0 kcal mol−1. Finally, the basis set incompleteness could add another 1.0 kcal mol−1 but is most often less severe. In principle, complete basis set limit results could be estimated for all methods yet such an approach is less established for the various DFT methods at hand. Further, different kind of basis sets might be needed for consistent treatment. Therefore, all results are compared for the same basis set. Again, the aforementioned error estimations should be regarded as conservative ones for challenging cases. For most of the values within the test set, the reliability should be higher especially because often the applied approximations have opposing effects and cancel to some extent. Therefore, each result deviating more than 3 kcal mol−1 form the reference result is regarded as an outlier in the following discussion.
4.2 Functional assessment
Based on the reference data, nine representative functionals are assessed. For comparison, the results regarding SCS-MP2, which is also often recommended for such computations, are also given. Key values for the assessment are listed in Table 2. Detailed results can be found in the ESI.†![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ), the mean absolute deviation (|
), the mean absolute deviation (|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) |), the median of the absolute deviation (|
|), the median of the absolute deviation (|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) |), the maximum (xmax) and minimum deviations (xmin), and the number of outliers (#). All energy values are in kcal mol−1
|), the maximum (xmax) and minimum deviations (xmin), and the number of outliers (#). All energy values are in kcal mol−1
| Functional |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
x max | x min | # |
|---|---|---|---|---|---|---|
| SCS-MP2(FC) | 0.4 | 1.0 | 0.6 | 4.6 | −3.7 | 6 |
| B2GP-PLYP-D3(FC) | 0.5 | 1.3 | 0.4 | 7.8 | −4.6 | 11 |
| B3LYP-D3 | 0.0 | 3.6 | 2.1 | 12.6 | −11.7 | 34 |
| PBE0-D3 | −0.5 | 2.1 | 2.0 | 6.0 | −7.1 | 22 |
| M06-2X | −0.2 | 1.9 | 1.1 | 8.7 | −8.6 | 21 |
| PW6B95-D3 | −0.6 | 1.8 | 1.6 | 5.7 | −5.5 | 14 |
| ωB97X-D | −0.4 | 2.0 | 1.5 | 5.3 | −8.2 | 21 |
| M11 | −0.3 | 2.4 | 1.5 | 6.3 | −14.6 | 34 |
| M11-L | −0.6 | 3.7 | 2.8 | 13.9 | −19.2 | 44 |
| oTPSS-D3 | −0.2 | 2.7 | 2.1 | 13.2 | −8.5 | 31 |
A standard criterion for evaluating quantum mechanical methods is the mean absolute deviation (MAD). SCS-MP2 shows the lowest MAD of 1.0 kcal mol−1, followed by B2GP-PLYP-D3 (1.3 kcal mol−1), PW6B95-D3 (1.8 kcal mol−1), M06-2X (1.9 kcal mol−1), ωB97X-D (2.0 kcal mol−1), PBE0-D3 (2.1 kcal mol−1), M11 (2.4 kcal mol−1), oTPSS-D3 (2.7 kcal mol−1), B3LYP-D3 (3.5 kcal mol−1) and M11-L (3.7 kcal mol−1).
These numbers hide to some extent the individual performance for a given set entry. To give an impression of that one can inspect the range of deviations for each method. From the smallest to the largest, the order is: SCS-MP2 (8.3 kcal mol−1), PW6B95-D3 (11.2 kcal mol−1), B2GP-PLYP-D3 (12.4 kcal mol−1), PBE0-D3 (13.1 kcal mol−1), ωB97X-D (13.5 kcal mol−1), M06-2X (17.3 kcal mol−1), M11 (20.9 kcal mol−1), oTPSS-D3 (21.7 kcal mol−1), B3LYP-D3 (24.3 kcal mol−1), and M11-L (33.1 kcal mol−1).
Further, MAD values are sensitive to outliers. An alternative criterion which can be used to assess methods is the median of the absolute deviations. Again, this changes the ranking of the methods under investigation: B2GP-PLYP-D3 (0.4 kcal mol−1), SCS-MP2 (0.6 kcal mol−1), M06-2X (1.1 kcal mol−1), M11 and ωB97X-D (1.5 kcal mol−1), PW6B95-D3 (1.6 kcal mol−1), PBE0-D3 (1.7 kcal mol−1), B3LYP-D3 (2.0 kcal mol−1), oTPSS-D3 (2.1 kcal mol−1) and M11-L (2.8 kcal mol−1).
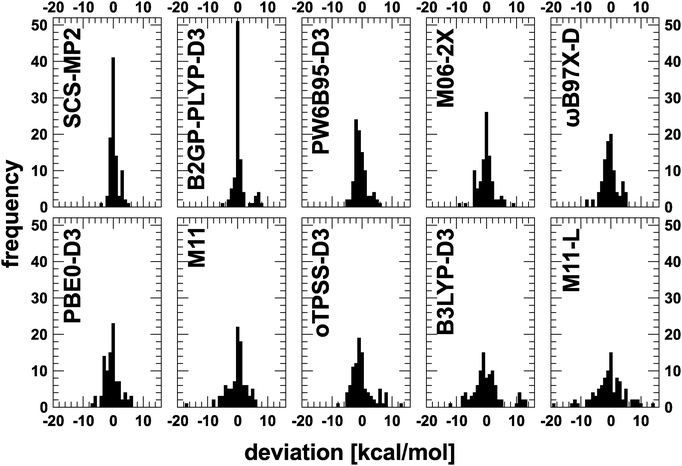
As a final way to compare all methods, the distribution of deviations for each methods is given in Fig. 2. SCS-MP2 and B2GP-PLYP-D3 show a sharp peak around a deviation of 0 kcal mol−1. For the latter a distinct group of outliers around 7 kcal mol−1 can be identified. For M11-L and B3LYP-D3, a completely different distribution, namely a flat and broad one, is obtained. The remaining functionals lie somewhere in between these two patterns. Interestingly, PW6B95-D3 is the only functional that shows it maximum not around 0 kcal mol−1, but around −2 kcal mol−1. These distributions can also be complemented by the number of outliers (deviations larger than 3 kcal mol−1) which is 6 for SCS-MP2, 11 for B2GP-PLYP-D3, 14 for PW6B95-D3, 21 for M06-2X and ωB97X-D, 22 for PBE0-D3, 31 for oTPSS-D3, 34 for M11 and B3LYP-D3, and 44 for M11-L.
Some of the functionals are supplemented with an empirical dispersion correction. For the present benchmark set, which contains relatively small molecules, the effect of the correction is negligible. For completeness, results without the correction are given in the ESI.† For some rare cases the effect is as large as 2.0 kcal mol−1, but most often it is well below 0.5 kcal mol−1. And there is no consistent improvement due to the correction so that the overall effect cancels for the statistics. Actual values for some cases with the largest isomerization energy change are listed in Table 3. As it is generally recommended to apply a dispersion correction, only these results are discussed in the following.
| Functional | Reaction label | ||||
|---|---|---|---|---|---|
| C.05 | C.06 | P.09 | S.10 | Ge.05 | |
| B2GP-PLYP-D3 | −0.6 | −0.2 | 0.7 | −0.8 | 0.8 |
| B3LYP-D3 | −1.6 | −0.7 | 1.4 | −1.9 | 1.4 |
| PBE0-D3 | −1.0 | 0.5 | 0.8 | −1.0 | 0.6 |
| PW6B95-D3 | −0.7 | −0.2 | 0.7 | −0.9 | 0.8 |
| ωB97X-D | −0.6 | 0.7 | −0.5 | −0.3 | 0.1 |
| oTPSS-D3 | −1.7 | −1.0 | 1.6 | −2.0 | 1.5 |
Now, the statistical key values are grouped by the row the heteroatom belongs to. The results are shown in Table 4. While also of empirical nature to some extent, SCS-MP2 is less likely to show a bias because of the rather small number of only two very general parameters needed to define the approach.28 Comparing the results of SCS-MP2 against the DFT methods, most of the latter show a similar performance dependency on the periodic table row of the heteroatom – the mean absolute deviations as well as the medians of the absolute deviations can be considered to be quite stable for increasing the atom size within a group for almost all functionals under consideration. The worst case is found for M11-L for which the median increases by 2.5 kcal mol−1 from first to third row results (3.1 kcal mol−1 for the MAD). It is also the only functional where a continuous relationship between error statistics and the element row can be identified.
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ), the mean absolute deviation (|
), the mean absolute deviation (|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) |), and the median of the absolute deviation (|
|), and the median of the absolute deviation (|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) |). All values are in kcal mol−1
|). All values are in kcal mol−1
| Functional | 1st row | 2nd row | 3rd row | ||||||
|---|---|---|---|---|---|---|---|---|---|
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
|
| SCS-MP2(FC) | 0.2 | 0.7 | 0.6 | 0.4 | 1.2 | 0.6 | 0.5 | 1.0 | 0.6 |
| B2GP-PLYP-D3(FC) | 0.6 | 1.3 | 0.4 | 0.6 | 1.3 | 0.7 | 0.4 | 1.2 | 0.3 |
| B3LYP-D3 | 0.4 | 3.5 | 1.7 | −0.1 | 3.8 | 2.2 | −0.3 | 3.4 | 1.8 |
| PBE0-D3 | −0.1 | 1.9 | 1.8 | −0.5 | 2.3 | 1.8 | −0.9 | 2.1 | 2.1 |
| M06-2X | 0.0 | 1.7 | 1.1 | −0.6 | 1.7 | 0.7 | −0.1 | 2.2 | 1.8 |
| PW6B95-D3 | −0.2 | 1.7 | 1.3 | −0.6 | 1.9 | 1.6 | −0.9 | 1.9 | 1.8 |
| ωB97X-D | 0.2 | 1.9 | 1.5 | −0.5 | 2.0 | 1.4 | −0.8 | 2.0 | 1.5 |
| M11 | 0.2 | 1.8 | 0.9 | −0.2 | 2.4 | 2.1 | −0.8 | 2.8 | 1.5 |
| M11-L | 0.4 | 1.8 | 0.7 | −0.2 | 4.1 | 2.9 | −1.9 | 4.9 | 3.2 |
| oTPSS-D3 | −0.6 | 2.7 | 2.3 | 0.0 | 2.6 | 2.1 | 0.0 | 2.7 | 1.5 |
To put these numbers into context, the results regarding reactions 1 to 7 for groups 14, 15, and 16 are also compared against each other. For each group of the periodic table, these reactions describe similar isomerizations. Because of this similarity, the functional performance should be very consistent for a given reaction when compared with the heteroatoms of the same row. Therefore, the results for the group-wise comparison should reveal the variation in the performance which has to be expected for each functional when it is applied to related problems. The statistical key values are given in Table 5.
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ), the mean absolute deviation (|
), the mean absolute deviation (|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) |), and the median of the absolute deviation (|
|), and the median of the absolute deviation (|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) |). All values are in kcal mol−1
|). All values are in kcal mol−1
| Functional | Group 14 | Group 15 | Group 16 | ||||||
|---|---|---|---|---|---|---|---|---|---|
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
|![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) | | |
|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | | |
|
| SCS-MP2(FC) | 0.3 | 1.2 | 0.7 | 0.5 | 1.0 | 0.8 | 0.4 | 1.0 | 0.5 |
| B2GP-PLYP-D3(FC) | 0.3 | 0.9 | 0.3 | 0.3 | 1.5 | 0.5 | 1.2 | 1.2 | 0.5 |
| B3LYP-D3 | −0.5 | 2.4 | 1.4 | −0.8 | 4.0 | 2.8 | 1.7 | 3.7 | 2.1 |
| PBE0-D3 | −1.3 | 2.0 | 2.1 | −0.7 | 2.6 | 2.3 | 0.4 | 1.9 | 1.8 |
| M06-2X | −0.2 | 1.5 | 0.6 | −0.4 | 2.3 | 1.5 | −0.1 | 1.9 | 1.5 |
| PW6B95-D3 | −1.3 | 1.6 | 1.4 | −1.0 | 2.2 | 1.8 | 0.5 | 1.8 | 1.8 |
| ωB97X-D | −0.4 | 2.1 | 2.4 | −0.3 | 2.3 | 2.1 | 0.4 | 1.9 | 1.4 |
| M11 | −0.3 | 2.3 | 1.5 | 0.3 | 2.5 | 2.1 | 0.3 | 2.4 | 1.8 |
| M11-L | −1.4 | 4.4 | 3.9 | −0.4 | 3.4 | 2.3 | 0.7 | 2.9 | 2.1 |
| oTPSS-D3 | −0.6 | 2.6 | 2.3 | −0.5 | 2.5 | 2.1 | 0.4 | 2.7 | 1.9 |
The variations in statistics which can be found are in the same range as in Table 4. Slight fluctuations can be related to the limited number of test cases and to the fact that, of course, the group-wise test sets are not completely identical. The same noise in functional statistics can also be assumed for the deviations for different rows of the periodic table. Therefore, any bias due to systematic dependency effects which are smaller than the general functional performance variation cannot be resolved. Besides very consistent results for almost all functionals, M11-L, stands out because the error statistics for a group-wise analysis deviate less than they do for a row-wise analysis. For the former, the maximum deviation of medians of the absolute error is only 1.5 kcal mol−1.
According to the arguments given before, such a performance indicates a dependency on the row of heteroatom involved in the reaction. To further analyse the performance of M11-L, for each reaction the relative change in the deviation with respect to data from first row atoms is plotted for the second and third row data sets. A dependency on the type of heteroatom should result in a systematic change for going to the heavier elements. The changes are plotted in Fig. 3 along with results regarding M11 and oTPSS-D3.
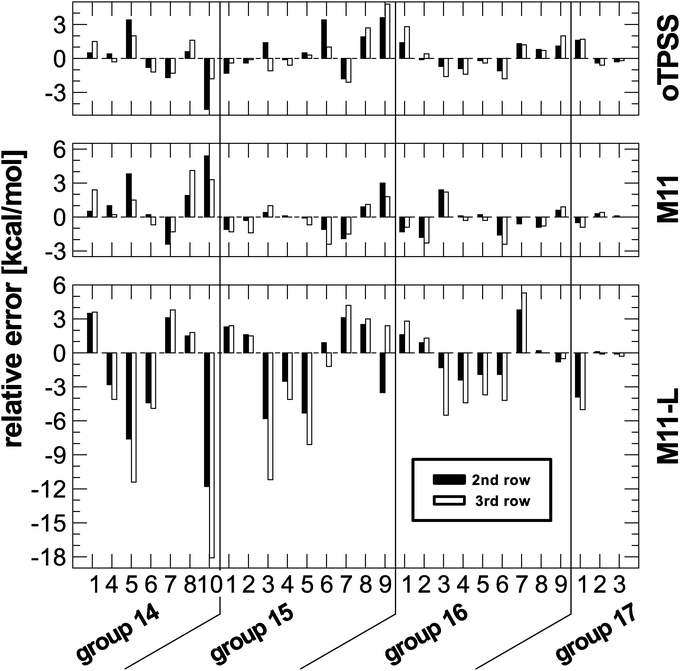 | ||
| Fig. 3 Relative change in deviations with respect to first row results for a given isomerization reaction set. | ||
The plot reveals that the M11-L performance shows systematic trends for almost all reactions considered here. The amount of deviation from reference data is increasing for the heavier heteroatoms. Such a pattern cannot be found for the other two functionals and also for none of the other functionals in the present study (see ESI†). Like M11-L, oTPSS is a meta-GGA functional containing a set of fitted parameters but with a very different functional form. On the other hand, the functional forms of M11 and M11-L are very similar, though the former belongs to the class of range-separated hybrid functionals. M11-L also incorporates the idea of range-separation but in a local fashion, termed dual-range (density functional) exchange. This is a unique characteristic and few studies with this approach of functional design can be found in the literature. Therefore, it is not possible to conclude from the present data if this could be a general problem or is just a fitting bias in the design of the functional. The comparison to the related functionals M11-L and oTPSS might hint of the latter. In any case, this deserves further analysis and is beyond the scope of the present paper.
5 Conclusion and summary
Nine representative functionals have been assessed for a set of isomerization reactions for which the key heteroatom has been successively substituted by a heavier member of the element group. This investigation was designed to reveal any bias which could be found for a given functional which is often trained only on a subset of elements during the development. The results are compared against very sophisticated reference data which have been computed at the SCS-MP2/cc-p(wC)V5Z level of theory corrected by CCSD(T)/cc-p(wC)VTZ values for higher correlation effects.Based on the data presented in this study no general bias can be identified. Most functionals show a stable performance downwards the periodic table and vary only to such an amount which has to be expected for similar but not identical chemical problems. Of course, this has to be expected for an exact density functional which only depends on the electron density and not on the external potential. But this cannot be guaranteed for an approximate density functional – at least when it is based on (some) empiricism. In one case, M11-L, some dependency on the heteroatom involved could be revealed. While this might be seen as a violation of the Hohenberg–Kohn theorems, one should remember that care has always to be taken when applying trained methods outside their proposed purposes. For the 1st row atoms, M11-L is among the best functionals in this test set and also has demonstrated its good performance before.38 The present test set can help to reparameterize the functional and might eliminate the bias while maintaining the general performance if no general flaw is found for local range-separated functionals.
That no general bias can be found for the given test set once more justifies the application of good functional approximations for very diverse tasks in quantum chemistry. Nevertheless, only a small though hopefully representative set of DFAs has been tested. Further, only isomerization energies have been considered. Although this is a very sensitive test for electronic structure methods, future studies should also take other properties into account to check how severe any bias for a specific group of elements is for a given DFA. For now, the present benchmark set can already serve as a first test to identify the possible problems in DFAs not considered so far or for new developments.
Yet, showing a constant performance across the periodic table is worth nothing if that means constantly poor results. None of the functionals can beat SCS-MP2 for this test set in terms of the error distribution and general reliability. At the same time it has a similar computational cost as the double-hybrid B2GP-PLYP-D3. The latter shows the next best performance. Even more interesting, if its outliers could be eliminated B2GP-PLYP-D3 should outperform SCS-MP2. That such an improved double-hybrid functional could be found might be seen from the fact that there are a few reactions for which all of the tested functionals show systematically deviations larger than 3 kcal mol−1. Most of these cases for which all functionals perform poorly can be related to reaction X.07 in which the aromatic system in the phenyl ring is destroyed. The aromatic system is always too stable. This indicates that the self-interaction error common to practically all approximate density functionals deteriorates the results.
Finding solutions to remedy the problem of self-interaction while maintaining the superior cost-performance ratio with respect to sophisticated wave function methods persists to be the great challenge in density functional development. Ideas like the range-separated double-hybrids,57,58 the MCY approach,59 or even higher-order approaches like the random-phase-approximation60 or the GW-method61 might be solutions. But these methods still have to prove that they do not loose the generality of common density functionals which are not only successful for main group chemistry but for problems all across the table. At least the present study emphasizes again the fact that functional performance is transferable to related chemistry.
References
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989 Search PubMed.
- W. Koch and C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, New York, Chichester, Brisbane, Singapore, Toronto, 2000 Search PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sáchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- X. Zheng, M. Liu, E. R. Johnson, J. Contreras-García and W. Yang, J. Chem. Phys., 2012, 137, 214106 CrossRef PubMed.
- K. E. Riley, M. Pitok, P. Jureka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CrossRef CAS.
- T. M. Henderson and G. E. Scuseria, Mol. Phys., 2010, 108, 2511–2517 CrossRef CAS.
- E. R. Johnson, J. Contreras-García and W. Yang, J. Chem. Theory Comput., 2012, 8, 2676–2681 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 669–676 CrossRef CAS.
- T. Schwabe and S. Grimme, J. Phys. Chem. Lett., 2010, 1, 201–204 CrossRef.
- M. Srebro, N. Govind, W. A. de Jong and J. Autschbach, J. Phys. Chem. A, 2011, 115, 10930–10943 CrossRef CAS PubMed.
- S. S. Leang, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2012, 136, 104101 CrossRef PubMed.
- M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003 CrossRef CAS.
- P. Pyykkö, Chem. Rev., 2012, 112, 371–384 CrossRef PubMed.
- S. Grimme, M. Steinmetz and M. Korth, J. Org. Chem., 2007, 72, 2118–2126 CrossRef CAS PubMed.
- R. Huenerbein, B. Schirmer, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 6940–6948 RSC.
- S. Luo, Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2011, 13, 13683–13689 RSC.
- T. Schwabe, R. Huenerbein and S. Grimme, Synlett, 2010, 1431–1441 CAS.
- T. Schwabe, J. Comput. Chem., 2012, 33, 2067–2072 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Enzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Adamo and V. J. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095 CrossRef CAS.
- A. Karton, A. Tarnopolsky, J.-F. Lamere, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 119, 525 CrossRef CAS.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 16615–16620 RSC.
- R. Peverati and D. G. Truhlar, J. Chem. Phys. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- R. Peverati and D. G. Truhlar, J. Chem. Phys. Lett., 2011, 3, 117–124 CrossRef.
- J. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- K. A. Peterson and J. T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- N. J. DeYonker, K. A. Peterson and A. K. Wilson, J. Phys. Chem. A, 2007, 111, 11383–11393 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. Helgaker, P. Jörgensen and J. Olsen, Molecular Electronic-Structure Theory, J. Wiley, New York, 2000 Search PubMed.
- F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 CrossRef CAS.
- T. Schwabe, J. Phys. Chem. A, 2013, 117, 2879–2883 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- E. Valeev, 2011, available from http://libint.valeyev.net.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 5, 908–919 CrossRef.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- TURBOMOLE GmbH, 2012, TURBOMOLE V6.4, developed by University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- J. H. Ángyán, I. C. Gerber, A. Savin and J. Toulouse, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 012510 CrossRef.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2009, 131, 174105 CrossRef PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 124, 091102 CrossRef PubMed.
- H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084–1101 CrossRef.
- M. J. van Setten, F. Weigend and F. Evers, J. Chem. Theory Comput., 2013, 9, 232–246 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details about reference data, results regarding all functionals, results regarding the effect of the dispersion correction, and plots showing trends in functional performances. See DOI: 10.1039/c4cp00772g |
| This journal is © the Owner Societies 2014 |