Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Are hot charge transfer states the primary cause of efficient free-charge generation in polymer:fullerene organic photovoltaic devices? A kinetic Monte Carlo study†
Matthew L.
Jones
a,
Reesha
Dyer
a,
Nigel
Clarke
b and
Chris
Groves
*a
aSchool of Engineering and Computing Sciences, Durham University, South Road, DH1 3LE, UK. E-mail: chris.groves@durham.ac.uk
bDepartment of Physics and Astronomy, Sheffield University, Hounsfield Road, S3 7RH, UK
First published on 19th June 2014
Abstract
Kinetic Monte Carlo simulations are used to examine the effect of high-energy, ‘hot’ delocalised charge transfer (HCT) states for donor:acceptor and mixed:aggregate blends, the latter relating to polymer:fullerene photovoltaic devices. Increased fullerene aggregation is shown to enhance charge generation and short-circuit device current – largely due to the increased production of HCT states at the aggregate interface. However, the instances where HCT states are predicted to give internal quantum efficiencies in the region of 50% do not correspond to HCT delocalisation or electron mobility measured in experiments. These data therefore suggest that HCT states are not the primary cause of high quantum efficiencies in some polymer:fullerene OPVs. Instead it is argued that HCT states are responsible for the fast charge generation seen in spectroscopy, but that regional variation in energy levels are the cause of long-term, efficient free-charge generation.
1. Introduction
The performance of bulk heterojunction organic photovoltaic devices (OPVs) has improved rapidly since their invention in 1995.1,2 Today, lab-made, single junction OPVs have almost reached 10% power conversion efficiency,3,4 seen by some as the threshold at which OPVs become commercially viable.5 These improvements in efficiency have come about largely by better matching the absorption spectrum of the blend components to sunlight,6 as well as optimising the processing conditions of the active layer.7 However, there is still active discussion8–11 as to the mechanism by which efficient, even >80% efficient,12,13 free-charge generation can be achieved in organic materials. Efficient operation is perhaps unexpected because the dielectric constant is small (ε ∼ 3), meaning that photoabsorption creates excitons with a high binding energy14 rather than free-charges, and the recombination rate of high-performance polymer:fullerene OPVs, is of the order 109 s−1.15–19To try to explain this apparent contradiction, the focus of the community has turned to the charge transfer (CT) state; the precursor of free charges which is formed by the dissociation of the exciton at the interface between electron-donating and electron-accepting components of the OPV. The traditional picture is that the photogenerated Frenkel (i.e. tightly bound) exciton dissociates to yield a bound CT state that is localised at the donor–acceptor interface. This bound CT state then requires a series of intermolecular hops driven by an energy gradient to successfully dissociate into free charges, a process that is expected to be both slow and inefficient.20 Bakulin et al.21 carried out detailed pump–push–probe measurements on a range of OPV blends and explained the resulting data by proposing exciton dissociation instead creates a high-energy, or ‘hot’ charge transfer (HCT) state with a delocalised, band-like character which in turn leads to reduced Coulomb interaction between the electron and hole parts of the wavefunction. The concept of HCT states is consistent with spectroscopy investigations which show free-charge generation is fast, i.e. in the hundreds of fs range,22–25 in some materials systems. Some have gone on to argue that the lifetime of the HCT state represents a time limit for efficient free-charge generation, as the Coulomb binding energy of the bound CT state formed once the HCT state cools is much larger than kT.25 The spatially separated character of HCT states is supported by quantum chemical calculations.21,26 Indeed, it has been suggested that Frenkel excitons generally dissociate to yield spatially separated electron–hole pairs.26,27 Later work has gone on to suggest that the delocalisation of HCT states is associated with fullerene aggregates,28,29 which is consistent with the correlation between the presence of fullerene aggregates and high performance in polymer:fullerene OPVs.30,31 These arguments when taken together appear to offer a compelling explanation why OPVs may show efficient charge generation.
However, while the existence of a HCT state is well established, its effect on OPV performance is still a matter of discussion. The literature discussed above mostly utilises spectroscopy or calculations of CT states and dynamics, and so are mostly concerned with short timescales (∼fs–ps) and small lengthscales (∼Å nm). Other long-time (∼μs) or steady-state measurements on OPV devices (therefore implying lengthscales of ∼100 nm) suggest that the efficiency of free-charge generation is largely unaffected by whether HCT or bound CT states are excited, at least at room temperature.32–34 Furthermore, other mechanisms have been suggested as to how free-charge generation from a bound CT state may be efficient.9,10,35 The resulting picture is not clear and poses difficulties as to how OPV technology should be developed further. For instance, if HCT states are the primary reason why OPVs show efficient performance then materials development should attempt to enhance structural rigidity and suppress torsional relaxation,21 while processing should seek to promote fullerene aggregation.28,29 If, on the other hand, HCT states are not the primary cause of efficient free-charge generation then other techniques may need to be employed.
In this paper we attempt to quantify the efficacy of HCT states by taking as a starting point the assumption that HCT states do indeed occur, and that upon cooling, the electron and hole polaron have obtained an enhanced mutual separation, r, as a result of initial delocalisation. We then use a modified kinetic Monte Carlo (KMC) model9,36 to examine the subsequent behaviour of the charge pair, and the consequent effect on OPV performance. The aim of this exercise will be to see whether HCTs can provide the quantum efficiencies seen in experiment for common polymer:fullerene OPV systems. We find that HCT states do indeed improve the efficiency of charge generation as anticipated, but that the degree of delocalisation required to obtain the performance seen in OPVs is in excess of that measured in experiment. We also show that the efficacy of HCT states depends strongly on morphology, and in particular, that HCT states are most effective when fullerene aggregates are dispersed throughout the molecularly mixed phase. However, none of the morphologies considered are predicted to give rise to efficient OPV performance as seen in experiment. Further investigations examining the interplay between kinetics and energetics of free-charge generation suggest that HCT states provide most significant benefit under two sets of conditions. The first occurs for when the degree of delocalisation, r is of the order of 10 nm, meaning the Coulomb binding energy approaches kT and separation becomes energetically favourable. The second occurs for small r (∼4 nm) and when electron mobility is small, meaning recombination is kinetically unfavourable. It is argued that neither circumstance is expected in polymer:fullerene OPVs and that high efficiency seen in such devices is most likely due to other mechanisms, or a combination.
The paper is arranged as follows. In Section 2 simulations, the morphologies used in this investigation are described in Section 2.1 and the KMC methodology explained in Section 2.2. In Section 3 Results, the effect of hot charge transfer states is then examined in the context of donor:acceptor blends in Section 3.1 and mixed:aggregate blends in Section 3.2, including both geminate pair separation and OPV device simulations. In Section 4, we propose reasons why HCT states are not as effective in producing charges as expected, and discuss alternative mechanisms, before concluding in Section 5.
2. Simulations
2.1 Morphologies
The morphology used in KMC modelling was derived from modified Cahn–Hilliard37 theory, which is described briefly here, the equations presented in ESI† (Section S1), and discussed in greater detail elsewhere.38 The simulation volume within the KMC model is a 3-dimensional, regular array of 1 nm3 lattice sites extending 128 nm in each direction. Each site has an associated local composition, Φ, where Φ = 1 represents only donor material and Φ = 0 represents only acceptor material. Initially, the value of Φ is set to the bulk donor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acceptor ratio with an additional small random perturbation, δ to seed the morphology. The volume is considered to be a polymer melt, and is then quenched such that spinodal decomposition is favoured. The thermodynamics and kinetics of morphology evolution during the quench are described by a modified Cahn–Hilliard equation.38,39 Phase separation is allowed to continue until the morphology features have developed to the desired size, whereupon the simulation is stopped.
acceptor ratio with an additional small random perturbation, δ to seed the morphology. The volume is considered to be a polymer melt, and is then quenched such that spinodal decomposition is favoured. The thermodynamics and kinetics of morphology evolution during the quench are described by a modified Cahn–Hilliard equation.38,39 Phase separation is allowed to continue until the morphology features have developed to the desired size, whereupon the simulation is stopped.
The Cahn–Hilliard free energy expression, and enhancements thereof,40 allow the simulation of multi-component bulk heterojunction morphologies, which have found extensive use in KMC investigations.38,39,41 Such methods have allowed for significant advancements towards a predictive model for morphology formation by considering the effect on morphology of, for example, spinodal phase segregation during evaporation42 and substrate-induced phase demixing.38,43 In general, such models have provided good agreement with experimental observations of morphology.44 We note that research is ongoing to incorporate material crystallisation in the morphology generation process,45 however in this investigation, we do not consider the effect of such kinetics.
The input parameters for the Cahn–Hilliard equations are the molecular weight of the donor and acceptor components, ND and NA respectively, and the initial donor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
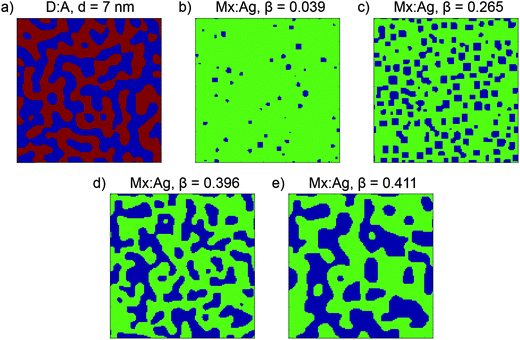
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acceptor volume ratio of the blend. Two sets of input parameters are used to generate morphologies for use in this paper; one results in morphologies similar to an all-polymer blend, which have ND/NA = 1 and a donor volume ratio of 0.5; the second results in morphologies similar to a polymer:fullerene blend, which have ND/NA = 30 and a donor volume ratio of 0.4, i.e. have a slight excess of a smaller molecular weight acceptor. The end result of Cahn–Hilliard simulations is a 3-dimensional array of Φ which represents the morphology, which is further processed for use in KMC simulations. For morphologies with ND/NA = 1, sites with Φ ≤ 0.5 are assigned as pure donor, whereas sites with Φ > 0.5 are assigned as pure acceptor, leading to morphologies of the type shown in Fig. 1a. Evolving these morphologies increases the average size of the donor and acceptor domains, d. Because these morphologies include only pure donor and acceptor phases, which conduct holes and electrons respectively, these are referred to as donor:acceptor morphologies, or D:A for brevity. For morphologies with NA/ND = 30, sites with Φ > 0.8 are assigned as an acceptor aggregate, and other sites as a molecularly-mixed phase, as shown in Fig. 1b–d. These morphologies are referred to as mixed:aggregate morphologies, or Mx:Ag. Evolving these morphologies increases the volume fraction of aggregated acceptor, β. We consider electrons to be able move in both aggregate and mixed regions, while holes are confined to the mixed phase only. Examining both D:A and Mx:Ag morphologies is important here as it allows us to separately examine the impact of mixed phases, which can both generate charge and transport electrons and holes, and HCT states. Further information about these morphologies is shown in the ESI† (Section S2). We note that polymer:fullerene OPVs can display 3-phase morphologies, i.e. donor, acceptor and mixed, however we do not consider these in this investigation since such morphologies will exhibit behaviour which is intermediate between the D:A and Mx:Ag morphologies used here.
acceptor volume ratio of the blend. Two sets of input parameters are used to generate morphologies for use in this paper; one results in morphologies similar to an all-polymer blend, which have ND/NA = 1 and a donor volume ratio of 0.5; the second results in morphologies similar to a polymer:fullerene blend, which have ND/NA = 30 and a donor volume ratio of 0.4, i.e. have a slight excess of a smaller molecular weight acceptor. The end result of Cahn–Hilliard simulations is a 3-dimensional array of Φ which represents the morphology, which is further processed for use in KMC simulations. For morphologies with ND/NA = 1, sites with Φ ≤ 0.5 are assigned as pure donor, whereas sites with Φ > 0.5 are assigned as pure acceptor, leading to morphologies of the type shown in Fig. 1a. Evolving these morphologies increases the average size of the donor and acceptor domains, d. Because these morphologies include only pure donor and acceptor phases, which conduct holes and electrons respectively, these are referred to as donor:acceptor morphologies, or D:A for brevity. For morphologies with NA/ND = 30, sites with Φ > 0.8 are assigned as an acceptor aggregate, and other sites as a molecularly-mixed phase, as shown in Fig. 1b–d. These morphologies are referred to as mixed:aggregate morphologies, or Mx:Ag. Evolving these morphologies increases the volume fraction of aggregated acceptor, β. We consider electrons to be able move in both aggregate and mixed regions, while holes are confined to the mixed phase only. Examining both D:A and Mx:Ag morphologies is important here as it allows us to separately examine the impact of mixed phases, which can both generate charge and transport electrons and holes, and HCT states. Further information about these morphologies is shown in the ESI† (Section S2). We note that polymer:fullerene OPVs can display 3-phase morphologies, i.e. donor, acceptor and mixed, however we do not consider these in this investigation since such morphologies will exhibit behaviour which is intermediate between the D:A and Mx:Ag morphologies used here.
For each cell within the morphology we additionally assign a random, Gaussian distributed energetic disorder. As high-performance polymer:fullerene OPVs are of primary interest here, we set the standard deviation of the Gaussian density of states to 50 meV, representative of the high mobility organic materials utilised in such devices.46,47 We note that Gaussian distributed energetic disorder is time-invariant.
2.2 Kinetic Monte Carlo simulations
Practically, the HCT state is implemented as follows. If an exciton is generated in a mixed phase, it dissociates immediately to yield an electron–hole pair with a mutual separation of 1 nm as suggested by experiment29 (however, at points in the current investigation we relax this assumptions to make HCT states occur more generally, but this is described more fully in the text later on). If the exciton is generated within a donor, acceptor or aggregate phase, and further diffuses to an interface, the exciton dissociates and immediately yields a separated electron–hole pair; the separated electron–hole pair being the cooled remains of the HCT state. This assumes that the HCT state cools to yield a separated charge pair on a timescale shorter than any of the other processes occurring within the device, which is in broad agreement with experiment.22,25 Furthermore, this assumes that delocalisation is associated with aggregated fullerene, as also been suggested by experiment.28,29 The position of the electron is determined by a 3-dimensional random walk which terminates when the mutual separation of the electron–hole pair reaches the pre-defined HCT separation, r. Hence HCT dissociation immediately results in the injection of an electron at a random position with pre-defined separation to the hole, r. The hole is always created at the interface between donor and acceptor (D:A morphologies) or mixed and aggregate (Mx:Ag morphologies) materials.
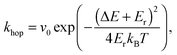 | (1) |
Behaviours for charges and excitons were determined by first calculating the rates for the various processes which can occur to the particle in question, and generating waiting times for each using the following equation:
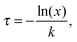 | (2) |
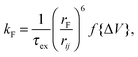 | (3) |
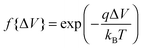 , whereas when ΔV < 0, f{ΔV} = 1. Here q is the electronic charge. This approach, which allows for microscopic variations in exciton transport due to disorder, was shown by Scheidler et al.51 to give excellent agreement with exciton decay dynamics in PPV. After each exciton hop, a check was performed to determine whether dissociation was permitted at the new location. If it was, the exciton immediately dissociated into charge carriers, implicitly assuming that exciton dissociation rate was much faster than other rates considered. If there was more than one option for dissociation (i.e. more than one interface was adjacent to the current site of the exciton), dissociation occurred at a randomly chosen interface. The carriers generated by exciton dissociation were then able to hop in the same manner as described above.
, whereas when ΔV < 0, f{ΔV} = 1. Here q is the electronic charge. This approach, which allows for microscopic variations in exciton transport due to disorder, was shown by Scheidler et al.51 to give excellent agreement with exciton decay dynamics in PPV. After each exciton hop, a check was performed to determine whether dissociation was permitted at the new location. If it was, the exciton immediately dissociated into charge carriers, implicitly assuming that exciton dissociation rate was much faster than other rates considered. If there was more than one option for dissociation (i.e. more than one interface was adjacent to the current site of the exciton), dissociation occurred at a randomly chosen interface. The carriers generated by exciton dissociation were then able to hop in the same manner as described above.
Charges were also injected into the device from both electrodes as dark (or diode) current. Injection rates were calculated as a Marcus hop (eqn (1)) of a carrier type from the corresponding electrode (holes from anode, electrons from cathode) to a site at the boundary of the simulation volume, using ΔE based on the bandgap, carrier injection barrier and potential of the destination site in a similar manner to Marsh et al.52 All parameters used in the simulations, including injection barriers and bandgaps, are included in the ESI† (Section S3).
Device simulations proceeded until the system had converged, usually after approximately 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photoinjections had been recorded. At this point the current density was calculated from the net rate of charges transferring out of the device. The power conversion efficiency (η) was calculated as a ratio of the output and input powers,
000 photoinjections had been recorded. At this point the current density was calculated from the net rate of charges transferring out of the device. The power conversion efficiency (η) was calculated as a ratio of the output and input powers,
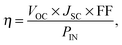 | (4) |
3. Results
3.1 Hot charge transfer states in donor:acceptor blends
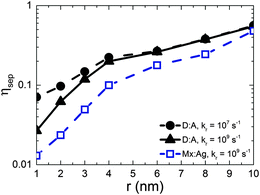
Fig. 2 shows the free-charge generation efficiency ηSEP as a function of HCT delocalisation, r for a D:A morphology. Two recombination rates are examined, kr = 1 × 107 s−1 which is similar to that found in all-polymer OPVs,50 and kr = 1 × 109 s−1, similar to that observed in polymer:fullerene OPVs.15–19 For bound CT states (r = 1 nm) it is seen that the higher recombination rate results in lower separation efficiency as expected. However, as r is increased, the separation efficiency increases for both recombination rates considered, with both curves intersecting at r beyond 4 nm.The free-charge generation efficiency measured here is most closely related to the internal quantum efficiency (IQE) of an OPV measured in experiment. Although the values of IQE measured can vary substantially depending on the treatment and manufacture of the device and the annealing conditions, efficient polymer:fullerene OPV systems typically have IQEs of the order of 50% or more. For example, unannealed P3HT:PC61BM devices produce an IQE of around 20% to 30%,53 while solvent54 and thermally annealed55 devices typically have IQE of approximately 65% and 80% respectively. Unannealed PTB7:PC71BM devices have an IQE of 65%,56 which increases to 85%57 after annealing. Other devices made from p-DTS(FBTTh2)2:PC71BM12 and PCDTBT:PC71BM13 have been reported to have IQEs that reach 80% and 100% respectively. In order to observe efficiencies close to 50% in the current simulations, it is necessary to have r = 10 nm. This contrasts with delocalisation of r ∼ 4 nm29 measured by experiment for DTS(FBTTh2)2:PC71BM and PCDTBT:PC71BM blends. It is difficult to reconcile IQE in excess of 80% with r ∼ 4 nm on the basis of the current KMC data.
Gélinas et al.29 note that the electro-absorption measurements are expected to be most sensitive to electron–hole separations of up to 5–6 nm, since the strength of the electro-absorption signal is proportional the dipolar field (i.e. ∝1/r). Hence it is possible that larger delocalisation occurs in these blends but it is not possible to detect with the electro-absorption technique. Another method to enquire whether HCT delocalisation occurs over larger lengthscales is quantum chemical calculations. Atomistic approaches to these calculations necessarily consider only a few molecules at the interface for computational reasons, and so maximal HCT state delocalisation is likely to be limited by the simulation volume (of the order Å nm).21,25 Troisi and co-workers suggest that long range exciton dissociation occurs with a rate which depends upon disorder,27 and in the limiting case of perfect order, the CT state separation is of the order of the chain length.26 However, TEM images on similar blends do not reveal the dimensions of fullerene aggregates in optimised blends12 so it is not currently possible to estimate the maximal extent of HCT delocalisation. Nonetheless, even if r were larger than suggested currently by experiment, the present KMC data suggest it would have to be significantly larger to be the sole cause of large IQE values seen in efficient OPVs.
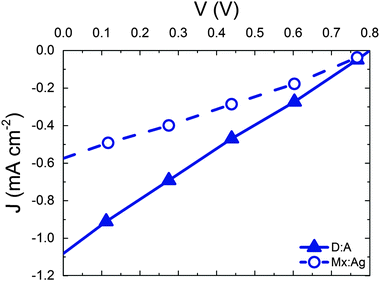
We now move on to consider the effect of r for D:A blends in the context of a complete OPV where both geminate and non-geminate recombination can occur. Fig. 3 shows the effect of varying r on the J–V curve and the consequent changes in power conversion efficiency, η for a D:A morphology with d = 7 nm and a recombination rate of kr = 1 × 109 s−1. The exciton dissociation and charge collection efficiencies for these morphologies are listed in the ESI† (Section S4). The J–V curve is largely unaffected when r is changed from 1 nm (i.e. a bound CT state) to r = 2 nm. Further increases in delocalisation beyond r = 2 nm results in an approximately linear increase in power conversion efficiency, η which is largely due to changes in the short circuit current, JSC. The approximately linear variation of η with r is in accordance with the approximately linear variation of ηSEP with r shown in Fig. 2.
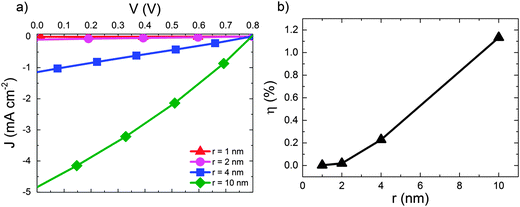 | ||
| Fig. 3 (a) J–V curves for device simulations with increasing r for D:A morphology with d = 7 nm. In all cases kr = 1 × 109 s−1. (b) The corresponding power conversion efficiencies, η. | ||
3.2 Hot charge transfer states in mixed:aggregate blends
Having considered the effect of HCT states in the idealised case of D:A morphologies, we now turn our attention to mixed:aggregate (Mx:Ag) morphologies, which are common in polymer:fullerene OPVs with high IQEs.30,31,58,59 Furthermore, polymer:fullerene blends are most strongly linked with the presence of HCT states.21,25,28,29 The details of charge generation and transport are, as mentioned previously, different in the case of the Mx:Ag morphologies: electrons are here assumed to move throughout the entire volume and holes are confined to the mixed phase, while delocalised HCT states occur only at the interface between mixed and aggregate regions. These assumptions, based on observations in experiment,28,29 would be expected to change the efficiency of both free-charge generation and OPV performance when compared to the D:A morphologies considered previously. Fig. 2 shows ηSEP for both a d = 7 nm D:A and a d = 7 nm, β = 0.396 Mx:Ag morphology. This clearly shows the negative effect of the mixed phase on free-charge generation both for bound CT states (r = 1 nm) and HCT states (r > 1 nm). This is perhaps to be expected since it has been reported previously that constraining charge transport to donor and acceptor regions improves free-charge generation.60 The presence of the mixed phase reduces the free-charge generation efficiency still further below that observed in experiment. Even when HCT states occur with a delocalisation in excess of that measured experimentally (r = 10 nm), ηSEP is predicted to only reach 10% for Mx:Ag morphologies.Fig. 4 compares the predicted J–V characteristics of the same two morphologies, where HCT states are assumed to be created with r = 4 nm. This shows that the mixed phase is especially detrimental to the short circuit current. We note as an aside that the total fraction of non-geminate recombination at short circuit for the Mx:Ag morphology was measured as 14%, whereas the fraction of non-geminate recombination at short circuit for the D:A morphology is only 0.1%. While it is perhaps expected that the lack of a phase-separated structure would increase non-geminate recombination,61 it is noteworthy that KMC models assuming a phase-separated D:A morphology typically predict geminate recombination as the major loss mechanism in OPVs.62,63 Therefore the presence of a mixed phase in the current KMC model appears to reconcile the predicted mode of recombination with that measured for some polymer:fullerene OPVs.64,65
In summary, although we predict that HCT states can be beneficial to the performance of polymer:fullerene OPVs, the presence of the mixed phase limits the efficiency that can be obtained. We note that this conclusion is not sensitive to our assumptions of when the HCT state is, and is not formed, since further simulations (in ESI† Section S5) show that allowing all dissociated excitons to form HCT states still leads to J–V characteristics which were inferior to the corresponding D:A morphology.
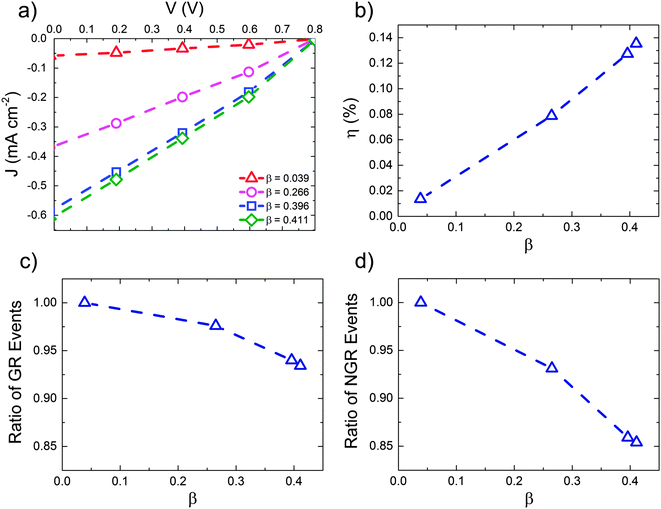
These data suggest that the form of the Mx:Ag morphology is important in determining the performance of the OPV when HCT states are present. Fig. 5 below examines this in more detail by showing the predicted J–V characteristics of Mx:Ag blends which vary in the proportion acceptor aggregate regions, β. In all cases we assume exciton dissociation at Mx:Ag interfaces result in HCT states with r = 4 nm, while in mixed phases exciton dissociation generate bound CT states with r = 1 nm. Again, the exciton dissociation and charge collection efficiencies for these morphologies are listed in the ESI† (Section S4).
The power conversion efficiency (panel (b)) is shown to increase mostly linearly with fullerene aggregate proportion, β over the range examined. Similar behaviour has been observed experimentally for P3HT:PC61BM devices with varying degree of fullerene aggregation.30 The number of charge recombination events (panels (c) and (d)) decrease approximately linearly with increasing aggregate proportion. Increased aggregation allows more HCT states to be formed, resulting in better overall free-charge generation. Increasing aggregation also leads to a reduction in the degree of non-geminate recombination, due to the fact that electrons are increasingly likely to inhabit aggregated regions where they are protected from recombination.61 Note, however, that further increases in aggregate proportion would at some point lead to reduced exciton dissociation efficiency and OPV performance due to a lack of heterojunctions.
Our simulations therefore demonstrate that morphology plays a role in the efficacy of HCT states, primarily via determining what fraction of generated excitons go on to form HCT states. We also show, however, that even with optimised Mx:Ag morphologies, and HCT delocalisation r = 4 nm associated with acceptor aggregates, the predicted power conversion efficiency of the OPV is not as high as that measured experimentally.
4. Discussion
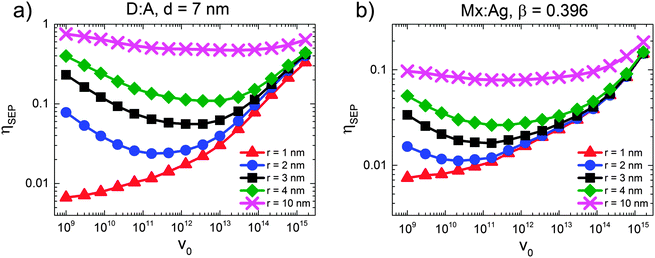
This poses the question as to why HCT states provide only moderately efficient free-charge generation in polymer:fullerene OPVs. In order to investigate this question further, we simulated the free-charge generation efficiency of HCT states as a function of electron mobility pre-factor (v0) for both D:A and Mx:Ag morphologies, as shown in Fig. 6. A range of r was considered, with r = 1 corresponding to bound CT states and r > 1 nm corresponding to HCT states, such that the difference between the r = 1 nm and r > 1 nm curves represents the benefit offered by delocalisation of the HCT state. Fig. 6 therefore examines the interplay between the energetics of free-charge generation, controlled by initial delocalisation, r, and the kinetics of free-charge generation, controlled by electron mobility pre-factor, v0. For HCT states the same general behaviour is observed for all curves, namely that ηSEP first decreases with increasing v0 (mobility prefactor), before eventually increasing when v0 increases further. This is counter-intuitive, since one might expect that an increase in mobility would always lead to an improvement in ηSEP. The point at which ηSEP begins to increase with v0 varies depending on r, but for orientation, v0 = 1012 s−1 which is close to the bottom of the parabola for most curves, corresponds to μ ∼ 1 × 10−2 cm2 V−1 s−1.Jailaubekov et al.25 anticipated that the benefit of HCT states to free-charge generation is time-limited, and so to some extent dependent on kinetics. This is because HCT states are expected to have Coulomb binding energies, EC > kT (i.e. r < 15–20 nm), hence they will relax to a bound CT state unless they separate into free charges first.20,66,67Fig. 6 shows that free-charge generation becomes less dependent on transport kinetics (v0) as delocalisation (r) increases. We attribute this to EC approaching kT, meaning that separation becomes more energetically favourable. However, we note that r in the region of 10 nm is not expected on the basis of current experiments.29 When r is of the order of a few nm, as anticipated by experiment, the benefit offered by HCT states is strongly dependent on the kinetics of charge transport (v0). While Jailaubekov et al.25 suggested that kinetics has a strong role to play in determining the efficacy of HCT state dissociation, the trends observed here are counter to what would be expected if transient HCT delocalisation sets a ‘time limit’ for free-charge generation, since both positive and negative dependencies on v0 are observed. We explain these trends as follows.
When r is small, the Coulomb binding energy is large, and so relaxation of the HCT state into a bound CT state is both fast and efficient. Therefore, in order to observe a benefit from the HCT state it is necessary to have slow electron transport (small v0) in order to allow the hole the opportunity to escape. Once one views low electron mobility as beneficial to charge separation when r is small but greater than 1 nm, it is possible to explain the reduction in ηSEP when mobility increases as shown in Fig. 6. In this region, increasing electron mobility reduces the likelihood that the electron will be trapped in a position where recombination is not possible, therefore making the electron more available for recombination and reducing ηSEP. We argue that this is unlikely to apply in polymer:fullerene OPVs, since the mobility of electrons in aggregated fullerene regions is expected to be large.68 Increasing the mobility (v0) still further is shown to increase ηSEP when r is small. However, in this case, the improvement in ηSEP is due to charge transport competing effectively with recombination rather than HCT states. On the basis of these simulations, the anticipated transient benefit of HCT states is anticipated to be small, and suggest that efficient free-charge generation is via the bound CT state.32–35
The current simulations seem to suggest that relaxation of the HCT state to a bound CT state is fast, in turn suggesting that free-charge generation proceeds from the bound CT state. This poses the question of how efficient charge generation is possible from the bound CT state. It has been suggested that polymer packing improves further away from the donor–acceptor interface, and that better packing leads to a reduced bandgap, in turn creating a cascaded energy heterojunction that drives charge separation.35,69,70 KMC simulations predict efficient (i.e. ηSEP > 80%), field-independent free-charge generation for cascaded energy heterojunctions using energy levels in the range reported by experiment and calculation.67,71 KMC has shown that cascades are more effective still if the mobility of charges is large over short lengthscales,72 as may be expected from microwave conductivity measurements.46 Aggregation of fullerenes also leads to a variation in the fullerene LUMO energy of the order of 100 meV,30 which in turn encourages electrons to transfer to the aggregate. Efficient free-charge generation via cascades67,71 contrasts with that via HCT states in an important detail. Both Groves71 and Burke and McGehee67 predict that substantial improvements in the free-charge generation efficiency begin to occur when the cascade energy (i.e. the energy offset encouraging charge separation) is in the region of 150–200 meV. This roughly coincides with the energy required to move a charge from a mutual separation of 1 nm to 2 nm (230 meV for ε = 3). Hence, cascaded energy heterojunctions are predicted to give efficient charge generation when the bound CT state always favours charge separation, as opposed to the transient advantage offered by HCT states.25
Although cascaded energy heterojunctions appear to explain efficient free-charge generation in systems where either the polymer packs or fullerene aggregates in localised regions, it is possible that similar energy gradients could be provided by other mechanisms. In particular, quantum chemical calculations have shown that electrostatic interactions between permanent charges on the donor and acceptor molecules can modify the energetic landscape in the few nanometres around the heterojunction.35,69,73–75 These interactions can either reduce or increase the barrier to charge separation depending upon the particular molecular packing35,73,74 and materials combination.35,75 Perhaps more generally, energetic gradients to drive charge separation could be provided by relaxation of charges within the density of states.69,76,77 However, in this case, a majority of KMC investigations appear to indicate that relaxation alone is insufficient to obtain the high efficiencies seen in polymer-fullerene OPVs.20,63
Of course, HCT states,21,22,25,26 spatial variation in energy levels due to aggregation or packing,35,67,69–71 and electrostatic interactions between donor and acceptor,35,69,73–75 are not mutually exclusive, and indeed, fullerene aggregation is seen to be a pre-requisite to the first two mechanisms in providing efficient free-charge generation. Consequently we speculate that HCT states are the cause of fast charge generation seen in spectroscopy, but that arrangement of energy levels in the region of the heterojunction is the cause of long-term separation of charges ultimately leading to high quantum efficiencies seen in devices.
5. Conclusions
We have used Monte Carlo simulations to show that HCT states enhance free-charge generation in both donor:acceptor morphologies and mixed:aggregate morphologies. Fullerene aggregation within the mixed phase is shown to enhance OPV efficiency, largely via the increased production of HCT states in the fullerene aggregate, leading to an enhanced short circuit current. However, in order to observe free-charge generation efficiencies seen in experiment, unphysical kinetics and HCT state delocalisation have to be assumed. One case which is predicted to give efficient free-charge generation is when delocalisation is of the order ∼10 nm, meaning that the Coulomb binding energy approaches kT and separation is energetically favoured. This delocalisation is larger than that observed in experiment (r ∼ 4 nm). The other case which provides efficient free-charge generation for smaller values of r (∼4 nm) occurs when the electron mobility is small and recombination is kinetically unfavourable. Small electron mobilities in the fullerene aggregates are not expected. Since neither circumstance are expected to occur, we suggest that HCT states are unlikely to be the sole reason why some polymer:fullerene OPVs have large efficiencies.Other KMC simulations have considered the effect of cascaded energy heterojunctions on free-charge generation and predicted efficient operation when considering cascade parameters taken from experiment,71 and still better performance when one includes locally high mobilities expected as a result of microwave conductivity measurements.67 Based on these data it would seem that variation in energy levels close to the heterojunction play a more significant role in efficient polymer:fullerene OPV operation than HCT states.
Associated content
Access to underlying research materials: the software code used to analyze the data is copyright to Durham University subject to license by Cambridge University Enterprise; the data is held by Durham University and can be accessed by contacting the corresponding author.Acknowledgements
MLJ has a scholarship funded by an EPSRC doctoral training award.References
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CAS.
- J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti and A. B. Holmes, Nature, 1995, 376, 498–500 CrossRef CAS.
- Y. Liang, Z. Xu, J. Xia, S. Tsai, Y. Wu, G. Li, C. Ray and L. Yu, Adv. Mater., 2010, 22, E135–E138 CrossRef CAS PubMed.
- Z. He, C. Zhong, S. Su, M. Xu, H. Wu and Y. Cao, Nat. Photonics, 2012, 6, 591–595 Search PubMed.
- C. J. Brabec, S. Gowrisanker, J. J. M. Halls, D. Laird, S. Jia and S. P. Williams, Adv. Mater., 2010, 22, 3839–3856 CrossRef CAS PubMed.
- Y. Li, Acc. Chem. Res., 2012, 45, 723–733 CrossRef CAS PubMed.
- C. J. Brabec, M. Heeney, I. McCulloch and J. Nelson, Chem. Soc. Rev., 2011, 40, 1185–1199 RSC.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed.
- C. Groves, Energy Environ. Sci., 2013, 6, 3202–3217 CAS.
- K. Vandewal, S. Himmelberger and A. Salleo, Macromolecules, 2013, 46, 6379–6387 CrossRef CAS.
- J. L. Brédas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1699 CrossRef PubMed.
- J. A. Love, C. M. Proctor, J. Liu, C. J. Takacs, A. Sharenko, T. S. van der Poll, A. J. Heeger, G. C. Bazan and T.-Q. Nguyen, Adv. Funct. Mater., 2013, 23, 5019–5026 CrossRef CAS.
- S. H. Park, A. Roy, S. Beaupre, S. Cho, N. Coates, J. S. Moon, D. Moses, M. Leclerc, K. Lee and A. J. Heeger, Nat. Photonics, 2009, 3, 297–302 CrossRef CAS.
- S. F. Alvarado, P. F. Seidler, D. G. Lidzey and D. D. C. Bradley, Phys. Rev. Lett., 1998, 81, 1082–1085 CrossRef CAS.
- I. A. Howard, R. Mauer, M. Meister and F. Laquai, J. Am. Chem. Soc., 2010, 132, 14866–14876 CrossRef CAS PubMed.
- I.-W. Hwang, D. Moses and A. J. Heeger, J. Phys. Chem. C, 2008, 112, 4350–4354 CAS.
- S. C. J. Meskers, P. A. van Hal, A. J. H. Spiering, J. C. Hummelen, A. F. G. van der Meer and R. A. J. Janssen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9917–9920 CrossRef CAS.
- S. De, T. Pascher, M. Maiti, K. G. Jespersen, T. Kesti, F. L. Zhang, O. Inganäs, A. Yartsev and V. Sundström, J. Am. Chem. Soc., 2007, 129, 8466–8472 CrossRef CAS PubMed.
- A. A. Bakulin, D. S. Martyanov, D. Y. Paraschuk, M. S. Psehnichnikov and P. H. M. Van Loosdrecht, J. Phys. Chem. B, 2008, 112, 13730–13737 CrossRef CAS PubMed.
- C. Groves, R. A. Marsh and N. C. Greenham, J. Chem. Phys., 2008, 129, 114903 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H. J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef CAS PubMed.
- I.-W. Hwang, C. Soci, D. Moses, Z. Zhu, D. Waller, R. Gaudiana, C. J. Brabec and A. J. Heeger, Adv. Mater., 2007, 19, 2307–2312 CrossRef CAS.
- F. Etzold, I. A. Howard, R. Mauer, M. Meister, T.-D. Kim, K.-S. Lee, N. S. Baek and F. Laquai, J. Am. Chem. Soc., 2012, 134, 10569–10583 CrossRef CAS PubMed.
- A. E. Jailaubekov, A. P. Willard, J. R. Tritsch, W. L. Chan, N. Sai, R. Gearba, L. G. Kaake, K. J. Williams, K. Leung, P. J. Rossky and X. Y. Zhu, Nat. Mater., 2013, 12, 66–73 CrossRef CAS PubMed.
- H. Vázquez and A. Troisi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 205304 CrossRef.
- A. Troisi, Faraday Discuss., 2013, 163, 377–392 RSC.
- B. M. Savoie, A. Rao, A. A. Bakulin, S. Gélinas, B. Movaghar, R. H. Friend, T. J. Marks and M. A. Ratner, J. Am. Chem. Soc., 2014, 136, 2876–2884 CrossRef CAS PubMed.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef PubMed.
- F. C. Jamieson, E. B. Domingo, T. McCarthy-Ward, M. Heeney, N. Stingelin and J. R. Durrant, Chem. Sci., 2012, 3, 485–492 RSC.
- B. A. Collins, Z. Li, J. R. Tumbleston, E. Gann, C. R. McNeill and H. Ade, Adv. Energy Mater., 2012, 3, 65–74 CrossRef.
- T. G. J. van der Hofstad, D. Di Nuzzo, M. van den Berg, R. A. J. Janssen and S. C. J. Meskers, Adv. Energy Mater., 2012, 2, 1095–1099 CrossRef CAS.
- K. Vanderwal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. J. Fréchet, A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Nat. Mater., 2014, 13, 63–68 CrossRef PubMed.
- J. Lee, K. Vandewal, S. R. Yost, M. E. Bahlke, L. Goris, M. A. Baldo, J. V. Manca and T. V. Voorhis, J. Am. Chem. Soc., 2010, 132, 11878–11880 CrossRef CAS PubMed.
- S. R. Yost and T. Van Voorhis, J. Phys. Chem. C, 2013, 117, 5617–5625 CAS.
- C. Groves, R. G. E. Kimber and A. B. Walker, J. Chem. Phys., 2010, 133, 144110 CrossRef PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS PubMed.
- B. P. Lyons, N. Clarke and C. Groves, J. Phys. Chem. C, 2011, 115, 22572–22577 CAS.
- B. P. Lyons, N. Clarke and C. Groves, Energy Environ. Sci., 2012, 5, 7657–7663 CAS.
- I. C. Henderson and N. Clarke, Macromol. Theory Simul., 2005, 14, 435–443 CrossRef CAS.
- M. L. Jones, B. Chakrabarti and C. Groves, J. Phys. Chem. C, 2014, 118, 85–91 CAS.
- S. Kouijzer, J. J. Michels, M. van den Berg, V. S. Gevaerts, M. Turbiez, M. M. Wienk and R. A. J. Janssen, J. Am. Chem. Soc., 2013, 135, 12057–12067 CrossRef CAS PubMed.
- O. Wodo and B. Ganapathysubramanian, Comput. Mater. Sci., 2012, 55, 113–126 CrossRef CAS PubMed.
- J. J. Michels and E. Moons, Macromolecules, 2013, 46, 8693–8701 CrossRef CAS.
- O. Wodo, S. Tirthapura, S. Chaudhary and B. Ganapathysubramanian, Org. Electron., 2012, 13, 1105–1113 CrossRef CAS PubMed.
- G. Dicker, M. P. de Haas, L. D. A. Siebbeles and J. M. Warman, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045203 CrossRef.
- R. C. I. MacKenzie, T. Kirchartz, G. F. A. Dibb and J. Nelson, J. Phys. Chem. C, 2011, 115, 9806–9813 CAS.
- S. A. Choulis, Y. Kim, J. Nelson, D. D. C. Bradley, M. Giles, M. Shkunov and I. McCulloch, Appl. Phys. Lett., 2004, 85, 3890–3892 CrossRef CAS PubMed.
- N. D. Treat, A. Varotto, C. J. Takacs, N. Batara, M. Al-Hashimi, M. J. Heeney, A. J. Heeger, F. Wudl, C. J. Hawker and M. L. Chabinyc, J. Am. Chem. Soc., 2012, 134, 15869–15879 CrossRef CAS PubMed.
- S. Westenhoff, I. A. Howard, J. M. Hodgkiss, K. R. Kirov, H. A. Bronstein, C. K. Williams, N. C. Greenham and R. H. Friend, J. Am. Chem. Soc., 2008, 130, 13653–13658 CrossRef CAS PubMed.
- M. Scheidler, U. Lemmer, R. Kersting, S. Karg, W. Riess, B. Cleve, R. F. Mahrt, H. Kurz, H. Bassler, E. O. Gobel and P. Thomas, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5536–5544 CrossRef CAS.
- R. A. Marsh, C. Groves and N. C. Greenham, J. Appl. Phys., 2007, 101, 083509 CrossRef PubMed.
- R. A. Marsh, J. M. Hodgkiss, S. Albert-Seifried and R. H. Friend, Nano Lett., 2010, 10, 923–930 CrossRef CAS PubMed.
- J. Jo, S.-I. Na, S.-S. Kim, T.-W. Lee, Y. Chung, S.-J. Kang, D. Vak and D.-Y. Kim, Adv. Funct. Mater., 2009, 19, 2398–2406 CrossRef CAS.
- S. Honda, T. Nogami, H. Ohkita, H. Benten and S. Ito, ACS Appl. Mater. Interfaces, 2009, 1, 804–810 CAS.
- B. A. Collins, Z. Li, J. R. Tumbleston, E. Gann, C. R. McNeill and H. Ade, Adv. Energy Mater., 2013, 3, 65–74 CrossRef CAS.
- H. Zhou, Y. Zhang, J. Seifter, S. D. Collins, C. Luo, G. C. Bazan, T.-Q. Nguyen and A. J. Heeger, Adv. Mater., 2013, 25, 1646–1652 CrossRef CAS PubMed.
- B. A. Collins, J. R. Tumbleston and H. Ade, J. Phys. Chem. Lett., 2011, 2, 3135–3145 CrossRef CAS.
- S. Shoaee, S. Subramaniyan, H. Xin, C. Keiderling, P. S. Tuladhar, F. Jamieson, S. A. Jenekhe and J. R. Durrant, Adv. Funct. Mater., 2013, 23, 3286–3298 CrossRef CAS.
- P. Peumans and S. R. Forrest, Chem. Phys. Lett., 2004, 398, 27–31 CrossRef CAS PubMed.
- C. Groves and N. C. Greenham, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155205 CrossRef.
- R. A. Marsh, C. Groves and N. C. Greenham, J. Appl. Phys., 2007, 101, 083509 CrossRef PubMed.
- C. Groves, J. C. Blakesley and N. C. Greenham, Nano Lett., 2010, 10, 1063–1069 CrossRef CAS PubMed.
- C. G. Shuttle, B. O'Regan, A. M. Ballantyne, J. Nelson, D. D. C. Bradley and J. R. Durrant, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113201 CrossRef.
- G. F. A. Dibb, F. C. Jamieson, A. Maurano, J. Nelson and J. R. Durrant, J. Phys. Chem. Lett., 2013, 803–808 CrossRef CAS.
- R. G. E. Kimber, A. B. Walker, G. E. Schroder-Turk and D. J. Cleaver, Phys. Chem. Chem. Phys., 2010, 12, 844–851 RSC.
- T. M. Burke and M. D. McGehee, Adv. Mater., 2014, 26, 1923–1928 CrossRef CAS PubMed.
- D. Veldmann, Ö. Ipek, S. C. J. Meskers, J. Sweelssen, M. M. Koetse, S. C. Veenstra, J. M. Kroon, S. S. van Bavel, J. Loos and R. A. J. Janssen, J. Am. Chem. Soc., 2008, 130, 7721–7735 CrossRef PubMed.
- G. D'Avino, S. Mothy, L. Muccioli, C. Zannoni, L. Wang, J. Cornil, D. Beljonne and F. Castet, J. Phys. Chem. C, 2013, 117, 12981–12990 Search PubMed.
- D. P. McMahon, D. L. Cheung and A. Troisi, J. Phys. Chem. Lett., 2011, 2, 2737–2741 CrossRef CAS.
- C. Groves, Energy Environ. Sci., 2013, 6, 1546–1551 CAS.
- T. M. Burke and M. D. McGehee, Adv. Mater., 2014, 26, 1923–1928, DOI:10.1002/adma.201304241.
- J. Idé, S. Mothy, A. Savoyant, A. Fritsch, P. Aurel, R. Méreau, L. Ducasse, J. Cornil, D. Beljonne and F. Castet, Int. J. Quantum Chem., 2012, 113, 580–584 CrossRef.
- J. Idé, R. Mereau, L. Ducasse, F. Castet, H. Bock, Y. Olivier, J. Cornil, D. Beljonne, G. D'Avino, O. M. Roscioni, L. Muccioli and C. Zannoni, J. Am. Chem. Soc., 2014, 136, 2911–2920 CrossRef PubMed.
- S. Mothy, M. Guillaume, J. Ide, F. Castet, L. Ducasse, J. Cornil and D. Beljonne, J. Phys. Chem. Lett., 2012, 3, 2374–2378 CrossRef CAS.
- H. van Eersel, R. A. J. Janssen and M. Kemerink, Adv. Funct. Mater., 2012, 22, 2700–2708 CrossRef CAS.
- U. Albrecht and H. Bassler, Chem. Phys. Lett., 1995, 235, 389–393 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp01626b |
| This journal is © the Owner Societies 2014 |