Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DFT studies of oxygen dissociation on the 116-atom platinum truncated octahedron particle†
Paul C.
Jennings‡
 a,
Hristiyan A.
Aleksandrov
bc,
Konstantin M.
Neyman
bd and
Roy L.
Johnston
*e
a,
Hristiyan A.
Aleksandrov
bc,
Konstantin M.
Neyman
bd and
Roy L.
Johnston
*e
aSchool of Chemical Engineering, University of Birmingham, Birmingham, UK
bDepartament de Química Física & IQTCUB, Universitat de Barcelona, Spain
cFaculty of Chemistry and Pharmacy, University of Sofia, Sofia, Bulgaria
dInstitució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona, Spain
eSchool of Chemistry, University of Birmingham, Birmingham, UK. E-mail: r.l.johnston@bham.ac.uk; Fax: +44 (0)121 414 4403; Tel: +44 (0)121 414 7477
First published on 15th July 2014
Abstract
Density functional theory calculations are performed to investigate oxygen dissociation on 116-atom truncated octahedron platinum particles. This work builds on results presented previously [Jennings et al., Nanoscale, 2014, 6, 1153], where it was shown that shell flexibility played an important role in facilitating fast oxygen dissociation. In this study, through investigation of the larger particle size, it is shown that oxygen dissociation on the (111) facet of pure platinum species is still aided by shell flexibility at larger sizes. Only the hollow sites close to the edges of the (111) facet mediate oxygen dissociation; oxygen is bound too weakly at other hollow sites for dissociation to occur. Further studies are performed on the (100) facet, which is larger for the Pt116 particle than for either the Pt38 or Pt79 ones. Much higher dissociation barriers are found on the (100) facet compared to the (111) facet, where the bridge sites are favourable for oxygen dissociation.
1 Introduction
The interest in platinum (Pt) systems is due in part to the relevance of Pt based catalysts in many industrial applications, such as catalysing the oxygen reduction reaction (ORR) in hydrogen fuel cells.1–4 For low temperature fuel cells, a common problem associated with the use of a Pt electrocatalyst is the strong Pt–O binding, which aids oxygen dissociation, but is responsible for reducing the rate of the ORR.5–7 Modelling of the ORR is a very active area of research, with emphasis on computing the overall mechanism,8–12 as well as chemisorption studies of specific intermediates within the reaction.13–15Oxygen chemisorption studies have been performed on a number of extended Pt surfaces,16–18 although there is also significant interest in the study of both free19–21 and supported particle systems.22,23 Nanoparticle models can offer a greater number of symmetry inequivalent sites at which to bind oxygen and in the size regime where “each atom counts”,24 properties are often dominated by quantum effects. For these structures, the under-coordinated surface atoms of the particles provide a diverse range of electronic environments at which to bind O.25 However, it should be noted that it is also possible to use particle models that are scalable with size.26–28 In the work presented here, focus is placed on investigating O2 dissociation on Pt particles. The behaviour of O2 dissociation on Pt surfaces has been studied extensively. Whilst this has predominantly focused on bulk systems,29–36 some studies have been performed on small particles.37–40
In work published previously, we showed that when Pt is alloyed with titanium (Ti) to produce core–shell Ti@Pt moieties, changes in the electronic structure of the nanoparticle result in weaker Pt–O binding, through filling of the Pt d-band;41,42 where similar trends have been found for a number of other Pt based alloy systems.43–45 In later studies, it was found that whilst the strong core–shell interactions could result in a favourable reduction of Pt–O binding energies, these strong Pt–M interactions also inhibited oxygen dissociation. Shell flexibility plays an important role in facilitating fast oxygen dissociation, where on pure Pt particles the outermost shell can distort in such a way as to reduce the O2 dissociation barrier from 0.4 eV on the (111) bulk slab, to <0.1 eV on the (111) facet of the particle.46
The previous studies on oxygen dissociation were performed on 38- and 79-atom particles.46 It is noted that other studies found significant variation in adsorption energies of O on small Pt particles, when nearby facets were modified;47 although, this appears less pronounced for particle sizes >80 atoms. Therefore, size effects potentially play an important role in O binding as well as flexibility of the Pt shell for the small particle sizes investigated previously. In the work presented here, O2 dissociation studies are performed on the larger truncated octahedron (TO) Pt116 nanoparticles, which should be in the range that scales with size. It allows the investigation of, not only the size dependance of (111) facet flexibility, but also perform a more detailed study of the (100) facet. Although in the previous studies the (100) facet exhibited far higher dissociation barriers, the Pt116(100) facet is larger and allows for additional O2 adsorption sites to be investigated.
2 Methodology
Calculations are performed using the Vienna Ab-initio Simulation Package (VASP) 5.2.48–51 For all atom types, the valence electrons are treated explicitly, while the ionic cores are represented by the projected augmented wave (PAW) method.52,53 Electronic exchange and correlation are described using the generalised gradient approximation (GGA) using the Perdew–Wang 91 (PW91) formula.54,55 The Methfessel–Paxton smearing method is used with a width of 0.1 eV (extrapolated for computing final energies at zero smearing) and an energy cutoff of 415.0 eV has been employed. All particles are placed in the centre of large enough supercells to ensure sufficient separation of 10 Å between periodic images. The Γ point is used to sample the Brillouin Zone. Atoms are then relaxed according to the calculated atomic forces, with convergence criteria for energies and forces required to be better than 1.0 × 10−4 eV per atom and 0.02 eV Å−1, respectively.Dissociation pathways are investigated using the Transition State Tools implementation of the VASP code, by first generating an approximate pathway using the Nudged Elastic Band (NEB) method,56 with further refinements achieved using the Dimer method.57 Charges are calculated using the Bader method.58,59
In order to assess the (atomic or molecular) oxygen adsorption strength to the Pt surface, the binding energy (Eb) is calculated, as defined in eqn (1).
| Eb = EAB − (EA + EB) | (1) |
| Eint = EAB − (EA* + EB*) | (2) |
| ΔEA = EA − EA* | (3) |
Although specific distortions, brought about by adsorption of oxygen, are discussed in detail, as a more general measure root mean squared displacements (RMSD) of atoms are calculated as defined in eqn (4).
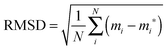 | (4) |
3 Results and discussion
3.1 Oxygen adsorption
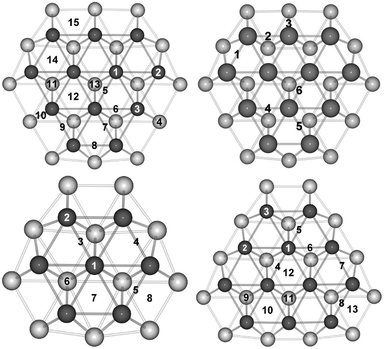
In the previous studies, the Pt79 TO model showed similar trends to the Pt38 TO, although further site dependent trends were observed for the 79-atom particle that were not present on the limited (111) facet of the 38-atom particle. Therefore, in this study, one further particle size is considered for the pure Pt system. On the surface of the 116-atom TO model there are 15 symmetry inequivalent sites which are depicted in Fig. 1. The results of atomic and molecular oxygen adsorption on Pt116 are presented in Table 1.| Site | Position | Pt116–O | Pt116–O2 |
|---|---|---|---|
| a Adsorbate migration to position 14. b Adsorbate migration to position 13. c Adsorbate migration to position 9. d Adsorbate migration to positions 9 and 10. e Adsorbate migration to position 12. f Adsorbate migration to position 11. | |||
| 1 | Top | —a | —b |
| 2 | Top | −4.26 | −0.66 |
| 3 | Top | −3.92 | —c |
| 4 | Top | −3.58 | —d |
| 5 | Bridge | −e | −0.83 |
| 6 | Bridge | —f | −0.93 |
| 7 | Bridge | —a | −1.17 |
| 8 | Bridge | −4.92 | −1.87 |
| 9 | Bridge | −5.02 | −1.68 |
| 10 | Bridge | −4.76 | −1.34 |
| 11 | hcp | −4.66 | −0.99 |
| 12 | fcc | −4.65 | −0.88 |
| 13 | hcp | −4.42 | −0.68 |
| 14 | fcc | −4.79 | −1.07 |
| 15 | 4-Fold hollow | —c | —d |
Atomic oxygen is preferentially adsorbed at site 9, the edge-bridge position between the (111) and (100) facets, with a binding energy of −5.02 eV. This is in agreement with the studies on the Pt79 model. Whilst the atomic oxygen preferentially binds to the hcp hollow site (more stable by ≥0.09 eV than the edge-bridge sites) on the 38-atom moiety, favourable binding is observed to the edge-bridge position between two (111) facets (strengthened by ≥0.06 eV compared to hollow sites). This shows that there is competition between atomic oxygen adsorption on the edge-bridge and hollow sites on the 38- and 79-atom particles. However, on the 116-atom particle, the edge-bridge site between the (111) and (100) facets are found to be ≥0.23 eV more stable when compared to the hollow positions. This indicates that, as the particle size increases, there is a move away from the hollow sites directed towards the edge-bridge sites. The exact edge-bridge position also varies as seen when comparing Pt79, where the edge-bridge position between two (111) facets is favourable, to Pt116, where the edge-bridge site between the (111) and (100) facets is favourable.
O2 is preferentially adsorbed at position 8, the edge-bridge site between the two (111) facets. This is in agreement with results for Pt79, although it is found that the edge-bridge site between the (111) and (100) facets is most favourable for Pt38. O2 at the edge-bridge site is found to be ≥0.17 eV lower in energy than at hollow sites on Pt38, suggesting more site preference for O2 binding when compared with atomic oxygen. This is also seen for the 79- and 116-atom species, where the preference for binding to edge-bridge sites over hollow sites is ≥0.70 and ≥0.80 eV, respectively. This also manifests size dependence, where the energy difference between the edge-bridge and hollow sites increases as particle size increases.
O2 dissociation is investigated for sites on both the (111) and (100) facets. For Pt116, bridge sites 8, 9 and 10 have been investigated as well as hollow sites 11, 12 and 14. O2 dissociation proceeds from an initial site and terminates at the central hollow position on the (111) facet (site 13). Any further migration of the atomic oxygen to other positions on the particle would lead to additional small barriers associated with moving between different sites but would have little importance. The central hollow site of the (111) facet was also investigated, although found to be unfavourable for O2 dissociation, which is likely due to the small (in magnitude) O2 binding energy of −0.68 eV.
3.2 Barriers for O2 dissociation
Representations of the minimised geometries for the initial, transition and final states (IS, TS and FS, respectively) can be found in the ESI,† Fig. S1–S6. For comparative purposes, the minimised geometries for the initial, transition and final states of the extended Pt(111) surface can be found in the ESI,† Fig. S7. A greater range of facet sites were studied for Pt116, these included similar (111) hollow sites to those investigated previously (positions 11, 12, 13 and 14) but also a greater range of bridge sites (positions 5, 6, 7, 8, 9, and 10). As with Pt79, the (111) hollow site at the centre of the (111) facet, position 13, is found to exhibit weak Pt–O binding. This explains why the attempted O2 dissociation studies were not successful, where the O2 molecule favours migration away from the initial facet position, towards a more favourable one, instead of dissociating.Relatively low binding energies are found for bridge positions 5, 6 and 7, −0.83 to −1.17 eV. Instead of O2 dissociation barriers being located for these positions, small barriers, ∼0.1 eV are found for O2 migration to a preferential site, e.g. an edge-hollow site. This suggests that, where possible, O2 migrates to favourable binding sites prior to dissociation. Details for the positions at which dissociation barriers were located are given in Table 2.
| ΔE(Pt116) | RMSD | ΔE(O2) | E int | E b | ΔE≠ | |
|---|---|---|---|---|---|---|
| a Values for ΔE(Ptsurf). b RMSD values for entire slab. | ||||||
| Initial state | ||||||
| Pt116-8 | 0.10 | 0.04 | 0.70 | −2.67 | 1.87 | |
| Pt116-9 | 0.38 | 0.14 | 0.56 | −2.63 | 1.68 | |
| Pt116-10 | 0.34 | 0.11 | 0.51 | −2.19 | −1.34 | |
| Pt116-11 | 0.20 | 0.07 | 0.84 | −2.03 | −0.99 | |
| Pt116-12 | 0.65 | 0.16 | 0.91 | −2.43 | −0.88 | |
| Pt116-14 | 0.23 | 0.07 | 0.91 | −2.21 | −1.07 | |
| Pt(111) slab | 0.17a | 0.03b | 0.64 | −1.67 | −0.86 | |
| Transition state | ||||||
| Pt116-8 | 0.21 | 0.09 | 5.15 | −6.91 | −1.56 | 0.32 |
| Pt116-9 | 0.47 | 0.16 | 5.58 | −7.33 | −1.27 | 0.41 |
| Pt116-10 | 0.44 | 0.14 | 5.84 | −6.92 | −0.64 | 0.69 |
| Pt116-11 | 0.84 | 0.21 | 2.35 | −4.11 | −0.91 | 0.08 |
| Pt116-12 | 0.72 | 0.17 | 2.81 | −4.33 | −0.80 | 0.07 |
| Pt116-14 | 0.41 | 0.10 | 3.35 | −4.69 | −0.93 | 0.14 |
| Pt(111) slab | 0.25a | 0.05b | 5.72 | −6.41 | −0.43 | 0.45 |
| Final state | ||||||
| Pt116-8 | 0.53 | 0.09 | 9.65 | −13.41 | −3.23 | |
| Pt116-9 | 0.52 | 0.12 | 9.31 | −12.77 | −2.94 | |
| Pt116-10 | 0.65 | 0.13 | 9.35 | −12.50 | −2.50 | |
| Pt116-11 | 1.03 | 0.16 | 9.22 | −12.56 | −2.30 | |
| Pt116-12 | 1.37 | 0.21 | 8.20 | −11.36 | −1.78 | |
| Pt116-14 | 0.72 | 0.13 | 9.49 | −12.41 | −2.19 | |
| Pt(111) slab | 0.39a | 0.05b | 6.34 | −9.12 | −2.39 | |
For Pt116 there are very low dissociation barriers for hollow positions 11, 12 and 14, at 0.08, 0.07 and 0.14 eV, respectively. Although the barrier at position 14 is slightly higher than those for 11 and 12, it is significantly lower than that of the bulk (∼0.40 eV46). Furthermore, it is comparable with that of position 9 on Pt79, which was found to be 0.21 eV. Whilst position 9 on Pt79 is the hcp hollow site adjacent to a (100) facet, position 14 on Pt116 is the fcc hollow site adjacent to another (111) facet site. There are few similarities between the two sites that could lead to this slightly higher dissociation barrier aside from the fact that they are both adjacent to the “short” edge of the (111) facet. On Pt79, there are two hollow positions adjacent to (111) facets, and only one adjacent to the (100) facets. For Pt116 there are two hollow sites adjacent to the (100) facets, but only one adjacent to the (111) facets. It is therefore likely that the facets on the “short” edge are slightly more difficult to distort, with the bridge bond between facets being more ridgid. However, as the central atoms of the (111) facet are more flexible, favourable distortions towards the centre of the facet are still possible, leading to these slightly higher dissociation barriers compared to other hollow positions on the (111) facet, but still lower than the Pt slab. Dissociation barriers for the Pt38 and Pt79 particles are presented in Table 3, along with those for the Pt116 particles.
| Pt38 | Pt79 | Pt116 | |||
|---|---|---|---|---|---|
| Site | ΔE≠ | Site | ΔE≠ | Site | ΔE≠ |
| a ΔE≠ for the Pt(111) surface is 0.45 eV. | |||||
| 5 | 0.32 | 8 | 0.34 | 8 | 0.32 |
| 6 | 0.04 | 9 | 0.21 | 9 | 0.41 |
| 7 | 0.00 | 10 | 0.00 | 10 | 0.69 |
| 11 | 0.05 | 11 | 0.08 | ||
| 12 | 0.07 | ||||
| 14 | 0.14 | ||||
3.3 Distortion energies
Studies of the IS reveal few trends in the distortion energies of Pt116 upon adsorption of O2. Compared to other positions, there is a small distortion energy for Pt116 when O2 is adsorbed on position 8, the edge-bridge between two (111) facets. When compared to the Pt slab, sites 8, 11 and 14 have similar distortion energies (≤0.07 eV difference). For Pt38, none of the nanoparticle distortion energies are close to that of the slab (≥0.25 eV difference). For Pt79, site 9 is 0.04 eV lower in energy than the slab, however other sites are ≥0.14 eV higher in energy. This shows a trend towards infinite surface like behaviour with increasing particle size. The greatest distortion energy on Pt116 is found for position 12, 0.65 eV, although the distortion energies for the various sites are generally in line with those for the 38- and 79-atom particles of ≤0.50 eV.At the TS, position 8 once again has the lowest distortion energy associated with it. The particle distortion energy for site 8 is similar to that of the slab, 0.21 and 0.25 eV, respectively. However, all other sites have significantly higher distortion energies associated with them, 0.44–0.84 eV. The greatest distortion energies are found for positions 11 and 12 which are indicative of low O2 dissociation barriers. The particle distortion energy for site 14 is similar to those of positions 9 and 10, although a significantly lower O2 dissociation barrier is found for 14 compared to 9 and 10. The dissociation barrier for position 14 lies between the other low barrier (111) hollow sites and the high barrier bridge sites. There is a slight increase in the distortion energies when comparing the IS and TS structures, where the TS ones tend to have greater distortion energies. Furthermore, the distortion energies at the TS for Pt116 tend to be greater than those for the Pt38 and Pt79 TS structures.
At the FS, the Pt116 distortion energies are all greater than for the Pt slab. Furthermore, positions 8 and 9 have comparable distortion energies, both ∼0.10 eV higher in energy than the slab model. The Pt116 distortion energies for positions 8 and 9 are lower than other sites as adsorption on the bridge positions typically leads to less distortion. Position 10 has a larger distortion energy compared to the other bridge positions. In this case, O2 dissociation occurs over the central atom of the (100) facet. This leads to similar distortions to the (111) facet, with the central atom being pulled out of the plane. However, for the (100) facet, this distortion does not lead to the very low dissociation barriers observed for the (111) facet. Instead, a high barrier of 0.69 eV is calculated. Position 14 has a higher distortion energy than the bridge sites, although this is lower than the distortion energy for the other hollow sites. As discussed previously, there is less distortion of the “short” facet edge, leading to a reduced distortion energy compared to positions 11 and 12.
RMSD is calculated for all particles, however only the atoms to which O2 is bound as well as nearest neighbour Pt atoms are accounted for. There are generally greater displacement associated with the TS and FS. This is expected as the oxygen binds more strongly to the Pt surface as the system progresses from the IS to the FS. There are fewer trends when comparing the various sites being studied. Generally, there is a large RMSD associated with sites 11 and 12 (particularly at the TS), which exhibit larger distortion energies and lower O2 dissociation barriers compared to other sites.
At the IS, the oxygen distortion energy shows that there is greater distortion of O2 on the hollow sites, positions 11, 12 and 14. This means that at the positions for which there are very low dissociation barriers, there is greater distortion, away from the gas phase structure, of O2. Conversely at the TS, this trend inverts, where higher O2 distortion barriers are found for the bridge sites, 8, 9 and 10. This shows that at the TS, there is less distortion of the O2 on the hollow sites.
3.4 Interaction energies
E int gives an idea of the strength of the O2 bond to the surface. From the IS studies it follows that there is little difference between the interaction energies for the various sites. This trend changes at the TS, where greater interaction energies are found for the bridge sites than for the hollow sites. Thus, at the bridge sites, where there is typically less distortion of Pt116 and greater distortion of O2, there is a stronger Pt–O interaction. This is the opposite trend to that of the hollow sites, where there is greater distortion of Pt116 and less of O2. Similar trends to this are found for the binding energy, although in this case the trends are not as obvious because Eb includes the energetic contributions of distortions compared to the gas phase structures.3.5 Geometric analysis
Calculated geometric parameters are listed in Table 4. At the IS, there is generally little difference in the O–O bond length for the various sites. However, at the TS, shorter O–O distances are found on the hollow sites, compared to the bridge sites. On the hollow sites, the O–O distances are on average only 0.25 Å longer at the TS compared to the IS. This compares to an 0.84 Å average increase in the O–O distances from the TS to the IS on the bridge sites. This trend is in good agreement with results of the previous studies on Pt38 and Pt79 which exhibit early transition states located on the (111) facet where O2 dissociation results in very small energetic barriers. As the Pt116 system progresses from the IS to the TS, the Pt–O bond lengths are shortest at the TS. Pt–O bond lengths are increased when comparing the FS to the TS, although those at the FS are generally still shorter than at the IS. This is due to the increased binding energies observed as the system progresses from the IS to the FS, leading to the reduction in the Pt–O bond length. Longer Pt–O bonds are observed when O2 is adsorbed on the hollow sites, compared to the bridge sites.| Site | O–O | Pt–O | Pt–Pt | Pt–Xcentre | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | IS | TS | FS | IS | TS | FS | |
| Pt116-8 | 1.40 | 2.00 | 5.58 | 1.97 | 1.82 | 1.94 | 2.781 | 3.032 | 2.982 | — | — | — |
| Pt116-9 | 1.38 | 2.21 | 3.24 | 1.96 | 1.80 | 1.94 | 3.162 | 3.222 | 2.912 | — | — | — |
| Pt116-10 | 1.38 | 2.47 | 3.29 | 1.98 | 1.81 | 1.95 | 3.103 | 3.143 | 2.933 | — | — | — |
| Pt116-11 | 1.42 | 1.62 | 3.13 | 2.12 | 2.01 | 2.05 | 2.782 | 2.782 | 2.862 | 4.03 | 4.65 | 4.48 |
| 2.764 | 2.314 | 3.124 | ||||||||||
| 2.875 | 3.195 | 2.885 | ||||||||||
| 3.006 | ||||||||||||
| Pt116-12 | 1.43 | 1.67 | 2.52 | 2.07 | 1.99 | 2.07 | 3.334 | 3.354 | 3.214 | 3.99 | 4.04 | 4.41 |
| 2.926 | 2.936 | 3.036 | ||||||||||
| Pt116-14 | 1.43 | 1.74 | 3.62 | 2.12 | 2.00 | 2.05 | 2.791 | 2.831 | 2.861 | 4.03 | 4.12 | 4.11 |
| 2.935 | 3.065 | 2.875 | ||||||||||
| 2.966 | ||||||||||||
When inspecting Pt–Pt bond lengths, several trends become apparent. On the bridge sites, the Pt–Pt TS bond is elongated compared to the IS, whilst the FS bond is generally shorter than those for the IS and TS. The TS will have the longest Pt–Pt bond because of the stronger Pt–O interactions when compared to the IS. The Pt–Pt bond lengths are then generally reduced for the FS because, whilst the Pt–O binding is stronger, it is only a single O atom occupying the site. The trends are less well defined for the hollow sites, although in this case, there are a greater number of bonds that can be distorted. This can lead to smaller distortion of a certain bond type, compared to the bridge sites where ≤2 bonds are being distorted. Pt–Xcentre values are calculated for all hollow sites. In all cases, there is a greater distortion of the central (111) facet atom at the TS and FS when compared to the IS. This shows that as the Pt–O interaction energy increases, the (111) facet distorts more.
3.6 Bader charge analysis
Results from the Bader charge analysis are given in Table 5. Charge density difference plots are shown in the ESI,† Fig. S8–S14. Consistent with previous studies,41,42,46,60 there is significant charge transfer from the Pt, which becomes positively charged, to the O, which becomes negatively charged. At the IS it is found that there is less charge transfer from Pt for site 8 compared to sites 9 and 10. Instead, the charge state of site 8 is comparable to the hollow sites, which are slightly less positively charged. When studying O2 charge, it is found that there is a greater charge compared to the O associated with the hollow sites. For the hollow sites, charge transfer is investigated for the three Pt atoms directly bonded to O2, instead of the two atoms of the bridge sites. This means that, although there is typically less charge transfer from one Pt atom, as there are more Pt atoms interacting with O, the average charge on the O is greater.| Site | Pt chargesa | O charges | ||||
|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | |
| a Pt atoms interacting directly with O atoms. | ||||||
| Pt116-8 | 0.19 | 0.46 | 0.32 | −0.33 | −0.54 | −0.75 |
| Pt116-9 | 0.29 | 0.51 | 0.44 | −0.33 | −0.58 | −0.72 |
| Pt116-10 | 0.28 | 0.49 | 0.45 | −0.31 | −0.59 | −0.73 |
| Pt116-11 | 0.20 | 0.28 | 0.31 | −0.36 | −0.45 | −0.77 |
| Pt116-12 | 0.24 | 0.31 | 0.39 | −0.38 | −0.48 | −0.75 |
| Pt116-14 | 0.19 | 0.28 | 0.30 | −0.37 | −0.49 | −0.76 |
The charge transfer at the TS is greater than that at the IS. As the O2 dissociates, the interaction energy increases, coupled with a greater transfer of charge from the Pt to the O. At the TS, there is greater charge transfer at the bridge sites which is due to the coordination number of the O, where each O atom is bonded to a single Pt atom. For the hollow sites the charge transfer is spread over three Pt atoms, which results in the smaller transfer of charge. A similar trend is observed for the FS, where once again, greater charge transfer is found than at the IS or TS. Each O atom is now strongly bonded to the Pt surface and able to extract a greater charge than the molecular O2. At the FS, there is less difference in charge transfer between the bridge and hollow sites. This is because the transferred charge is spread over a greater number of atoms at each site.
4 Conclusions
We have presented a comprehensive study of size effects on O2 dissociation of Pt particles considering the Pt116 particle and comparing with the previously obtained results for smaller Pt particles. Most of the trends observed in the previous studies on Pt38 and Pt79 species are also seen for the larger Pt116. It is seen that the small O2 dissociation barriers, first calculated on Pt38, were not due to the small particle size. For the Pt116 model much lower dissociation barriers are obtained on the (111) facet hollow sites at the edge between (111) and (100) facets, 0.07 eV, when compared to the Pt(111) slab, 0.45 eV. A slightly higher dissociation barrier, 0.14 eV, is found for the other hollow site located close to the edge between two neighbouring (111) facets, although this is significantly lower than for the Pt slab, or other bridge sites on the Pt116 particle.For Pt116, other sites were also investigated: these included bridge sites on the (111) and (100) facets as well as the edge bridge sites between neighbouring (111) facets and between (111) and (100) facets. When studying the bridge sites on the (111) facet, it was found that the O2 would, instead of dissociating, overcome low barriers to migrate to hollow sites. Both edge bridge sites exhibited similar characteristics. On the other hand, it was found that there was a higher dissociation barrier for the bridge site at (100) facets, when compared to the edge bridge sites. This demonstrates that O2 dissociation will occur preferentially on (111) facets near the nanoparticle edges and the advantages of particles with greater numbers of (111) facet sites compared to (100) facet sites.
Acknowledgements
This research was funded through the RCUK doctoral training centre in hydrogen, fuel cells and their applications (EP/G037116/1). Financial support was also provided by the EU (FP7-NMP.2012.1.1-1 project ChipCAT, Ref. No. 310191), the Generalitat de Catalunya (2014SGR97, XRQTC) and the Spanish MICINN (CTQ2012-34969). The authors thank COST Actions MP0903 and CM1104. Much of the initial work was performed under the HPC-EUROPA2 project (project number: 228398) with the support of the European Commission – Capacities Area – Research Infrastructures. The computations described in this paper were performed in part using The University of Birmingham's BlueBEAR HPC service, which was purchased through HEFCE SRIF-3 funds, and via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/F067496). This work made use of the facilities of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. H. A. A. thanks the Spanish Ministerio de Educación for a post-doctoral grant (SB2010-0172), Bulgarian Science Fund (grant DCVP 02/1) and FP7 project BeyondEverest for support.References
- A. Chandan, M. Hattenberger, A. El-kharouf, S. Du, A. Dhir, V. Self, B. G. Pollet, A. Ingram and W. Bujalski, J. Power Sources, 2013, 231, 264–278 CrossRef CAS PubMed.
- S. Guo, S. Zhang and S. Sun, Angew. Chem., Int. Ed., 2013, 52, 8526–8544 CrossRef CAS PubMed.
- Z. Liu, L. Ma, J. Zhang, K. Hongsirikarn and J. G. Goodwin, Catal. Rev., 2013, 55, 255–288 CAS.
- L. Su, W. Jia, C.-M. Li and Y. Lei, ChemSusChem, 2014, 7, 361–378 CrossRef CAS PubMed.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS.
- T. P. Johansson, E. T. Ulrikkeholm, P. Hernandez-Fernandez, P. Malacrida, H. A. Hansen, A. S. Bandarenka, J. K. Nørskov, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Top. Catal., 2013, 57, 245–254 CrossRef.
- A. B. Anderson and T. V. Albu, J. Electrochem. Soc., 2000, 147, 4229 CrossRef CAS PubMed.
- R. Jinnouchi, Microscale Thermophys. Eng., 2003, 7, 15–31 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. A. Keith, G. Jerkiewicz and T. Jacob, ChemPhysChem, 2010, 11, 2779–2794 CrossRef CAS PubMed.
- Y. Sha, T. H. Yu, B. V. Merinov, P. Shirvanian and W. A. Goddard, J. Phys. Chem. Lett., 2011, 2, 572–576 CrossRef CAS.
- M. T. M. Koper, T. E. Shubina and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 686–692 CrossRef CAS.
- J. Seminario, L. Agapito, L. Yan and P. Balbuena, Chem. Phys. Lett., 2005, 410, 275–281 CrossRef CAS PubMed.
- B. Han, C. Miranda and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075410 CrossRef.
- Q. Ge, P. Hu, D. A. King, M.-H. Lee, J. A. White and M. C. Payne, J. Chem. Phys., 1997, 106, 1210 CrossRef CAS PubMed.
- K. Bleakley and P. Hu, J. Am. Chem. Soc., 1999, 121, 7644–7652 CrossRef CAS.
- H. Tang, A. Van der Ven and B. Trout, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045420 CrossRef.
- X. Lin, N. J. Ramer, A. M. Rappe, K. C. Hass, W. F. Schneider and B. L. Trout, J. Phys. Chem. B, 2001, 105, 7739–7747 CrossRef CAS.
- T. Li and P. B. Balbuena, J. Phys. Chem. B, 2001, 105, 9943–9952 CrossRef CAS.
- T. Jacob, R. P. Muller and W. A. Goddard, J. Phys. Chem. B, 2003, 107, 9465–9476 CrossRef CAS.
- G. N. Vayssilov, Y. Lykhach, A. Migani, T. Staudt, G. P. Petrova, N. Tsud, T. Skála, A. Bruix, F. Illas, K. C. Prince, V. Matoln, K. M. Neyman and J. Libuda, Nat. Mater., 2011, 10, 310–315 CrossRef CAS PubMed.
- T. Q. Nguyen, M. C. S. Escaño, H. Nakanishi, H. Kasai, H. Maekawa, K. Osumi and K. Sato, Appl. Surf. Sci., 2014, 288, 244–250 CrossRef CAS PubMed.
- U. Heiz, A. Sanchez, S. Abbet and W.-D. Schneider, J. Am. Chem. Soc., 1999, 121, 3214–3217 CrossRef CAS.
- R. L. Johnston, Atomic & Molecular Clusters, Taylor & Francis, London, 2002, p. 208 Search PubMed.
- S. M. Kozlov and K. M. Neyman, Top. Catal., 2013, 56, 867–873 CrossRef CAS PubMed.
- H. A. Aleksandrov, F. Viñes, W. Ludwig, S. Schauermann and K. M. Neyman, Chem. – Eur. J., 2013, 19, 1335–1345 CrossRef CAS PubMed.
- F. Viñes, Y. Lykhach, T. Staudt, M. P. A. Lorenz, C. Papp, H.-P. Steinrück, J. Libuda, K. M. Neyman and A. Görling, Chem. – Eur. J., 2010, 16, 6530–6539 CrossRef PubMed.
- R. B. Getman, Y. Xu and W. F. Schneider, J. Phys. Chem. C, 2008, 112, 9559–9572 CAS.
- A. Smeltz, R. Getman, W. Schneider and F. Ribeiro, Catal. Today, 2008, 136, 84–92 CrossRef CAS PubMed.
- R. Getman, W. Schneider, A. Smeltz, W. Delgass and F. Ribeiro, Phys. Rev. Lett., 2009, 102, 076101 CrossRef CAS.
- W. Chen, D. Schmidt, W. F. Schneider and C. Wolverton, J. Phys. Chem. C, 2011, 115, 17915–17924 CAS.
- J. M. Bray and W. F. Schneider, Langmuir, 2011, 27, 8177–8186 CrossRef CAS PubMed.
- Q. Fu, J. Yang and Y. Luo, J. Phys. Chem. C, 2011, 115, 6864–6869 CAS.
- M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2, 2648–2663 CrossRef CAS.
- D. J. Schmidt, W. Chen, C. Wolverton and W. F. Schneider, J. Chem. Theory Comput., 2012, 8, 264–273 CrossRef CAS.
- Y. Xu, W. A. Shelton and W. F. Schneider, J. Phys. Chem. A, 2006, 110, 5839–5846 CrossRef CAS PubMed.
- D.-H. Lim and J. Wilcox, J. Phys. Chem. C, 2011, 115, 22742–22747 CAS.
- M. Kettner, W. B. Schneider and A. A. Auer, J. Phys. Chem. C, 2012, 116, 15432–15438 CAS.
- D. Cheng and W. Wang, Nanoscale, 2012, 4, 2408–2415 RSC.
- P. C. Jennings, B. G. Pollet and R. L. Johnston, Phys. Chem. Chem. Phys., 2012, 14, 3134–3139 RSC.
- P. C. Jennings, B. G. Pollet and R. L. Johnston, J. Phys. Chem. C, 2012, 116, 15241–15250 CAS.
- B. Hammer and J. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- S. J. Yoo, S. J. Hwang, J.-G. Lee, S.-C. Lee, T.-H. Lim, Y.-E. Sung, A. Wieckowski and S.-K. Kim, Energy Environ. Sci., 2012, 5, 7521–7525 CAS.
- P. C. Jennings, H. A. Aleksandrov, K. M. Neyman and R. L. Johnston, Nanoscale, 2014, 6, 1153–1165 RSC.
- A. H. Larsen, J. Kleis, K. S. Thygesen, J. K. Nørskov and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245429 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- J. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978 CrossRef CAS.
- D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 074103 CrossRef PubMed.
- J. Kästner and P. Sherwood, J. Chem. Phys., 2008, 128, 014106 CrossRef PubMed.
- R. F. W. Bader, Atoms in Molecules: a Quantum Theory, Oxford University Press, New York, 1994 Search PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- P. C. Jennings and R. L. Johnston, Comput. Theor. Chem., 2013, 1021, 91–100 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Showing images of all initial, transition and final states for the sites investigated. See DOI: 10.1039/c4cp02147a |
| ‡ Present address: Department of Energy Conversion and Storage, Technical University of Denmark, Roskilde, Denmark. |
| This journal is © the Owner Societies 2014 |