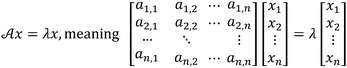The use of principal component analysis and discriminant analysis in differential sensing routines
Sara Stewarta,
Michelle Adams Ivyb and
Eric V. Anslyn*a
aInstitute for Cell and Molecular Biology, The University of Texas at Austin, 1 University Station A4800, Austin, Texas 78712, USA
bDepartment of Chemistry and Biochemistry, The University of Texas at Austin, 1 University Station A1590, Austin, Texas 78712, USA. E-mail: anslyn@austin.utexas.edu; Fax: +1 512 471 7791; Tel: +1 512 471 0068
First published on 2nd September 2013
Abstract
Statistical analysis techniques such as principal component analysis (PCA) and discriminant analysis (DA) have become an integral part of data analysis for differential sensing. These multivariate statistical tools, while extremely versatile and useful, are sometimes used as “black boxes”. Our aim in this paper is to improve the general understanding of how PCA and DA process and display differential sensing data, which should lead to the ability to better interpret the final results. With various sets of model data, we explore several topics, such as how to choose an appropriate number of hosts for an array, selectivity compared to cross-reactivity, when to add hosts, how to obtain the best visually representative plot of a data set, and when arrays are not necessary. We also include items at the end of the paper as general recommendations which readers can follow when using PCA or DA in a practical application. Through this paper we hope to present these statistical analysis methods in a manner such that chemists gain further insight into approaches that optimize the discriminatory power of their arrays.
Key learning points(1) This review is intended to advance the readers ability in interpret PCA and DA plots.(2) We would like the reader to better understand how certain types of chemical behaviour translate to plot behaviour. (3) Thirdly we would like readers to understand what modifications can be done to their data analysis to improve data representation with these methods. (4) Furthermore we would like the reader to understand some pitfalls common to these methods and how to avoid them. (5) Finally, through this work, it is hoped that an increased understanding of multivariate statistical analysis tools is gained, which aids in the interpretation of complex data sets, specifically those seen in differential sensing routines. |
Introduction
Differential sensing has become an increasingly important concept in the field of supramolecular chemistry, as trends in research shift from using lock-and-key receptors to employing less selective receptors in array sensing.1–6 Modeled after the mammalian olfactory senses, differential sensing employs a collection of low selectivity receptors which signal a specific pattern for each analyte or complex solution. In turn, each analyte or solution is discriminated from others by a unique fingerprint. In practice, the fingerprint, consisting of various fluorescence, absorbance, or electrode data cannot be easily analyzed by individual calibration curves for the purpose of analyte and solution identification and differentiation.To alleviate such difficulties, chemists have explored the use of statistical analysis techniques such as principal component analysis (PCA) and discriminant analysis (DA). Although these techniques are becoming particularly important for differential sensing purposes,7–16 these techniques are sometimes used as a “black box”. PCA and DA are widely utilized across multiple fields of academia and industry, and thus there are numerous reviews and tutorials on these techniques available to study.17–21 However, these articles are often heavily laden with mathematical symbols and derivations, or with seemingly unrelated examples, that are challenging to translate to differential sensing. For this reason, we see the present need for a qualitative explanation of these techniques to help chemists interpret PCA and DA plots that result from differential sensing studies. Our aim is to present PCA and DA to chemists in a manner which will shed light on the types of receptor arrays which lead to certain plots, and to give a few general criteria for obtaining optimal PCA and DA plots. This information ultimately can be utilized to refine differential sensing systems for better analyte and solution discrimination and differentiation.
Background
Both PCA and DA are statistical analysis techniques, which produce score plots for the analytes or solutions tested. These score plots consist of a coordinate system with axes in a two, three, or higher dimensionality space, with the goal of revealing the coordinate system in which the test analytes are best discriminated. Both PCA and DA generate these score plots by decomposing the raw data by a matrix technique, in which the eigenvectors of the matrix produce axes mentioned above and the eigenvalues give a measure of the level of discrimination that exists in the data. However, the manner in which each of these techniques arrives at their corresponding eigenvectors and eigenvalues is slightly different.To explore how PCA and DA work, a relevant analogy can be made to a more familiar eigenvalue problem (see Scheme 1 for how eigenvalue problems are written). Most chemists know that the Schrödinger equation plays a fundamental role in quantum mechanics (eqn (1)). This differential equation is usually simplified and reduced to a problem involving the eigenvectors and eigenvalues of a square matrix.22 The eigenvectors of this matrix represent the molecular orbitals with which we are all familiar, and the eigenvalues give the orbital energies that correspond roughly to the ionization potentials of the molecules. This classic equation is just one of many examples of eigenvalue problems, which play roles in fields as diverse as signal processing and civil engineering. Simply stated, when a matrix multiplies one of its eigenvectors, the result is proportional to the eigenvector (it has the same directional sense), where the constant of proportionality is the eigenvalue.22
| HΨ = EΨ | (1) |
What differentiates one eigenvalue problem from another is the way that the elements of the square matrix are defined. In the Schrödinger equation describing electrons in molecules, the matrix elements are quite complicated integrals involving the “basis functions” (models of atomic orbitals) that describe the problem, and the eigenvectors are linear combinations of the basis functions, giving a mathematical description of the molecular orbitals.
In PCA (eqn (2)), the square matrix C is referred to as the co-variance matrix, while v is the set of the eigenvectors, and D is the set of eigenvalues. Because the goal of PCA is to find the greatest extents of variance in a set of data, the square matrix is a function of variance. Specifically, in PCA, the matrix reflects co-variance. Deriving the co-variance matrix C is the key to PCA, just like deriving the Hamiltonian matrix is key to solving the Schrödinger equation.
| Cv = Dv | (2) |
To create the co-variance matrix, we first take a matrix of experimental observations (m) for different samples (n) to make an m × n data matrix. For example, in array sensing the observations may be absorbances at various wavelengths for different receptors mixed with the different analytes. The samples (number = n) are the individual analytes and replicates of the analytes. If we record 50 absorbance values with 5 receptors we would have 250 experimental observations (m = 50 × 5) for every sample. Next, for each sample n, the variance in the data (experimental observations) is derived from the standard deviation, presented in eqn (3), where N equals the number of total observations in a group, xi is a single observation within a group and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i is the mean of all the observations in a group. Variance is the square of the standard deviation (eqn (4)).
i is the mean of all the observations in a group. Variance is the square of the standard deviation (eqn (4)).
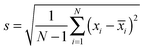 | (3) |
| Var(X) = s2 | (4) |
In our example, the data for which variance is calculated consists of all the absorbance values for the series of receptors. So far, this would mean that for each sample (n of these), corresponding to potentially a large set of data (m observations), we simply have one number – variance. The goal of PCA is to seek how the variance of one sample correlates with the variance of another sample. To do this, the method calculates co-variance, defined as in eqn (5). In this formula xi is a single observation in a group, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i is the mean of all the observations in a group, yi is a single observation in a different group and ȳi is the mean of all observations in that different group.
i is the mean of all the observations in a group, yi is a single observation in a different group and ȳi is the mean of all observations in that different group.
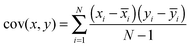 | (5) |
Importantly, there is a co-variance value for each sample relative to each other sample. Hence, for n samples there will be n × n co-variance values. These values can therefore be arranged into the square co-variance matrix (see Scheme 2) and this sets the stage for an eigenvalue problem as discussed above. The matrix is symmetric across the diagonal, because the co-variance of, for example sample 3 with sample 5, must be the same as between 5 and 3. In Pearson's co-variance, a specific type of PCA plot, which normalizes the data set before running the PCA algorithm, the diagonal elements of the co-variance matrix will be equal to 1.23
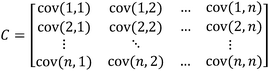 | ||
| Scheme 2 An n × n matrix used in PCA, where cov = co-variance, and the variance of the data for each sample samples is labeled with a number up to n samples. | ||
In the original data matrix, one can define a vector for each sample in an m dimensional space. After PCA, each sample consists as a vector in n dimensional space, where each dimension reflects decreasing extents of variance between the samples. The x, y, z… coordinates for each sample in the new space are called the scores for that sample, and the score values along each axis reflect the extent to which the samples differ along the variance expressed by that axis. The extent of variance along each principal component axis is the eigenvalue for that axis.
The above example presents what is generally called eigenvalue value decomposition (EVD). We have used it as an example, along with molecular orbital theory (MOT), in order to allow the reader to better conceptualize what the underlying mechanics of PCA are. However this is, in fact, only one approach to solve the eigenvalues and is limited by requiring a square matrix. While this is a legitimate method of calculating the eigenvalues, it is very computationally taxing. A more generalized approach to the problem would be singular value decomposition (SVD). PCA can be thought of in the general form presented in eqn (6) where T and P′ are matrices which capture the underlying data pattern of X, which is in this case the covariance matrix.24
| X = TP′ | (6) |
For the purposes of PCA, T is a matrix where the columns contain the factor scores for each component and the P′ is a matrix where the rows contain the loading scores. Fundamentally the factor scores are the coordinates of each sample and loading scores are the coordinates of each variable in a data reduced space.25,26
SVD has the form presented in eqn (7). In this case the columns of V are termed the right singular vectors and are equivalent to the columns in P. U is equivalent to T except
| X = UDV′ | (7) |
Another alternative to EVD for solving for eigenvectors is Nonlinear Iterative Partial Least Squares (NIPALS). In this method possible loadings and score values are set initially and iteratively modified until convergence between the previous values and new values is attained.27,28
More simply, PCA rotates and combines the original data such that each new orthogonal axis explains the most possible variance. This is referred to as a change of basis. This results in the apparent shifting of the data points such that they are centered around the origin of each axis. It is here where the real strength of PCA arises. It is generally safe to assume that the most important variables are those with the greatest variance. However it is not always apparent which combination of variables will yield a vector which explains the most variance. Furthermore, when a large data set is generated, such as for spectroscopic data, there is a fair amount of redundancy between variables. PCA fundamentally reduces the dimensionality of the data removing redundancy and finding collinear variables and expressing them across a single axis. In essence, PCA finds the axis that best fits an n dimensional space of data and projects those axes in a simpler space.29
The eigenvectors of any matrix, not just with PCA, can be viewed as a “coordinate system” that is optimal for the problem under consideration. For example, if one does PCA for a set of x,y data points, the eigenvectors correspond to two lines in the x,y plane. Along one of these lines, the variance of the data points is maximized (the data exhibits a wide range of values along that axis), while the other axis has the opposite behaviour (the data exhibits a narrow range of values). While it can be quite easy to see – by eye – what these axes are in a two-dimensional case, the generalization to more dimensions is less easily visualized but no less straightforwardly amenable to computation.
Discriminant analysis (DA) is another eigenvalue problem, and has many features in common with PCA. The main difference between DA and PCA is that with PCA there is no bias placed on finding the greatest variance between samples. This means that replicates of the same analytes are treated identically as different sets of analytes. Therefore, clustering of the samples in PCA means that the variance between these samples is indeed smaller than the variance with other samples. In DA, the mathematics place a bias toward clustering repetitive samples (called a class) and separating them from repetitions of a different set of analytes (a different class). Unlike PCA variance is not the parameter used to distinguish data in DA. Instead DA fundamentally finds the best way to organize data in order to maximize class discrimination. For this manuscript the percent captured values for the PCA plots represent variance captured and the percent captured values for the DA plots is discrimination captured.
An important distinction that needs to be made here is the precise form of DA used. For the sake of simplicity the more general form of DA, called canonical discriminate analysis (CDA) will be used here. In the most basic sense CDA identifies some combination of variables which maximize the Euclidean distance between groups while minimizing the distance between members of a group. There are other forms of discriminate analysis such as linear discriminate analysis (LDA) and quadratic discriminate analysis (QDA). LDA differs from CDA in that rather than relying on both with-in and between group data to classify, LDA uses distance from a centroid to classify data.30 QDA is a more complex application of the likelihood classification, but rather than finding the linear combination of variables it identifies a quadratic surface which minimizes misclassifications.31
CDA is a function which maximizes the difference between the means of differing classes, while minimizing the difference within a class. This is done by defining the scatter within a class and the scatter between the classes. Scatter is defined by matrices which are analogous in form to the co-variance matrices used in PCA.20 Importantly, with CDA two matrices are used, one for between class scatter (SB) and one for within class scatter (SW) (i.e. variance). Given this, the eigenvalue problem is formulated as in eqn (8). The inverse of the within class scatter matrix multiplied by the between class scatter matrix acts to maximize between class scatter while minimizing within class scatter. The eigenvectors (w) represent weighted combinations of scatter within and between the samples, while the eigenvalues (J) represent the extent that scatter is best maximized between classes and minimized with classes. The J values are analogous to the extent of variance eigenvalues found in PCA. Because DA has a bias built into the mathematical approach, it is called a “supervised” routine, while PCA is “unsupervised”. Consequently, due to the supervised nature of DA, the resulting plots often show better analyte classification than a corresponding PCA plot.
| Sw−1SBw = Jw | (8) |
Now that a summary of the Schrödinger equation and PCA/DA eigenvalue problems has been given, we can draw an analogy between the results of the two kinds of problems. The eigenvectors of the Schrödinger equation are linear combinations of atomic orbitals we interpret as molecular orbitals. Each value of the eigenvector is the coefficient of the atomic orbital that contributes to the molecular orbital, and it acts as a weighting factor for that atomic orbital. Each element in an eigenvector for a particular eigenvalue from PCA is the coordinate position of individual samples along different axes in the n-dimensional space. The dimensions in this new space are orthogonal, and are referred to as PC 1, 2,…n, where each PC is associated with an eigenvalue. The most important eigenvalues from the Schrödinger equation are those associated with the HOMO and LUMO, meaning the orbitals near the middle of the energies. In PCA, the eigenvalues are the extent of variance carried by each axis in the n-dimensional space. It is the first few principle coordinates that are the most important because they reflect the greatest amount of variance between the samples.
In a PCA or DA plot resulting from differential sensing, the response from multiple receptors can contribute to each axis in the plot, although some receptors often have a much larger contribution to a particular axis than others. The power of PCA and DA becomes most apparent in the cases that have data sets with a large number of receptors, spectral data, or other experimental data where it is nearly impossible to comprehensively evaluate the raw data with a few simple calibration curves. When there are many more variables than samples, DA in particular may not perform well due to an issue called “over-fitting” which will be discussed later in this manuscript.
As already mentioned, PCA and DA are common techniques employed to analyze the data that result from differential sensing. The receptors used in this technique are commonly referred to as differential, or cross-reactive. The terms are often synonymous, and we use them and likely will continue to use them in this manner. However, for purposes of this concept article, we give them slightly different definitions. Differential receptors simply show different responses from each other to the analytes. Cross-reactive receptors actually have differences in their trends of affinities to the analytes, meaning that some receptors have higher affinities to some analytes, while the corresponding cross-reactive receptors prefer different analytes. This means that cross-reactive receptors are a subset of differential receptors.
It is important to note that PCA and DA are not the only algorithms used for pattern recognition. Factor analysis (FA), partial least squares (PLS), and maximum redundancy analysis (MRA), and hierarchical clustering are examples of alternatives.23,27,32
Model setup
In order to illustrate the use of PCA and DA in differential sensing we will present a variety of artificial datasets that show behavior similar to what one might see in an array sensing experiment. A set of five hosts (receptors) and five guests (analytes or mixtures) are created where each host–guest measurement is modeled as if it was repeated five times. The measurements are host:guest binding constants (Ka values), although they could represent any kind of data such as spectral intensities. However, by using Ka values the discussion naturally has lessons related to the selectivity of the receptors.For each scenario, values were selected to represent the Ka of each host:guest pair. For each pair, five values representing repetitions were randomly generated, following a normal distribution.32 This distribution was set such that the mean of the values was equal to the Ka's selected to represent the host:guest pair. The 0.5 to 5 standard deviations (σ) of the distributions of Ka values for each host:guest pair were used in order to simulate a range of variances within repetitions. For each scenario presented we have included a summary of the mean Ka values used and the σ-value used.
Exploration of PCA and DA
Lock-and-key array versus cross-reactive array
Most times when examining DA and PCA score plots, receptor performance may not be entirely known. However, careful examination of the plot results can shed some light on how a receptor is performing. Consider a situation in which there is a panel of antibody-like receptors that are highly selective, each to different individual guests (Fig. 1A) and a very low σ relative to the Ka values. The resulting score plot shows that each guest occupies a distinct location in the PCA plot. G1, G3, and G4 are discriminated primarily across the F1 axis (principal component 1, PC1) while G2 and G5 are discriminated primarily across the F3 axis (principal component 3, PC3). (Note that F1 was plotted versus F3. This was chosen in order to better display the visual separation of each of the guests. We will be discussing methods and rational for improving visual discrimination later in this review.) It is important to note that approximately 50% of the variance is found in the F2, F4, and F5 axes. In this particular case all of the guests can be visually discriminated by two axes, though there is still significant discrimination in the remaining axes.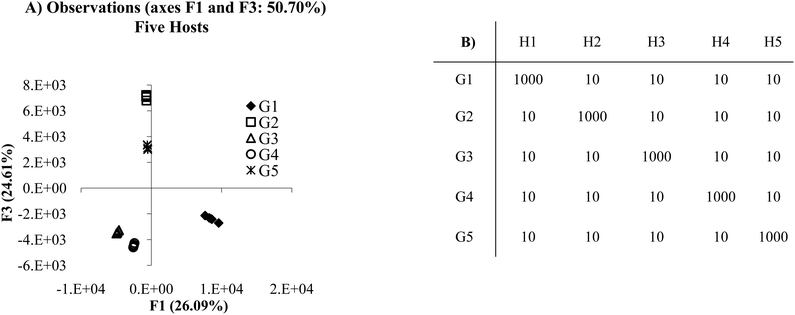 | ||
| Fig. 1 (A) PCA plot of the antibody-like scenario. (B) Mean Ka values for the “antibody like” scenario. In this example, each host:guest behaves in a very specific manner. For example, guest 1 (G1) and host 1 (H1) have a very high affinity for each other relative to the other host:guest pairs (0.5 standard deviations). | ||
Similar results can be achieved through lower selectivity but fully cross-reactive receptors (Fig. 2A). Fig. 2A presents a plot in which each receptor is cross-reactive with all other receptors. In this case, because each of the host:guest pairs behaves in a unique manner each guest is separated from the others in both the F1 and F2 axes. From this example, it seems that there is very little difference in using a panel of receptors that have antibody like behavior as opposed to cross-reactive behavior, since discrimination of analytes can be effectively achieved in both circumstances. In these models each host responds in an unambiguously different manner to all the guests. This situation is ideal for optimal discrimination. However, quality discrimination can still be achieved with small differences between responses to guests for an array of hosts, as is the case in most cross-reactive arrays, since each receptor behaves in a sufficiently unique manner.
On one hand it may seem that these conclusions support the notion for utilizing cross-reactive arrays in all scenarios. However, despite the power cross reactive arrays may show for discriminating similar targets, they are not well suited for all cases. When a specific target or targets need to be identified from a complex solution, cross-reactive arrays may fall short. Further, the advantages that cross-reactive arrays show to subtle variations in a target may be rendered useless by a large concentration of background competing analytes. In cases like this, a very specific receptor, that is not perturbed by compounds in the background would obviously be far superior to a cross reactive array.
 | ||
| Fig. 2 (A) PCA plot of the cross-reactive scenario. (B) Mean Ka values for the cross-reactive scenario. In this example, each host:guest behaves in a very unique manner. For example, guest 1 (G1) and host 1 (H1) have lower affinity for each other than the affinity of H1 for any of the other guests, whereas host 2 (H2) has the lowest affinity for G2 relative to the other host:guest pairs (2 standard deviations). | ||
Choosing the best number of hosts for an array
Care must be taken in selecting the correct number of hosts, be it high selectivity or cross-reactive array. Studying what is termed as the 2n rule may be helpful in such a case. Fig. 3A portrays the same data as Fig. 1A but using four hosts instead of five. This is an example where the 2n rule can explain the similarities between the two figures. The analysis reveals that a lack of a signal can be just as important as a measurable single in an array setting. In Fig. 3A, guest 3 does not respond to the hosts. Its behavior is therefore different than the other guests and can easily be separated from the remaining guests. Essentially, in arrays where there is high selectivity, fewer hosts than guests (2n) can be used to achieve optimal discrimination in many cases.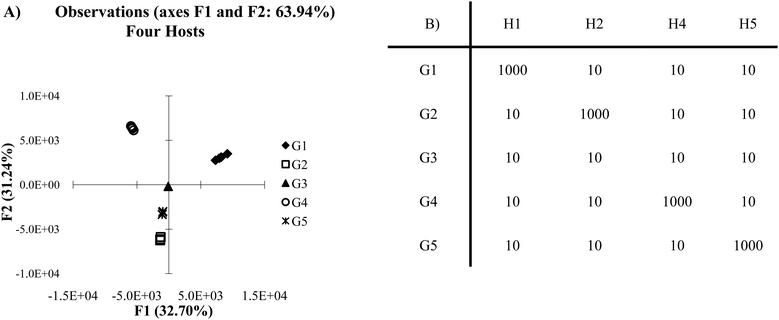 | ||
| Fig. 3 (A) PCA plot of antibody-like scenario with four hosts. (B) The same data sets as presented in Fig. 1B, however one of the hosts has been omitted (0.5 standard deviations). | ||
This can be thought of in terms of a combination of 1s and 0s (this is the source of the 2; 2 options 1 or 0). An antibody like sensor can be considered “perfect,” when presented with its target, it has maximum signal and can be assigned a 1. When presented with a non-target analyte it has no signal and can be assigned a 0. A combination of 2 receptors could have the values (1,1), (0,1), (1,0) or (0,0) giving four unique combination. Thus the number of possible combinations and set of perfect receptors is equal to 2n. Not all “perfect” sensor systems are capable of displaying all four possible combinations. Frequently, systems of highly selective sensors (like antibodies) are designed in such a way to eliminate the possibility of the (1,1) situation. One further consideration for this scheme is a restriction on the (0,0) response. As with any signal, having multiple guests that respond in the same manner limits the discriminatory power of the assay. While this limitation exists for all guests, there can commonly be more guests that show no response than those that will. Thus, for full classification, it is important to ensure there is only one guest that shows a null response to all receptors in the array.
Cross-reactive arrays are not limited by being constrained by on and off values. Rather, they are limited only by their ability to create a reproducible and sufficiently unique pattern of binding for each target. When a single host is removed from the cross-reactive data set in Fig. 2A, the score plot still retains a high level of discrimination (Fig. 4A). However, guests 2 and 4 begin to show overlap in a two-dimensional plot. This is due to the lack of a sufficient number of hosts behaving in a distinctly unique manner. Also, in the cross-reactive case an increase can be seen in the overall variance of PC1 and PC2, from 69.74% to 75.17%. This is due to the properties of the data set itself. In x–y plots of multivariate data, there is variance found in each of the variables but only two dimensions are displayed. Therefore, in a five variable array, the variance is distributed across five dimensions. When a variable is removed from the system, there are fewer dimensions across which the variance can be distributed.
 | ||
| Fig. 4 (A) PCA plot of cross-reactive scenario with four hosts. (B) The same data set as presented in Fig. 2B, however, one of the hosts has been omitted (2 standard deviations). | ||
When to add hosts to an array
An array in which every host:guest pair generates a signal which contains sample variance comparable in intensity to background noise occurs when different host:guest pairs show very similar affinities to analytes, for example, see the first five host:guest pairs in Fig. 5E. This can be considered analogous to the antibody-like scenario, except with much lower selectivity. The following section will explore a similar situation found in cross-reactive systems where the affinity for each host:guest pair varies only slightly. | ||
| Fig. 5 (A) PCA plot of overlapping data set with 5 hosts (B) DA plot overlapping data set with 5 hosts (C) PCA plot of overlapping data set with ten plots (D) LDA plot of over lapping data set with ten hosts (E) mean Ka values (×100) for each host guest pair (5 standard deviations). | ||
In Fig. 5 clustering of the various guests may roughly exist, but the groups are not readily distinguishable. This is due to a high standard deviation between the repetitions, relative to the magnitude of the Ka values for all the guest groups. Fig. 5A is the PCA plot of the data, which appears as total scatter. However, even with DA (Fig. 5B), the method falls short of completely discriminating the analyte classes.
One possible reason for this lack of discrimination has to do with what characteristics are being used to classify the data. As is typical with PCA, it is assumed that variance between groups of guests is sufficient to categorize data. DA on the other hand requires information about class membership to group the data. This situation is hinted at by the difference in variance captured by the PCA in Fig. 5A and the percent of discrimination captured by the DA in Fig. 5B. If the amount of variance captured by the first few PCs in PCA is low then it is possible that variance is not a good classifier. However, this leads to the debate of how many axes are appropriate to include in a model. There are arguments that in cross-reactive sensing routines including many axes to account for a large amount of the variance is a more appropriate method, indicating that variance dispersed across many sensor combinations is the discriminatory element.33 The counter point to this is that by including many axes in the analysis, the ability of PCA to reduce the dimensionality is neglected. To some extent this is a philosophical question we will not be exploring here. However, careful consideration of what exactly a researcher wished to achieve as well as how the data is expected to behave may allow one to decide what the best model approach may be. While the DA appears to be superior to the PCA in 5A due the increased amount of discrimination captured, it likely will perform poorly as a predictive model. This is due to the model relying on all data points in order to create the classifier model. If a leave one out cross validation is performed one can see that the model loses its predictive power.
In cases like this, adding additional hosts can improve the data discrimination by reinforcing difficult to observe patterns in the data sets. Fig. 5C and D show the PCA and DA plots obtained when ten hosts are considered, rather than the five used for Fig. 5A and B. The five new hosts were chosen to respond identically to the first five. This could represent additional replicates in the system, or additional hosts where the deviation from other hosts is subtle. Now we see that each guest is more localized in the PCA plot, though overlap still exists. In the DA plot (Fig. 5D), there exists a much tighter clustering of the guests. The improvement can be further supported by considering the jack-knife analysis for the five host data set DA plot (76%), and the improved jack-knife analysis for the ten host data set DA plot (84%). This analysis means that the identity of each guest was correctly predicted 76% or 84% of the time. Please see the section on validation for a more detailed explanation of this method.
The reason additional hosts improved the discriminatory power of this system is that each host responds to the guests in a specific manner that is not easily observed due to a high amount of noise in the system. In such circumstances, differentiation of analytes can be achieved by adding additional hosts that either reinforce observed patterns, by adding additional hosts with similar behaviour to other hosts (as the example presented here does), or by adding additional hosts with wholly unique behaviour. This situation, where adding hosts to a high noise system increases the discriminatory power of an array, is called “co-linearity”.34 When this data set is expanded to 20 hosts (Fig. 6) – a situation which in this case could be considered as having many more hosts than guests; the amount of variance captured across the first few PCs decreases. This is not unexpected as each PC captures a portion of the variance; as the number of PCs increase the amount of variance captured by each PC decreases. Visual examination of the first 2 PCs appears to show superior grouping of the samples. However when a validation method is applied is it is found that the model has very poor predictive power, in this case the Jack knife analysis yields a 12% correct classification rate.
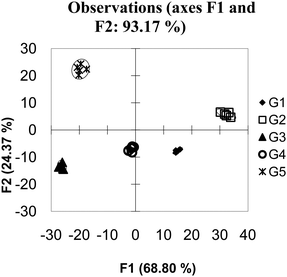 | ||
| Fig. 6 PCA of overlapping data with 20 hosts. The data has been “over-fit”. | ||
This is a situation referred to as over-fitting, and is a common trap many researchers fall into. Even in the most random data set, it is possible to find an equation which can perfectly group the data by whatever parameter the researcher wants. If too much data is used, however, the equation is only relevant to the presently available data. Any new data is not likely to follow the lines of discrimination resulting in a model that only predicts itself. When examining the quality of a PCA or DA one must be cognizant that adding more variables can appear to make a better fitting model while reducing the predicative power of the model.35
High dimensionality in an array and determining host performance
High dimensionality in PCA and DA plots is often a goal for many authors during the statistical analysis of their data.10,11,36–38 High dimensionality is defined in PCA and DA as a large number of principal components or discriminating axes, all of which carry a significant extent of the total differentiation. High dimensionality is desirable in cases where very similar analytes need to be differentiated. However, in many circumstances where high dimensionality exists, a two or three-dimensional plot, while mathematically aiding in the differentiation of analytes, may not lead to an optimal pictorial representation of discriminated data. High dimensionality, and thus more principal components or discriminating axes, is obtained by adding more cross-reactive or highly selective receptors to an array. This makes sense, as the number of discriminating axes possible in a PCA or DA plot is directly correlated to the number of receptor variables.The math behind the decomposition of a data set in PCA into its corresponding eigenvectors necessitates that the number of eigenvectors which emerge from the calculation be equal to the number of receptors in the array or the number of samples, whichever of these two numbers is smaller.23 Similarly the number if eigenvectors which can emerge from a DA is equal to the number of classes minus one.39 However, this correlation between the number of eigenvectors and number of receptors often leads to an incorrect conclusion: Each discriminating axis represents one receptor (variable). To further understand why this conclusion is a misconception, we must turn to loading plots, which are simultaneously generated when PCA and DA plots are produced Loading plots show the influence which each receptor, or variable, has on the corresponding discriminating axis. Each receptor is represented by a vector in a loading plot. The x,y coordinates (or higher coordinates) of each vector indicates the extent to which each receptor contributes to a discriminating axis. Vectors of (1,0) or (−1,0) most influence the discrimination of analytes along the x-axis (F1), with the vector (−1,0) best discriminating analytes on the left side of F1 and vector (1,0) best discriminating analytes on the right side of F1. Conversely, vectors (0,−1) or (0,1) most influence the lower half of the y-axis or the upper half of the y-axis, respectively. Receptors with vectors of intermediary x,y values indicate contributions to both axes. Thus, the loading plot becomes very useful in analyzing which receptors or variables are most useful for discrimination, thus aiding in determining receptor performance.
Similar to a loading plot is a biplot. Biplots are most commonly seen in conjunction with PCA plots, where the loading plot of the PCA plot is superimposed onto its corresponding PCA plot. In these plots, the receptors which most influence a particular data point are located close in vector space to the data point. The proximity of a receptor vector endpoint to a data point allows further analysis of the array system to determine whether the receptor is important for discriminating that particular analyte.
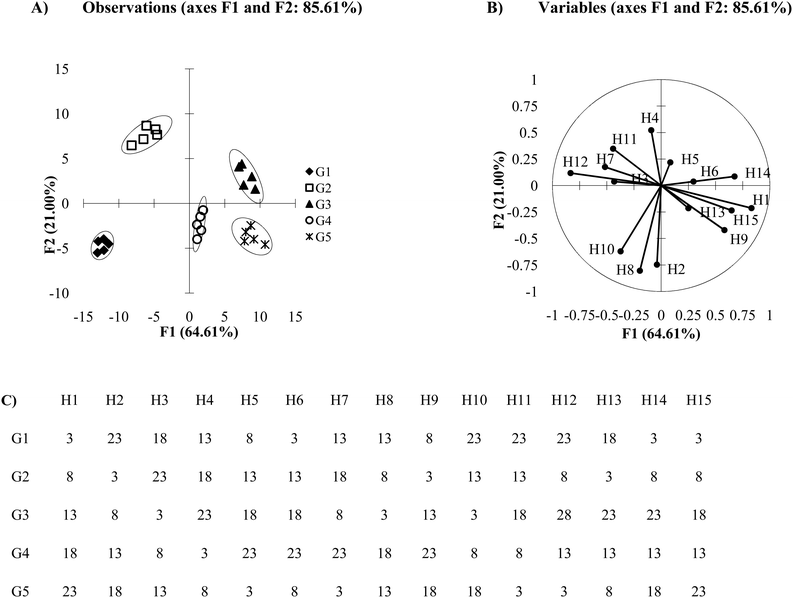
The loading plot or biplots make it clear that the differing principal components can be made up from several responses of receptors. Both loading plots and biplots are important plots to analyze once PCA or DA results have been generated. They allow the user to probe the importance of the receptors in an array, which in turn provides information to improve and modify the array to obtain the best results. The DA plot in Fig. 7A was derived from an array consisting of 15 receptors, where Fig. 7C shows the mean Ka values used for this simulation. These values were chosen to maximize the dissimilarity between the behavior of each host:guest interaction in order to observe how each receptor can contribute to multiple axes. In the loading plot (Fig. 7B), we see that the first axis (F1) discriminates analytes based on the data from all the receptors, except H2 which shows a close to zero value as an x-component in its line ending vector. The second axis (F2) discriminates analytes based on the data from nearly all the receptors, because most receptors contain a non-zero value as a y-component in their line ending vector (H3 and H6 are near zero). Receptors H2, H8, H10, and H4 contribute the most to the discrimination seen with the F2 axis because the absolute value of their y-component is larger than the absolute value of the y-vector components of the other receptors. Therefore, each discriminating axis contains contributions from multiple variables.
Care must be taken not to rely on loading plots and biplots exclusively for receptor selection. While it is likely that H2 and H8 are the primary contributors to the position of G4 in Fig. 7A, the precise relationships between the host‘s influence on the guest's position cannot be determined. Biplots are useful tools for approximating the host's influence, however for a more exact measure and for optimal variable selection a factor analysis could be performed. This method uses the loadings and biplots in PCA and applies a set of rules and criterions in order to quantify the relative significance each factor has on the data structure of the model.23 This gives a quantitative estimation of the importance of each factor. That being said, in many cases PCA will yield equivalent results to a factor analysis.40
The misconception that each discriminating axis represents one receptor in an array is most likely a result of the direct correlation seen between the number of receptors (variables) in an array and the number of discriminating axes obtained. Another reason for this misunderstanding may be that in high dimensionality systems with a large number of receptors, it is often the case that only a few of the receptors have pertinent contribution to a particular discriminating axis, while the other variables in the array have a very small contribution that can be considered negligible.
Obtaining the best visually representative plot
After running PCA or DA algorithms, many statistical programs automatically generate a two-dimensional plot using the two discriminating axes which contain the maximum variance or discrimination. Oftentimes, this leads to a satisfactory plot, however, there are circumstances where this automatically generated two-dimensional PCA or DA plot may not be the best visual representation of the data. In cases such as this, it becomes important to consider all of the components computed by the statistical analysis program. Fig. 8A shows an example where a two-dimensional plot of the data shows considerable overlap between the analytes G1 and G5. The Ka and σ values employed in this example (presented in Fig. 8C) were chosen to generate this coincidental overlap.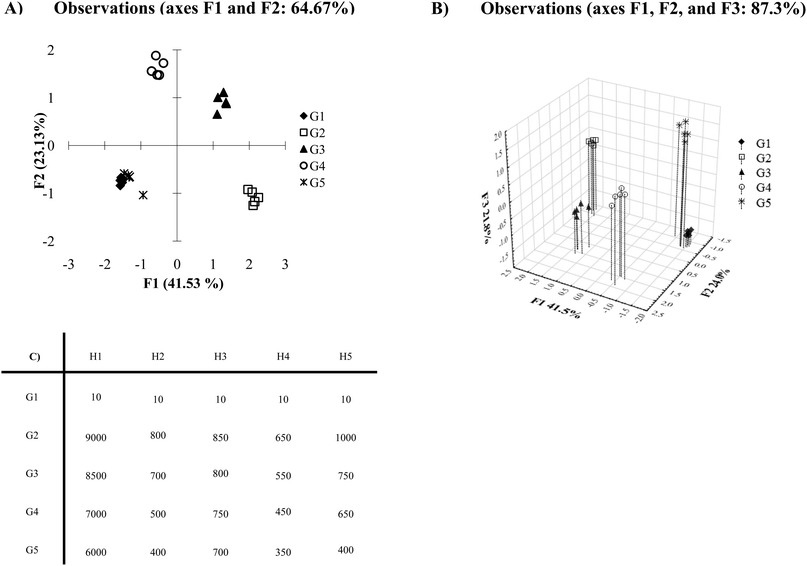 | ||
| Fig. 8 (A) PCA plot with a large variance data set. (B) Three-dimensional PCA plot of the data set. (C) Mean Ka values of inconsistent variance data (data for G1 contains 0.5 standard deviations, data for G2–G5 with Ka values of 10 contains 0.5 standard deviations, data for G2–G5 with Ka values of 20 contains 1 standard deviation, data for G2–G5 with Ka values of 30 contains 1.5 standard deviations, data for G2–G5 with Ka values of 40 contains 2 standard deviations). | ||
Once we examine the three-dimensional plot, which takes into account a third discriminating component (Fig. 8B), we see excellent discrimination of all the analytes. If any other of the discriminating axes calculated by the PCA or DA algorithms hold a substantial discriminating percentage (i.e. >5%), it would be beneficial to further examine those axes in addition to the two greatest discriminatory axes. For instance, there may be circumstances where a third and fourth discriminating component is important to differentiate a data set. In this case, an examination of the plots generated from all combinations of the first through fourth axes may be necessary (i.e. compare plots – 1 vs. 2, 1 vs. 3, 1 vs. 4, 2 vs. 3, 2 vs. 4, etc.). Thus, careful consideration of all components may lead to the best visual representation of differentiated data.
To specifically optimize PCA plots, there exist rotation methods which often aid in simplifying the discriminating axes for easier interpretation. Although there are several methods, varimax rotation introduced by Kaiser in 195841 is the most common. Varimax works by searching for a rotation of the original discriminating axes which maximizes the variance of the squared loading scores. The advantage of utilizing varimax is that the new plot may be easier to analyse because each axis represents a response from one, or only a few receptors.42 This tends to lead to loading scores (i.e. placements within the PCA plot) which have a wide range of values and emphasize clustering.23
Including blank or control responses in an array
Another factor which should be considered when selecting data to be discriminated by PCA or DA is whether to include blank or control responses in the data set. Oftentimes, researchers are eager to show the excellent response which their receptor array shows towards the desired analytes versus a blank or control sample. However, inclusion of blank or control data within the data set evaluated by PCA or DA can lead to artificial discrimination in the plot. The generated plot becomes skewed from the blank or control sample data. Take the following example (Fig. 9A), where G1 represents blank or control samples, which do not respond to the receptor array. In this example, the F1 discrimination is dominated by the response difference between the blank/control samples and the analytes being tested. Here, a large fraction of the F2 axis instead becomes the differentiation that is seen within the analytes tested. Once we remove the blank/control from our data set, the plot shown in Fig. 9B is generated. It is not necessarily incorrect to include the blank or control in the data set being evaluated by PCA or DA. If the researcher's primary goal is to differentiate non-responsive samples (i.e. blanks or controls) from response samples, then including the blank/controls in the data set is appropriate. However, usually the goal is to differentiate analytes, and thus, an omission of the blank/control samples from the PCA or DA data set is generally most sensible.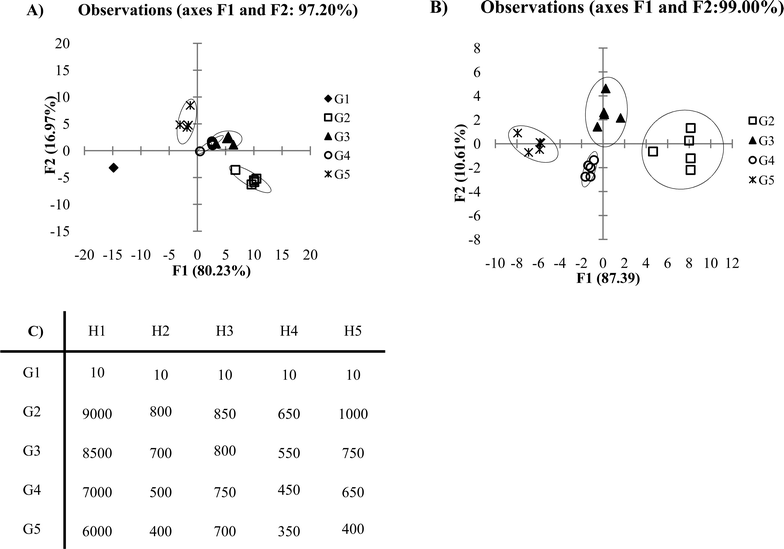 | ||
| Fig. 9 (A) DA plot of low variance data with blank included in the data set. (B) DA plot with blank excluded from data set. (C) Ka values of low variance data (0.5 standard deviations). | ||
Circumstances when arrays may not be necessary
PCA and DA find their greatest utility in circumstances where data is obtained from cross-reactive receptors. However, in cases where high cross-reactivity is not seen within receptors, repetitive data may exist which does not assist in the differentiation of the analytes. In these types of circumstances, an array of receptors may not be necessary and instead, one single receptor is sufficient for analyte discrimination. Take for example a case where there are several receptors which have nearly identical signal response trends, with only slight differences between receptors in their intensity of overall response to the set of analytes (Fig. 10C). We see that the corresponding PCA and DA plots (Fig. 10A and B) for this example shows the data tightly clustered according to analyte identity along the F1 axis. Variance of the F2 axis however, is misleading as the variance arises solely from the noise found within analyte groupings for the array. In this case, both of these plots would be better represented in a two dimensional graph (analyte vs. signal) plotted from the data obtained with only one of the receptors from the original array. Thus, the use of an array and corresponding multivariate statistical analysis tools are both unnecessary here. In circumstances like this, one receptor is sufficient for the purpose of analyte differentiation. To prevent such a case where unnecessary work and time have been spent planning, engineering, and executing an array when only one receptor from the array is needed to accomplish the desired goal of analyte differentiation, it is prudent to always be observant for arrays in which receptors give highly similar response trends.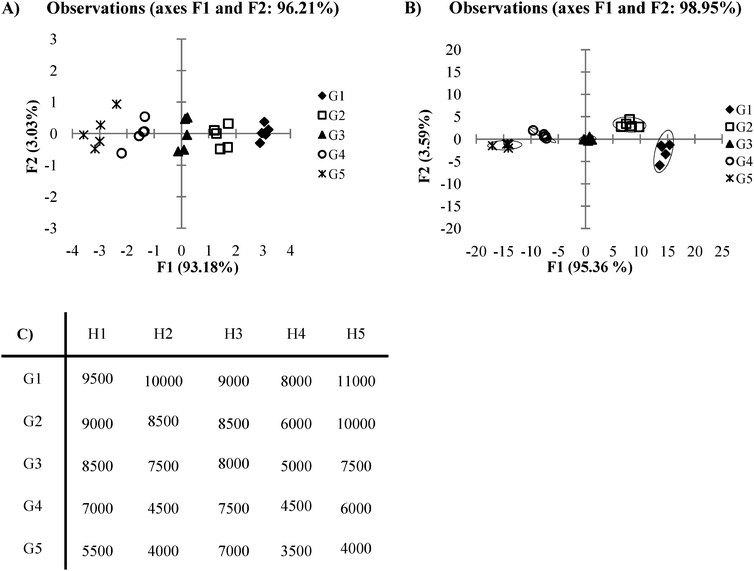 | ||
| Fig. 10 (A) A PCA plot of data where an array is not needed. (B) An LDA plot of date where an array is not needed. (C) Ka values for a plot where an array is not needed (0.5 standard deviations). | ||
Practical application of PCA and DA
Using PCA and DA together and validation techniques
PCA and DA are both methods which are best used conjunctively to optimize data analysis. Typically, PCA is run first to assist in uncovering general trends in the data set. Once PCA is run, a DA is run to specifically investigate the classification and grouping trends present in the data set. Although sometimes the graphs obtained for a data set with PCA and DA look similar, occasionally both methods can identify different patterns in the data set. For this reason, we generally recommend running both of these methods on a data set and simultaneously studying the outcomes of these analyses for trends.As already mentioned, it is often very common for a DA plot to look better than its corresponding PCA plot. Therefore, as we have mentioned a few times, validation techniques are simultaneously run with trained models to allow users to evaluate the validity of the model for their data set. A common initial validation technique for DA is the jack-knife analysis, also known as the “leave-one-out” analysis. In this validation technique, data for one or several samples are removed from the data set and a new model is constructed. The classification of this removed analyte is then estimated from the new model and compared to its previous classification. This entire process is completed with every analyte in the data set, and the resulting number is the percentage of classifications which were correctly identified.23
In addition to validation techniques for DA, most computer software programs give an option to display confidence ellipses for the grouped data. These ellipses generally represent a 95% confidence limit for a specific analyte group; typically calculated using the Hotelling T2 statistic. These confidence ellipses help the user to more easily identify how close each sample is to the group consensus; the centroid. On this note, however, we strongly discourage the incorporation of arbitrarily drawn circles which encompass analyte groups, as these may be mistaken for confidence ellipses. A more relevant statistic for assessing the quality of classification would be the use of bootstrapping in order to approximate to true characteristics of the population. Briefly, a bootstrap method resamples data from a sample population in order to create an expected distribution of the data. This process is repeated many times, often several thousands, until a reasonably accurate distribution is generated. This allows the researcher to generate confidence intervals directly related to the true distribution of the data rather than make assumptions when using the T2 statistic.43
These techniques can be used to validate PCA data as well as DA data. While not considered a classification method in and of itself, PCA scores can be used for classification. Most software packages support validation methods for both DA and PCA though the exact title may vary. One software package may use the term “predictive PCA”44 while another may call it “principal component regression”.
If the final goal of these methods is to classify unknown data, an external validation data set should be used. This is data for which the researcher knows the class (though if possible blinding the experimenter should be considered) but was not used to develop the model. This can include data that was collected as part of an experiment but not used in the model or data collected as part of another experiment. There are a variety of methods used to quantify the predictive power of a model using an external data set. The precise method used should be selected to best reflect how the model is expected to be used and the availability/quality of external data.44
Pre-processing data
Pre-processing data is often an important step to take into consideration before running multivariate analysis methods. Frequently data is preprocessed by transformation in order to achieve certain data structures. Linearity, for example is a requirement for many models; log transformation can be used to bring data into this shape. When using attributes of the data, such as variance, to identify differences in the data, it is often prudent to normalize the data to eliminate variation that does not contribute to classification. A common method to achieve this is called centering. This involves setting the mean of each variable to some constant number. Frequently this value is zero, however it can also be some value that has meaning for the data set.Typically, scaling is used in conjunction with centering to further normalize the variables to each other. With scaling, variables with large values are fundamentally “shrunk” while variables with small variables are “stretched” to put them on the same footing.45 Without these steps it is often the case that the primary vector of variance is defined by the mean of the data. This limits the utility of the model by obscuring latent variables which are more powerful for discrimination.46
Another method commonly used to remove noise from data is referred to as smoothing. One of the simplest examples of this is the moving average. In this example a window of points is averaged together to generate a single point in their place. The window is then shifted through the entire data set point by point until each new point represents an average of a subset of points. This method reduces the impact of especially high or low values in the data set.47 There are many different methods used to smooth and remove noise from a data set, such as the Fourier transformation or the Savitzky–Golay smoothing filter.48
Pearson's correlation is considered to be a normalization method where the standard deviation is used to scale the data between −1 and +1.33 Correlation methods are always applied when the data set being used contains different units (i.e. absorbance and fluorescence data both contained within a data set). There are four main methods of executing these methods: (1) covariance about the origin, (2) covariance about the mean, (3) correlation about the origin, and (4) correlation about the mean. Rozett and Petersen give a detailed analysis of these methods and their advantages and disadvantages.49 In the context of differential sensing, covariance about the origin is the typical approach. Using this pre-processing method prevents the loss of data around the zero point of the experimental scale and avoids the loss of information regarding the relative size and relative error associated with the data from different receptors.23
It is important to note that because pre-processing of data can be key to obtaining the best differentiating model for the data set, some programs which run PCA often include a pre-processing step in the program calculations. In these cases, additional pre-processing may not be necessary for the user and the raw data can be used directly.
Experimental setup
Lastly, it is important to note that researchers must take care in their experimental setup to avoid any inherent experimental design flaws which could cause artificial trends. Take for example, microarrays. It has been shown in the literature that if care is not taken with the experimental design one can generate spurious discrimination, where the differences are due to artifacts, such as the days on which the arrays were performed.50 Thoughtful care must be taken to ensure that uniform conditions and parameters are applied to each analyte. In addition, when judging the validity of an array one must also consider the differences between laboratory conditions and real-world conditions. In order to validate the performance of an array, one must try to replicate real-world conditions and variability.It is also important to note the difference between technical replicates and experimental replicates. Technical replicates involve replicated data which were derived from using the same stock solutions. These types of replicates help to evaluate pipetting accuracy and the homogeneity of the solutions or media being tested. Experimental replicates require the entire experiment to be reproduced including the growing of cells and preparation of stock solutions. These types of replicates are very useful in preventing results which discriminate data based on irrelevant variables such as the petri dish in which the cells were grown, the well plate in which the array was run, and the conditions in which the solutions or media were stored. Not all systems may require the incorporation of both technical replicates and experimental replicates in a data set, but a clear understanding of the benefits which arise from each different type of replicate may prevent false or unsupported discrimination in a plot, thus avoiding incorrect conclusions.
Conclusions
In this work, the use of statistical analysis tools such as DA and PCA have been discussed in the context of differential sensing. Additionally, a number of key observations regarding the relationships between the data in an array and the corresponding plots have been presented through model data sets. (1) Cross-reactive arrays have demonstrated high discriminatory power and are particularly advantageous over a lock-and-key array when differentiating similar analytes. (2) Optimizing the number of hosts based on the behavior of an array is an important aspect in designing an array; in particular, the presented examples have emphasized how to choose the best number of hosts for an array and how to recognize circumstances in which adding additional hosts to the array is beneficial. (3) High dimensionality and the benefits and consequences of incorporating high dimensionality into an array were discussed, as well as the importance of investigating the data provided by loading plots and biplots for analyzing receptor performance. (4) The model data sets have shown how to analyze PCA or DA data to obtain the best visual plot representation possible, assuming that visual representation is a goal, and thus learning to not rely exclusively on variance or differentiation as a measure for the quality of an array. (5) The effect of blank or control samples on the appearance of the plot, and the circumstances when an array may not be necessary for differentiating purposes, were explored. (6) Lastly, the implementation of PCA and DA as statistical analysis tools for working up data obtained by sensing arrays was discussed, highlighting the use of validation techniques to probe the effectiveness of the model at representing the data and learning how to avoid bias from experimental design.Acknowledgements
The Anslyn research group has been continually funded by the NSF, NIH (most recently R01 GM077437) and the Welch Foundation (F-1151) for developing differential sensing routines for over a decade, and we are grateful for their support.References
- J. J. Lavigne and E. V. Anslyn, Angew. Chem., Int. Ed., 2001, 40, 3118 CrossRef CAS.
- E. V. Anslyn, J. Org. Chem., 2007, 72, 687 CrossRef CAS PubMed.
- B. E. Collins and E. V. Anslyn, Chem.–Eur. J., 2007, 13, 4700 CrossRef CAS PubMed.
- B. E. Collins, A. T. Wright and E. V. Anslyn, Top. Curr. Chem., 2007, 277, 181 CrossRef CAS.
- O. R. Miranda, B. Creran and V. M. Rotello, Curr. Opin. Chem. Biol., 2010, 14, 728 CrossRef CAS PubMed.
- A. P. Umali and E. V. Anslyn, Curr. Opin. Chem. Biol., 2010, 14, 685 CrossRef CAS PubMed.
- T. Hirsch, H. Kettenberger, O. S. Wolfbeis and V. M. Mirsky, Chem. Commun., 2003, 432 RSC.
- A. Buryak and K. Severin, J. Am. Chem. Soc., 2005, 127, 3700 CrossRef CAS PubMed.
- H. Zhou, L. Baldini, J. Hong, A. J. Wilson and A. D. Hamilton, J. Am. Chem. Soc., 2006, 128, 2421 CrossRef CAS PubMed.
- M. A. Palacios, R. Nishiyabu, M. Marquez and P. Anzenbacher, J. Am. Chem. Soc., 2007, 129, 7538 CrossRef CAS PubMed.
- S. Stewart, A. Syrett, A. Pothukuchy, S. Bhadra, A. Ellington and E. V. Anslyn, ChemBioChem, 2011, 12, 2021 CrossRef CAS PubMed.
- A. D. Hughes, I. C. Glenn, A. D. Patrick, A. Ellington and E. V. Anslyn, Chem.–Eur. J., 2008, 14, 1822 CrossRef CAS PubMed.
- S. H. Shabbir, L. A. Joyce, G. M. da Cruz, V. M. Lynch, S. Sorey and E. V. Anslyn, J. Am. Chem. Soc., 2009, 131, 13125 CrossRef CAS PubMed.
- A. Bajaj, O. R. Miranda, R. Phillips, I. B. Kim, D. J. Jerry, U. H. F. Bunz and V. M. Rotello, J. Am. Chem. Soc., 2010, 132, 1018 CrossRef CAS PubMed.
- A. Bajaj, S. Rana, O. R. Miranda, J. C. Yawe, D. J. Jerry, U. H. F. Bunz and V. M. Rotello, Chem. Sci., 2010, 1, 134 RSC.
- T. Takeuchi, J. Montenegro, A. Hennig and S. Matile, Chem. Sci., 2011, 2, 303 RSC.
- W. R. Klecka, Discriminant Analysis, Sage Publications, California, 1980 Search PubMed.
- K. Fukunaga, Statistical Pattern Recognition, Academic Press, California, 2nd edn, 1990 Search PubMed.
- D. Coomans and D. L. Massart, Hard Modeling in Supervised Pattern Recognition, in Data Handling in Science and Technology, ed. R. G. Brereton, Elsevier, Amsterdam, 1992 Search PubMed.
- A. J. Izenman, Modern Multivariate Statistical Techniques, Springer, New York, 2008 Search PubMed.
- S. Theodoridis and K. Koutroumbas, Pattern Recognition, Elsevier, Amsterdam, 4th edn, 2009 Search PubMed.
- G. A. Korn and T. M. Korn, Mathematical Handbook for Scientists and Engineers, Definitions, Theorems, and Formulas for Reference and Review, McGraw-Hill, New York, 1961 Search PubMed.
- E. R. Malinowski, Factor Analysis in Chemistry, Wiley-VCH, New York, 3rd edn, 2002 Search PubMed.
- S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2(1), 37 CrossRef CAS.
- M. Wall, A. Rechtsteiner and L. Rocha, A practical approach to microarray data analysis, Springer, 2003, p. 9 Search PubMed.
- V. Kelma and A. Laub, IEEE Trans. Autom. Control, 1980, 25(2), 164 CrossRef.
- H. Wold, Nonlinear Iterative Partial Least Squares (NIPLAS) Modelling: Some Current Developments, Univ., Department of Statistics, 1973 Search PubMed.
- H. Risvik, Principal Component Analysis (PCA) & NIPALS algorithm, 2007 Search PubMed.
- B. K. Lavine and W. S. Rayens, Comprehensive. Chemometrics., Elsevier, Amsterdam, 2009 Search PubMed.
- J. H. Friedman, J. Am. Stat. Assoc., 1989, 84, 165N CrossRef.
- N. Bratchell, Chemom. Intell. Lab. Syst., 1987, 6(2), 105 CrossRef.
- M. L. Samuels and J. A. Witmer, Statistics for the Life Sciences, Prentice Hall, New Jersey, 3rd edn, 2003 Search PubMed.
- M. C. Janzen, J. B. Ponder, D. P. Bailey, C. K. Ingison and K. S. Suslick, Anal. Chem., 2006, 78, 3591 CrossRef CAS PubMed.
- B. K. Slinker and S. A. Glantz, Am. J. Phys., 1985, 249, R1 CAS.
- R. D. Tobias, Proc. Ann. SAS Users Group Int. Conf., 20th, Orlando, FL, 1995.
- K. S. Suslick, MRS Bull., 2004, 29, 720 CrossRef CAS.
- K. S. Suslick, N. A. Rakow and A. Sen, Tetrahedron, 2004, 60, 11133 CrossRef CAS PubMed.
- C. Zhang, D. P. Bailey and K. S. Suslick, J. Agric. Food Chem., 2006, 54, 4925 CrossRef CAS PubMed.
- R. A. Johnson and D. W. Wichern, Applied multivariate statistical analysis, Englewood Cliffs, NJ, Prentice hall, vol. 4, 1992 Search PubMed.
- L. R. Fabrigar, D. T. Wegener and R. C. MacCullem, Psychological Methods, 1999, 4(3), 272 CrossRef.
- H. F. Kaiser, Psychometrika, 1958, 23, 187 CrossRef.
- H. Abdi, Factor Rotation in Factor Analyses, in The SAGE Encyclopedia of Social Science Research Methods, ed. M. S. Lewis-Beck, A. E. Bryman and T. F. Liao, Sage Publications, California, 2003 Search PubMed.
- R. Wehrens, H. Putter and L. Buydens, Chemom. Intell. Lab. Syst., 2000, 54(1), 35 CrossRef CAS.
- L. Eriksson, E. Johansson, N. Kettaneh-Wold, J. Trygg, C. Wikström and S. Wold, Multi and Megavariate Data Analysis Part 1 Basic Principles and Applications, Umetrics AB, 2006 Search PubMed.
- V. Consonni, D. Ballabio and T. Todeschini, J. Chemom., 2010, 24(3–4), 194 CrossRef CAS.
- J. Han, M. Kamber and J. Pei, Data mining concepts and Techniques, Elsevier, Amsterdam, 3rd edn, 2011 Search PubMed.
- J. C. Miller and J. N. Miller, Statistics for analytical chemistry, 1988 Search PubMed.
- V. J. Barclay, R. F. Bonner and I. P. Hamilton, Anal. Chem., 1997, 69(1), 78 CrossRef CAS.
- R. W. Rozett and E. M. Petersen, Anal. Chem., 1975, 47, 1301 CrossRef CAS.
- J. J. Chen, R. R. Delongchamp, C. A. Tsai, H. M. Hsueh, F. Sistare, K. L. Thompson, V. G. Desai and J. C. Fuscoe, Bioinformatics, 2004, 20, 1436 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |