Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synergy between Lewis acid sites and hydroxyl groups for the isomerization of glucose to fructose over Sn-containing zeolites: a theoretical perspective†
Guanna
Li
a,
Evgeny A.
Pidko
*ab and
Emiel J. M.
Hensen
*a
aInorganic Materials Chemistry group, Schuit Institute of Catalysis, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: e.a.pidko@tue.nl; e.j.m.hensen@tue.nl
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
First published on 22nd April 2014
Abstract
The mechanism of glucose isomerization to fructose catalyzed by Lewis acidic Sn sites in the framework of MOR, BEA, MFI and MWW zeolites was investigated by periodic DFT calculations. The main focus was on the influence of the nature of the active site and the zeolite topology on the rate-controlling hydride shift step. A general finding is that the Sn-catalyzed isomerization of glucose is strongly promoted by proximate hydroxyl groups. These hydroxyl groups can derive from co-adsorbed water molecules or internal silanols. The cooperative action of such proton donors with the Lewis acidic Sn sites results in more effective compensation of the negative charge developing on the O1 atom of glucose during the rate-controlling hydride shift reaction step. The variation in the shape of the micropores with a zeolite topology affects the mode and strength of carbohydrate adsorption, which is dominated by van der Waals forces. Their influence on the intrinsic reactivity of intrazeolite Sn sites is small. We propose that higher glucose adsorption energy in the narrower micropores of 10-membered ring zeolites (e.g., Sn-MFI and Sn-MWW) adversely affects the intrachannel diffusion compared to that in the zeolites with larger pores. The high catalytic performance of Sn-MWW towards glucose transformation is due to the lower barrier for the hydride shift step resulting from the presence of a relatively strong acidic bridging silanol group next to the Lewis acidic Sn site.
Introduction
Platform chemicals such as 5-hydroxymethylfurfural (HMF), levulinic acid and lactic acid may serve in the future as versatile intermediates for the production of a wide range of important chemicals from carbohydrate biomass feedstock.1–5 The main constituents of second generation biomass, cellulose and hemicellulose, can be efficiently hydrolyzed into monosaccharide building blocks such as glucose and xylose using Brønsted acid catalysts.6–8 The valorization of glucose, which is the most abundant sugar monomer in biomass, to platform chemicals is challenging and is currently only possible with relatively modest yields of desired products.9,10 Comparatively, the conversion of fructose to platform molecules by Brønsted or Lewis acid catalysts can be typically carried out with higher yields and under milder reaction conditions.11–13 The catalytic isomerization of glucose to fructose (aldose–ketose isomerization) is therefore considered to be an important step for the efficient valorization of glucose to platform chemicals such as HMF or lactic acid.14–16Currently, the industrial process for fructose production utilizes D-glucose/xylose isomerase enzyme for the conversion of glucose.17 Despite good performance, enzyme integration into a value chain for large-scale production of biorenewable bulk chemicals and fuels is problematic. Thus, an important challenge is to develop chemocatalysts for aldose–ketose isomerization.18 Among different homogeneous19–23 and heterogeneous24–28 catalysts developed so far, the Lewis acidic large-pore zeolite Sn-BEA is particularly active in selective glucose conversion.9,29–33 Sn-BEA offers the possibility of converting glucose with high selectivity to lactic acid,32,33 while its good isomerization activity can be used in combination with mineral acids to convert glucose into HMF.9
Density functional theory (DFT) calculations have been instrumental in progressing our understanding about zeolite catalysis.34 Recently, they have also been successfully employed to understand better the mechanisms of the conversion of biomass constituents.35–37 The nature of the active site in Sn-BEA for glucose activation has been the subject of a number of theoretical studies.38–41 It has been found that isolated Sn species incorporated into the zeolite lattice are the active sites for glucose activation.42,43 There are strong indications that partially hydrolyzed lattice Sn sites such as (SiFOF)3SnOH (where SiF and OF stand for the silicon and oxygen atoms of the zeolite framework, respectively) are more reactive than tetrahedral lattice Sn(IV) sites (Sn(OFSiF)4).38–40,44 Partial hydrolysis of lattice Sn(IV) atoms may enhance the flexibility of their coordination environment, which is beneficial for the coordination and activation of bulky carbohydrate molecules.41
The key elementary steps in glucose to fructose isomerization by zeolite Sn sites involve transformation of the open (acyclic) forms of the carbohydrates (Scheme 1).45 Coordination of the open form of glucose (Glu) to a lattice Sn site is followed by deprotonation of the O2H hydroxyl group resulting in an anionic o-Glu intermediate. The subsequent hydride shift (H-shift) between C2 and C1 atoms of the sugar is the key step that converts the aldose to the ketose form. Fructose formation occurs by protonation of the anionic O1 center in the adsorbed ketose intermediate (o-Fru). Previous experimental and theoretical studies30,38,45 indicate that the H-shift reaction is the rate-controlling step.
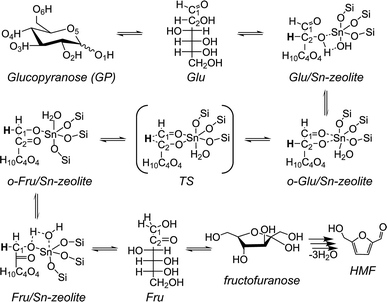 | ||
| Scheme 1 A proposed mechanism for glucose isomerization to fructose over the partially hydrolyzed (SiFOF)3SnOH framework site in zeolites. | ||
It has been found that Sn-BEA is preferred for glucose conversion compared to other Sn-containing zeolites and Sn-containing silicas such as Sn-MFI and Sn-MCM-41.29,46–48 However, a recent study showed that the Sn-MWW zeolite (MWW has 10-membered ring pores nearly similar in size to MFI) also displays good performance in glucose conversion to lactic acid in water and methyl lactate in methanol, which involves isomerization as an intermediate step.49 Tentatively, the effect of the zeolite topology may be related to differences in the flexibility of the partially hydrolyzed Sn framework species, or in the diffusion rate or adsorption modes of the reactants and products as a function of the pore size. Besides, the dimension and shape of the zeolite micropores may also influence the transition states relevant for the glucose isomerization reaction.
In this work, we investigated by theoretical methods the reaction mechanism of the glucose to fructose isomerization catalyzed by four Sn-containing zeolite models of mordenite (MOR), Beta (BEA), MFI and MWW topologies. We employed full periodic models of these structures and explored the reactivity of partially hydrolyzed lattice Sn sites. We specifically addressed the influence of the confinement effects and the local zeolite environment of the Sn sites on their catalytic reactivity towards the aldose–ketose isomerization reaction.
Computational details
DFT calculations were performed using the Vienna ab initio Simulation Package (VASP 5.2).50 The generalized gradient exchange–correlation PBE functional was used.51 The electron–ion interactions were described by the projector augmented wave (PAW) method.52 Geometry optimization was carried out using a plane-wave basis set with a cutoff of 400 eV. The calculations were assumed to be converged when the forces on each atom were less than 0.05 eV Å−1. Brillouin zone-sampling was restricted to the Γ point. The optimized cell parameters for all-silica zeolite models are listed in Table S1.†For all four topologies, one of the framework Si atoms was substituted by Sn followed by H2O dissociation over a Sn–O–Si moiety resulting in a partially hydrolyzed (SiFOF)3SnOH⋯HOFSiF active site model. Sn atoms were introduced at T6, T12, T3 and T8 tetrahedral sites of BEA, MFI, MOR and MWW frameworks, respectively (Fig. 1). These sites are located either at the intersection of the channels (T12 of MFI and T3 of MOR) or at relatively flexible rings (T6 of BEA and T8 of MWW). This choice was made based on the consideration of the accessibility of the site to the sugar reactant. These specific locations of Sn in the zeolite frameworks were selected with a view towards systematic analysis of the influence of the zeolite topology on the different reaction paths for aldose–ketose isomerization. The resulting models do not necessarily correspond to the most thermodynamically stable lattice Sn substitution.39 We should note, however, that the exact location of heteroatoms introduced during the hydrothermal zeolite synthesis is influenced by both thermodynamic and kinetic factors and their distribution in the final material depends therefore on the particular synthesis conditions. Furthermore, the intrinsic stability of particular Sn substitutions is expected to be of minor importance for Sn distribution in the materials prepared by post-synthetic methodologies.24,49,53–55 The acyclic forms of D-glucose (Glu) and D-fructose (Fru) were used as the initial and final states in studying the mechanism of isomerization. In our considerations, we assume that the partially hydrolyzed SnOH site can be formed in all of the investigated zeolites. Moreover, reactant and product diffusion will not be considered explicitly here, although we will discuss this point briefly in the discussion.
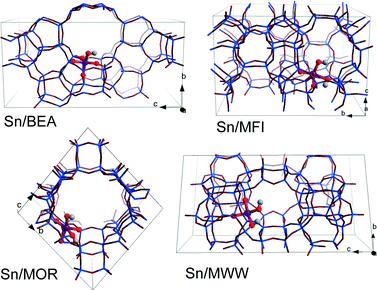 | ||
| Fig. 1 Optimized structures and locations of partially hydrolyzed Sn sites in T6-BEA, T3-MOR, T12-MFI, and T8-MWW periodic zeolite models. | ||
The minimum reaction energy path and the corresponding transition state were determined using the nudged elastic band method (NEB) with improved tangent estimate.56 The maximum energy geometry along the reaction path obtained by the NEB method was further optimized using a quasi-Newton algorithm. In this step, only the extra-framework atoms and the first coordination sphere of Sn were relaxed. Frequency analysis of the stationary points was performed by means of the finite difference method as implemented in VASP. Small displacements (0.02 Å) were used to estimate the numerical Hessian matrix. The transition states were confirmed by the presence of a single imaginary frequency corresponding to the reaction path. To account for the van der Waals (vdW) interactions between zeolite voids and carbohydrates, all DFT calculated energies were corrected by performing single point energy calculations using the DFT-D2 method57 as implemented in VASP 5.2.
The reaction Gibbs free energies were calculated at a reaction temperature of 373 K and a pressure of 1 atm by the corrected DFT-D2 electronic energy of each reaction intermediate with zero-point energy (Ezpe) and TSv entropy terms computed within the ideal gas approximation under the assumption of constant internal thermal energy. For the isolated Glu reactant and the Fru product, the internal thermal energies due to translation (Et) and rotational motion (Er) items were included in the Gibbs free energy.
Results
Earlier mechanistic studies evidence that the rate-controlling step in the glucose to fructose isomerization reaction is the H-shift between the C1 and C2 atoms of the anionic acyclic glucose (o-Glu) intermediate coordinated to a lattice Sn site.30,38,45 Before the H-shift step, the carbohydrate adsorbs on the partially hydrolyzed SnOH site followed by deprotonation of its O2H hydroxyl group. Assuming that the initial sugar activation step by SnOH is a facile process,38 we focus on analysing the effect of zeolite topology and local geometry of the active site on the important H-shift step. Several starting configurations of the o-Glu intermediate were generated by varying the geometry of the (SiFOF)3SnOH⋯HOFSiF site. All energies are given relative to the most stable configuration of the initial (SiFOF)3SnOH⋯HOFSiF active site and an isolated acyclic glucose molecule.Sn-BEA
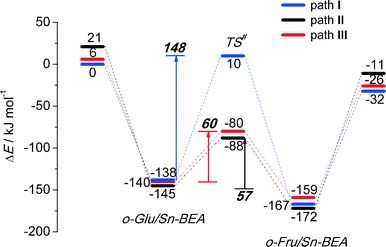
Reaction energy diagrams for the isomerization of o-Glu to o-Fru over the partially hydrolyzed SnOH site of Sn-BEA are shown in Fig. 2. The optimized structures of the reaction intermediates and transition states are given in Fig. 3. The adsorption of Glu to Sn-BEA followed by its deprotonation at the O2H site resulting in o-Glu/Sn-BEA and co-adsorbed water (Sn⋯H2O) is favorable by 140–170 kJ mol−1, depending on the configuration of the confined o-Glu species (Fig. 3). All adsorption complexes show a monodentate coordination of o-Glu to Sn via the anionic O2 site. The optimized r(Sn⋯O2) distances are similar for all o-Glu/Sn-BEA complexes. In configuration I (o-GluI/Sn-BEA), the O1 carbonyl group is 3.6 Å away from the Sn atom and no hydrogen bonding between the o-Glu and hydroxyl groups of the active site (Sn⋯H2O and HOFSiF) occurs. Hydrogen bonding of the O1 carbonyl with a H2O molecule coordinated to lattice Sn (o-GluII/Sn-BEA, Fig. 3, path II) or with an adjacent SiFOFH group (o-GluIII/Sn-BEA, Fig. 3, path III) slightly stabilizes the o-Glu intermediate in configurations II and III, respectively. In spite of the very different binding modes of o-Glu, their stabilities do not differ substantially. The activated sugar intermediates also have similar geometries. The different starting configurations, however, result in pronounced differences in the reaction pathways for the aldose–ketose isomerization.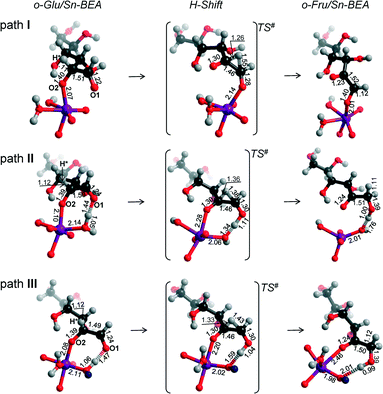 | ||
| Fig. 3 Local structures of reaction intermediates and transition states for the aldose–ketose isomerization of o-Glu over the SnOH site in a periodic Sn-BEA model. | ||
The H-shift of o-GluI/Sn-BEA is catalyzed by the Lewis acidic Sn site. In the course of the reaction, the shift of the H* atom from the C2 to C1 atom of glucose is accompanied by redistribution of the negative charge from the C2O2 moiety to C1O1, resulting in the cleavage of Sn⋯O2 with concomitant formation of a new Sn⋯O1 bond. Bader charge analysis indicates a net charge transfer from the C2O2 moiety to C1O1 during the H* shift (Tables S2–S4†) for all three reaction paths. The charge is delocalized over these moieties in the respective transition state structures. The length of the new Sn⋯O1 bond is close to the corresponding bond length in the o-FruI/Sn-BEA reaction product (Fig. 3, path I). We propose that monodentate sugar coordination is maintained along the reaction path because the weak interaction with the slightly electrophilic C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O2 keto group formed during this reaction cannot compensate for the energy losses associated with the perturbations of the Sn site that would be necessary to form bidentate O1,O2 coordination. Monodentate binding of the anionic sugar with the Lewis acid will only stabilize the negative charge at the O1 position in the transition state. This monodentate binding is the cause of the high activation barrier of 148 kJ mol−1 for the H-shift in o-GluI/Sn-BEA. The activation barriers are substantially lower for the reactions of o-GluII/Sn-BEA (57 kJ mol−1) and o-GluIII/Sn-BEA (60 kJ mol−1) because these transition states involve an additional hydrogen bond between the active site and the aldehyde C1
O2 keto group formed during this reaction cannot compensate for the energy losses associated with the perturbations of the Sn site that would be necessary to form bidentate O1,O2 coordination. Monodentate binding of the anionic sugar with the Lewis acid will only stabilize the negative charge at the O1 position in the transition state. This monodentate binding is the cause of the high activation barrier of 148 kJ mol−1 for the H-shift in o-GluI/Sn-BEA. The activation barriers are substantially lower for the reactions of o-GluII/Sn-BEA (57 kJ mol−1) and o-GluIII/Sn-BEA (60 kJ mol−1) because these transition states involve an additional hydrogen bond between the active site and the aldehyde C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 group (Fig. 2). In both cases, the H-shift reaction proceeds simultaneously with protonation of the terminal O1 site by either the Sn⋯H2O or SiFOFH group resulting in direct formation of the open form of fructose.
O1 group (Fig. 2). In both cases, the H-shift reaction proceeds simultaneously with protonation of the terminal O1 site by either the Sn⋯H2O or SiFOFH group resulting in direct formation of the open form of fructose.
The drastic decrease in the activation barrier points to the crucial role of the H-bonding resulting in direct stabilization of the negative charge redistributing between O1 and O2 sites. In a previous computational study,39 we have shown that the non-cooperative H-shift involving bidentate coordination of o-Glu to SnOH species located at the T9 lattice site of the desilicated Sn-BEA zeolite can proceed with a substantially lower barrier of 94 kJ mol−1. Nevertheless, this value is still higher than the barrier computed for the cooperative paths II and III (~60 kJ mol−1).
For paths II and III, the H-shift is accompanied by proton transfer to the O1 site from, respectively, pre-coordinated water and a silanol group adjacent to the Sn site. The relatively short r(O1⋯H) distances in the corresponding TS structures (1.11 and 1.04 Å, respectively, for TSII and TSIII) imply that the proton transfer is effectively completed prior to the H-shift. At the same time, the Sn⋯O1 distance is only slightly elongated in TSII and TSIII compared to the initial o-Glu/Sn-BEA. These observations indicate a strong interaction of both oxygen centers with the zeolite active site during the H-shift reaction, resulting in better stabilization of the TS structures and, accordingly, lower activation barriers for paths II and III. For the unfavorable TS of configuration I, only O1 interacts with the Sn site through a relatively short Sn⋯O1 bond (2.14 Å, Fig. 3, path I) and the O2 moiety is not directly stabilized by interactions with the electrophilic groups of the zeolite.
These results imply that, besides direct coordination of the carbohydrate to the Lewis acidic Sn site, the pre-activation of the terminal C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 carbonyl group in glucose via hydrogen bonding is necessary to facilitate the H-shift reaction (Fig. 2). For the current Sn-BEA model, this beneficial hydrogen bond can be formed with a water molecule, which is co-adsorbed to the Sn site, or a vicinal silanol group. These interactions strongly decrease the barrier of the aldose–ketose isomerization (57–60 kJ mol−1 for paths II and III) compared to the case where the reaction proceeds without assistance of a hydroxyl group (148 kJ mol−1, path I).
O1 carbonyl group in glucose via hydrogen bonding is necessary to facilitate the H-shift reaction (Fig. 2). For the current Sn-BEA model, this beneficial hydrogen bond can be formed with a water molecule, which is co-adsorbed to the Sn site, or a vicinal silanol group. These interactions strongly decrease the barrier of the aldose–ketose isomerization (57–60 kJ mol−1 for paths II and III) compared to the case where the reaction proceeds without assistance of a hydroxyl group (148 kJ mol−1, path I).
Sn-MOR
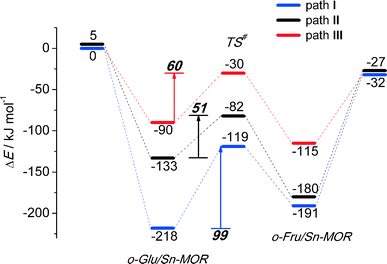
In the exploration of glucose isomerization over Sn-MOR, we assumed that the reaction proceeds via a mechanism essentially similar to that identified for Sn-BEA. Accordingly, three o-Glu/Sn-MOR configurations were compared. The corresponding reaction energy diagrams for the H-shift reaction are shown in Fig. 4. The optimized local structures and key geometrical parameters of transition states and intermediates involved are summarized in Fig. 5. Different from Sn-BEA, the stabilities of o-Glu/Sn-MOR complexes show strong dependency on the adsorption mode (Fig. 4). The most stable complex (o-GluI/Sn-MOR) involves bidentate binding of glucose to the Lewis acidic Sn site via O1 and O2 moieties of the carbohydrate (r(Sn–O1) = 2.27 Å and r(Sn–O2) = 2.09 Å, Fig. 5, path I). The formation of this complex via adsorption and deprotonation of glucose by Sn-MOR is exothermic by −218 kJ mol−1. The alternative configurations II (−133 kJ mol−1) and III (−90 kJ mol−1) are much less stable, because of the monodentate coordination of o-Glu.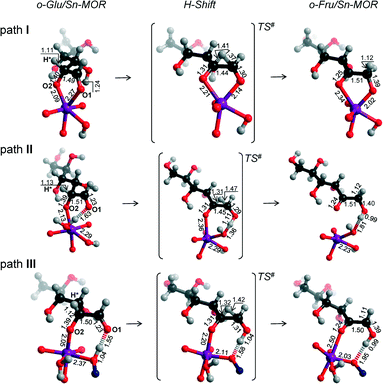 | ||
| Fig. 5 Local structures of reaction intermediates and transition states for the aldose–ketose isomerization of o-Glu over the SnOH site in a periodic Sn-MOR model. | ||
The trends in the energetics and geometries during the H-shift reaction over Sn-MOR are similar to those reported for Sn-BEA. Low H-shift barriers of 51 and 60 kJ mol−1 are found for the reaction promoted through additional hydrogen bonding between the aldehyde C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 group and co-adsorbed H2O (path II) or the vicinal silanol group (path III). Although these values are close to those found for the corresponding paths in Sn-BEA (Fig. 2), the activation barrier for the H-shift involving only the Sn site is much lower for Sn-MOR (99 kJ mol−1) than for the partially hydrolyzed Sn-BEA model considered in this study (148 kJ mol−1). This value is close to the barrier of 94 kJ mol−1 predicted for the H-shift reaction in a bidentate o-Glu complex with a SnOH site in desilicated Sn-BEA.39 This is the consequence of the better compensation of the negative charges on O1 and O2 sites in the TS due to bidentate coordination of the sugar intermediate to the Lewis acidic Sn center in Sn-MOR. The results listed in Table S2† show that the net charges at C2O2 and C1O1 moieties and the Sn atom of the TS complex in Sn-MOR are, respectively, −1.55 e−, −1.78 e− and 2.29 e−. In the zeolite Sn-BEA, the corresponding values are, −1.85 e−, −1.78 e−, and 2.35 e−. This indicates a more pronounced charge transfer between the carbohydrate and Sn during the transformation of the bidentately coordinated o-Glu in Sn-MOR compared to that of the monodentate o-Glu/Sn-BEA structure. The bidentate adsorption mode was not stable in the current model of Sn-BEA probably because of the strong coordination with H2O that restricts the accessibility of Sn. Despite the beneficial effect of the bidentate coordination in Sn-MOR, the calculations predict that the cooperative paths involving a vicinal hydroxyl group are the dominant reaction pathways.
O1 group and co-adsorbed H2O (path II) or the vicinal silanol group (path III). Although these values are close to those found for the corresponding paths in Sn-BEA (Fig. 2), the activation barrier for the H-shift involving only the Sn site is much lower for Sn-MOR (99 kJ mol−1) than for the partially hydrolyzed Sn-BEA model considered in this study (148 kJ mol−1). This value is close to the barrier of 94 kJ mol−1 predicted for the H-shift reaction in a bidentate o-Glu complex with a SnOH site in desilicated Sn-BEA.39 This is the consequence of the better compensation of the negative charges on O1 and O2 sites in the TS due to bidentate coordination of the sugar intermediate to the Lewis acidic Sn center in Sn-MOR. The results listed in Table S2† show that the net charges at C2O2 and C1O1 moieties and the Sn atom of the TS complex in Sn-MOR are, respectively, −1.55 e−, −1.78 e− and 2.29 e−. In the zeolite Sn-BEA, the corresponding values are, −1.85 e−, −1.78 e−, and 2.35 e−. This indicates a more pronounced charge transfer between the carbohydrate and Sn during the transformation of the bidentately coordinated o-Glu in Sn-MOR compared to that of the monodentate o-Glu/Sn-BEA structure. The bidentate adsorption mode was not stable in the current model of Sn-BEA probably because of the strong coordination with H2O that restricts the accessibility of Sn. Despite the beneficial effect of the bidentate coordination in Sn-MOR, the calculations predict that the cooperative paths involving a vicinal hydroxyl group are the dominant reaction pathways.
Sn-MFI
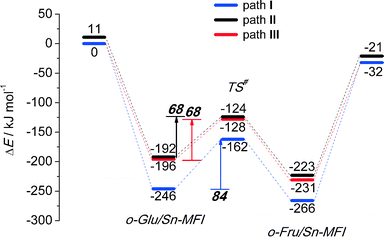
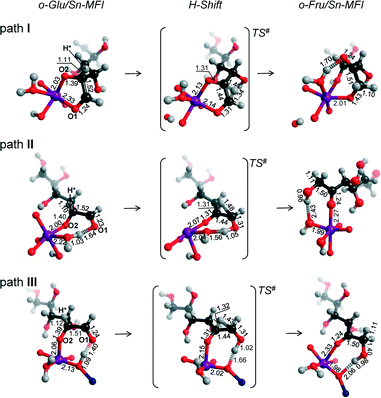
We also considered the isomerization reaction by Sn-MFI. A brief investigation of the relevant literature has shown that Sn-MFI zeolites are not active in selective glucose conversion.47,48 The energy profiles for o-Glu isomerization over Sn-MFI are shown in Fig. 6. The formation of the o-Glu intermediate in Sn-MFI channels is more favorable than in Sn-MOR and Sn-BEA. The reaction energies fall in the range of −192 to −246 kJ mol−1 for the adsorption and deprotonation of glucose over SnOH in Sn-MFI.Similar to the Sn-MOR zeolite, the o-GluI/Sn-MFI complex featuring a bidentate coordination of the carbohydrate to Sn (r(Sn–O1) = 2.33 Å and r(Sn–O2) = 2.03 Å, Fig. 7, path I) is the most stable. Configurations II and III, in which the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 carbonyl group is hydrogen bonded with co-adsorbed water or a silanol group, respectively, are approximately 50 kJ mol−1 less stable. In these o-Glu/Sn-MFI structures, glucose forms a monodentate adsorption complex with the Sn site with r(Sn–O2) = 2.00 Å and 2.06 Å (Fig. 7, path II and III, respectively). Comparison of the energies computed with and without correction for van der Waals interactions (vdW) evidenced a strong contribution of dispersion interactions to the stabilization of the o-Glu intermediate in zeolite voids (see the ESI† for pure DFT energies without vdW correction). Indeed, the vdW contribution to the stabilization of carbohydrate intermediates in the larger pores of zeolites Sn-BEA and Sn-MOR is in the range of 174–200 kJ mol−1. In zeolites Sn-MFI and Sn-MWW, the vdW stabilization is much stronger (220–242 kJ mol−1) because of a tighter confinement of the sugar intermediate in their narrower channels. Similar to Sn-BEA and Sn-MOR, the H-shift reaction for paths II and III in Sn-MFI proceed with protonation of the O1 group with a barrier of 68 kJ mol−1. The non-cooperative path involving the bidentate o-Glu⋯Sn complex (path I) proceeds with an activation barrier of 84 kJ mol−1.
O1 carbonyl group is hydrogen bonded with co-adsorbed water or a silanol group, respectively, are approximately 50 kJ mol−1 less stable. In these o-Glu/Sn-MFI structures, glucose forms a monodentate adsorption complex with the Sn site with r(Sn–O2) = 2.00 Å and 2.06 Å (Fig. 7, path II and III, respectively). Comparison of the energies computed with and without correction for van der Waals interactions (vdW) evidenced a strong contribution of dispersion interactions to the stabilization of the o-Glu intermediate in zeolite voids (see the ESI† for pure DFT energies without vdW correction). Indeed, the vdW contribution to the stabilization of carbohydrate intermediates in the larger pores of zeolites Sn-BEA and Sn-MOR is in the range of 174–200 kJ mol−1. In zeolites Sn-MFI and Sn-MWW, the vdW stabilization is much stronger (220–242 kJ mol−1) because of a tighter confinement of the sugar intermediate in their narrower channels. Similar to Sn-BEA and Sn-MOR, the H-shift reaction for paths II and III in Sn-MFI proceed with protonation of the O1 group with a barrier of 68 kJ mol−1. The non-cooperative path involving the bidentate o-Glu⋯Sn complex (path I) proceeds with an activation barrier of 84 kJ mol−1.
 | ||
| Fig. 7 Local structures of reaction intermediates and transition states for the aldose–ketose isomerization of o-Glu over the SnOH site in a periodic Sn-MFI model. | ||
Independent of the starting o-Glu configuration, the sugar moieties in the transition states show similar geometries. They have similar r(C1–O1) and r(C2–O2) bond lengths of 1.31 Å and r(C1–C2) bond lengths of 1.44 Å. The short r(O1⋯H) distances in the TSs of configuration II (1.05 Å) and configuration III (1.02 Å) point to complete protonation of the aldehyde moiety prior to the formation of the C1–H* bond during the H-shift elementary reaction step.
Sn-MWW
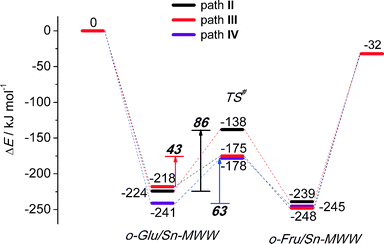
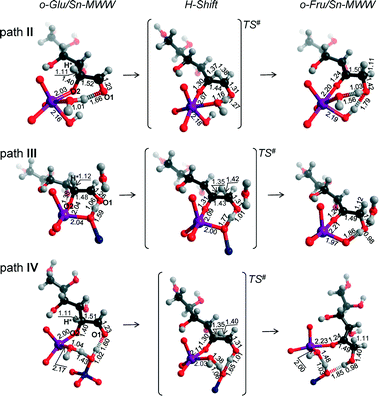
Although the MWW structure features even smaller pores than MFI, Sn-MWW has recently been shown to be active in the catalytic transformation of glucose.49 The expected strong confinement of anionic glucose intermediates within the relatively small MWW micropores is reflected in very high stabilization energies in the range of 218–241 kJ mol−1 computed for o-Glu/Sn-MWW complexes (Fig. 8). For Sn-MWW, we did not find a stable configuration involving o-Glu interaction with lattice Sn without additional stabilization through hydrogen bonding of the aldehyde C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 moiety. This is likely the consequence of the tight confinement in the pores of this zeolite. Besides the two hydroxyl-stabilized configurations II and III, we also found another configuration denoted as IV (Fig. 9) similar to the one previously proposed by Vlachos and co-workers for the Sn-BEA zeolite on the basis of cluster DFT calculations.41 In this configuration, the adsorbed H2O molecule, the SiFOFH group and the carbonyl group of o-Glu form a hydrogen bonding network. The concerted proton transfer through this hydrogen bonding network to O1 has been proposed to be crucial for the facile aldose–ketose isomerization reaction.41 Attempts to construct a similar adsorption complex in the periodic models of Sn-BEA, Sn-MOR and Sn-MFI zeolites were not successful. The activation barriers for the H-shift reaction over Sn-MWW are 86, 43 and 63 kJ mol−1, respectively for paths II, III and IV. The structural properties of the intermediates and transition states involved (Fig. 9) are similar to those described above for other zeolite topologies.
O1 moiety. This is likely the consequence of the tight confinement in the pores of this zeolite. Besides the two hydroxyl-stabilized configurations II and III, we also found another configuration denoted as IV (Fig. 9) similar to the one previously proposed by Vlachos and co-workers for the Sn-BEA zeolite on the basis of cluster DFT calculations.41 In this configuration, the adsorbed H2O molecule, the SiFOFH group and the carbonyl group of o-Glu form a hydrogen bonding network. The concerted proton transfer through this hydrogen bonding network to O1 has been proposed to be crucial for the facile aldose–ketose isomerization reaction.41 Attempts to construct a similar adsorption complex in the periodic models of Sn-BEA, Sn-MOR and Sn-MFI zeolites were not successful. The activation barriers for the H-shift reaction over Sn-MWW are 86, 43 and 63 kJ mol−1, respectively for paths II, III and IV. The structural properties of the intermediates and transition states involved (Fig. 9) are similar to those described above for other zeolite topologies.
 | ||
| Fig. 9 Local structures of reaction intermediates and transition states for the aldose–ketose isomerization of o-Glu over the SnOH site in a periodic Sn-MWW model. | ||
Discussion
The present DFT calculations provide compelling evidence for the strong beneficial effect of the presence of hydroxyl groups in close proximity to partially hydrolyzed Lewis acidic lattice Sn centers that catalyze the H-shift reaction in sugar. This is the crucial step in the isomerization of glucose to fructose over Sn-containing zeolites. The conversion of glucose starts by its adsorption on the partially hydrolyzed SnOH lattice sites followed by the deprotonation of the hydroxyl O2H group. This results in the anionic o-Glu intermediate and a water molecule, both coordinated to Sn. Hydrogen bonding between the aldehyde C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 group and coordinated water increases the electrophilicity of the C1 atom, thereby promoting directly the H-shift between C2 and C1. The interaction with the proton donor also stabilizes the negative charge developing at the O1 site during the isomerization reaction. As a result of the cooperative action between the Lewis acidic Sn site and the coordinated water molecule, the rate-controlling step of the aldose–ketose isomerization involves a simultaneous C2–C1 H-shift reaction and the protonation of the O1 site resulting in the direct formation of acyclic fructose and the regeneration of the initial SnOH site. For Sn-BEA, the activation barrier for the water-assisted H-shift reaction is only 57 kJ mol−1 (path II, Fig. 2), which is almost 100 kJ mol−1 lower than the barrier for the path catalyzed only by the Lewis acidic Sn center in Sn-BEA (path I, Fig. 2). We speculate that a similar mechanism is relevant in the presence of other proton donors. In this study, the promoting effect of a vicinal silanol group formed together with the SnOH active species via the partial hydrolysis of the tetrahedral Sn center in the zeolite framework provides such an example. The activation barrier predicted for this path over Sn-BEA (60 kJ mol−1, path III, Fig. 2) is almost the same as that of the water-assisted reaction. The computed trends are very similar for Sn-MOR and Sn-MFI (Fig. 4 and 6). The water-assisted path over Sn-MWW is more difficult (86 kJ mol−1). Interestingly, the active center in Sn-MWW consists of the Lewis acidic SnOH species that forms a short coordination bond with the vicinal silanol group (Fig. 9). This interaction effectively enhances the acidity of the silanol group resulting in a very low barrier for the SiFOFH-promoted isomerization reaction (43 kJ mol−1). On the other hand, it leads to a decreased acidity of the co-adsorbed H2O in configuration II resulting in a higher barrier for the water-assisted isomerization reaction. The direct interaction between the silanol group and the Sn site can be broken by the introduction of a water molecule resulting in the formation of an intermolecular hydrogen bonding network Sn⋯H2O⋯SiFOFH. The isomerization reaction assisted by a concerted proton transfer through this network (path IV) shows a barrier close to that identified for H2O and SiFOFH-assisted paths over Sn-BEA, Sn-MOR and Sn-MFI.
O1 group and coordinated water increases the electrophilicity of the C1 atom, thereby promoting directly the H-shift between C2 and C1. The interaction with the proton donor also stabilizes the negative charge developing at the O1 site during the isomerization reaction. As a result of the cooperative action between the Lewis acidic Sn site and the coordinated water molecule, the rate-controlling step of the aldose–ketose isomerization involves a simultaneous C2–C1 H-shift reaction and the protonation of the O1 site resulting in the direct formation of acyclic fructose and the regeneration of the initial SnOH site. For Sn-BEA, the activation barrier for the water-assisted H-shift reaction is only 57 kJ mol−1 (path II, Fig. 2), which is almost 100 kJ mol−1 lower than the barrier for the path catalyzed only by the Lewis acidic Sn center in Sn-BEA (path I, Fig. 2). We speculate that a similar mechanism is relevant in the presence of other proton donors. In this study, the promoting effect of a vicinal silanol group formed together with the SnOH active species via the partial hydrolysis of the tetrahedral Sn center in the zeolite framework provides such an example. The activation barrier predicted for this path over Sn-BEA (60 kJ mol−1, path III, Fig. 2) is almost the same as that of the water-assisted reaction. The computed trends are very similar for Sn-MOR and Sn-MFI (Fig. 4 and 6). The water-assisted path over Sn-MWW is more difficult (86 kJ mol−1). Interestingly, the active center in Sn-MWW consists of the Lewis acidic SnOH species that forms a short coordination bond with the vicinal silanol group (Fig. 9). This interaction effectively enhances the acidity of the silanol group resulting in a very low barrier for the SiFOFH-promoted isomerization reaction (43 kJ mol−1). On the other hand, it leads to a decreased acidity of the co-adsorbed H2O in configuration II resulting in a higher barrier for the water-assisted isomerization reaction. The direct interaction between the silanol group and the Sn site can be broken by the introduction of a water molecule resulting in the formation of an intermolecular hydrogen bonding network Sn⋯H2O⋯SiFOFH. The isomerization reaction assisted by a concerted proton transfer through this network (path IV) shows a barrier close to that identified for H2O and SiFOFH-assisted paths over Sn-BEA, Sn-MOR and Sn-MFI.
To analyze in more detail the influence of the zeolite topology on the isomerization reaction we compared the energies of similar reaction paths for different zeolites in Fig. 10 and 11, assisted by co-adsorbed water and vicinal silanol, respectively. For the water-assisted path, the lowest activation barriers are predicted for the large pore Sn-BEA and Sn-MOR zeolites (57 and 51 kJ mol−1, respectively). When the reaction occurs in narrower pores of Sn-MFI the barrier is slightly higher (68 kJ mol−1). This reaction is least favorable for Sn-MWW (86 kJ mol−1). The barrier differences are less significant when the reaction is promoted by a vicinal silanol group. Zeolites Sn-BEA, Sn-MOR and Sn-MFI promote the respective reaction with activation barriers in the 60–70 kJ mol−1 range. The much lower barrier of 43 kJ mol−1 predicted for Sn-MWW is due to the higher acidity of the bridging SiFOFH group acting as a proton-donor in the course of the H-shift reaction assisting the Lewis acidic Sn site. These findings provide an explanation for the high catalytic performance of Sn-MWW.49 The pronounced catalytic activity of Sn-MWW in glucose conversion may be explained by the low reaction barrier for the H-shift step. Nevertheless, one cannot exclude the beneficial role of other factors such as the increased mesoporosity and high density of defects generated upon the post-synthetic modification of the MWW material. This can promote the accessibility of the active intrazeolitic Sn sites. The low activity of Sn-MFI is tentatively attributed to slow diffusion of sugars in the narrow pores of MFI. Furthermore, previous studies48 did not evidence the formation of partially hydrolyzed SnOH sites in Sn-MFI. Accordingly, the limited performance of Sn-MFI may also be explained by the absence of catalytically active partially hydrolyzed Sn sites in the zeolite micropores.
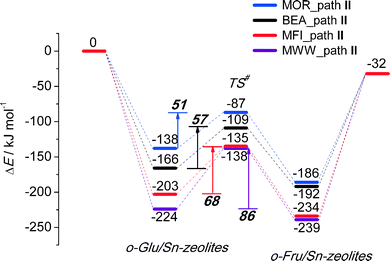 | ||
| Fig. 10 Reaction energy diagram of o-Glu to o-Fru over the SnOH site in path II promoted by Sn⋯H2O⋯O1 hydrogen bonding in Sn-BEA, Sn-MOR, Sn-MFI and Sn-MWW. | ||
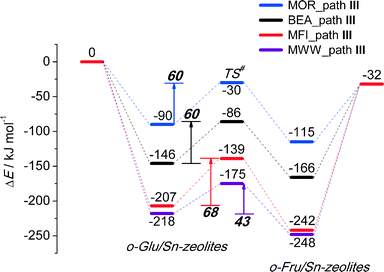 | ||
| Fig. 11 Reaction energy diagram of o-Glu to o-Fru over the SnOH site in path III of the SiOH⋯O1 hydrogen bond mode in Sn-BEA, Sn-MOR, Sn-MFI and Sn-MWW. | ||
The application of Sn-modified zeolite catalysts for glucose isomerization has been frequently compared to the catalytic action of the D-xylose isomerase enzyme.38 The present work further supports this supposition. Kovalevsky et al. investigated the reaction mechanism of enzymatic sugar conversion.58 It was demonstrated that the isomerization reaction was triggered by the interaction with a “catalytic” water molecule coordinated by a metal cofactor close to the active site of the enzyme. The polarized water pre-activates the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 aldehyde moiety of aldose via a metal⋯H2O⋯O1 hydrogen bond and effectively increases the positive charge of the C1 atom of the carbohydrate. The concerted action of the metal cofactors and the “catalytic” water molecule is essential to promote the C2–C1 H-shift by the enzyme. The present study hints at a very similar hydrogen bond promotion of the H-shift reaction over Sn-modified zeolites. Co-adsorbed water binding to the Sn site and a silanol group nearby the Sn center can donate their protons to the C1
O1 aldehyde moiety of aldose via a metal⋯H2O⋯O1 hydrogen bond and effectively increases the positive charge of the C1 atom of the carbohydrate. The concerted action of the metal cofactors and the “catalytic” water molecule is essential to promote the C2–C1 H-shift by the enzyme. The present study hints at a very similar hydrogen bond promotion of the H-shift reaction over Sn-modified zeolites. Co-adsorbed water binding to the Sn site and a silanol group nearby the Sn center can donate their protons to the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 carbonyl group. This interaction compensates the negative charge developing at the O2 atom of the sugar and, in this way, promotes the rate-controlling H-shift reaction. The present work points to the generality of this cooperative mechanism for aldose–ketose isomerization reaction in Sn-modified zeolites. As glucose isomerization is usually carried out in aqueous solutions, one may envision that solvent molecules present in the zeolite micropores can promote the Sn-catalyzed reactions.59 Alternatively, the pre-activation of the C1
O1 carbonyl group. This interaction compensates the negative charge developing at the O2 atom of the sugar and, in this way, promotes the rate-controlling H-shift reaction. The present work points to the generality of this cooperative mechanism for aldose–ketose isomerization reaction in Sn-modified zeolites. As glucose isomerization is usually carried out in aqueous solutions, one may envision that solvent molecules present in the zeolite micropores can promote the Sn-catalyzed reactions.59 Alternatively, the pre-activation of the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 carbonyl moiety can occur through a hydrogen bonding network consisting of zeolite defects neighboring the Lewis acidic site as previously proposed by Yang et al.39
O1 carbonyl moiety can occur through a hydrogen bonding network consisting of zeolite defects neighboring the Lewis acidic site as previously proposed by Yang et al.39
The differences in size and shape of the zeolite channels affect the thermodynamic stability of the o-Glu and o-Fru intermediates. They will also affect the diffusion rates of the reactant and product in the zeolite micropores. The dominant effect of vdW interactions on the stabilization of carbohydrate species in zeolites is evident from the comparison of reaction energies calculated with and without dispersion corrections (see Fig. S1–S4 in the ESI†). The vdW stabilization of the reaction intermediates in Sn-BEA and Sn-MOR is 174–200 kJ mol−1, independent of the reaction path. This vdW contribution to the stabilization energies of carbohydrate intermediates is higher for Sn-MWW and Sn-MFI (220–242 kJ mol−1). Although the stabilities of the carbohydrate intermediates are strongly affected by different dimensions of the zeolite voids, confinement effects only slightly influence the intrinsic reactivity of framework Sn sites. The reaction and activation Gibbs free energies at a reaction temperature of 373 K for reaction path II over the four Sn-zeolite models considered in this study are summarized in Fig. S5–S8.† The results point to a strong influence of the entropy on the adsorption and desorption steps, while the entropy contribution to the activation barrier of the H-shift reaction and, accordingly, the intrinsic activity of intrazeolite SnOH Lewis acid sites is relatively small.
Conclusion
The reaction mechanism of glucose isomerization to fructose over Sn-containing zeolites Sn-MOR, Sn-BEA, Sn-MFI and Sn-MWW was studied by periodic DFT calculations. A partially hydrolyzed (SiFOF)3SnOH group in the zeolite framework was investigated as the active site for the isomerization reaction. For each zeolite topology three distinct reaction mechanisms were considered, namely the reaction promoted only by the Lewis acidic Sn center and two cooperative paths involving synergy between the lattice Sn site and vicinal proton-donating groups from co-adsorbed water or an internal silanol. It is demonstrated that independent of the zeolite topology, the rate-controlling H-shift elementary step is strongly facilitated when the aldehyde C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O1 moiety of o-Glu is pre-activated by a proton donor located in the vicinity of the Lewis acidic Sn site. This cooperative action of the lattice Sn and hydrogen bond donor allows for efficient stabilization of the negative charge redistributing between the O2 and O1 moieties of the adsorbed carbohydrate during the H-shift reaction. The cooperative paths involve concerted C2–C1 H-shift and O1 protonation. These mechanistic insights provide a conceptual bridge between heterogeneous Lewis acid glucose conversion catalysts and enzymatic systems.
O1 moiety of o-Glu is pre-activated by a proton donor located in the vicinity of the Lewis acidic Sn site. This cooperative action of the lattice Sn and hydrogen bond donor allows for efficient stabilization of the negative charge redistributing between the O2 and O1 moieties of the adsorbed carbohydrate during the H-shift reaction. The cooperative paths involve concerted C2–C1 H-shift and O1 protonation. These mechanistic insights provide a conceptual bridge between heterogeneous Lewis acid glucose conversion catalysts and enzymatic systems.
Although the size and shape of the zeolite pores have only a minor influence on the intrinsic reactivity of the lattice Sn centers, they affect very strongly the thermodynamic stabilities of adsorbed o-Glu and o-Fru intermediates inside the zeolite channels. The increased vdW stabilization of carbohydrates adsorbed in narrow pore zeolites is proposed to limit the diffusion of the substrates and products inside the zeolite resulting thus in the effective decrease in the accessibility of the lattice Sn sites. This suggests that the low activity of Sn-MFI is due to slow diffusion of the carbohydrates in its micropores. It is proposed that the good performance of Sn-MWW in glucose isomerization as compared to inactive Sn-MFI having pores of a similar size can be explained by the high reactivity of a small fraction of accessible sites containing more acidic bridging silanol groups cooperating with the Lewis acidic Sn site.
Acknowledgements
This work was financially supported by the European Union FP7 NMP project NOVACAM (Novel cheap and abundant materials for catalytic biomass conversion, FP7-NMP-2013-EU-Japan-604319). SurfSARA and NWO are acknowledged for providing access to the supercomputer facilities.Notes and references
- R.-J. van Putten, J. C. van der Waal, E. de Jong, C. B. Rasrendra, H. J. Heeres and J. G. de Vries, Chem. Rev., 2013, 113, 1499–1597 CrossRef CAS PubMed.
- D. M. Alonso, J. Q. Bond and J. A. Dumesic, Green Chem., 2010, 12, 1493–1513 RSC.
- J. N. Chheda, G. W. Huber and J. A. Dumesic, Angew. Chem., Int. Ed., 2007, 46, 7164–7183 CrossRef CAS PubMed.
- B. Girisuta, L. P. B. M. Janssen and H. J. Heeres, Ind. Eng. Chem. Res., 2007, 46, 1696–1708 CrossRef CAS.
- M. Dusselier, P. Van Wouwe, A. Dewaele, E. Makshina and B. F. Sels, Energy Environ. Sci., 2013, 6, 1415–1442 CAS.
- R. Rinaldi, R. Palkovits and F. Schüth, Angew. Chem., Int. Ed., 2008, 47, 8047–8050 CrossRef CAS PubMed.
- C.-H. Zhou, X. Xia, C.-X. Lin, D.-S. Tong and J. Beltramini, Chem. Soc. Rev., 2011, 40, 5588–5617 RSC.
- S. Dutta, S. De, B. Saha and M. I. Alam, Catal. Sci. Technol., 2012, 2, 2025–2036 CAS.
- E. Nikolla, Y. Román-Leshkov, M. Moliner and M. E. Davis, ACS Catal., 2011, 1, 408–410 CrossRef CAS.
- O. O. James, S. Maity, L. A. Usman, K. O. Ajanaku, O. O. Ajani, T. O. Siyanbola, S. Sahu and R. Chaubey, Energy Environ. Sci., 2010, 3, 1833–1850 CAS.
- T. D. Swift, C. Bagia, V. Choudhary, G. Peklaris, V. Nikolakis and D. G. Vlachos, ACS Catal., 2013, 4, 259–267 CrossRef.
- L. Lai and Y. Zhang, ChemSusChem, 2010, 3, 1257–1259 CrossRef CAS PubMed.
- Q. Lu, H.-T. Liao, Y. Zhang, J.-J. Zhang and C.-Q. Dong, J. Fuel Chem. Technol., 2013, 41, 1070–1076 CrossRef CAS.
- V. Choudhary, R. I. Burnett, D. G. Vlachos and S. I. Sandler, J. Phys. Chem. C, 2012, 116, 5116–5120 CAS.
- T. Ståhlberg, S. Rodriguez-Rodriguez, P. Fristrup and A. Riisager, Chem. – Eur. J., 2011, 17, 1456–1464 CrossRef PubMed.
- G. Yang, E. A. Pidko and E. J. M. Hensen, J. Catal., 2012, 295, 122–132 CrossRef CAS PubMed.
- T. D. Fenn, D. Ringe and G. A. Petsko, Biochemistry, 2004, 43, 6464–6474 CrossRef CAS PubMed.
- T. Wang, M. W. Nolte and B. H. Shanks, Green Chem., 2014, 16, 548–572 RSC.
- E. A. Pidko, V. Degirmenci, R. A. van Santen and E. J. M. Hensen, Angew. Chem., 2010, 122, 2584–2588 CrossRef.
- E. A. Pidko, V. Degirmenci and E. J. M. Hensen, ChemCatChem, 2012, 4, 1263–1271 CrossRef CAS.
- H. Zhao, J. E. Holladay, H. Brown and Z. C. Zhang, Science, 2007, 316, 1597–1600 CrossRef CAS PubMed.
- V. Choudhary, S. H. Mushrif, C. Ho, A. Anderko, V. Nikolakis, N. S. Marinkovic, A. I. Frenkel, S. I. Sandler and D. G. Vlachos, J. Am. Chem. Soc., 2013, 135, 3997–4006 CrossRef CAS PubMed.
- M. E. Zakrzewska, E. Bogel-Łukasik and R. Bogel-Łukasik, Chem. Rev., 2010, 111, 397–417 CrossRef PubMed.
- F. de Clippel, M. Dusselier, R. Van Rompaey, P. Vanelderen, J. Dijkmans, E. Makshina, L. Giebeler, S. Oswald, G. V. Baron, J. F. M. Denayer, P. P. Pescarmona, P. A. Jacobs and B. F. Sels, J. Am. Chem. Soc., 2012, 134, 10089–10101 CrossRef CAS PubMed.
- Y. Román-Leshkov and M. E. Davis, ACS Catal., 2011, 1, 1566–1580 CrossRef.
- E. Taarning, C. M. Osmundsen, X. Yang, B. Voss, S. I. Andersen and C. H. Christensen, Energy Environ. Sci., 2011, 4, 793–804 CAS.
- M. Moliner, Dalton Trans., 2014, 43, 4197–4208 RSC.
- S. Saravanamurugan, M. Paniagua, J. A. Melero and A. Riisager, J. Am. Chem. Soc., 2013, 135, 5246–5249 CrossRef CAS PubMed.
- M. Moliner, Y. Román-Leshkov and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6164–6168 CrossRef CAS PubMed.
- Y. Román-Leshkov, M. Moliner, J. A. Labinger and M. E. Davis, Angew. Chem., Int. Ed., 2010, 49, 8954–8957 CrossRef PubMed.
- J. Dijkmans, D. Gabriels, M. Dusselier, F. de Clippel, P. Vanelderen, K. Houthoofd, A. Malfliet, Y. Pontikes and B. F. Sels, Green Chem., 2013, 15, 2777–2785 RSC.
- M. S. Holm, S. Saravanamurugan and E. Taarning, Science, 2010, 328, 602–605 CrossRef CAS PubMed.
- M. S. Holm, Y. J. Pagan-Torres, S. Saravanamurugan, A. Riisager, J. A. Dumesic and E. Taarning, Green Chem., 2012, 14, 702–706 RSC.
- J. B. Nicholas, Top. Catal., 1997, 4, 157–171 CrossRef CAS.
- V. Choudhary, S. Caratzoulas and D. G. Vlachos, Carbohydr. Res., 2013, 368, 89–95 CrossRef CAS PubMed.
- G. Yang, E. A. Pidko and E. J. M. Hensen, J. Phys. Chem. C, 2013, 117, 3976–3986 CAS.
- L. Cheng, L. A. Curtiss, R. S. Assary, J. Greeley, T. Kerber and J. Sauer, J. Phys. Chem. C, 2011, 115, 21785–21790 CAS.
- R. Bermejo-Deval, R. S. Assary, E. Nikolla, M. Moliner, Y. Román-Leshkov, S.-J. Hwang, A. Palsdottir, D. Silverman, R. F. Lobo, L. A. Curtiss and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9727–9732 CrossRef CAS PubMed.
- G. Yang, E. A. Pidko and E. J. M. Hensen, ChemSusChem, 2013, 6, 1688–1696 CrossRef CAS PubMed.
- M. Boronat, P. Concepción, A. Corma, M. Renz and S. Valencia, J. Catal., 2005, 234, 111–118 CrossRef CAS PubMed.
- N. Rai, S. Caratzoulas and D. G. Vlachos, ACS Catal., 2013, 3, 2294–2298 CrossRef CAS.
- R. Bermejo-Deval, R. Gounder and M. E. Davis, ACS Catal., 2012, 2, 2705–2713 CrossRef CAS.
- S. Roy, K. Bakhmutsky, E. Mahmoud, R. F. Lobo and R. J. Gorte, ACS Catal., 2013, 3, 573–580 CrossRef CAS.
- R. S. Assary and L. A. Curtiss, J. Phys. Chem. A, 2011, 115, 8754–8760 CrossRef CAS PubMed.
- V. Choudhary, A. B. Pinar, R. F. Lobo, D. G. Vlachos and S. I. Sandler, ChemSusChem, 2013, 6, 2369–2376 CrossRef CAS PubMed.
- J. Jae, G. A. Tompsett, A. J. Foster, K. D. Hammond, S. M. Auerbach, R. F. Lobo and G. W. Huber, J. Catal., 2011, 279, 257–268 CrossRef CAS PubMed.
- C. M. Lew, N. Rajabbeigi and M. Tsapatsis, Microporous Mesoporous Mater., 2012, 153, 55–58 CrossRef CAS PubMed.
- C. M. Osmundsen, M. S. Holm, S. Dahl and E. Taarning, Proc. R. Soc. A, 2012, 468, 2000–2016 CrossRef CAS.
- Q. Guo, F. Fan, E. A. Pidko, W. N. P. van der Graaff, Z. Feng, C. Li and E. J. M. Hensen, ChemSusChem, 2013, 6, 1352–1356 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- C. Hammond, S. Conrad and I. Hermans, Angew. Chem., Int. Ed., 2012, 51, 11736–11739 CrossRef CAS PubMed.
- J. Dijkmans, D. Gabriels, M. Dusselier, F. de Clippel, P. Vanelderen, K. Houthooft, A. Malfliet, Y. Pontikes and B. F. Sels, Green Chem., 2013, 15, 2777 RSC.
- J. Dědeček, Z. Sobalík and B. Wichterlová, Catal. Rev.: Sci. Eng., 2012, 54, 135–223 Search PubMed.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Y. Kovalevsky, L. Hanson, S. Z. Fisher, M. Mustyakimov, S. A. Mason, V. Trevor Forsyth, M. P. Blakeley, D. A. Keen, T. Wagner, H. L. Carrell, A. K. Katz, J. P. Glusker and P. Langan, Structure, 2010, 18, 688–699 CrossRef CAS PubMed.
- P. Nava, Y. Carissan, J. Drujon, F. Grau, J. Godeau, S. Antoniotti, E. Duñach and S. Humbel, ChemCatChem, 2014, 6, 500–507 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: DFT computed reaction energy diagrams, reaction Gibbs free energy diagrams for reaction path II, optimized lattice parameters of zeolite models and analysis of Bader atomic charges. See DOI: 10.1039/c4cy00186a |
| This journal is © The Royal Society of Chemistry 2014 |