Coordination and conformational isomers in mononuclear iron complexes with pertinence to the [FeFe] hydrogenase active site

Abstract

A series of six mononuclear iron complexes of the type [Fe(X-bdt)(P^R₂N^Ph₂)(CO)] (P^R₂N^Ph₂ = 1,5-diaza-3,7-diphosphaoctane, bdt = benzenedithiolate with X = H, Cl₂ or Me and R = Ph, Bn, Cyc or tert-Bu) was prepared. This new class of penta-coordinate iron complexes contains a free coordination site and a pendant base as essential structural features of the [FeFe]-hydrogenase active site. The bidentate nature of the P^R₂N^Ph₂ ligands was found to be crucial for the preferential formation of coordinatively unsaturated penta-coordinate complexes, which is supported by first principle calculations. IR-spectroscopic data suggest the presence of coordination isomers around the metal center, as well as multiple possible conformers of the P^R₂N^Ph₂ ligand. This finding is further corroborated by X-ray crystallographic and computational studies. ³¹P{¹H}-NMR- and IR-spectroscopic as well as electrochemical measurements show that the electronic properties of the complexes are strongly, and independently, influenced by the P-substituents at the P^R₂N^Ph₂ ligand as well as by modifications of the bdt bridge. These results illustrate the advantages of this modular platform, which allows independent and selective tuning through site specific modifications. Potential catalytic intermediates, namely singly reduced and protonated complexes, have been further investigated by spectroscopic methods and exhibit remarkable stability. Finally, their general capacity for electro-catalytic reduction of protons to molecular hydrogen was verified.

---

Introduction

With a globally increasing energy demand and limited fossil fuel resources, the development of efficient and sustainable proton reduction catalysts is at the heart of a future “Hydrogen Economy”.¹ Particular enzymes, so-called hydrogenases (H₂ases),² catalyze the reversible (inter)conversion of protons to molecular hydrogen and thus provide inspiration for the development of new synthetic catalysts.^3,4 As H₂ases are based on abundant metals in their active sites, functional synthetic models may someday become alternatives to expensive noble metal catalysts.⁵ Consequently, many attempts have been made to prepare complexes that mimic the active sites of hydrogenases, in particular those of [FeFe] H₂ases (Fig. 1), in structure and function.⁶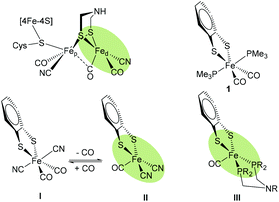

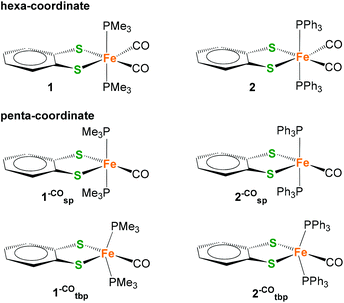
Fig. 1 Schematic structure of the H_ox state of [FeFe] H₂ase active site highlighting the free coordination site in the distal iron (Fe_d) (top left). Hexa-coordiante (1 and I¹⁴) and penta-coordinate (II and III) mononuclear model complexes of Fe_d.

In the active site of [FeFe] H₂ases, two low-valent Fe centers are interconnected by a bidentate dithiolate bridge, with biologically unusual carbon monoxide and cyanide ligands occupying most of the coordination sphere around the metals. The presence of an open coordination site at the Fe_d, i.e. the Fe center distal to the [4Fe4S] cluster, allows for substrate binding. An amine in the second coordination sphere is thought to shuttle protons to and from the active site.⁷

To this end, a broad range of dinuclear complexes as structural and functional models of the [FeFe] H₂ases have been developed. Despite sometimes very close similarity to the natural active site, catalysis with high turnover rates and low overpotential remains elusive. One of the major reasons for the lack of activity is the stability of hydrides that bridge the two Fe centers.^8,9 The formation of such bridging hydrides is not observed in the enzyme as ligand rearrangements are precluded due to hydrogen bonding from the protein matrix to the cyanide ligands, which is supported by experimental and theoretical evidence.^10–13

As the catalytically important elemental steps in hydrogen formation are assumed to proceed exclusively at Fe_d (Fig. 1),^15–17 our interests veered towards developing mononuclear complexes as functional models of Fe_d and by that avoiding the potential occurrence of bridging hydrides.^10,11,13,18 The desired structural features of these models include a primary ligand environment with maximum similarity to Fe_d, a free coordination site for substrate binding (i.e. protons, hydrogen or hydride) and an amine in the second coordination sphere as the potential proton shuttle.^19–22

The work presented in this paper summarizes our latest results in this endeavor, and discusses experimental and theoretical insights into factors that determine the conditions under which Fe(II) complexes prefer to be penta- or hexa-coordinate. A novel series of penta-coordinate Fe complexes was prepared and their preferred coordination and conformation geometry was investigated by spectroscopic techniques and first principles DFT calculations. Further spectroscopic and electrochemical investigations show that the complexes’ reduction potentials can be tuned by two orthogonal strategies and that the complexes are catalysts for the electrochemical reduction of protons at a relatively mild overpotential.

Results and discussion

More than a decade ago, Rauchfuss and co-workers reported on a mononuclear Fe complex [(bdt)Fe(CN)₂(CO)₂]²⁻I (Fig. 1) that contains two sulfide ligands, two cyanides and two CO ligands.¹⁴ Interestingly, it was found that one CO ligand binds very weakly and can be removed simply by purging with argon to afford the penta-coordinate [(bdt)Fe(CN)₂(CO)]²⁻ (II). In terms of coordination isomers, octahedrally coordinated I features the cyanides trans to each other, while square pyramidal II has the CO in the apical position (Fig. 1).¹⁴ Similarly, Darensbourg et al. reported weak and reversible binding of a third CO ligand to (2-amidothio-phenylate)Fe(CO)₂P(Cy₃) giving a hexa-coordinate complex.²³

The trimethylphosphine (PMe₃) analogue [(bdt)Fe(PMe₃)₂(CO)₂] 1 was presented a few years later,²⁴ and exhibits an equivalent coordination geometry as I. Complex 1 however features stronger Fe–CO bonds and the penta-coordinate version cannot be obtained by purging with argon. Penta-coordinate Fe complexes with phosphine ligands could however be afforded by tethering the phosphines into a bidentate ligand. The resulting penta-coordinate (bdt)Fe(PNP)(CO) (III, PNP = Ph₂PCH₂NRCH₂PPh₂, R = CH₃, CH₂CF₃) features both P-ligands in the base of the square pyramidal geometry, similar to the situation in II. Penta-coordinate II and III can only be obtained when the sulfides are part of an aromatic dithiolate (bdt) ligand, pointing towards a non-innocence of this ligand.^25,26

Considering the appeal of penta-coordinate iron complexes as catalysts for proton/hydrogen conversion, our first objective was to identify factors that determine their coordination number and conformational freedom. Particular focus was on whether or how the different donor strength and steric requirements of the PMe₃ ligands in 1 compared to the PPh₂ units in the PNP ligand of III affect these properties. For this purpose, [(bdt)Fe(PPh₃)₂(CO)₂] 2, i.e. the PPh₃ analogue of 1, was prepared (Scheme 1).

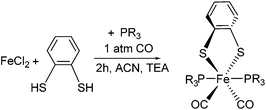Scheme 1 One-step synthesis of hexa-coordinate iron complexes 1 (R = CH₃) and 2 (R = C₆H₅). Reaction conditions: 3 h, 40 °C, 1 atm CO, Et₃N, CH₃CN.

Complex 2 is a hexa-coordinate species with an IR spectrum that is almost identical to that of 1, thus suggesting that the different electronic and spatial properties of PMe₃ compared to PPh_n (n = 2, 3) do not determine whether a complex is penta- or hexa-coordinate. Calculated symmetrical and anti-symmetrical CO-stretching frequencies are given in Table 1. The calculated IR parameters agree well with the measured ones and indicate that the PMe₃vs. PPh₃ ligand does not significantly affect the C=O bond strengths and vibrations. Yu et al. have shown that BP86/TZVP generally gives Fe–CO stretching frequencies in better agreement with experiment than B3LYP/TZVP calculations.²⁷ This is also corroborated by our results. The consideration of solvent effects by COSMO (Conductor-Like-Screening Model)²⁸ calculations does not lead to an improvement of IR frequencies (see ESI†). When applying the scaling factor by Yu et al., IR frequencies of 1954 and 2001 cm⁻¹ for 1 and 1941 and 1994 cm⁻¹ for 2 were obtained which agree well with the experimental data.

Table 1 Calculated and experimental CO stretching frequencies in solution, CO binding affinities for complexes 1 and 2 in acetonitrile and relative free energy differences for pentacoordinate complexes

Cpd.		ν/cm^−1 COasym	ν/cm^−1 COsym	CO binding free energy^c relative to		Rel. free energy^c sp vs. tbp
				sp	tbp
sp = square pyramidal; tbp = trigonal bipyramidal.a In DCM.^18b Scaled gas phase B3LYP/TZVP frequencies.^27c kcal mol^−1.
1	BP86	1920	1982	−39	−14	+25
	B3LYP	2019 (1954)^b	2071 (2001)^b	−27	−6	+21
	Exp.^a	1958	2014	—	—	—
2	BP86	1911	1973	−27	−5	+22
	B3LYP	2020 (1941)^b	2074 (1994)^b	−12	+1	+13
	Exp.^a	1969	2014	—	—	—

---

In order to investigate the prevalence of hexa-coordinate complexes 1 and 2, we determined the CO-binding free energies of the second CO ligand of complexes 1 and 2 by removing one of the equatorial CO ligands to give putative penta-coordinate low-spin Fe(II) complexes 1^–CO and 2^–CO. As for all five-coordinate 3d metal complexes, trigonal-bipyramidal (tbp) and square-pyramidal (sp) coordination modes or hybrids thereof can be expected. In general, the principal factors that determine the configuration are electrostatic and steric repulsion between ligands, the nature of the metal–ligand bond and the crystal field stabilization energy (omitting crystal packing effects). With regard to ligand–ligand repulsion, it can generally be expected that the trigonal bipyramid is the more stable regular structure.

Formal removal of one equatorial CO ligand from hexa-coordinate complexes 1 and 2 gives square-pyramidal 1^–CO_sp and 2^–co_sp with almost unchanged P–Fe–P angles, for example, of 177° in 1^–CO_sp compared to 171° in 1. Calculated 1,2^–CO_sp feature a bdt-S in the apical position which is different from the geometry of PNP complexes III which have a CO ligand in the axial site instead. The square-pyramidal coordination modes in 1,2^–CO_sp are characterized as local minima on the potential energy surface. There are, however, global energy minima which stem from a distortion of the PMe₃ and PPh₃ ligands that leads to changes in S–Fe–P angles from ∼90° to larger angles. The result is a geometry that is best described as a distorted trigonal-bipyramidal coordination in which the trigonal plane is defined by the two P and one S (see Fig. 2, bottom). The structural re-orientation is also characterized by a large change in the P–Fe–P angle from 163° in hexa-coordinate 2 to 102° in penta-coordinate 2^–CO_tbp.

Fig. 2 Conceivable coordination isomers that arise from the formal removal of one CO ligand from experimentally observed hexa-coordinate complexes 1 and 2. sp = square pyramidal; tbp = trigonal bipyramidal.

1,2 ^–CO _tbp are both energetically and entropically favored (see ESI†) compared to their 1,2^–CO_sp analogues. For example, 1,2^–CO_sp is higher in Gibbs energy by 28 kcal mol⁻¹ (BP86+D3/TZVP) and 20 kcal mol⁻¹ (B3LYP+D3/TZVP) compared to their respective trigonal-bipyramidal analogue. The consideration of solvent effects (acetonitrile) does not qualitatively change the picture (21 kcal mol⁻¹ BP86+D3/TZVP and 13 kcal mol⁻¹ B3LYP+D3/TZVP). Whereas the consideration of the organic solvent increases the difference in free energies by 5–6 kcal mol⁻¹ for 1^–CO, it diminishes the free energy differences for 2^–CO by 7 kcal mol⁻¹. This is consistent with the increase in solvent accessible surface for PPh₃vs. PMe₃ ligands and the decreased solubility of PPh₃ in acetonitrile.

The different coordination modes of 1,2^–CO also have a large effect on the energetics of binding a sixth CO ligand. While coordination of the second CO ligand to 1,2^–CO_sp is characterized by strong negative CO binding free energies (see Table 1), exogenous CO binding to the ligand-distorted 1,2^–CO_tb is very weak if not almost energetically unfavorable (data in the ESI†).

From the above considerations on monodentate phosphine ligands, it is clear that tethering of the P-ligands into bidentate motifs as in PNP ligands in III is essential to gain access to penta-coordinate structures, especially if they are to display a square-pyramidal coordination mode with the associated vacant coordination site that is necessary for substrate binding. A further potentially beneficial design feature for catalysis is the inclusion of an amine in the second coordination sphere. It has previously been shown that the capacity of the N in the second coordination sphere to shuttle protons to a metal site can be increased by introduction of a second six-membered ring. In analogy to what has been observed for related Ni(P^R₂N^R′₂)₂ complexes, steric congestion in the resulting 1,5-diaza-3,7-diphosphaoctane ligands (P^R₂N^R′₂) promotes a conformation of the complex in which one nitrogen base resides above the metal center.^22,29 We thus decided to introduce P₂N₂ ligands also to our penta-coordinate Fe complexes and targeted structures of the general type 3, depicted in Fig. 3.

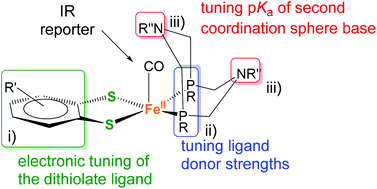Fig. 3 Modular design of mononuclear pentacoordinate iron complexes containing a P^R₂N^Ph₂ ligand and its three different possible sites (i)–(iii) of independent modifications.

A great advantage of this structural platform is that it offers multiple possibilities to fine-tune the complexes’ electronic properties (Fig. 3). Traditional and structurally more closely related di-nuclear models of the [FeFe] H₂ase active site are more limited in this sense. In detail, these variations include (i) the benzenedithiolate (bdt) bridge, (ii) the phosphine ligand(s) and (iii) the substituent at the amine(s). The latter predominantly changes the basicity of the amine site (i.e. as a potential proton shuttle), while alterations of (i) and (ii) affect the metal's reduction potential. With this general architecture, we aimed to investigate the potential of orthogonal tuning by variation of sites (i) to (ii).

The motif could in principle also feature a free coordination site for substrate binding, as well as a CO ligand that is a useful IR probe to detect changes of the metal-oxidation state, the influence of the modifications on the metal's electronic content, and potentially even conformational changes of the 6-membered FePCNCP heterocycles.

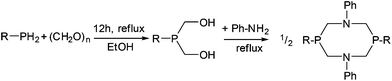
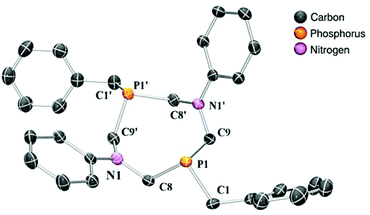
In this study, four different P^R₂N^Ph₂ ligands were prepared that carry identical N-phenyl substituent, but vary in the P-substituent (for a: R = Ph (phenyl), b: R = Bn (benzyl), c: R = Cyc (cyclo-hexyl) and d: R = ^tBu (tert-butyl)) (Scheme 2). The P₂N₂ ligands were synthesized according to published procedures by the reaction of a primary phosphine with formaldehyde (in situ generated from para-formaldehyde), resulting in the corresponding bis(hydroxymethyl)phosphine, which was used without further purification.^30,31 This intermediate reacts in a subsequent condensation with aniline, forming the desired cyclic bisphosphine ligand (Scheme 2). The P^R₂N^Ph₂ ligands could be isolated by crystallization in moderate to good overall yields. We were able to grow single crystals suitable for X-ray diffraction of ligand P^Bn₂N^Ph₂ from a chloroform solution (Fig. 4).

Scheme 2 Synthesis of cyclic bisphosphine ligands a–d (P^R₂N^Ph₂) starting from primary phosphines and aniline: a: R = Ph (phenyl), b: R = Bn (benzyl), c: R = Cyc (cyclo-hexyl) and d: R = ^tBu (tert-butyl).

Fig. 4 ORTEP representation of ligand P^Bn₂N^Ph₂ (thermal ellipsoids at a probability level of 50%). Hydrogen atoms are omitted for clarity. The solid state structure shows the conformational flexibility of this ligand allowing to adjust the P⋯P distance according to the geometric requirements (see also structures of 3a and 3c). Symmetry related atoms are created by a two-fold crystallographic symmetry (2 − x, 2 − y, z). Selected distances and angles: P1–C1 1.8567(17), P1–C9 1.8655(16), P1–C8 1.8686(16), P1⋯P1′ 4.0903(5), C1–P1–C9 97.43(8), C1–P1–C8 95.58(8), C9–P1–C8 99.11(8).

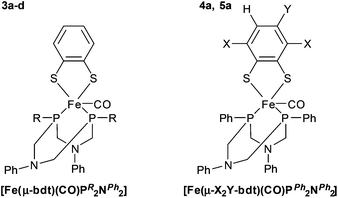
To gain insight into the impact of the P-substituents on relevant molecular properties, Fe complexes 3a–d were synthesized by a one-pot reaction of Fe(II)Cl₂, benzene-1,2-dithiolate (bdt) and the respective P^R₂N^Ph₂ ligand in an acetonitrile solution containing triethylamine under an atmosphere of CO (see Scheme SI-1 in the ESI†). Chromatographic workup with deaerated solvents yields all complexes in excellent yields (≥80%) as dark green solids (Fig. 5, left).

Fig. 5 Overview of the mononuclear penta-coordinate Fe(II)-complexes, with its different substitutions at the bisphosphine ligand (3a R = Ph; 3b: R = benzyl; 3c: R = cyclo-hexyl; 3d: R = tert-Bu; left) and at the dithiolate bridge (4a: X = Cl, Y = H; 5a: X = H, Y = CH₃; right side).

In order to investigate the impact of electronic variations introduced by different substituents on the dithiolate bridge, two additional iron complexes 4a and 5a were prepared using 3,6-dichloro-1,2-benzenedithiol (Cl₂-bdt) and 4-methyl-1,2-benzenedithiol (Me-bdt), respectively, together with the parent P^Ph₂N^Ph₂ ligand a (Fig. 5, right, Scheme ESI-1†). While 4a was only obtained in moderate yields (49%), complex 5a could be isolated in 85% yield, both as dark green solids. The lower yield of the Cl₂-bdt substituted complex is most likely related to the electron withdrawing character of Cl₂-bdt and is in agreement with previous observations for dinuclear [Fe₂(dithiolate)(CO)₆] analogues.^15,24 While 3a–5a with P-phenyl groups are fairly stable compounds, stability drops significantly when changing to alkyl substituents at the phosphorus (Fig. 5). This behavior is in line with the expected stability of aromatic vs. aliphatic phosphines and also explains the lower yields for the aliphatic substituted complexes 3c and 3d (80 and 82%) compared to the aromatic derivatives 3a and 3b (94 and 96%).³²

³¹P{¹H}-NMR spectroscopic investigations of all mononuclear complexes show a single resonance in the expected region, which indicates symmetric nature of the complex and/or fast dynamic behavior in solution, which was also observed for structurally related compounds.^33–35 Electronic differences of the phosphine ligands are well reflected in their ³¹P{¹H}-NMR shifts which range from +65 to almost +90 ppm. On the other hand, variations of the bdt bridge only have a marginal influence on ³¹P{¹H}-NMR chemical shifts (3a: 68.0, 4a: 68.2, and 5a: 68.1 ppm, Table 3), supporting the notion that orthogonal tuning of the electronic properties of the central metal using either strategy (i) or (ii) may be feasible.

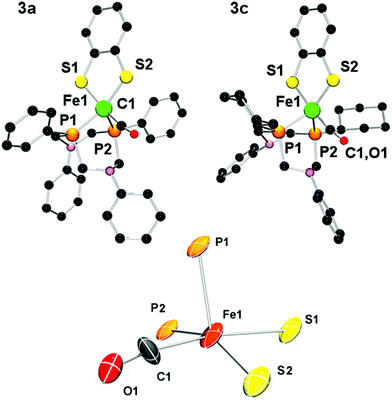
Single crystals of complexes 3a and 3c suitable for X-ray crystallographic analysis could be obtained, and their solid state structure is displayed in Fig. 6. As expected, the mononuclear iron complexes exhibit a coordination number of five. To our great surprise, however, the apical position is not occupied by a CO ligand as in the PNP complexes of type III, but by one of the phosphorus centers of the P₂N₂ ligand. The CO ligand lies in a position trans to one sulfur of the bdt bridge instead.

Fig. 6 Molecular structures of 3a and 3c (top) and detailed view of the Fe(II) coordination mode of 3a (bottom). Note that compound 3c crystallizes with two independent complex molecules per unit cell and only one is depicted here. Thermal ellipsoids are drawn at 50% probability level. Hydrogen atoms and co-crystallized solvent molecules are omitted for clarity.

The coordination environment also exhibits substantial deviation from the ideal geometry and can be viewed as either a distorted trigonal-bipyramidal or square-pyramidal coordination. A summary of relevant structural parameters from crystallographic and theoretical investigations is given in Table 2. The distorted geometry of 3a in the crystal (hereafter denoted as 3a^cryst) facilitates a dense molecular packing of four symmetry-related molecules per unit cell with CH⋯π-interactions between the P-phenyl ring of P^Ph₂N^Ph₂ and an N-phenyl of a neighboring molecule (see ESI†). In order to describe the geometry of the complexes we employed Addison's τ value.³⁶ For complex 3a this value (0.22) supports a highly distorted square-pyramidal complex.

Table 2 Selected bond lengths (Å) and angles (°) for complexes 3a (calculated and X-ray) and 3c

Compounds	3a^cryst (Exp.)	3a^cryst (Calc.)	3c (Exp.)
ap = apical, bas = basal, Exp. = experimental, Calc. = calculated.
Fe1–C1	1.77	1.76	1.74/1.77
Fe1–S1/Fe1–S2	2.21/2.17	2.25/2.21	2.21/2.18
			2.20/2.18
Fe1–P1/Fe1–P2	2.14/2.17	2.16 ap/2.19 bas	2.15/2.15
S1–Fe1–S2	88.7	88.7	88.8
S1–Fe1–P1	93.1	103.3	90.7
S2–Fe1–P1	123.9	119.3	123.9
S2–Fe1–C1	83.4	83.4	82.5
P1–Fe1–P2	80.5	83.0	81.7
S1–Fe1–P2	93.1	88.5	96.9
C1–Fe1–P2	92.0	96.8	95.8

---

Considering that the ligand orientations in 3a^cryst are such that proton shuttling from the N to the metal would not be feasible, it was investigated whether 3a^cryst is also the preferred coordination isomer in solution. In a conformational search, a second minimum 3a′ was found in addition to the conformation in 3a^cryst. In 3a′, the two bdt-S coordinate to the Fe-center in the Fe–P–P plane and the CO ligand occupies an apical position, resulting in a square-pyramidal coordination sphere (see ESI†). The coordination in 3a′ thus resembles that found in the PNP-type complexes III. Both 3a^cryst and 3a′ are local minima in solution and in the gas phase and only differ by rotation of the bdt-ligand. Both GGA (generalized gradient approximation) and hybrid functionals give a very consistent picture here. The square-pyramidal configuration 3a′ was found to be lower in Gibbs energy by 6.6 kcal mol⁻¹ and 6.8 kcal mol⁻¹ for BP86+D3/TZVP, COSMO(acetonitrile) and B3LYP+D3/TZVP, COSMO(acetonitrile), respectively. However, calculations with a def2-TZVP basis set at the BP86+D3/COSMO(acetonitrile) level show smaller energy differences of max. 3 kcal mol⁻¹ (vide infra).

In the square-pyramidal 3a′ orientation, the Fe–CO distance is 1.75 Å, which leads to a C=O stretching frequency of 2051 cm⁻¹ (B3LYP+D3/TZP) and 2004 cm⁻¹ (B3LYP+D3/TZVP (acetonitrile)). In the distorted trigonal-bipyramidal coordination in 3a^cryst, the Fe–CO bond is longer (1.80 Å), which leads to a lower C=O stretching frequency (2043 cm⁻¹ in the gas phase and 1995 cm⁻¹ in the organic solvent). The calculated difference between the two coordination isomers is thus about 8 cm⁻¹ which would make it difficult, but not impossible, to distinguish them by FTIR spectroscopy (see ESI†).

The stabilization of 3a′ over the crystallized form 3a^cryst was analyzed in detail. The major contribution to 3a′ being lower in energy is from a reduction of steric repulsion of the bulky bidentate ligands. Thermal corrections and entropic effects favor the distorted trigonal-bipyramidal arrangement as in 3a^cryst over 3a′ but cannot compensate for the energetic differences. Both BP86 and B3LYP give a very consistent picture and the effect of solvent consideration amounts to an extra stabilization by 1.5–2 kcal mol⁻¹ of 3a′.

Of the two isomers only 3a′, as opposed to 3a^cryst, contains an open coordination site to afford a hexa-coordinate octahedral complex. In 3a^cryst this coordination site is blocked by the distorted trigonal-bipyramidally arranged bulky bidentate ligand. Whereas the square-pyramidal complexes 1^–CO_sq and 2^–CO_sq easily accommodate CO (see above), their trigonal bipyramidal isomers are only weak CO-binders. This is in agreement with the results obtained for 3a′.

3a′ is able to accommodate an additional CO ligand and yield a hexa-coordinate octahedral complex. The calculated CO ligand binding affinity for 3a′, however, shows that coordination of this additional sixth axial ligand, i.e. the second CO ligand, to 3a′ is very weak, if at all, and may be thermodynamically unfavorable by 0.5 (BP86) to 4.8 kcal mol⁻¹ (B3LYP). 3a_cryst is not able to afford an additional CO ligand. It converts to the structure of 3a′ with an extra CO.

In the crystal structure of 3c we found two crystallographically independent entities in the unit cell. Interestingly, their geometries differ significantly which further indicates the possible co-occurrence of several isomers. While the structure containing Fe1 features a τ-value of 0.25 and is similar to the crystal structure of 3a (τ = 0.22), the second entity (containing Fe2) is better described as a hybrid of a trigonal bipyramidal and a square-pyramidal geometry (τ = 0.53).

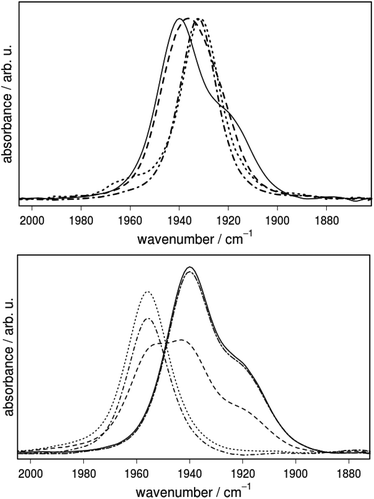
In general the stretching vibrations of CO ligands are excellent probes for changes in electron density of their coordinating metal centers. To test the hypothesis of orthogonal tuning, the extent to which the different substituents at the P-centers affect the electron density at the Fe center was investigated by IR spectroscopy (Fig. 7, Table 3). The vibrational frequencies decrease in the order 3a (1939) > 3b (1936) > 3d (1932) and 3c (1931 cm⁻¹), which is in line with the increasing donor strength of the respective phosphine ligands. Furthermore, the vibrational frequencies of 3a were compared with those of the Cl₂-bdt (4a) and Me-bdt (5a) analogues to elucidate the influence of variations in the dithiolate bridge on the metal center (Table 3 and ESI†). The introduction of electron withdrawing chloride substituents shifts ν_CO to slightly higher wavenumbers, from 1939 (3a) to 1946 cm⁻¹ (4a), while a methyl group has almost no effect (1938 cm⁻¹, 5a).

Fig. 7 Top: normalized IR spectra of 3a (line), 3b (dashed), 3c (dotted) and 3d (dash-dotted) in acetonitrile in the region of the carbonyl stretching vibrations. Bottom: IR spectra of 3a in the absence of acid (line), with 1 eq. (dashed), 2 eq. (dotted), and 5 eq. (dash-dotted) of triflic acid and deprotonated with 5 eq. triethylamine (dash long dotted). Acetonitrile at ambient temperatures.

Table 3 Summary of selected spectroscopic data for the mononuclear complexes 3a–d, 4a and 5a

	^31P-NMR	IR		Echem
	δ P [ppm]	ν CO, ACN [cm^−1]	ν CO, ACN [cm^−1] protonated^a	E red,1/2, ACN [V]
sh = shoulder, redox data vs. the Fc/Fc^+ couple.a Protonated with trifluoromethanesulfonic acid (triflic acid).b 3d with p-toluenesulfonic acid (TsOH).c Not determined due to decomposition.
3a	68.0	1939, 1919(sh)	1956	−1.65
3b	64.9	1936	1956	−1.70
3c	78.2	1931	1943	−1.78
3d	89.7	1932	1943^b	−1.82
4a	68.2	1946, 1925(sh)	n.d.^c	−1.57
5a	68.1	1938, 1917(sh)	1989	−1.72

---

Interestingly, the IR spectra of the complexes that contain phenyl substituents at the phosphorus center (3a–5a) do not exhibit only one absorption band, but contain a clearly visible shoulder at lower energy (Fig. 7). This shoulder is not visible in the IR spectra of single crystals of 3a–5a and thus has to arise from a process that is only enabled in solution. As described above, potential coordination isomers in solution may offer an explanation for the experimentally observed shoulder; however, they hardly account for the Δν of 20 cm⁻¹ between the peak in the IR absorption and the shoulder.

The following computational analysis offers an alternative explanation. It reveals a more complex picture that takes into account the conformational flexibility of the P₂N₂ ligand, and in particular the geometry of the N-substituent in the vicinity of the CO ligand, as well as coordination isomers.

The boat conformations of the heterocycle in which N₍₁₎ points towards the CO ligand are termed endo-isomers 3a′_endo and 3a^cryst_endo, while the chair conformations are termed exo (Fig. 8) in analogy to the nomenclature used by DuBois and co-workers.^22,37 Further discrimination by the remote heterocycle, including N₍₂₎, can be subdivided once more into endo and exo conformers giving rise to e.g. endo/exo structures (Fig. 8).

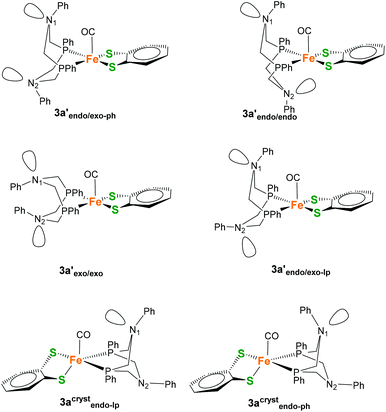Fig. 8 Potential coordination isomers 3a′ and 3a^cryst with different exo/endo conformations of the 6-membered FePCNCP heterocycles as well as different orientations of the N-Ph substituent.

During the calculations (BP86+D3/def2-TZVP/COSMO), it was noticed that a simple endo/exo differentiation between the two isomers is in some cases insufficient to fully describe the conformations of the 6-membered ring systems, as the potential energy surface shows multiple minima. It was found, for example, that 3a^cryst_endo can exist in two different geometries that differ in the orientation of the N-lone pair (lp) or N-phenyl (ph) substituent relative to the CO ligand, giving rise to isomers 3a^cryst_endo-lp and 3a^cryst_endo-ph (Fig. 8). The former isomer was found to be the lowest in energy of all considered isomers, while the latter is 1.4 kcal mol⁻¹ higher in Gibbs energy. In general the different endo and exo isomers for 3a′ and 3a^cryst that are found on the PES are energetically rather similar, and only differ by max. 3 kcal mol⁻¹ in Gibbs energy. The energetically most favorable square-pyramidal isomer is 3a′_endo/exo-lp which gives rise to a C=O stretching frequency of 1900 cm⁻¹ while the corresponding 3a^cryst_endo-ph does not exhibit substantial differences in CO vibrations (1899 cm⁻¹). A second conformer, differing in the orientation of the Ph at N₁ (3a^cryst_endo-lp) which has the lone pair of N₁ pointing towards the CO probe, causes a 12 cm⁻¹ shift to lower wavenumbers (1887 cm⁻¹). However, similar carbonyl vibrations are found also for the square-pyramidal isomer 3a′_endo/exo-ph (1886 cm⁻¹) which differs from 3a′_endo/exo-lp only in the orientation of the remote N₂-Ph substituent. Two additional conformations could be identified that are shifted to significantly higher (1922 cm⁻¹) and lower (1877 cm⁻¹) wavenumbers for 3a′_endo/endo and 3a′_exo/exo, respectively. Since we are interested in relative free energy differences between conformers, small differences of maximum 3.0 kcal mol⁻¹ let us assume that the experimentally observed CO stretching vibrations including the observed shoulder are a superposition of all isomers. In nitrogen substituted six-membered rings, both ring inversion and nitrogen inversion are hard to discriminate experimentally since they are both of similar barrier heights. Only upon introduction of a planar sp²-hybridized carbon atom into the six-membered ring, nitrogen inversion barriers of 8 and 9 kcal mol⁻¹ could be obtained.³⁸ Due to the high dimensionality of the potential energy surface, barrier heights for the individual inversion steps were not obtained but we can estimate them to be of the order of ∼9–10 kcal mol⁻¹ each.

Support for the assignment that the shoulder in the IR spectrum of 3a–5a arises from different P^Ph₂N^Ph₂ conformations is provided by the observation that addition of acid leads to an IR spectrum that is characterized by one single band (Fig. 7, bottom). Complex 3a has multiple protonation sites. Protonation of one of the thiolate S atoms is one possibility. The second and more probable possibility is protonation of one of the amine nitrogen atoms. No matter in which ring conformation, protonation of either of the two nitrogen atoms is possible. Their proton affinities are almost identical. Kinetically preferred may be a shared proton between the amine sites. This would enforce an exo/exo conformation of both rings and explain the simplified IR spectrum of the protonated form. In such a case, protonation leads to a shift of the main band by 17 cm⁻¹, which is well in agreement with computational results which predict a shift in CO stretching frequencies to higher wavenumbers by 9 cm⁻¹ (BP86+D3/TZVP COSMO). In analogy to well-studied Ni(P₂N₂)²⁺ complexes, protonation can be expected to lead to a species where the proton resides between the two six-membered rings. In this conformation, the N₍₁₎ has to be in an exo orientation, and can thus not inflict varying impacts on the CO ligand. The calculated proton binding affinity for such a situation is −272 kcal mol⁻¹ (BP86+D3/TZVP).

From the above considerations, it is clear that the CO ligand is not only an indicator of changes to the electronic density at the Fe center, but will also sense the presence of coordination isomers in solution or conformational changes at the nitrogen. Both nitrogen inversion that brings the phenyl ring in close proximity to the CO ligand as well as rotation of the bdt-ligand that converts a trigonal-bipyramidal to a square-pyramidal coordination mode lead to distinct changes in ν_CO vibration frequency.

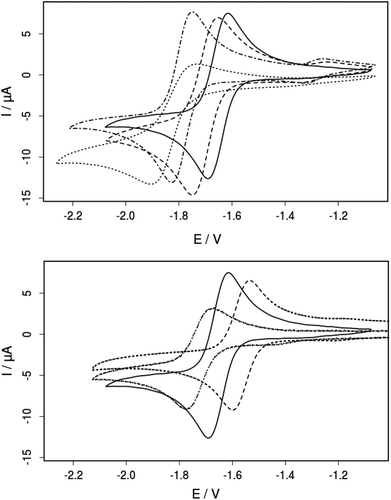
The electrochemical properties of 3a–d, 4a and 5a were studied by cyclic voltammetry in acetonitrile solution (Fig. 9, Table 3). All complexes show a reversible one-electron reduction assigned to the formal Fe^II/I-couple. The half-wave potentials of compounds 3a–d decrease in the order of −1.65 (3a) > −1.70 (3b) > −1.78 (3d) > −1.82 V (3c) vs. Fc/Fc⁺, consistent with the observed shifts in the IR absorption maxima of the carbonyl stretching vibrations (Fig. 7; Table 3). The reduction potentials are in agreement with the electron donating properties of the P-substituents and in the same range as those of other penta-coordinate iron complexes.^26,39 Furthermore, the influence of the substitution pattern at the bridge was investigated. As expected, the electron withdrawing chloride substituents in 4a shift the reduction potential to a more positive value (−1.57 V) whereas the electron donating methyl group in 5a leads to a more negative reduction potential (−1.72 V) compared to that of the unsubstituted complex 3a (−1.65 V). As evident from ³¹P-NMR spectroscopy, substitution at the dithiolate bridge has only marginal effects on the compounds’ ³¹P chemical shifts, despite the fact that the electronic properties of the iron centers are significantly influenced. These findings clearly demonstrate that orthogonal tuning of the complexes’ electronics is possible, either by changes of the P-substituent or the introduction of bdt-substituents (strategies (i) and (ii) in Fig. 3).

Fig. 9 Top: cyclic voltammograms of 3a (line), 3b (dashed), 3c (dotted) and 3d (dash-dotted). Bottom: CVs of 3a (line), 4a (dashed) and 5a (dotted) with a concentration of 1.0 M in acetonitrile. Conditions: scan rate of 100 mV s⁻¹, 0.1 M (Bu)₄NPF₆ as a supporting electrolyte.

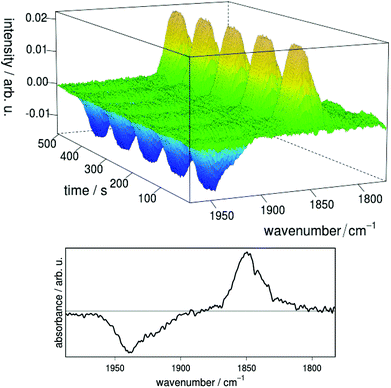
The reversibility of the electrochemical reduction and the stability of the produced anion were demonstrated by FTIR spectro-electrochemistry on complex 3a (Fig. 10). When a constant potential of −1.8 V vs. Ag/Ag⁺ is applied, the reduced species 3a^red is produced, giving rise to a new band located at 1850 cm⁻¹ in the IR difference spectra with respect to the 3a background spectrum. At the same time a negative signal corresponding to depletion of 3a appears at 1939 cm⁻¹. The shift in IR absorption maximum to lower vibrational frequencies for 3a^red can be explained by the higher electron density at the iron center resulting in stronger back-bonding to CO-based π*-orbitals as compared to 3a. Quantitative re-oxidation of 3a was achieved at a potential of −1.4 V vs. Ag/Ag⁺. No significant decomposition of the catalyst was observed after 20 reduction–reoxidation cycles, indicating high reversibility and a remarkably stable singly reduced species.

Fig. 10 Fully reversible reduction–reoxidation cycles of complex 3a in acetonitrile solution, monitored by FTIR spectro-electrochemistry. Time-depended FTIR spectra of 3a^red induced by reduction of 3a at −1.8 V and reoxidation at −1.4 V vs. Ag/Ag⁺, respectively, measured against the IR spectrum of 3a as the background. The reduction–reoxidation cycles (first five of 20 cycles are shown, cycle length 100 sec) were performed without any loss or decomposition of the compound.

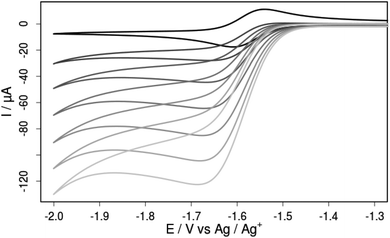
The addition of increasing amounts of acetic acid (AcOH) to an acetonitrile solution of compound 3a gives rise to increasing cathodic peak currents in the cyclic voltammograms that are attributable to catalytic turnover (Fig. 11). Background hydrogen production at glassy carbon is negligible at this potential as confirmed by cyclic voltammetry and bulk electrolysis control experiments at a constant potential of −1.68 V vs. Fc/Fc⁺ (Fig. ESI-21†). Bulk electrolysis with 3a in the presence of 100 equivalents of AcOH at the same constant potential also leads to a substantially enhanced cathodic current compared to experiments in the absence of 3a. Comparison of the passed charge with the amount of produced hydrogen as monitored by means of in situ GC analysis suggests a Faradaic yield close to unity and shows that 3a can catalyze proton reduction even with very weak acids like acetic acid (pK_a = 22.3 in acetonitrile) at a mild overpotential of merely 290 mV.

Fig. 11 Cyclic voltammograms of 3a (1.0 mM) in acetonitrile solution in the absence (black) and presence (grey curves) of increasing AcOH concentrations (in steps of 50 eq. from 0 to 300 eq.). The increase in current in the presence of acid indicates that the proton reduction is catalyzed by the iron complex.

Conclusion

Based on the idea that functional mimics of the [FeFe] H₂ase only require the Fe_d site, a series of six mononuclear iron model complexes was prepared. The different behavior of monodentate vs. bidentate ligands in their tendency to form hexa- and penta-coordinated complexes, respectively, could be rationalized by first principle calculations. Simple phosphine ligands, i.e. PMe₃ and PPh₃, form hexa-coordinate complexes, and the loss of one CO ligand was calculated to be energetically unfavorable. The use of chelating P^R₂N^Ph₂ bisphosphine ligands leads to selective formation of coordinatively unsaturated penta-coordinate Fe(II)-complexes with the general formula [Fe(X-bdt)(P^R₂N^Ph₂)(CO)] (with X = H, Cl₂ or Me and R = Ph, Bn, Cyc or tert-Bu). Two main coordination isomers of this complex are found by ab initio calculations, namely a trigonal-bipyramidal and a distorted square-pyramidal structure. Furthermore, the P^R₂N^Ph₂ ligand leads to a variety of conformational isomers depending on the orientation of the six-membered FePCNCP rings (endo/exo) as well as the orientation of N-phenyl substituent (endo-lp/endo-Ph). The almost isoenergetic isomers reveal significant shifts of the CO stretching vibrations and may all contribute to the experimentally observed shoulder in the IR spectrum of 3a. Protonation of the P^R₂N^Ph₂ ligand greatly restricts this conformational freedom.

The design of complexes of type 3 (Fig. 3) enables facile and independent variations of the complexes’ properties through specific modifications on the bdt bridge and the phosphine ligands. Spectroscopic studies clearly demonstrate the orthogonal and independent tuning of the complexes’ properties by variation of (i) the dithiolate bridge and (ii) the P-substituent. Electrochemical experiments show electrocatalytic proton reduction, even from weak acids like acetic acid at modest overpotentials. The mononuclear complexes can be reversibly protonated and reduced and are extraordinarily stable in their ground, singly protonated and singly reduced states, making them good candidates for further mechanistic investigations.

Experimental section

General information

If not stated otherwise all reactions were performed under an inert argon atmosphere using standard Schlenk techniques. All reagents were obtained from commercial suppliers and used without further purification.

NMR spectroscopy

¹H-NMR spectra were recorded on a JEOL Eclipse+ spectrometer operating at a proton frequency of 400 MHz at 25 °C. The spectra were referenced to a deuterated solvent as an internal standard (CHCl₃: δ_H = 7.26 ppm) and the measured values for δ are given in ppm. ¹³C{¹H}-NMR and ³¹P{¹H}-NMR measurements were recorded on the same instrument and referenced internally to solvent peaks or externally to H₃PO_4(aq.) (85%), respectively.

FTIR spectroscopy

IR absorption spectra of 3a–d, 4a and 5a were recorded in the spectral range of 2100–1800 cm⁻¹ with a resolution of 2 cm⁻¹ on a Perkin Elmer SpectrumOne FTIR spectrometer and the protonation studies were recorded on a Bruker (IFS 66 v/S) FTIR spectrometer. The IR measurements were performed with a liquid-sample-cell (Specac Omni-Cell) using CaF₂ windows with 0.5 mm PTFE spacers in acetonitrile or dichloromethane.

Electrochemistry

Cyclic voltammograms were obtained using an Autolab potentiostat with a GPES electrochemical interface (Eco Chemie) and a standard three electrode setup. The working electrode was a glassy carbon disc (diameter 3 mm, freshly polished), while a glassy carbon stick was used as a counter electrode. As a reference electrode a non-aqueous Ag/Ag⁺ electrode (CH Instruments, 10 mM AgNO₃ in acetonitrile) with a potential of 80 mV (vs. the ferrocene/ferrocenium (Fc/Fc⁺) couple) was used. Ferrocene was used as an internal standard and all reported potentials are quoted vs. the Fc/Fc⁺ couple. All measurements were conducted with oven dried glassware, freshly distilled dry CH₃CN and 0.1 M tetrabutylammonium-hexafluorophosphate (Bu)₄NPF₆ (Fluka, electrochemical grade) as a supporting electrolyte.

Spectro-electrochemistry

FTIR spectro-electrochemical experiments were performed in an OTTLE-type (optically transparent thin-layer electrode) cell. A platinum mesh was sandwiched as the working electrode between CaF₂ windows and the path length of the cell was 120 μm. The spectra were recorded on a Bruker FTIR spectrometer (IFS 66v/S) between 2200 and 1800 cm⁻¹ and with a resolution of 2 cm⁻¹. UV/vis absorption spectro-electrochemical spectra were recorded between 250 and 800 nm on a diode array UV/vis spectrometer (8543 spectrometer, Agilent) in an acetonitrile solution. A quartz cell cuvette with a 10 mm pathlength was used.

X-ray crystallography

Crystallographic data sets were collected from single crystal samples mounted on a loop fibre and coated with N-paratone oil (Hampton Research). The collection was performed using a Bruker SMART APEX diffractometer equipped with an APEXII CCD detector, a graphite monochromator and a 3-circle goniometer. The crystal-to-detector distance was 5.0 cm, and the data collection was carried out in 512 × 512 pixel mode. The initial unit cell parameters were determined by a least-squares fit of the angular setting of strong reflections, collected by a 30 degrees scan in 12 frames over three different parts of the reciprocal space (36 frames total). Cell refinement and data reduction were performed with SAINT V7.68A (Bruker AXS) on the final data. Absorption correction was done by multi-scan methods using SADABS96 (Sheldrick). The structure was solved by direct methods and refined using SHELXL97.⁴⁰ All non-H atoms were refined by full-matrix least-squares with anisotropic displacement parameters while hydrogen atoms were placed in idealized positions. Refinement of F² was performed against all reflections. The weighted R-factor wR and goodness of fit S are based on F². Crystal structure data were deposited at the Cambridge Crystallographic Data Centre (CCDC 822967, 972155–972156).

Computational details

All calculations were performed with Orca version 2.9.⁴¹ The BP86^42,43 GGA exchange-correlation functional and the B3LYP hybrid^44–47 exchange-correlation functionals were used together with dispersive corrections due to Grimme.^48,49 An Ahlrichs TZVP basis set⁵⁰ was used for initial structure optimizations. The def2-TZVP basis set⁵¹ was used for vibrational assignment of conformers from numerically calculated second derivatives. Thermochemical corrections were applied for T = 298.15 K and p = 1 atm. Solvent effects for acetonitrile were included in a Conductor-Like-Screening Model (COSMO).²⁸ The proton binding affinity is calculated as the Gibbs energy difference between protonated and unprotonated species at ambient temperature, normal pressure and in an implicit solvation model.

Bulk electrolysis with in situ GC detection

All procedures were done in a glove box under an argon atmosphere. An Autolab potentiostat with a GPES electrochemical interface (EcoChemie) was used with a three electrode setup consisting of a non-aqueous Ag/Ag⁺ reference electrode (+80 mV vs. Fc/Fc⁺), a platinum mesh counter electrode and a 0.44 cm² glassy carbon rod working electrode. The counter and reference electrodes were separated from the sample compartment by means of glass frits. The 130 ml gaseous head-space was sampled in situ with a CP4900 Micro-GC (Varian) equipped with a 5 Å molsieve column and argon as a carrier gas. The GC was calibrated electrochemically in two separate runs by reduction of acetic acid with a 2 mm diameter Pt disk working electrode at −1.58 V vs. Fc/Fc⁺. Assuming 100% charge to hydrogen conversion efficiency, the amount of produced hydrogen was calculated from the charge passed through the electrode and the hydrogen peak area correlated to this amount. (Bu)₄NPF₆ dried at 85 °C was used for 0.1 M supporting electrolyte solutions in anhydrous acetonitrile. All bulk electrolysis experiments were performed on 6 ml samples at −1.68 V vs. Fc/Fc⁺ under rapid stirring. Acid backgrounds were measured as averages of two independent runs. The overpotential was determined from the applied potential of the bulk electrolysis experiments as described by Artero et al.⁵²

Synthesis

Preparation of the bisphosphine ligands P^R₂N^Ph₂. The cyclic 1,5-diaza-3,7-diphosphacyclooctane ligands (P^R₂N^Ph₂) were prepared according to literature methods³¹, and the resulting data were identical to those reported earlier.

The synthesis of the hexanuclear complex 2 [Fe(bdt)(PPh₃)₂CO₂] was performed under an Ar atmosphere starting from the single precursors. Therefore, a Schlenk vessel was loaded with FeCl₂ (51 mg, 0.4 mmol), an excess of PPh₃ (4.0 mmol) and 13 ml freshly degassed acetonitrile. After this, a second Schlenk was filled with acetonitrile (5 ml), 1,2-benzenedithiole (57 mg, 0.4 mmol) and Et₃N (TEA, 0.15 ml). These solutions were combined and vigorously stirred for 3 h at room temperature, resulting in a deep red suspension. The solid precipitate was filtered, washed and dried in vacuo. Yield: 55% (0.17 g), C₄₄H₃₄O₂S₂P₂Fe₁ (776.64 g mol⁻¹), EA calcd: C 68.04, H 4.41, S 8.26; found: C 68.84, H 3.44, S 8.49. ¹H-NMR (400 MHz, CDCl₃): δ_H = 7.23–7.71 (m, 32H, PPH₃ and bdt), 8.17 (m, 2H, bdt) ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 60.1 ppm. IR (DCM): ν_CO = 2014 and 1940 cm⁻¹.

General procedure for the preparation of [Fe(X-bdt)(P^R₂N^Ph₂)(CO)]complexes. In a Schlenk vessel FeCl₂ (51 mg, 0.4 mmol) and one equivalent of the respective bisphosphane ligand (P^R₂N^Ph₂) (0.4 mmol) were mixed with 15 ml degassed acetonitrile under a CO atmosphere. Subsequently, this suspension was treated with a combined acetonitrile solution (5 ml) of the respective dithiol ligand (X-bdt, 0.4 mmol) and Et₃N (TEA, 0.15 ml). The reaction solution turned first quickly to violet and then to dark green. After three hours of stirring and gently heating at 40 °C the solvent was removed under reduced pressure. The solid residue was purified by chromatography on a silica gel column with a degassed CH₂Cl₂–n-hexane (8 : 2) mixture as an eluent. If necessary, a further purification could be obtained by recrystallization from CH₂Cl₂–n-heptane in the absence of oxygen. Finally, a dark green powder was obtained after removal of all volatiles under vacuum.

[Fe(μ-bdt)(P^Ph₂N^Ph₂)(CO)] 3a (Ph = phenyl). Yield: 94%, C₃₅H₃₂N₂O₁S₂P₂Fe₁ (678.59 g mol⁻¹), EA calcd: C 61.95, H 4.75, N 4.13; found: C 61.69, H 4.83, N 4.10. ¹H-NMR (400 MHz, CDCl₃): δ_H = 3.91 (m, 4H, CH₂), 4.04 (m, 2H, CH₂), 4.80 (m, 2H, CH₂), 6.9–7.4 (m, 22H, phenyl), 8.15 (dd, J = 6.0, 3.2 Hz, 2H) ppm. ¹³C{¹H}-NMR (75.5 MHz, CD₂Cl₂): δ_C = 53.09 (dt, J = 38.2, 16.7 Hz, CH₂) 128.88 (d, J = 10.1 Hz), 128.96 (d, J = 15.9 Hz) 129.39 (d, J = 23.0 Hz), 131.29 (t, J = 18.5 Hz), 131.95 (t, J = 5.4 Hz), 152.25 (dt, J = 18.5, 8.8 Hz), 156.69 (t, J = 3.6 Hz, 0H), 152.87 (t, J = 8.3 Hz), 214.96 (t, J = 23.1 Hz, CO) ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 68.0 ppm. IR (CH₃CN): ν_CO = 1939 cm⁻¹.

[Fe(μ-bdt)(P^Bn₂N^Ph₂)(CO)] 3b (Bn = benzyl). Yield: 96%, C₃₇H₃₆N₂O₁S₂P₂Fe₁ (706.62 g mol⁻¹), EA calcd: C 62.89, H 5.14, N 3.96; found: C 62.33, H 5.30, N 3.86. ¹H-NMR (400 MHz, CDCl₃): δ_H = 3.43 (dd, J = 121.1, 14.1 Hz, 4H, CH₂), 3.80 (s, 4H, benzyl), 3.82 (ddt, J = 146.5, 14.2, 3.4 Hz, 4H, CH₂), 6.57 (dt, J = 59.9, 13.7 Hz, 4H), 6.86 (t, J = 7.3 Hz, 2H), 7.16 (m, 4H), 7.20–7.30 (m, 18 H) ppm. ¹³C{¹H}-NMR (75.5 MHz, CDCl₃): δ_C = 36.00 (ps. t, J = 7.4 Hz, benzyl), 51.28 (d, J = 355.7, 16.3 Hz, CH₂), 117.94, 118.25, 121.61 (d, J = 27.0 Hz), 121.77, 127.48, 129.19 (d, J = 13.0 Hz), 129.43 (d, J = 12.5 Hz), 129.97 (t, J = 2.0 Hz), 132.65 (t, J = 4.0 Hz), 151.98 (dt, J = 16.0, 7.4 Hz), 156.85 (t, J = 5.7 Hz), 214.96 (t, J = 22.8 Hz, CO) ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 64.9 ppm. IR (CH₃CN): ν_CO = 1936 cm⁻¹.

[Fe(μ-bdt)(P^Cyc₂N^Ph₂)(CO)] 3c (Cyc = cyclo-hexyl). Yield: 80%, C₃₅H₄₄N₂O₁S₂P₂Fe₁ (690.66 g mol⁻¹), EA calcd: C 60.87, H 8.09, N 4.06; found: C 60.53, H 7.82, N 4.03. ¹H-NMR (400 MHz, CDCl₃): δ_H = 0.75 (m, 2H), 1.08 (m, 4H), 1.36 (m, 4H), 1.55 (br.s. 6H), 1.72 (m, 4H), 3.31 (d, J = 13.3 Hz, 2H), 3.53 (d, J = 13.4 Hz, 2H), 3.65 (m, 2H), 4.47 (dt, J = 12.9, 3.9 Hz, 2H), 7.00 (q, J = 7.2 Hz, 2H), 7.08 (ps.t., J = 7.7 Hz, 4H), 7.14 (m, 1H) 7.33 (ps.t., J = 7.6 Hz, 4H), 8.12 (m, 1H) ppm. ¹³C{¹H}-NMR (75.5 MHz, CDCl₃): δ_C = 26.45 (dt, J = 16.9, 6.1 Hz), 26.87, 27.76, 38.94 (t, J = 9.7 Hz), 49.88 (dt 16.8, 102.6 Hz), 119.06, 119.30, 121.23, 122.01, 122.35, 128.93, 129.45, 129.61, 152.90 (dt, J = 18.0, 8.5 Hz), 155.76 (t, J = 3.1 Hz), 214.82 (CO) ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 78.2 ppm. IR (CH₃CN): ν_CO = 1931 cm⁻¹.

[Fe(μ-bdt)(P^tB₂N^Ph₂)(CO)] 3d (tB = tert-butyl). Yield: 82%, C₃₁H₄₀N₂O₁S₂P₂Fe₁ (638.59 g mol⁻¹), EA calcd: C 58.31, H 6.31, N 4.39; found: C 58.30, H 6.40, N 4.50. ¹H-NMR (400 MHz, CDCl₃): δ_H = 0.92 (m, 18H, t-Bu), 3.23 (d, J = 13.3 Hz, 2H, CH₂), 3.53 (d, J = 13.5 Hz, 2H, CH₂), 3.72 (m, 2H, CH₂), 4.71 (m, 2H, CH₂), 7.02 (m, 2H), 7.10–7.16 (m, 6H), 7.35 (dd, J = 16.2, 8.8 Hz, 4H), 8.12 (m, 2H) ppm. Due to the low solubility of this complex no ¹³C NMR could be obtained. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 89.7 ppm. IR (CH₃CN): ν_CO = 1932 cm⁻¹.

[Fe(μ-Cl₂bdt)(P^Ph₂N^Ph₂)(CO)] 4a (μ-Cl₂bdt = 3,6-dichloro-1,2-benzenedithiolate). Yield: 49%, C₃₅H₃₀N₂O₁S₂P₂Cl₂Fe₁ (747.43 g mol⁻¹), EA calcd: C 56.24, H 4.05, N 3.75; found: C 55.82, H 4.86, N 4.18. ¹H-NMR (400 MHz, CDCl₃): δ_H = 3.84–4.10 (m, 6H, CH₂), 4.46 (t, J = 13.6 Hz, 1H, CH₂), 4.92 (dt, J = 13.5, 4.0 Hz, 1H, CH₂), 6.70 (m, 2H), 6.98 (t, J = 7.3 Hz, 1H), 7.02–7.10 (m, 2H), 7.14–7.24 (m, 5H), 7.26–7.40 (m, 8H), 7.47 (m, 1H), 7.61 (m, 1H) ppm. ¹³C{¹H}-NMR (75.5 MHz, CDCl₃): δ_C = 53.17(d, J = 110.8 Hz, CH₂), ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 68.1 ppm. IR (CH₃CN): ν_CO = 1947 cm⁻¹.

[Fe(μ-Mebdt)(P^Ph₂N^Ph₂)(CO)] 5a (μ-Mebdt = 4-methyl-1,2-benzenedithiolate). Yield: 85%, C₃₆H₃₂N₂O₁S₂P₂Fe₁ (690.56 g mol⁻¹), EA calcd: C 62.43, H 4.95, N 4.04; found: C 62.34, H 5.37, N 3.73. ¹H-NMR (400 MHz, CDCl₃): δ_H = 2.40 (s, 3H, Me), 3.88 (dt, J = 13.2, 2.9 Hz, 2H, CH₂), 3.94 (t, J = 13.3 Hz, 2H, CH₂), 4.04 (dt, J = 13.3, 6.6 Hz, 2H, CH₂), 4.80 (dt, J = 13.3, 3.9 Hz, 2H, CH₂), 6.95 (t, J = 7.3 Hz, 1H), 7.00–7.05 (m, 2H), 7.08 (dd, J = 8.7, 1.0 Hz, 2H), 7.16 (dd, J = 8.7, 1.0 Hz, 2H), 7.20–7.40 (m, 14H), 7.96 (br.s., 1H), 8.03 (d, J = 8.1 Hz, 1H) ppm. ¹³C{¹H}-NMR (75.5 MHz, CD₂Cl₂): δ_C = 20.91 (s, Me), 53.43 (dt, J = n.d., 19.0 Hz, CH₂), 118.96, 119.57, 122.03, 122.61, 123.53, 128.95, 129.21 (t, J = 4.9 Hz), 129.51, 129.74 (d, J = 24.6 Hz), 131.61, 131.78 (d, J = 7.7 Hz), 132.32 (t, J = 5.4 Hz), 152.65 (dt, J = 18.3, 8.7 Hz), 155.82 (d, J = 295.6 Hz), 215.25 (d, J = 22.4 Hz; CO) ppm. ³¹P{¹H}-NMR (161.8 MHz, CDCl₃): δ_P = 68.2 ppm. IR (CH₃CN): ν_CO = 1938 cm⁻¹.

Funding sources

A.O. is grateful to the Austrian Science Fund (FWF) for an Erwin-Schrödinger fellowship (J3193-N17). M.K. thanks the Wenner-Gren Foundation and S.T. thanks the German Academic Exchange Service (DAAD) for a PostDoc fellowship. M.S. is grateful to the Max-Planck-Society for the Advancement of Science and the Excellence Initiative “Research Center for Dynamic Systems: Biosystems Engineering” for financial support. Further financial support from the Swedish Research Council, the Knut and Alice Wallenberg Foundation and the Swedish Energy Agency is gratefully acknowledged.

Author contributions

The manuscript was written and approved through contributions of all authors.

The authors declare no competing financial interest.

Acknowledgements

We acknowledge Dr Marie-Pierre Santoni (Uppsala University) for help in measuring the crystal structure of complex 3a and Mohammad Mirmohades (Uppsala University) for assistance with the IR protonation studies. Dr Reiner Lomoth is acknowledged for valuable discussions.

Notes and references

1. N. Armaroli and V. Balzani, Angew. Chem., Int. Ed., 2007, 46, 52–66.
2. V. Balzani, A. Credi and M. Venturi, ChemSusChem, 2008, 1, 26–58.
3. C. Tard, X. Liu, S. K. Ibrahim, M. Bruschi, L. D. Gioia, S. C. Davies, X. Yang, L.-S. Wang, G. Sawers and C. J. Pickett, Nature, 2005, 433, 610–613.
4. M. Y. Darensbourg, Nature, 2005, 433, 589–591.
5. S. Styring, Faraday Discuss., 2012, 155, 357–376.
6. T. Faunce, S. Styring, M. R. Wasielewski, G. W. Brudvig, A. W. Rutherford, J. Messinger, A. F. Lee, C. L. Hill, H. deGroot, M. Fontecave, D. R. MacFarlane, B. Hankamer, D. G. Nocera, D. M. Tiede, H. Dau, W. Hillier, L. Wang and R. Amal, Energy Environ. Sci., 2013, 6, 1074–1076.
7. Y. Nicolet, C. Piras, P. Legrand, C. E. Hatchikian and J. C. Fontecilla-Camps, Structure, 1999, 7, 13–23.
8. A. Jablonskyte, J. A. Wright and C. J. Pickett, Dalton Trans., 2010, 39, 3026–3034.
9. X. Zhao, I. P. Georgakaki, M. L. Miller, J. C. Yarbrough and M. Y. Darensbourg, J. Am. Chem. Soc., 2001, 123, 9710–9711.
10. B. E. Barton and T. B. Rauchfuss, Inorg. Chem., 2008, 47, 2261–2263.
11. J. I. van der Vlugt, T. B. Rauchfuss, C. M. Whaley and S. R. Wilson, J. Am. Chem. Soc., 2005, 127, 16012–16013.
12. A. R. Finkelmann, M. T. Stiebritz and M. Reiher, Chem. Sci., 2014, 5, 215–221.
13. R. Zaffaroni, T. B. Rauchfuss, D. L. Gray, L. De Gioia and G. Zampella, J. Am. Chem. Soc., 2012, 134, 19260–19269.
14. T. B. Rauchfuss, S. M. Contakes, S. C. N. Hsu, M. A. Reynolds and S. R. Wilson, J. Am. Chem. Soc., 2001, 123, 6933–6934.
15. P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Chem. Rev., 2007, 107, 4414–4435.
16. J.-F. Capon, F. Gloaguen, F. Y. Pétillon, P. Schollhammer and J. Talarmin, Coord. Chem. Rev., 2009, 253, 1476–1494.
17. D. L. DuBois and R. M. Bullock, Eur. J. Inorg. Chem., 2011, 2011, 1017–1027.
18. S. Kaur-Ghumaan, L. Schwartz, R. Lomoth, M. Stein and S. Ott, Angew. Chem., Int. Ed., 2010, 49, 8033–8036.
19. T. Liu, D. L. DuBois and R. M. Bullock, Nat. Chem., 2013, 5, 228–233.
20. A. D. Wilson, R. K. Shoemaker, A. Miedaner, J. T. Muckerman, D. L. DuBois and M. R. DuBois, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6951–6956.
21. M. L. Helm, M. P. Stewart, R. M. Bullock, M. R. DuBois and D. L. DuBois, Science, 2011, 333, 863–866.
22. M. O'Hagan, M.-H. Ho, J. Y. Yang, A. M. Appel, M. R. DuBois, S. Raugei, W. J. Shaw, D. L. DuBois and R. M. Bullock, J. Am. Chem. Soc., 2012, 134, 19409–19424.
23. T. Liu, B. Li, C. V. Popescu, A. Bilko, L. M. Pérez, M. B. Hall and M. Y. Darensbourg, Chem.–Eur. J., 2010, 16, 3083–3089.
24. L. Schwartz, P. S. Singh, L. Eriksson, R. Lomoth and S. Ott, C. R. Chim., 2008, 11, 875–889.
25. D. Streich, M. Karnahl, Y. Astuti, C. W. Cady, L. Hammarström, R. Lomoth and S. Ott, Eur. J. Inorg. Chem., 2011, 2011, 1106–1111.
26. M. Beyler, S. Ezzaher, M. Karnahl, M.-P. Santoni, R. Lomoth and S. Ott, Chem. Commun., 2011, 47, 11662–11664.
27. L. Yu, C. Greco, M. Bruschi, U. Ryde, L. De Gioia and M. Reiher, Inorg. Chem., 2011, 50, 3888–3900.
28. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
29. J. Y. Yang, S. E. Smith, T. Liu, W. G. Dougherty, W. A. Hoffert, W. S. Kassel, M. R. DuBois, D. L. DuBois and R. M. Bullock, J. Am. Chem. Soc., 2013, 135, 9700–9712.
30. G. M. Jacobsen, R. K. Shoemaker, M. J. McNevin, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2007, 26, 5003–5009.
31. G. Märkl, G. Y. Jin and C. Schoerner, Tetrahedron Lett., 1980, 21, 1409–1412.
32. T. E. Barder and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 5096–5101.
33. S. Ezzaher, A. Gogoll, C. Bruhn and S. Ott, Chem. Commun., 2010, 46, 5775–5777.
34. M. Karnahl, S. Tschierlei, O. F. Erdem, S. Pullen, M.-P. Santoni, E. J. Reijerse, W. Lubitz and S. Ott, Dalton Trans., 2012, 41, 12468–12477.
35. S. Lounissi, J.-F. Capon, F. Gloaguen, F. Matoussi, F. Y. Petillon, P. Schollhammer and J. Talarmin, Chem. Commun., 2011, 47, 878–880.
36. A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
37. U. J. Kilgore, M. P. Stewart, M. L. Helm, W. G. Dougherty, W. S. Kassel, M. R. DuBois, D. L. DuBois and R. M. Bullock, Inorg. Chem., 2011, 50, 10908–10918.
38. J. M. Lehn, in Dynamic Stereochemistry, Springer, Berlin, Heidelberg, 1970, vol. 15/3, pp. 311–377.
39. J. M. Gardner, M. Beyler, M. Karnahl, S. Tschierlei, S. Ott and L. Hammarström, J. Am. Chem. Soc., 2012, 134, 19322–19325.
40. G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, A64, 112–122.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
42. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
43. J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 1200–1211.
46. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
47. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
48. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
49. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
50. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
51. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
52. V. Fourmond, P.-A. Jacques, M. Fontecave and V. Artero, Inorg. Chem., 2010, 49, 10338–10347.

---

Footnotes

† Electronic supplementary information (ESI) available: Crystallographic, NMR and IR data of the complexes 3a–d, 4a and 5a. UV/vis-SEC and electrochemical spectra of 3a as well as its catalytic activity. Further details concerning the DFT calculations. CCDC 822967, 972155, and 972156. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3dt53268b

‡ Contributed equally and should be both considered as first authors.

§ Present address: Leibniz-Institute for Catalysis at the University of Rostock, Albert-Einstein-Straße 29a, 18059 Rostock, Germany.

¶ Present address: Institute of Physics, University of Rostock, Universitätsplatz 3, 18055 Rostock, Germany.

---