Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Proton conductivity of hexagonal and cubic BaTi1−xScxO3−δ (0.1 ≤ x ≤ 0.8)
Seikh M. H.
Rahman
 *a,
Stefan T.
Norberg
a,
Christopher S.
Knee
a,
Jordi J.
Biendicho
bc,
Stephen
Hull
c and
Sten G.
Eriksson
a
*a,
Stefan T.
Norberg
a,
Christopher S.
Knee
a,
Jordi J.
Biendicho
bc,
Stephen
Hull
c and
Sten G.
Eriksson
a
aDepartment of Chemical and Biological Engineering, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden. E-mail: habibur@chalmers.se; Fax: +46 (0)31 772 2853; Tel: +46 (0)31 772 2906
bDepartment of Material and Environmental Chemistry, Stockholm University, SE-106 91 Stockholm, Sweden
cThe ISIS Facility, STFC Rutherford Appleton Laboratory, Chilton, Didcot, OX11 0QX, UK
First published on 22nd July 2014
Abstract
BaTi1−xScxO3−δ (x = 0.1–0.8) was prepared via solid state reaction. High resolution X-ray powder diffraction was used to characterise the synthesised materials. It was found that low substitution (x = 0.1 and 0.2) of Ti4+ for Sc3+ gives a hexagonal perovskite structure, whereas high substitution (x = 0.5–0.7) results in a cubic perovskite structure. Thermogravimetric analysis revealed significant levels of protons in both as-prepared and hydrated samples. Electrical conductivity was measured by AC impedance methods under oxygen, argon and under dry and humid, both H2O and D2O, conditions for BaTi1−xScxO3−δ (x = 0.2, 0.6 and 0.7). In the temperature range of 150–600 °C, under humid conditions, the conductivity is significantly higher than that under the dry conditions. The increase in conductivity is especially prominent for the cubic phases, indicating that protons are the dominant charge carriers. The proton conductivity of hexagonal BaTi0.8Sc0.2O3−δ is approx. two orders of magnitude lower than that of the more heavily substituted cubic phases. Conductivity is also found to be higher in dry O2 than in Ar in the whole temperature range of 150–1000 °C, characteristic of a significant contribution from p-type charge carriers under oxidising atmospheres. Greater Sc3+ substitution leads to a higher proton concentration and the highest proton conductivity (σ ∼ 2 × 10−3 S cm−1 at 600 °C) is found for the BaTi0.3Sc0.7O3−δ composition.
1 Introduction
Proton conducting oxides have the unique property that hydrogen can be transported with high selectivity due to ionic conduction of protons. They have a wide range of energy related applications including their use as electrolyte materials in fuel cells, steam electrolysers, and for hydrogen and humidity sensors.1–5 Amongst these uses, protonic ceramic fuel cells (PCFCs), utilising hydrogen as fuel, stand out as a promising technology for future, clean energy generation. These devices produce electricity through direct electro-chemical reactions, where chemical energy is converted into electricity more efficiently than any process in which fuel is burnt. Materials possessing both proton and electronic conductivity are potential membrane materials for hydrogen separation from gas mixtures.6 This approach can be used for production of hydrogen from fossil fuels or for pre-combustion CO2 capture.However, the success of these technologies relies on the invention of novel chemically stable electrolyte materials with high protonic conductivity (>0.01 S cm−1) at intermediate temperatures (200–600 °C). Since the breakthrough work on proton conducting perovskite oxides by Iwahara et al.2 during the 1980s, acceptor-doped perovskites (with the most common formula, A2+B1−x4+Mx3+O3−δ2−) have been actively studied in the search for improved proton conducting materials.
The majority of the investigated materials are either alkaline earth cerates or zirconates.1,5,7–9 In contrast, relatively few studies have focused on proton conductivity in alkaline earth titanate compounds, e.g. BaZr0.45Ti0.45Y0.1O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and BaTi0.5In0.5O3−δ.11,12 Brownmillerite phases such as Ba2In2O5
10 and BaTi0.5In0.5O3−δ.11,12 Brownmillerite phases such as Ba2In2O5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,14 and Ba2Sc2O5
13,14 and Ba2Sc2O5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 based oxides have also been investigated as potential proton conductors. Addition of Ti to Ba2In2O5 results in the formation of perovskite-like oxygen deficient compounds Ba2(In1−xTix)2O5+x (0 ≤ x ≤ 1) that show much higher proton conduction than the brownmillerite parent phase.16–18 Recently findings on the structure and conductivity of 50 mol% Sc doped BaTiO3, i.e. BaTi0.5Sc0.5O3−δ, were reported in ref. 19, and indicated promising levels of proton conductivity in this cubic phase. In this paper, the crystal structure and conductivities of BaTi1−xScxO3−δ (x = 0.1, 0.2, 0.6 and 0.7) will be discussed with an emphasis on proton conduction and compared with 50 mol% Sc doped BaTiO3.19 The samples will be referred to as BTS10, BTS20, etc. where the number represents the percentage of Ti4+ substituted by Sc3+. The phases are characterised by X-ray powder diffraction, thermogravimetric analysis and electrochemical impedance spectroscopy under controlled atmospheres. A compositionally driven structural transition is found that impacts profoundly on the mobility of the protons in the materials. In addition, the 60 and 70% Sc substituted samples show an approximate one order of magnitude increase in proton conduction over that found for BTS50.19
15 based oxides have also been investigated as potential proton conductors. Addition of Ti to Ba2In2O5 results in the formation of perovskite-like oxygen deficient compounds Ba2(In1−xTix)2O5+x (0 ≤ x ≤ 1) that show much higher proton conduction than the brownmillerite parent phase.16–18 Recently findings on the structure and conductivity of 50 mol% Sc doped BaTiO3, i.e. BaTi0.5Sc0.5O3−δ, were reported in ref. 19, and indicated promising levels of proton conductivity in this cubic phase. In this paper, the crystal structure and conductivities of BaTi1−xScxO3−δ (x = 0.1, 0.2, 0.6 and 0.7) will be discussed with an emphasis on proton conduction and compared with 50 mol% Sc doped BaTiO3.19 The samples will be referred to as BTS10, BTS20, etc. where the number represents the percentage of Ti4+ substituted by Sc3+. The phases are characterised by X-ray powder diffraction, thermogravimetric analysis and electrochemical impedance spectroscopy under controlled atmospheres. A compositionally driven structural transition is found that impacts profoundly on the mobility of the protons in the materials. In addition, the 60 and 70% Sc substituted samples show an approximate one order of magnitude increase in proton conduction over that found for BTS50.19
2 Experimental
2.1 Synthesis
BaTi1−xScxO3−δ (x = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8) compositions were prepared by the conventional solid state sintering method using Sc2O3 (Sigma Aldrich, 99.9%), BaCO3 (Sigma Aldrich, ≥99%), and TiO2 (Merck, 99.8%) according to stoichiometric ratios. These carbonates and oxides were mixed using a mortar and pestle with ethanol to help the process of homogenization. The mixed powders were heated at 1000 °C for 12 h, ground a second time and thereafter pelletized and reheated at 1200 °C for 12 h. This procedure was repeated two more times with the exception of heating to 1300 °C and 1400 °C, respectively. After the 1400 °C sintering, the BTS10 and BTS20 samples were judged to be pure from long X-ray diffraction scans. The BTS60 and BTS70 samples required further heating and were reground and heated at 1500 °C for 18 h, followed by a heating cycle at 1550 °C for 48 h. After the final sintering step the so called as-sintered or as-prepared pellets for the x = 0.1, 0.2, 0.6 and 0.7 samples showed a density corresponding to approx. 77–89% of the theoretical values obtained from the cell volumes determined by X-ray diffraction. The obtained densities for the BTS10 and BTS20 samples were at the higher end of this range.Portions of the as-prepared BTS10, 20, 60 and 70 samples, in powder form, were hydrated at 185 °C under a humid atmosphere for a period of two days and thus the hydrated samples are obtained. In the process N2(g) saturated with water vapour at 76.2 °C, corresponding to a water partial pressure, p(H2O) ≈ 0.40 atm, was passed through a closed tube furnace.
2.2 Characterisation
The X-ray powder diffraction (XRPD) measurements were carried out at ambient temperature using a Bruker AXS D8 ADVANCE VARIO powder diffractometer (CuKα1 = 1.54056 Å) equipped with a solid-state LynxEye detector and a germanium primary monochromator. Short 30 minute scans covering the 2θ range 20–65° were performed in order to check the phase purity and progress of synthesis. Longer, high resolution, scans (2θ range 10–120°, with a step size of 0.0092° and 3.9 s collections per step) were used for structural characterisation of samples. The data were analysed by the Rietveld method20 using the GSAS program with EXPGUI interface.21,22 Thermogravimetric analysis (TGA) was carried out on as-prepared and hydrated powder samples on heating from room temperature to 1000 °C. The experiments were performed with a NETZSCH STA 409 PC instrument with a heating rate of 20 °C min−1 in a stream of N2 (nitrogen contains ≤5 ppm H2O) with a gas flow rate of 20 ml min−1.A Solartron 1260 frequency response analyser connected to a ProboStat (NorECs, Norway) conductivity cell was used to measure impedance over the frequency range 4.5 MHz to 100 mHz and the applied sine wave amplitude was 1 V rms. Impedance measurements were performed on sintered pellets of BTS20, BTS60 and BTS70 samples with approx. 10 mm diameters. Platinum paste was used to ensure good Ohmic contacts. The Pt electrode area, used to extract the final conductivity, values ranged between 0.5 and 0.74 cm2. Impedance data were then collected following a similar procedure as described elsewhere for BaTi0.5Sc0.5O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 under wet gas conditions being provided by bubbling the gas through either H2O or D2O at RT.
19 under wet gas conditions being provided by bubbling the gas through either H2O or D2O at RT.
An additional 10 mm diameter pellet (thickness 1.6 mm and electrode area 0.74 cm2) of the same batch of BTS70 material was further characterised by impedance spectroscopy as a function of temperature and oxygen partial pressures. A ProboStat measurement cell was connected to a gas mixer that could provide gases with known partial compositions of different gases. Drying of the gas was achieved by running the gas through a column of P2O5. A Solartron 1260 impedance spectrometer was used for the conductivity measurements. Isotherms (at temperatures from 1000 to 400 °C) were measured versus the partial pressure of oxygen in the range 2.5 × 10−4 to 2.5 × 10−1 atm under dry conditions (∼30 ppm H2O). The impedance was monitored versus time under each new set of conditions to ensure that equilibrium was achieved before taking a measurement. The oxygen partial pressure was measured, using a zirconia ceramic gas sensor and atmospheric air, with p(O2) = 0.209, as a reference.
The least squares refinement program Z-View (Scribner Associates Inc.) was used to fit the obtained impedance data. The brick-layer model23,24 was employed to represent the electrical response of the samples. Each arc from the experimental data was represented by a parallel combination of a resistance (R) and a constant-phase element (CPE). The CPE is an empirical impedance function that substitutes the uniquely capacitive element, in order to account for the depression of the semicircles when the sample presents non-Debye behaviour.23,24 Due to high impedance at temperatures below 200 °C, the resistance could not be extracted reliably. It was difficult to separate the bulk and grain-boundary conductivity especially for the BTS60–BTS70 samples. Therefore, in this study, the total conductivity is plotted for these samples except for BTS20. For BTS20, up to 650 °C, under wet Ar conditions, bulk conductivity is extracted.
Microstructure and chemical composition of the sintered pellets of BTS20 and BTS70 were characterised by scanning electron microscopy (Leo Ultra 55 FEG SEM) in conjunction with energy dispersive X-ray spectroscopy (EDX, Oxford INCA systems) operated with an acceleration potential of 2–20 kV and a secondary electron detector. The exposed top surface of the samples after the impedance analysis was polished in preparation for the EDX and images were taken on the fractured bulk areas of the pellets.
3 Results
The findings of the phase formation of the BaTi1−xScxO3−δ revealed a complex dependency on the level of Sc doping with two distinct regions of phase pure samples being of particular interest. For BTS10 and BTS20, the patterns could be fully indexed using the ideal hexagonal 6H perovskite structure with space group P63/mmc, whereas cubic phases, seen for BTS60 and 70, are indexed with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The samples with x = 0.3 and 0.4 revealed diffraction patterns that were clearly bi-phasic in nature. Analysis of long scan XRPD data on BTS30 showed that the main phase adopts a hexagonal structure similar to BTS20. Through comparison with the ICDD database,25 we were not able to reliably identify the second phase but speculate that it could be formed due to a different stacking arrangement of corner sharing and face sharing octahedra than found in the 6H-polytype. Similarly, we were not able to identify the structure of the x = 0.8 sample. These compositions were consequently not comprehensively characterised and hence are not discussed further in this study.
m space group. The samples with x = 0.3 and 0.4 revealed diffraction patterns that were clearly bi-phasic in nature. Analysis of long scan XRPD data on BTS30 showed that the main phase adopts a hexagonal structure similar to BTS20. Through comparison with the ICDD database,25 we were not able to reliably identify the second phase but speculate that it could be formed due to a different stacking arrangement of corner sharing and face sharing octahedra than found in the 6H-polytype. Similarly, we were not able to identify the structure of the x = 0.8 sample. These compositions were consequently not comprehensively characterised and hence are not discussed further in this study.
Rietveld refinement for the hexagonal systems was carried out using the structure reported by Akimoto et al.26 as a starting model. The lattice parameters for the initial model were first obtained using the program CELLREF.27 Scale factor, 12 background parameters (shifted Chebyshev as implemented in GSAS) and 6 peak-shape parameters (pseudo-Voigt function ‘type 2’ as implemented in GSAS, refining the Gaussian parameters Gw, Gu and Gv, Lorentzian parameter LY along with shift and asymmetry parameters) were refined independently for each data set. The unit-cell parameters and a global isotropic atomic displacement parameter (ADP) were initially refined along with the instrumental parameters described above. Ti and Sc were distributed statistically according to the expected stoichiometry across both B sites of the hexagonal structure and the occupancies kept fixed. Atomic coordinates and ADPs were refined using constraints to keep them equal for Ti and Sc. It was not possible to reliably refine the oxygen site occupancies so these were fixed at values determined from the TGA data that indicated partial hydration of the as-prepared materials due to filling of oxygen vacancies as per eqn (1). For BTS20, all the vacant oxygen sites were allocated to the O(1) site, as this gave more satisfactory Uiso values. The data from the new cubic compositions BTS60 and BTS70 were analysed in a similar way using the starting model of BaTi0.5Sc0.5O3−δ.19
| H2O(g) + O×O + V˙˙O ↔ 2OH˙O | (1) |
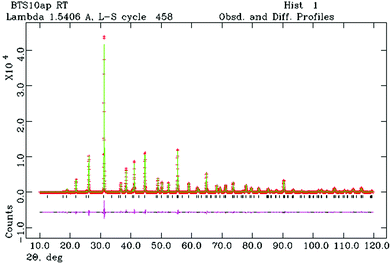
Fig. 1 shows the final Rietveld plot for hexagonal BTS10. The Rietveld plots for BTS20, BTS60 and BTS70 had similar quality but are not included for brevity. A summary of the structural parameters obtained from the Rietveld analyses are presented in Tables 1 and 2. The hexagonal and cubic crystal structures are shown in Fig. 2a and 2b, respectively. In Fig. 3 the normalised unit cell volumes versus mol% Sc3+ for the compositions of BaTi1−xScxO3−δ (x = 0.1, 0.2. 0.5, 0.6 and 0.7) are shown.
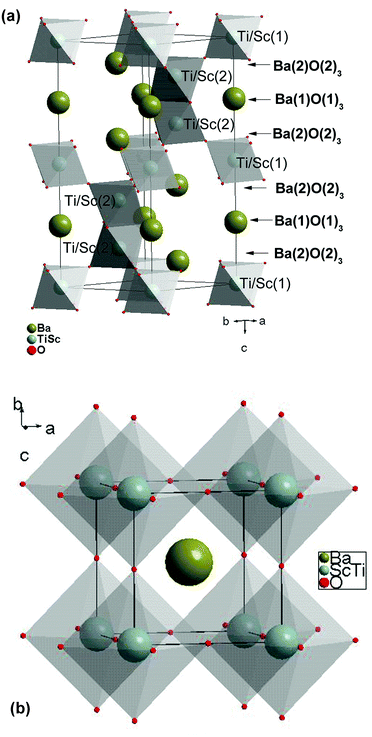 | ||
| Fig. 2 Polyhedral representation of the crystal structures of (a) hexagonal BTS10 (viewed along the ab-axis) and (b) cubic BTS70. | ||
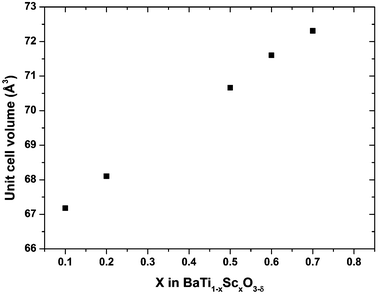 | ||
| Fig. 3 The unit cell volumes for BaTi1−xScxO3−δ ceramics. For the x = 0.1 and 0.2 hexagonal phases (Z = 6) the unit cell volume is reduced to equivalent cubic values. | ||
| BaTi0.9Sc0.1O3−δ (BTS10) | BaTi0.8Sc0.2O3−δ (BTS20) | |
|---|---|---|
| a (Å) | 5.7517(1) | 5.7732(1) |
| c (Å) | 14.0682(2) | 14.1567(2) |
| Cell volume (Å3) | 403.06(1) | 408.62(1) |
| Ba(1) 2b (0,0,1/4) | ||
| U iso (Å2) | 0.0102(2) | 0.0136(4) |
| Occ. factor | 1.0 | 1.0 |
| Ba(2) 4f (1/3,2/3,z) | 0.09565(7) | 0.09505(7) |
| U iso (Å2) | 0.0102(2) | 0.0136(4) |
| Occ. factor | 1.0 | 1.0 |
| Ti/Sc(1) 2a (0,0,0) | ||
| U iso (Å2) | 0.0080(11) | 0.0059(12) |
| Occ. factor | 0.9/0.1 | 0.8/0.2 |
| Ti/Sc(2) 4f (1/3,2/3,z) | 0.84732(15) | 0.84821(18) |
| U iso (Å2) | 0.0115(9) | 0.0200(12) |
| Occ. factor | 0.9/0.1 | 0.8/0.2 |
| O(1) 6h (x,y,1/4) | 0.5161(7), 0.0321(14) | 0.5179(9), 0.0357(17) |
| U iso (Å2) | 0.0081(19) | 0.022(3) |
| Occ. factor | 0.99 | 0.93 |
| O(2) 12k (x,y,z) | 0.8361(6), 0.6722(12), 0.0813(3) | 0.8326(6), 0.6651(13), 0.0834(3) |
| U iso (Å2) | 0.0015(13) | 0.0045(14) |
| Occ. factor | 0.99 | 1.0 |
| Bond distances (Å) | ||
| Ba(1)–O(1) | 2.881(1) × 6 | 2.892(1) × 6 |
| Ba(1)–O(2) | 2.881(5) × 6 | 2.892(5) × 6 |
| Ba(2)–O(1) | 2.883(1) × 3 | 2.866(6) × 3 |
| Ba(2)–O(2) | 2.883(1) × 6 | 2.892(1) × 6 |
| Ba(2)–O(2) | 3.008(1) × 3 | 3.023(5) × 3 |
| Ti(1)/Sc(1)–O(2) | 1.993(5) × 6 | 2.049(6) × 6 |
| Ti(2)/Sc(2)–O(1) | 2.031(5) × 3 | 2.036(6) × 3 |
| Ti(2)/Sc(2)–O(2) | 1.964(6) × 3 | 1.921(6) × 3 |
| χ 2 | 4.18 | 5.43 |
| R wp (%) | 6.34 | 7.02 |
| R Bragg (%) | 5.46 | 5.47 |
| No. of variables | 35 | 32 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Note that oxygen contents were fixed based on the level of hydration determined from TGA data
m). Note that oxygen contents were fixed based on the level of hydration determined from TGA data
| BaTi0.4Sc0.6O3−δ (BTS60) | BaTi0.3Sc0.7O3−δ (BTS70) | |
|---|---|---|
| Cell parameter, a (Å) | 4.1523(1) | 4.1673(1) |
| Ba(1) 1b (1/2,1/2,1/2) | ||
| U iso (Å2) | 0.0242(2) | 0.0245(2) |
| Occ. factor | 1.0 | 1.0 |
| Ti/Sc(1) 1a (0,0,0) | ||
| U iso (Å2) | 0.0239(4) | 0.0206(4) |
| Occ. factor | 0.4/0.6 | 0.3/0.7 |
| O(1) 3d (1/2,0,0) | ||
| U iso (Å2) | 0.0223(8) | 0.0179(7) |
| Occ. factor | 0.93 | 0.94 |
| Bond distances (Å) | ||
| Ba–O(1) | 2.936(1) × 12 | 2.947(1) × 12 |
| Ti/Sc–O(1) | 2.076(1) × 6 | 2.083(1) × 6 |
| χ 2 | 5.78 | 5.29 |
| R wp (%) | 7.28 | 7.11 |
| R Bragg (%) | 4.4 | 5.8 |
| No. of fitted parameters | 23 | 23 |
Fig. 4a and b present the TGA scans for as-prepared and hydrated BaTi1−xScxO3−δ ceramics (a) 0.1 ≤ x ≤ 0.2 and (b) 0.5 ≤ x ≤ 0.7. All the samples show significant mass losses with onset temperatures >250 °C consistent with hydration of oxygen vacancies introduced via acceptor doping. For BTS50, the data are taken from ref. 19.
The SEM images obtained for the bulk areas of the BTS20 and BTS70 pellets used for conductivity measurements are shown in Fig. 5. They reveal the grain size for both samples to be in the range of ∼1–6 μm. EDX analysis on areas of grains show the Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti
Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sc compositions are 97.5(10)
Sc compositions are 97.5(10)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : 80.8(4)
: 80.8(4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : 21.7(6) and 95.2(8)
: 21.7(6) and 95.2(8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : 34.4(13)
: 34.4(13)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : 70.4(5) for BTS20 and BTS70, respectively, indicating that the sample stoichiometry is close to the expected values. The potentially greater Ba deficiency suggested for BTS70 is consistent with the higher final sintering temperature used during its preparation.
: 70.4(5) for BTS20 and BTS70, respectively, indicating that the sample stoichiometry is close to the expected values. The potentially greater Ba deficiency suggested for BTS70 is consistent with the higher final sintering temperature used during its preparation.
Fig. 6 compares the complex plane plots for BTS20 at 450 °C under different environments during the cooling cycle of the measurements, together with a typical equivalent circuit used to extract the conductivity data. The extracted true capacitance values of the distributed responses in Fig. 6b have been calculated using the equation C = Q1/αR(1/α−1),28 where Q and α are related to the CPE and R is the resistance. Under wet Ar conditions, the larger first semicircle, seen at higher frequencies, yielded a capacitance of 5.7 × 10−12 F cm−1, representative of a bulk process and the second one gave a value of 9.19 × 10−10 F cm−1, typical of grain boundary capacitance. The lower frequency tail is attributed to the electrode response. A drop in resistance is apparent for the dry O2 run in comparison to the dry Ar data, and an even greater drop of resistance is clear for the data recorded under wet O2 and wet Ar compared to dry condition runs (from the apparent resistance scale on the x-axis).
The Arrhenius plots of total (bulk + grain boundary) conductivity for the BTS20 and BTS70, determined from fitting of the full frequency range, are shown in Fig. 7a and b and Fig. 8a and b, respectively. The BTS20 sample shows higher conductivity in wet Ar than dry Ar in the low temperature region (below 600 °C) with an isotope effect proving that proton conductivity is dominant. In the higher temperature region the conductivity values under dry and wet Ar conditions merge as protonic charge carriers become less stable. The conductivity in dry O2 is higher than that under dry/wet Ar conditions and even marginally higher than wet O2 run (below 550 °C), indicating a strong influence of p(O2) on the total conductivity. From the extracted bulk conductivity plot of BTS20 in Fig. 7a, it is evident that bulk conductivity and not the grain boundary contribution, is dominant for the total conductivity, in the shown temperature range.
 | ||
| Fig. 7 Conductivity vs. 1/T of BTS20 measured under (a) Ar (total and bulk) and (b) O2 (total only) conditions during cooling. | ||
 | ||
| Fig. 8 Total conductivity vs. 1/T of BTS70 measured (a) under dry and wet (Ar), (b) under dry (Ar, O2), wet and heavy water conditions under O2. | ||
The overall trends are similar for the BTS70 sample (Fig. 8), with large enhancements of conductivity observed in wet gas, albeit here the conductivity values, particularly those at T < 600 °C in wet gas, are significantly higher than those of BTS20. A noteworthy isotope effect is also evident (see Fig. 8b), and confirms that protons dominate the conductivity for T ≤ 600 °C. Subtracting the dry state conductivity from the wet gas (Ar) run reveals the overall proton conduction, which is also plotted in Fig. 8a. For both BTS20 and BTS70 the proton conductivity is of the same order of magnitude as the wet Ar data, and it starts to decrease in values above 500 °C for hexagonal BTS20 (see transference number in Fig. 11 below) and 600 °C for cubic BTS70. In Fig. 8b the conductivity data are also compared with the cooling scan performed in dry Ar. The data demonstrate that the dry Ar run is consistently approximately one order of magnitude lower than the dry O2 run throughout the temperature window, as was found for BTS50.19
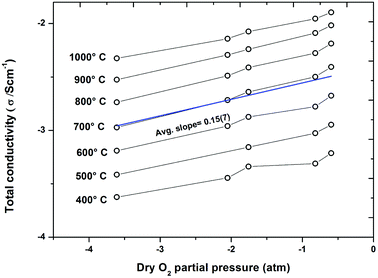
Fig. 9 compares the total conductivity of the series BaTi1−xScxO3−δ for x = 0.2, and 0.5 ≤ x ≤ 0.7 in wet Ar (cooling runs). The BTS50 data are taken from ref. 19. The proton conductivity increases markedly when changing the Sc content from 20% to 50%, while the BTS60 and BTS70 are very similar, and for the latter phase reaches the maximum at 600 ± 50 °C. Finally, Fig. 10 displays conductivity isotherms collected as a function of p(O2) in the dry state on BTS70.
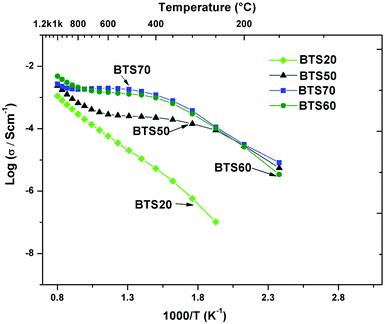 | ||
| Fig. 9 Total conductivity vs. 1/T of BaTi1−xScxO3−δ series: BTS20 (Fig. 6a), BTS50,19 BTS60 and BTS70 (Fig. 7a) in wet Ar. | ||
4 Discussion
4.1 Structure
For BTS20, the Rietveld analysis indicates that all oxygen vacancies occur in the O(1) h-layer sites between face-sharing octahedra. This result is in good agreement with the existing literature on oxygen deficient 6H-BaTiO3-type perovskites,31 BaTi1−xGaxO3−x/2 for x = 0.08,32 h-Ba(Ti,Fe)O3−δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 and 6H-BaFeO2.79.35 However, in BTS10, the oxygen vacancy is uniformly distributed within the O(1) and O(2) sites as per the refinement of laboratory XRD data. Neutron diffraction studies would be required to confirm the suggested vacancy ordering and further probe the potential for Ti and Sc ordering. As can be seen from Fig. 3 the cell volume of the hexagonal phases increases with the incremental amount of Sc3+. This expansion is expected as Sc3+ (ionic radius of 0.745 Å in 6-fold coordination)36 is larger compared to Ti4+ (ionic radius of 0.605 Å).36
34 and 6H-BaFeO2.79.35 However, in BTS10, the oxygen vacancy is uniformly distributed within the O(1) and O(2) sites as per the refinement of laboratory XRD data. Neutron diffraction studies would be required to confirm the suggested vacancy ordering and further probe the potential for Ti and Sc ordering. As can be seen from Fig. 3 the cell volume of the hexagonal phases increases with the incremental amount of Sc3+. This expansion is expected as Sc3+ (ionic radius of 0.745 Å in 6-fold coordination)36 is larger compared to Ti4+ (ionic radius of 0.605 Å).36
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m perovskite structure. For BTS60 and BTS70, there is no evidence of a larger unit cell that would reflect long range ordering of the Ti and Sc ions at the B-site. Therefore the materials are classed as oxygen deficient, B-site disordered, perovskites. These phases can be thought of as if synthesized from the parent BaTiO3 perovskite by substitution of 60–70% of the tetravalent Ti4+ ions by trivalent Sc3+ ions, respectively. Hence charge compensating oxygen vacancies (V˙˙O) were created and these appear to be distributed randomly over the single oxygen site to a first approximation. Once more an expansion of the unit cell is seen for increasing levels of Sc (Fig. 3).
m perovskite structure. For BTS60 and BTS70, there is no evidence of a larger unit cell that would reflect long range ordering of the Ti and Sc ions at the B-site. Therefore the materials are classed as oxygen deficient, B-site disordered, perovskites. These phases can be thought of as if synthesized from the parent BaTiO3 perovskite by substitution of 60–70% of the tetravalent Ti4+ ions by trivalent Sc3+ ions, respectively. Hence charge compensating oxygen vacancies (V˙˙O) were created and these appear to be distributed randomly over the single oxygen site to a first approximation. Once more an expansion of the unit cell is seen for increasing levels of Sc (Fig. 3).
4.2 TGA
Based on the stoichiometric formula of BaTi1−xScxO3−x/2, a maximum of x/2 moles of oxygen vacancies “per chemical formula” can be made in the dried sample. Protons can then be incorporated as an outcome of filling of the oxygen vacancies by hydroxyl groups, OH−, as presented in eqn (1) (in Kröger–Vink notation).The TGA data provide evidence of significant proton concentrations in the BaTi1−xScxO3−x/2 samples (Fig. 4). When heated from RT to 1000 °C, water vapour evolved from the samples in the interval 200 °C < T < 550 °C as the stability of the protonic defects decreased. From the data it is apparent that the as-prepared materials contained significant levels of protons and that the hydrated samples show even higher levels of filling of the available oxygen vacancies, i.e., between a minimum of 74% (cubic BTS50) and maximum of 99% (hexagonal BTS20). Hydration enthalpies of acceptor doped oxides are typically exothermic. At temperatures above 250 °C the equilibrium of the hydration reaction (eqn (1)) is pushed to the left hand side and de-hydration of the samples start. At temperatures close to 500 °C, the dehydration is almost completed, but, BTS70 in particular, shows a tendency to retain protons at even higher temperatures.
4.3 Conductivity
The conductivity data reveal that the major differences in the crystal structures related to the connectivity of the Ti/ScO6−δ octahedra are strongly reflected in the proton conductivity, as is apparent from Fig. 9. For hexagonal BTS20 the conductivity in wet Ar at 400 °C is at least two orders of magnitude lower than the values observed for the cubic BTS50, 60 and 70 samples. A comparison of the activation energies derived from the total conductivity below 450 °C in wet Ar, gives 0.80 eV for BTS20 versus 0.48 eV for BTS70. The latter value represents a good agreement with literature values of proton conducting perovskites,37 whilst the former value is very high and indicates the mobility of protons through the hexagonal structure is not favourable. The ability to separate the dominant bulk contribution for the BTS20 sample, from which a similar high activation energy of 0.77 eV for proton conduction was obtained, allows us to directly relate the conductivity to the material's crystal structure in this manner. Taken together with the TGA results that show a high level of protonation for BTS20 is possible, then it seems that low proton mobility is the critical factor in determining the modest level of proton conductivity observed for the hexagonal phase.For BTS60 and 70 samples under wet conditions and in the interval of 350–650 °C a “plateau-like” region evolves that is characteristic of the behaviour of other heavily doped cubic perovskites such as BaZr1−xMxO3−δ (M = In3+ and Yb3+),8,38–41 and 50 mol% In3+ and Sc3+ substituted BaTiO3.11,19 This may be deduced as a result of decrease of the concentration of proton charge carriers coupled to an increase in diffusivity of the protons that remain.9 However, at T > 700 °C the majority of protons have left the samples and the conductivity reflects a new dominant transport process with either electron hole or oxide ion conduction.42
The reduction in the total conductivity obtained below 550 °C for the D2O run (Fig. 7a and 8b) is in line with the expected isotope effect and provides further confirmation that the conductivity is predominantly protonic for both the hexagonal and cubic phases studied. At 250 °C to 500 °C, σH+/σD+ = 3.04 to 1.65 for BTS20 whereas for BTS70, σH+/σD+ lies in the range of 3.6 to 1.6 in the temperature interval of 150 °C to 500 °C. These findings are in line with previous results for perovskites which show a large scatter between 1.6 and 4.11,19,43
Assuming proton conduction has no significant effect on the contribution of other charge carriers, the pure protonic conductivity σH can be calculated as the difference between the conductivity in H2O-saturated Ar, σwet, and the conductivity of water-free sample obtained during the cooling cycle in dry Ar, σdry![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,44 as shown in Fig. 8a:
13,44 as shown in Fig. 8a:
| σH+ = σwet − σdry | (2) |
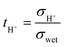
The transference number for proton conduction (tH+) in wet Ar can then be calculated from eqn (3). The temperature dependence of tH+ for BTS20, BTS60 and BTS70 is plotted in Fig. 11:
 | (3) |
The conductivity plots presented in Fig. 7 and 8 reveal the expected strong dependence on p(H2O) on these samples for T < 600 °C and, in addition, a significant effect of p(O2) is also seen in these isobars. The conductivity isotherms (Fig. 10) performed on the BTS70 sample further characterise the enhancements of conductivity as a function of p(O2). In the presence of oxygen acceptor-doped oxide ion vacancies may be charge compensated via the absorption of oxygen to produce electron holes as described in eqn (4) below:
| ½O2(g) + V˙˙O → O×O + 2h˙ | (4) |
This reaction competes with the creation of [OH˙O] defects described in eqn (1). From the equilibrium equations for reactions (1) and (4), given below, it is apparent that protonic and p-type electronic conductivity depend respectively on the water vapour pressure and oxygen partial pressure:42
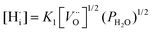 | (5) |
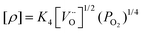 | (6) |
Fitting of the isotherms for BTS70 shown in Fig. 10 gives an average exponent value of ∼0.15, which is less than the expected value of 0.25, for pure p-type conduction. The results indicate that all BTS samples display mixed oxide ionic and electronic conduction, particularly under wet O2 and within the T interval 600–1000 °C. Estimated from the isobar data the p-type enhancement for BTS50, 60 and 70 is significantly greater than for the closely related BaTi0.5In0.5O3−δ (BTI50) phase determined from our previous study.11 This indicates that there is a greater electronic contribution when Sc is used as the acceptor dopant ion for these BaTi1−xMxO3−δ systems.
5 Conclusions
10–20 mol% scandium substituted BaTiO3, showed single phase materials and crystallise with a hexagonal 6H-BaTiO3 structure whereas samples with 50% to 70% of the Ti substituted by Sc adopt phase pure, primitive cubic, perovskites. Hydration behaviour indicates the filling of oxide ion vacancies by significant levels of proton defects for all materials studied. The effect of water vapour partial pressure, and the presence of an isotope effect, reveals that protons are the dominating charge carriers at temperatures below 600 °C; the conductivity of the cubic BTS50–BTS70 materials displays an enhancement of close to two orders of magnitude in wet gas runs at T ≤ 300 °C. The proton conductivity of hexagonal BTS20 is significantly lower indicating that the crystal structure is not as favourable for proton transport as the cubic perovskite. All of the BaTi1−xScxO3−δ samples show a meaningful contribution from p-type electron conductivity throughout the studied temperature window. The highest proton conductivity was achieved for the 70 mol% Sc substituted BaTiO3 that reaches a value of ∼0.002 S cm−1 at 600 °C in wet Ar, comparable to the best performing materials based on BaZrO3 and BaCeO3 doped with 10–20% yttrium. Further studies of the chemical stability, hydration behaviour and sinterability of the cubic phases aimed at further enhancing the proton conductivity are in progress.Acknowledgements
The authors thank the Swedish Energy Agency (STEM) for project funding. STN, CSK and SGE also thank Vetenskapsrådet (Swedish Research Council) for funding. We are also thankful to Zohreh G. Tari, Chalmers University of Technology, for helping with the synthesis of materials.References
- T. Norby, Solid State Ionics, 1999, 125(1–4), 1 CrossRef CAS.
- H. Iwahara, T. Esaka, H. Uchida and N. Maeda, Solid State Ionics, 1981, 3–4(Aug), 359 CrossRef CAS.
- H. Iwahara, T. Yajima, T. Hibino, K. Ozaki and H. Suzuki, Solid State Ionics, 1993, 61(1–3), 65 CrossRef CAS.
- T. Norby and Y. Larring, Curr. Opin. Solid State Mater. Sci., 1997, 2(5), 593 CrossRef CAS.
- T. Norby, in Perovskite Oxide for Solid Oxide Fuel Cells, ed. T. Ishihara, Springer, USA, 2009, pp. 217–241 Search PubMed.
- T. Norby and R. Haugsrud, Membranes for Energy Conversion, Wiley-VCH Verlag GmbH & Co. KGaA, 2008, pp. 169–216 Search PubMed.
- A. Orera and P. R. Slater, Chem. Mater., 2010, 22(3), 675 CrossRef CAS.
- I. Ahmed, S. G. Eriksson, E. Ahlberg, C. S. Knee, P. Berastegui, L. Johansson, H. Rundlof, M. Karlsson, A. Matic and L. Borjesson, Solid State Ionics, 2006, 177(17–18), 1395 CrossRef CAS PubMed.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333 CrossRef CAS.
- K. D. Kreuer, S. Adams, W. Munch, A. Fuchs, U. Klock and J. Maier, Solid State Ionics, 2001, 145(1–4), 295 CrossRef CAS.
- S. M. H. Rahman, C. S. Knee, I. Ahmed, S. G. Eriksson and R. Haugsrud, Int. J. Hydrogen Energy, 2012, 37(9), 7975 CrossRef CAS PubMed.
- S. T. Norberg, S. M. H. Rahman, S. Hull, C. S. Knee and S. G. Eriksson, J. Phys.: Condens. Matter, 2013, 25(45), 454214 CrossRef PubMed.
- G. B. Zhang and D. M. Smyth, Solid State Ionics, 1995, 82(3–4), 153 CrossRef CAS.
- I. Animitsa, N. Tarasova and Y. Filinkova, Solid State Ionics, 2012, 207, 29 CrossRef CAS PubMed.
- I. E. Animitsa, N. A. Kochetova and A. R. Shaikhlislamova, Russ. J. Electrochem., 2007, 43, 708 CrossRef CAS.
- E. Quarez, S. Noirault, M. T. Caldes and O. Joubert, J. Power Sources, 2010, 195(4), 1136 CrossRef CAS PubMed.
- V. Jayaraman, A. Magrez, M. Caldes, O. Joubert, F. Taulelle, J. Rodriguez-Carvajal, Y. Piffard and L. Brohan, Solid State Ionics, 2004, 170(1–2), 25 CrossRef CAS.
- V. Jayaraman, A. Magrez, M. Caldes, O. Joubert, M. Ganne, Y. Piffard and L. Brohan, Solid State Ionics, 2004, 170(1–2), 17 CrossRef CAS.
- S. M. H. Rahman, I. Ahmed, R. Haugsrud, S. G. Eriksson and C. S. Knee, Solid State Ionics, 2014, 255, 140 CrossRef CAS PubMed.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65 CrossRef CAS.
- A. C. Larson and R. B. V. Dreele, Los Alamos National Laboratory Report LAUR 86-748, 2004.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210 CrossRef CAS.
- J. R. Macdonald and W. B. Johnson, Impedance Spectroscopy, John Wiley & Sons, Inc., 2005, pp. 1–26 Search PubMed.
- J. R. Macdonald, J. Electroanal. Chem., 1987, 223(1–2), 25 CrossRef CAS.
- PDF-4+ 2010 (Database), ed. S. Kabekkodu, International Centre for Diffraction Data, Newtown Square, PA, USA Search PubMed.
- J. Akimoto, Y. Gotoh and Y. Oosawa, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1994, 50(2), 160 CrossRef.
- J. laugier and B. Bochu, LMGP-Suite Suite of Programs for the interpretation of X-ray Experiments, 2000 Search PubMed.
- E. Barsoukov and J. R. Macdonald, Impedance spectroscopy: theory, experiment, and applications, John Wiley & Sons, 2005 Search PubMed.
- R. H. Buttner and E. N. Maslen, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48(6), 764 CrossRef.
- C.-R. Xin, J. Zhang, Y. Liu, Q.-L. Zhang, H. Yang and D. Cheng, Mater. Res. Bull., 2013, 48(6), 2220 CrossRef CAS PubMed.
- D. C. Sinclair, J. M. S. Skakle, F. D. Morrison, R. I. Smith and T. P. Beales, J. Mater. Chem., 1999, 9(6), 1327 RSC.
- A. Feteira, G. M. Keith, M. J. Rampling, C. A. Kirk, I. M. Reaney, K. Sarma, N. Mc. Alford and D. C. Sinclair, Cryst. Eng., 2002, 5(3), 439 CrossRef CAS.
- R. H. Mitchell, Perovskites: modern and ancient, Almaz Press, Thunder Bay, 2002 Search PubMed.
- I. E. Grey, C. Li, L. M. D. Cranswick, R. S. Roth and T. A. Vanderah, J. Solid State Chem., 1998, 135(2), 312 CrossRef CAS.
- A. Jacobson, Acta Crystallogr., Sect. B: Struct. Sci., 1976, 32(4), 1087 CrossRef.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1976, 32(5), 751 CrossRef.
- K. D. Kreuer, Solid State Ionics, 1999, 125(1–4), 285 CrossRef CAS.
- I. Ahmed, S. G. Eriksson, E. Ahlberg, C. S. Knee, M. Karlsson, A. Matic, D. Engberg and L. Borjesson, Solid State Ionics, 2006, 177(26–32), 2357 CrossRef CAS PubMed.
- I. Ahmed, S. G. Eriksson, E. Ahlberg and C. S. Knee, Solid State Ionics, 2008, 179(21–26), 1155 CrossRef CAS PubMed.
- I. Ahmed, C. S. Knee, S.-G. Eriksson, E. Ahlberg, M. Karlsson, A. Matic and L. Borjesson, J. Electrochem. Soc., 2008, 155(11), P97 CrossRef CAS PubMed.
- S. M. Rahman, I. Ahmed and S. G. Eriksson, Appl. Mech. Mater., 2012, 110, 1181 Search PubMed.
- N. Bonanos, Solid State Ionics, 1992, 53(Part 2), 967 Search PubMed.
- A. S. Nowick and A. V. Vaysleyb, Solid State Ionics, 1997, 97(1–4), 17 CrossRef CAS.
- S. V. Chernov, Y. A. Dobrovolsky, S. Y. Istomin, E. V. Antipov, J. Grins, G. Svensson, N. V. Tarakina, A. M. Abakumov, G. Van Tendeloo, S. G. Eriksson and S. M. Rahman, Inorg. Chem., 2012, 51(2), 1094 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |