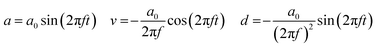Piezoelectric and ferroelectric materials and structures for energy harvesting applications
C. R.
Bowen
*a,
H. A.
Kim
a,
P. M.
Weaver
b and
S.
Dunn
c
aDepartment of Mechanical Engineering, University of Bath, Bath, BA2 7AY, UK. E-mail: c.r.bowen@bath.ac.uk
bNational Physical Laboratory, Hampton Road, Teddington TW11 0LW, UK
cCentre for Materials Research, School of Engineering and Materials Science, Queen Mary University of London, London E1 4NS, UK
First published on 1st November 2013
Abstract
This review provides a detailed overview of the energy harvesting technologies associated with piezoelectric materials along with the closely related sub-classes of pyroelectrics and ferroelectrics. These properties are, in many cases, present in the same material, providing the intriguing prospect of a material that can harvest energy from multiple sources including vibration, thermal fluctuations and light. Piezoelectric materials are initially discussed in the context of harvesting mechanical energy from vibrations using inertial energy harvesting, which relies on the resistance of a mass to acceleration, and kinematic energy harvesting which directly couples the energy harvester to the relative movement of different parts of a source. Issues related to mode of operation, loss mechanisms and using non-linearity to enhance the operating frequency range are described along with the potential materials that could be employed for harvesting vibrations at elevated temperatures. In addition to inorganic piezoelectric materials, compliant piezoelectric materials are also discussed. Piezoelectric energy harvesting devices are complex multi-physics systems requiring advanced methodologies to maximise their performance. The research effort to develop optimisation methods for complex piezoelectric energy harvesters is then reviewed. The use of ferroelectric or multi-ferroic materials to convert light into chemical or electrical energy is then described in applications where the internal electric field can prevent electron–hole recombination or enhance chemical reactions at the ferroelectric surface. Finally, pyroelectric harvesting generates power from temperature fluctuations and this review covers the modes of pyroelectric harvesting such as simple resistive loading and Olsen cycles. Nano-scale pyroelectric systems and novel micro-electro-mechanical-systems designed to increase the operating frequency are discussed.
Broader contextEnergy harvesting remains a topic of intense interest and this review provides an overview of the variety of energy harvesting mechanisms employed by piezoelectrics and their subclasses of pyroelectrics and ferroelectrics. The most common application is mechanical energy harvesting using inertial energy harvesting and kinematic energy for applications such as autonomous and self-powered low-power electronic devices. Other harvesting applications being considered are (i) the use of ferroelectric or multi-ferroic materials to convert light into chemical or electrical energy and (ii) the use of pyroelectric materials to generate electrical energy from temperature fluctuations. The multi-functional capability of piezoelectric materials provides the intriguing prospect of a material that can harvest energy from multiple sources; however the optimisation of such harvesting devices for specific applications continues to be a complex task. |
1. Introduction
Energy harvesting continues to receive both industrial and academic interest since it provides a route for the realisation of autonomous and self-powered low-power electronic devices, e.g. for wireless sensor networks or consumable electronics. An excellent commercial example is the recent system developed by Perpetuum which converts the vibration of rolling stock into electrical power for the wireless communication of sensors that predict the failure of rail wheel bearings.1The ability to deliver sustainable power to a wireless system network by energy harvesting is attractive not only because of the cost of batteries; it also removes the additional time and cost that is necessary to replace and maintain the batteries and the labour required to install complex wired systems. This is particularly relevant to the installation of sensor networks in areas that are either inhospitable or difficult to reach; this includes safety-monitoring devices,1 structure-embedded micro-sensors and medical implants. There are also environmental benefits associated with limiting the disposal of batteries.
Energy harvesting devices therefore provide a ‘battery-less’ solution by scavenging energy from ambient energy sources such as vibrations, heat, light, water etc., and converting it into a useable form, often electrical power.2 While the energy harvesting technologies are continuously improving there are also similar advances in microprocessor technology leading to an increase in power efficiency and reduced power consumption. Local electrical energy storage solutions are also improving, for example the development of super-capacitors3 and even ‘structural power’.4 It is this convergence of technologies that will ultimately lead to successful energy harvesting products and systems.
As a result of its topical nature, there are already a number of excellent reviews in the area of energy harvesting, which often concentrate on nano-scale materials and devices (‘nanogenerators’) 5–13 or surveys of the various potential devices and systems.14–19 The aim of this review is to provide an overview of the energy harvesting technologies associated with the family of ‘piezoelectric’ materials along with its sub-classes of ‘pyroelectrics’ and ‘ferroelectrics’.
These materials are particularly attractive for a number of energy harvesting applications. This includes the potential to convert mechanical vibrations into electrical energy via the direct piezoelectric effect, the conversion of thermal fluctuations into electrical energy via the pyroelectric effect and finally the exciting prospect of using the internal electric fields present in ferroelectrics or strained piezoelectric materials to influence electron–hole recombination in solar-cell devices or chemical reactions, such as water-splitting.
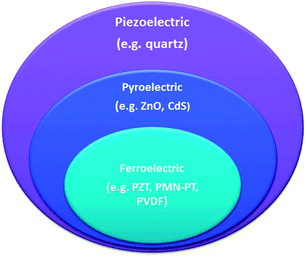
Fig. 1 shows the relationships between these materials in that all ferroelectrics are both pyroelectric and piezoelectric and all pyroelectrics are piezoelectric. Since these properties are, in many cases, present in the same material, it provides the intriguing prospect of a material that can harvest energy from multiple sources including vibration, thermal fluctuations and light.
2. Piezoelectric mechanical energy harvesters
Mechanical energy harvesting converts energy from movement or vibration into electrical energy. There are a wide variety of sources of mechanical energy including vibrations from industrial machinery and transport,1 fluid flow such as air movements,20,21 direct human action from walking,22 or in-body motion such as chest and heart movement to power pacemakers23 and orthopaedic implants.22 Many of these sources are also used for large scale power generation e.g. wind power, but energy harvesting technologies are mainly focussed on very small scale power generation at the point of use, typically to power small electronic devices where mains or battery power does not provide a viable or convenient solution.In general there are two main ways of extracting energy from a mechanical source, described in this review as ‘inertial’ and ‘kinematic’.
Inertial energy harvesting relies on the resistance to acceleration of a mass. This creates a force in a mass-spring system when the source (the base) is moved. These systems are widely used for vibration harvesting and are connected to the base at a single point. When the base moves a vibration is set up in the mass-spring system, from which electrical energy can be extracted. The amplitude of the vibration is not simply related to the base amplitude since the vibration amplitude of a system at resonance can be significantly larger than the amplitude of the base movement.
Kinematic energy harvesting directly couples the energy harvester to the relative movement of different parts of the source. Examples include harvesting energy from the bending of a tyre wall to monitor type pressure,24 or the flexing and extension of limbs to power mobile communications.25 Kinematic energy harvesting mechanisms do not rely on inertia or resonance. Since the strain in the harvester is directly coupled to a flexing or extension of the source, they are connected at more than one point.
An electro-mechanical energy harvester extracts energy from the motion of a source and converts it to electrical energy that is delivered to a load as shown in Fig. 2.
To best understand the operation of an energy harvester, it is useful to know:
(i) the characteristics of the energy source,
(ii) the way in which energy is transferred from the source to the energy harvester,
(iii) the electromechanical conversion in the energy harvesting transducer,
(iv) how the energy is transferred from the energy harvester to the electrical load.
Losses can be incurred, not just within the energy harvesting transducer,26 but at all stages in this process. It is clear that the effectiveness of the transducer is not the only factor, and that performance can be dominated by losses in the transfer of energy across these system boundaries.
For vibration energy harvesting, the simplest vibration source is a single frequency sinusoid which is characterised by its frequency and amplitude. The amplitude is most commonly defined by the acceleration, but could equally be defined by the velocity or the displacement as these are simply related through the frequency:
There are numerous technologies for using motion to generate electrical power. Electromagnetic generators are a well-established means of converting mechanical to electrical energy and have been deployed successfully for vibration energy harvesting.1 These technologies use established manufacturing and engineering methods and are effective both in terms of cost and performance at sizes from a few cm3 upwards. However, performance and manufacturability decline rapidly at smaller length scales, so the technology is generally unsuitable for small scale energy harvesting applications (<1 cm3 or less). Piezoelectric materials provide solid state conversion between electrical and mechanical energy and can be manufactured at small scales and integrated into micro-scale devices or even electronic circuits. Power density for piezoelectric transduction exceeds that for electromagnetic generators below around 0.5 cm3.30
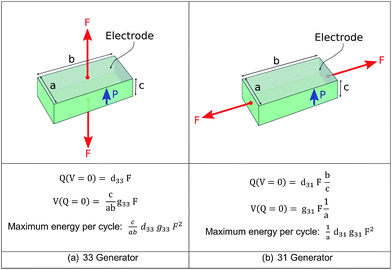
A piezoelectric material undergoes a change in electrical polarisation when a mechanical stress is applied. This can induce an electrical current in an external circuit and therefore be used as an electromechanical generator. To produce electrical energy the piezoelectric material must be able to generate both charge and voltage. Most piezoelectric materials of technological importance for energy harvesting possess a well-defined polar axis, and the energy harvesting performance depends on the direction of the applied strain relative to this polar axis. In a piezoelectric ceramic or ferroelectric polymer the polar axis is the poling direction, whilst for non-ferroelectric crystalline materials such as zinc oxide (ZnO) or aluminium nitride (AlN) this is defined by the crystal orientation. In these cases, the polar axis is referred to as the ‘3’ direction. By symmetry all directions in the plane at right angles to the polar axis are equivalent and are referred to as the ‘1’ direction; this is typical for most ceramic piezoelectrics. A stress can be applied either in the direction of the polar axis, or at right angles to it, resulting in two configurations commonly used for piezoelectric generators, termed ‘33’ and ‘31’ in Fig. 3. Other configurations are possible, and the situation is more complex for materials with lower symmetry, but these two configurations cover most situations of practical piezoelectric energy harvesters.
The energy harvesting performance is directly related to the piezoelectric coefficients, but the applied stress or strain is also an important factor. This is why the coupling between the mechanical source and the piezoelectric material is a critical factor in determining the energy harvesting performance. The energy output also depends on the ability of the piezoelectric material to sustain an applied force or to repeatedly undergo a recoverable strain. It is particularly important for kinematic energy harvesters; it is these limits in the strength and elasticity of the materials that may be the dominant factors in energy harvesting performance rather than just the piezoelectric coefficients.
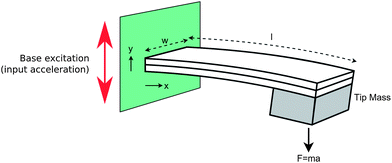
Piezoelectric vibration harvesters exploit the same piezoelectric properties, but the strain in the piezoelectric material is created by the inertia of a suspended mass undergoing acceleration, rather than being directly deformed by the source. Again, there are many ways of achieving this coupling, but perhaps one of the most common is the piezoelectric cantilever (Fig. 4).
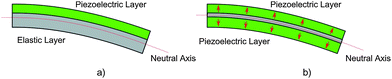
The cantilever is clamped at one end (the root) to the vibration source. A mass is fixed to the other end. When the base accelerates, the inertia of the tip mass bends the cantilever. Simple bending a piezoelectric element creates equal and opposite strains on the inside and outside of the bend. These cancel, so no net current is generated. To be effective as a generator it is necessary to move the piezoelectric layer away from the neutral axis. This is usually accomplished either by fixing the piezoelectric material to a non-piezoelectric elastic layer, or by joining two piezoelectric layers poled in opposite directions. These are referred to as unimorph of bimorph configurations as shown in Fig. 5.
These devices are usually operated at or close to resonance, where the amplitude of the tip oscillation is only limited by the losses from the mechanical system resulting from the energy harvested as well as internal and external losses due to friction, internal electrical losses and air damping. This means that the most effective energy harvester does not necessarily employ the material with the highest piezoelectric coefficients. Lead zirconate titanate (PZT) ceramic is one of the most widely used piezoelectric materials and is obtainable in a range of compositions from “hard” materials which have low losses but small piezoelectric coupling, through to “soft” materials with much higher piezoelectric coupling, but also much higher losses (Table 1 shows some data for these materials). Some studies have shown that the hard materials with much smaller piezoelectric coefficients can produce larger power output than soft materials.31 However, this depends on the magnitude of the electrical power harvested compared to other sources of loss i.e. the efficiency, and for many systems non-harvested losses dominate. In this case a strong coupling would be most effective. This demonstrates the importance of efficiency, not only in controlling the loading of the source, but also in optimising power output and material selection. Piezoelectric energy harvesters do not operate under the same thermodynamic constraints as thermal converters and, in theory, the efficiency of conversion could reach 100%.32 In practice the losses are usually significantly bigger than the energy converted, and efficiencies of 20% are more typical.33 In some cases the mechanical source is not an infinite supply, and the harvesting of energy damps the vibration producing it. In these cases, one can only hope to extract at most the power available from the source and this is best done with a high efficiency, low loss harvester.
| Material | GaN | AlN | CdS | ZnO | α-quartz | BaTiO3 | PZT-4 ‘hard PZT’ | PZT-5H ‘soft PZT’ | PMN–PT | LiNbO3 | PVDF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Piezoelectric | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Pyroelectric | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Ferroelectric | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Const. strain rel. perm. (εs33) | 11.2 (ref. 188) | 10.0 (ref. 189) | 9.53 (ref. 190) | 8.84 (ref. 191) | 4.63 (ref. 192) | 910 (ref. 193) | 635 (ref. 193) | 1470 (ref. 193) | 680 (ref. 194) | 27.9 (ref. 195) | 5–13 (ref. 196) |
| Const. stress rel. perm. (εT33) | — | 11.9 (ref. 197) | 10.33 (ref. 190) | 11.0 (ref. 191) | 4.63 (ref. 192) | 1200 (ref. 193) | 1300 (ref. 193) | 3400 (ref. 193) | 8200 (ref. 194) | 28.7 (ref. 195) | 7.6 (ref. 198) |
| d 33 pC N−1 | 3.7 (ref. 199), 13.2 (NW)51 | 5 (ref. 199) | 10.3 (ref. 190) | 12.4 (ref. 200) 14.3–26.7 (nanobelt)50 | d 11 = −2.3 (ref. 192) | 149 (ref. 193) | 289 (ref. 193) | 593 (ref. 193) | 2820 (ref. 194) | 6 (ref. 195) | −33 (ref. 198) |
| d 31 pC N−1 | −1.9 (ref. 199) −9.4 (NW)51 | −2 (ref. 199) | −5.18 (ref. 190) | −5.0 (ref. 200) | — | −58 (ref. 193) | −123 (ref. 193) | −274 (ref. 193) | −1330 (ref. 194) | −1.0 (ref. 195) | 21 (ref. 198) |
| d 15 pC N−1 | 3.1 (ref. 201) | 3.6 (ref. 201) | −13.98 (ref. 190) | −8.3 (ref. 200) | d 14 = 0.67 (ref. 192) | 242 (ref. 193) | 495 (ref. 193) | 741 (ref. 193) | 146 (ref. 194) | 69 (ref. 202) | −27 (ref. 198) |
| Mechanical quality (Qm) | 2800 (ref. 203) (NW) | 2490 (ref. 204) | ∼1000 (ref. 205) (NW) | 1770 (ref. 204) | 105–106 (ref. 202) | 400 (ref. 193) | 500 (ref. 193) | 65 (ref. 193) | 43–2050 (ref. 204 and 206) | 104 (ref. 207) | 3–10 (ref. 208) |
| Electro-mechanical coupling (k33) | — | 0.23 (ref. 204) | 0.26 (ref. 190) | 0.48 (ref. 200) | 0.1 (ref. 209) | 0.49 (ref. 210) | 0.7 (ref. 211) | 0.75 (ref. 211) | 0.94 (ref. 194) | 0.23 (ref. 202) | 0.19 (ref. 209) |
| Pyro. coeff. -p (μC m−2 K−1) | 4.8 (ref. 212) | 6–8 (ref. 213) | 4 (ref. 161) | 9.4 (ref. 161) | — | 200 (ref. 161) | 260 (ref. 161) –533 (ref. 157) (PZT) | 260 (ref. 161) –533 (ref. 157) (PZT) | 1790 (ref. 214) | 83 (ref. 161) | 33 (ref. 157) |
| sE11 (pPa−1) | 3.326 (ref. 215) | 2.854 (ref. 215) | 20.69 (ref. 216) | 7.86 (ref. 216) | 12.77 (ref. 192) | 8.6 (ref. 193) | 12.3 (ref. 193) | 16.4 (ref. 193) | 69.0 (ref. 194) | 5.83 (ref. 195) | 365 (ref. 198) |
| sE33 (pPa−1) | 2.915 (ref. 215) | 2.824 (ref. 215) | 16.97 (ref. 216) | 6.94 (ref. 216) | 9.73 (ref. 192) | 9.1 (ref. 193) | 15.5 (ref. 193) | 20.8 (ref. 193) | 119.6 (ref. 194) | 5.02 (ref. 195) | 472 (ref. 198) |
Loss mechanisms can be quite subtle. Air friction and losses associated with the clamping arrangements can be significant. Internal losses due to ferroelastic hysteresis and inelastic behaviour at joints and interfaces can also contribute. Electrical losses can occur internally even before any energy is transferred to the load. These are due to capacitive loading of regions of the piezoelectric element that are not being strained significantly; charge flows from the high strain regions to the low strain regions resulting in loss. The tip of the cantilever is only subjected to a small strain, so concentrating the piezoelectric material towards the root provides the most effective use of material. A recent study showed that for a rectangular cantilever, a piezoelectric coverage of exactly 2/3 of the beam area produced the maximum power output.26 Positioning the piezoelectric material under the clamp can also significantly increase losses. It should therefore be avoided, although thinning of the structure at the root can reduce stiffness and cause the maximum strain to be developed away from the piezoelectric region and thus reducing overall effectiveness. Optimisation methodologies can be used to maximise harvester performance and will be discussed later in the review.
Since the maximum oscillation amplitude in a resonant device is determined by the losses, an efficient device could produce very large amplitude oscillations resulting in damage to the device. This means that a practical constraint of the power output of a resonant energy harvester may well be determined by material strength and reliability considerations rather than piezoelectric coefficients.
One of the main limitations of a resonant harvester is that the power output decreases rapidly away from the resonant frequency.34 This means that they are only effective in a situation where there is a large component of vibration amplitude at or near to the resonant frequency. To overcome this limitation a number of strategies have been pursued to increase the bandwidth35,36 including tuneable resonators, multi-frequency arrays, and non-linear oscillators. Non-linearity is often introduced by engineering two stable states (bistability). Above a specific amplitude the system can switch between the two states in a highly non-linear, non-resonant and chaotic manner. This lack of a well-defined resonant frequency means that the device is effective across a wider frequency range. A recent study of the use of a non-linear piezoelectric harvester to power a heart pacemaker37 showed that the device was effective from 7 beats per minute to 700 beats per minute. The pacemaker harvester used opposing permanent magnets to create the bistability. Recent reviews on bistable harvesting38,39 have classified the potential methods to induce bistability, such as employing magnetic attraction or repulsion on cantilever structures and imparting mechanical bistability into a piezoelectric structure, for example by engineering asymmetric composite laminates supporting the piezoelectric,40 as in Fig. 6.
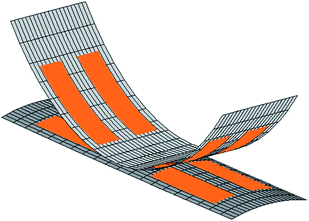 | ||
| Fig. 6 Two stable states of a bistable [0P/0/90/90P]T laminate.40 Orange regions are locations of piezoelectric material. Reprinted with permission from.40 Copyright [2012], American Institute of Physics. | ||
It was stated earlier that an important advantage of piezoelectric materials for energy harvesting was in their scalability to small device size. Integrating the piezoelectric element with silicon electronics using MEMS (Micro-Electro-Mechanical System) fabrication methods offers the promise of low cost high volume self-powered electronic devices and much work has gone into developing devices and processes to make this possible.30 High performance piezoelectric materials such as PZT can present problems with regard to process compatibility, but significant progress has been made in integrating CMOS compatible materials such as AlN. Although the piezoelectric coefficients of AlN are lower than those of PZT (see Table 1), Elfrink et al.41 demonstrated that the piezoelectric coupling compared more favourably due to its low dielectric constant and it is also a lead free alternative.42 Microgen recently announced that they would begin commercial scale production of AlN based piezoelectric MEMS energy harvesters in 2013.43 Effective micro-scale development requires measurement techniques for measuring piezoelectric performance at the scale of interest, so recent work has developed MEMS metrology devices to measure piezoelectric performance at the micro-scale, potentially in situ or in production.44
As well as efforts to develop small scale piezoelectric harvesters, there is also strong research interest in developing nanostructured materials to provide novel energy harvesting devices and routes to production.5,9 Zinc oxide is a piezoelectric material that can be grown as nanorods on a large scale and significant improvements in energy harvesting performance have been reported.6,12,45,46 Power densities in the region of 0.2 W cm−3 have been reported47 based on measurements of peak short circuit current and open circuit voltage for an impulsive mechanical excitation. Recent work on measurement techniques for nano-generators has shown that, in common with the inertial vibration harvesters described above, the output power is dependent on the electrical load, and that the power delivered to the load, averaged over multiple loading cycles, will be smaller than the instantaneous peak power48 and dependent on the source of excitation. The ability to produce a material that is both functional and manufactured through low cost and energy efficient processes is valuable when considering the development of a new energy harvesting system. When compared with a number of materials such as PZT there are clear environmental benefits. However, since ZnO is non-ferroelectric its piezoelectric coefficients (d33, d31, d15), like AlN and gallium nitride (GaN), are relatively small in comparison with PZT (see Table 1). Computational investigation of size effects in ZnO nanowires have shown that piezoelectric properties may be enhanced as the diameter of the nanorods is reduced below around 1.5 nm,49 although current growth methods produce nanorods with diameters in the range 10–100 nm.50 Experiments have also shown a possible increase the piezoelectric effect in GaN nanowires compared to bulk51 while nano-scale ferroelectrics have been recently reviewed by Varghese et al.52
The operation of piezoelectric materials to enhance energy conversion from a variety of natural sources relies on the development of the piezoelectric potential through strain in the material. As piezoelectrics, and indeed ferroelectrics, can be treated as semi-conductors that can sustain a crystal dipole there is an intimate relationship between the semi-conductor properties of the material and any device behaviour resulting from a strain. This relationship has long been understood for piezoelectric materials with early reports correctly identifying barrier height changes in III–V structures53 and strain induced piezoelectric effects in GaN optoelectronic devices.54 These reports have led to a variety of devices being produced that exploit these relationships for a range of piezoelectric materials. The development of such devices has rapidly come to maturity and there are now a large number of applications where the piezoelectric, or ferroelectric nature, of a device is harnessed to generate energy under a controlled environment.48 There is also now growing evidence that ferroelectric materials, such as BaTiO3, LiNbO3 and PbZrxTi1−xO3 are true semi-conductors. For example, undoped PZT is a wide band gap semiconductor with a band gap of between 2.6 eV and 3.5 eV.55 The material also exhibits p type conductivity due to the presence of low valence impurities substituting for higher valence Pb ions. This causes A-site (Pb ion) vacancies to act as electron acceptors, leading to the production of holes.56 The behaviour is modified due to the non-centrosymmetric crystal structure and that this can be used to enhance a number of interesting device and materials performance parameters, such as photo-voltaic performance or photochemical yield.
2.1. High-temperature harvesting
A considerable amount of research has concentrated on vibration harvesting at ambient temperatures since one motivation is to power low-power electronic devices and wireless systems. However there are a number of applications, such as power, transport or oil/gas/space exploration, where there is a need to operate at higher temperatures. As an example, temperatures up to 600 °C are widely encountered in engines of different types and industrial processes.In terms of the piezoelectric material for high temperature energy harvesting many ferroelectric materials are characterised by a Curie temperature below 600 °C. For example, PZT based ferroelectrics have a Curie temperatures below 400 °C and gradual reduction in power with temperature up to 150 °C has been reported for soft PZT harvesters.57 Comyn et al.58 have recently processed bismuth ferrite based polycrystalline ceramics with Curie temperatures up to 650 °C and bismuth titanate, another ferroelectric, has been shown to be stable up to 500 °C and has been considered as a potential material for use at the ambient temperature of Venus (460 °C).59
In addition to ferroelectrics, wide band gap materials with wurtzite structures are of interest. GaN is a potential piezoelectric material that exhibits the semiconductor and piezoelectric properties that is advantageous for the realization of high temperature harvesting. While the piezoelectric coefficients are not as high as ferroelectrics (compare GaN with the PZTs in Table 1), GaN nanowires have demonstrated high piezoelectric coefficients51 and piezoelectric sensors based on GaN have been reported.60 For interest, piezoelectric data for nanowires (NW) have been included in Table 1 for comparison with the bulk material. Due to their wide band gap, these materials are expected to operate in a broad temperature range and retain low conductivity, and being semiconductor has the potential to integrate with device electronics associated with the energy harvester. In terms of device electronics, the relatively narrow band gap of silicon results in device functionality being degraded at ∼350 to 400 °C as the intrinsic densities of electrons and holes become significant compared with doping densities. The use of wide band gap materials, such as GaN or silicon carbide (SiC), is one possible solution for harvesting in hostile environments.61
Another potential high temperature material is AlN which, like GaN, has a wurtzite structure and does not exhibit a phase transition on heating and has a melting point of 2000 °C62 and c-axis orientated thin films of AlN have been used in high temperature transducers.63 Piezoelectric activity in AlN has been reported at temperatures as high as 1150 °C and the material also has low electrical conductivity owing to its large band gap. AlN can be used at low oxygen partial pressures, an advantage if the transducer must operate under reducing conditions to prevent oxidation of packaging.
Lithium niobate (LiNbO3) is another option for high temperature piezoelectric actuation and has been considered for high temperature actuation and sensing in harsh environments for applications such as ultrasonic drills, corers, and rock abrasion tools.64 Under shear conditions LiNbO3 possesses relatively large piezoelectric (see d15 in Table 1) and electro-mechanical coupling coefficients, a pre-requisite for efficient energy conversion, and a very high Curie temperature of 1142–1210 °C.65,66 By using high purity LiNbO3 single crystal materials transducers operating at temperatures up to 1000 °C have been reported with no significant oxygen loss or resistance change over 600 °C,15,65 but there is less work on energy harvesting using this material.67 Bedekar et al.68 have shown that yttrium calcium oxyborate YCa4O(BO3)3 and lanthanum gallium silicate La3Ga5SiO14 exhibit stable piezoelectric and dielectric properties up to 1000 °C. Gadolinium calcium oxyborate piezoelectric single crystals have also been considered for ultra-high temperature (>1000 °C) applications.69 Zhang et al.70 have provided an excellent overview of piezoelectric sensor materials for high temperatures which provides potential new insights for high temperature vibration harvesting. While there is evidence of research on using piezoelectric materials for high temperature transducers, such as sensors, there is less work specifically on harvesting and the associated circuits and storage challenges under extreme conditions.
2.2. Compliant piezoelectrics
Many of the materials described above (e.g. PZT, GaN, ZnO, LiNbO3) are inorganic and are inherently hard, high stiffness and brittle with the potential to fracture at low tensile strains.71 Polymeric materials that exhibit piezoelectric behaviour are of interest for harvesting due to their flexibility, toughness, low density, biocompatibility and low-cost. Example applications include wearable or implanted devices72 where the material is subjected to bending or stretching by limb motion or lung and cavity expansion during respiration.11 The most common piezoelectric polymer is polyvinylidene difluoride (PVDF) whose piezoelectric behaviour originates from orientated molecular dipoles which are formed by a combination of mechanical deformation and electrical poling of β-phase PVDF.71 The material has a failure strain of 2% or higher;11 however the material has relatively low piezoelectric and electro-mechanical coupling coefficients compared to many of the inorganic piezoelectrics (see Table 1). Example applications include harvesting footsteps (using foils),73 respiration (using microbelts),74 rainfall and wind.75 As with the inorganic materials, methods of manufacturing PVDF at the nanoscale have been developed by employing electro-spinning using a needle11 or disc71 to form nano-fibre webs. The formation of β-phase PVDF for optimum piezoelectric properties can be promoted since the electrospinning process can be undertaken under high electric field and mechanical stress.Ferroelectret polymers have been explored for vibration harvesting to a lesser extent. In this case their piezoelectric properties originate from internally charged voids.76,77 Their potential advantage over PVDF are the higher piezoelectric coefficients (d33 > 200 pC N−1) and greater compliance,78e.g. s11 ∼ 1100 pPa−1;79 although they have low electromechanical coupling coefficients, k33 < 0.1,80 and the output voltage was observed to degrade at lower temperatures compared to PVDF.76 Other attempts to create flexible piezoelectric structures is the use of fine scale ‘wavy’ PZT ribbons on flexible rubber substrates to allow stretching and flexing modes for harvesting biomechanical energy.81,82 In this way the high piezoelectric activity of the PZT material can be exploited, especially when enhanced by operating in a buckling mode. Such piezoelectric ‘nano-ribbons’ have been also used to form a biocompatible interface with cells to act as sensors, with the potential to act a harvester of biomechanical sources.83 Bio-piezoelectric devices have also been considered based on genetically modified bacterial viruses (M13 phages) with an aligned protein coat structure to form the necessary electrical dipole.84
In summary, whilst piezoelectric transducers have been studied for many years both as sensors and actuators, it is only recently that significant attention has been devoted to their use as an energy source. Whilst the fundamental principles of piezoelectric coupling of electrical and mechanical energies are unchanged, there are many complexities associated with their application to energy production that have only recently been addressed. As the technology develops new opportunities will arise for new materials, techniques and innovations. It is crucial that these are supported by strong scientific underpinning of the technology and reliable measurements. As the technology moves towards production scale-up and wider market penetration this knowledge will need to be transferred to industrial standards for device performance and reliability.
3. Optimisation for piezo-based harvesting
Energy harvesting devices are complex multi-physics systems requiring advanced methodologies to maximise their performance. This section reviews the research that optimises this complex system via mathematical programming or population-based optimisation techniques such as the genetic algorithm. By far the most literature to date considered mechanical vibration to electrical energy conversion via piezoelectrics.85,86 Due to simplicity and the existence of the well-understood models, cantilever beams remain to be the favourite system for optimisation although researchers are beginning to optimise two-dimensional plates in the last few years. Design optimisation for such systems comprises of a coupled consideration of three elements. The first is the dynamic response of structures, which is a mature field. The second is the electrical circuit to condition the voltage generated in which there has been active development.87–91 The final element is the coupled electro-mechanics which represents the key step in energy harvesting and poses a challenging multi-physics problem to the optimisation community. Some research has optimised material properties, e.g. optimisation of the microscopic crystallite configuration to maximise the electromechanical coupling in specific ferroelectric materials.92 However, the majority of research has been taken a structural optimisation approach to piezoelectric energy harvesting systems. This section takes a closer look at these research efforts and the methods employed.The most common configurations for optimisation studies are cantilevered beam and plates, examples of which are shown in Fig. 7.
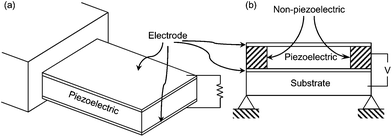 | ||
| Fig. 7 Common piezoelectric energy harvesting configurations: (a) cantilevered beam; (b) cross-section of a plate. | ||
Studies have shown that the lay-out and configuration of the piezoelectric materials can have a significant influence on the energy harvesting performance.93–96 Dietl and Garcia94 used a combination of the constrained pattern search algorithm and gradient search method using MATLAB to optimise the width of a bimorph cantilever beam with a tip mass to maximise the voltage generation over time. The first two modes of vibration were included for the optimisation study and it was found that the optimum beam tapered down from the root then widened again near tip. Other researchers also found higher and more uniform strain areas could be achieved by a trapezoidal tapered beam along the span95 and through-thickness,96 thus increasing the specific output power per unit volume. Similarly, Goldschmidtboeing and Woias97 obtained an optimum configuration for a unimorph cantilever beam of planform geometry that was a triangle for a single excitation mode. Here, they defined the optimum performance metrics to be its efficiency characterised by the output power and the maximum tolerable amplitude, taking into account the stress homogeneity. Interestingly, they found the planform shape to have little impact on the overall efficiency but is highly sensitive to stress which, in turn, influences the tolerable vibration amplitude. This supports Wang's observation that under a static load the planform structure has little influence on the efficiency of the electrical energy conversion, but a trapezoidal cross-section enhances the output voltage.98 In contrast to the linear energy harvester optimisation presented in this review, Betts et al.40 optimised a nonlinear bistable piezo-composite energy harvester, described earlier in this review, using sequential quadratic programming. The design space was highly nonlinear and multimodal however, they were able to consistently find all local and global optima by employing multiple starting solutions.40 As with the above studies, the dimensional parameters of the rectangular plate geometry were optimised to maximise the energy output characterised by the maximum strain. Due to the nonlinear nature of the bistable structure, the strain is large and the power output can be as much as an order of magnitude greater than a linear harvester with an added benefit of harvesting appreciable energy over a broad spectrum of excitation frequencies.99
The investigations of the shape of the structure for energy harvesting have so far been somewhat limited in that the majority of the literature either constructs a simplified analytical model or a reduced order model and then conducts the optimisation analytically or study a small set of geometries. Using linear elasticity, much of the understanding of the optimum energy harvesting performance relates to positioning the piezoelectric material in high strain areas and in these cases the lowest bending mode is usually most beneficial. As such work only considers quadrilateral and triangular geometries, the design space is inherently limited and the understanding of the optimum design and potential of energy harvesting are also limited. Park et al.100 opened up the design space by applying shape optimisation to the beam planform. Since there was limited space in their application domain, they specify a maximum length of the cantilever beam and they allow an arbitrary width variation to maximise the output power, as shown in Fig. 8. The optimum solution is demonstrated to achieve 37% improvement compared with the rectangular planform of the same volume.
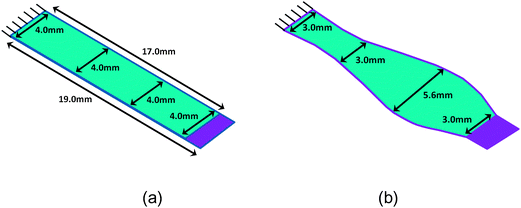 | ||
| Fig. 8 (a) Initial and (b) optimum bimorph beam shape for piezoelectric cantilever beam for maximum power by rotary motion.100 The bimorph is in parallel connection clamped at upper left hand side end of the beam, as in Fig. 7a. Blue is the piezoelectric and purple is the substrate where the tip region is deflected. Length dimensions are fixed. Adapted from ref. 100. | ||
One key feature that researchers consistently agree on is the importance of considering the coupling of the electro-mechanical behaviour of the harvester.101 Research is addressing this complex multi-physics problem by employing stochastic optimisation which does not require an analytical model or gradient sensitivities. Gonsalez et al. combined a genetic algorithm (GA), which is a heuristic search algorithm based on natural selection to evolve a population of potential solutions, with a reduced order model to maximise the power output of a piezo-substrate beam combination. This approach enabled optimisation of the piezoelectric and substrate thickness, mechanical loss factor and electrical impedance.102 Benkhelifa et al. also used a well-established genetic algorithm for multiple objectives, MOGA-II, to maximise the power and voltage outputs whilst minimising the size of a bimorph piezoelectric beam subjected to a single excitation frequency.103 Bourisli and Al-Ajmi optimised a unimorph cantilever beam to maximise the conversion of mechanical to electrical for the first three vibration modes using a GA.104 Their subject of interest was the optimum piezoelectric coverage pattern for different substrate materials: brass, steel and aluminium. The studies revealed that the optimum designs are not influenced by the choice of the substrate materials, and the optimum piezoelectric material locations coincided with the regions of maximum strain for each vibration mode; this agrees with the finding of other researchers', as discussed previously. It is worth at this stage to note the optimisation studies of Hadas et al.;105 although their application domain was electromagnetic vibration energy harvesting, they applied a Self-Organisation Migrating Algorithm (SOMA) which mimics the behaviour of wild animal groups. For their numerical studies of multi-objective optimisation, SOMA was considered superior to GA although they are both able to find the optimum solutions. Gurav et al. studied the maximisation of the power output of MEMS based energy harvesters.106 In order to address the challenges in manufacturing and control of material properties and microstructure, uncertainty-based design optimisation was applied to determine an optimum combination of geometric variables.
Returning to the starting point where the shape has a significant effect on an energy harvester, the approaches so far consider only a small number of geometrical variables and have explored a small design space, mainly studying well-defined geometries such as rectangles and trapezoids. In addition, the complex multi-physics dynamics of energy harvesting is not well understood and an “intuitive” design may not be an optimum. In order to explore a greater design space to include unintuitive designs, researchers have developed topology optimisation for linear energy harvesters. Topology optimisation is a class of structural optimisation that provides the most creative solution independent of the preconceived or initial design. As such it is gaining popularity in many different domains of physics.107 Two categories of approaches have emerged over the past three decades. The traditional elemental approach is to formulate the design problem as a material distribution problem where each small unit or element of material is considered to be a design variable which can take either 1 (material) or 0 (void). The design space therefore becomes the distribution of material and voids, which represents the topology or the general layout solution.108 The most popular methodology in this category of approaches is termed, Solid Isotropic Material with Penalisation or SIMP. The alternative approach is commonly referred to as the Level Set Method which represents the structural boundaries as a set of implicit signed distance functions and the boundaries are moved to minimise the objective function, thus producing the topologically optimum solution.109,110
Topology optimisation has been applied to piezoelectric energy harvesting systems. The more common approach is an extension of SIMP where the key approach is to relax the binary design variables to a continuous variable between 0 and 1 (0 < x ≤ 1) then penalise the infeasible solutions where x ∉ {0, 1} using a power law. Extending this to the piezoelectric problem, the power law is applied to stiffness, piezoelectric and dielectric parameters.111 Researchers found that the choice of the three exponents can lead to different solutions or even non-convergence, thus they need to be carefully selected.112,113 The alternative level set method avoids the challenges associated with using the power law114 and both the ‘31’ and ‘33’ operation modes, shown in Fig. 3, have been considered using this approach.
Chen et al.114 applied the level set method to optimise a cylindrical energy harvester using two materials that operated in −33 mode, Fig. 7. Optimisation for multiple materials was achieved by a ‘Reconciled Level Set’ method.115 Sun and Kim116 also optimised two materials in a magneto-electro-elastic laminate composite. In their study the thickness of each material was optimised using a micro-mechanics based model under a static load. They found that the SIMP-type material interpolation model was unable to converge to a solution with distinct phase states for this complex multi-physics problem. However, by far the more common configurations considered in the topology optimisation literature remain to be simple flat cantilevered beams and plates as in Fig. 9,111–113,117–119 albeit there are variations, e.g. with or without substrates, with or without tip mass. Rupp et al.117 optimised the electrical circuit parameters simultaneously with the general layout, Fig. 10. Their numerical studies showed that the simultaneous optimisation of both structural topology and circuit did not fundamentally change the topological designs, but did influence the optimal resistance of the circuit.
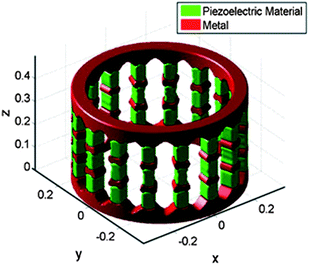 | ||
| Fig. 9 Optimum topology for piezoelectric (green) and metal (red) of a multi-material cylindrical energy harvester operating in −33 mode, as in Fig. 2a, using the level set method.114 Mechanical loads to be harvested are in the z-direction. Reprinted from,114 with permission from Elsevier. | ||
 | ||
| Fig. 10 Optimal distribution of material for a cantilever beam in the (a) piezoelectric layer (red) and (b) mass layer (green).117 Permission granted from Sage Publishing Ltd. | ||
For energy harvesters designed for quasi-static applications or at an excitation frequency much lower than the resonance frequency, the optimisation objective tends to be to maximise the electromechanical coupling coefficient, k, since it represents an efficiency of conversion between mechanical and electrical energies,112,116,118,119,120eqn (1) and (2).
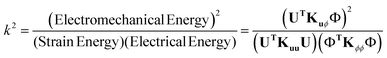 | (1) |
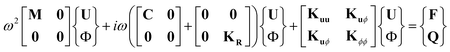 | (2) |
For dynamic applications, the harvested power for the given vibration environment is maximised,117,120–122eqn (3). Wein et al.122 added a stress constraint to their optimisation to control the peak stress in a piezoelectric and substrate composite system using linear elasticity so that the device can sustain an applied force or to repeatedly undergo a recoverable strain. It is interesting to note that Chen et al.114 optimised a dynamic system but used a mean steady-state energy conversion efficiency, η, similar to k, as shown in eqn (4). By manipulating each energy term, they conveniently converted this time domain objective function into a frequency domain and showed that η ≤ k2.
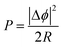 | (3) |
 | (4) |
Most dynamic optimisation studies considered a single frequency environment and the structural layout was optimised to “tune” its resonant modes to the excitation frequency. In a recent advance by Lin et al.,121 they optimised a cantilevered beam energy harvester for broadband random vibration; see Fig. 11 where black represents the material, 1, white is void, 0, and grey is an intermediate density between 0 and 1. When comparing solutions for objective functions (eqn (1)) and (eqn (3)) and indeed, for a broadband environment, it can be seen that their topological designs are fundamentally different. Thus, more research is needed in dynamics and particularly for broadband and random ambient vibration conditions. We also note that there exists very little research beyond the cantilever beam and plate configurations and optimisation of more recently developed harvesters such as piezoelectric nanogenerators would be a fruitful avenue for future research.
 | ||
| Fig. 11 Optimum cantilever beam topology of piezoelectric material under excitation frequencies 10 Hz–400 Hz.121 The beam is configured as in Fig. 7a, clamped on upper left side. Black represents the material is 1 and white is void, 0. Grey is an intermediate density between 0 and 1. Permission granted from Springer. | ||
4. Piezoelectric for light harvesting into chemical or electrical energy
The use of functional materials and specifically ferroelectric or multi-ferroic materials to convert light into chemical or electrical energy has generated broad interest in the last ten years. This follows from the initial research on semiconductor photocatalysis after the discovery that titania (TiO2) photochemical electrodes could split water using ultraviolet light.123 Since this work the photocatalytic oxidation of organic contaminants using TiO2-based semiconductors as a photocatalyst has been extensively investigated. This is due to the excellent photochemical stability, high-efficiency, low cost, and non-toxicity of such semi-conductor materials. However, the photo-efficiency of TiO2 is limited by its restricted absorption in the visible-light region. Only 4% of terrestrial radiation is suitable for the photoexcitation of TiO2124 rendering the process impractical due to the inefficiency of photocatalysis. A number of alternative systems have been investigated to generate systems that are photoactive under visible light stimulation. These include over 50 different semi-conductor systems, so called ‘z-system’ couples, doping and modification of wide band gap materials such as the doping of TiO2 and recently the use of plasmonic nanostructures grown on the surface of the catalyst. Among the new systems that are being investigated include ferroelectric and multi-ferroic materials, such as bismuth ferrite which are both ferroelectric and ferromagnetic. These activities include photocatalysis (light to chemical energy conversion) and photovoltaic (light to electrical energy conversion) devices and applications.A significant benefit of TiO2 is that it is photostable under illumination in aqueous environments. For photostability the band positions of the semiconductor must ‘pinch’ the oxidation–reduction (REDOX) couples of available reactants and products. If the photocatalyst does not do this then it may be liable to photocorrosion.125 This is a well-known problem for many narrow band gap semiconductors such as cadmium telluride (CdTe).
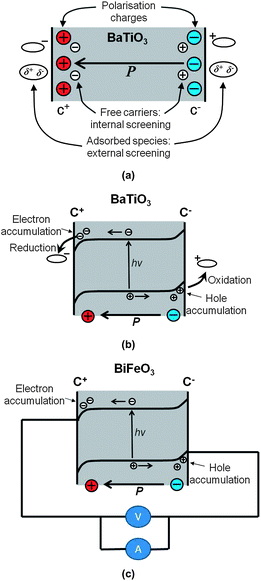
In recent years there has been growing interest in the use of ‘functional’ photocatalysts such as those from the perovskite ABO3 family such as ferroelectric barium titanate (BaTiO3). These materials demonstrate some unique catalytic properties that arise from the non-centrosymmetric nature of their crystal structure. In essence the internal electric field of a ferroelectric exhibits a spontaneous polarisation that acts like an internal p–n junction. We term this a ‘self-junction’ as carriers are influenced by the field within, and inherent to, the material. This, largely, determines the band bending at the interface and the surface where the mobile carriers can accumulate and to a large extent also determines both the photochemistry and the photovoltaic behaviour of the ferroelectric material.
It is typical for a semiconductor to experience movement of free carriers due to differences in local chemical potential that result in band bending when in contact with an ionic solution. In ferroelectric materials the depolarising fields screen the surface charge by drawing electrons to the positive C+ face and holes to the negative C− face126 (Fig. 12a). A further contribution comes from screening due to the externally absorbed charged species. These regions of carrier accumulation induce bending at the surface causing downward bending at the C+ face and upward bending at the C− face. It has been shown that this band bending is sufficiently dominating that it determines the band bending irrespective of the chemical environment around the catalyst such as the solution or the dissolved species. This results in a spatially distinct REDOX chemistry.127,128 Reduction occurs at the C+ face due to electron accumulation and oxidation at the C− face129 (Fig. 12b). The separation of carriers by the depolarisation fields also suppresses recombination rates thereby increasing carrier lifetimes. Evidence for this is provided by the long photo-luminescence of up to 9 μs in ferroelectric LiNbO3.130
These intriguing properties of ferroelectrics have led to growing interest in their photochemistry. Selective deposition of metal nano-particles has been extensively investigated131–137 and a wide range of different materials including PZT, barium titanate and lithium niobate have been used as a catalyst. Ferroelectrics have also been used to drive photocatalytic reactions such as artificial photo synthesis138 and water splitting.139 An investigation of different compositions of BaTiO3 to split water140 showed the reactivity of the materials to increase with strength of polarization. Most perovskite based ferroelectrics rely on a Ti–O tetrahedra arrangement that is shared with TiO2 and therefore have similar band gaps and band positions to TiO2. This means that these systems have a band gap that exceeds 3 eV and so much of the solar spectrum will not induce excited carriers. There are a number of exceptions to this but one material that has gained significant interest is BiFeO3 as this material demonstrates multi-ferroic properties and has a band gap that ranges from 2.2 to 2.7 eV depending on synthetic method. Perovskite – type BiFeO3 (BFO) materials have attracted much interest due to their multiferroic properties exhibited at room temperature.141,142 In particular, BFO thin films have been intensively investigated as novel materials for nonvolatile memory143 and magnetoelectric switching.144 In addition, there is increasing interest in these materials for photocatalytic processes under visible-light illumination.145 There are reports in the literature that BFO can split water146 and is an effective photocatalyst147 but recently there is some doubt regarding the photostability148 of BFO under illumination in an aqueous environment.
The low band gap and the generation of a ‘self-junction’ also make the production of photovoltaic devices149 with a single material possible when using a material such as BFO. Devices of this nature have been demonstrated by a number of groups using multi-ferroic BFO sandwiched between two metal or degenerately conductive semiconductor electrodes. Since the initial discovery a number of groups have been studying these systems including those of Liang150 and Ramesh.151 In these cases the ferroelectric dipole of the BFO effectively separates the photoinduced electrons and holes to drive an external current in the circuit (Fig. 12c). The nature of BFO enables light from the visible part of the spectrum to be absorbed and the anomalous photovoltage152 effect of a ferroelectric material enables a potential that exceeds the band gap to be generated.
5. Pyroelectric based harvesting
The pyroelectric effect is an intriguing possibility for converting heat into electricity. Large amounts of waste heat are lost as a by-product of power, refrigeration, or heat pump cycles153 and in 2009 half of the energy consumed in the United States was wasted in the form of low grade waste heat.154While thermoelectric materials are able to generate electrical power from temperature gradients, pyroelectric materials produce power from temperature fluctuations.155 The pyroelectric effect is exhibited by polar materials due to a temperature dependence of its electrical polarisation2 and will be discussed in more detail later. Pyroelectric materials are of interest due to their high thermodynamic efficiency and, unlike thermoelectrics, they do not require bulky heat sinks to maintain a temperature gradient.156 One of the technical challenges in pyroelectric harvesting systems is to develop methods to generate temperature oscillations to harvest power. Efforts to transform a temperature gradient into a time variable temperature include cyclic pumping.157 The pumping power consumed can be a small fraction (<2%) of the harvested energy,157–159 making the process feasible. Naturally occurring temperature changes to harvest are more rare but examples include changes in ambient temperature, the human body, exhaust gases and natural temperature variations caused by convection and solar energy.2 An additional challenge is that the inherent large thermal mass of materials generally restricts pyroelectric harvesters to low frequency operation (<1 Hz)160 compared to vibration harvesters; although efforts to increase frequency will be described later.
5.1. Origin of the pyroelectric effect
Pyroelectric materials are polar and have a spontaneous polarization Ps in the absence of an applied electric field, where Ps is the average electric dipole moment per unit volume.161 The polarisation leads to a layer of bound charge on each flat surface of the material and free charges (ions or electrons) are attracted to the charged surfaces to form a layer of unbound charge. Pyroelectric behaviour originates from the polarization level being dependent on material temperature. For example, when the material is heated (dT/dt > 0) its polarisation level decreases as dipoles lose their orientation and the level of unbound charges on the material surface decreases;161 this results in an electric current and power generation. Similarly, as the pyroelectric is cooled (dT/dt < 0) the dipoles regain their orientation leading to an increase in the level of polarization, thus reversing the electric current flow. It is worth noting that due to the polar nature of pyroelectrics, they are also piezoelectric, although not all piezoelectrics are pyroelectric (see Fig. 1). In can also be seen in Fig. 1 that ferroelectric materials are a sub-class of pyroelectric materials which have a spontaneous polarization which can be switched (e.g. Ps to -Ps) by reversing the direction of the applied electric field. As can be seen in Table 1, ferroelectric materials generally have both larger pyroelectric, and piezoelectric, coefficients than non-ferroelectrics; however if a ferroelectric is heated beyond the Curie temperature (TCurie) it undergoes a phase transition where the spontaneous polarization and both the pyroelectric and piezoelectric behaviour vanishes. While the loss of piezoelectric properties above the Curie temperature is a disadvantage for vibration harvesters, the phase transition at the Curie temperature has attracted some interest for pyroelectric harvesting since the material has the potential to discharge a large amount of electrical energy if the phase transition occurs under a high applied electric field.162Eqn (5) describes the relationship between charge (Q), generated current (ip), rate of temperature change (dT/dt), surface area of the element (A) and pyroelectric coefficient (p):2
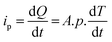 | (5) |
The pyroelectric coefficient is defined by,
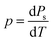 | (6) |
5.2. Direct pyroelectric power (resistive loading)
A simple approach to pyroelectric energy harvesting is to connect the material to a resistive electrical load and subject it to a temperature change. For example, pyroelectric cells fabricated using screen-printed PZT films and commercial polyvinylidene difluoride (PVDF) films were examined as potential pyroelectric power sources for autonomous sensors.163 Pyroelectric currents in the order of 10−7 A and charges in the order of 10−5 C were achieved for temperature changes from 300 K to 360 K in over 100 s, which agreed with a first order electrical model based on a current source and an output impedance.163 Guyomar et al.164 developed a pyroelectric micro-generator comprised of PVDF films that produced 0.32 mW for a 7 K temperature amplitude at 0.2 Hz. A synchronised switch harvesting on inductor (SSHI) was used to improve the effectiveness of energy conversion. Increased power could be produced by increasing the temperature amplitude, frequency and using a material with higher pyroelectric coefficients, such as lead magnesium niobate–lead titanate (PMN–PT) single crystals (see Table 1). Simply increasing amount of material to increase power is not straightforward since it also restricts the ability of the material to follow temperature variations unless it is in thin-film form; this concept relates to the design and manufacture of nano-scale harvesters which are described later. Xie et al.155 examined pyroelectric harvesting using thin devices generating ∼0.2 to 0.3 μW based on PMN–PT, PVDF and PZT-5A with experimental peak power densities of 0.33, 0.20 and 0.12 μW cm−2 respectively. This work again indicated that large area and high pyroelectric coefficients are advantageous. While the power levels are low compared to vibration or thermoelectric harvesters one advantage of this approach is a large range of working temperatures is possible.157 It is also possible to consider to harvesting natural temperature variations; for example Sebald et al.157 measured the temperature fluctuations of a coat fabric as it moved from inside to outside conditions several times per day. Power peaks up to 0.2 mW cm−3 were predicted and a mean power of 1 μW cm−3 was determined within 24 h; again thinner structures than those considered can provide faster temperature variations.5.3. Olsen cycle
In an effort to increase the power generated by pyroelectric harvesting, other approaches have been examined. The aim of the Olsen cycle is to subject the material to two isotherms and two constant electric field lines; this is an electrical analogue of the Ericsson heat engine cycle.165Fig. 13 presents a typical Olsen cycle as an electric displacement versus electric field diagram (D–E diagram). The process can be considered as charging a capacitor to a high electric field at low temperature and then to discharge it by initially heating166 and finally reducing the electrical field to further discharge it. These steps act to effectively reverse the direction of conventional polarisation-field hysteresis loops which convert electrical energy into heat.167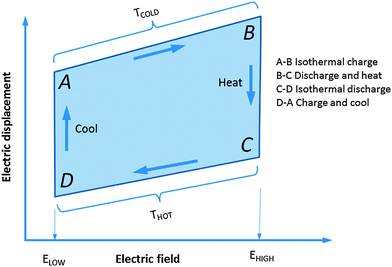 | ||
| Fig. 13 Olsen cycle, adapted from.171 | ||
The area enclosed by the Olsen cycle (also termed Ericsson cycles) in Fig. 13 is the electrical energy produced per unit volume of material per cycle. Process A–B consists of increasing the electric field from ELOW to EHIGH isothermally at a low temperature TCOLD. Process B–C corresponds to heating the material from temperature TCOLD to THOT under a constant electric field EHIGH. Process C–D consists of reducing the electric field from EHIGH to ELOW under isothermal conditions at THOT. Finally, the cycle is closed by cooling the material to TCOLD under constant electric field ELOW. Stirling cycles are also possible, however, it has been shown experimentally that Olsen produce more power than Stirling cycles.168
Successive dipping of a slab of pyroelectric material sandwiched between electrodes into fluid baths at TCOLD at and THOT at the specified electric fields EHIGH to ELOW provides a simple way to perform the Olsen cycle. The energy harvesting capability of [001] oriented 68PbMg1/3Nb2/3O3–32PbTiO3 (PMN–32PT) single crystal was measured by Kandilian et al.166 by successively dipping the material in oil baths at temperatures 80 °C and 170 °C and cycling the electric field between 2 and 9 kV cm−1. This produced an energy density of 100 mJ cm−3 per cycle, corresponding to 4.92 mW cm−3. It was estimated 40% of this energy resulted from the strain polarization due to the rhombohedral to tetragonal phase transition. Sebald et al.169 compared Olsen-based cycles compared to direct (resistive) pyroelectric harvesting and estimated that Ericsson provides one hundred times more energy. For a 0.90Pb(Mg1/3 Nb2/3)O3-0.10PbTiO3 ceramic the harvested energy reached 186 mJ cm−3 for a 50 °C temperature change and field change of 3.5 kV mm−1; based on operating at a frequency of 2 Hz with a 10 °C temperature change a power level of 100 mW cm−3 was considered feasible. In addition to dipping experiments pistons have been used to drive a working fluid repeatedly between a heat source and cold heat exchanger.170
To generate high levels of power from the Olsen cycle the ability to apply large electric fields is advantageous, to maximise EHIGH in Fig. 13, and materials with a high dielectric strength are therefore desirable. While polycrystalline ceramics have a dielectric strength of 3–4 kV mm−1, single crystals can withstand electric fields up to 12–14 kV mm−1, and oriented thin films electric fields up to 60–80 kV mm−1.172 Polymer based PVDF materials are attractive materials because of their low cost, mechanical flexibility (compliance) and have been used at electric fields up to 120 kV mm−1.173 Composite materials are also attracting interest174.
In addition to increasing the maximum applied field, it is also of interest to work near a phase transition where the polarization is strongly influenced by temperature variations.166 This has been examined for a range of ferroelectric materials that exhibit phase transitions such ferroelectric–ferroelectric172 and ferroelectric-to-paraelectric.166 One disadvantage of this approach is that the working temperature range of the harvester is limited to the vicinity of the phase transition in terms of both electric field and temperature,158 unlike the linear (resistive) pyroelectric approach. Recently, Mischenko et al.175 observed a ‘giant’ electrocaloric effect (the converse of the pyroelectric effect) where there is a change in material temperature due to a change in the applied electric field under adiabatic conditions. This was observed in thin films of PbZr0.95T0.05O3 with reported temperature variations of 12 °C under electric fields of 30 kV mm−1 to 78 kV mm−1 at 220 °C.175 The electrocaloric effect of this material was said to be enhanced in the vicinity of a phase transition suggesting that the pyroelectric effect also increases near this transition and a potentially interesting material choice for harvesting applications.
5.4. Nanoscale pyroelectric systems
For pyroelectric harvesters the operating frequency of the device is often small (much less than 1 Hz). For example in fluid based systems the operating frequency is limited by heat transfer between the pyroelectric and the working fluid subject to oscillatory flow between hot and cold sources. The restriction of pyroelectric harvesters to low frequencies limits the power generation capability and using heat transfer at the nanoscale offers one potential solution. Nanoscale radiative heat transfer has been examined by Fang et al.176 who considered radiative heat transfer between a pyroelectric element and hot and cold surfaces since it has a faster response compared to convection. If the surfaces are separated by a distance smaller than a characteristic wavelength (given by Wien's displacement law) the net radiation flux in a vacuum between two surfaces can be increased by several orders of magnitude. A device using 60/40 porous poly(vinylidene fluoride–trifluoroethylene) achieved a 0.2% efficiency and a 0.84 mW cm−2 electrical power output for the cold (273 K) and hot sources (388 K). A pyroelectric plate made from 0.9PMN–PT composite thin films achieved a higher efficiency (1.3%) and a larger power output (6.5 mW cm−2) for a temperature oscillation amplitude of 10 K at a temperature of 343 K at a relatively high frequency of 5 Hz.A simple approach to improve the rate of temperature change and increase the pyroelectric current is to reduce the thickness of the pyroelectric, such as using thin films of material. Yang et al.177 demonstrated a flexible hybrid energy cell for simultaneously harvesting thermal, mechanical, and solar energies. A ZnO based layer was used for harvesting solar energy while a PVDF-based pyroelectric and piezoelectric nanogenerator was built on its bottom surface for harvesting thermal and mechanical energies. A pyroelectric coefficient of ∼44 μC m−2 K−1 was measured. Pyroelectric nanogenerators based on ZnO,178 PZT179 and lead-free KbNO3180 nanowires and thin films have also been examined.
The size of the pyroelectric element has also been used in an attempt to tailor the phase transition temperatures in ferroelectric nanowire structures, enabling the development of systems with a tunable ‘giant’ pyroelectric response.181 It was shown that it is possible to tune the pyroelectric coefficient by changing the nanowire radius and the nature of the surrounding media e.g. template material, gas or gel, since the ferroelectric–ambient interface determines the surface energy properties. While the efficiency of these nanoscale materials for heat power converters was predicted to be relatively low at room temperature it was noted that as the temperature decreased the efficiency tends to the maximal Carnot cycle efficiency, making it suitable for low temperatures, e.g. outer space applications.
5.5. Novel pyroelectric systems
This final pyroelectric section considers some non-conventional and interesting approaches to pyroelectric harvesting. Since all pyroelectric materials are piezoelectric (Fig. 1) it is surprising there are limited detailed studies examining combined mechanical vibration and thermal harvesting. This has been considered by Yang et al.177 for nanogenerators and Erturun et al.182 examined combined harvesting using a heating lamp directed at a vibrating beam. Both effects were initially investigated independently and then coupled. In some cases the combination of beam vibration with thermal cycling had a negative effect on scavenged energy and this indicates the potential complexities in such an approach unless the system is designed so that both piezoelectric and pyroelectric effects are used to constructively control the degree of unbound charge. Nevertheless the development of ‘piezo-pyro-harvesters’ potentially offers an interesting method of enhancing power.Oak Ridge National Laboratory183 have designed a MEMS based cantilever harvesting system based on a thermally cycled pyroelectric capacitor that acts as a bimorph. The cantilever is placed between two surfaces, one heated by waste heat and the other is a cooler heat sink surface (Fig. 14). Proof masses are located at the tip of the bimorph cantilever to ensure good thermal contact to the hot and cold surfaces. When the bimorph is heated it deforms due to a thermal expansion mismatch between the cantilever layers and this leads to the proof mass contacting the cold surface, making the structure cool and deform in the reverse direction and eventually making contact to the hot surface. This repeated deformation ultimately leads to the cantilever alternately contacting the hot and cold surfaces at the resonant frequency of the cantilever to generate a pyroelectric current. The MEMS approach employed to fabricate the device means that large arrays of devices (106) could be used to increase power and this interesting approach allows the device to potentially operate at high frequencies, up to 20 Hz or higher.184,185
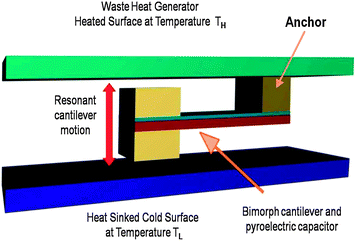 | ||
| Fig. 14 Pyroelectric energy harvester consisting of a bimaterial cantilever which alternately contacts hot and cold surfaces and generates a current in the pyroelectric capacitor.184 Permission granted from SPIE and S.R. Hunter. | ||
Another approach to increase operating frequency uses liquid-based switchable thermal interfaces to convert a spatial temperature gradient into temporal temperature oscillations.156 In this work a plate containing a pyroelectric material is oscillated up and down between a high temperature source and a cold heat sink and repeatedly makes thermal contact to undergo temperature oscillations. In the thermally conducting state, the pyroelectric is pressed against the hot or cold surface using a linear actuator and liquid droplets at the interface deform to make them merge into a continuous thin liquid layer of low thermal resistance. In the non-thermally conducting state, the pyroelectric material is physically separated from the hot and cold surfaces and the liquid on the pyroelectric interface exists as discrete droplets. By creating a hydrophilic pattern of the surfaces the rupture distance was reduced, thus reducing the distance required and increasing the potential operating frequency. A device was demonstrated at frequencies of the order of 1 Hz with a power density of 113 mW cm−3.
As discussed above a temperature change alters the degree of polarisation, leading to an electric current; this is termed the primary pyroelectric effect and is relevant to perfectly clamped materials under constant strain.161 In many cases a secondary pyroelectric effect is present since thermal expansion induces a strain that alters the electric displacement via the piezoelectric effect. This secondary contribution can be significant contribution to the overall pyroelectric coefficient and data for a variety of data has been collected in an excellent review of pyroelectric and electrocaloric materials by Li et al.186 Chang et al.187 examined laminate structures with differing thermal expansion and stiffness characteristics to enhance the contribution of the secondary pyroelectric coefficient for energy harvesting. A laminate based PZT and stainless steel showed an improvement in pyroelectric coefficient of 88%. Mane et al.2 observed that the pyroelectric energy harvested by pre-stressed PZT composites was 40% larger than with simple PZT ceramics. Tertiary pyroelectricity is also possible since non-uniform heating generates non-uniform stresses that result in polarization through the piezoelectric effect.161 The secondary and tertiary effects therefore have potential for enhanced thermal harvesting.
6. Conclusions
Energy harvesting remains a topic of intense interest and this review provides a timely overview of the variety of energy harvesting mechanisms employed by piezoelectric and related materials. By far the most common application is mechanical energy harvesting using inertial energy harvesting and kinematic energy. Piezoelectric materials provide solid state conversion between electrical and mechanical energy and can be manufactured at small scales and integrated into micro-scale devices or even electronic circuits. There are a number of potential materials and device configurations and properties and loss mechanism need also be considered, along with the potential scale of the system (cm to nm). One of the main limitations of resonant based devices is that their power output decreases rapidly away from the resonant frequency and non-linearity can be introduced to enable more ‘broadband’ harvesting. As vibration harvesting matures it is likely that they will need to be deployed in more hostile environments and candidate materials for such applications include high Curie temperature ferroelectric and wide-band gap materials such as GaN and AlN; although the associated circuits and storage challenges under extreme conditions must also be met. In applications where a high strain is required more compliant systems based on polymers or composite systems are being considered.The electro-mechanical coupling in piezoelectric based devices and the complex dynamic response harvester devices means that optimisation of the harvesting device remains a complex task. In many cases simplified analytical models or reduced order models are used to optimise analytically or study a small set of geometries. A variety of approaches are however available to maximise performance in terms of efficiency or total power; this can include methods to optimise an ‘initial’ design or topology optimisation which has the potential to develop the creative solution independent of the preconceived or initial design. To date most optimisation studies have concentrated on mechanical energy harvesting, although there is potential to apply these approaches to other systems, such as pyroelectric harvesting or even combined harvesting systems.
Piezoelectrics are finding uses in other harvesting applications, such as ferroelectric or multi-ferroic materials to convert light into chemical or electrical energy. Specific areas of interest include photocatalysis and photovoltaic (light to electrical energy conversion) devices. These ‘functional’ photocatalysts that convert light to chemical energy possess unique catalytic properties due to their non-centrosymmetric crystal structure where the internal electric field of a ferroelectric exhibits a spontaneous polarisation that acts like an internal p–n junction. Band bending at the interface and the surface where the mobile carriers accumulate can results in a spatially distinct REDOX chemistry. Reduction occurs at the C+ face due to electron accumulation and oxidation at the C− face. In photovoltaic applications (light to electrical energy conversion) the ferroelectric dipole can effectively separate the photoinduced electrons and holes to drive an external current in the circuit. Such mechanism offers intriguing possibility for light harvesting in future devices.
The use of pyroelectric harvesting to generate electrical energy from temperature fluctuations is less well studied. Although the efficiencies can be high for some thermal and electric cycles the inherent low frequency of temperature fluctuations limits the amount of power that can be harvested. Resistive loading of the pyroelectric current is relatively simple and can operate in a range of operating environments. Approaches such a employing the Olsen cycle and phase changes can increase the power generated, but tend to require operation within specific temperature and electric field ranges. Operation of pyroelectric harvesters at the nano-scale may offer opportunities for operation at higher frequencies or the creation of materials with improved pyroelectric coefficients. Because pyroelectric materials are also piezoelectric, novel designs that use thermal fluctuations or gradients to generate to mechanical motion or addition of strain to enhance the secondary pyroelectric coefficients are also of interest. Surprisingly little work has attempted to combine both piezoelectric and pyroelectric based harvesting mechanisms.
In summary, piezoelectrics, pyroelectrics and ferroelectric represent important materials for energy harvesting applications not any due to their efficiency, ease of use, scale, integration with electronics but also because of their versatility and the variety of modes that they can be deployed. In addition to new materials and greater understanding of their use in energy harvesting applications it is also crucial that the harvesting community is supported by strong scientific underpinning of the technology and reliable measurements.
Acknowledgements
C. R. Bowen would like to acknowledge funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement no. 320963 on Novel Energy Materials, Engineering Science and Integrated Systems (NEMESIS). P. M. Weaver would like to acknowledge funding through the European Metrology Research Programme (EMRP) Project ENG02 “Metrology for Energy Harvesting” and the UK National Measurement System. The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union.References
- http://www.perpetuum.com/rail/ .
- P. Mane, J. Xie, K. K. Leang and K. Mossi, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58, 10–17 CrossRef PubMed.
- M. J. Guan and W. H. Liao, J. Intell. Mater. Syst. Struct., 2008, 19, 671–680 CrossRef PubMed.
- S. R. Anton, A. Erturk and D. J. Inman, Smart Mater. Struct., 2010, 19, 115021 CrossRef.
- Z. L. Wang and W. Wu, Angew. Chem., 2012, 51, 2–24 CrossRef.
- Z. L. Wang, MRS Bull., 2012, 37, 814–827 CrossRef CAS.
- Z. L. Wang, Adv. Mater., 2012, 24, 4632–4646 CrossRef CAS PubMed.
- Z. L. Wang, R. Yang, J. Zhou, Y. Qin, C. Xu, Y. Hu and S. Xu, Mater. Sci. Eng., R, 2010, 70, 320–329 CrossRef PubMed.
- Z. L. Wang, G. Zhu, Y. Yang, S. Wang and C. Pan, Mater. Today, 2012, 15, 532–543 CrossRef CAS.
- X. Wang, Nano Energy, 2012, 1, 13–24 CrossRef CAS PubMed.
- Y. Qi and M. C. McAlpine, Eng. Environ. Sci., 2010, 3, 1275–1285 RSC.
- Z. L. Wang, Mater. Sci. Eng., R, 2009, 64, 33–71 CrossRef PubMed.
- P. Hiralal, H. Unalan and G. A. J. Amaratunga, Nanotechnology, 2012, 23, 194002 CrossRef PubMed.
- H. B. Radousky and H. Liang, Nanotechnology, 2012, 23, 502001 CrossRef CAS PubMed.
- K. A. Cook-Chennault, N. Thambi and A. M. Sastry, Smart Mater. Struct., 2008, 17, 043001 CrossRef.
- H. S. Kim, J. H. Kim and J. Kim, International Journal of Precision Engineering and Manufacturing, 2011, 12, 1129–1141 CrossRef.
- H. A. Sodano, D. J. Inman and G. Park, Shock and Vibration Digest, 2004, 36, 197–205 CrossRef PubMed.
- A. Nechibvute, A. Chawanda and P. Luhanga, Smart Mater. Res., 2012, 2012, 853481 Search PubMed.
- P. D. Mitcheson, E. M. Yeatman, G. K. Rao, A. S. Holmes and T. C. Green, Proc. IEEE, 2008, 96, 1457–1486 CrossRef.
- C. A. K. Kwuimy, G. Litak, M. Borowiec and C. Nataraj, Appl. Phys. Lett., 2012, 100, 024103 CrossRef.
- J. A. C Dias, C. De Marqui and A. Erturk, Appl. Phys. Lett., 2013, 102, 044101 CrossRef.
- S. P. Beeby, M. J. Tudor and N. M. White, Meas. Sci. Technol., 2006, 17, R175–R195 CrossRef CAS.
- M. A. Karami and D. J. Inman, Appl. Phys. Lett., 2012, 100, 042901 CrossRef.
- D. A. van den Ende, H. Van de Wiel, W. Groen and S. van der Zwaag, Smart Mater. Struct., 2012, 21, 015011 CrossRef.
- J. M. Donelan, Q. Li, V. Naing, J. A. Hoffer, D. J. Weber and A. D. Kuo, Science, 2008, 319, 807–810 CrossRef CAS PubMed.
- M. Stewart, P. M. Weaver and M. Cain, Appl. Phys. Lett., 2012, 100, 073901 CrossRef.
- S. Roundy, P. Wright and J. Rabaey, Computer Communications, 2003, 26, 1131–1144 CrossRef.
- University of Southampton, Next Generation Energy-Harvesting Electronics: Holistic Approach, http://www.holistic.ecs.soton.ac.uk/.
- I. Neri, F. Travasso, R. Mincigrucci, H. Vocca, F. Orfei and L. Gammaitoni, J. Intell. Mater. Syst. Struct., 2012, 23, 2095–2101 CrossRef PubMed.
- S. Kim, S. Priya and I. Kanno, MRS Bull., 2012, 37, 1039–1050 CrossRef CAS.
- A. Erturk and D. J. Inman, Piezoelectric Energy Harvesting, Wiley, 2011, p. 314 Search PubMed.
- M. Umeda, K. Nakamura and S. Ueha, Jpn. J. Appl. Phys., 1996, 35, 3267–3273 CrossRef CAS.
- J. Cho, R. Richards, D. Bahr, C. Richards and M. Anderson, Appl. Phys. Lett., 2006, 89, 104107 CrossRef.
- A. Erturk and D. J. Inman, Smart Mater. Struct., 2009, 18, 025009 CrossRef.
- D. Zhu, M. J. Tudor and S. P. Beeby, Meas. Sci. Technol., 2010, 21, 022001 CrossRef.
- L. Tang, Y. Yang and C. K. Soh, Broadband Vibration Energy Harvesting Techniques Advances in Energy Harvesting Methods, in Advances in Energy Harvesting Methods, Springer, 2013, pp. 17–61 Search PubMed.
- M. A. Karami and D. J. Inman, Appl. Phys. Lett., 2012, 100, 042901 CrossRef.
- R. L. Harne and K. W. Wang, Smart Mater. Struct., 2013, 22, 023001 CrossRef.
- S. P. Pellegrini, N. Tolou, M. Schenk and J. L. Herder, J. Intell. Mater. Syst. Struct., 2013, 24, 1303–1312 CrossRef PubMed.
- D. N. Betts, H. A. Kim, C. R. Bowen and D. J. Inman, Appl. Phys. Lett., 2012, 100, 114104 CrossRef.
- R. Elfrink, T. M. Kamel, M. Goedbloed, S. Matova, D. Hohlfeld, Y. Andel and R. van Schaijk, J. Micromech. Microeng., 2009, 19, 094005 CrossRef.
- R. Andosca, T. Gus McDonald, V. Genoa, S. Rosenberg, J. Keating, C. Benedixen and J. Wu, Sens. Actuators, A, 2012, 178, 76–87 CrossRef CAS PubMed.
- http://www.microgensystems.co/ .
- J. Wooldridge, A. Muniz-Piniella, M. Stewart, T. A. V. Shean, P. M. Weaver and M. G. Cain, J. Micromech. Microeng., 2013, 23, 035028 CrossRef.
- J. Briscoe, M. Stewart, M. Vopson, M. Cain, P. M. Weaver and S. Dunn, Adv. Energy. Mater., 2012, 2, 1261–1268 CrossRef CAS.
- J. Briscoe, E. Bilotti and S. Dunn, Appl. Phys. Lett., 2012, 101, 093902 CrossRef.
- Y. Hu, L. Lin, Y. Zhang and Z. Wang, Adv. Mater., 2012, 24, 110–114 CrossRef CAS PubMed.
- J. Briscoe, N. Jalali, P. Woolliams, M. Stewart, P. M. Weaver, M. Cain and S. Dunn, Energy Environ. Sci., 2013, 6, 3035–3045 CAS.
- R. Agrawal and H. D. Espinosa, Nano Lett., 2011, 11, 786–790 CrossRef CAS PubMed.
- H. D. Espinosa, R. A. Bernal and M. Minary-Jolandan, Adv. Mater., 2012, 24, 4656–4675 CrossRef CAS PubMed.
- M. Minary-Jolandan, R. A. Bernal, I. Kuljanishvili, V. Parpoil and H. D. Espinosa, Nano Lett., 2012, 12, 970–976 CrossRef CAS PubMed.
- J. Varghese, R. W. Whatmore and J. D. Holmes, J. Mater. Chem. C, 2013, 1, 2618–2638 RSC.
- E. T. Yu, X. Z. Dang, P. M. Asbeck, S. S. Lau and G. J. Sullivan, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1999, 17, 1742–1749 CrossRef CAS.
- C. A. Flory and G. Hasnain, IEEE J. Quantum Electron., 2001, 37, 244–253 CrossRef CAS.
- B. Nagaraj, S. Aggarwal, T. Song, T. Sawhney and R. Ramesh, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 16022–16027 CrossRef CAS.
- B. Jaffe, W. Cook and H. Jaffe, Piezoelectric Ceramics, Academic Press, London, 1971 Search PubMed.
- S. Kim, J. Park, H. Ahn, D. Liu and D. Kim, Microelectron. J., 2011, 42, 988–991 CrossRef CAS PubMed.
- T. P. Comyn, S. P. McBride and A. J. Bell, Mater. Lett., 2004, 58, 3844–3846 CrossRef CAS PubMed.
- S. Sherrit, X. Bao, Y. Bar-Cohen, and Z. Chang, Resonance analysis of high-temperature piezoelectric materials for actuation and sensing, in Smart Structures and Materials 2004: Active Materials: Behavior and Mechanics, San Diego, 2004, vol. 5387 Search PubMed.
- E. D. Le Boulbar, M. J. Edwards, S. Vittoz, G. Vanko, K. Brinkfeldt, L. Rufer, P. Johander, T. Lalinský, C. R. Bowen and D. W. E. Allsopp, Sens. Actuators, A, 2013, 194, 247–251 CrossRef CAS PubMed.
- J. M. R. Kudimi, F. Mohd-Yasina and S. Dimitrijev, Proced. Eng., 2012, 47, 1165–1172 CrossRef CAS PubMed.
- D. Damjanovic, Curr. Opin. Solid State Mater. Sci., 1998, 3, 469–473 CrossRef CAS.
- R. Hou, D. Hutson, K. J. Kirk and Y. Q. Fu, J. Appl. Phys., 2012, 111, 074510 CrossRef.
- X. Bao, Y. Bar-Cohen, J. Scott, S. Sherrit, S. Widholm, M. Badescu, T. Shrout and B. Jones, Ultrasonic/sonic drill for high temperature application, in Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, 2010, vol. 7647 Search PubMed.
- A. Baba, C. T. Searfass and B. R. Tittmann, Appl. Phys. Lett., 2010, 97, 232901 CrossRef.
- D. B. Fraser and W. Warner, J. Appl. Phys., 1966, 37, 3853–3854 CrossRef CAS.
- R. W. C. Lewis, D. W. E. Allsopp, P. Shields, A. Šatka, S. Yu, V. Y. Topolov and C. R. Bowen, Ferroelectrics, 2012, 429, 62–68 CrossRef CAS.
- V. Bedekar, J. Oliver, S. Zhang and S. Priya, Jpn. J. Appl. Phys., 2009, 48, 091406 CrossRef.
- S. Zhang, E. Frantz, R. Xia, W. Everson, J. Randi, D. W. Snyder and T. R. Shrout, J. Appl. Phys., 2008, 104, 084103 CrossRef.
- S. Zhang and F. Yu, J. Am. Ceram. Soc., 2011, 94, 3153–3170 CrossRef CAS.
- J. Fang, H. Niu, H. Wang, X. Wang and T. Lin, Energy Environ. Sci, 2013, 6, 2196–2202 CAS.
- J. Chang, M. Dommer, C. Chang and L. Lin, Nano Energy, 2012, 1, 356–371 CrossRef CAS PubMed.
- J. Kymissis, C. Kendall, J. Paradiso and N. Gershenfeld, in Proc. 2nd IEEE Int. Symp. Wearable Computers, Pitsburg, 1998, pp. 132–139 Search PubMed.
- C. Sun, J. Shi, D. J. Bayerl and X. Wang, Energy Environ. Sci., 2011, 4, 4508–4512 CAS.
- D. Vatansever, R. L. Hadimani, T. Shah and E. Siores, Smart Mater. Struct., 2011, 20, 055019 CrossRef.
- I. Patel, E. Siores and T. Shah, Sens. Actuators, A, 2010, 159, 213–218 CrossRef CAS PubMed.
- S. Bauer, R. Gerhard-Multhaupt and G. M. Sessler, Phys. Today, 2004, 57, 37–43 CrossRef CAS.
- S. R. Anton and K. M. Farinholt, Proc. SPIE, 2012, 8341, 83410G CrossRef PubMed.
- A. Mellinger, IEEE Trans. Dielectr. Electr. Insul., 2003, 10, 842–861 CrossRef CAS.
- M. Wegener, E. Tuncer, R. Gerhard-Multhaupt and S. Bauer, Elastic properties and electromechanical coupling factor of inflated polypropylene ferroelectrets, in 2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena, Kansas City, 2006, pp. 752–755 Search PubMed.
- Y. Qi, N. T. Jafferis, K. Lyons, C. M. Lee, H. Ahmad and M. C. McAlpine, Nano Lett., 2010, 10, 524–528 CrossRef CAS PubMed.
- Y. Qi, T. D. Nguyen, B. Lisko, P. K. Purohit and C. M. McAlpine, Nano Lett., 2011, 11, 1331–1336 CrossRef CAS PubMed.
- T. D. Nguyen, N. Deshmukh, J. M. Nagarah, T. Kramer, P. K. Purohit, M. J. Berry and M. C. McAlpine, Nat. Nanotechnol., 2012, 7, 587–593 CrossRef CAS PubMed.
- B. Y. Lee, J. Zhang, C. Zueger, W. J. Chung, S. Y. Yoo, E. Wang, J. Meyer, R. Ramesh and S. W. Lee, Nat. Nanotechnol., 2012, 7, 351–356 CrossRef CAS PubMed.
- P. Glynne-Jones, S. P. Beeby and N. M. White, IEE Proc.: Sci., Meas. Technol., 2001, 148, 68–72 CrossRef.
- T. Sterken, K. Baert, C. VanHoof, R. Puers, G. Borghs and P. Fiorini, Comparative modelling for vibration scavengers, in Proc. IEEE Sensors, Vienna, 2004, pp. 1249–1252 Search PubMed.
- G. K. Ottman, H. F. Hofmann and G. A. Lesieutre, IEEE Transactions on Power Electronics, 2003, 18, 696–703 CrossRef.
- G. A. Lesieutre, G. K. Ottman and H. F. Hofmann, Journal of Sound and Vibration, 2004, 269, 991–1001 CrossRef.
- E. Lefeuvre, A. Badel, C. Richard and D. Guyomar, J. Intell. Mater. Syst. Struct., 2005, 16, 865–876 CrossRef PubMed.
- Y. C. Shu and I. C. Lien, J. Micromech. Microeng., 2006, 16, 2429–2438 CrossRef.
- E. Lefeuvre, A. Badel, C. Richard and D. Guyomar, J. Electroceram., 2007, 19, 349–355 CrossRef.
- K. P. Jayachandran, J. M. Guedes and H. C. Rodrigues, J. Appl. Phys., 2010, 108, 024101 CrossRef.
- M. I. Friswell and A. Sondipon, J. Appl. Phys., 2010, 108, 014901 CrossRef.
- J. M. Dietl and E. Garcia, J. Intell. Mater. Syst. Struct., 2010, 21, 633–646 CrossRef PubMed.
- D. Benasciutti, L. Moro, S. Zelenika and E. Brusa, Microsyst. Technol., 2010, 16, 657–668 CrossRef PubMed.
- S. Paquin and Y. St-Amant, Smart Mater. Struct., 2010, 19, 105020 CrossRef.
- F. Goldschmidtboeing and P. Woias, J. Micromech. Microeng., 2008, 18, 104013 CrossRef.
- L. Wang, Design, fabrication and experimental analysis of piezoelectric energy harvesters with non-traditional geometries, The State University of New Jersey, 2011 Search PubMed.
- A. F. Arrieta, P. Hagedorn, A. Erturk and D. J. Inman, Appl. Phys. Lett., 2010, 97, 104102 CrossRef.
- J. Park, S. Lee and B. M. Kwak, Journal of Mechanical Science and Technology, 2012, 26, 137–143 CrossRef PubMed.
- C. D. Richards, M. J. Anderson, D. F. Bahr and R. F. Richards, J. Micromech. Microeng., 2004, 14, 717–721 CrossRef CAS.
- C. G. Gonsalez, S. B. Shiki, M. J. Brennan, S. da Silva and V. L. Juni, Piezoelectric energy harvesting system optimization, in 2nd International Conference on Engineering Optimization, September 6–9, Lisbon, 2010 Search PubMed.
- E. Benkhelifa, M. Moniri, A. Tiwari and A. G. de Rueda, Evolutionary multi-objective design optimisation of energy harvesting MEMS, in IEEE Congress on Evolutionary Computation (CEC), 5–8 June, Barcelona, 2011 Search PubMed.
- R. I. Bourisli and M. A. Al-Ajmi, J. Intell. Mater. Syst. Struct., 2010, 21, 907–914 CrossRef PubMed.
- Z. Hadas, J. Kurfurst, C. Ondrusek and V. Singule, Microsyst. Technol., 2012, 18, 1003–1014 CrossRef PubMed.
- S. Gurav, A. Kasyap, M. Sheplak, L. Cattafesta, R. Haftka, J. Goosen and F. van Keulen, Uncertainty-based design optimization of a micro piezoelectric composite energy reclamation device, in 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, New York, 2004 Search PubMed.
- M. P. Bendsøe, E. Lund, N. Olhoff and O. Sigmund, Control Cybernet., 2005, 34, 7–35 Search PubMed.
- M. P. Bendsøe and O. Sigmund, Topology Optimization – Theory, Methods and Applications, Springer Verlag, Berlin, 2003 Search PubMed.
- G. Allaire, F. Jouve and A. M. Toader, J. Comput. Phys., 2004, 194, 363–393 CrossRef PubMed.
- P. D. Dunning and H. A. Kim, International Journal for Numerical Methods in Biomedical Engineering, 2013, 93, 118–134 CrossRef.
- P. H. Nakasone and E. C. N. Silva, Proc. of SPIE, 2009, 7286, 728603 CrossRef PubMed.
- J. E. Kim, D. S. Kim and Y. Y. Kim, Computer Methods in Applied Mechanics and Engineering, 2010, 199, 3153–3168 CrossRef PubMed.
- J. Y. Noh and G. H. Yoon, Advances in Engineering Software, 2012, 53, 45–60 CrossRef PubMed.
- S. Chen, S. Gonella, W. Chen and W. K. Liu, Computer Methods in Applied Mechanics and Engineering, 2010, 199, 2532–2543 CrossRef PubMed.
- B. Merriman, J. K. Bence and S. Osher, J. Comput. Phys., 1994, 112, 334–363 CrossRef.
- K. H. Sun and Y. Y. Kim, Smart Mater. Struct., 2010, 19, 055008 CrossRef.
- C. J. Rupp, A. Evgrafov, K. Maute and M. L. Dunn, J. Int. Mater. Sys. Struct., 2009, 20, 1923–1939 CrossRef PubMed.
- F. Wein, E. Weller, T. Albach, A. Sutor and L. Reinhard, Topology optimisation of a piezoelectric energy harvester, in Sensor and Test Conference, Proceeding II C6.1, Nurnberg, 2009 Search PubMed.
- B. Zheng, C. J. Chang and H. C. Gea, Structural and Multidisciplinary Optimization, 2009, 38, 17–23 CrossRef PubMed.
- S. L. Vatanabe, G. H. Paulino and E. C. N. Silva, Composites, Part B, 2012, 43, 2646–2654 CrossRef PubMed.
- Z. Q. Lin, H. C. Gea and S. T. Liu, Acta Mech. Sin., 2011, 27, 730–737 CrossRef PubMed.
- F. Wein, M. Kaltenbacher and M. Stingl, Structural and Multidisciplinary Optimization, 2013, 48, 173–185 CrossRef.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS.
- A. L. Linsebigler, G. Lu and J. T. Yates Jr, Chem. Rev., 1995, 95, 735–758 CrossRef CAS.
- V. Pleskov, Semiconductor Photochemistry, Springer, New York, 1986 Search PubMed.
- J. F. Scott, Ferroelectric memories, Springer, Berlin, 2000 Search PubMed.
- S. Dunn, D. Cullen, E. Abad-Garcia, C. Bertoni, R. Carter, D. Howorth and R. W. Whatmore, Appl. Phys. Lett., 2004, 85, 3537 CrossRef CAS.
- J. Garra, J. M. Vohs and D. A. Bonnell, Surf. Sci., 2009, 603, 1106–1114 CrossRef CAS PubMed.
- J. L. Giocondi and G. S. Rohrer, J. Phys. Chem. B, 2001, 105, 8275–8277 CrossRef CAS.
- A. Harhira, L. Guilbert, P. Bourson and H. Rinnert, Phys. Status Solidi C, 2007, 4, 926–929 CrossRef CAS.
- P. M. Jones and S. Dunn, J. Phys. D: Appl. Phys., 2009, 42, 065408 CrossRef.
- S. Dunn and D. Tiwari, Appl. Phys. Lett., 2008, 93, 092905 CrossRef.
- P. M. Jones, D. E. Gallardo and S. Dunn, Chem. Mater., 2008, 20, 5901–5906 CrossRef CAS.
- S. Dunn, P. M. Jones and D. E. Gallardo, J. Am. Chem. Soc., 2007, 129, 8724–8728 CrossRef CAS PubMed.
- S. Dunn, D. Tiwari, P. M. Jones and D. E. Gallardo, J. Mater. Chem., 2007, 17, 4460–4463 RSC.
- P. M. Jones and S. Dunn, Nanotechnology, 2007, 18, 185702 CrossRef.
- J. L. Giocondi and G. S. Rohrer, MRS Proceedings, 2000, 654, AA7.4.1 CrossRef PubMed.
- J. L. Giocondi and G. S. Rohrer, Chem. Mater., 2001, 13, 241–242 CrossRef CAS.
- K. Saito, K. Kogaa and A. Kudo, Dalton Trans., 2011, 40, 3909–3913 RSC.
- J. Xu, G. Zhang, F. Li, X. Zhang, Q. Sun, S. Liu, F. Song, Y. Kong, X. Chen, H. Qiao, J. Yao and Z. Lijuan, Opt. Lett., 2000, 25, 129–131 CrossRef CAS.
- J. R. Teague, R. Gerson and W. J. James, Solid State Commun., 1970, 8, 1073–1074 CrossRef CAS.
- I. Sosnowskat, T. Peterlin-Neumaier and E. Steichele, J. Phys. C: Solid State Phys., 1982, 15, 4835–4846 CrossRef.
- D. Lebeugle, D. Colson, A. Forget and M. Viret, Appl. Phys. Lett., 2007, 91, 022907 CrossRef.
- S. M. Wu, S. A. Cybart, P. Yu, M. D. Rossell, J. X. Zhang, R. Ramesh and R. C. Dynes, Nat. Mater., 2010, 9, 756–761 CrossRef CAS PubMed.
- F. Gao, X. Chen, K. Yin, S. Dong, Z. Ren, F. Yuan, T. Yu, Z. Zou and J. M. Liu, Adv. Mater., 2007, 19, 2889–2892 CrossRef CAS.
- J. Deng, S. Banerjee, S. K. Mohapatra, Y. R. Smith and M. Misra, Journal of Fundamentals of Renewable Energy and Applications, 2011, 1, R101204 CrossRef.
- Y. Zhang, A. M. Schultz, P. A. Salvador and G. S. Rohrer, J. Mater. Chem., 2011, 21, 4168–4174 RSC.
- C. Hengky, X. Moya, N. D. Mathur and S. Dunn, RSC Adv., 2012, 2, 11843–11849 RSC.
- T. Choi, S. Lee, Y. J. Choi, V. Kiryukhin and S. W. Cheong, Science, 2009, 324, 63–66 CrossRef CAS PubMed.
- W. Ji, K. Yao and Y. C. Liang, Adv. Mater., 2010, 22, 1763–1766 CrossRef CAS PubMed.
- S. Y. Yang, L. W. Martin, S. J. Byrnes, T. E. Conry, S. R. Basu, D. Paran, L. Reichertz, J. Ihlefeld, C. Adamo, A. Melville, Y. H. Chu, C. H. Yang, J. L. Musfeldt, D. G. Schlom, J. W. Ager and R. Ramesh, Appl. Phys. Lett., 2009, 95, 062909 CrossRef.
- S. Y. Yang, J. Seidel, S. J. Byrnes, P. Shafer, C. H. Yang, M. D. Rossell, P. Yu, Y. H. Chu, J. F. Scott, J. W. Ager, L. W. Martin and R. Ramesh, Nat. Nanotechnol., 2010, 5, 143–147 CrossRef CAS PubMed.
- F. Y. Lee, A. Navid and L. Pilon, Appl. Therm. Eng., 2012, 37, 30–37 CrossRef CAS PubMed.
- I. M. McKinley, R. Kandilian and L. Pilon, Smart Mater. Struct., 2012, 21, 035015 CrossRef.
- J. Xie, X. P. Mane, C. W. Green, K. M. Mossi and K. K. Leang, J. Intell. Mater. Syst. Struct., 2010, 21, 243–249 CrossRef CAS PubMed.
- G. Chaa and Y. Jia, High power density pyroelectric energy harvesting incorporating switchable liquid-based thermal interfaces, in IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS), 2012, pp. 1241–1244 Search PubMed.
- G. Sebald, D. Guyomar and A. Agbossu, Smart Mater. Struct., 2009, 18, 125006 CrossRef.
- A. Khodayari, S. Pruvost, G. Sebald, D. Guyomar and S. Mohammadi, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56, 693–698 CrossRef PubMed.
- A. A. Sklar, A numerical investigation of a thermodielectric power generation system, PhD Dissertation Georgia Institute of Technology, 2005 Search PubMed.
- H. Maiwa, Y. Ishizone and W. Sakamoto, Thermal and vibrational energy harvesting using PZT- and BT- based ceramics, in IEEE, Applications of Ferroelectrics, Aviero, 2012, pp. 1–4 Search PubMed.
- S. B. Lang, Phys. Today, 2005, 58, 31–36 CrossRef CAS.
- A. Navid and L. Pilon, Smart Mater. Struct., 2011, 20, 025012 CrossRef.
- A. Cuadras, M. Gasulla and V. Ferrari, Sens. Actuators, A, 2010, 158, 132–139 CrossRef CAS PubMed.
- D. Guyomar, G. Sebald, E. Lefeuvre and A. Khodayari, J. Intell. Mater. Syst. Struct., 2009, 20, 265–271 CrossRef PubMed.
- R. B. Olsen, D. A. Bruno, J. M. Briscoe and E. W. Jacobs, J. Appl. Phys., 1985, 58, 2854–2860 CrossRef CAS.
- R. Kandilian, A. Navid and L. Pilon, Smart Mater. Struct., 2011, 20, 055020 CrossRef.
- R. A. Olsen, J. Energy, 1982, 6, 91–95 CrossRef.
- A. Navid, D. Vanderpool, A. Bah and L. Pilon, Int. J. Heat Mass Transfer, 2010, 53, 4060–4070 CrossRef CAS PubMed.
- G. Sebald, S. Pruvost and D. Guyomar, Smart Mater. Struct., 2008, 17, 015012 CrossRef.
- H. Nguyen, A. Navid and L. Pilon, Appl. Therm. Eng., 2010, 30, 2127–2137 CrossRef CAS PubMed.
- F. Y. Lee, S. Goljahi, I. M. McKinley, C. S. Lynch and L. Pilon, Smart Mater. Struct., 2012, 21, 025021 CrossRef.
- D. Guyomar, S. Pruvost and G. Seblad, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55, 279–285 CrossRef PubMed.
- G. Cha and Y. S. Ju, Smart Mater. Struct., 2012, 21, 022001 CrossRef.
- G. Sebald, E. Lefeuvre and D. Guyomar, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55, 538–551 CrossRef PubMed.
- A. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270–1271 CrossRef CAS PubMed.
- J. Fang, H. Frederich and L. Pilon, J. Heat Transfer, 2010, 132, 092701 CrossRef.
- Y. Yang, H. Zhang, G. Zhu, S. Lee, Z. Lin and Z. L. Wang, ACS Nano, 2013, 7, 785–790 CrossRef CAS PubMed.
- Y. Yang, W. Guo, K. C. Pradel, G. Zhu, Y. Zhou, Y. Zhang, Y. Hu, L. Lin and Z. L. Wang, Nano Lett., 2012, 12, 2833–2838 CrossRef CAS PubMed.
- Y. Yang, S. Wang, Y. Zhang and Z. L. Wang, Nano Lett., 2012, 12, 6408–6413 CrossRef CAS PubMed.
- Y. Yang, J. H. Jung, B. K. Yun, F. Zhang, K. C. Pradel, W. Guo and Z. L. Wang, Adv. Mater., 2012, 24, 5357–5362 CrossRef CAS PubMed.
- A. N. Morozovska, E. A. Eliseev, G. S. Svechnikov and S. V. Kalinin, J. Appl. Phys., 2010, 108, 042009 CrossRef.
- U. Erturun, R. Waxman, C. Green, M. L. Richeson and K. Mossi, Energy scavenging combining piezoelectric and pyroelectric effects, in ASME 2010 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Philadelphia, 2010 Search PubMed.
- Mems based pyroelectric thermal energy harvester US Patent Pub. no. US 20120056504 A1, 2012.
- S. R. Hunter, N. V. Lavrik, T. Bannuru, S. Mostafa, S. Rajic and P. G. Datskos, Proc. SPIE, 2011, 8035, 80350V CrossRef PubMed.
- S. R. Hunter, N. V. Lavrik, S. Mostafa, S. Rajic and P. G. Datskos, Proc. SPIE, 2012, 8377, 83770D CrossRef PubMed.
- X. Li, S. G. Lu, X. Z. Chen, H. Gu, X. Qian and Q. M. Zhang, J. Mater. Chem., 2013, 1, 23–37 CAS.
- H. H. S. Chang and Z. Huang, Smart Mater. Struct., 2010, 19, 065018 CrossRef.
- L. Qin and Q. Wang, J. Appl. Phys., 2010, 107, 114102 CrossRef.
- L. Qin and Q. Wang, J. Appl. Phys., 2010, 108, 104510 CrossRef.
- H. Joffe, D. Berlincourt, H. H. A. Krueger and L. R. Shiozawa, Piezoelectric properties of cadmium sulphide crystals, in 14th Annual Symposium on Frequency Control, Atlantic City, 1960 Search PubMed.
- K. F. Young and H. P. R. Frederikse, J. Phys. Chem. Ref. Data, 1973, 2, 313–409 CrossRef.
- J. Erhart, E. Kittinger and J. Přívratská, Fundamentals of Piezoelectric Sensorics, Springer, New York, 2010 Search PubMed.
- G. Hayward, J. Bennett and R. Hamilton, J. Acoust. Soc. Am., 1995, 98, 2187–2196 CrossRef PubMed.
- R. Zhang, B. Jiang and W. Cao, J. Appl. Phys., 2001, 90, 3471 CrossRef CAS.
- R. S. Weis and T. K. Gaylord, Appl. Phys. A: Mater. Sci. Process., 1985, 37, 191–203 CrossRef.
- K. K. Shung, J. M. Cannata and Q. F. Zhou, J. Electroceram., 2007, 19, 139–145 CrossRef CAS PubMed.
- T. Kamiya, Jpn. J. Appl. Phys., 1996, 35, 4421–4426 CrossRef CAS.
- R. S. Dahiya and M. Valle, Appendix A Fundamentals of piezoelectricity, Springer, 2013 Search PubMed.
- I. L. Guy, S. Muensit and E. M. Goldys, Appl. Phys. Lett., 1999, 75, 4133 CrossRef CAS.
- D. F. Crisler, J. J. Cupal and A. R. Moore, Proc. IEEE, 1968, 56, 225–226 CrossRef CAS.
- S. Muensit, E. M. Goldys and I. L. Guy, Appl. Phys. Lett., 1999, 75, 3965 CrossRef CAS.
- R. C. Turner, P. A. Fuierer, R. E. Newnham and T. R. Shrout, Appl. Acoust., 1994, 41, 299–324 CrossRef.
- C. Y. Nam, P. Jaroenapibal, D. Tham, D. E. Luzzi, S. Evoy and J. E. Fischer, Nano Lett., 2006, 6, 153–158 CrossRef CAS PubMed.
- S. Tadigadapa and K. Mateti, Meas. Sci. Technol., 2009, 20, 092001 CrossRef.
- P. Gao, K. Liu, L. Liu, Z. Wang, Z. Liao, Z. Xu, W. Wang, X. Bai, E. Wang and Y. Li, J. Electron Microsc., 2010, 59, 285–289 CrossRef CAS PubMed.
- K. C. C. Cheng, H. L. W. Chan, C. L. Choy, Q. Yin, H. Luo and Z. Yin, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50, 1177–1183 CrossRef.
- G. Ohlendorf, D. Richter, J. Sauerwald and H. Fritze, Diffusion Fundamentals, 2008, 8, 6.1–6.7 Search PubMed.
- K. Uchino, Introduction to Piezoelectric Actuators and Transducers, Penn State University, 2003 Search PubMed.
- C. R. Hill, J. C. Bamber and G. R. ter Haar, Physical Principles of Medical Ultrasonics, John Wiley & Sons, West Sussex, 2004 Search PubMed.
- K. Hong, H. Xu, H. Konishi and X. Li, J. Phys. Chem. Lett., 2010, 1, 997–1002 CrossRef CAS.
- D. Berlincourt and H. H. A. Krueger, Technical Publication TP-226 Properties of Piezoelectricity Ceramics.
- W. S. Yan, R. Zhang, L. Xie, Q. Xiu, Y. D. Zheng, Z. G. Liu, S. Xu and Z. H. He, Appl. Phys. Lett., 2009, 94, 242111 CrossRef.
- V. Fuflyigin, E. Salley, A. Osinsky and P. Norris, Appl. Phys. Lett., 2000, 77, 3075 CrossRef CAS.
- G. Sebald, E. Lefeuvre and D. Guyomar, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55, 538–551 CrossRef PubMed.
- C. Wood and D. Jena, Polarization effects in semiconductors: From Ab Initio theory to device, Springer-Verlag, New York, 2010 Search PubMed.
- S. A. Wilson, R. P. J. Jourdain, Q. Zhang, R. A. Dorey, C. R. Bowen, M. Willander, Q. U. Waha, S. M. Al-hilli, O. Nur, E. Quandt, C. Johanssong, E. Pagounis, M. Kohl, J. Matovic, B. Samelk, W. van der Wijngaartk, E. W. H. Jager, D. Carlsson, Z. Djinovic and M. Wegener, Mater. Sci. Eng., R, 2007, 56, 1–129 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2014 |