Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Design and cost considerations for practical solar-hydrogen generators†
Claudia A.
Rodriguez‡
,
Miguel A.
Modestino‡
*,
Demetri
Psaltis
and
Christophe
Moser
School of Engineering, École Polytechnique Fédéral de Lausanne (EPFL), Station 17, 1015, Lausanne, Switzerland. E-mail: miguel.modestino@epfl.ch; Tel: +41 21 69 33446
First published on 21st October 2014
Abstract
Solar-hydrogen generation represents a promising alternative to fossil fuels for the large-scale implementation of a clean-fuel transportation infrastructure. A significant amount of research resources has been allocated to the development of photoelectrochemical components (i.e. photovoltaic and water splitting catalysts) that are able to spontaneously split water in the presence of solar irradiation, which has led to major advances in the solar-fuels field. At the same time, only limited attention has been given to understanding the key aspects that drive economically viable solar-fuel generators. This study presents a generalized approach to understand the economic factors behind the design of solar-hydrogen generators composed of photovoltaic components integrated with water electrolyzers. It evaluates the underpinning effects of the material selection for the light absorption and water splitting components on the cost of the generated fuel ($ per Kg of H2). The results presented in this work provide insights into important engineering aspects related to the sizing of devices and the use of light concentration components that, when optimized, can lead to costs below $2.90 per kilogram of hydrogen after compression and distribution. Most significantly, the analysis demonstrates that the cost of hydrogen is defined primarily by the light-absorbing component (up to 97% of the cost) while the material selection for the electrolysis components has, to a large extent, minor effects. The findings presented here can help direct research and development efforts towards the fabrication of deployable solar-hydrogen generators that are cost competitive with commercial energy sources.
Broader contextRecent economic and environmental factors have triggered a strong interest towards the implementation of clean-energy generation technologies such as electricity generation from renewable sources (e.g. solar and wind), whose output is fed into the electrical grid for immediate use. An attractive alternative is the implementation of stand-alone solutions that couple energy capture and storage into the same process, so that renewable energy can be harvested and used as needed. Solar-fuel generators represent a promising technology that can accomplish this task by storing solar energy in the form of energy-rich fuels, such as hydrogen, that can be used at a later stage for either transportation or electricity generation. These generators are based on light-absorbing components that can collect sun-light and generate electrical charges which can subsequently be used for electrochemical fuel production. The analysis presented here explores fundamental aspects of the design of cost-effective solar-hydrogen generators in terms of materials selection and device configurations. It demonstrates that in cost-optimized devices, the light-absorbing component dominates the cost of the generated fuel. Furthermore, this work shows that hydrogen generated from solar sources can be competitive with that obtained from non-renewables, and it points towards design strategies that can significantly aid in the reduction of solar-fuels production costs. |
Introduction
The need for the development of scalable, practical and clean energy capture, generation and storage systems has spurred vast amounts of research in the recent years.1,2 Solar energy is ubiquitous to the clean-energy discussion given its scale (∼120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TW average irradiation at the earth's surface).3 Despite it being the largest energy source of the planet, direct solar-energy utilization only accounts for less than 0.06% of the global electricity generation.4,5 Economic and implementation challenges are the most important causes for the low dissemination of solar-driven energy generation systems. The price of photovoltaic (PV) modules has declined significantly in the past decade (5–7% annually)6 leading to a continued increase in their deployment and grid integration. However this energy is of intermitted nature and adds complexity in balancing the grid load. The challenge of efficiently using intermittent sources of energy has resulted in significant interest towards the development of economically viable and scalable energy storage solutions. Currently, energy storage takes place in its vast majority via pumped-hydroelectrical systems (more than 99% of storage, with a total 127 GW capacity).7,8 Although this solution is economically viable in certain instances, its implementation is constrained by geographical factors and can only serve as a mean of central energy storage with limited usability in the transportation sector. Less wide-spread technologies for energy storage include compressed air, flywheel systems, thermal storage systems and batteries, some of which can be used for both stationary and mobile energy generation.
000 TW average irradiation at the earth's surface).3 Despite it being the largest energy source of the planet, direct solar-energy utilization only accounts for less than 0.06% of the global electricity generation.4,5 Economic and implementation challenges are the most important causes for the low dissemination of solar-driven energy generation systems. The price of photovoltaic (PV) modules has declined significantly in the past decade (5–7% annually)6 leading to a continued increase in their deployment and grid integration. However this energy is of intermitted nature and adds complexity in balancing the grid load. The challenge of efficiently using intermittent sources of energy has resulted in significant interest towards the development of economically viable and scalable energy storage solutions. Currently, energy storage takes place in its vast majority via pumped-hydroelectrical systems (more than 99% of storage, with a total 127 GW capacity).7,8 Although this solution is economically viable in certain instances, its implementation is constrained by geographical factors and can only serve as a mean of central energy storage with limited usability in the transportation sector. Less wide-spread technologies for energy storage include compressed air, flywheel systems, thermal storage systems and batteries, some of which can be used for both stationary and mobile energy generation.
A potential solution for the capture and storage of solar energy is integrated solar-fuel generators (i.e. off-grid). These devices both capture solar energy and convert it in energy rich molecules that can be readily used as fuels for transportation and stationary energy generation.2,9–15 Since the first demonstrations of photoelectrochemical water-splitting in 1970's,16 large amounts of research resources have been devoted to the development of scalable components (light absorbing and catalytic) for solar fuel generating systems.17–24 Additionally, recent studies have started to tackle questions regarding the overall design and operation of such systems.25–31
Even though there has been significant progress in understanding the physical challenges for the fabrication of practical solar-fuel generators, the analysis of the techno-economical implications for their deployment has been limited. These cost implications are extremely important for realizing commercial implementations of solar-fuels technologies. One of the main challenges for the cost estimation of solar-hydrogen systems is the lack of reference demonstrators on which to base calculations. Despite this challenge, several studies in the literature have provided insights in the cost and energy requirements for solar-hydrogen production using designs believed to be promising candidates.32–35 In order to circumvent the limitations posed by the lack of practical systems, the work presented here uses a technology agnostic approach to analyse the importance of component selection (light absorption, catalytic, and separation), sizing of components, and operating parameters. Additionally, a comprehensive sensitivity analysis on systems parameters (both physical and economic factors) is carried out to elucidate their overall impact on the cost of hydrogen produced. This approach allows for a fair comparison between solar-hydrogen generation systems on a cost-based figure of merit ($ per Kg of H2).
Methodology
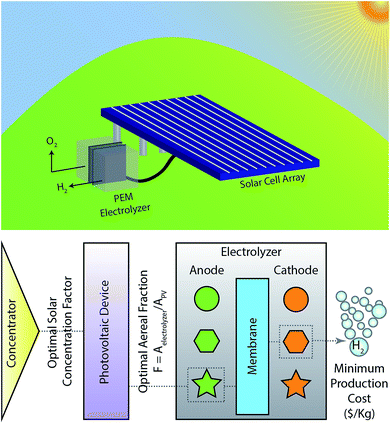
The systems that were studied consisted of photovoltaic (PV) cells electrically coupled with an electrolyzer, with the possibility of a solar concentrator feeding concentrated sunlight to the photovoltaic cell (Fig. 1). The operating conditions for a given PV and electrolyzer were estimated from the current characteristics of each of the components with the purpose of calculating the production rate of hydrogen; the photovoltaic's output curve was obtained from experimental measurements, while the electrolyzer's load curve was modeled following methods from the literature.25–27 In summary, the potential (V) in the electrolyzer is described as.| V = E0 + ηanode + ηcathode + ηohm | (1) |
The PV's output curve was adjusted to behave according to the irradiation of a high radiation zone in Arizona. Average hour irradiance values per month were used to calculate the hourly hydrogen production rate for each of the systems.20 Different material combinations were studied as the electrolyzer's catalysts; these include Platinum, Nickel Molibdenum, and Nickel for the cathodic reaction, and Iridium Oxide, Rutherium Oxide, and Cobalt Oxide (Co2O3) for the anodic reaction.15 Kinetic parameters for these materials were obtained from the literature and are referred in detail in the ESI.† Nafion® membranes were chosen as the material for ionic transport and gas separation. The model developed here assumed a membrane-electrode assembly (MEA) configuration where the catalysts are dispersed in a catalysts layer that is pressed against the membranes.36,37 It is important to point out that some of the earth-abundant catalysts selected in this analysis are only stable under neutral-to-basic conditions, and the use of Nafion membranes will result in a local acidic environment at the catalyst interface. This will result in additional challenges for the implementation of those catalysts (requiring the use of stable alkaline membranes), but the cost analysis presented here was used to provide insights on design constraints.
As the performance of integrated systems varies depending on the PV and the catalytic components chosen, it is necessary to define system design parameters that can be tuned in order to obtain cost-optimum devices. The relative size of the PV and electrolysis components is one of the most important parameters as it defines how efficiently devices can operate (both in terms of cost and performance). For example, for a given size of PV, if the available area for electrolysis increases, the solar-hydrogen efficiency will increase as well, due to the lower electrochemical load in the device. On the other hand, the price of the overall system will increase as larger electrolyzers will need to be installed. Therefore in this study we define a non-dimensional geometric parameter, F, as the ratio between the areas used for electrolysis and that used for light absorption by the PV. As this work focusses in understanding design parameters for cost-effective solar-hydrogen generators, the value of F was optimized in order to minimize the hydrogen production cost in $ per Kg. Evidently, the optimal value of F, changes depending on the photovoltaic and electrolyzer combination selected. Given this, for a selected PV component, a hydrogen price comparison was made for different electrolyzers with all possible combinations from the materials mentioned above.
The cost function (eqn (2)) used to find optimal values for F is based on the levelized cost of hydrogen production (LCHP).
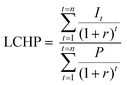 | (2) |
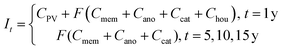 | (3) |
The prices for solar modules and catalysts were obtained from publicly disclosed reports from industry and government agencies,38,39 and they were converted to units of $ per cm2 of PV or MEA component respectively. Membrane and electrolyzer's housing prices were estimated to be similar to those corresponding equivalent components in fuel cells. Importantly, these prices were extracted from mass production cost estimates, which is relevant for solar-fuel generators deployed in large scale.40 Lastly, a life-span (t) of 20 years was assumed for the PV components and 5 years for the MEA components,37 with a yearly discount rate (r) of 2%. Given this, the initial investment in year 1 accounts for the costs of all of the systems components, and in year 5, 10, and 15 additional investment is required for the replacement of the MEAs in the electrolyzer. It is important to point out that the scope of our cost analysis was limited to the simplified device topology described herein. Within this framework only the cost of critical components for solar-hydrogen were accounted for, which allowed for an evaluation of devices with varying components, configurations, and operating conditions. No compression, storage or distribution costs were included in the analysis, as these costs would likely not vary between different material systems. As a reference, previous studies have estimated these latter costs at approximately $2 per kg per kilogram of H2.41 Furthermore, costs associated with the installation, operation, maintenance, and overall management of a large scale H2 production plant were not considered. It is expected that these additional costs can be very significant; as an example in electricity production these costs can exceed for more than 600% the costs associated with the PV device alone.42 Further details regarding the cost function are given in the ESI.†
Lastly, a sensitivity analysis was performed to understand the impact of the variability of the parameters used in the model on the H2 price. A full factorial analysis was carried out using lower and upper bounds for each of the parameters. Results allowed us to identify parameters that had high impact on the price of hydrogen and reduce concerns about the variability of kinetic values in the literature for catalytic materials and photovoltaic prices.
Results and discussion
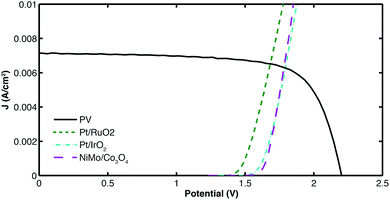
The first design component considered by this study was the electrolyzer material selection. Different material combinations for the electrolyzer were compared based on the cost of hydrogen produced and considering an 11% efficient a-Si/a-Si/μc-Si PV cell fabricated by the Swiss Center for Electronics and Microtechnology (CSEM). Earth-abundant multijunction thin-film silicon cells are promising for solar-fuels generators as their output current–voltage can be readily tuned to achieve a voltage high enough to split water (>1.23 V), and due to their relatively low cost.19,43 The graph in Fig. 2 shows the load curve (dashed) representing current consumption by the electrolyzer to generate hydrogen and the current generation curve (solid) by the PV cell mentioned above as a function of voltage. The operating point of the system occurs at the intersection of the load curve and the PV curve. Three load curves are plotted and correspond to different electrodes material combinations. Each load curve is the result of an optimized value of F (ratio between electrolysis area and PV area) to obtain the lowest H2 production cost for each of them.In order to better understand the effect of F in the production costs, Fig. 3(a) shows the load and PV curves of three systems based on Pt/IrO2 electrolyzers that are designed with different F ratios. In Fig. 3(b) the behaviour of the H2 production cost as a function of F is presented, showing a cost minimum for Fopt = 0.0058. The observed cost behaviour is due to the two factors that determine the levelized cost of hydrogen production (eqn (2)): It (component costs) and P (H2 production rate). Both of these factors increase with F (F = 1 means same area for PV and electrolysis): It will increase due to a larger electrolysis area, and the production rate of hydrogen P is proportional to the operating current which increases with F because of the lower electrolyzer's load (as observed in Fig. 3(a)). As the cost depends on the ratio between It and P, an optimal value of F can be found by balancing these two factors. The effects of F on It and P are clearly shown in Fig. S4 and S5 in the ESI.† Values higher than Fopt will result in more expensive H2 production arising from higher capital costs, while values below Fopt result in higher cost of hydrogen due to lower production.
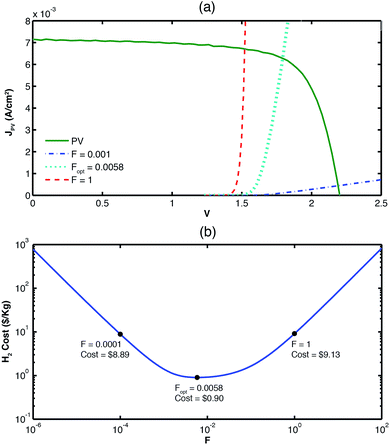 | ||
| Fig. 3 Top graph shows how the operation of the electrolyzer changes with the geometric factor, F. The bottom figure shows how the cost varies as a function of F. | ||
For all the systems studied in this paper, optimal F values tend to be small (≪1) resulting in a high PV cost contribution. This result is due to the fact that PV components under unconcentrated solar irradiation operate at current densities <10 mA cm−2, while MEA based electrolyzers can hold current densities up to several A cm−2 at voltage ranges that correspond to those output by the PV. It is also important to point out that mass transport limitations in the electrolyzer were not considered, and they are expected to be significant when F is small, due to the increased current density through the electrolysis system. As an example, in the case of Pt/IrO2 catalyst combination (Optimal F value = 0.0058), the current density in the electrolyzer is expected to be 1.38 A cm−2. As this value is in the operational limit of commercial electrolyzers,37 the continuing development of robust electrolyzers that can operate at high current densities is of crucial importance for the realization of cost-optimal solar-hydrogen systems. These high current densities are achievable in commercial MEAs based on noble metal catalysts,37 but achieving them with earth-abundant catalyst systems is yet to be demonstrated.
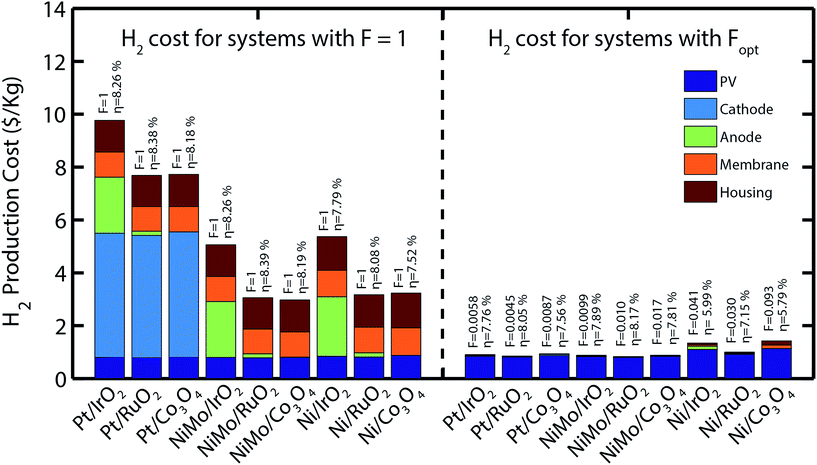
Following the geometrical design optimization described above, the hydrogen production price for every combination of catalysts was calculated. Fig. 4 (left graph) shows the price of H2 for all possible combinations of catalysts with F = 1 (corresponding to the dimensions of solar-fuel generators based on photoelectrodes) and (right graph) an optimized value for F. The cost contribution for each of the components is also displayed. Results show that optimized systems can produce hydrogen as low as $0.90 per kg (Pt/IrO2), which is only $0.54 per kilogram lower than the highest price obtained from a system using (Ni/Co3O4). Furthermore, optimized systems can provide a saving of up to $8.22 per kilogram of hydrogen when compared to the case of F = 1 (Pt/IrO2). It is important to point out that systems with F = 1 show higher sun to hydrogen efficiencies (i.e. more kilograms of hydrogen per Watt of sunlight) than optimized systems, but the additional costs associated with larger electrolysis units impacts significantly the hydrogen production cost. By taking these additional costs into account, the resulting cost of hydrogen is comparable to those reported by other studies.32,34 Given that the largest price contribution for all systems corresponds to the PV component, its price was chosen as one of the most important parameters for the sensitivity analysis. Physical and cost parameters associated with the anode and cathode components were also included in the sensitivity analysis to verify that these components have a low price contribution for hydrogen production.
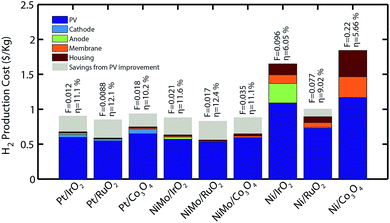
Given the high impact of PV in the hydrogen price, a similar analysis was carried out to understand the impact of efficiency improvement in solar cells. A 16% a-Si/a-Si/μc-Si photovoltaic was modelled based on expected performance improvements in PV manufacturing. Results on Fig. 5 show a price reduction between 11–33% for most systems when using higher efficiency cells. For these systems, F has been optimized for the new PV component, therefore resulting in different electrolyzer sizes. This analysis was also carried for devices operating with series connected crystalline silicon cells (necessary to generate a voltage >1.23 V since the open circuit voltage is limited to ∼0.7 V), and comparable production costs were obtained as presented in the ESI.†
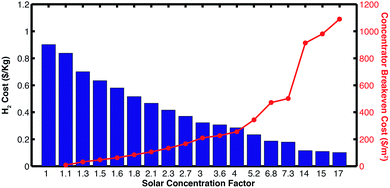
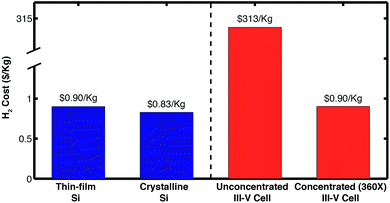
Another viable alternative for reducing the impact in the hydrogen price by the photovoltaic component is to include a solar concentrator in the system. With available data of the PV component under concentration, a price analysis with concentration was carried out for the Pt/IrO2 combination; this material system was selected due to the low impact on the catalyst selection, as demonstrated above, and the commercial availability of PEM electrolyzers that use this catalysts combination. Fig. 6 shows hydrogen's price reduction with the use of solar concentration. The graph also shows the breakeven cost of the solar concentrator and tracking components for solar-hydrogen production. These results suggest that the cost of hydrogen could be reduced to as low as $0.11 per kilogram, allowing the cost of the concentrator to be of up to $1090 per m2 for a concentration factor of 17× (these values are comparable to those from similar concentration cost analysis studies).33 Also, the results show that the contributions from the electrolysis part of the systems become comparable to the ones from the PV components as concentration increases. A similar type of analysis can be performed to select the type of photovoltaic cells that would be most benefited by certain type of concentrators. As an example, high-performing PV systems based on III–V elements can result in further cost savings when light is concentrated above 360 times (Detailed results in the ESI†). Fig. 7 presents a comparison between the hydrogen production cost from different solar-hydrogen generators based on various PV technologies (i.e. thin-film Silicon, crystalline Silicon and III–V cells). The results demonstrate that both thin-film and crystalline Silicon based devices can produce H2 at similar costs, while devices based on high-performing III–V cells are only viable at large solar concentration factors due to their high cost.
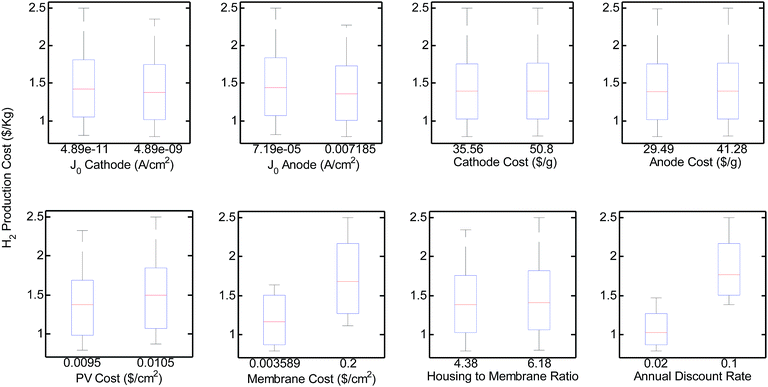
Lastly, results from the sensitivity analysis (presented in Fig. 8) show that the cost of hydrogen production from unconcentrated sunlight is expected to fall between 0.79–2.5$ per kg allowing for reasonable variations in the cost and physical parameters used in the model. Concerns about the accuracy of photovoltaic costs reported by industry are reduced as all systems are equally impacted by this parameter and have limited impact in the conclusions regarding optimal system design. Similarly, concerns about inconsistency in literature of the kinetic values for electrocatalytic materials (i.e. J0 of anode and cathode) are soothed, as they do not significantly impact the price of hydrogen. The price of membranes has a strong impact on the overall production costs. New inexpensive membrane materials or cost reductions from mass production of Nafion can help push the technology towards deployment. Moreover, the uncertainty in the cost of MEA based electrolysis systems can result in significant variations on the H2 production cost. This study based the cost of electrolyzers' peripheral components, herein referred as MEA housing, on large scale production estimates for fuel cells (as a ratio to the membrane cost). Large variations on the MEA housing costs can tilt the cost balance towards the electrolyzer system. As an example, Fig. S9† demonstrates that if the housing cost was 3 orders of magnitude larger than anticipated in this study, the ratio between the H2 production cost associated with the electrolyzer and that associated with the PV could raise to above 0.6. Under these conditions, the electrolyzer costs will start to approach to comparable levels to the cost contribution from the PV component, which will still dominate. Fig. S9† also shows that even under this extreme scenario, the optimal F values and H2 production costs are expected to only experience minor changes. Additionally, the cost of capital, reflected as the discount rate, can have an impact on the overall costs. For the base case of thin-film Si PVs and Pt/IrO2 electrolyzers, varying the discount rate from 2 to 10% can result in an increase in 74% on the H2 production cost. This result reflects the importance of government aid in the deployment and derisking of the technology to assure lower capital costs.
The sensitivity of the optimal F factor on the factors discussed above was also studied. As it can be seen in Fig. S10 in the ESI,† the values of Fopt for the systems can vary by a factor of ∼4, but still the optimal areas for electrolysis in systems without solar concentrators are at least 2 orders magnitude lower than the areas covered by the PV units. These results are a consequence of the fact that all of the optimized systems discussed in this study operate near the maximum power point of the PV.
Conclusions
The results presented in this study provide a general vision on the importance of different design parameters in integrated solar-hydrogen generators. This analysis suggests that a PV-Electrolyzer approach can be commercially viable and compete with other hydrogen production methods (e.g. electrolysis powered from polluting energy sources, steam reforming). Also, the results derived from the analysis provide some clear recommendations for the development of economically viable solar-hydrogen generators:(1) In cost-optimized PV-Electrolysis devices, the light absorption component occupies areas that are significantly larger than the MEA component (>102 larger). This leads to systems where the hydrogen production cost is expected to be dominated by the PV component, and suggests that the viability of solar-fuel systems is tightly bound to their price and performance.
(2) Materials selection for the catalytic components in the electrolysis units does not significantly affect the cost of hydrogen production, and current MEA system that use Pt/IrO2 catalyst can be integrated as viable components.
(3) The implementation of solar-concentrators can provide additional cost savings, if their base capital cost is lower than the cost reduction achieved by the reduction in PV area (e.g. $1090 per m2 for 17× concentration factor). Their use is particularly important for systems that integrate next-generation III–V PV components that can withstand large solar concentrations and have significantly larger costs.
Considering the price similarity among systems, a new selection criteria should to be used for the electrolyzer composition such as material availability or cost of land. Although, in examples from Fig. 4, the areal dimension of the system is determined by the photovoltaic's area, some systems produce more hydrogen than others per areal coverage (a difference of 41% when comparing systems with highest to lowest production rates). This is due to the increased solar-fuel efficiency of systems that use noble metals. Evidently, when choosing between material systems with similar prices, selecting the one with the highest production rate will result in cost savings from the land requirement for a given fuel production goal. Taking land value into consideration, classical electrolysis systems with noble metal catalysts would look as the most promising candidates, as their highest catalytic efficiency outweigh their higher cost. On the other hand, materials availability constraints would motivate the implementation of solar-hydrogen generation systems based on earth-abundant components, especially for large scale deployment.
Despite the fact that this study focussed on the cost-analysis of electrically integrated PV-Electrolysis systems, it can provide guidance regarding the cost-efficiency of alternative solar-fuels solutions (i.e. grid integration of decoupled PV and electrolyzers, and integrated photoelectrochemical (PEC) systems based on photocatalysts). In the case of grid-distributed energy capture and hydrogen generations, significant implementation advantages can be attained via decoupling the two components at the expense of efficiency losses and additional expenses coming from the introduction of power inverters. For PEC systems, technoeconomic challenges arise from constraining the area for water splitting to that of the light absorbing units. On the other hand, these highly integrated systems could be advantageous when concentrated sunlight is used, as the fraction of the cost associated with the electrolyzer becomes significant (33% for the case of 17×), and thermal management would be needed for PV cooling and to potentially use the excess heat in the electrolysis processes.
Future technoeconomic studies should explore the different cost advantages between different degrees of integration, as well as implications of materials availability on large scale implementations of solar-fuel devices. The economic insights provided by this study can help direct research efforts towards critical aspects in the development of cost-effective solar-hydrogen generators and ultimately enable the commercial deployment of artificial photosynthesis systems.
Acknowledgements
This material is based upon work performed with the financial support of the Nano-Tera.ch initiative, as part of the Solar Hydrogen Integrated Nano Electrolysis project (Grant # 530 101). The authors would also like to thank Prof. Sophia Haussener and Dr Mikael Dumortier (EPFL) for helpful discussions and Dr Didier Domine (CSEM) for providing assistance with the performance and cost information of the photovoltaic components.Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed
.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed
.
- D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890–1898 CrossRef CAS PubMed
.
- H. Zhang and P. K. Shen, Chem. Soc. Rev., 2012, 41, 2382–2394 RSC
.
- Key World Energy Statistics, http://www.iea.org/publications/freepublications/publication/kwes.pdf, 2012.
-
D. Feldman, G. Barbose, R. M. Margolis, R. Wiser, N. Darghouth and A. Goodrich, Photovoltaic (PV) Pricing Trends: Historical, Recent, and Near-Term Projections, U.S. Department of Energy, 2012 Search PubMed
.
-
The Economist, Packing some power, 2012 Search PubMed
.
- C. L. Choi and A. P. Alivisatos, Annu. Rev. Phys. Chem., 2010, 61, 369–389 CrossRef CAS PubMed
.
- A. J. Bard and M. A. Fox, Acc. Chem. Res., 1995, 28, 141–145 CrossRef CAS
.
- K. S. Joya, Y. F. Joya, K. Ocakoglu and R. van de Krol, Angew. Chem., Int. Ed., 2013, 52, 10426–10437 CrossRef CAS PubMed
.
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed
.
- J. M. Thomas, Energy Environ. Sci., 2014, 7, 19–20 CAS
.
-
H. J. Lewerenz, L. Peter, F. Schuth, T. S. Zhao and H. Frei, Photoelectrochemical Water Splitting: Materials, Processes and Architectures, Royal Society of Chemistry, 2013 Search PubMed
.
- E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazabal and J. Perez-Ramirez, Energy Environ. Sci., 2013, 6, 3112–3135 CAS
.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed
.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed
.
- M. A. Modestino, K. A. Walczak, A. Berger, C. M. Evans, S. Haussener, C. Koval, J. S. Newman, J. W. Ager and R. A. Segalman, Energy Environ. Sci., 2014, 7, 297–301 CAS
.
- S. Y. Reece, J. A. Hamel, K. Sung, T. D. Jarvi, A. J. Esswein, J. J. H. Pijpers and D. G. Nocera, Science, 2011, 334, 645–648 CrossRef CAS PubMed
.
- F. F. Abdi, L. Han, A. H. M. Smets, M. Zeman, B. Dam and R. van de Krol, Nat. Commun., 2013, 4, 2195 Search PubMed
.
- G. Peharz, F. Dimroth and U. Wittstadt, Int. J. Hydrogen Energy, 2007, 32, 3248–3252 CrossRef CAS
.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS PubMed
.
- O. Khaselev, A. Bansal and J. A. Turner, Int. J. Hydrogen Energy, 2001, 26, 127–132 CrossRef CAS
.
- M. R. Shaner, K. T. Fountaine, S. Ardo, R. H. Coridan, H. A. Atwater and N. S. Lewis, Energy Environ. Sci., 2014, 7, 779–790 CAS
.
- Y. Lin, C. Battaglia, M. Boccard, M. Hettick, Z. Yu, C. Ballif, J. W. Ager and A. Javey, Nano Lett., 2013, 13, 5615–5618 CrossRef CAS PubMed
.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 CAS
.
- S. Haussener, S. Hu, C. Xiang, A. Z. Weber and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3605–3618 CAS
.
- M. T. Winkler, C. R. Cox, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1076–E1082 CrossRef CAS
.
- M. R. Shaner, K. T. Fountaine and H.-J. Lewerenz, Appl. Phys. Lett., 2013, 103, 143905 CrossRef
.
- C. Xiang, Y. Chen and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3713–3721 CAS
.
- J. Newman, J. Electrochem. Soc., 2013, 160, F309–F311 CrossRef CAS
.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 CAS
.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 CAS
.
-
J. R. Thompson, R. D. McConnell and M. Mosleh, Cost analysis of a concentrator photovoltaic hydrogen production system, 2005 Search PubMed
.
-
B. D. James, G. N. Baum, J. Perez, K. N. Baum and O. V. Square, Technoeconomic Analysis of Photoelectrochemical (PEC) Hydrogen Production, 2009, https://www1.eere.energy.gov/hydrogenandfuelcells/pdfs/pec_technoeconomic_analysis.pdf Search PubMed
.
- P. Zhai, S. Haussener, J. Ager, R. Sathre, K. Walczak, J. Greenblatt and T. McKone, Energy Environ. Sci., 2013, 6, 2380–2389 CAS
.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS
.
- K. E. Ayers, E. B. Anderson, C. Capuano, B. Carter, L. Dalton, G. Hanlon, J. Manco and M. Niedzwiecki, ECS Trans., 2010, 33, 3–15 CAS
.
-
I. R. E. Agency, Renewable Energy Technologies: Cost Analysis Series, 2012, http://www.irena.org Search PubMed
.
-
U. S. D. o. t. I. a. U. S. G. Survey, Mineral Commodity Summaries, 2013 Search PubMed
.
-
B. D. James and J. A. Kalinoski, Mass production cost estimation for direct H2 PEM fuel cell systems for automotive applications, 2008 Search PubMed
.
-
J. Genovese, Current (2009) State-of-the-Art Hydrogen Production Cost Estimate Using Water Electrolysis: Independent Review, National Renewable Energy Laboratory, 2009 Search PubMed
.
-
U.S.EIA, Levelized Cost and Levelized Avoided Cost of New Generation Resources in the Annual Energy Outlook 2014, 2014, http://www.eia.gov/forecasts/aeo/pdf/electricity_generation.pdf Search PubMed
.
- D. G. Nocera, Acc. Chem. Res., 2012, 45, 767–776 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the physical and cost model, sensitivity analysis parameters, cost optimization of solar-fuel generators based on crystalline Silicon and III–V PV cells, comparison of H2 production costs with commercial electricity prices, and sensitivity analysis on optimized F values. See DOI: 10.1039/c4ee01453g |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2014 |