The influence of matrix (an)isotropy on cardiomyocyte contraction in engineered cardiac microtissues

Abstract

In the cardiac microenvironment, cardiomyocytes (CMs) are embedded in an aligned and structured extracellular matrix (ECM) to maintain the coordinated contractile function of the heart. The cardiac fibroblast (cFB) is the main cell type responsible for producing and remodeling this matrix. In cardiac diseases, however, adverse remodeling and CM death may lead to deterioration of the aligned myocardial structure. Here, we present an in vitro cardiac model system with uniaxial and biaxial constraints to induce (an)isotropy in 3D microtissues, thereby mimicking ‘healthy’ aligned and ‘diseased’ disorganized cardiac matrices. A mixture of neonatal mouse CMs and cFBs was resuspended in a collagen–matrigel hydrogel and seeded to form microtissues to recapitulate the in vivo cellular composition. Matrix disarray led to a stellate cell shape and a disorganized sarcomere organization, while CMs in aligned matrices were more elongated and had aligned sarcomeres. Although matrix disarray has no detrimental effect on the force generated by the CMs, it did have a negative effect on the homogeneity of contraction force distribution. Furthermore, proliferation of the cFBs affected microtissue contraction as indicated by the negative correlation between the percentage of cFBs in the microtissues and their beating frequency. These results suggest that in regeneration of the diseased heart, reorganization of the disorganized matrix will contribute to recover the coordinated contraction but restoring the ratio in cellular composition (CMs and cFBs) is also a prerequisite to completely regain tissue function.

---

Insight, innovation, integration

In vitro cardiac tissue models can be used to mimic healthy aligned and diseased disorganized cardiac tissue to give more insight into the influence of (an)isotropy on tissue contraction in cardiac disease. We created microscale tissue gauges to engineer 3D isotropic and anisotropic cardiac tissues. With this technology we showed that matrix disorganization affects the direction and distribution of cardiomyocyte contraction force although it has no effect on contraction force magnitude. Furthermore, our results indicate a threshold value for the percentage of cFBs that correlates with a rapid reduction in frequency of the microtissues to almost zero. This cardiac tissue model mimics in vivo characteristics of heart diseases, and will be further tested as an in vitro screening assay for new cardiac therapies.

Introduction

The myocardial microenvironment is composed of cardiomyocytes (CMs) and non-myocytes embedded in an aligned and structured extracellular matrix (ECM), which is mainly produced by the cardiac fibroblasts (cFBs).¹ Cells and ECM proteins are connected via cell–cell and cell–matrix interactions to maintain this structural organization and enable coordinated contraction of the heart. During cardiac disease, such as ischemia and myocardial infarction, the myocardial microenvironment changes in response to pathological cues. The most common effects of heart disease are loss of CMs, followed by tissue repair and remodeling, ultimately leading to fibrosis, due to adverse matrix remodeling.^2,3 It is generally believed that fibrosis leads to deterioration of the aligned myocardial tissue structure,¹ especially when combined with massive CM death. While the influence of microenvironmental changes on CM function has been extensively studied at the cellular level,^4–6 the impact of changes in structural organization on local tissue function is still unclear.

The importance of alignment of CMs in coordinated contraction is not only proven by the native cardiac structure, but also in in vitro studies. Alignment of CMs has been induced by microcontact printing parallel lines of matrix proteins onto 2D substrates.^4–6 These studies demonstrated that alignment improves CM calcium handling and contractile properties when compared to randomly oriented cell monolayers.^4–6 In 3D, researchers have mimicked matrix alignment by using electrospun scaffolds and showed that scaffold fiber alignment induced alignment of the cardiac cells.^7,8 Black et al. created fibrin based cardiac tissues using rat neonatal CMs and measured twitch forces in aligned and disorganized 3D tissues.⁹ They reported that when paced at 1 Hz, aligned cardiac tissues generated a higher contraction force compared to disorganized tissues, caused by improved gap junction formation.⁹ Desroches et al. used scaffold-free 3D microtissues to study cellular distribution, function and cell–cell interactions in a 3D environment.¹⁰ Interestingly, they demonstrated that neonatal rat CMs and cFBs in these microtissues recapitulated the in vivo cellular distribution, depending on their cellular composition, functional calcium handling as well as rhythmic contraction, indicating the importance of using additional cell types next to CMs to create in vitro cardiac tissue models.¹⁰ The effects of other cell types, mainly (myo)fibroblasts, on CM function have also been extensively studied.^11–13 Paracrine factors of cFBs¹¹ and mechanical¹² and electrical coupling¹³ of cFBs and CMs have all shown to affect the conduction velocity in cardiac cell monolayers.

Although these studies address the effects of different microenvironments on CM function, most studies did not provide insight into the evolution with time. As cells synthesize and remodel their own matrix, and matrix composition and organization in turn influence cell function, there is a dynamic interplay between cells and their microenvironment. We therefore aimed at monitoring changes in cell (CM) function in response to their environment in time to further understand the transient changes in CM contractile behavior in different microenvironments.

Currently available model systems do not allow for simultaneous manipulation of the matrix architecture and monitoring of cardiac tissue composition and function over time. Therefore, we used a previously developed microfabricated tissue gauge (μTUG) design^14,15 and adapted this to create microtissues with either uniaxial or biaxial constraints to manipulate matrix organization into an aligned (anisotropic) or disorganized (isotropic) organization. While alignment is chosen to represent a “healthy” tissue organization, the disorganized matrix structure is used to mimic a “diseased” tissue organization. The relatively small size of the tissues allows for real-time monitoring of the complete constructs using microscopy, whereas the use of arrays of tissues enables higher throughput data collection. Cardiac microtissues were created using a mixed cell population isolated from neonatal mouse hearts, representing a healthy cellular composition. The microtissues were expected to develop a more disease-like cellular composition with culture time, since cFBs proliferate with time and CMs do not proliferate.¹³ To study the effect of matrix alignment we compared a number of features, i.e. cellular structure and composition, contraction force, beating frequency, and homogeneity of contraction between anisotropic and isotropic microtissues during one week of culture. Using this model system we showed that matrix disorganization affects the direction and homogeneity of cardiac tissue contraction although it has no detrimental effect on the force of contraction. Furthermore our results suggest a negative correlation between fibroblast proliferation and contraction frequency.

Materials and methods

Ethical statement

Animal experiments were approved by the Animal Experiments Committee of the Leiden University Medical Center and conformed to the Guide for the Care and Use of Laboratory Animals as stated by the National Institutes of Health.

Cell isolation and culture

Neonatal cardiomyocytes (CMs) and cardiac fibroblasts (cFBs) were isolated from 1–3 day old C57/BL6 mouse hearts as described before.¹⁶ Cells were cultured in high glucose DMEM (Lonza), supplemented with 10% heat-inactivated fetal bovine serum, 1% L-glutamine, and 1% penicillin/streptomycin. To remove most of the cFBS, the isolated cells were first seeded in uncoated culture flasks to let cFBs adhere. Non-attached cells were considered to be the CM-enriched cell population.¹⁶ The enriched CMs were plated at a concentration of 5 × 10⁴ cells per cm² on six-well plates coated with 1% gelatin and 10 μg ml⁻¹ fibronectin for four days before they were used for microtissue fabrication or staining.

μTUG fabrication

The design of the μTUG system was adapted from the system developed by Legant et al., which was fabricated using soft lithography.¹⁴ Each microwell contains polydimethylsiloxane (PDMS, Sylgard 184, Dow-Corning) microposts, providing biaxial (12 posts) or uniaxial (4 posts) constraints of the tissues (Fig. 1A–C). In short, multilayered masters were manufactured by UV-induced polymerization of the SU-8 photoresist (Microchem) spin coated on silicon wafers. Exposure and alignment were performed on a Karl Suss MJB3 mask aligner (Suss Microtec). The SU-8 masters were made non-adhesive via overnight silanization with (tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane under vacuum. Molds were created by casting a prepolymer to curing agent ratio of 10 : 1 w/w PDMS on the masters and incubating at 60 °C for 48 hours. The PDMS molds were treated in a plasma oxidizer (1 min at 100 Watt) and made non-adhesive via overnight silanization to facilitate release of the molds from the μTUG system. PDMS was then casted on these molds and substrates were replicated on glass bottom cell culture dishes. After careful removal of the molds, μTUGs were sterilized in 70% ethanol followed by exposure to UV for 15 minutes. Furthermore, μTUGs were treated for at least 15 minutes with 0.2% Pluronic F127 (BASF) to reduce cell adhesion.

Fig. 1 μTUG system with uniaxial or biaxial constraints to manipulate tissue organization. (A) The cell seeded hydrogels compacted around the posts to form microtissues. (B) Collagen (CNA-35 OG, green) and cells (CTO, red) in uniaxially and biaxially constrained tissues had an aligned and random orientation, respectively. (C) Isotropic and anisotropic collagen organization was confirmed by image analysis showing the highest fiber fractions in the direction of the constraints and was consistent at day two, four, and seven. Scale bars represent 100 μm. Error bars represent SD for N = 10 from one representative experiment.

Microtissue seeding

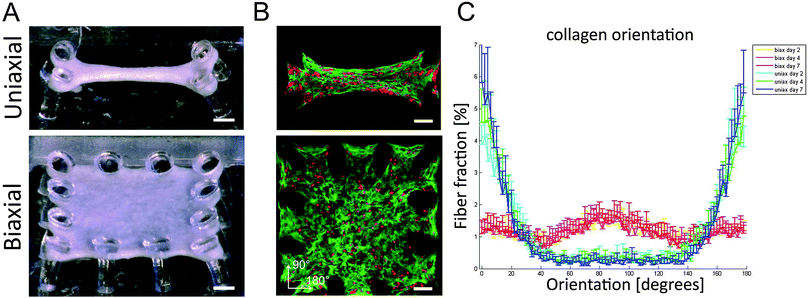
A gel mixture was prepared by mixing 50% Collagen type I (BD Biosciences, 3.2 mg ml⁻¹), 39% CM culture medium, 3% 0.25 M NaOH, and 8% growth factor-reduced Matrigel (BD Biosciences), added to the well of the μTUG system, and centrifuged to spin the hydrogel into the microwells. After trypsinization, enriched CMs were resuspended in the hydrogel at a density of 1 × 10⁶ cells per ml, and centrifuged again to spin the cells into the microwells. After spinning, excessive gel was aspirated leaving 0.14 μl or 0.25 μl of gel volume in the microwells with uniaxial or biaxial constraints, respectively. The cell seeded gel polymerized in an incubator at 37 °C, 5% CO₂ for 10 minutes, by inverting the petridish and adding sterile water to the lid to prevent dehydration of the tissues. Subsequently, culture medium was added to the microtissues and changed every two to three days. Cells compacted the matrix around the microposts creating uniaxially anchored microtissues of 875 × 375 μm and biaxially anchored microtissues of 875 × 875 μm (Fig. 1A).

Immunofluorescence, confocal microscopy, and image analysis

Viable fluorescent probes, CNA35-OG¹⁷ and Cell Tracker Orange (CTO, Invitrogen Molecular Probes), were used to visualize collagen and cells in the microtissues at day two, four, and seven, using two-photon confocal laser scanning microscopy (Zeiss LSM 510 META NLO). To determine the orientation and the ratio of CMs and cFBs and to study CM maturation, immunohistochemistry was performed using α-actinin as a CM label and vimentin as a FB label on monolayers at day zero and microtissues at day two, four, and seven. Cells and microtissues were fixed in 10% formalin for 10 minutes, followed by storage in PBS. For double staining of α-actinin and vimentin, samples were permeabilized with 0.5% Triton-X-100 and incubated with 10% horse serum prior to incubation with antibodies against α-actinin (Sigma-Aldrich) and vimentin (Cell Signaling) overnight. The next day, samples were washed in PBS, incubated with secondary antibodies Alexa 488 (Invitrogen) and Alexa 555 (Molecular Probes), counterstained with DAPI, and then embedded in Mowiol. Monolayers were imaged on a fluorescence microscope (Zeiss Axiovert 200M) and microtissues on a two-photon confocal laser scanning microscope. The resulting images were analysed in Mathematica to quantify collagen and cell orientation as described before.^18,19 In short, the probability that a pixel belongs to a fiber-like structure was calculated, based on the vesselness measure defined by Frangi et al.²⁰ To determine the percentage of cFBs in the microtissues, α-actinin and vimentin positive cells were counted using ImageJ in images taken in the middle of the constructs. Sarcomere length was measured in ImageJ as the distance between adjacent α-actinin bands. Sarcomere width was measured in ImageJ as the length of individual α-actinin bands.

Force measurement

Micropost displacement caused by spontaneous beating of CMs was monitored over time using a high speed camera mounted on a Zeiss observer microscope. Movies were recorded at day two, four, and seven for each experimental group. Micropost displacement was tracked and analyzed using feature detection software in Mathematica and Matlab, based on the use of the Hough transform. The Hough transform is a feature extraction technique used in image analysis to detect known shapes based on a voting procedure of the pixels in the image.²¹ More votes on one point means a greater probability of the point being the center of a circle. Once all microposts were detected in the first frame, they were tracked throughout all frames of the movie to get the displacement of the microposts over time. Finite element analysis was used to calculate the force–displacement relationship, leading to a spring constant of 0.7 μN μm⁻¹ for our system (see ESI,† Fig. S1). Dynamic contraction forces were then calculated from displacements by using this displacement–force relationship. Contraction forces of all microposts were summed to obtain the total contraction force per microtissue. To account for the difference in the cell number between anisotropic and isotropic microtissues, the measured forces were corrected for initial microwell volume, representative of the initial cell numbers. Beating frequency was deducted from the Fourier spectrum of the signal.

Computational strain analysis

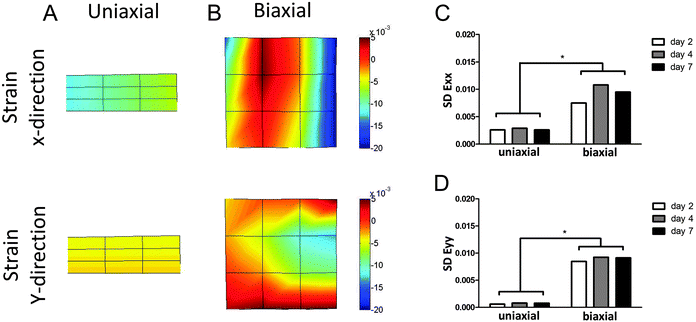
The μTUG system was used to measure displacements at multiple microposts per tissue. This information was used to calculate local strains in the microtissues. In analogy with the finite element method, a polynomial approximation of the displacement field within each microtissue was determined from the measured displacements at the microposts and the shape functions. A 2D third-order quadrilateral serendipity element (12 nodes) was used in the case of a biaxial tissue, or a 2D first-order quadrilateral element (4 nodes) for a uniaxial tissue. Subsequently, the deformation gradient tensor F was determined at 16 equally distributed locations within each tissue from the spatial gradients of the displacement field. The deformation gradient tensor F was then used to calculate the Green–Lagrange strain (E = 0.5(F^T·F − I)) at each location. The standard deviation (SD) of the normal strain in x- (E_xx) and y-directions (E_yy) was calculated as a measure of the homogeneity of force distribution.

Statistical analysis

All data are represented as mean ± standard deviation. Statistical analysis was performed with GraphPad Prism software. Comparisons of parameters between two groups were made using the unpaired T-test, multiple comparisons between groups were made using two-way analysis of variance (ANOVA) with the Bonferroni post-hoc test, and comparisons of variance between two groups were made using the F-test of equal variance. Differences were considered statistically different when P < 0.05.

Results

Microtissue constraints determine collagen organization

In this study, both healthy aligned and diseased disorganized cardiac tissues were successfully mimicked by seeding cardiac cells in μTUGs with uniaxial or biaxial constraints to manipulate tissue organization (Fig. 1A). By using a viable probe to stain the collagen,¹⁷ matrix organization could be followed over time in the same sample. Confocal microscopy on microtissues stained with CNA-35 OG and CTO at day two, four, and seven showed that cells were embedded in a collagen matrix and distributed homogenously throughout the microtissues in both designs (Fig. 1B). Orientation analysis of the collagen network showed that uniaxial anchoring resulted in anisotropy of the collagen with the highest fiber fraction oriented at 180°, which is the direction of the constraints. Biaxial anchoring did not result in a preferred fiber orientation and this tissue architecture is therefore considered isotropic. The collagen organization was present from day two and did not change over time (Fig. 1C). Thus, constraining the tissues uniaxially or biaxially using the microposts resulted in the desired anisotropic and isotropic collagen organization, mimicking healthy and diseased myocardium.

Matrix (an)isotropy has no effect on cellular composition in microtissues

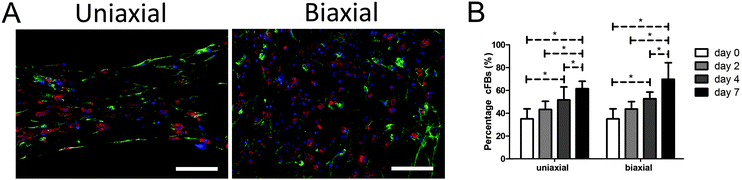
CMs and cFBs were equally distributed throughout all microtissues (Fig. 2A). Despite purifying the CM population due to adherence of cFBs to plastic, at the day of microtissue seeding, the cell population contained 35 ± 9% cFBs. At day two of culture microtissues consisted already of 43 ± 7% cFBs and this increased to 52 ± 10% at day four and 65 ± 11% cFBs at day seven (Fig. 2B). Tissue organization did not have any influence on the percentage of cFBs in the microtissues as no differences were observed between anisotropic and isotropic microtissues (Fig. 2B).

Fig. 2 The percentage of cFBs in the microtissues increased over time. (A) CMs (α-actinin, red) and cFBs (vimentin, green) were distributed throughout the microtissues in uniaxially and biaxially constrained microtissues, here shown at day two of culture (nuclei in blue). (B) Percentage of cFBs increased equally in both uniaxially and biaxially constrained microtissues. Scale bars represent 100 μm. Error bars represent SD of N ≥ 8 from two independent experiments.

Matrix anisotropy enhances cell and sarcomere alignment in microtissues

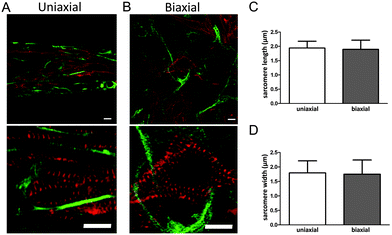
For efficient contraction, CMs need to mature and develop an organized sarcomere structure. Maturation of CMs was investigated by staining the microtissues for α-actinin, which is a protein that organizes into a striated pattern when the sarcomeric proteins develop into a mature structure. Although CMs still had a round shape, α-actinin was visible from day two, indicating a developing sarcomere structure (Fig. 2A). After seven days, CMs were more spread and obtained an organized sarcomere structure in both anisotropic and isotropic microtissues (Fig. 3A and B).

Fig. 3 Sarcomere organization in anisotropic and isotropic microtissues. (A) Matrix alignment induced alignment of the CMs and cFBs and concomitant sarcomere organization. (B) A disorganized matrix induced random cell orientation and a stellate cell shape. Although CMs develop a mature sarcomere structure, the individual sarcomeres do not have the same orientation throughout the cell. (C) Sarcomere length was not significantly different between uniaxially or biaxially constrained microtissues. (D) Sarcomere width was not affected by matrix organization. Error bars represent N = 100 sarcomeres measured in 20 different CMs. Scale bars represent 10 μm.

However, CMs in anisotropic microtissues (Fig. 3A) were more aligned compared to CMs in isotropic microtissues that obtained a more stellate shape and random orientation (Fig. 3B and ESI,† Fig. S2).

The alignment of cells in anisotropic microtissues also resulted in a better alignment of the sarcomeres (Fig. 3). Next to sarcomere alignment, sarcomere length and width are important for the contractile function of the CMs.^22–24

Determination of the sarcomere length using ImageJ indicated a length of ∼1.9 μm in both anisotropic and isotropic tissues. Sarcomere width was found to be ∼1.8 μm in both groups. Although the exact values may not be as accurate as measured with other techniques,^25,26 this indicates that matrix organization did not influence sarcomere length or width in our microtissues. Together, matrix alignment improved organization of the sarcomeres and alignment of the cells.

Microtissue contraction frequency is not affected by matrix organization

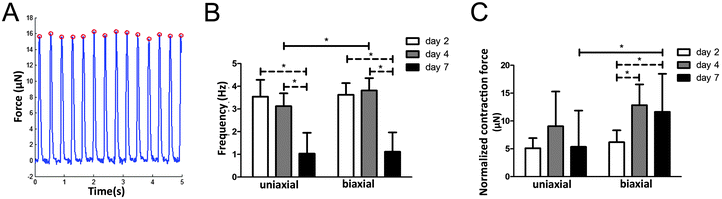
The μTUG system containing arrays of flexible microposts was used to measure the contractile properties in anisotropic and isotropic tissues. To investigate the effect of matrix organization on microtissue contractile behavior, displacement of microposts caused by spontaneous beating of CMs was monitored for seven days.

Single beating CMs were observed within the microtissues from day one of culture while synchronized beating that caused micropost displacement (Fig. 4A) could be observed from day two of culture in both groups. At day two, the beating frequency of anisotropic microtissues (3.5 ± 0.7 Hz) was not significantly different from isotropic microtissues (3.6 ± 0.5 Hz) (ESI,† Movies S1 and S2). At day 4, the beating frequency of both groups did not significantly change compared to day 2, although the frequency of the anisotropic tissues (3.1 ± 0.6 Hz) was significantly lower than that of the isotropic tissues (3.8 ± 0.5 Hz) (ESI,† Movies S3 and S4). While the beating frequency remained rather constant over the first four days of culture, at day seven, a large decrease in frequency was observed in both groups (65% decrease in anisotropic microtissues, 70% decrease in isotropic microtissues). This resulted in a frequency of 1.0 ± 0.9 Hz for the anisotropic microtissues and a frequency of 1.1 ± 0.9 Hz for the isotropic microtissues (Fig. 4B, ESI,† Movies S5 and S6). Interestingly, despite the small significant difference at day 4, matrix organization did not have a strong effect on the beating frequency of the microtissues. Apart from tissue organization, cellular composition may also affect microtissue contractile properties. To assess for a possible correlation between cFB numbers and microtissue beating frequency, the percentage of cFBs per experimental group was averaged and plotted against the frequency measured in the same experiment. Interestingly, a threshold value for the percentage of cFBs of around 55% was found to correlate with a reduction of the frequency from 3.5 Hz to almost 0 Hz (ESI,† Fig. S3).

Fig. 4 Contraction force and frequency of uniaxially and biaxially constrained microtissues. (A) Total absolute contraction force over time for a representative microtissue, peaks indicate the dynamic contraction force. (B) Frequency decreased on day seven in both groups. (C) Dynamic contraction force normalized for microtissue volume increased over time in biaxially constrained microtissues. On day 7 the contraction force in biaxially constrained microtissues was significantly higher compared to uniaxially constrained microtissues. Error bars represent SD of N ≥ 18 from two independent experiments.

Matrix disarray does not decrease the ability of CMs to generate contractile forces

Next to beating frequency, also the dynamic contraction force was calculated from micropost displacements. While contraction force in isotropic microtissues increased over time, no significant increase was found for the anisotropic microtissues. On day seven, contraction force was even lower in anisotropic microtissues (5.4 ± 6.5 μN) compared to isotropic microtissues (11.6 ± 6.8 μN) (Fig. 4C). To check for an effect of cFB numbers on microtissue contraction force, the average percentage of cFBs per experimental group was also plotted against the contraction force measured in the same experiment, but no correlation was found. Due to the alignment of the matrix and cells in the uniaxially constrained tissues, it was expected that contraction in these tissues is mainly in the direction of the alignment. In the anisotropic microtissues, contraction force in the direction of alignment was 59 ± 10% of the total contraction, while in the isotropic tissues the distribution was 50 ± 6% in both directions. So even if we take just one direction into account, the anisotropic microtissues were not able to generate higher force compared to isotropic microtissues. Together, these results suggest that in 3D, a disorganized matrix organization alone does not decrease the ability of the CMs to generate contractile forces.

Direction of contraction force and homogeneity of contraction force distribution are disturbed by matrix disorganization

The μTUG system was used to measure displacements at multiple microposts per tissue, to calculate local strains. This enabled the investigation of contractile behavior of the microtissues in more detail than by just looking at total contraction force. The standard deviation (SD) of the strains in the microtissues (Fig. 5A and B) was calculated as a measure of homogeneity of force distribution. If all CMs in the microtissues generate the same force, the strain throughout the tissue will be equal, resulting in a very small SD. On the other hand, a heterogeneous force distribution will be represented by a large SD of the strain. The SD of strains in both x- and y-directions was significantly different between the two groups on all time points (Fig. 5C and D). This indicates that the contraction force is much more homogenously distributed in anisotropic microtissues, compared to isotropic microtissues. Surprisingly, this homogeneous contraction did not lead to higher contractile forces. This suggests that matrix disorganization only influences the direction and homogeneity of contraction and not the total contraction force or frequency of the microtissues.

Fig. 5 Distribution of strains in anisotropic microtissues was more homogeneous compared to isotropic microtissues. (A) Strains in x- and y-directions in an anisotropic microtissue were homogenously distributed. (B) Strains in x- and y-directions in an isotropic microtissue were very heterogeneously distributed. (C, D) Mean SD of N ≥ 16 from two independent experiments showed a higher standard deviation of the strains in both directions in the biaxially constrained microtissues compared to the uniaxially constrained microtissues, reflecting the heterogeneity in force distribution.

Discussion

Knowledge on CM contractile behavior in response to changes in their microenvironment is still limited. Although recent research has shown the importance of matrix alignment for CM function, the dynamic interplay between cells and their environment makes this a complex phenomenon which is not yet fully understood. As the presence of cFBs helps to recapitulate the in vivo cellular distribution,¹⁰ we used enriched CMs isolated from neonatal mouse hearts to create engineered cardiac tissue. As the cFBs are expected to proliferate during culture and the CMs do not proliferate,¹³ depletion of fibroblasts was performed before microtissue seeding. Despite this approach, 43 ± 7% cFBs were found in our samples at day two, which is comparable to the amount of non-CMs in neonatal murine hearts,²⁷ thereby indicating the presence of a healthy cellular composition in our microtissues at this time point. Where the percentage of cFBs in the adult heart stabilizes over time, in our study it increased to more than 60% at day seven.

The high proliferation of cFBs was previously described in 2D in vitro cultures using rat cardiac cells in which the percentage of cFBs increased from 16% at day one of culture to 37% at day four and 62% at day nine.¹³

The CMs and cFBs that were seeded in a collagen–matrigel mixture compacted around the micropost and self sorted into a heterogeneous cell distribution similar to the cardiac microtissues of Desroches et al.¹⁰ After two days of culture, the CMs in the microtissues started to beat synchronously, resulting in displacement of the microposts. Interestingly, matrix disarray did not negatively affect the beating frequency. The average microtissue beating frequency of 3.5 Hz at day two and four was relatively higher than the frequency between 2 Hz and 3 Hz that has been previously reported for mouse engineered cardiac tissues.²⁸ However, the explored in vitro frequencies do not reach the in vivo frequency of a mouse heart, which is around 10 Hz,²⁹ probably caused by the differences in organization, composition and maturation of the CMs.

At day seven, we measured a large decrease in frequency in both groups (65% decrease in anisotropic microtissues, 70% decrease in isotropic microtissues). The increase in the cFB number during culture and the decrease in frequency at day seven raised the suggestion of a relation between these two effects. Indeed we found a negative correlation between the percentage of cFBs and the beating frequency. Interestingly, our results suggest a threshold of around 55% cFB which correlates with the sudden reduction in frequency from 3.5 Hz to almost 0 Hz. At day 4 of culture, microtissues contained already 52 ± 10% cFBs. In cardiac cell monolayers it has been shown that proliferation of cFBs reduces the conduction velocity probably by inhibiting contraction signal propagation between CMs.¹³ Surprisingly, we did not see a decrease in frequency at this time point, suggesting that the CMs can still propagate their conduction signals. Only when the percentage of cFB increased even more, the frequency drastically decreased to almost 0 Hz. More cFBs could also lead to a higher matrix production, which in turn may stiffen the matrix over time and may affect beating of the CMs. For single CMs in 2D, it has been shown that higher substrate stiffness leads to a decrease in beating.³⁰

Next to beating frequency, we also investigated the effect of matrix (an)isotropy on the force of contraction in microtissues. Our anisotropic tissues did not show higher contraction forces than isotropic tissues, while previous studies showed that alignment of cells improved the contractile strength of the tissues.^5,6,9

The contradiction between our data and previous data could be caused by the fact that previous studies all used electrical stimulation, while our study concentrated on spontaneous contraction. Furthermore, where previous studies^5,6 used the curvature of the substrate in just one direction as a measure of contraction force, in our study the displacement of the microposts in all directions was used. So to compare our results to these studies,^5,6 only forces in one direction should be considered. However, our data showed that even if we considered forces in just one direction, alignment of the matrix did not lead to higher contractile forces.

A limitation of our study is that the alignment of collagen in the anisotropic microtissues may cause local increases in stiffness that could possibly affect CM contraction. Previous 2D studies have showed that CM contraction force increased on stiffer substrates.^23,31 Although the exact effect of stiffness on sarcomere properties remains unclear, most studies found differences in sarcomere length and/or width when changing substrate stiffness.^23,24,32

To the best of our knowledge, this is the first study describing strain distributions in cardiac microtissues. Our data showed a more homogenous contraction force distribution in anisotropic microtissues compared to isotropic microtissues, probably caused by the improved organization and morphology of CMs in these tissues. A quantitative analysis of cell orientation showed that matrix alignment induced alignment of cells. In the CMs, this also led to alignment of the sarcomeres, while a more stellate cell shape resulted in disarray of the sarcomeres. However, alignment or disarray of sarcomeres did not affect sarcomere length and width, which were found to be similar in anisotropic and isotropic microtissues. Although a previous study in 2D showed that CM contractility is a function of cell shape which coincides with sarcomere organization,²² our data did not confirm this for a 3D environment. In 2D, myocyte shape regulates alignment of sarcomeres and thereby CM contractility.²² Our data showed similar sarcomere lengths for the different cell shapes found in anisotropic and isotropic tissues, indicating that in 3D, cell shape does not coincide with sarcomere length. Although the heterogeneity of force distribution that we showed in isotropic microtissues did not negatively affect total contraction force and frequency, in the native heart this inhomogeneity might decrease efficient pump function.

Conclusion

Our data showed that the described μTUG system was suitable to mimic (dis)organization of the cardiac microenvironment. Disorganization of the microenvironment did not negatively affect the force that could be generated by CMs, although it did have a negative effect on the direction and homogeneity of contraction force distribution. This is probably caused by the differences in cell shape and sarcomere organization dictated by the matrix organization. Cellular composition however, did influence microtissue contraction as indicated by the negative correlation between the percentage of cFBs and the beating frequency of the microtissues. This suggests that in regeneration of the diseased heart, not only reorganization of the disorganized matrix will contribute to restore the coordinated contraction but to completely restore tissue function, repair of the cellular composition is also of importance.

Acknowledgements

The authors thank Kirsten Lodder and Prof. Marie-Jose Goumans of the department of Molecular and Cellular Biology at the Leiden University Medical Center (LUMC) for assistance with the mouse neonatal cardiac cells isolation. Christine Obbink-Huizer and Inge van Loosdregt of the department of Biomedical Engineering at the Eindhoven University of Technology (TU/e) are acknowledged for finite element modeling of the microposts and for the preparation of the μTUG molds, respectively. This work was supported by a grant from the Dutch government to the Netherlands Institute for Regenerative Medicine (NIRM, grant No. FES0908) and funded by the NIH RESBIO technology resource center and the Penn Center for Engineering Cells and Regeneration.

References

1. K. R. Chien, J. J. Domian and K. K. Parker, Science, 2008, 322, 1494–1497.
2. A. F. Bayomy, M. Bauer, Y. Qiu and R. Liao, Life Sci., 2012, 91, 823–827.
3. V. I. Kapelko, Exp. Clin. Cardiol., 2001, 6, 41–49.
4. T. Pong, W. J. Adams, M. A. Bray, A. W. Feinberg, S. P. Sheehy, A. A. Werdich and K. K. Parker, Exp. Biol. Med., 2011, 236, 366–373.
5. A. W. Feinberg, P. W. Alford, H. Jin, C. M. Ripplinger, A. A. Werdich, S. P. Sheehy, A. Grosberg and K. K. Parker, Biomaterials, 2012, 33, 5732–5741.
6. A. Grosberg, P. W. Alford, M. L. McCain and K. K. Parker, Lab Chip, 2011, 11, 4165–4173.
7. Y. Orlova, N. Magome, L. Liu, Y. Chen and K. Agladze, Biomaterials, 2011, 32, 5615–5624.
8. C. W. Hsiao, M. Y. Bai, Y. Chang, M. F. Chung, T. Y. Lee, C. T. Wu, B. Maiti, Z. X. Liao, R. K. Li and H. W. Sung, Biomaterials, 2013, 34, 1063–1072.
9. L. D. Black 3rd, J. D. Meyers, J. S. Weinbaum, Y. A. Shvelidze and R. T. Tranquillo, Tissue Eng., Part A, 2009, 15, 3099–3108.
10. B. R. Desroches, P. Zhang, B.-R. Choi, M. E. King, A. E. Maldonado, W. Li, A. Rago, G. Liu, N. Nath, K. M. Hartmann, B. Yang, G. Koren, J. R. Morgan and U. Mende, Am. J. Physiol.: Heart Circ. Physiol., 2012, 302, H2031–H2042.
11. D. M. Pedrotty, R. Y. Klinger, R. D. Kirkton and N. Bursac, Cardiovasc. Res., 2009, 83, 688–697.
12. S. A. Thompon, C. R. Copeland, D. H. Reich and L. Tung, Circulation, 2011, 123, 2083–2093.
13. S. F. Askar, A. A. Ramkisoensing, M. J. Schalij, B. O. Bingen, J. Swildens, A. van der Laarse, D. E. Atsma, A. A. de Vries, D. L. Ypey and D. A. Pijnappels, Cardiovasc. Res., 2011, 90, 295–304.
14. W. R. Legant, A. Pathak, M. T. Yang, V. S. Deshpande, R. M. McMeeking and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10097–10102.
15. T. Boudou, W. R. Legant, A. Mu, M. A. Borochin, N. Thavandiran, M. Radisic, P. W. Zandstra, J. A. Epstein, K. B. Margulies and C. S. Chen, Tissue Eng., Part A, 2012, 18, 910–919.
16. A. Weeke-Klimp, N. A. Bax, A. R. Bellu, E. M. Winter, J. Vrolijk, J. Plantinga, S. Maas, M. Brinker, E. A. Mahtab, A. C. Gittenberger-de Groot, M. J. van Luyn, M. C. Harmsen and H. Lie-Venema, J. Mol. Cell. Cardiol., 2010, 49, 606–616.
17. K. N. Krahn, C. V. Bouten, S. van Tuijl, M. A. van Zandvoort and M. Merkx, Anal. Biochem., 2006, 15, 177–185.
18. D. W. van der Schaft, A. C. van Spreeuwel, H. C. van Assen and F. P. Baaijens, Tissue Eng., Part A, 2011, 17, 2857–2865.
19. J. Foolen, V. S. Deshpande, F. M. Kanters and F. P. Baaijens, Biomaterials, 2012, 33, 7508–7518.
20. A. F. Frangi, W. J. Niesen, K. L. Vinken and M. A. Viergever, MICCAI, 1998, 1496, 130–137.
21. D. H. Ballard, Pattern Recogn., 1980, 13, 111–122.
22. P. L. Kuo, H. Lee, M. A. Bray, N. A. Geisse, Y. T. Huang, W. J. Adams, S. P. Sheehy and K. K. Parker, Am. J. Pathol., 2012, 181, 2030–2037.
23. A. G. Rodriguez, S. J. Han, M. Regnier and N. J. Sniadecki, Biophys. J., 2011, 101, 2455–2464.
24. S. Majkut, T. Idema, J. Swift, C. Krieger, A. Liu and D. E. Discher, Curr. Biol., 2013, 23, 1–6.
25. G. Bub, P. Camelliti, C. Bollensdorff, D. J. Stuckey, G. Picton, R. A. Burton, K. Clarke and P. Kohl, Am. J. Physiol.: Heart Circ. Physiol., 2010, 298, H1616–H1625.
26. S. H. Huang, C. D. Hsiao, D. S. Lin, C. Y. Chow, C. J. Chang and I. Liau, PLoS One, 2011, 6, e24764.
27. I. Banerjee, J. W. Fuseler, R. L. Price, T. K. Borg and T. A. Baudino, Am. J. Physiol.: Heart Circ. Physiol., 2007, 293, H1883–H1891.
28. A. Stohr, F. W. Friedrich, F. Flenner, B. Geertz, A. Eder, S. Schaaf, M. N. Hirt, J. Uebeler, S. Schlossarek, L. Carrier, A. Hansen and T. Eschenhagen, J. Mol. Cell. Cardiol., 2013, 63, 189–198.
29. V. Chu, J. M. Otero, O. Lopez, J. P. Morgan, I. Amende and T. G. Hampton, BMC Physiol., 2001, 6.
30. A. J. Engler, C. Carag-Krieger, C. P. Johnson, M. Raab, H. Tang, D. W. Speicher, J. W. Sanger, J. M. Sanger and D. E. Disher, J. Cell Sci., 2008, 121, 3794–3802.
31. N. Hersch, B. Wolters, G. Dreissen, R. Springer, N. Kirchgeßner, R. Merkerl and B. Hoffmann, Biol. Open, 2012, 2, 351–361.
32. J. G. Jacot, A. D. McCulloch and J. H. Omens, Biophys. J., 2008, 95, 3479–3487.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ib40219c

---