High-precision copper and iron isotope analysis of igneous rock standards by MC-ICP-MS
Sheng-Ao
Liu
*a,
Dandan
Li
a,
Shuguang
Li
a,
Fang-Zhen
Teng
ab,
Shan
Ke
a,
Yongsheng
He
a and
Yinghuai
Lu
a
aState Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, Beijing 100083, China. E-mail: lsa@mail.ustc.edu.cn; Fax: +86 10 82322382; Tel: +86 10 82322382
bIsotope Laboratory, Department of Earth and Space Sciences, University of Washington, Seattle, WA 98195, USA
First published on 9th October 2013
Abstract
Stable isotopic systematics of Cu and Fe are two important tracers for geological and biological processes. Generally, separation of Cu and Fe from a matrix was achieved by two independent, completely different methods. In this study, we report a method for one-step anion-exchange separation of Cu and Fe from a matrix for igneous rocks using strong anion resin AG-MP-1M. Cu and Fe isotopic ratios were measured by multi-collector inductively coupled plasma mass-spectrometry (Neptune plus) using a sample–standard bracketing method. External normalization using Zn to correct for instrumental bias was also adopted for Cu isotopic measurement of some samples. In addition, all parameters that could affect the accuracy and precision of isotopic measurements were examined. Long-term external reproducibility better than ±0.05‰ (2SD) for δ65Cu and ±0.049‰ (2SD) for δ56Fe was routinely obtained. Cu and Fe isotopic compositions of commercially accessible igneous rock standards including basalt, diabase, amphibolite, andesite and granodiorite were measured using this method. δ65Cu values of igneous rock standards vary from −0.01 to +0.39‰ (n = 11) with an overall range (0.40‰) that exceeds about 8 times that of the current analytical precision. The improved precisions of stable Cu isotopic analysis thus demonstrate that igneous rocks are not homogeneous in Cu isotopic composition. The procedure for one-step separation of Cu and Fe and high-precision analysis of Cu and Fe isotopic ratios have an important advantage for economical and efficient study of stable Cu and Fe isotopic systematics in geological and biological fields.
1. Introduction
Copper is a transition metal and has two stable isotopes of mass 63 and 65, whose average abundances are 69.17% and 30.83%, respectively.1 Natural variations in stable Cu isotope abundances have been observed since the 1950s.2 The search by Walker et al. using thermal ionization mass spectrometry (TIMS) had identified a total range of ∼9‰ in 65Cu/63Cu ratios in Cu-rich minerals, sediments and organic samples, although the precision (1–1.5‰) they achieved was relatively poor compared with the modern standard. In the past decade, lots of high-precision Cu isotopic data obtained using MC-ICP-MS have been reported.3–12 These new results have provided profound insights into processes that link planetary accretion in high-temperature environments as well as inorganic and biological chemistry in low temperature supergene environments. However, Cu isotopic ratios of most igneous rocks span a narrow range of <±0.4‰.12 Application of Cu isotopes to high-temperature geochemistry thus requires high-precision and accurate analyses.In the recent decade, Fe isotope geochemistry has gained particular interest due to its relatively high planetary abundance, multiple redox states and biological utilization. For instance, over 5‰ δ56Fe variation has been observed during low temperature geological and biological processes.13–15 High-temperature equilibrium Fe isotope fractionation is, however, limited as well. Recently, high-precision Fe isotope data better than ±0.03‰ have been obtained using high-resolution (HR) MC-ICP-MS.16
With the development of analytical precision, the combined utilization of Cu and Fe isotopes as geochemical and biological tracers has been recently undertaken on both experimental and field work.6,17,18 The combined use of Cu and Fe isotopes has an important advantage because Cu and Fe behave distinctly in several aspects. For example, Cu(II) is more fluid-mobile than Cu(I) and Fe(III) is less mobile than Fe(II). This difference may result in contrasting behaviors of Cu and Fe isotopes during mineral dissolution. Typically, Cu and Fe in rocks or aqueous solutions were purified by two independent, completely different methods, using anion resin AG-MP-1 and AG-X4 or X8 respectively. In an original paper, Maréchal et al.4 managed one-step anion-exchange separation of Cu and Fe using strong anion resin AG-MP-1 by involving stepwise decreases in concentrations of hydrochloric acid. Regrettably, they did not measure Fe isotopes along with Cu isotopes after chemical purification, and thus the quality of Fe isotope data obtained using this method was unknown. In a recent paper, Borrok et al.6 outlined a method to separate Cu and Fe through a single anion-exchange column and measure Cu and Fe isotopic ratios in complex aqueous solutions. They obtained 2σ precisions better than ∼±0.1‰ for Cu and Fe isotopic analysis. Because most rocks have remarkably different chemical compositions from aqueous solutions, the procedures for isolation of Cu and Fe from a matrix could be different for rocks and aqueous systems. To date, no systematic study has been carried out to separate Cu and Fe in a single column for rocks and to measure their isotopic compositions with high precision. In addition, Cu cannot be completely separated from Fe using the AG-X4 or X8 resin, but high Cu/Fe (>20) can cause significant offset on δ56Fe ratio analysis of >0.2‰.16 Therefore, accurate analysis of Fe isotopes on samples with high Cu/Fe (e.g., Cu-rich sulfides) is impossible using the general procedure.
In this paper, we report a method for one-step anion-exchange separation of Cu and Fe from matrix elements for igneous rocks using strong anion resin AG-MP-1M. We measured both Cu and Fe isotopic compositions of eleven commercially accessible igneous rock standards (e.g., BHVO-2, BIR-1 and BCR-2, etc.) using this method. All parameters that could potentially affect the quality of isotopic analysis were well evaluated. A long-term external reproducibility of better than ±0.05‰ (2SD) for δ65Cu and δ56Fe measurements has been obtained.
2. Analytical methods
The detailed procedures for sample dissolution, column chemistry and instrumental analysis are presented in the following three separate sections.2.1 Sample dissolution
Copper concentration in the analyzed igneous rock standards mostly varies from ∼20 to ∼200 μg g−1, and thus 10–20 mg samples were weighed to contain at least ∼0.4 μg Cu for isotopic analysis. The amounts of iron in the weighed samples are typically <1 mg. The samples were dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) mixture of double-distilled HF and HNO3 in Savillex screw-top beakers, followed by heating at 160 °C on a hotplate in an exhaust hood (Class 100). The solutions were dried down at 150 °C to expel the fluorine. The dried residues were refluxed with a 1
1 (v/v) mixture of double-distilled HF and HNO3 in Savillex screw-top beakers, followed by heating at 160 °C on a hotplate in an exhaust hood (Class 100). The solutions were dried down at 150 °C to expel the fluorine. The dried residues were refluxed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (v/v) mixed HNO3 and HCl, followed by heating and then evaporating to dryness at 80 °C. The samples were refluxed with concentrated HNO3 until complete dissolution was achieved, and subsequently dried down at 80 °C. 1 ml of 8 N HCl + 0.001% H2O2 was added to the beaker and the sample was heated to dryness. This process was repeated three times to ensure that all cations were converted to chloride species. The final material was dissolved in 1 ml of 8 N HCl + 0.001% H2O2 in preparation for ion-exchange separation.
3 (v/v) mixed HNO3 and HCl, followed by heating and then evaporating to dryness at 80 °C. The samples were refluxed with concentrated HNO3 until complete dissolution was achieved, and subsequently dried down at 80 °C. 1 ml of 8 N HCl + 0.001% H2O2 was added to the beaker and the sample was heated to dryness. This process was repeated three times to ensure that all cations were converted to chloride species. The final material was dissolved in 1 ml of 8 N HCl + 0.001% H2O2 in preparation for ion-exchange separation.
2.2 Ion-exchange chromatography
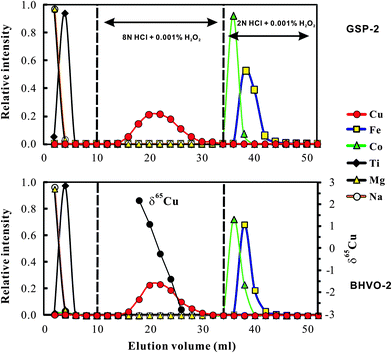
The chemical purification method in this study is modified from Maréchal et al.4 The major difference between this study and Maréchal et al.4 is that we used 8 N HCl for Cu separation from matrix elements instead of 7 N HCl used by Maréchal et al.4 Bio-Rad AG-MP-1M strong anion exchange resin (100–200 mesh; chloride form) was used for separation of Cu and Fe from matrix elements. The resin was pre-cleaned with 0.5 N HNO3 and 8 N HCl alternating with MQ H2O (18.2 MΩ) 12 times. The pre-cleaned column (4 mm in diameter and 9 cm long; Poly-Prep Chromatography) was filled with pre-cleaned AG-MP-1M resin, and washed with 7 ml 0.5 N HNO3 and 5 ml 8 N HCl alternating with MQ H2O three times. The volume of resin was adjusted to 2 ml in 8 N HCl. 7 ml of 8 N HCl was added to the column for conditioning and then samples dissolved in 1 ml 8 N HCl (+0.001% H2O2) were loaded onto the column. Matrix elements (e.g. Na, Mg, Al, K, Ca, Ti, Cr, Ni and Mn) were eluted in the first 10 ml 8 N HCl, leaving Fe, Co, Cu and Zn retained on the resin. The one-step anion-exchange chromatographic method, involving stepwise decreases in concentrations of hydrochloric acid, can separate Cu and Fe from other ions.4 Copper was collected in the following 24 ml of 8 N HCl. Iron fraction was collected in the following 18 ml of 2 N HCl. Analysis of basalt and granodiorite samples yields consistent elution curves (Fig. 1), suggesting that this method is suitable to samples with various matrix compositions. Both the Cu and Fe fractions were evaporated to dryness, dissolved in 3% (m/m) HNO3, and then re-evaporated to dryness and re-dissolved in 3% HNO3 to remove all chlorine prior to isotopic ratio analysis.Total procedural blanks (from sample dissolution to mass spectrometry) were routinely measured and had a long-term average of ∼1.5 ng (1–2 ng, n = 10) for Cu and ∼6 ng (2–10 ng; n = 10) for Fe, which are considered neglected during mass spectrometry. The contribution from blank is still insignificant when the amount of Cu loaded is as low as ∼0.4 μg (see Section 3.4).
2.3 Mass spectrometry
Copper and iron isotopic ratios were measured by a sample–standard bracketing method using a Thermo-Finnigan Neptune plus MC-ICP-MS at the Isotope Geochemistry Laboratory of the China University of Geosciences, Beijing. The sample–standard bracketing (SSB) method has been successfully used for Cu and Fe isotopic analysis.6,9,16,19 Element-doping using Zn or Ni as an external standard was also commonly adopted to correct for instrumental mass bias during Cu isotopic analysis.1,3,4 We performed external normalizing using Zn-doping with an aim to evaluate whether there is significant difference in precisions between the two methods. The results will be discussed in Section 3.5.The instrument is equipped with a Cetac ASX-110 automatic sampler and a PFA Teflon self-aspirating micronebulizer system. The mass spectrometry parameters are outlined in Table 1. Prior to sample introduction, samples and standards were diluted to produce ∼100 ppb Cu solution and ∼1 ppm Fe solution in 3% (m/m) HNO3 respectively. The uptake rate was ∼50 or 100 μl min−1, and no difference in accuracy and precision was found at different uptake rates. The take-up time was 80 s. Prior to each analysis sequential rinses of two separate 3% HNO3 of 100 s were used to reduce baselines to <1 mv on the 63Cu and 56Fe channels.
| Instrument parameters | |
|---|---|
| a LR: low-resolution; HR: high-resolution. | |
| Rf power | 1250 W |
| Cooling Ar | ∼16 l min−1 |
| Auxiliary Ar | ∼1.0 l min−1 |
| Nebuliser Ar | ∼1.0 l min−1 |
| Extraction voltage (hard) | −2000 V |
| Vacuum | 4–8 × 10−9 Pa |
| Cu sensitivity | ∼60 V ppm−1 (LR) |
| Fe sensitivity | ∼10 V ppm−1 (HR) |
| Cones | Ni (X) |
| Sample uptake | ∼50 μl min−1 |
The sampler and skimmer cones are made of Ni, and the high-sensitivity (X) cones are used to increase transmission by a factor of 2–3 relative to the routine H-cones. For example, the 63Cu signal was typically ∼6 V/100 ppb when we used the X-cone. The high sensitivity allows samples containing ∼0.2 μg Cu to be measured for at least four blocks of 40 cycles each (100 ppb in 2 ml solution). This is particularly important for measurement of samples with a small amount of Cu but a large amount of Fe, which is true for most silicates and Fe-sulfides. Otherwise, this needs considerable amounts of digested rocks, which may exceed the loading capacity of the column. Cu isotopic ratios were analyzed in low-resolution mode with 63Cu in the Central cup and 65Cu in the H2 Faraday cup. A measurement consists of at least four blocks of 40 cycles of ∼10 s each, and thus each value reported is the average of at least 160 ratios. Cu isotopic data are reported in standard δ-notation in per mil relative to standard reference material (SRM) NIST 976:
| δ65Cu = ((65Cu/63Cu)sample/(65Cu/63Cu)NIST 976 − 1) × 1000 |
Iron isotopic ratios were measured in high-resolution mode (M/ΔM = ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). 53Cr, 54(Fe, Cr), 56Fe, 57Fe, 58(Fe, Ni) and 60Ni isotopes were measured in the static mode by Faraday cups at Low 3, Low 1, Central, High 1, High 2 and High 4 positions, respectively. The measured 53Cr was used to correct any 54Cr interference on 54Fe. The 56Fe signal was ∼10 V for the analyzed 1 ppm solution using the X-cone. The 54Fe signal is typically >500 mV which is important to obtain high-precision iron isotopic measurement.16 A measurement consists of four blocks of 40 cycles of ∼8 s each. Fe isotope data are reported in standard δ-notation in per mil relative to the reference material IRMM-014, as follows:
000). 53Cr, 54(Fe, Cr), 56Fe, 57Fe, 58(Fe, Ni) and 60Ni isotopes were measured in the static mode by Faraday cups at Low 3, Low 1, Central, High 1, High 2 and High 4 positions, respectively. The measured 53Cr was used to correct any 54Cr interference on 54Fe. The 56Fe signal was ∼10 V for the analyzed 1 ppm solution using the X-cone. The 54Fe signal is typically >500 mV which is important to obtain high-precision iron isotopic measurement.16 A measurement consists of four blocks of 40 cycles of ∼8 s each. Fe isotope data are reported in standard δ-notation in per mil relative to the reference material IRMM-014, as follows:
| δxFe = ((xFe/54Fe)sample/(xFe/54Fe)IRMM-014 − 1) × 1000 |
3. Accuracy and precision check
In the following sections, we address several important parameters that can lessen the quality of Cu and Fe isotopic analysis. These parameters include incomplete recovery, the effects of matrix elements (Co, Na, Ti and Fe) on the instrumental mass bias, amounts of loaded Cu and Fe, storage of Cu and Fe standard solution, acid molarity, and Cu–Fe concentration of samples.3.1 Incomplete recovery
Significant Cu and Fe isotope fractionations can occur during ion-exchange chromatography due to incomplete recovery of Cu (ref. 9 and 20) or Fe.21 Similar ion-exchange fractionation has also been found for other metal isotopes, e.g., Mg.22,23 Cu and Fe that were eluted earlier were always isotopically heavier than those eluted later, probably reflecting isotope fractionation between the resin bound and the free Cu or Fe species. We obtained similar results by analyzing the Cu cuts at a 2 ml interval eluted from USGS basalt standard BHVO-2 (Fig. 1). For example, Cu that occurs at the 17–18 ml cut is >5‰ heavier in δ65Cu than that eluted at the 25–26 ml cut (Fig. 1). Calculation with the fractionation factor shows that ∼90% recovery will produce up to 0.4‰ shift of measured δ65Cu values relative to the true value. Similar isotope fractionation was observed during Fe elution. Therefore, to reduce the impact from chemical purification and achieve accurate Cu and Fe isotope data, complete recovery must be achieved.The Cu and Fe recovery in this study has been estimated in two ways. The first was to collect the Cu cut (total 24 ml) or Fe (18 ml) eluted from natural samples (BHVO-2 and GSP-2) and then compare them with the total Cu or Fe signal in all cuts (52 ml; Fig. 1). This way yielded a recovery of Cu = 99.7 ± 0.8% (2SD, n = 5) and Fe = 99.9 ± 0.6% (2SD, n = 5). The second was to purify a given amount of pure Cu and Fe solutions and check the yields. This yielded a recovery of Cu = 99.9 ± 0.5% (2SD, n = 9) and 100.4 ± 0.8% (2SD, n = 9). Clearly, both methods yielded complete recovery for Cu and Fe during chemical purification.
3.2 Acid molarity and concentration mismatch
The possible influence of acid molarity and Cu or Fe concentration of samples and standards on isotopic analysis must be evaluated when using the sample–standard bracketing method. The effect of acid molarity on Cu isotopic analysis was evaluated by changing the acid molarity of samples (NIST 976 was used here) at certain acid molarity of bracketing standards (3% HNO3; 0.325 N) and the same Cu concentration (100 ppb). The results indicate that for high acid molarity the observed effect is a shift towards heavy isotopic composition (Table 2). For example, a 10% difference of acid molarity between samples and standards caused a shift of δ65Cu values by larger than 0.3‰. To eliminate the effect of acid molarity, the same batch of newly made 3% HNO3 was always used for samples and bracketing standards in this study.| Name | Ti/Cu | δ 65Cu | 2SD | Name | Co/Cu | δ 65Cu/δ56Fe | 2SD/2SD |
|---|---|---|---|---|---|---|---|
| Ti doping test | Co doping test | ||||||
| Ti1 | 0.001 | −0.01 | 0.05 | Co1 | 0.001 | 0.00/−0.01 | 0.04/0.05 |
| Ti2 | 0.01 | −0.02 | 0.05 | Co2 | 0.01 | 0.01/0.01 | 0.04/0.04 |
| Ti3 | 0.1 | 0.00 | 0.03 | Co3 | 0.1 | 0.03/0.00 | 0.04/0.04 |
| Ti4 | 0.3 | 0.07 | 0.04 | Co4 | 0.5 | −0.01/−0.02 | 0.06/0.02 |
| Ti5 | 0.5 | 0.14 | 0.05 | Co5 | 1 | 0.02/−0.03 | 0.02/0.03 |
| Ti6 | 1.0 | 0.28 | 0.05 | Co6 | 2 | 0.04/−0.03 | 0.05/0.04 |
| Ti7 | 10 | 3.20 | 0.07 | Co7 | 5 | 0.05/0.01 | 0.02/0.04 |
| Co8 | 10 | 0.05 | 0.04 | ||||
| Na doping test | Na/Cu | Fe doping test | Fe/Cu | ||||
| Na1 | 0.1 | 0.00 | 0.04 | Fe1 | 0.1 | −0.02 | 0.07 |
| Na2 | 0.5 | −0.01 | 0.06 | Fe2 | 0.5 | −0.02 | 0.04 |
| Na3 | 1 | −0.02 | 0.03 | Fe3 | 1 | −0.05 | 0.03 |
| Na4 | 1.2 | −0.04 | 0.03 | Fe4 | 2 | −0.10 | 0.02 |
| Na5 | 1.5 | −0.05 | 0.04 | Fe5 | 4 | −0.23 | 0.03 |
| Na6 | 2 | −0.08 | 0.04 | ||||
| Na7 | 5 | −0.18 | 0.06 | ||||
| Concentration match test | Without on-peak zero correction | Concentration match test | On-peak zero correction | ||||
| Test | C sample/Cstandard | Test | C sample/Cstandard | ||||
| CM-1 | 0.1 | −4.39 | 0.06 | CM-C1 | 0.1 | −0.01 | 0.04 |
| CM-2 | 0.2 | −2.03 | 0.06 | CM-C2 | 0.2 | 0.05 | 0.07 |
| CM-3 | 0.5 | −0.55 | 0.04 | CM-C3 | 0.5 | 0.01 | 0.04 |
| CM-4 | 0.7 | −0.31 | 0.03 | CM-C4 | 0.7 | 0.03 | 0.05 |
| CM-5 | 0.8 | −0.15 | 0.02 | CM-C5 | 0.8 | −0.02 | 0.04 |
| CM-6 | 0.9 | −0.01 | 0.06 | CM-C6 | 0.9 | 0.01 | 0.05 |
| CM-7 | 1.0 | 0.02 | 0.05 | CM-C7 | 1 | 0.01 | 0.06 |
| CM-8 | 1.1 | 0.08 | 0.02 | CM-C8 | 1.1 | 0.00 | 0.06 |
| CM-9 | 1.2 | 0.10 | 0.05 | CM-C9 | 1.2 | 0.01 | 0.06 |
| CM-10 | 1.3 | 0.16 | 0.03 | CM-C10 | 1.5 | 0.00 | 0.04 |
| CM-11 | 1.5 | 0.20 | 0.02 | CM-C11 | 1.6 | 0.03 | 0.06 |
| CM-12 | 2 | 0.32 | 0.06 | CM-C12 | 2 | 0.01 | 0.06 |
| CM-13 | 5 | 0.47 | 0.06 | CM-C13 | 5 | 0.00 | 0.06 |
| Acid match | Acid molarity (sample/std.) | Acid match | Acid molarity (sample/std.) | ||||
| AM-1 | 0.3 | −2.04 | 0.07 | AM-6 | 1.1 | 0.33 | 0.05 |
| AM-2 | 0.5 | −1.16 | 0.06 | AM-7 | 1.2 | 0.44 | 0.06 |
| AM-3 | 0.7 | −0.72 | 0.07 | AM-8 | 1.3 | 1.07 | 0.07 |
| AM-4 | 0.8 | −0.41 | 0.05 | AM-9 | 1.7 | 1.1 | 0.07 |
| AM-5 | 1.0 | 0.04 | 0.05 | ||||
The effect of the Cu concentration on Cu isotopic analysis was evaluated by changing the Cu concentration of samples (NIST 976 was used here) at certain Cu concentrations of bracketing standards (100 ppb). The results demonstrate that imperfect concentration match (>10%) can largely affect the accuracy of Cu isotopic measurements (Fig. 2a). The positive correlation between δ65Cu and the concentration ratio of sample to standard (Csample/Cstandard) suggests a small interference on 63Cu relative to 65Cu when concentrations of the sample and standard are inconsistent. We modeled the effect by assuming no interference on 65Cu. Consequently, δ65Cu values of NIST 976 Cu standard solutions relative to the standard itself can be calculated as follows:24
| δ65Cu = 1000 × f × (R − 1)/(R + f) |
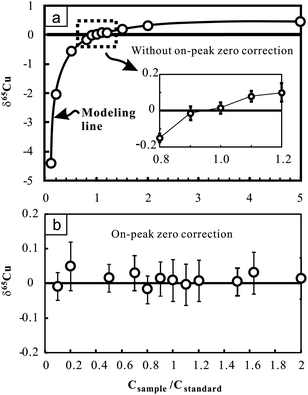 | ||
| Fig. 2 Cu isotopic ratio variation of pure Cu standard solutions (NIST 976) with changing Cu concentrations relative to the bracketing standard (NIST 976) with certain Cu concentration (100 ppb). Results obtained without on-peak zero correction (upper figure) and those obtained with on-peak zero correction (lower figure) are presented for comparison. The bold line in the upper figure indicates the modeling results by assuming that there is only interference on 63Cu. See text for details. The errors (2SD) were calculated on the basis of four times replicate measurements in an analytical session. Data are reported in Table 2. | ||
Nevertheless, when on-peak zero (OPZ) correction was applied, up to 90% concentration difference between samples and standards yields results which are still close to zero within analytical uncertainty (Fig. 2b). This suggests that limited interference on 63Cu can be effectively offset when blank contribution from acid was reasonably corrected. However, given that the composition of blanks may greatly vary with time, this correction may not be prevalent under different working conditions. For Fe isotopic analysis, up to 80% concentration difference between samples and standards also yields consistent results within analytical uncertainty when OPZ correction was applied. During the course of sample analysis, the concentration of Cu or Fe in samples is strictly set within ±10% of the standards and OPZ correction was always used.
3.3 Matrix effect
The potential molecular spectral interferents for Cu isotopic analysis include 47Ti16O, 23Na40Ar on 63Cu, 25Mg40Ar and 47Ti18O on 65Cu, etc.8 We found that Cu isotopic analysis in our working conditions is sensitive to the presence of matrix Na, Fe and Ti (Fig. 3a–c). The influence of Na on Cu isotopic analysis towards a light isotopic composition is likely a result of (23Na40Ar)+ interference on the lighter isotope of Cu (63Cu). The significant effect of Fe on Cu (and Zn) isotopic measurement was previously found by Archer and Vance.25 By contrast, Zhu et al.5 showed that Fe/Cu molar ratios up to 15 cause insignificant influence on Cu isotopic analysis using the Nu Instruments. The reason for these differences is unclear. There is no known molecular spectral interference from iron on mass 63 or 65. The significant influence of Fe on Cu isotopic analysis found in this study, however, points out that chemical purification may be necessary for Cu isotopic analysis of Fe-bearing Cu sulfides (e.g., chalcopyrite).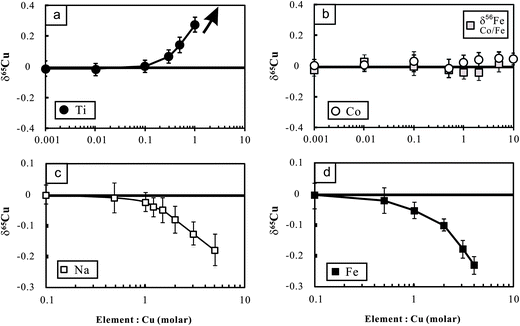 | ||
| Fig. 3 Cu isotopic variations of NIST Cu standard solutions spiked with different amounts of Ti, Co, Fe and Na relative to the unspiked Cu solution. The Cu concentration for samples and bracketing standards (NIST 976) is the same (100 ppb). The variations of Fe isotopic composition with Co/Fe are also plotted in this figure. The errors (2SD) were calculated based on four times replicate measurements. Data are reported in Table 2. | ||
The polyatomic interference from Ti on Cu isotopic analysis may be attributed to the oxides of Ti (16O47Ti and 16O49Ti) on mass 63 and 65 respectively. In addition, the hydroxides (16O1H) of 48Ti and 46Ti also have the same mass number with the two isotopes of Cu.12 Because 47Ti (7.44%) has higher natural abundance than 49Ti (5.41%), the contributions from polyatomic ions of Ti-oxides would lower the mass 65/mass 63 ratio. By contrast, 48Ti (73.72%) is more abundant than 46Ti (8.25%), and thus the contribution from polyatomic ions of Ti-hydroxides would cause the measured results towards heavy δ65Cu values when Ti is present.12 Li et al.12 found significant influence of Ti on Cu isotopic analysis towards heavy isotopic compositions using a Nu Plasma MC-ICP-MS. By contrast, Bigalke et al.7 reported a remarkable influence of Ti on Cu isotopic ratio analysis towards a light value, using the Neptune MC-ICP-MS. We measured a set of Cu-free Ti solutions with concentrations varying from 100 ppb to 1 ppm in low-resolution mode. The results showed that signals of both mass 63 and 65 increased significantly compared with the blank baseline (3% HNO3) but the mass 65/mass 53 ratios also increased from ∼0.47 to ∼0.76. This clearly demonstrates a major interference of Ti on mass 65 over 63. We also performed high-resolution (M/ΔM = ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) measurement for a mixed Ti and Cu solution (each 1 ppm) on the mass 63 and 65. There was no clearly visible shoulder, particularly at mass 65. The reasons remain unresolved.
000) measurement for a mixed Ti and Cu solution (each 1 ppm) on the mass 63 and 65. There was no clearly visible shoulder, particularly at mass 65. The reasons remain unresolved.
To overcome the matrix interference, the only way would be sufficient purification. Analysis of the Cu cuts eluted from basaltic and granitic rocks shows that the ratios of major ions (Mg, Ca, Fe, Na, Mn, etc.) to Cu were less than 0.01 after one time purification. The ratios can be markedly reduced (<0.001) after double column chemistry. The low signal of matrix elements yielded neglected influence on Cu isotopic measurement (Fig. 3). Titanium, however, was commonly found in the Cu cuts eluted from these rocks, with Ti/Cu up to ∼0.3 (e.g., basalt BHVO-2) after one purification due to high Ti/Cu in the rocks (>100). The modest Ti/Cu ratio of 0.3 would cause an offset of ∼0.15‰ relative to the true δ65Cu value (Fig. 3a). A second purification is thus needed. After double column chemistry, Ti/Cu can be reduced to less than 0.03 for all analyzed samples which contributed neglectful influence on Cu isotope ratio analysis.
Different from Cu, only one column chemistry has been undertaken for Fe in all analyzed rock samples. After single column chemistry, the ratios of all ions to Fe were found to be less than 0.01. The signal ratio of 53Cr/54Fe is commonly at or below the level of 10−5. Such low signals of interferents did not generate any detectable influence on Fe isotopic measurement. It is noted that Co was completely separated from Cu in the 8 N HCl medium but it was shifted into the fraction of Fe in 2 N HCl. Experiments were thus designed to evaluate the possible interference of Co on Fe isotopic analysis. The results show that Co/Fe ratios up to 5 did not produce detectable impact on Fe isotopic analysis (Fig. 3b).
3.4 The amount of loaded Cu/Fe and Cu/Fe solution storage
Because Cu in most rocks only constitutes a small amount, it is necessary to evaluate any possible effect of the amount of loaded Cu on the accuracy of Cu isotopic analysis by considering the contribution from the blank. Therefore, different amounts of in-house mono-elemental Cu standards (GSB Cu; >99.99%) from 0.4 to 20 μg were routinely purified over an eleven month period. For comparison, the purified samples were measured against the unprocessed in-house standard itself. The results yielded consistent δ65Cu values within analytical uncertainty for all samples containing Cu from 0.4 to 20 μg, with a weighted average δ65Cu = 0.006 ± 0.05‰ (2SD; n = 21) relative to the unprocessed standard (Fig. 4). This suggests that the contribution from blank (averaged ∼1.5 ng) is still insignificant when the amount of Cu loaded to the column is as low as 0.4 μg (blank: sample = ∼0.3%). A calculation should indicate that contamination of the sample with 0.3% blank, for which an extreme positive δ65Cu value of +10‰ (ref. 26) is assumed, would cause an undetectable shift (+0.03‰) on Cu isotopic composition. If the extreme negative value (∼−17‰)26 is assumed, the shift would be ca. +0.05‰. Furthermore, the average δ65Cu values of all purified samples are close to zero relative to the unpurified standards, suggesting that no Cu isotope fractionation has been generated during chemical purification. The loaded amounts of Fe in all samples analyzed in this study range from ∼0.6 to 0.9 mg, which are one hundred thousand times larger than the total procedural blank (∼6 ng). The blank contributions on Fe isotopic analysis are thus considered neglectful.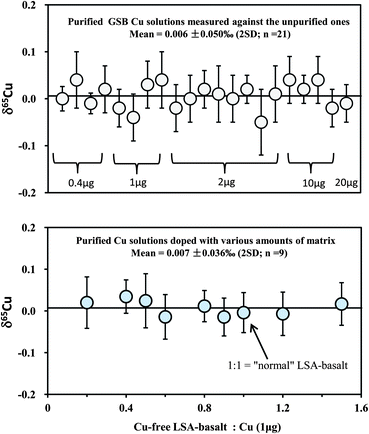 | ||
Fig. 4 Test of the effect of the amount of loaded Cu on the accuracy of Cu isotopic analysis (upper diagram). In-house mono-element standard solutions (GSB Cu) were prepared to contain different amounts of Cu (0.4–20 μg) and were purified through column chemistry. Cu isotopic ratios were measured relative to the in-house standard itself. A set of solutions with 1 μg pure Cu (NIST 976), mixed with various amounts of synthetic Cu-free LSA-basalt, were processed through column chemistry (twice) and measured against NIST 976 (lower diagram). The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu-free LSA-basalt to Cu is equal to that in the “normal” Cu-containing LSA-basalt. The errors (2SD) were based on four times replicate measurements. Data are reported in Table 3. 1 ratio of Cu-free LSA-basalt to Cu is equal to that in the “normal” Cu-containing LSA-basalt. The errors (2SD) were based on four times replicate measurements. Data are reported in Table 3. | ||
To avoid an important systematic bias, it is critical to ensure that no isotopic changes occur in the bracketing standard. One primary concern is the effect of long-term storage of working standards in plastic bottles. Significant deviation of isotopic ratios of standards with time has been observed for Mg.27 Storage of the pure, concentrated GSB Cu and IRMM-014 Fe standards (100 ppm) in 50 ml clean fluorinated plastic (Teflon®) bottles for one year has not caused any detectable deviations in Cu and Fe isotopic ratios. This indicates that no any systematic bias occurred in the bracketing standards, and thus, the samples analyzed.
3.5 Cu isotopic analysis with Zn-doping
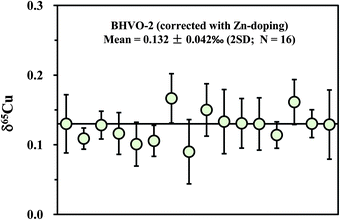
Apart from the SSB method, external (inter-element) normalization using Zn or Ni was also commonly pursued to correct for instrumental mass bias during Cu isotopic measurement.1,3,4 Compared with the external normalization, sample–standard bracketing does not require either introduction of a known 66/68Zn/64Zn ratio or removal of natural Zn in a sample. By contrast, Zn must be completely removed and an external standard with known 66/68Zn/64Zn ratio must be introduced before isotopic analysis. Compared with external normalization, however, sample–standard bracketing may not account for machine drift such as variations in the plasma, temperature, etc. We measured a processed (twice) natural basalt sample (BHVO-2) by using Zn (SRM 3168a standard solution) as an external standard. Mass fractionation was first corrected with the exponential mass bias function.4 The delta values were then calculated by calibrating the mass bias-corrected Cu isotopic ratios against the mean of two adjacent standards (NIST 976). The slopes (S) on the plot of ln64Zn/66Zn versus ln63Cu/65Cu, measured in mixed Cu + Zn (each 100 ppb) standard solutions, slightly vary on different days (from 0.99 to 1.10) but are almost constant within one session (24 h). The inconstant variation of S with time has been previously observed.4 The 65Cu/63Cu ratios were therefore calculated by reference to the standard regression line measured on each day. The measured results for BHVO-2 are plotted in Fig. 6. The average δ65Cu value is +0.132 ± 0.042‰ (2SD; n = 16). This value is in agreement within uncertainty with the result measured by the SSB method (+0.150 ± 0.050‰). Compared with the SSB method, it seems that there is no significant improvement of the analytical precision. This may be in part due to the stability of the machines that have either constant or negligible drift.3.6 Precision and accuracy check
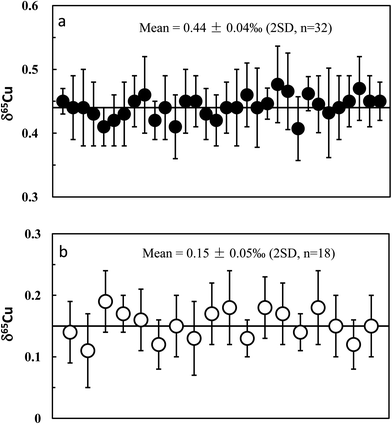
Repeat analyses of the in-house Cu standards (GSB Cu) and well-studied igneous rock standards allow evaluation of our long-term analytical precision and accuracy. Long-term analysis of the GSB Cu solutions over a six month period gave an average δ65Cu of +0.44 ± 0.04‰ (2SD; n = 32) relative to NIST 976 (Fig. 5a). The precision reflects the long-term external reproducibility of pure Cu solution measurement. Compared with the precision obtained from processed GSB Cu solution (±0.05‰; 2SD), the results indicate that the purification processes do not result in a significant shift in analytical precision. A synthetic “basalt” (LSA-basalt) was made to have a chemical composition similar to the average LCC28 by spiking the Cu standard (NIST 976) with Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe
Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn
Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr
Cr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti
Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na
Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mg
Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K
K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al
Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca
Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn = 1
Mn = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2500
2500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4
3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190
190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1700
1700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4500
4500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2600
2600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. The “basalt” sample was processed through column chemistry (two times) as the same as done for the natural rock samples. The long-term analysis (over ten months) yielded a mean δ65Cu = −0.004 ± 0.048‰ (2SD; n = 9; Table 3). This value is identical within uncertainty to zero, indicating accurate and precise Cu isotopic analysis.
30. The “basalt” sample was processed through column chemistry (two times) as the same as done for the natural rock samples. The long-term analysis (over ten months) yielded a mean δ65Cu = −0.004 ± 0.048‰ (2SD; n = 9; Table 3). This value is identical within uncertainty to zero, indicating accurate and precise Cu isotopic analysis.
| Sample type | Cu (μg/g) | Session | δ 65Cu | 2SD | n | Ti/Cu after purification | Commentsb |
|---|---|---|---|---|---|---|---|
a The times of repeat measurements of the same purification solution by MC-ICP-MS. 2SD = 2 times the standard deviation of the population of n repeat measurements of a sample solution.
b All samples were processed two times through column chemistry except the one of the standard BHVO-2 as indicated. 10 or 20 mg denotes the weight of primary sample powder which was dissolved and loaded into the column.
c 1 μg Cu (NIST 976 standard) was spiked with various amounts of Cu-free LSA-basalt (Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr Cr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mg Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn = 2500 Mn = 2500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4 3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1700 1700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4500 4500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2600 2600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30). The “mixed” sample was processed through column chemistry as the same as done for the samples. If no isotope fractionation occurs during column chemistry the value should be close to zero. 30). The “mixed” sample was processed through column chemistry as the same as done for the samples. If no isotope fractionation occurs during column chemistry the value should be close to zero.
|
|||||||
| BHVO-2, Basalt, Hawaiian, USA | 127 | 1 | 0.14 | 0.05 | 4 | 0.20 | 1–3 used the same bulk raw solution; 1 was processed only one time, each 10 mg |
| 2 | 0.11 | 0.06 | 4 | 0.01 | |||
| 3 | 0.19 | 0.05 | 4 | 0.01 | |||
| 4 | 0.17 | 0.03 | 4 | 0.01 | Merged from Cu cuts, 20 mg | ||
| 5 | 0.16 | 0.05 | 4 | <0.01 | New digestion; 20 mg | ||
| 6 | 0.12 | 0.04 | 4 | 0.01 | New digestion, 10 mg | ||
| 7 | 0.15 | 0.05 | 4 | 0.02 | New digestion, 10 mg | ||
| 8 | 0.13 | 0.06 | 4 | 0.01 | New digestion, 10 mg | ||
| 9 | 0.17 | 0.05 | 4 | 0.01 | 9–13 used the same bulk raw solution, each 10 mg | ||
| 10 | 0.18 | 0.06 | 4 | <0.01 | |||
| 11 | 0.13 | 0.03 | 4 | <0.01 | |||
| 12 | 0.18 | 0.05 | 4 | 0.01 | |||
| 13 | 0.17 | 0.05 | 4 | 0.01 | |||
| 14 | 0.14 | 0.03 | 4 | 0.01 | 13–15 used the sample purified solution measured in different days (over 3 months) | ||
| 15 | 0.18 | 0.06 | 4 | 0.01 | |||
| 16 | 0.15 | 0.05 | 6 | <0.01 | 16 and 17 used the same bulk raw solution, each 10 mg | ||
| 17 | 0.12 | 0.04 | 6 | <0.01 | |||
| 18 | 0.15 | 0.05 | 6 | 0.01 | New digestion, 10 mg | ||
| Average (n = 18) | 0.15 | 0.05 | This study | ||||
| 0.10 | 0.10 | Weinstein et al. (2011) | |||||
| BIR-1a, Basalt, Iceland | 125 | 1 | −0.02 | 0.05 | 2 | <0.01 | 1 and 2 used the same bulk raw solution, each 10 mg |
| 2 | 0.01 | 0.04 | 4 | <0.01 | |||
| 3 | 0.02 | 0.05 | 4 | <0.01 | New digestion, 20 mg | ||
| 4 | 0.01 | 0.05 | 6 | <0.01 | 4 and 5 used the sample purified solution measured on different days (over 2 months). | ||
| 5 | −0.03 | 0.06 | 4 | <0.01 | |||
| 6 | 0.03 | 0.05 | 6 | <0.01 | New digestion, 10mg | ||
| Average (n = 6) | 0.00 | 0.05 | This study | ||||
| BIR-1, Basalt, Iceland | 125 | 1 | −0.02 | 0.05 | 4 | <0.01 | 1 and 2 used the same bulk raw solution, each 10 mg |
| 2 | −0.01 | 0.04 | 6 | <0.01 | |||
| 3 | −0.03 | 0.04 | 4 | <0.01 | New digestion, 10 mg | ||
| 4 | 0.01 | 0.05 | 4 | 0.01 | New digestion, 20 mg | ||
| 5 | 0.02 | 0.04 | 4 | <0.01 | New digestion, 10 mg | ||
| Average (n = 5) | −0.01 | 0.04 | This study | ||||
| −0.02 | 0.10 | Li et al. (2009) | |||||
| JB-3, Basalt, Japan | 199 | 1 | 0.18 | 0.07 | 4 | 0.01 | 1 and 2 used the same bulk raw solution, each 10 mg |
| 2 | 0.16 | 0.03 | 4 | 0.01 | |||
| 3 | 0.15 | 0.06 | 4 | <0.01 | New digestion, 20 mg | ||
| Average (n = 3) | 0.16 | 0.03 | This study | ||||
| BCR-2 | 19 | 1 | 0.22 | 0.05 | 4 | 0.02 | New digestion, 20 mg |
| Basalt, USGS | 2 | 0.22 | 0.04 | 4 | 0.03 | New digestion, 20 mg | |
| Average (n = 2) | 0.22 | 0.04 | |||||
| 0.22 | 0.06 | Bigalke et al. (2010a) | |||||
| 0.18 | 0.09 | Bigalke et al. (2011) | |||||
| GSP-2, Granodiorite, USGS | 43 | 1 | 0.32 | 0.05 | 4 | 0.01 | 1 and 2 used the same bulk raw solution, each 20 mg |
| 2 | 0.31 | 0.05 | 4 | 0.01 | |||
| 3 | 0.28 | 0.03 | 4 | <0.01 | New digestion, 20 mg | ||
| Average (n = 3) | 0.30 | 0.04 | This study | ||||
| 0.35 | 0.06 | Bigalke et al. (2010b) | |||||
| 0.25 | 0.03 | Bigalke et al. (2010a) | |||||
| AGV-2, Andesite, USGS | 1 | 0.06 | 0.04 | 4 | 0.01 | New digestion, 20 mg | |
| 2 | 0.05 | 0.04 | 0.01 | New digestion, 20 mg | |||
| Average (n = 2) | 0.05 | 0.04 | This study | ||||
| 0.10 | 0.10 | Weinstein et al. (2011) | |||||
| GBW07105, Basalt, China | 49 | 1 | 0.09 | 0.06 | 4 | 0.03 | New digestion, 20 mg |
| 2 | 0.11 | 0.07 | 4 | 0.02 | New digestion, 10 mg | ||
| 3 | 0.08 | 0.04 | 4 | 0.02 | 3 and 4 used the same bulk raw solution, each 20 mg | ||
| 4 | 0.09 | 0.06 | 4 | 0.02 | |||
| Average (n = 4) | 0.09 | 0.03 | This study | ||||
| GBW07122, Amphibolite, China | 84 | 1 | 0.38 | 0.04 | 4 | <0.01 | 1 and 2 used the same bulk raw solution, each 20 mg |
| 2 | 0.43 | 0.06 | 4 | 0.01 | |||
| 3 | 0.37 | 0.07 | 4 | 0.01 | New digestion, 10 mg, | ||
| Average (n = 3) | 0.39 | 0.06 | This study | ||||
| W-2a, Diabase, Virginia | 110 | 1 | 0.10 | 0.08 | 4 | <0.01 | 1 and 2 used the same bulk raw solution, each 10 mg |
| 2 | 0.11 | 0.05 | 4 | <0.01 | |||
| 3 | 0.11 | 0.04 | 4 | <0.01 | New digestion, 10 mg | ||
| Average (n = 2) | 0.11 | 0.02 | <0.01 | This study | |||
| JA-1 | 42 | 1 | 0.31 | 0.04 | 4 | <0.01 | 1 and 2 used the same bulk raw solution, each 10 mg |
| 2 | 0.28 | 0.07 | 4 | <0.01 | |||
| 3 | 0.29 | 0.04 | 4 | <0.01 | New digestion, 20 mg | ||
| Average (n = 2) | 0.29 | 0.03 | This study | ||||
Cu-free LSA-basalt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu Cu |
|||||||
| Mixed Cu + LSA-basaltc | 0.2 | 0.02 | 0.06 | 4 | — | ||
| 0.4 | 0.03 | 0.04 | 4 | — | |||
| 0.5 | 0.02 | 0.06 | 4 | — | |||
| 0.6 | −0.01 | 0.05 | 4 | — | |||
| 0.8 | 0.01 | 0.04 | 4 | — | |||
| 0.9 | −0.01 | 0.05 | 4 | — | |||
| 1.0 | 0.00 | 0.05 | 4 | — | Mean of 9 repeat analyses | ||
| 1.2 | −0.01 | 0.05 | 4 | — | |||
| 1.5 | 0.02 | 0.05 | 4 | — | |||
| Average (n = 9) | 0.007 | 0.036 | |||||
In addition, we separated a set of synthetic solutions with a fixed amount of Cu contained in solution of variable ionic strength. The aim was to test the effect of the amount of matrix on Cu purification. NIST 976 Cu standard (1 μg) was mixed with the remade Cu-free LSA-basalt, with the ratios of Cu-free LSA-basalt to Cu varying from 0.2 to 1.5 (note that the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is equal to that in the original Cu-containing LSA-basalt). All mixed samples were processed through column and all values were close to zero with an average δ65Cu = 0.007 ± 0.038‰ (2SD; n = 9) (Fig. 4). The results indicate that Cu can be well separated from the matrix for considerably high ions/Cu samples with complete recovery.
1 is equal to that in the original Cu-containing LSA-basalt). All mixed samples were processed through column and all values were close to zero with an average δ65Cu = 0.007 ± 0.038‰ (2SD; n = 9) (Fig. 4). The results indicate that Cu can be well separated from the matrix for considerably high ions/Cu samples with complete recovery.
At least two repeat measurements were performed over a ten month period for all igneous rock geostandards in this study. These analyses include independent digestion of the same rock powder, duplicate column chemistry using aliquots of the same bulk raw solution, different amounts of loaded Cu, duplicate measurements of purified Cu solutions on different days, as well as combination of Cu cuts (Table 2). Hawaiian basalt BHVO-2 was most frequently analyzed, which has an average δ65Cu = +0.15‰ ± 0.05‰ (2SD; n = 18). The consistent values among samples with independent digestion suggest homogeneous Cu isotopic composition of the rock powers of basalt standard BHVO-2 (Fig. 5b). A purified solution was measured on different days (over 3 months) and yielded consistent results (Table 3), again suggesting that the Cu isotopic composition of the Cu solution did not deviate with time. The δ65Cu value of BHVO-2 obtained here is lightly heavier than but similar within uncertainty to the value (+0.10 ± 0.10‰; 2SD) reported by Weinstein et al.29 Given the most frequent analyses, we recommend a reference δ65Cu value of +0.15‰ for the international basalt standard material BHVO-2.
The Columbia River basalt standard (BCR-2) has an average δ65Cu = +0.22 ± 0.04‰ (2SD). This δ65Cu value is in agreement within uncertainty with that (+0.22 ± 0.06‰) reported by Bigalke et al.30 and +0.18 ± 0.09‰ reported by Bigalke et al.7 The USGS granodiorite standard GSP-2 has an average δ65Cu = +0.30 ± 0.04‰ (2SD). Bigalke et al.7,30 reported two values (+0.25 ± 0.05‰ and +0.35‰) for GSP-2, with a difference of 0.10‰. The value obtained in this study is slightly different but agrees within uncertainty with their results. The Icelandic basalt standard BIR-1a has an average Cu isotopic composition equivalent to the NIST 976 Cu standard, with δ65Cu = 0.00 ± 0.05‰ (2SD; n = 6). Another set (BIR-1) of the Icelandic basalt standard has an average δ65Cu = −0.01 ± 0.04‰ (2SD; n = 5) identical to the value of BIR-1a. The value for BIR-1 reported here is in agreement with the value (−0.02 ± 0.10‰) reported by Li et al.12
| Sample | Sessiona | δ 56Fe | 2SD | δ 57Fe | 2SD | n | Comments |
|---|---|---|---|---|---|---|---|
| a All samples were processed through only one column chemistry. The session numbers correspond to the same numbers as in Cu isotopic analysis (Table 3), during which Cu and Fe were eluted through a single column. b Iron in the LSA-basalt was made from the GSB Fe solution and the purified (one time) samples were measured against the original GSB Fe solution. | |||||||
| BHVO-2 | 1 | 0.085 | 0.059 | 0.140 | 0.038 | 4 | 1–3 used the same bulk raw solution |
| 2 | 0.137 | 0.025 | 0.190 | 0.074 | 4 | ||
| 3 | 0.143 | 0.020 | 0.197 | 0.061 | 4 | ||
| 4 | 0.148 | 0.050 | 0.246 | 0.042 | 4 | New digestion | |
| 5 | 0.149 | 0.043 | 0.239 | 0.063 | 4 | New digestion | |
| 6 | 0.132 | 0.043 | 0.223 | 0.029 | 4 | New digestion | |
| 7 | 0.111 | 0.040 | 0.191 | 0.038 | 4 | New digestion | |
| 8 | 0.090 | 0.047 | 0.167 | 0.037 | 4 | New digestion | |
| 9 | 0.116 | 0.042 | 0.192 | 0.057 | 4 | 9 and 10 used the same bulk raw solution | |
| 10 | 0.109 | 0.048 | 0.189 | 0.054 | 4 | ||
| 11 | 0.124 | 0.038 | 0.199 | 0.052 | 4 | New digestion | |
| 12 | 0.114 | 0.041 | 0.175 | 0.049 | 4 | New digestion | |
| Average (n = 12) | 0.121 | 0.049 | 0.175 | 0.064 | |||
| BIR-1a | 0.060 | 0.042 | 0.085 | 0.072 | 9 | ||
| BIR-1 | 0.078 | 0.027 | 0.130 | 0.069 | 4 | ||
| JB-3 | 1 | 0.099 | 0.033 | 0.149 | 0.046 | 4 | |
| 2 | 0.103 | 0.050 | 0.171 | 0.059 | 4 | ||
| BCR-2 | 0.107 | 0.025 | 0.170 | 0.013 | 3 | ||
| GSP-2 | 1 | 0.173 | 0.031 | 0.250 | 0.067 | 4 | New digestion |
| 2 | 0.164 | 0.060 | 0.246 | 0.089 | 4 | New digestion | |
| AGV-2 | 0.106 | 0.036 | 0.179 | 0.025 | 4 | ||
| GBW07105 | 0.146 | 0.035 | 0.221 | 0.056 | 4 | ||
| GBW07122 | 0.069 | 0.020 | 0.096 | 0.069 | 4 | ||
| W-2a | 0.036 | 0.053 | 0.054 | 0.016 | 3 | ||
| JA-1 | 0.057 | 0.019 | 0.100 | 0.048 | 3 | ||
| LSA-basaltb | −0.008 | 0.041 | −0.010 | 0.059 | 40 | ||
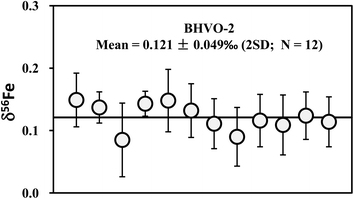 | ||
| Fig. 7 Long-term analyses of Fe isotopic compositions of international basalt standard BHVO-2. The data are reported in Table 4. The mean δ56Fe value is 0.121 ± 0.049‰ (2SD; n = 12). | ||
The Cu and Fe isotopic results obtained in this study are plotted against the literature data in Fig. 8a and b. Our data are generally consistent with literature data for all analyzed standards. In summary, accurate and precise analysis of Cu and Fe isotopic ratios can be achieved using the established procedure. A long-term external reproducibility better than ±0.05‰ (2SD) of both δ65Cu and δ56Fe measurement for silicate rocks can be routinely obtained. This allows for economical and efficient study of stable Cu and Fe isotopic systematics in geological and biological fields.
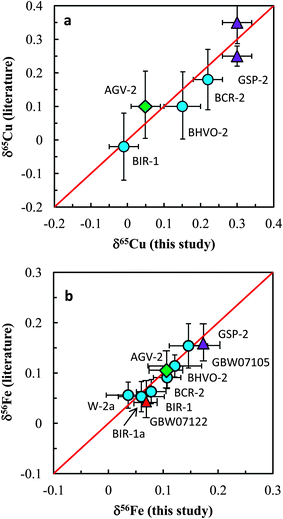 | ||
| Fig. 8 Comparison of Cu and Fe isotopic compositions of igneous rock standards reported in this study and those reported in the literature. The data from this study and literature are listed in Tables 3 and 4. Iron isotopic data of igneous rock standards are widely available in the literature and only the data from Carddock and Dauphas32 are plotted here for comparison. | ||
4. Copper and iron isotopic composition of igneous rock standards
Totally eleven international igneous rock standards were analyzed in this study. The δ56Fe values of all standards are in the range of ±0.10‰. However, the overall range of δ65Cu is up to 0.40‰ (−0.01 to +0.39‰). Basalt standards BIR-1 and BIR-1a have the lightest Cu isotopic composition of zero among all geostandards analyzed, and the amphibolite standard from China (GBW07122) has the heaviest Cu isotopic composition (+0.39‰). Given the long-term reproducibility of Cu isotopic analysis (±0.05‰; 2SD) routinely obtained in this study, we conclude that the range can be significantly discriminated, which represents about 8 times that of the analytical precision.Previous studies have suggested a similar Cu isotopic composition among mid-oceanic ridge basalt (MORB),31 oceanic island basalt (OIB),23 continental basalt,25 peridotite33 and granite.12 A mean value of zero relative to NIST 976 has been recommended for the Cu isotopic composition of these silicate reservoirs in the Earth. The bulk silicate Earth (BSE) is thus believed to have δ65Cu close to zero. However, the results from some natural rock standards obtained in this study have shown that Cu isotopic compositions of basalts or diabases (BCR-2, BIR-1, JB-3, W-2a and GBW07105) are significantly different (Fig. 9). Although only two andesite geostandards (AGV-2 and JA-1) have been analyzed, they also have different Cu isotopic compositions (Fig. 9). This suggests that the Cu isotopic composition of intermediate-felsic rocks is also not homogeneous.
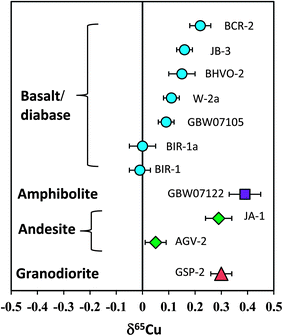 | ||
| Fig. 9 Cu isotopic composition of silicate rock standards reported in this study. The results clearly demonstrate that the Cu isotopic composition of igneous rocks, including basaltic and felsic rocks, is not homogeneous. The overall δ65Cu variation can be distinguished by the current analytical precision. Data are reported in Table 3. | ||
If one assumes that these rock standards were significantly free to surface alteration after intrusion or eruption, the detectable Cu isotopic variation among igneous rocks should reflect either high-temperature magmatic processes or isotopic heterogeneity in the source regions. Cu isotope fractionation during crystal-melt differentiation of granitic magmas may be small as revealed by a granite study,12 although they reported an overall δ65Cu variation of >0.4‰. It is currently unclear that to what extents these variations reflect magmatic differentiation. A detailed evaluation of these mechanisms is beyond the scope of the present study. Nevertheless, the results indicate that Cu isotopic variations should not be confined to the realm of biology or low temperature aqueous geochemistry but may also occur at high temperature magmatic processes. This makes the Cu isotope a potential tracer for high-temperature magmatic processes in addition to its wide application to low-temperature geochemistry. Further studies are needed to better address (i) to what extents Cu isotopic compositions of igneous rocks may vary and (ii) how these variations were caused.
5. Conclusion
We reported a method for high-precision Cu and Fe isotopic ratio analysis by MC-ICP-MS using the sample–standard bracketing method. Cu and Fe were separated from the matrix through a single column using strong anion resin AG-MP-1M. Several important parameters such as incomplete recovery, acid molarity and concentration mismatch, and isobaric interference from matrix elements (Ti, Na, and Fe) were found to significantly affect the accuracy and precision of isotopic ratio measurements. After these parameters were fully addressed, long-term external reproducibility better than ±0.05‰ (2SD) for δ65Cu and δ56Fe has been routinely obtained.Cu and Fe isotopic compositions of eleven commercially accessible igneous rock standards including basalt, diabase, amphibolite, andesite and granodiorite were measured. Their Fe isotopic compositions are relatively uniform, whereas Cu isotopic compositions vary significantly from −0.01 to +0.39‰. The 0.40‰ range exceeds about 8 times that of the external analytical precision. The results thus demonstrate that igneous rocks may not be homogeneous in Cu isotopic composition, and the Cu isotope could be used to trace high-temperature magma processes in addition to its wide application to low-temperature geochemistry.
Acknowledgements
This work is supported by the National Natural Foundation of China (41203013) to SAL. We are grateful to Prof. X.-K. Zhu for kindly providing us with the SRM Cu standard NIST 976. We thank the editor Harriet Brewerton and two anonymous reviewers for very constructive and helpful comments which largely improved the manuscript.Notes and references
- W. R. Shields, T. J. Murphy and E. L. Garner, J. Res. Natl. Bur. Stand., Sect. A, 1964, 68, 589–592 CrossRef
.
- E. C. Walker, F. Cuttitta and F. E. Senftle, Geochim. Cosmochim. Acta, 1958, 15, 183–194 CrossRef CAS
.
- R. Mathur, L. Jin, V. Prush, J. Paul, C. Ebersole, A. Fornadel, J. Z. Williams and S. Brantley, Chem. Geol., 2012, 304–305, 175–184 CrossRef CAS PubMed
.
- C. N. Maréchal, P. Télouk and F. Albarède, Chem. Geol., 1999, 156, 251–273 CrossRef
.
- X. K. Zhu, R. K. O'Nions, Y. Guo, N. S. Belshaw and D. Rickard, Chem. Geol., 2000, 163, 139–149 CrossRef CAS
.
- D. M. Borrok, R. B. Wanty, W. I. Ridley, R. Wolf, P. J. Lamothe and M. Adams, Chem. Geol., 2007, 242, 400–414 CrossRef CAS PubMed
.
- M. Bigalke, S. Weyer and W. Wilcke, Geochim. Cosmochim. Acta, 2011, 75, 3119–3134 CrossRef CAS PubMed
.
- T. F. D. Mason, D. J. Weiss, M. S. A. Horstwood, R. R. Parrish, S. S. Russell, E. Mullane and B. J. Coles, J. Anal. At. Spectrom., 2004, 19, 209–217 RSC
.
- X. K. Zhu, Y. Guo, R. J. P. Williams, R. K. O'Nions, A. Matthews, N. S. Belshaw, G. W. Canters, E. C. de Waal, U. Weser, B. K. Burgess and B. Salvato, Earth Planet. Sci. Lett., 2002, 200, 47–62 CrossRef CAS
.
- J.-M. Luck, D. B. Othman and F. Albarède, Geochim. Cosmochim. Acta, 2005, 69, 5351–5363 CrossRef CAS PubMed
.
- J. Bermin, D. Vance, C. Archer and P. J. Statham, Chem. Geol., 2006, 226, 280–297 CrossRef CAS PubMed
.
- W. Q. Li, S. E. Jackson, N. J. Pearson, O. Alard and B. W. Chappell, Chem. Geol., 2009, 258, 38–49 CrossRef CAS PubMed
.
- B. L. Beard, C. M. Johnson, L. Cox, H. Sun, K. H. Nealson and C. Aguilar, Science, 1999, 285, 1889–1892 CrossRef CAS
.
- C. M. Johnson, B. L. Beard, C. Klein, N. J. Beukes and E. E. Roden, Geochim. Cosmochim. Acta, 2008, 72, 151–169 CrossRef CAS PubMed
.
- M. S. Fantle and D. J. DePaolo, Earth Planet. Sci. Lett., 2004, 228, 547–562 CrossRef CAS PubMed
.
- N. Dauphas, A. Pourmand and F.-Z. Teng, Chem. Geol., 2009, 267, 175–184 CrossRef CAS PubMed
.
- A. Fernandez and D. M. Borrok, Chem. Geol., 2009, 264, 1–12 CrossRef CAS PubMed
.
- S. Graham, N. Pearson, S. Jackson, W. Griffin and S. Y. O'Reilly, Chem. Geol., 2004, 207, 147–169 CrossRef CAS PubMed
.
- P. B. Larson, K. Maher, F. C. Ramos, Z. Chang, M. Gaspar and L. D. Meinert, Chem. Geol., 2003, 201, 337–350 CrossRef CAS PubMed
.
- C. Maréchal and F. Albarède, Geochim. Cosmochim. Acta, 2002, 66, 1499–1509 CrossRef
.
- A. Anbar, J. Roe, J. Barling and K. Nealson, Science, 2000, 288, 126–128 CrossRef CAS
.
- F.-Z. Teng, M. Wadhwa and R. T. Helz, Earth Planet. Sci. Lett., 2007, 261, 84–92 CrossRef CAS PubMed
.
- J. A. Baker, M. Schiller and M. Bizzarro, Geochim. Cosmochim. Acta, 2012, 77, 415–431 CrossRef CAS PubMed
.
- X. K. Zhu, A. Makishima, Y. Guo, N. S. Belshaw and R. K. O'Nions, Int. J. Mass Spectrom., 2002, 220, 21–29 CrossRef CAS
.
- C. Archer and D. Vance, J. Anal. At. Spectrom., 2004, 19, 656–665 RSC
.
- R. Mathur, S. Titley, F. Barra, S. Brantley, M. Wilson, A. Phillips, F. Munizaga, V. Maksaev, J. Vervoort and G. Hart, J. Geochem. Explor., 2009, 102, 1–6 CrossRef CAS PubMed
.
- F. Huang, J. Glessner, A. Ianno, C. Lundstrom and Z. Zhang, Chem. Geol., 2009, 268, 15–23 CrossRef CAS PubMed
.
- R. L. Rudnick and S. Gao, Treatise Geochem., 2003, 1–64 CrossRef
.
- C. Weinstein, F. Moynier, K. Wang, R. Paniello, J. Foriel, J. Catalano and S. Pichat, Chem. Geol., 2011, 286, 266–271 CAS
.
- M. Bigalke, S. Weyer and W. Wilcke, Soil Sci. Soc. Am. J., 2010, 74, 60–73 CrossRef CAS
.
- M.-A. Millet, J. A. Baker and C. E. Payne, Chem. Geol., 2012, 304–305, 18–25 CrossRef CAS PubMed
.
- P. R. Carddock and N. Dauphas, Geostand. Geoanal. Res., 2010, 35, 101–123 CrossRef
.
- B. Othman, D. Luck, J. M. Bodinier, N. T. Arndt and F. Albarede, Geochim. Cosmochim. Acta, 2006, 70, A46 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |