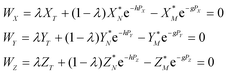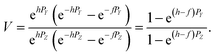Precise determination of δ88Sr in rocks, minerals, and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes
Leonid A.
Neymark
*a,
Wayne R.
Premo
a,
Nikolay N.
Mel'nikov
b and
Poul
Emsbo
c
aUS Geological Survey, Denver Federal Center, Box 25046, MS 963, Denver, CO 80225, USA. E-mail: lneymark@usgs.gov; Tel: +1 (303) 236 7898
bInstitute of Precambrian Geology and Geochronology, Russian Academy of Sciences, nab. Makarova 2, St. Petersburg, 199034, Russia
cUS Geological Survey, Denver Federal Center, Box 25046, MS 973, Denver, CO 80225, USA
First published on 31st October 2013
Abstract
We present strontium isotopic (88Sr/86Sr and 87Sr/86Sr) results obtained by 87Sr–84Sr double spike thermal ionization mass-spectrometry (DS-TIMS) for several standards as well as natural water samples and mineral samples of abiogenic and biogenic origin. The detailed data reduction algorithm and a user-friendly Sr-specific stand-alone computer program used for the spike calibration and the data reduction are also presented. Accuracy and precision of our δ88Sr measurements, calculated as permil (‰) deviations from the NIST SRM-987 standard, were evaluated by analyzing the NASS-6 seawater standard, which yielded δ88Sr = 0.378 ± 0.009‰. The first DS-TIMS data for the NIST SRM-607 potassium feldspar standard and for several US Geological Survey carbonate, phosphate, and silicate standards (EN-1, MAPS-4, MAPS-5, G-3, BCR-2, and BHVO-2) are also reported. Data obtained during this work for Sr-bearing solids and natural waters show a range of δ88Sr values of about 2.4‰, the widest observed so far in terrestrial materials. This range is easily resolvable analytically because the demonstrated external error (±SD, standard deviation) for measured δ88Sr values is typically ≤0.02‰. It is shown that the “true” 87Sr/86Sr value obtained by the DS-TIMS or any other external normalization method combines radiogenic and mass-dependent mass-fractionation effects, which cannot be separated. Therefore, the “true” 87Sr/86Sr and the δ87Sr parameter derived from it are not useful isotope tracers. Data presented in this paper for a wide range of naturally occurring sample types demonstrate the potential of the δ88Sr isotope tracer in combination with the traditional radiogenic 87Sr/86Sr tracer for studying a variety of biological, hydrological, and geological processes.
1. Introduction
Variations in the radiogenic isotopic composition of Sr (87Sr/86Sr) are widely used as a tracer in a variety of biological, hydrological, and geological processes. Until recently, the stable Sr isotopic ratio (88Sr/86Sr) was used for internal normalization to correct for instrumental mass bias, thus masking natural mass-dependent Sr isotopic fractionation. The pioneering work of Patchett1,2 demonstrated up to 1.5‰ amu−1 mass-dependent Sr isotopic variation in the meteorite Allende. Subsequent studies based on newly developed MC-ICPMS and double-spike (DS) TIMS methods have begun to document 88Sr/86Sr variability in terrestrial samples.3–10 These studies highlight the unique potential for this isotope system, especially when combined with measurements of radiogenic Sr (87Sr/86Sr). Namely, this area of study opens up an entirely new direction in the field of non-traditional stable isotope geochemistry because high-precision Sr isotope composition records information about both the source of Sr and processes causing mass-dependent isotope fractionation.The natural processes responsible for strontium isotope fractionation currently are not well understood. The documented Sr isotope fractionation in carbonates is apparently controlled by temperature.3 Also, it was shown10 that the fractionation may increase at higher precipitation rates. First ICPMS measurements of igneous rocks lead to the estimation of the δ88Sr† ∼0.27‰ value in bulk silicate Earth,11 which is lower than δ88Sr ∼ 0.39‰ in modern oceanic water, the highest δ88Sr reported so far. Marine carbonates (both inorganic and biogenic) are variably depleted in 88Sr compared to the water from which they precipitated.3,4,10 The most negative rock δ88Sr value measured to date, −0.42‰, was from a carbonate rock in South China and was ascribed to enhanced isotopic fractionation during precipitation from the originally 88Sr-depleted seawater.12 Knudson et al.8 reported even more negative δ88Sr values measured by MC-ICPMS in biological samples and stated that different Sr isotopic signatures can be observed in different trophic levels as organisms preferentially incorporate the lighter isotope of Sr.
In this paper we present first 88Sr/86Sr ratio results obtained by 87Sr–84Sr double spike TIMS for several USGS standards as well as for natural water samples and mineral samples of biogenic and abiogenic origin. The double-spike calibration routine, detailed DS algorithm, and the DS data reduction method based on the stand-alone Sr-specific user-friendly computer program that corrects for Rb interference, calculates Sr concentrations and “true” 88Sr/86Sr, 87Sr/86Sr, and δ88Sr values are also presented. We also discuss the lack of usefulness of the externally corrected for instrumental mass-fractionation “true” 87Sr/86Sr and δ87Sr values as geochemical tracers.
2. Experimental methods
2.1. Sample preparation
During this study, we analyzed several different types of materials, including fossils (conodonts, Megalodon shark tooth, coral), modern fauna (dolphin tooth, acantharia, clam shell), abiogenic sulfate and carbonate minerals (celestite, strontianite, calcite), silicate whole-rocks (basalt and granite), and waters (groundwater and brine). Although the procedures used to process these materials vary and are presented individually, the procedure for the separation of Sr from all samples is essentially identical. Prior to spiking, small aliquots of water or dissolved solid samples were analyzed to determine the concentration of Sr in the solution using a Plasma Quad-III ICP-MS. Obtaining accurate Sr concentrations for the unknowns is crucial for optimizing the sample/spike ratio in the spiked aliquot using the double-spike method.Conodonts (tooth-like microfossils of extinct marine chordates) were separated from the host rock using standard techniques described by Collinson13 and then better preserved fragments were handpicked for isotope analysis. Handpicking was performed dry with stainless steel tweezers. A selected number of conodont elements (normally one to six; enough for our desired Sr yield) were transferred to an aluminum weigh pan and weighed on a Cahn 4100 microbalance with a precision level of about ±0.000003 g, and then transferred into a pre-cleaned 7 ml PFA Teflon™ vial containing about 1 ml of 0.1 M HCl. HCl was used to pre-clean the conodonts, decanted three times prior to digestion with 1 M HNO3, and then dried.
Samples of dentine and enamel from phosphatic fossil (Miocene/Pliocene) Megalodon shark tooth (samples ST-E and ST-D) were micro-drilled using a dental burr mounted in a hand-held rotary drill. A pre-powdered sample of bulk modern dolphin tooth (DT-1) was available because it is used in the USGS Denver stable isotope laboratory as an internal carbon and nitrogen isotope reference material. Similarly, a powdered sample of ∼120 ka-old Acropora coral (Acrop-1) was also available because it is used in the USGS Denver radiogenic isotope laboratory as an internal U-series dating reference material. All of these carbonate and phosphate samples were digested in a specific volume of 6 M HNO3.
Acantharia cysts (Acan-1) from the Bahamas were handpicked and processed similar to the conodonts, except that they were dissolved immediately after weighing to avoid chemical leaching of their extremely delicate structure. Acantharia are abundant oceanic protists, and are the only organisms known to form entire mineral skeletons of celestite (strontium sulfate, SrSO4). They also have the capacity to completely change their morphology over the course of their life cycle in order to form cysts. The extreme Sr content of acantharia (∼47.5% by weight) is thought to produce enough Sr to outweigh any potential Sr surface contamination that was not eliminated due to a lack of surface leaching of the sample during processing.
Sulfate samples (acantharia Acan-1, celestite Cel-1, MAD-1, and OH-1) were dissolved in a mixture of 0.02 M hydroxylamine–HCl (NH2OH–HCl) and 2 M nitric acid (HNO3) after the methods by Puchelt and Setiobudi.14 Carbonate mineral samples (strontianite FI-1) were dissolved in 1 M HCl. Groundwater and brine samples were dried down and then chemically processed like solid samples.
Water standard NASS-6 was prepared in the same manner as the water/brine samples. Other standards, both carbonate and phosphate, were prepared in the same method as unknowns of the same chemical composition. The silicate standards SRM-607, BCR-2, G-3, and BHVO-2 were prepared in much the same manner except dissolution was achieved using concentrated ultrapure HF and HNO3 in 7 ml PFA Teflon™ vials.
2.2. Chemical separation of Sr
Two aliquots of about 1 microgram of Sr per specimen were taken from each of the final solutions of known Sr concentration. One aliquot was spiked with about 100–200 microliters of a84Sr–87Sr double spike solution, and both separates were dried down on a hot plate. A few drops of concentrated HNO3 and hydrogen peroxide (H2O2) were added to help breakdown of any remaining organic components, the samples were re-dried, and then dissolved in 6 M HNO3 for Sr separation chemistry. Samples of Sr sulfates (acantharia, celestite) and carbonate (strontianite) were measured by TIMS with no further ion-exchange chemical separation of Sr.Sr was separated from the major cations (e.g. Ca, Mg, Fe, etc.) in Ca-carbonate and silicate samples using a strontium-specific Eichrom Sr resin and a method that was slightly modified from De Muynck et al.15 The resin was pre-cleaned in deionized water (Milli-Q filtration) by five decantations. Small (0.25 ml volume), PFA Teflon™ columns were made in-house using 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 shrinkable tubing with FEP Teflon™ frits. These columns were filled with the Sr resin and the resin was cleaned with both deionized water and 6 M HCl prior to conditioning with 6 M HNO3. About 0.4 ml of the dissolved sample were loaded onto each column and then washed with about 8 ml of 6 M HNO3 and Sr was eluted with about 4 ml of 0.05 M HNO3. The Sr separates were dried down and then a few drops each of concentrated HNO3 and H2O2 were added to the residues of each separate and dried down again with 5 microliters of ultrapure phosphoric acid (H3PO4). The total blank for this process determined by ID-TIMS did not exceed 0.2 ng Sr, which was negligible considering the amount of Sr analyzed.
1 shrinkable tubing with FEP Teflon™ frits. These columns were filled with the Sr resin and the resin was cleaned with both deionized water and 6 M HCl prior to conditioning with 6 M HNO3. About 0.4 ml of the dissolved sample were loaded onto each column and then washed with about 8 ml of 6 M HNO3 and Sr was eluted with about 4 ml of 0.05 M HNO3. The Sr separates were dried down and then a few drops each of concentrated HNO3 and H2O2 were added to the residues of each separate and dried down again with 5 microliters of ultrapure phosphoric acid (H3PO4). The total blank for this process determined by ID-TIMS did not exceed 0.2 ng Sr, which was negligible considering the amount of Sr analyzed.
2.3. 87Sr–84Sr double spike preparation
Our double-spike (DS) preparation was similar to the one described by Krabbenhöft et al.6 Two powdered Sr-carbonates enriched in 84Sr (1 mg from Oak Ridge National Laboratory, ORNL) and in 87Sr (30 mg from ISOFLEX USA) were purchased in order to prepare a 87Sr–84Sr DS solution. The vendors-certified isotopic compositions of these spikes are given in Table 1. The certified abundance of Rb is 5 ppm in the 84Sr carbonate, but was not reported for the 87Sr carbonate, for which our ICP-MS analyses yielded a Rb concentration of 2 ppm. The latter value is lower than the 87Rb content of <56 ppm reported by ref. 6 for 87Sr-enriched spike from ORNL. Both of these Rb concentrations in the 84Sr and 87Sr spikes are negligible for samples analyzed without chemical separation of Sr and are irrelevant for samples passed through the Sr resin. The carbonate powders were dissolved in a specific volume of high-purity Seastar™ 6 M HNO3. Based on the certified isotopic compositions we mixed the two 84Sr- and 87Sr-enriched solutions to reach the DS 84Sr/87Sr ratio of ∼1.2 recommended by Rudge et al.16 The spike calibration procedure is described in Section 3.1.2.4. TIMS analysis
Strontium isotope measurements were conducted at the USGS Denver radiogenic isotope laboratory, using the static mode on the TRITON (ThermoFisher Scientific) 9-collector mass spectrometer which operates in positive ion mode with a 10 kV acceleration voltage and 1011 ohm resistors for the Faraday cups. Between 500 and 1000 ng of Sr were loaded on outgassed Re filaments with a Ta2O5 activator. All measurements were conducted in fully automatic mode with the targeted 88Sr intensity of 8 V, which was commonly achieved at the filament temperature of about 1400 °C. Strontium sulfate and carbonate samples measured without chromatographic separation of Sr provided intense and stable ion beams, similar to chemically purified Sr separates. An ion beam of 85Rb was monitored to correct for the interfering 87Rb. Measured 85Rb/86Sr ratios in accepted analyses never exceeded a value of 1 × 10−5. A mass-spectrometric run comprised 14 blocks of data and each block consisted of 11 scans with an 8 seconds integration time and a 3 seconds idle time. Before each block the baseline (deflected beam) was measured for 80 s and the amplifier rotation was performed. Within-run uncertainties (2 SE, 2 standard errors) for conventionally fractionation-corrected isotope ratios using the accepted 88Sr/86Sr value of 8.375209 were typically ∼0.0008% for 87Sr/86Sr and 0.002–0.004% for 84Sr/86Sr in unspiked samples. Unspiked National Institute of Standards and Technology (NIST) SrCO3 standard SRM-987 was run after each five unknowns and its average was used to determine a normalization factor for measured 87Sr/86Sr values as R = 87Sr/86SrNIST average/0.710248. This normalization factor was then applied to the 87Sr/86Sr ratio of all unknowns run in the same turret of 21 samples and the errors were propagated to include the uncertainty of the correction.2.5. Double spike algorithm and the data reduction program
The measured Sr isotope ratios of natural samples are affected by three isotopic fractionation processes, of which the first is natural and the second and third occur during chemical separation of Sr using the ion-exchange resin4,17 and the evaporation of Sr in the ion source of the mass spectrometer.18 The magnitude of mass-dependent isotope fractionation introduced in the laboratory may be comparable to, or even significantly larger than, the natural fractionation. The DS method (internal standard) was developed19–28 to correct for the bias (mass discrimination) introduced by chemical separation and TIMS analysis. This method relies on the laws describing mass-dependent isotope effects occurring during evaporation of atoms (molecules) in the ion source of the mass spectrometer. In its simplest form, the DS method consists of adding to an unknown sample two isotopes of the analyte (Sr in our case), which are absent in the sample.19,29 The ratio of these added isotopes should be precisely known. If the fractionation law is the same for all isotopes of the analyzed element, it is possible to calculate the “true” isotope ratios of the sample from the known spike compositions and measured isotope ratios in unspiked and double-spiked sample aliquots. Because pure artificial isotopes are not always available, in the general case of double isotope dilution, the isotopic analysis is possible for elements with at least four stable isotopes, which is the case for Sr.Various mathematical models have been proposed to describe the mass discrimination in the ion source.23,30,31 The exponential model of Wasserburg et al.31 is considered to be the most accurate. According to this model, the “true” isotope ratios of Sr (XN, YN, and ZN) in the sample are related to their measured values (X*N, Y*N, and Z*N) by
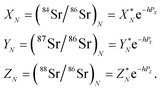 | (1) |
In eqn (1)h is a fractionation factor in the unspiked run, m84, m86, m87, and m88 are the atomic masses of corresponding Sr isotopes, and 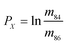 ,
, 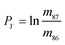 , and
, and 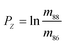 . Similarly, the ratios measured in the spiked run are
. Similarly, the ratios measured in the spiked run are
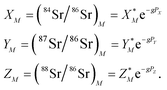 | (2) |
Indices N and M in eqn (1) and (2) correspond to unspiked and spiked runs, respectively, and g is a fractionation factor in the spiked run.
Combining eqn (1) and (2) with isotope dilution equations,32 namely,
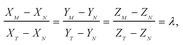 | (3) |
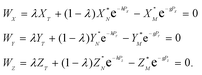 | (4) |
In eqn (4)h, g and λ are the unknowns, the subscript T denotes a spike (tracer), and λ is the mixing ratio between the sample and the spike. The algorithm for solving eqn (4) was constructed following the recommendations of Rudge et al.16 and is given in Appendix A.
A stand-alone Windows-based computer program written in Turbo Pascal on the basis of this algorithm uses two input files in *.csv format for each sample analyzed and does not require any additional software to run (i.e. Excel or Matlab). The input files consist of baseline-corrected intensities of isotopes in each spectrum for spiked (n spectra) and unspiked (m spectra) runs so that n is not necessarily equal to m. The program also corrects mass 87 for 87Rb interference using the beam intensity at mass 85. The raw isotope ratios are calculated for each spectrum and then the isotopic ratios of each spectrum from the spiked and unspiked runs are used for calculations of the “true” 88Sr/86Sr and 87Sr/86Sr isotopic ratios, which are corrected for instrumental mass fractionation. The data processing consists of two steps: (i) the solutions are obtained using the linear model of mass discrimination (see Appendix A) and (ii) the values of mass-bias coefficients (α and β) and λ from the linear model are used as starting values for iterations in the second stage of calculations, which use the exponential mass-fractionation model. The iterations in the second stage converge rapidly and the time it takes to process an array of 154 × 154 spectra is typically less than a second. After rejection of outliers beyond a user-defined 2 or 3σ thresholds, the calculated mean values and their standard deviations as well as standard errors are reported for “true” 88Sr/86SrN, δ88Sr, and “true” 87Sr/86SrN in the sample. These “true” ratios are calculated using fractionation factors in the unspiked and spiked runs and the mixing ratio between the sample and the spike as it is described in Appendix A. The “true” 87Sr/86SrN ratio is not equivalent to the traditional 88Sr/86Sr-normalized 87Sr/86Sr ratio reported by studies of radiogenic Sr isotope ratios because it includes the “combination” of the radiogenic effect and the natural mass-dependent fractionation.
The program also calculates the Sr concentration in the sample, plots a histogram of calculated δ88Sr values, and uses the Monte Carlo method33,34 to calculate the predicted minimum standard deviation of δ88Sr based on the precision of the mass-spectrometric analysis and on the measured 84Sr/86Sr in the sample/spike mixture. The program also has an additional mode for the DS calibration using the same exponential model of mass-fractionation. In the DS calibration mode two *.csv input files are used (i) measured raw intensities of masses 84, 85, 86, 87, and 88 for the pure spike isotope composition run and (ii) the raw intensities data for a SRM-987 + DS mixture run. This Windows-based stand-alone program is available upon request from N. Mel'nikov (E-mail: nickm46@mail.ru).
3. Results
3.1. Spike calibration
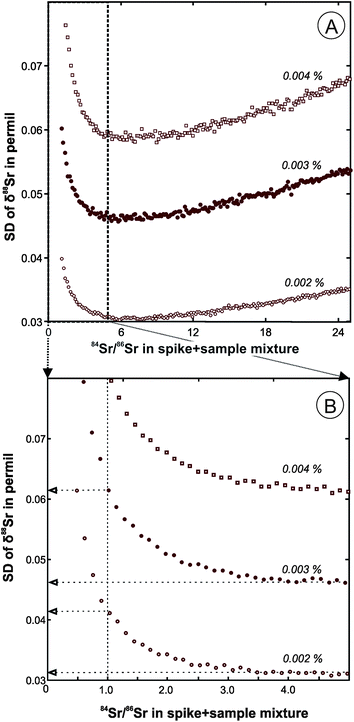
The double spike calibration was conducted in two steps. First, a DS aliquot containing a large amount of 84Sr (about 200 ng) was used to conduct a single mass-spectrometric analysis of pure spike to obtain preliminary estimates of its isotopic composition. The raw fractionation-uncorrected data for a pure spike run and the raw data for a series of DS + SRM-987 mixtures were used to calculate fractionation-corrected values of isotope abundances of 84Sr, 86Sr, 87Sr, and 88Sr in the DS (Table 1) using the program described in the previous section. The SRM-987 solution used in the mixtures had a known concentration, so the analyses of the mixture were also used to evaluate the total Sr concentration in the DS spike (0.028 μmol Sr per g). The mixtures were prepared with targeted 84Sr/86Sr values in the range from 1 to 5. The optimal 84Sr/86Sr ratio in a DS + sample mixture of ∼5 was estimated based on predicted standard deviations of δ88Sr values for our DS compositions (Fig. 1A), but lower values are preferred in order to conserve the DS. For a typical 84Sr/86Sr error of ∼0.002% in an unspiked run, a decrease of 84Sr/86Sr in a spiked run from the optimal value of 5 to 1 causes only a slight decrease in the anticipated precision of the δ88Sr (SD value increases from 0.03 to 0.04‰; Fig. 1B). For a 84Sr/86Sr error of ∼0.001% and optimal spiking, the within-run δ88Sr SD can be further reduced to 0.016‰, but it can only be achieved in practice by higher signal to noise ratios that would require about four times larger ion beam intensities than those typical of our runs.Because the DS isotope abundances estimated in the first step of the DS calibration are based on a single pure DS run, we consider these values to be preliminary estimates of the DS isotopic composition. The second step of the spike calibration was conducted using the DS + SRM-987 mixtures together with a series of unspiked SRM-987 runs to calculate more statistically representative δ88Sr values in the SRM-987 measured with our spike. Preliminary estimates of the DS isotopic composition obtained from the pure DS runs were used for this DS calibration step. This DS calibration routine was repeated periodically and the running average δ88Sr value of −0.024 ± 0.009‰ (2SE, n = 61) for about two years of SRM-987 measurements is given in Table 2. Because the expected value for δ88Sr in SRM-987 is equal to zero, all results for unknowns were corrected for the −0.024‰ bias and the final error was propagated to include its 2SE uncertainty of 0.009‰ (Table 2).
| Sample ID | Sample type | Sampling location/source | Number of replicates | 87Sr/86Sra | ±2SE | δ 87Srb ‰ | ±SD‰ | δ 88Sr‰ | ±SD‰ | ±2SE‰ | δ 87Sr/δ88Sr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Conventionally calculated values corrected for mass-fractionation using 88Sr/86Sr = 8.375209 and normalized for the instrumental bias using 87Sr86Sr = 0.710248 in NIST SRM-987. b This parameter is not a useful geochemical tracer (see text for discussion). c n.a. – not applicable. d Long-term average used to adjust δ88Sr data for unknowns. | |||||||||||
| Standards | |||||||||||
| SRM-987 | SrCO3, NIST Sr isotope standard | Spex Industries, Inc., Metuchen, NJ | 61 | n.a.c | n.a. | n.a. | n.a. | −0.024d | 0.032 | 0.009 | n.a. |
| SRM-607 | Potassium feldspar (KFsp) NIST standard | Kingman Feldspar mine, Arizona | 6 | 1.200680 | 6 × 10−5 | 0.154 | 0.017 | 0.180 | 0.021 | 0.017 | 0.86 |
| NASS-6 | NRC Canada, sea water standard | Sandy Cove, Nova Scotia | 8 | 0.709179 | 5 × 10−6 | 0.164 | 0.007 | 0.378 | 0.013 | 0.009 | 0.43 |
| EN-1 | CaCO3, USGS standard, shell of giant clam Tridacna gigas | Bikini Atoll, Enewetak lagoon, S. Pacific | 28 | 0.709176 | 3 × 10−6 | 0.114 | 0.009 | 0.259 | 0.018 | 0.007 | 0.44 |
| MAPS-4 | USGS standard, synthetic Ca3(PO4)2, modern bone proxy | n.a. | 8 | 0.7078 | 6 × 10−6 | 0.030 | 0.006 | 0.071 | 0.011 | 0.008 | 0.42 |
| MAPS-5 | USGS standard, synthetic Ca3(PO4)2, fossilized bone proxy | n.a. | 6 | 0.70791 | 5 × 10−6 | 0.078 | 0.009 | 0.162 | 0.018 | 0.014 | 0.49 |
| BCR-2 | USGS standard, Columbia River basalt | Bridal Veil Flow Quarry, Oregon | 3 | 0.705004 | 5 × 10−6 | 0.146 | 0.005 | 0.277 | 0.009 | 0.010 | 0.53 |
| BHVO-2 | USGS standard, Hawaiian basalt | Halemaumau Crater, Hawaii | 3 | 0.703469 | 5 × 10−6 | 0.137 | 0.005 | 0.254 | 0.008 | 0.009 | 0.54 |
| G-3 | USGS standard, granite | Sullivan Quarry, Rhode Island | 3 | 0.709970 | 5 × 10−6 | 0.177 | 0.003 | 0.338 | 0.005 | 0.006 | 0.53 |
| Biogenic samples | |||||||||||
| Acan-1 | SrSO4, Acantharia cyst | Bahamas, N. Atlantic | 8 | 0.709173 | 4 × 10−6 | 0.088 | 0.013 | 0.165 | 0.026 | 0.018 | 0.53 |
| Acrop-1 | Aragonite CaCO3, ∼120 ka-old Acropora palmata coral | Haiti, Carribian | 3 | 0.709167 | 9 × 10−6 | 0.070 | 0.010 | 0.161 | 0.020 | 0.023 | 0.43 |
| Cono-V77 | Early Ordovician conodonts, apatite | Nevada | 3 | 0.708931 | 6 × 10−6 | −0.526 | 0.010 | −1.059 | 0.020 | 0.023 | 0.50 |
| Cono-V4 | Early Silurian conodonts, apatite | Nevada | 3 | 0.708176 | 6 × 10−6 | −0.449 | 0.003 | −0.859 | 0.007 | 0.008 | 0.52 |
| SP-5A | Early Mississippian Lower crenulata conodonts, apatite | Bridger Range, Montana | 4 | 0.708183 | 5 × 10−6 | −0.064 | 0.002 | −0.130 | 0.004 | 0.004 | 0.49 |
| PNR-1 | Middle Devonian conodonts, apatite | Pinyon Range, Nevada | 6 | 0.707951 | 5 × 10−6 | 0.045 | 0.004 | 0.104 | 0.009 | 0.007 | 0.43 |
| Cono-V109 | Late Mississippian conodonts, apatite | Alaska | 6 | 0.708008 | 5 × 10−6 | 0.138 | 0.009 | 0.305 | 0.018 | 0.015 | 0.45 |
| BCT-14 | Conodont Early marginifera, apatite | Pahrangat Range, Nevada | 6 | 0.708329 | 6 × 10−6 | −0.200 | 0.010 | −0.348 | 0.019 | 0.016 | 0.57 |
| ST-E | Miocene shark (megalodon) tooth, enamel, apatite | S. Carolina | 2 | 0.709001 | 6 × 10−6 | 0.044 | 0.009 | 0.095 | 0.018 | 0.025 | 0.46 |
| ST-D | Miocene shark (megalodon) tooth, dentine, apatite | S. Carolina | 4 | 0.709014 | 6 × 10−6 | 0.115 | 0.004 | 0.250 | 0.007 | 0.007 | 0.46 |
| DT-1 | Dolphin tooth (bulk), apatite | Sarasota Bay, Florida | 4 | 0.709091 | 9 × 10−6 | −0.157 | 0.007 | −0.287 | 0.013 | 0.013 | 0.55 |
| Water samples | |||||||||||
| Salsbury 24-35-1H | Produced formation water (brine) from shale | Bakken Formation, Montana | 4 | 0.710789 | 6 × 10−6 | 0.700 | 0.004 | 1.373 | 0.007 | 0.007 | 0.51 |
| State 21-28H | Produced formation water (brine) from shale | Bakken Formation, N. Dakota | 4 | 0.710805 | 6 × 10−6 | 0.672 | 0.007 | 1.301 | 0.014 | 0.014 | 0.52 |
| PW1 | Produced formation water (brine) from limestone | Charles Formation, Montana | 6 | 0.708002 | 6 × 10−6 | 0.055 | 0.019 | 0.133 | 0.032 | 0.026 | 0.41 |
| Average of 4 samples | Groundwater | Dunn County, N. Dakota | 4 | n.a. | n.a. | 0.172 | 0.028 | 0.354 | 0.055 | 0.055 | 0.49 |
| Rock and mineral samples | |||||||||||
| Cel-1 | SrSO4, celestite | Kara-Kum Desert, Turkmenistan | 8 | 0.707758 | 1 × 10−5 | 0.475 | 0.009 | 0.928 | 0.018 | 0.012 | 0.51 |
| MAD-1 | SrSO4, celestite | Madagascar | 4 | 0.708053 | 6 × 10−6 | −0.018 | 0.013 | −0.034 | 0.026 | 0.026 | 0.54 |
| MAD-2 | SrSO4, celestite | Madagascar | 4 | 0.708073 | 6 × 10−6 | −0.011 | 0.012 | −0.022 | 0.023 | 0.023 | 0.48 |
| OH-1 | SrSO4, celestite | Ohio | 6 | 0.708521 | 6 × 10−6 | 0.053 | 0.012 | 0.126 | 0.020 | 0.016 | 0.42 |
| FI-1 | SrCO3, strontianite | Fidalgo Island, Washington | 6 | 0.704818 | 6 × 10−6 | 0.034 | 0.016 | 0.063 | 0.030 | 0.025 | 0.53 |
3.2. Data for standards and unknowns
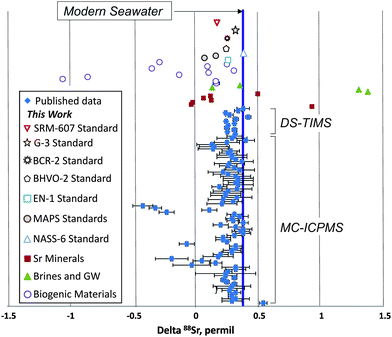
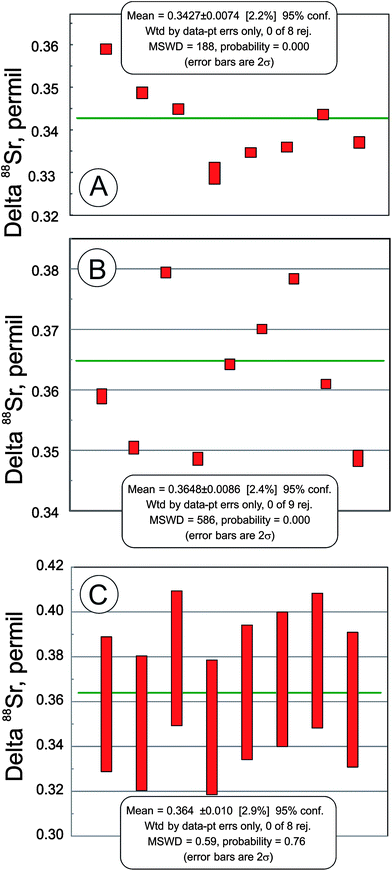
In addition to the NIST SRM-987 Sr isotope standard, we analyzed several other standards as well as unknown water and mineral samples. The results of these analyses are presented in Table 2 and in Fig. 2. A typical run with an optimal sample/spike ratio shows a symmetrical distribution of individual δ88Sr values (Fig. 3) with a standard deviation of ∼0.05–0.06‰. The standard error of the mean, calculated by our program and by the DS-toolbox,16 SE = SD/√n, where n is a total number of individual within-run δ88Sr values, is not the best representation of the precision for our analyses. Weighted averages for replicate analyses that used within-run 2SE as a weighing factor were calculated using the Isoplot program.37 Theoretically, if the scatter of the replicate analyses is caused by random within-run errors, the mean square of weighted deviates (MSWD) value should be equal to one. For our measurements MSWD is ≫1 in all cases, thus indicating the presence of a substantial external error. For example, δ88Sr values for eight replicate unspiked runs of the NASS-6 standard calculated with data for a single spiked DS + NASS-6 run gave an MSWD value of 188 (probability of fit = 0) (Fig. 4A). An even larger value of MSWD = 586 (probability of fit = 0) was obtained when the δ88Sr values for a single unspiked run were calculated with nine separate spiked runs (Fig. 4B). However, the MSWD value is <1 and the probability of the fit is >0 when the 2SE error of ±0.03‰ was ascribed to individual δ88Sr values (Fig. 4C). The external SD values calculated for several replicate analyses of the same unknown samples were ≤0.02‰ in most cases (Table 2). The 2SE value of ±0.03‰ is our preferred parameter to represent the precision of the δ88Sr data calculated from typical runs, for which no replicate analyses were conducted.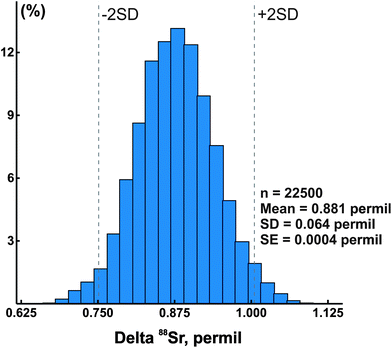 | ||
| Fig. 3 A histogram of calculated delta 88Sr values for a typical sample run. SE – standard error, SD – standard deviation, and n – total number of calculated delta values. | ||
Our mean δ88Sr value of 0.378 ± 0.009‰ (2SE, n = 8) for the seawater standard NASS-6 (Table 2 and Fig. 2) is within the error of the 0.381 ± 0.010‰ value reported for the IAPSO seawater standard by Fietzke and Eisenhauer,3 0.370 ± 0.026‰ by Liu et al.,35 and 0.386 ± 0.005‰ given for this standard by Krabbenhöft et al.6 The NASS-6 results are also within the error of the average δ88Sr = 0.382 ± 0.011‰ of the seawater standard IAPSO and samples from different marine environments (shallow brackish Baltic Sea, N- and E-Atlantic, Mediterranean Sea) reported by Liebetrau et al.38 Comparison of our data for seawater with previous studies shows that the DS-TIMS method and the data reduction routine presented here produce accurate δ88Sr values.
In addition to the seawater standard, we conducted a series of replicate analyses of the USGS carbonate standard EN-1 and of two synthetic phosphate standards MAPS-4 and MAPS-5 that mimic the chemical compositions of live and fossilized bones, respectively. We also analyzed three USGS silicate standards BCR-2 (Columbia River basalt), BHVO-2 (Hawaiian basalt), and G-3 (granite). Data for the modern giant clam shell EN-1 standard (δ88Sr = 0.259 ± 0.010‰, Table 2) show a 0.12‰ δ88Sr offset from the modern seawater value. The synthetic standards MAPS-4 and MAPS-5 yielded lower δ88Sr values of 0.067 ± 0.008 and 0.162 ± 0.013‰, respectively. The silicate standards BCR-2, BHVO-2, and G-3 yielded δ88Sr values of 0.277 ± 0.014, 0.254 ± 0.013, and 0.338 ± 0.011‰, respectively (Table 2 and Fig. 2). Our DS-TIMS δ88Sr results for these materials are within the error of published yet less precise ICP-MS data for BCR-2, BHVO-2, and G-2 USGS silicate standards.11,39,40 Our δ88Sr value of 0.180 ± 0.017 for the NIST SRM-607 potassium feldspar standard (Table 2 and Fig. 2) is appreciably larger than the δ88Sr value of −0.07 ± 0.06 determined for this material by MC-ICPMS.39
Several Sr minerals (celestite and strontianite) showed a wide range of δ88Sr values from 0.928 ± 0.012 to −0.014 ± 0.017‰. Biogenic SrSO4 from acantharia (δ88Sr = 0.165 ± 0.023‰) shows a strong 0.23‰ offset from the modern seawater value. The variability of δ88Sr values observed in abiogenic celestite samples indicates that the stable Sr isotope fractionation may depend not only on the mineral chemistry, but also on other parameters such as parent water Sr isotopic composition and, probably, precipitation rates, as demonstrated for synthetic calcite.10 The highest δ88Sr value of 1.373 ± 0.007‰ was measured in a brine sample from the oil-producing Bakken Formation black shale. A brine sample from a carbonate host rock has a much lower δ88Sr value of 0.133 ± 0.030‰. These brines are thought to be potential groundwater contaminants by produced waters. Although the origin of this large range of δ88Sr values in brines is unknown, the observed difference between the brines and regional groundwaters (which gave a mean δ88Sr value of 0.354 ± 0.055‰; Table 2) makes this parameter a promising tool in addition to more commonly used 87Sr/86Sr and elemental tracers of groundwater/brine mixing and also may help to better understand the origin of deep-seated continental brines.
The lowest δ88Sr value of −1.059 ± 0.023‰ was measured in an Ordovician conodont sample (Table 2). This result combined with the brine data defines a total range of δ88Sr values obtained during this work of >2.4‰, which is the widest range reported so far for terrestrial samples (Fig. 2). This range of δ88Sr values is 80 times larger than the typical TIMS-DS external error of ≤0.03‰ demonstrated in previous studies6,41 and in our measurements. A significant variability of stable Sr isotopes was observed in different conodont species (Table 2). A negative δ88Sr value of −0.287 ± 0.013‰ was measured for a bulk dolphin tooth sample and a measurable difference of 0.14‰ between δ88Sr was obtained for fossil shark tooth dentine and enamel. These “vital effects” may open the door for potential biological applications using precise stable Sr isotope data.
3.3. Are the “true” 87Sr/86Sr and δ87Sr values useful geochemical tracers?
The “true” 87Sr/86SrN ratio is not equivalent to the traditional 88Sr/86Sr-normalized 87Sr/86SrSample CN ratio reported by studies of radiogenic Sr isotope ratios because it includes the “combination” of the radiogenic effect and the natural mass-dependent fractionation. Ohno et al.12 and Liu et al.35 proposed to calculate the δ87Sr value using a formula δ87Sr = 1000 × {[(87Sr/86Sr)N/(87Sr/86Sr)SRM987 − 1] − [(87Sr/86Sr)Sample CN/(87Sr/86Sr)SRM987 − 1]}‰, which includes “true” 87Sr/86SrN in the sample, the conventionally normalized ratio (87Sr/86Sr)Sample CN and supposedly separates the radiogenic and the natural mass-dependent fractionation effects. In its simplified form this formula transforms to δ87Sr = 1000 × [(87Sr/86Sr)N − (87Sr/86Sr)Sample CN]/(87Sr/86Sr)SRM987. This δ87Sr value should not be confused with the δ87Sr parameter defined in several publications (e.g.ref. 36) as deviation of conventionally normalized 87Sr/86Sr measured in a sample from the 87Sr/86Sr in the modern seawater.The δ88Sr and δ87Sr values for all samples except the SRM-607 NIST standard show a very good linear correlation (Fig. 5) with an R2 value of 0.9964. The regression line goes through the origin of the coordinates and has a slope of ∼0.5. According to Ohno et al.12 and Liu et al.35 this relationship should mean that the natural mass-fractionation effects are a factor of two smaller for 87Sr/86Sr than for 88Sr/86Sr, which is expected considering the mass differences of isotopes and should provide evidence for natural mass-dependent isotope fractionation for both 87Sr and 88Sr. However, as it is shown in Appendix B, δ88Sr and δ87Sr values are not independent and the way the δ87Sr value is calculated makes it a function of the δ88Sr value. The observed linear correlation and δ87Sr ≈ 0.5 × δ88Sr relationship are artifacts of the measured 87Sr/86Sr ratios of most samples being close to this ratio in the NIST SRM-987 standard. These relationships should not hold for samples with significantly more radiogenic Sr than in the NIST standard. Indeed, data for the NIST potassium feldspar standard SRM-607, which contains radiogenic Sr with 87Sr/86Sr ≈ 1.20 (Table 2), confirm this reasoning because its δ87Sr ≈ 0.86 × δ88Sr, but not ∼0.5 × δ88Sr as it is for other samples, which have 87Sr/86Sr ratios of ∼0.7 (close to the 87Sr/86Sr in the NIST SRM-987 standard; Table 2). Our conclusion is that the natural mass-fractionation effect and the radiogenic effect cannot be separated for the “true” 87Sr/86Sr and, therefore, the δ87Sr value calculated using the approach by Ohno et al.12 and Liu et al.35 does not bear any useful independent information. The “true” 87Sr/86Sr value obtained by the DS-TIMS or any other external normalization method combines both the radiogenic and mass-dependent fractionation effects, and thus, may be less useful as an isotope tracer compared to the conventional 87Sr/86Sr radiogenic tracer.
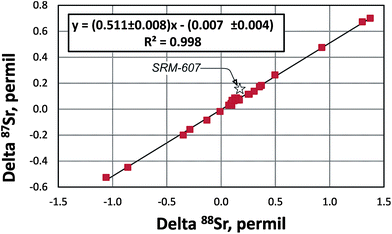 | ||
| Fig. 5 The delta 88Sr (δ88Sr) versus delta 87Sr (δ87Sr) diagram for samples analyzed during this study (data from Table 2). δ87Sr is calculated using a formula from Ohno et al.12 and Liu et al.35 (see Appendix B). R – correlation coefficient. | ||
4. Conclusions
We used a 87Sr–84Sr double spike to eliminate the effects of isotope fractionation during ion chromatographic separation of Sr and TIMS analysis and precisely measure the δ88Sr values of natural materials. A Sr-specific user-friendly computer program was developed for the double-spike data reduction. It was confirmed that a digestion routine using a mixture of 0.02 M hydroxylamine–HCl and 2 N nitric acid can be successfully applied to Sr sulfates, and the TIMS analysis of these Sr-rich minerals can be conducted without the chromatographic separation and purification of Sr. Our DS-TIMS δ88Sr data for a variety of standards and unknowns show external reproducibility of better than 0.02‰ (1SD). Observed agreement of our seawater data with previous studies shows that the method presented here produces accurate results.The mass-fractionation effect and the radiogenic ingrowth effect cannot be separated for 87Sr/86Sr and, therefore, the δ87Sr based on the “true” 87Sr/86Sr determined using external correction for mass-dependent instrumental discrimination in DS-TIMS or MC-ICPMS does not bear any useful information about 87Sr mass-fractionation in nature.
A total range of δ88Sr values reported here is ∼2.4‰, which is the widest range observed so far in terrestrial samples. This range of δ88Sr values is 80 times larger than the typical DS-TIMS external error thus demonstrating a potential of the δ88Sr isotope tracer in combination with the traditional radiogenic 87Sr/86Sr tracer for studying a variety of biological, hydrological, and geological processes.
Appendix A
To solve eqn (4) in the main text, an initial estimate of values for the unknowns h, g (fractionation factors in the unspiked and spiked runs, respectively) and λ (the mixing ratio between the sample and the spike) is required. These estimated values are obtained using a linear model of mass-fractionation,42 which is based on a geometric representation of the DS problem.25 According to the linear model the measured isotope ratios X*N = 84Sr/86Sr, Y*N = 87Sr/86Sr, and Z*N = 88Sr/86Sr are linked with the “true” isotope ratios XN, YN, and ZNvia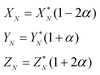 | (A.1) |
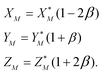 | (A.2) |
In eqn (A.1) and (A.2)α and β are fractionation factors in the unspiked and spiked runs, respectively. These equations define two straight lines in the XYZ isotope ratios space which intercept a third line defined by eqn (3) in the main text. The plane containing the line (A.1) and the point of the spike isotopic composition is defined by
| PX + QY + RZ + S = 0. | (A.3) |
The coefficients P, Q, R, and S in the plane eqn (A.3) are calculated first and then the unknown α, β and λ values are obtained. Because both the DS isotopic composition and the line defined by eqn (A.1) belong to the (A.3) plane, the solution for the coefficients P, Q, R, and S is
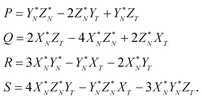 | (A.4) |
The value of the coefficient β in eqn (A.2) is defined by the intersection of the line (A.2) with the plane (A.3) and is given by
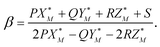 | (A.5) |
The isotope ratios XM, YM, and ZM are calculated using formula (A.2), after which the isotope ratio XN is defined by
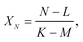 | (A.6) |
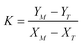 ,
, 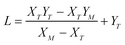 , M = −Y*N/2X*N, and N = 3Y*N/2,
, M = −Y*N/2X*N, and N = 3Y*N/2,
The values of α and λ are calculated via
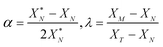 | (A.7) |
Eqn (A.1) and (A.2) are used to calculate values of ZN and ZM, which then are used to redefine linear model mass-fractionation factors α and β in terms of the exponential model of mass-discrimination (exponential model mass-fractionation factors h and g) so that h = ln(Z*N/ZN)/PZ and g = ln(Z*M/ZM)/PZ.
Eqn (4) in the main text, which is repeated below
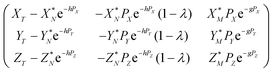 | (A.8) |
For brevity, the elements of the Jacobian matrix are denoted by
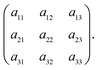 | (A.9) |
The functions Wx, WY and WZ are calculated using the starting values for the variables h, g, and λ from (A.5) and (A.7) based on the linear mass-fractionation model. If one or more of these values exceed a predefined threshold (e.g., 10−12), then the next iteration step starts. For each iteration step, the determinant Q of the matrix (A.8) is calculated using the current values of the h, g and λ. Then, the new values for h, g and λ, denoted by h′, g′ and λ′, are calculated from
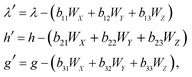 | (A.10) |
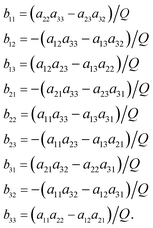 | (A.11) |
Finally, the values of h, g and λ are recalculated again until the user-prescribed accuracy is achieved.
Appendix B
A “true” 87Sr/86Sr value determined by the DS-TIMS or external correction using bracketing by MC-ICPMS reflects both the radiogenic effect and the isotopic fractionation effect in nature. In order to separate these two effects the δ87Sr parameter was introduced,12,35 which is calculated using the formula δ87Sr = [(87Sr/86SrSample)/(87Sr/86Sr)NIST − 1]ext. × 1000 − [(87Sr/86SrSample)/(87Sr/86Sr)NIST − 1]int. × 1000, where subscripts “ext.” and “int.” represent the externally corrected (“true”) and internally corrected (conventional) isotopic data, respectively. It was also stated that this δ87Sr value, similar to δ88Sr, shows the degree of natural mass-dependent isotopic fractionation. Ohno et al.12 and Liu et al.35 reported δ87Sr ≈ 0.5 δ88Sr for each sample from their datasets, and also present a linear correlation between the δ87Sr and δ88Sr values (Fig. 2b in Ohno et al.12), and interpret this correlation as representing mass-dependent isotopic fractionation of both 87Sr and 88Sr that occurred in those samples. We also observed similar correlation (Fig. 5), but question this interpretation because δ87Sr and δ88Sr values are not independent and are mathematically linked through the calculation process.Using notations accepted in our paper (see Appendix A) the δ87Sr formula from Ohno et al.12 and Liu et al.35 can be rewritten as
| δ87Sr = [(YN − YC)/YSRM987] × 1000, | (B.1) |
According to the exponential model of mass-fractionation,
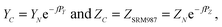 | (B.2) |
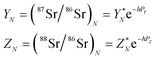 | (B.3) |
It can be shown that from the δ87Sr definition given by (B.1)
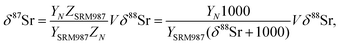 | (B.4) |
For a set of samples with non-radiogenic Sr for which YN/YSRM987 ≈ 1, eqn (B.4) corresponds to a straight line passing through the origin of coordinates in the δ88Sr–δ87Sr plot with a slope of ½, because δ88Sr ≪1000 and V ≈ 0.5 for realistic h and f values. Also, according to (B.4) the ratio δ87Sr/δ88Sr should be >0.5 in samples with more radiogenic Sr than in SRM-987 and <0.5 in samples that are less radiogenic than SRM-987. Therefore, the observation of δ87Sr ≈ ½ δ88Sr reported in our paper as well as in Ohno et al.12 and Liu et al.35 and the presence of good linear correlation between these values is just an artifact of small variations of 87Sr/86Sr values around the value of this ratio in the NIST standard SRM-987 and, therefore, cannot be interpreted as a proof of natural mass-dependent fractionation for the 87Sr.
Acknowledgements
The authors are grateful to B.A. Galperin for his helpful suggestions on the mathematical aspects of the work. We also thank Z. Peterman and R. Bernstein for providing some samples for this study. A. Pietruszka and three anonymous JAAS reviewers provided detailed comments that helped to improve the manuscript. Any use of trade, product, or firm names in this publication is for descriptive purposes only and does not imply endorsement by the U.S. Government.References
- P. J. Patchett, Earth Planet. Sci. Lett., 1980, 50, 181–188 CrossRef CAS.
- P. J. Patchett, Nature, 1980, 283, 438–441 CrossRef CAS.
- J. Fietzke and A. Eisenhauer, Geochem., Geophys., Geosyst., 2006, 7(8) CrossRef CAS.
- T. Ohno and T. Hirata, Anal. Sci., 2007, 23, 1275–1280 CrossRef CAS.
- L. Halicz, I. Segal, N. Fruchter, M. Stein and B. Lazar, Earth Planet. Sci. Lett., 2008, 272, 406–411 CrossRef CAS PubMed.
- A. Krabbenhöft, J. Fietzke, A. Eisenhauer, V. Liebetrau, F. Böhm and H. Vollstaedt, J. Anal. At. Spectrom., 2009, 24, 1267–1271 RSC.
- G. F. de Souza, B. C. Reynolds, M. Kiczka and B. Bourdon, Geochim. Cosmochim. Acta, 2010, 74, 2596–2614 CrossRef CAS PubMed.
- K. J. Knudson, H. P. Williams, J. E. Buikstra, P. D. Tomczak, G. W. Gordon and A. D. Anbar, J. Archaeol. Sci., 2010, 37, 2352–2364 CrossRef PubMed.
- Y. Sawaki, T. Ohno, M. Tahata, T. Komiya, T. Hirata, S. Maruyama, B. F. Windley, J. Hand, D. Shud and L. Yong, Precambrian Res., 2010, 176, 46–64 CrossRef CAS PubMed.
- F. Böhm, A. Eisenhauer, J. Tang, M. Dietzel, A. Krabbenhöft, B. Kisakürek and C. Horn, Geochim. Cosmochim. Acta, 2012, 93, 300–314 CrossRef PubMed.
- F. Moynier, A. Agranier, D. C. Hezel and A. Bouvier, Earth Planet. Sci. Lett., 2010, 300, 359–366 CrossRef CAS PubMed.
- T. Ohno, T. Komiya, Y. Ueno, T. Hirata and S. Maruyama, Gondwana Res., 2008, 14, 126–133 CrossRef CAS PubMed.
- C. Collinson, State of Illinois Geological Survey Circular, Department of Registration and Education, Urbana, State of Illinois, 1963, http://www.ideals.illinois.edu/bitstream/handle/2142/35164/collectionprepar343coll.pdf?sequence=2 Search PubMed.
- H. Puchelt, I. J. Setiobudi and Z. Fresenius, Anal. Chem., 1989, 335, 692–694 CrossRef CAS.
- D. De Muynck, G. Huelga-Suarez, L. Van Heghe, P. Degryse and F. Vanhaecke, J. Anal. At. Spectrom., 2009, 24, 1498–1510 RSC.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS PubMed.
- O. I. Takao, O. Hideki, H. Morikazu and K. Hidetake, Sep. Sci. Technol., 1992, 25, 631–643 Search PubMed.
- T. Suzuki, C. Kanaki, M. Nomura and Y. Fujii, Rev. Sci. Instrum., 2012, 83, 02B506 CrossRef CAS PubMed.
- L. A. Dietz, C. F. Pachucki and G. A. Land, Anal. Chem., 1962, 34, 709–710 CrossRef CAS.
- M. H. Dodson, J. Sci. Instrum., 1963, 40, 289–295 CrossRef.
- M. H. Dodson, J. Sci. Instrum., 1969, 2, 490–498 Search PubMed.
- M. H. Dodson, Geochim. Cosmochim. Acta, 1970, 34, 1241–1244 CrossRef CAS.
- L. E. Long, Earth Planet. Sci. Lett., 1966, 1, 289–292 CrossRef CAS.
- W. Compston and V. M. Oversby, J. Geophys. Res., 1969, 74, 4338–4348 CrossRef CAS.
- M. J. Dallwitz, Chem. Geol., 1970, 11, 311–314 CrossRef.
- N. H. Gale, Chem. Geol., 1970, 6, 305–310 CrossRef CAS.
- A. W. Hofmann, Earth Planet. Sci. Lett., 1971, 10, 397–403 CrossRef CAS.
- R. Russell, J. Geophys. Res., 1971, 76, 4949–4953 CrossRef.
- W. Todt, R. A. Cliff, A. Hanser and A. W. Hofmann, in Earth Processes: Reading the Isotopic Code, ed. A. Basu and S. Hart, American Geophysical Union Geophysical Monograph, 1996, vol. 95, pp. 429–437 Search PubMed.
- W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090 CrossRef CAS.
- G. J. Wasserburg, S. B. Jacobsen, D. J. DePaolo, M. T. McCulloch and T. Wen, Geochim. Cosmochim. Acta, 1981, 45, 2311–2323 CrossRef CAS.
- R. K. Webster, in Methods in Geochemistry, ed. A. A. Smales and L. R. Wagner, Interscience, N-Y, 1960, pp. 202–246 Search PubMed.
- G. M. Anderson, Geochim. Cosmochim. Acta, 1976, 40, 1533–1538 CrossRef CAS.
- N. N. Mel'nikov, Geochem. Int., 2010, 48, 876–886 Search PubMed.
- H.-C. Liu, C.-F. You, K.-F. Huang and C.-H. Chung, Talanta, 2012, 88, 338–344 CrossRef CAS PubMed.
- L. A. Derry, L. S. Keto, S. B. Jacobsen, A. H. Knoll and K. Swett, Geochim. Cosmochim. Acta, 1989, 53, 2331–2339 CrossRef CAS.
- K. R. Ludwig, Berkeley Geochronological Center Special Publication, 2003, 4, 70 Search PubMed.
- V. Liebetrau, A. Eisenhauer, A. Krabbenhöft, J. Fietzke, F. Böhm, A. Rüggeberg and K. Gürs, Geochim. Cosmochim. Acta, 2009, 73, A762 Search PubMed.
- B. L. A. Charlier, G. M. Nowell, I. J. Parkinson, S. P. Kelley, D. G. Pearson and K. W. Burton, Earth Planet. Sci. Lett., 2012, 329–330, 31–40 CrossRef CAS PubMed.
- J.-L. Ma, G.-J. Wei, Y. Liu, Z. Y. Ren, Y.-G. Xu and Y.-H. Yang, Chin. Sci. Bull., 2013, 58, 3111–3118 CrossRef CAS PubMed.
- N. Shalev, I. Segal, B. Lazar, I. Gavrieli, J. Fietzke, A. Eisenhauer and L. Halicz, J. Anal. At. Spectrom., 2013, 28, 940–944 RSC.
- N. N. Mel'nikov, Geochem. Int., 2005, 43, 1228–1234 Search PubMed.
Footnote |
| † The δ88Sr value in permil (‰) is calculated versus the accepted 88Sr/86SrSRM987 value of 8.375209 in NIST standard SRM-987 via formula δ88Sr = [(88Sr/86Sr)N/(88Sr/86Sr)SRM987 − 1] × 1000‰. |
| This journal is © The Royal Society of Chemistry 2014 |