Expansion and rupture of charged microcapsules†
Sujit S.
Datta‡
,
Alireza
Abbaspourrad‡
and
David A.
Weitz
*
Department of Physics and SEAS, Harvard University, Cambridge, MA 02138, USA. E-mail: weitz@seas.harvard.edu
First published on 11th October 2013
Abstract
We study the deformations of pH-responsive spherical microcapsules – micrometer-scale liquid drops surrounded by thin, solid shells – under the influence of electrostatic forces. When exposed to a large concentration of NaOH, the microcapsules become highly charged, and expand isotropically. We find that the extent of this expansion can be understood by coupling electrostatics with shell theory; moreover, the expansion dynamics is well described by Darcy's law for fluid flow through the microcapsule shell. Unexpectedly, however, below a threshold NaOH concentration, the microcapsules begin to disintegrate, and eventually rupture; they then expand non-uniformly, ultimately forming large, jellyfish-like structures. Our results highlight the fascinating range of behaviors exhibited by pH-responsive microcapsules, driven by the interplay between electrostatic and mechanical forces.
Microcapsules – micrometer-scale liquid drops, each surrounded by a thin, solid shell – are promising candidates for the encapsulation and controlled release of many technologically important active materials. These applications often require microcapsules to have unique mechanical properties, such as the ability to withstand large deformations. One common way of characterizing this behavior is to monitor how a microcapsule responds to forces exerted on its shell. These can be mechanical forces, externally imposed by poking, squeezing, or uniformly pressurizing the microcapsule.1–4 Alternatively, these forces can be generated by physico-chemical modifications to the shell itself, such as charging it; under certain conditions, the repulsion between the charges on the shell can cause it to deform. Electrostatic forces arise in many applications of soft matter, and consequently, this approach is frequently used to induce deformations in a variety of bulk materials.5,6 Nevertheless, systematic investigations of how electrostatic forces deform microcapsules are scarce.7–9 Thus, despite their prevalence in many real-world situations, a full understanding of how these forces affect microcapsules is lacking.
In this Communication, we study the deformations of spherical microcapsules exposed to a pH stimulus. We choose NaOH as the stimulus; when exposed to this base, the microcapsule shells become highly charged. For large NaOH concentrations, the microcapsules expand isotropically. We find that the extent of the microcapsule expansion can be understood by coupling electrostatics with shell theory; moreover, the dynamics of this expansion is well described by Darcy's law for flow through the porous microcapsule shell. Surprisingly, below a threshold NaOH concentration, the microcapsules begin to disintegrate, and eventually rupture; they then expand non-uniformly, ultimately forming large, jellyfish-like structures. Our results thus highlight the rich behavior exhibited by microcapsules, driven by the interplay between electrostatic and mechanical forces.
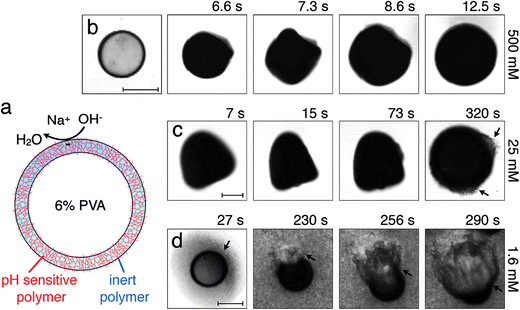
We fabricate monodisperse thin-shelled microcapsules using water-in-oil-in-water (W/O/W) double emulsion templates prepared by microfluidics.10,11 The inner and outer phases are 6 wt% and 10 wt% solutions of polyvinyl alcohol (PVA), respectively, while the middle oil phase is a mixture of a pH-responsive polymer, poly(acrylic acid-block-methyl methacrylate), suspended in tetrahydrofuran (THF), and another photo-polymerizable pH-unresponsive monomer, ethylene glycol phenyl ether methacrylate.12 We use UV light to polymerize the pH-unresponsive monomer in situ, immediately as the double emulsions are generated, forming a covalently cross-linked network around the inner core. This network is a solid characterized by a Young's modulus E ≈ 600 MPa;13 it is impermeable to hydrated Na+ and OH− ions, but is permeable to water.4,14 We then collect the microcapsules in water adjusted to have pH = 6, and let the THF evaporate; this forces the pH-responsive polymer to precipitate within the matrix provided by the cross-linked pH-unresponsive polymer, completing the formation of a solid, hybrid shell,12 schematized in Fig. 1(a). We then remove the supernatant, and repeatedly wash the microcapsules with pure water, to remove any surfactant from the continuous phase.
When exposed to NaOH, the pH-responsive polymer chains at the microcapsule exteriors become highly charged and repel each other;11,12,15 this repulsion is screened by any residual Na+ or OH− ions. To probe the microcapsule deformations under these conditions, we immerse them in an aqueous solution with cNaOH = 500 mM, and monitor them using optical microscopy. Strikingly, the hybrid microcapsules quickly become opaque, reflecting the development of heterogeneities in the shell, and abruptly expand in irregular shapes, which may reflect slight variations in the shell structure. Representative optical micrographs of this process are shown in Fig. 1(b) and Movie S1.† The microcapsules ultimately expand into spheres, due to the charging of the shell, as shown by the last frame of Fig. 1(b); this entire process occurs over a timescale of ∼10 s.
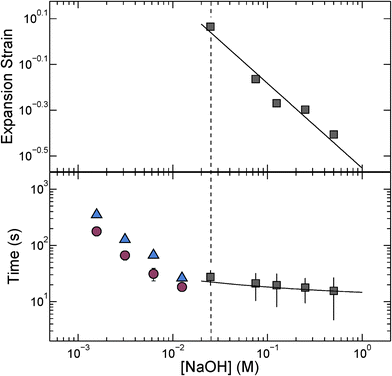
We quantify this behavior by measuring the maximal expansion, γ ≡ (Rf − R0)/R0, where R0 and Rf are the average initial and final microcapsule radii, respectively. We also measure the average time taken for the microcapsules to expand into their final spherical shapes, τ. To elucidate the expansion behavior, we explore even lower values of cNaOH. Intriguingly, γ increases strongly with decreasing cNaOH, as shown in the upper panel of Fig. 2, reaching a value exceeding 1 at cNaOH = 25 mM; the expansion time τ concomitantly increases, but only weakly, as shown by the grey squares in the lower panel of Fig. 2. Unexpectedly, at cNaOH = 25 mM, the microcapsules also begin to disintegrate, forming fragments of size ∼1 μm, as indicated by the arrows in Fig. 1(c). At even smaller cNaOH, the microcapsules first disintegrate, as shown by the first frame of Fig. 1(d); this ultimately results in the formation of a hole in each shell after a time delay τ1 ∼ 10–100 s. The microcapsules then begin to intermittently expand outward, starting at the hole perimeters, as exemplified by the last three frames of Fig. 1(d) and Movie S2;† the region of the shell that expands is indicated by the arrow in each frame. This process occurs over a time period τ2 ∼ 10–100 s; the expansion then stops, leaving wrinkled jellyfish-like structures, approximately 300 μm in size, as shown in Movie S2.† These structures are presumably composed of the covalently cross-linked pH-unresponsive polymer, with the pH-responsive polymer attached to their surfaces. Intriguingly, the expansion and rupture behavior we observe seems to be independent of the PVA concentration, and thus, the osmotic pressure, within the microcapsule core: we observe qualitatively similar behavior using microcapsules containing either 1 wt% PVA, or just pure water, within their cores.
The isotropic expansion at high cNaOH ≥ 25 mM is due to the charging of the microcapsule shells: when exposed to NaOH, the pH-responsive polymers at the microcapsule exteriors become highly charged, leading to a surface charge density σ. We thus expect that the repulsion between the charges on each spherically-symmetric shell leads to a force, directed radially outward, on the shell. We estimate11,16 the magnitude of the resultant electrostatic pressure as pe ≈ σ2κ−1/εε0R, where ε ≈ 80 is the dielectric constant of water, ε0 is the permittivity of free space, R is the time-dependent radius of the spherical microcapsule, and κ−1 is the length over which the repulsive interactions are screened. The quantity of NaOH required to fully charge the shell surface is small;11 consequently, the excess Na+ and OH− ions, which screen the surface charges on the shell, have a concentration approximately equal to cNaOH, and thus 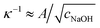 , with A ≡ 0.304 nm M1/2.17 As the microcapsule expands isotropically, a tensile stress builds up within its shell; this resists the expansion. We use shell theory to estimate this stress, pm = Eh(1/R0 − 1/R), where h ≈ 3 μm is the average shell thickness, measured using scanning electron microscopy.18 We thus expect that the microcapsules expand until the electrostatic pressure and tensile stress balance each other; this yields a maximal expansion strain
, with A ≡ 0.304 nm M1/2.17 As the microcapsule expands isotropically, a tensile stress builds up within its shell; this resists the expansion. We use shell theory to estimate this stress, pm = Eh(1/R0 − 1/R), where h ≈ 3 μm is the average shell thickness, measured using scanning electron microscopy.18 We thus expect that the microcapsules expand until the electrostatic pressure and tensile stress balance each other; this yields a maximal expansion strain 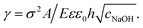 We test this prediction using our measurements of γ. We find γ ∼ cNaOH−1/2, as shown by the line in the top panel of Fig. 2, consistent with the theoretical prediction; fitting the experimental data yields an estimate of σ ≈ 300 e nm−2, where e is the charge of an electron. These results suggest that the microcapsule expansion can be understood by coupling electrostatics with shell theory.
We test this prediction using our measurements of γ. We find γ ∼ cNaOH−1/2, as shown by the line in the top panel of Fig. 2, consistent with the theoretical prediction; fitting the experimental data yields an estimate of σ ≈ 300 e nm−2, where e is the charge of an electron. These results suggest that the microcapsule expansion can be understood by coupling electrostatics with shell theory.
Within this picture, the Na+ and OH− ions screen the repulsion between the charges on the microcapsule shells. As an additional test of this idea, we expose the microcapsules to a 25 mM NaOH solution, also containing 500 mM NaCl; we expect the Na+ and Cl− ions to similarly screen the repulsion between the charges on the microcapsule shells. Consistent with our expectation, the microcapsules do not disintegrate, unlike microcapsules exposed to only 25 mM NaOH. Instead, they expand slightly, reaching a maximal expansion strain γ ≈ 0.4, much smaller than that expected for cNaOH = 25 mM. This value of the strain is instead comparable to that expected for cNaOH = 525 mM, as estimated using the line in the top panel of Fig. 2, thus confirming the validity of our picture. As a final test of this picture, we explore the reversibility of the expansion process by exposing microcapsules, initially charged at 25 mM NaOH and allowed to fully expand to a maximal strain γ ≈ 1.1, to a solution that also contains 500 mM NaCl. Consistent with the picture presented here, we find that the microcapsules shrink upon exposure to NaCl, ultimately reaching a strain γ ≈ 0.4; this provides further support that the Na+ and Cl− ions screen the repulsion between the charges on the microcapsule shells. Moreover, it indicates that the expansion process is reversible under the conditions explored here.
The microcapsules expand to their maximal size over a time period τ. We hypothesize that this behavior reflects the dynamics of the fluid flow into the microcapsule cores, through their porous shells, as they expand.4 We estimate this inflow rate using Darcy's law, pe − pm = μhṘ/3k, where μ ≈ 1 mPa s is the viscosity of water and k is the shell permeability; this yields a characteristic expansion time τ = μR02(1 + γ)/3Ek. We use our measurements of τ, as well as the fit to the measurements of γ shown in the top panel of Fig. 2, to directly test this prediction. We find excellent agreement between the data and the theoretical prediction, as shown by the solid line in the bottom panel of Fig. 2; fitting the experimental data yields a shell permeability k ≈ 10−21 m2. This value provides an approximate estimate for the permeability: while we make the simplifying assumption that k is a constant, it likely changes during the expansion process. However, the agreement between the data and the theoretical prediction thus suggests that the dynamics of the microcapsule expansion can be understood using Darcy's law.
As cNaOH decreases, the screening length κ−1 increases; consequently, the stress in the microcapsule shell increases, ultimately reaching pm = pe ≈ 10 MPa at cNaOH = 25 mM. For even smaller cNaOH, the microcapsules begin to disintegrate into ∼1 μm fragments, and eventually rupture. We hypothesize that, under these conditions, the stress that builds up in the shell exceeds the stress required to fracture it. To test this hypothesis, we estimate the fracture stress19 using the Griffith criterion, 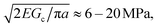 where Gc ∼ 0.1–1 J m−2 is the surface energy per unit area of the shell material and a ≈ 1 μm is the characteristic size of a shell fragment, measured using optical microscopy. Interestingly, this value is in good agreement with our estimate of the maximal stress that develops in the shell, pm ≈ 10 MPa, suggesting that the observed disintegration at cNaOH ≤ 25 mM reflects the fracturing of the microcapsule shell.
where Gc ∼ 0.1–1 J m−2 is the surface energy per unit area of the shell material and a ≈ 1 μm is the characteristic size of a shell fragment, measured using optical microscopy. Interestingly, this value is in good agreement with our estimate of the maximal stress that develops in the shell, pm ≈ 10 MPa, suggesting that the observed disintegration at cNaOH ≤ 25 mM reflects the fracturing of the microcapsule shell.
Finally, we monitor the dynamics of the disintegration, rupture, and subsequent expansion of the microcapsule shell that occurs at cNaOH < 25 mM. Intriguingly, both the time period over which the shell fractures before a hole forms in it, τ1, and the time period over which the shell subsequently expands into a jellyfish-like structure, τ2, both increase with decreasing cNaOH, as shown by the blue triangles and red circles in Fig. 2, respectively. A complete understanding of these dynamics remains a puzzle requiring further inquiry.
Our work highlights the fascinating range of structures exhibited by pH-responsive microcapsules, driven by the interplay between electrostatic and mechanical forces. Intriguingly, many of the morphologies we observe are reminiscent of structures, also induced by electrostatic effects, that often occur in other soft matter systems, such as viruses16,20,21 and red blood cells.22
It is a pleasure to acknowledge Esther Amstad, Michael Brenner, Alberto Fernandez-Nieves, Rodrigo Guerra, and Zhigang Suo for stimulating discussions, and the anonymous reviewers for useful feedback on the manuscript. This work was supported by the NSF (DMR-1006546) and the Harvard MRSEC (DMR-0820484). SSD acknowledges funding from ConocoPhillips. AA acknowledges Evonik Industries for generously donating the Eudragit S-100 polymer used.
References
- V. D. Gordon, X. Chen, J. W. Hutchinson, A. R. Bausch, M. Marquez and D. A. Weitz, J. Am. Chem. Soc., 2004, 126, 14117 CrossRef CAS PubMed.
- H. M. Wyss, T. Franke, E. Mele and D. A. Weitz, Soft Matter, 2010, 6, 4550 RSC.
- A. Fery, F. Dubreuil and H. Mohwald, New J. Phys., 2004, 6, 18 CrossRef.
- S. S. Datta, S. H. Kim, J. Paulose, A. Abbaspourrad, D. R. Nelson and D. A. Weitz, Phys. Rev. Lett., 2012, 109, 134302 CrossRef.
- W. T. S. Huck, Mater. Today, 2008, 11, 24 CrossRef CAS.
- Z. Suo, MRS Bull., 2012, 37, 218 CrossRef CAS.
- B. G. D. Geest, S. D. Koker, J. Demeester, S. C. D. Smedt and W. E. Hennink, Polym. Chem., 2010, 1, 137 RSC.
- B.-S. Kim and O. I. Vinogradova, J. Phys. Chem. B, 2004, 108, 8161 CrossRef CAS.
- K. Kohler, P. M. Biesheuvel, R. Weinkamer, H. Mohwald and G. B. Sukhorukov, Phys. Rev. Lett., 2006, 97, 188301 CrossRef.
- A. S. Utada, E. Lorenceau, D. R. Link, P. D. Kaplan, H. A. Stone and D. A. Weitz, Science, 2005, 308, 537 CrossRef CAS PubMed.
- Further details are available in the ESI.†.
- A. Abbaspourrad, S. S. Datta and D. A. Weitz, Langmuir, 2013 DOI:10.1021/la403064f , in press.
- T. H. Lin, W. H. Huang, I. K. Jun and P. Jiang, Chem. Mater., 2009, 21, 2039 CrossRef CAS.
- S. H. Kim, S. J. Jeon and S. M. Yang, J. Am. Chem. Soc., 2008, 130, 6040 CrossRef CAS PubMed.
- A. San Miguel, J. Scrimgeour, J. E. Curtis and S. H. Behrens, Soft Matter, 2010, 6, 3163 RSC.
- A. Siber and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061906 CrossRef.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Elsevier, 3rd edn, 1986 Search PubMed.
- T. L. Anderson, Fracture Mechanics: Fundamentals and Applications, CRC Press, 3rd edn, 2004 Search PubMed.
- W. K. Kegel and P. van der Schoot, Biophys. J., 2004, 86, 3905 CrossRef CAS PubMed.
- A. L. Bozic, A. Siber and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041916 CrossRef.
- M. D. Betterton and M. P. Brenner, Phys. Rev. Lett., 1999, 82, 1598 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and theoretical details, movies showing microcapsule expansion and rupture. See DOI: 10.1039/c3mh00099k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2014 |