Computational study of diastereoselective ortho-lithiations of chiral ferrocenes†
Andrea
Škvorcová
and
Radovan
Šebesta
*
Department of Organic Chemistry, Faculty of Natural Sciences, Comenius University, Mlynska dolina CH-2, SK-84215, Bratislava, Slovak Republic. E-mail: radovan.sebesta@fns.uniba.sk; Tel: +421 2 60296208
First published on 4th October 2013
Abstract
Diastereoselective ortho-lithiations serve for the preparation of many important chiral ferrocenes, however diastereoselections of these lithiations are explained only by simple steric models. We elucidated ortho-lithiations of three important ferrocenes based on DFT calculations. The calculations showed that simple models of transition states involving ferrocenyl substrates and lithium bases can only in some cases account for the experimental results. Transition state models, which include solvent or coordinating additives as distinct entities bound to lithium, can satisfactorily explain diastereoselection of the ortho-lithiations of chiral ferrocenes.
Introduction
Ferrocene derivatives with planar chirality serve as successful ligands in transition metal catalysed reactions.1–3 One of the key steps in their synthesis is usually an introduction of planar chirality by ortho-metalation, such as palladation,4,5 magnetisation,6–9 or lithiation. The most versatile and frequently used method is ortho-lithiation. The crucial element of this reaction is the presence of an ortho-directing group, which can coordinate and direct the approach of an alkyllithium or lithium dialkylamide base. If the ortho-directing group is chiral, two diastereoisomers of lithium intermediates are formed (Scheme 1). These Li-intermediates can then be trapped with a variety of electrophiles leading to planar chiral 1,2-disubstituted ferrocene derivatives.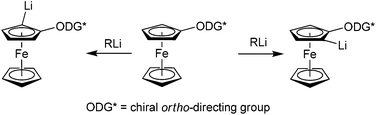 | ||
| Scheme 1 Formation of two possible lithium intermediates evolved from a chiral ferrocene derivative. | ||
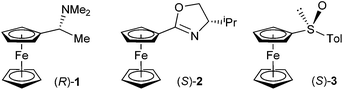
Ugi and co-workers described the first diastereoselective ortho-lithiations of ferrocene derivative – N,N-dimethyl-1-ferrocenylethylamine (Ugi amine).10 Based on this reaction Hayashi developed chiral amino phosphanes, which later culminated in the development of ferrocenyl diphosphines such as the Josiphos family of chiral ligands.11 Apart from the Ugi amine, other amines can serve as ortho-directing groups.12–14 Nitrogen, as a stronger nucleophile, serves as a directing atom in oxazolines, which form the basis of another important group of chiral ligands. Three research groups described ortho-lithiations of ferrocenyl oxazolines almost simultaneously.15–17 Other nitrogen based ortho-directing groups are hydrazones,18,19 azepines,20 sulfoximines,21 and imidazolines.22 Oxygen performs the ortho-directing function in sulfoxides23 acetals,24 methoxy-derivatives,25 and alcohols.26 The structures of the major products of diastereoselective ortho-lithiations have been well established experimentally, either by X-ray or NMR; however, a detailed understanding of the reasons for the observed diastereoselectivity is lacking. It is usually explained by empirical consideration based on simple models of transition states or even intermediates. DFT calculations, only recently started to help explain the underlying reasons for diastereoselection in ortho-lithiations of ferrocene derivatives.27,28 We have studied diastereoselective ortho-lithiations of ferrocenophanes29 and have suggested the mechanism of dilithiation reaction leading to the Taniaphos family of ligands.30 A lack of understanding of the lithiation of ferrocenes prompted us to investigate diastereoselective ortho-lithiations of three relevant ferrocene compounds by DFT calculations. Although many factors, such as steric demands or aggregation of alkyllithium reagent, solvent, additive and size of the substituent on a chiral stereogenic centre, seem to influence the diastereoselectivity of ortho-lithiations we argue that even a rather simplistic model including only ferrocene substrate and a lithium base can account, at least on a qualitative level, for the observed diastereoselection. On the basis of these facts, we decided to provide a theoretical explanation for the experimentally observed diastereoselective lithiations on ferrocene derivatives 1–3, which are essential for the synthesis of useful chiral ferrocenyl ligands (Fig. 1).
For the compounds 1–3, Table 1 summarizes experimental results obtained by ortho-lithiation.3
| Compound | Base | Additive | E+ | Solvent | dr | Major diastereomer |
|---|---|---|---|---|---|---|
| (R)-1 | n-BuLi | — | PPh2 | Et2O | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
(R,Rp) |
| (S)-2 | s-BuLi | — | Me3Si | THF | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(S,Sp) |
| (S)-2 | s-BuLi | TMEDA | Me3Si | Hexane | 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(S,Sp) |
| (S)-3 | LDA | — | Me3Si | THF | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(S,Rp) |
Results and discussion
The calculations were performed at DFT level using the BP86 functional, because it has been well tested on a variety of compound classes including the main group elements as well as transition metals and their compounds. As a basis set, we used Ahlrich's triple-zeta basis set def2-TZVP. For more details see Experimental. We have calculated complete energy profiles for the lithiation of derivatives 1–3, to gain a better understanding of the processes. Calculations of reaction profiles began from isolated starting materials. Firstly, we located complexes, which were likely to be formed between lithium base and the directing atom of the ferrocene derivative. The complexation of lithium alkyl or amide bases on ortho-directing atoms is thermodynamically favoured. The origin of stabilization can be attributed to a favourable binding energy between the relatively concentrated positive charge of the small lithium atom and negative charge of the electron pair.31 This fact is in accordance with the concept of complex-induced proximity effect, described by Snieckus and Beak.32 Already the approach of bases followed by coordination of the free electron pair predicts the formation of transition states. A different situation occurred when the solvent or additive was included in the calculations. The energy of the system did not decrease in the complexation step (the energy difference was just 0–8 kJ mol−1). The major energy gain was observed as a result of Li-coordination with solvent or an additive.ortho-Lithiation of Ugi amine (1)
Homochiral Ugi amine (1) was the first chiral ferrocenyl amine subjected to diastereoselective lithiations.2 Ugi in his seminal work observed the formation of two diastereoisomers in the ratio of 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
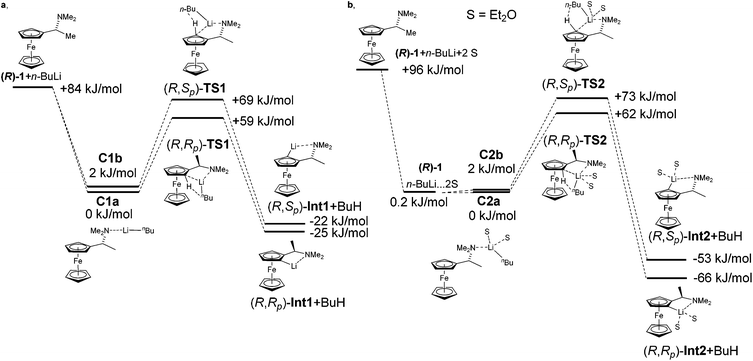
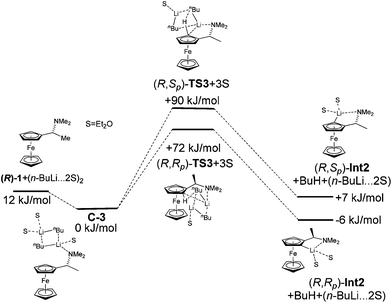
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. Hayashi later described the same diastereomeric ratio in the preparation of ferrocenyl amino phosphines.33 Observed diastereoselectivity was explained by strong repulsion of a methyl group with ferrocene moiety in a non-favoured (R,Sp) transition state. This repulsion is not present in the favoured (R,Rp) transition state. Fig. 2 shows energy profiles for the lithiation of amine (R)-1 without inclusion of Et2O (2a) and with two molecules of Et2O coordinated to lithium (2b). Table 2 gathers relative energies for the reactants, the transitions states and lithiated intermediates of the lithiation of amine (R)-1 with n-BuLi with and without Et2O.
4. Hayashi later described the same diastereomeric ratio in the preparation of ferrocenyl amino phosphines.33 Observed diastereoselectivity was explained by strong repulsion of a methyl group with ferrocene moiety in a non-favoured (R,Sp) transition state. This repulsion is not present in the favoured (R,Rp) transition state. Fig. 2 shows energy profiles for the lithiation of amine (R)-1 without inclusion of Et2O (2a) and with two molecules of Et2O coordinated to lithium (2b). Table 2 gathers relative energies for the reactants, the transitions states and lithiated intermediates of the lithiation of amine (R)-1 with n-BuLi with and without Et2O.
| Compound | ΔErel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (kJ mol−1) a (kJ mol−1) |
Compound | ΔErel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (kJ mol−1) b (kJ mol−1) |
Compound | ΔErel (kJ mol−1) |
|---|---|---|---|---|---|
| a RI-DFT, BP86, def2-TZVP. b RI-DFT-COSMO (ε = 4.33), BP86, def2-TZVP single point. | |||||
| (R)-1 + n-BuLi | 83.5 | (R)-1 + n-BuLi | 45.2 | (R)-1 + n-BuLi + 2Et2O | 95.5 |
| — | — | — | — | (R)-1 + n-BuLi·2Et2O | 0.2 |
| (R)-1·n-BuLi (C1a) | 0.0 | (R)-1·n-BuLi (C1a) | 0.0 | (R)-1·n-BuLi·2Et2O (C2a) | 0.0 |
| (R)-1·n-BuLi (C1b) | 2.5 | (R)-1·n-BuLi (C1b) | 3.6 | (R)-1·n-BuLi·2Et2O (C2b) | 1.8 |
| (R,Rp)-TS1 | 59.3 | (R,Rp)-TS1 | 72.7 | (R,Rp)-TS2 | 62.1 |
| (R,Sp)-TS1 | 68.7 | (R,Sp)-TS1 | 77.1 | (R,Sp)-TS2 | 73.1 |
| (R,Rp)-Int1 + BuH | −25.0 | (R,Rp)-Int1 + BuH | −38.0 | (R,Rp)-Int2 + BuH | −66.0 |
| (R,Sp)-Int1 + BuH | −21.9 | (R,Sp)-Int1 + BuH | −33.9 | (R,Sp)-Int2 + BuH | −52.7 |
The complex C1a leads to transition state (R,Rp)-TS1 and C1b to transition state (R,Sp)-TS1. From the two calculated diastereomeric transition states, (R,Rp)-TS1 is energetically more favoured (ΔE = 12 kJ mol−1) than (R,Sp)-TS1. This fact is in accordance with the experimentally observed configurations of products. The fact that transition state TS1 indeed connects starting material with product was confirmed by performing a potential energy scan (see ESI†).
Experimental data show that the course of lithiation often heavily depends on the solvent. The importance of solvation of lithium compounds is well known. Moreover, solvation can influence the formation of transition states or stabilization of the resulting Li-intermediates.34 Taking this fact into account, we proposed to simulate the effect of solvation of Li-derivatives firstly as a dielectric medium and secondly by two molecules of Et2O, which are included not just as a dielectric medium, but as defined molecules coordinated to lithium.
The calculation performed with COSMO (Et2O, ε = 4.33) resulted in an energy difference of transition states TS-1 of just 4 kJ mol−1. This result suggests that the solvent in the lithiation did not have influence just as a dielectric medium, but that the solvent molecules needed to be explicitly coordinated on lithium with a direct effect on diastereoselectivity of the reaction.
Interestingly, the inclusion of solvent resulted in approximately the same energy difference between the two diastereomeric transition states. A significant change was observed in the relative energies of lithiated products (R,Rp)-Int2, (R,Sp)-Int2. The energy difference increased to ΔErel = 13 kJ mol−1. The inclusion of solvent in the calculation did not affect the formation of transition states but a stabilization of Li-intermediates.
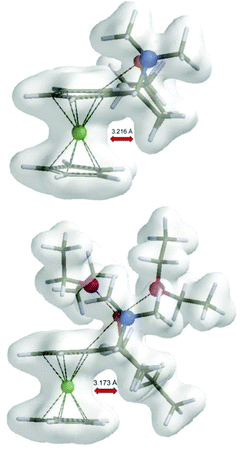
By examination of electron density maps of the calculated transition states TS1, it was possible to see steric repulsions, which were responsible for differences between the transition states. In accordance with Ugi's explanation, there indeed seems to be repulsion of the methyl group with a ferrocene moiety in the non-preferred transition states (R,Sp)-TS1 (Fe–H(CH3) 3.216 Å) and (R,Sp)-TS2 (Fe–H(CH3) 3.173 Å) (Fig. 3). The methyl group, in preferred transition states, is located in the plane of the cyclopentadienyl (Cp) ring.
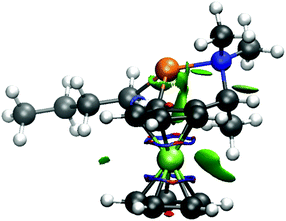
The repulsion of methyl group by the ferrocene skeleton can be visualized by a NCI plot (Fig. 4).35
The alkyllithium bases are present as aggregates in solution. As this can also influence the formation of transition states, we performed a calculation of the lithiation of amine (R)-1 with n-BuLi-dimer. Although in n-BuLi solutions aggregates up to a hexamer can exist, the presence of an amine coordinating atom, such as nitrogen, will likely decrease the aggregation (Fig. 5).
Therefore we used the n-BuLi-dimer as a model for the aggregated species. The energy difference between the two diastereomeric transition states increased to 18 kJ mol−1 and the correct diastereomer was predicted as being more favourable. The reason for the bigger energy difference between the transition states is probably the increased steric interactions in the presence of n-BuLi-dimer in complexes and transition states. The relative energies of the reactants, the transitions states and the resulting Li-intermediates of the lithiation of amine (R)-1 are summarized in Table 3.
| Compound | ΔE (kJ mol−1) |
|---|---|
| (R)-1 + (n-BuLi·2Et2O)2 | 12.4 |
| (R)-1·(n-BuLi)2·3Et2O (C3) + Et2O | 0.0 |
| (R,Rp)-TS3 + 3Et2O | 71.7 |
| (R,Sp)-TS3 + 3Et2O | 89.7 |
| (R,Rp)-Int2 + BuH + (n-BuLi·2Et2O) | −5.9 |
| (R,Sp)-Int2 + BuH + (n-BuLi·2Et2O) | 7.4 |
ortho-Lithiation of ferrocenyl oxazoline 2
Diastereoselective ortho-lithiations of ferrocenyl oxazolines leads to several useful chiral ligands.36,37 Quenching of the respective lithium intermediates with chlorophosphines gives oxazolinyl phosphines.15,17 The reaction with ketones leads to corresponding hydroxyl oxazolines.38 Other electrophiles such as disulfides and diselenides were also used for the synthesis of chiral ligands. ortho-Lithiation of oxazoline is directed by nitrogen as the stronger nucleophile. Sammakia proved this fact by bridging the oxazoline moiety with the unsubstituted Cp-ring, thus restricting rotation around the Cp–C(N) bond.39 Although Sammakia, Richards, and Uemura performed reactions under different conditions (solvent, additive, base), the major diastereoisomer of product was always the same. The experiments resulted only in different diastereomeric ratios. The first experiment performed with n-BuLi in Et2O offered product in the diastereomeric ratio of 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. An improvement was reached in the presence of s-BuLi as the base and THF as the solvent. The diastereoselectivity of lithiations changed to 8
1. An improvement was reached in the presence of s-BuLi as the base and THF as the solvent. The diastereoselectivity of lithiations changed to 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The presence of TMEDA dramatically increased the diastereoselectivity to 100
1. The presence of TMEDA dramatically increased the diastereoselectivity to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (both in diethylether and hexane). The most significant improvement occurred by a change of n-BuLi to s-BuLi where diastereomeric ratio increased to 500
1 (both in diethylether and hexane). The most significant improvement occurred by a change of n-BuLi to s-BuLi where diastereomeric ratio increased to 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.39 On the basis of the observed results, the authors explained the formation of the major (S,Rp) diastereomer by a simple model, in which the repulsion of the i-Pr group from the oxazoline moiety with lithium base is responsible for the diastereoselectivity (Fig. 6).
1.39 On the basis of the observed results, the authors explained the formation of the major (S,Rp) diastereomer by a simple model, in which the repulsion of the i-Pr group from the oxazoline moiety with lithium base is responsible for the diastereoselectivity (Fig. 6).
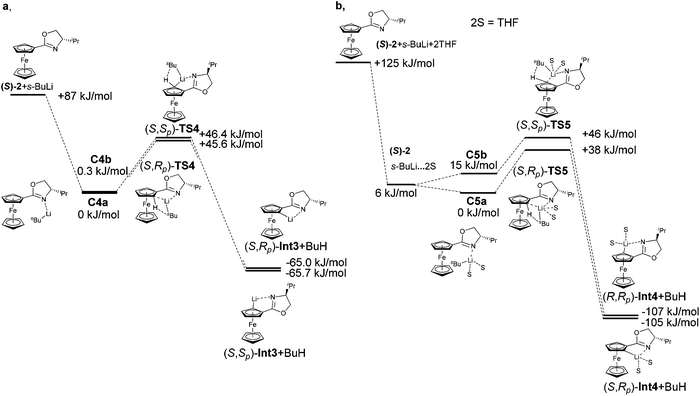
The calculations suggest that this simple model may not be sufficient to account for the observed diastereoselection. Diastereomeric transition states TS4 composed of oxazoline 2 and s-BuLi showed only a negligible energy difference ∼1 kJ mol−1. The situation manifests itself already in the calculation of complexes. The energy difference between complexes C4a and C4b was just 0.27 kJ mol−1. As is shown in Table 1, a major influence of THF was experimentally observed. The calculation of transition states, where two molecules of THF are included, confirmed the experimental results. Also, in this case it is not sufficient to include solvent only as the dielectric medium. The energies of the transition states were the same and neither transition state was favoured. However, the experimentally observed diastereoselectivity of the lithiation of compound 2 in THF is 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The calculation of lithiation, where two THF molecules were coordinated on the lithium atom observed a preferred formation of the less hindered transition state (S,Rp)-TS5 by 7.4 kJ mol−1. While in the transition states TS4, we did not observe any repulsion of the i-Pr group with base or ferrocene skeleton, in TS5, THF molecules showed repulsion of the i-Pr group with approaching base. This fact made one transition state more favourable and the diastereoselectivity changed. This theoretical result confirmed the experimental observations of Sammakia and co-workers.39
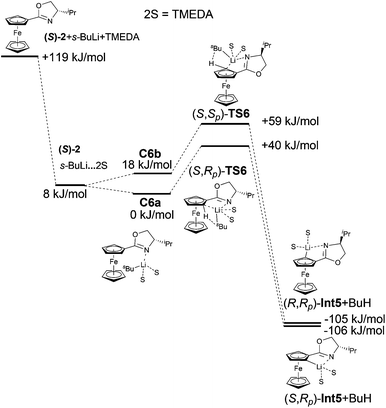
The inclusion of strongly chelating agent N,N,N′,N′-tetramethylethylenediamine (TMEDA) had a significant impact on the results. As this sterically bulky compound coordinated to lithium, it filled the space around lithium and thus helped increase steric interactions between the base and the substrate.
This effect was manifested both in complexation and was followed by the formation of transition states. It is confirmed by the large energy difference between complexes C6a and C6b. The formation of C6b was less favoured and therefore the formation of (S,Sp)-TS6 was not preferred. The calculated transition state (S,Rp)-TS6 is by 19 kJ mol−1 more stable than (S,Sp)-TS6. These calculated results correlate with the experimentally obtained major diastereomer (Fig. 7). The relative energies of the reactants, the transitions states and the resulting Li-intermediates of the lithiation reactions of oxazoline (S)-2, both with and without TMEDA and THF, are summarized in Tables 4 and 5.
| Compound | ΔEa (kJ mol−1) | Compound | ΔEb (kJ mol−1) |
|---|---|---|---|
| a RI-DFT, BP86, def2-TZVP. b RI-DFT-COSMO (ε = 7.58), BP86, def2-TZVP single point. | |||
| (S)-2 + s-BuLi | 86.9 | (S)-2 + s-BuLi | 37.5 |
| (S)-2·s-BuLi (C4a) | 0.0 | (S)-2·s-BuLi (C4a) | 0.0 |
| (S)-2·s-BuLi (C4b) | 0.3 | (S)-2·s-BuLi (C4b) | 0.1 |
| (S,Rp)-TS4 | 45.6 | (S,Rp)-TS4 | 57.8 |
| (S,Sp)-TS4 | 46.4 | (S,Sp)-TS4 | 57.9 |
| (S,Rp)-Int3 + BuH | −65.0 | (S,Rp)-Int3 + BuH | −79.1 |
| (S,Sp)-Int3 + BuH | −65.7 | (S,Sp)-Int3 + BuH | −80.7 |
| Compound | ΔE (kJ mol−1) |
|---|---|
| (S)-2 + s-BuLi + 2THF | 124.7 |
| (S)-2 + s-BuLi·2THF | 6.3 |
| (S)-2·s-BuLi·2THF (C5a) | 0.0 |
| (S)-2·s-BuLi·2THF (C5b) | 14.6 |
| (S,Rp)-TS5 | 38.6 |
| (S,Sp)-TS5 | 46.0 |
| (S,Rp)-Int4 + BuH | −106.6 |
| (S,Sp)-Int4 + BuH | −105.4 |
| (S)-2 + s-BuLi + TMEDA | 119.4 |
| (S)-2 + s-BuLi·TMEDA | 7.7 |
| (S)-2·s-BuLi·TMEDA (C6a) | 0.0 |
| (S)-2·s-BuLi·TMEDA (C6b) | 18.1 |
| (S,Rp)-TS6 | 39.9 |
| (S,Sp)-TS6 | 59.2 |
| (S,Rp)-Int5 + BuH | −106.3 |
| (S,Sp)-Int5 + BuH | −105.0 |
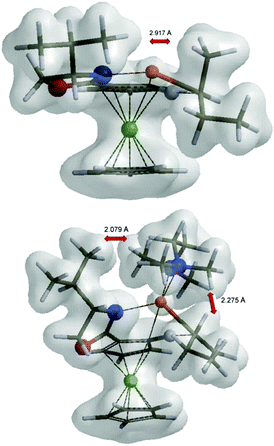
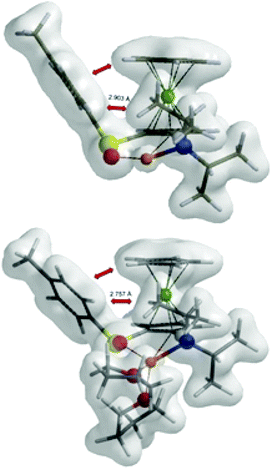
Inspection of the electron density maps of diastereomeric transition states TS4 shows that the distance between i-Pr group oriented up and alkyllithium base is sufficiently large (2.92 Å) and no repulsion is observed. On the other hand, the presence of TMEDA, as a bulky additive coordinated to the alkyllithium base, leads to larger repulsion with the i-Pr group in (S,Sp)-TS6 and thus the formation of (S,Rp)-TS6 is favoured (Fig. 8).
ortho-Lithiation of ferrocenyl sulfoxide 3
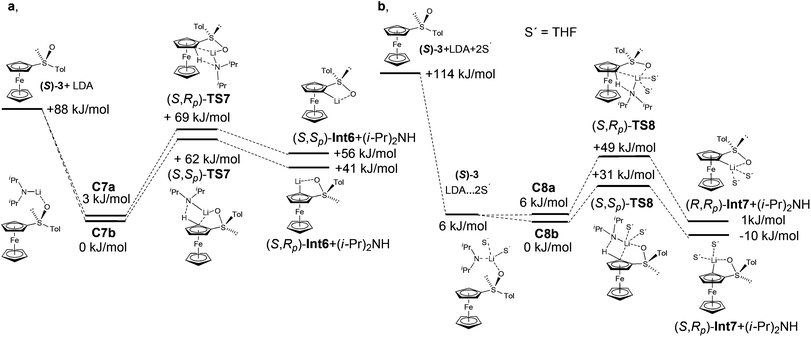
Diastereoselective ortho-lithiations and electrophilic quenching of ferrocenyl sulfoxide is another useful transformation because the sulfoxide group allows facile modification and thus preparation of chiral ligands. A sulfoxide lithiation strategy led to successful ligands such as the second generation of Taniaphos40 and related ligands,41 diphosphanes with only planar chirality,42 or Carretero's Fesulphos family of ligands.43 In the original report, Kagan and co-workers described lithiation of sulfoxide 3 with n-BuLi.23 They later found a more convenient procedure for the lithiation of ferrocenyl sulfoxide 3 with LDA, because butyl lithium also attacks the C–S bond.44 The lithiation proceeds preferentially in the pro-S position. To the best of our knowledge, however, no explanation can be found for the observed diastereoselectivity in the lithiation of sulfoxide 3.At the beginning of this part of the study, we have realized that LDA conformations play an important role and significantly influence the results. Energy differences of up to ΔErel = 5 kJ mol−1 were found (see ESI†). The formation of complex C7a is more favored (3.5 kJ mol−1) than the formation of complex C7b (Fig. 9 and Table 6).
| Compound | ΔEa (kJ mol−1) | Compound | ΔEb (kJ mol−1) | Compound | ΔEa (kJ mol−1) |
|---|---|---|---|---|---|
| a RI-DFT, BP86, def2-TZVP. b RI-DFT-COSMO (ε = 7.58), BP86, def2-TZVP, single point. | |||||
| (S)-3 + LDA | 88.5 | (S)-3 + LDA | 36.4 | (S)-3 + LDA + 2THF | 114.3 |
| — | — | — | — | (S)-3 + LDA·2THF | 5.9 |
| (S)-3·LDA (C7b) | 0.0 | (S)-3·LDA (C7b) | 0.0 | (S)-3 + LDA·2THF (C8b) | 0.0 |
| (S)-3·LDA (C7a) | 3.5 | (S)-3·LDA (C7a) | 1.6 | (S)-3 + LDA·2THF (C8a) | 6.5 |
| (S,Rp)-TS7 | 68.8 | (S,Rp)-TS7 | 74.8 | (S,Rp)-TS8 | 49.5 |
| (S,Sp)-TS7 | 62.0 | (S,Sp)-TS7 | 61.4 | (S,Sp)-TS8 | 30.7 |
| (S,Rp)-Int6 + (i-Pr)2NH | 55.5 | (S,Rp)-Int6 + (i-Pr)2NH | 26.5 | (S,Rp)-Int7 +(i-Pr)2NH | 1.1 |
| (S,Sp)-Int6 + (i-Pr)2NH | 40.8 | (S,Sp)-Int6 + (i-Pr)2NH | 12.5 | (S,Sp)-Int7 +(i-Pr)2NH | −9.5 |
Diastereoselection seems to be induced by the orientation of a tosyl group. While the tosyl group in C7a and (S,Sp)-TS7 is oriented over the ferrocene skeleton, the position of this group in C7b and (S,Rp)-TS7 is near the ferrocene moiety (Fig. 10).
The inclusion of the solvent in the calculation increased the energy difference between the complexes and the transition states. The coordination of two molecules of THF on lithium increased the steric demands of the lithium base. The repulsion of LDA with a tosyl group is observed in non-favoured transition state (S,Rp)-TS8. On the other hand, this repulsion is not possible in the transition state (S,Sp)-TS8, because the tosyl group is oriented on the opposite side. The energetically favoured transition states lead to the product (S,Rp)-Int7, which is in accordance with experiment (Fig. 9 and Table 6).
Conclusion
In conclusion, diastereoselective ortho-lithiations of three key ferrocene derivatives were studied by DFT calculations. Calculations can in all examples predict the formation of the experimentally obtained major diastereoisomer. The involvement of solvents or additives influenced energy differences of transition states for compounds 2 and 3. Coordinated solvent or additive increases the steric interactions between the Li-base and ferrocenyl substrate, which helps to differentiate between the diastereomeric transition states.The electron density maps of transition states help observe interactions in the diastereomeric transition states. Table 7 summarizes the bonding distances, energy differences for complexes, transition states and intermediates of the studied lithiations.
| (R)-1 | (S)-2 | (S)-3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Int | Int1 | Int2 | Int2 e | Int3 | Int4 | Int5 | Int6 | Int7 |
| a Energy of calculated complexes, transition states and intermediates are displayed in kJ mol−1. b Distances between hydrogen and base in complexes displayed in Å. c Distance between hydrogen and ferrocenyl carbon displayed in Å. d Distance between ferrocenyl carbon and lithium displayed in Å. e Intermediates produced when BuLi-dimer was considered. | ||||||||
| C | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| ΔE C-a | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.5 | 6.5 |
| d(H–C)b | 3.01 | 3.40 | 2.74 | 2.56 | 2.61 | 4.34 | 2.48 | |
| ΔE C-b | 2.5 | 1.8 | — | 0.3 | 14.6 | 18.1 | 0.0 | 0.0 |
| d(H–C)b | 2.97 | 3.48 | 2.72 | 2.73 | 3.85 | 4.36 | 5.69 | |
| TS | TS1 | TS2 | TS3 | TS4 | TS5 | TS6 | TS7 | TS8 |
| ΔE (Rp)-TS | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.8 | 18.7 |
| d(H–C)c | 1.40 | 1.44 | 1.34 | 1.37 | 1.41 | 1.40 | 1.43 | 1.45 |
| d(C–Li)d | 2.11 | 2.40 | 2.63 | 2.30 | 2.75 | 2.68 | 2.56 | 3.11 |
| ΔE (Sp)-TS | 9.4 | 10.9 | 18.0 | 0.8 | 7.4 | 19.3 | 0.0 | 0.0 |
| d(H–C)c | 1.43 | 1.44 | 1.35 | 1.36 | 1.41 | 1.39 | 1.45 | 1.43 |
| d(C–Li)d | 2.14 | 2.38 | 2.60 | 2.26 | 2.77 | 2.64 | 2.90 | 3.45 |
| Int | Int1 | Int2 | Int2e | Int3 | Int4 | Int5 | Int6 | Int7 |
| ΔE (Rp)-Int | 0.0 | 0.0 | 0.00 | 0.7 | 0.0 | 0.0 | 14.7 | 10.6 |
| ΔE (Sp)-Int | 3.1 | 13.3 | 13.3 | 0.0 | 1.2 | 1.3 | 0.0 | 0.0 |
The NCI plot software was use for visualization of non-covalent repulsions in transition states.
Experimental
All structures were first pre-optimized at the semiempirical PM3 level using the Spartan 8 program package.45 Transition states were optimized at DFT level using BP86 functional and 6-31G* basis set in Spartan 8. Finally transition states were refined at RI-DFT,46,47 level with the BP86 functional48 using def2-TZVP basis set49 as implemented in the Turbomole package.50 Minima were also optimized at RI-DFT level (BP86/TZVP). The empirical dispersion correction was evaluated by performing a single point calculation with DTF-D3 as implemented in Turbomole. However, these calculations did not correlate well with the experimental results.51 Searching for conformers of LDA and (i-Pr)2NH was performed with HF level and (6-31G*) basis set in Spartan 8. Final conformers of LDA and (i-Pr)2NH were optimized at DFT level with the BP86 functional using def2-TZVP basis set as implemented in the Turbomole package. All structures were characterized by frequency calculations at RI-DFT level52 with the BP86 functional using def2-TZVP. All transition states have only one imaginary vibration corresponding to C–H bond breaking (verified by visualization); minima have only real vibrations.Acknowledgements
Financial support from Slovak Grant Agency VEGA, grant no. 1/0623/12 is gratefully acknowledged.Notes and references
- P. Štepnička, Ferrocene: Ligands, Materials and Biomolecules, Wiley, Chichester, 2008 Search PubMed.
- A. Togni and T. Hayashi, Ferrocenes, VCH, Weinheim, 1995 Search PubMed.
- L.-X. Dai and X.-L. Hou, Chiral Ferrocenes in Asymmetric Catalysis, Wiley-VCH, Weinheim, 2010 Search PubMed.
- V. I. Sokolov, L. L. Troitskaya and O. A. Reutov, J. Organomet. Chem., 1979, 182, 537–546 CrossRef CAS.
- L. L. Troitskaya, Z. A. Starikova, T. V. Demeshchik, S. T. Ovseenko, E. V. Vorontsov and V. I. Sokolov, J. Organomet. Chem., 2005, 690, 3976–3982 CrossRef CAS PubMed.
- A. H. Stoll, P. Mayer and P. Knochel, Organometallics, 2007, 26, 6694–6697 CrossRef CAS.
- P. C. Andrikopoulos, D. R. Armstrong, W. Clegg, C. J. Gilfillan, E. Hevia, A. R. Kennedy, R. E. Mulvey, C. T. O'Hara, J. A. Parkinson and D. M. Tooke, J. Am. Chem. Soc., 2004, 126, 11612–11620 CrossRef CAS PubMed.
- K. W. Henderson, A. R. Kennedy, R. E. Mulvey, C. T. O'Hara and R. B. Rowlings, Chem. Commun., 2001, 1678–1679 RSC.
- W. Clegg, K. W. Henderson, A. R. Kennedy, R. E. Mulvey, C. T. O'Hara, R. B. Rowlings and D. M. Tooke, Angew. Chem., Int. Ed., 2001, 40, 3902–3905 CrossRef CAS.
- D. Marquarding, H. Klusacek, G. Gokel, P. Hoffmann and I. Ugi, J. Am. Chem. Soc., 1970, 92, 5389–5393 CrossRef CAS.
- A. Togni, C. Breutel, A. Schnyder, F. Spindler, H. Landert and A. Tijani, J. Am. Chem. Soc., 1994, 116, 4062–4066 CrossRef CAS.
- C. Ganter and T. Wagner, Chem. Ber., 1995, 128, 1157–1161 CrossRef CAS.
- L. Xiao, R. Kitzler and W. Weissensteiner, J. Org. Chem., 2001, 66, 8912–8919 CrossRef CAS PubMed.
- M. Widhalm, U. Nettekoven and K. Mereiter, Tetrahedron: Asymmetry, 1999, 10, 4369–4391 CrossRef CAS.
- C. J. Richards, T. Damalidis, D. E. Hibbs and M. B. Hursthouse, Synlett, 1995, 74–76 CrossRef CAS PubMed.
- T. Sammakia, H. A. Latham and D. R. Schaad, J. Org. Chem., 1995, 60, 10–11 CrossRef CAS.
- Y. Nishibayashi and S. Uemura, Synlett, 1995, 79–81 CrossRef CAS PubMed.
- D. Enders, R. Peters, R. Lochtman and G. Raabe, Angew. Chem., Int. Ed., 1999, 38, 2421–2423 CrossRef CAS.
- D. Enders, R. Peters, R. Lochtman and J. Runsink, Eur. J. Org. Chem., 2000, 2839–2850 CrossRef CAS.
- M. Widhalm, K. Mereiter and M. Bourghida, Tetrahedron: Asymmetry, 1998, 9, 2983–2986 CrossRef CAS.
- C. Bolm, M. Kesselgruber, K. Muñiz and G. Raabe, Organometallics, 2000, 19, 1648–1651 CrossRef CAS.
- R. Peters and D. F. Fischer, Org. Lett., 2005, 7, 4137–4140 CrossRef CAS PubMed.
- F. Rebière, O. Riant, L. Ricard and H. B. Kagan, Angew. Chem., Int. Ed. Engl., 1993, 32, 568–570 CrossRef.
- O. Riant, O. Samuel and H. B. Kagan, J. Am. Chem. Soc., 1993, 115, 5835–5836 CrossRef CAS.
- M. Lotz, T. Ireland, K. Tappe and P. Knochel, Chirality, 2000, 12, 389–395 CrossRef CAS.
- B. J. Ueberbacher, H. Griengl and H. Weber, Chem. Commun., 2008, 3287–3289 RSC.
- C. Metallinos, J. Zaifman, T. Dudding, L. Van Belle and K. Taban, Adv. Synth. Catal., 2010, 352, 1967–1982 CrossRef CAS.
- C. Metallinos, J. John, J. Nelson, T. Dudding and L. Belding, Adv. Synth. Catal., 2013, 355, 1211–1219 CrossRef CAS.
- A. Škvorcová, E. Rakovský, J. Kožíšek and R. Šebesta, J. Organomet. Chem., 2011, 696, 2600–2606 CrossRef PubMed.
- A. Almássy, A. Škvorcová, B. Horváth, F. Bilčík, V. Bariak, E. Rakovský and R. Šebesta, Eur. J. Org. Chem., 2013, 111–116 CrossRef.
- U. Olsher, R. M. Izatt, J. S. Bradshaw and N. K. Dalley, Chem. Rev., 1991, 91, 137–164 CrossRef CAS.
- M. C. Whisler, S. MacNeil, V. Snieckus and P. Beak, Angew. Chem., Int. Ed., 2004, 43, 2206–2225 CrossRef CAS PubMed.
- T. Hayashi, Pure Appl. Chem., 1988, 60, 7–12 CrossRef CAS.
- B. L. Lucht and D. B. Collum, J. Am. Chem. Soc., 1995, 117, 9863–9874 CrossRef CAS.
- (a) E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed; (b) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theor. Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- O. B. Sutcliffe and M. R. Bryce, Tetrahedron: Asymmetry, 2003, 14, 2297–2325 CrossRef CAS.
- Y. Miyake, Y. Nishibayashi and S. Uemura, Synlett, 2008, 1747–1758 CAS.
- C. Bolm, K. Muñiz Fernández, A. Seger and G. Raabe, Synlett, 1997, 1052 Search PubMed.
- T. Sammakia and H. A. Latham, J. Org. Chem., 1995, 60, 6002–6003 CrossRef CAS.
- M. Lotz, K. Polborn and P. Knochel, Angew. Chem., Int. Ed., 2002, 41, 4708–4711 CrossRef CAS PubMed.
- M. N. Cheemala and P. Knochel, Org. Lett., 2007, 9, 3089–3092 CrossRef CAS PubMed.
- G. Argouarch, O. Samuel, O. Riant, J.-C. Daran and H. B. Kagan, Eur. J. Org. Chem., 2000, 2893–2899 CrossRef CAS.
- S. Cabrera, O. Garcia Mancheno, R. Gomez Arrayas, I. Alonso, P. Mauleon and J. C. Carretero, Pure Appl. Chem., 2006, 78, 257–265 CrossRef CAS.
- O. Riant, G. Argouarch, D. Guillaneux, O. Samuel and H. B. Kagan, J. Org. Chem., 1998, 63, 3511–3514 CrossRef CAS.
- Spartan ‘08, Wavefunction, Inc., Irvine, CA Search PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- TURBOMOLE V6.4, TURBOMOLE GmbH, Karlsruhe, 2012 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2004, 384, 103–107 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Energies and Cartesian coordinates of all calculated structures, imaginary frequencies and NCI plots for transition states, table of LDA conformers, and potential energy scan for lithiations of amine (R)-1. See DOI: 10.1039/c3ob41339j |
| This journal is © The Royal Society of Chemistry 2014 |