Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The thermodynamics of the self-assembly of covalently linked oligomeric naphthalenediimides into helical organic nanotubes†
Koujiro
Tambara
a,
John-Carl
Olsen
b,
David E.
Hansen
c and
G. Dan
Pantoş
*d
aUniversity Chemical Laboratory, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: kt287@cam.ac.uk; Tel: +44 (0)1223 336300
bSchool of Sciences, Indiana University Kokomo, Kokomo, IN 46904, USA. E-mail: olsenj@iuk.edu; Tel: +1 (765) 455 9207
cW.M. Keck Science Department of Claremont McKenna, Pitzer, and Scripps Colleges, 925 N. Mills Avenue, Claremont, CA 91711, USA. E-mail: dhansen@kecksci.claremont.edu; Tel: +1 (909) 607 2565
dDepartment of Chemistry, University of Bath, Bath BA2 7AY, UK. E-mail: g.d.pantos@bath.ac.uk; Tel: +44 (0)1225 384376
First published on 13th November 2013
Abstract
The mechanism and thermodynamic functions of the self-assembly of a family of covalently linked oligomeric naphthalenediimides (NDIs) were investigated through variable-temperature NMR and CD studies. The NDIs were shown to self-assemble into helical supramolecular nanotubes via an isodesmic polymerisation mechanism, and regardless of the oligomer length a surprising entropy–enthalpy compensation was observed.
Introduction
Here we report a detailed study of the thermodynamic functions and supramolecular self-assembly mechanism of a family of homologous NDIs. The spontaneous supramolecular self-assembly of amino acid derived NDI nanotubes has been reported by the Sanders group.1 Using one such NDI – derived from S-trityl protected L-cysteine – as a model system for this process due to its enhanced solubility in chlorinated aprotic solvents, the thermodynamic functions and supramolecular self-assembly mechanism were investigated.2 The self-assembly of a quasi-one dimensional supramolecular polymer such as an NDI nanotube occurs through either an isodesmic or cooperative mechanism.3–7 In an isodesmic polymerisation process, the addition of a monomer to the growing polymer is governed by a single equilibrium constant, Ke, regardless of the size or length of the polymer. Consequently, a broad distribution in the degree of polymerisation is often observed for this type of process, even when conditions that favour polymerisation – such as low temperature, exceptionally high association constant and/or high concentrations – are employed. On the other hand, a cooperative mechanism involves two different equilibrium constants: the initial formation of a nucleation core governed by one equilibrium constant, Kn, which precedes the elongation process governed by the elongation equilibrium constant, Ke. If Ke ≫ Kn, the initial unfavourable activation step is followed by a rapid elongation in the growing chain (Fig. 1). | ||
| Fig. 1 Top: the equilibria for isodesmic and cooperative polymerisation mechanisms. Bottom: graphical representation of the isodesmic vs. cooperative mechanism, reproduced from ref. 3. | ||
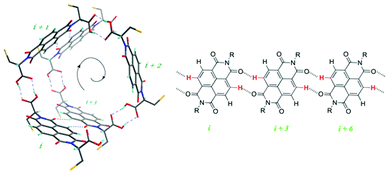
In chiral, helical supramolecular architectures, a cooperative growth mechanism is typically observed due to the fact that the number of interactions between each monomer increases as the first turn of the helix is completed.4 In the case of NDI nanotubes, a similar outcome was initially hypothesised: the 1st, 2nd, and 3rd NDI residues in the nanotube are held together solely by carboxylic acid dimerisations. All adjacent NDI residues thereafter are held together by carboxylic acid dimerisations as well, but after completion of the first turn of the helix (in other words, upon incorporation of the 4th residue), there are additional interactions between ith and i + 3rd residues in the form of C–H⋯O non-classical hydrogen bonds (Fig. 2).8
However, the Sanders group recently reported the isodesmic growth mechanism for NDI nanotubes,2 a finding attributed to the phenomenon of entropy–enthalpy compensation, in which the enthalpic gain of forming the aforementioned additional non-classical hydrogen bond is offset by the entropic cost resulting from the reduced degrees of freedom of incorporating a monomer NDI into a nanotube. Building on this work – in which the self-assembly process of monomeric NDIs into nanotubes was investigated – the investigation of the self-assembly process of a series of covalently linked, oligomeric NDIs was conceived (Fig. 3).
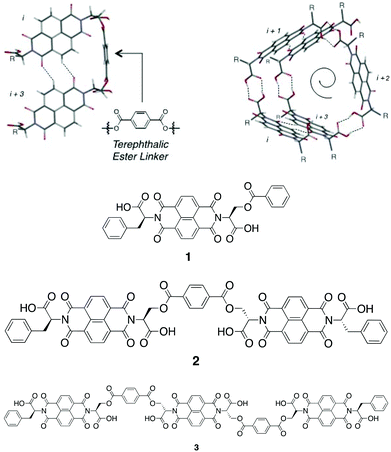 | ||
| Fig. 3 Top: molecular model of the terephthalate ester linker (left) in relation to the overall nanotubular structure (right), where R represents the amino acid side-chains.9Bottom: molecular structure of NDIs 1–3. | ||
Samples of NDIs 1–3 were obtained directly from John-Carl Olsen, who had synthesized them as reported in the initial studies published on these compounds.9 The terephthalate moiety was selected as the covalent linker on account of its geometric suitability, as determined from molecular modeling (Top, Fig. 3). The amino acid derivatives chosen for N-functionalisation were L-serine and L-phenylalanine: the former was selected as a precursor to the terephthalate ester linkages (or, for 1, the benzoate side-chain), whilst the latter was selected to provide good solubility in organic solvents and also to provide minimal hydrogen bonding competitors, as this would disrupt nanotube formation.
Experimental
VT NMR experiments were undertaken on a Bruker 400 MHz spectrometer with the following parameters for each temperature recorded: number of dummy scans = 2, number of scans = 16, equilibration time = 300 s. Where a mixture of solvents was used, 1,1,2,2-tetrachloroethane (TCE) was added to the NDI first, followed by the second solvent before sonication. The temperature was regulated by the heating element in the instrument for high temperatures, and with a liquid nitrogen cooling inlet for low temperatures. The experiments were recorded from high temperature to low temperature.VT CD experiments were undertaken on Applied Photophysics Chirascan Circular Dichroism Spectrophotometer with the following parameters: monochromator bandwidth = 1 nm, sampling time-per-point = 1 second, number of repeats per scan = 2, scanning increments = 1 nm, temperature equilibration time = 300 s. The spectrum of the control solvent was pre-recorded and autosubtracted from subsequent scans. The temperature was regulated by a Peltier thermoelectric temperature controller using a water cooling system (maximum temperature = 95 °C). The experiments were recorded from high temperature to low temperature.
Results and discussion
VT NMR studies
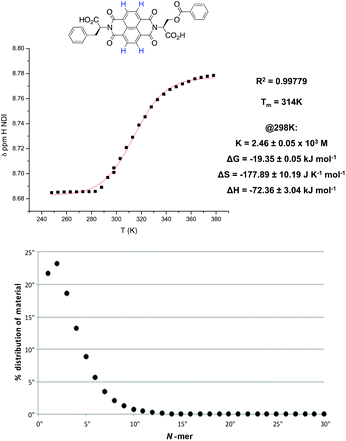
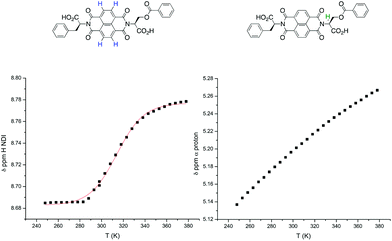
In the previous study by the Sanders group,2 a plot of the NDI proton chemical shift – which is highly dependent on temperature – in VT NMR was fitted to an isodesmic model to yield thermodynamic functions for the assembly process. Therefore, VT NMR was first conducted on 1 using TCE as the solvent due to its high boiling point and polarity similar to that of chloroform (Fig. 4).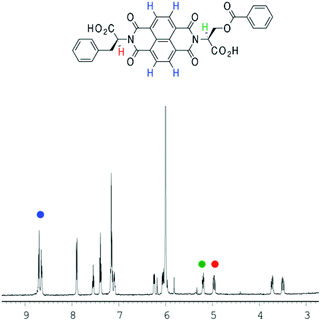 | ||
| Fig. 4 The partial 1H-NMR spectrum of 1 (d2-TCE, 1 × 10−3 M). The different protons (NDI in blue; two α protons in green and red) plotted for fitting have been highlighted. | ||
In the NDI nanotubes, the presence of the non-classical C–H⋯O hydrogen bonding pattern involving the NDI proton means that any significant change in its chemical shift is a direct result of NDI monomer incorporation into the growing nanotube chain. On the other hand, the α proton forms no significant non-covalent interactions in the nanotubular structure, and therefore the chemical shift of the NDI proton was plotted as a function of temperature, and the graph fitted to an isodesmic model (Fig. 5). The good fit of the data suggests that the self-assembly process is indeed isodesmic, as was observed earlier for an NDI derived from S-trityl protected L-cysteine; the thermodynamic functions and the melting temperature (Tm) for the assembly process were calculated using the published methodology.2
Dimeric NDI 2 showed limited solubility in TCE that could be overcome by the addition of tetrahydrofuran (THF). However, because of its hydrogen-bond acceptor abilities and hence its potential to disrupt the formation of nanotubes, the proportion of THF to TCE was kept to a minimum: thus, a 2% THF in TCE (v/v) solvent mixture was employed for NDI 2 (Fig. 6).
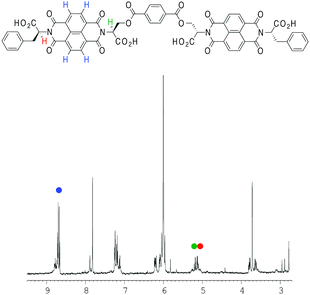 | ||
| Fig. 6 1H NMR spectrum of 2 (2% THF in TCE, v/v). The different protons (NDI in blue; two α protons in green and red) plotted for fitting have been highlighted. | ||
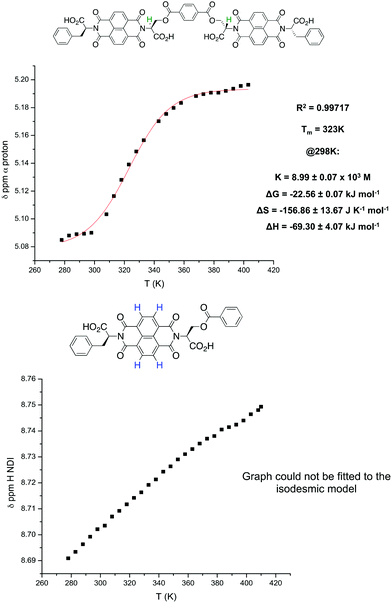
VT NMR studies using this solvent system revealed the following features: first, a plot of the chemical shift of the NDI protons as a function of temperature yielded a graph with a poor fit to the isodesmic model, yet a plot of the chemical shift of the α protons yielded a smooth sigmoid that could be fitted to an isodesmic model (Fig. 7); and secondly, the thermodynamic functions calculated from both protons yielded a larger value for the melting temperature (Tm) for the nanotube than that obtained for monomer 1 in pure TCE, despite the presence of THF.
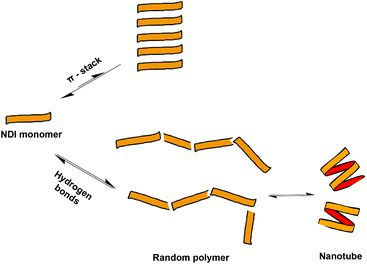
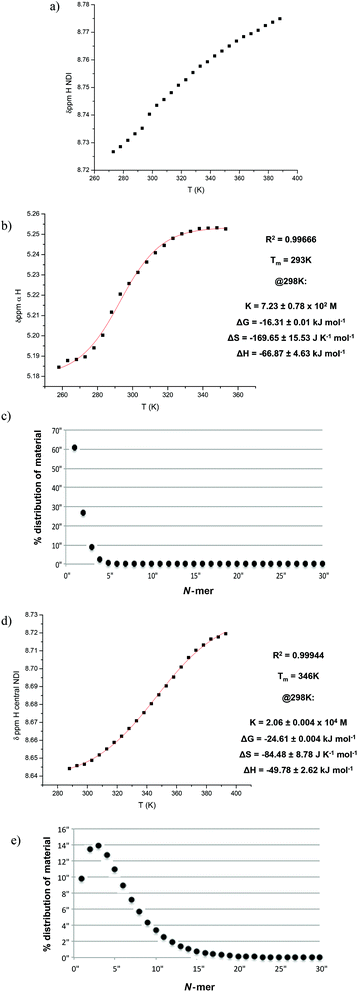
The melting temperature is defined as the temperature at which the degree of aggregation is 0.5, therefore it directly reflects the stability of the resulting nanotube, suggesting that the nanotubes formed by dimer 2 (Fig. 8) are significantly more stable and resistant to hydrogen bonding competitors than those formed from monomer 1, a result consistent with the earlier work on these molecules.9 As a comparison, the corresponding experiment for 1 in 2% THF yielded a linear graph (total loss of sigmoidal character), indicating that the addition of 2% THF was sufficient to prevent the formation of nanotubes altogether. The origins of this increased robustness in 2 in the presence of hydrogen bond competitors lies in the covalent linker group. The possible NDI aggregates in solution are hypothesised to be in equilibrium with each other (Fig. 9), where the population distribution is governed by the thermodynamic stability of each member, thus effectively forming a Dynamic Combinatorial Library.
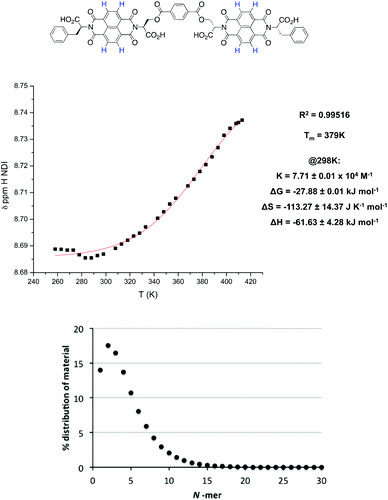 | ||
| Fig. 8 Top: the isodesmic fitting and thermodynamic functions for the NDI proton of 2 in 2% THF in TCE at 5 × 10−4 M. Bottom: the percentage distribution of material as a function of polymer length. | ||
By covalently connecting together the NDI units with a terephthalate linker (2), the π-stacked aggregates and random polymers have fewer accessible conformational states as compared with the analogous structures formed from ‘monomeric’ NDIs (such as 1, with its single NDI core)—as a result, covalent linking makes the formation of the π-stacked aggregates and random polymers entropically less favourable. In contrast, the additional entropic cost to nanotube formation brought on by covalent linking is expected to be negligible since the nanotubes have limited conformational flexibility to begin with and their structure is expected to be little affected by the introduction of the terephthalate linker (Top, Fig. 3). As a result, nanotube formation is comparatively favoured for the oligomeric NDIs. Furthermore, because of the decreased degrees of freedom in the free unaggregated state of the linked NDIs, the entropic penalty of incorporating the dimer 2 and trimer 3 into a nanotube is also decreased.
A first inspection and comparison of the NDI proton plot against the α proton plot for 2 reveals a significant discrepancy (373 K vs. 323 K) in the value of Tm (and hence in the values of the thermodynamic functions that depend of the value of Tm). Given the involvement of the NDI but not the α protons in the non-classical C–H⋯O hydrogen bonding pattern in the nanotube, it can be said that these two protons monitor different processes within the overall equilibrium of the system (Fig. 9). Consequently, the values of the thermodynamic functions calculated from these two different protons may contain errors that cannot be accounted for or directly compared to one another due to the different factors affecting their (de)shielding. A comparison of the NDI and α protons of 1 in TCE (Fig. 10) illustrates this: whilst the NDI plot produces a sigmoidal trace that gives a good fit to the isodesmic model, the α proton plot produces a near-linear trace that gives a very poor fit. For these reasons, the melting temperature values obtained from monitoring different protons are instructive more as a guideline rather than a quantitative measurement. A quantitative dimension of these data is added when comparing values obtained for different molecules in which protons involved in similar processes are observed.
Trimeric NDI 3 showed very limited solubility in the 2% THF solvent system, with any significant solubility being observed only at 4% THF in TCE. With this solvent system, however, all sigmoidal character was lost for all VT NMR plots of 1 and 2 regardless of the monitored proton, and thus a different solvent system was required.
1,4-Dioxane as the solubilising agent
As an alternative to THF, 1,4-dioxane was selected as the solubilising agent for the oligomeric NDIs based on its structural similarity to THF. 1% dioxane in TCE was established as a solvent system across all NDIs, involving a compromise between the need for solubility and the need to minimise the disruptive effect of dioxane on nanotube formation. VT NMR studies on NDIs 1–3 using this solvent system provided a comparable set of melting curves for the formation of nanotubes (Fig. 11). The trend observed for the thermodynamic functions and Tm values were consistent with expectations based on the entropic arguments outlined earlier.The Tm values obtained from all the VT NMR studies are summarised in Table 1 (which also includes some data obtained using 3% 1,4-dioxane in TCE as solvent). Since a solvent system that enabled direct comparison of 1–3 could not be obtained (NDI 1 did not form nanotubes in 1% dioxane), the trends in Tm values were instructive as guidelines rather than direct quantitative measures.
| NDI | Proton plotted | Solvent system | T m (K) |
|---|---|---|---|
| 1 | NDI | TCE | 314 |
| 1 | NDI | 2% THF | N/A |
| 1 | NDI | 1% Dioxane | N/A |
| 2 | NDI | 2% THF | 379 |
| 2 | α | 2% THF | 323 |
| 2 | α | 1% Dioxane | 293 |
| 2 | α | 3% Dioxane | N/A |
| 3 | NDI | 1% Dioxane | 346 |
| 3 | α | 3% Dioxane | 299 |
VT CD studies
To complement the VT NMR data and to quantitatively investigate the formation of nanotubes at lower concentrations of NDI, VT CD experiments were carried out on 1–3 (see ESI† for raw data).For NDI 1 in TCE, the presence of an aromatic side-group (phenylalanine), coupled with the low concentrations required for CD spectroscopy, led to the formation of π-stacked aggregates instead of nanotubes; previous studies by us and Govindaraju,10 also using NDIs containing aromatic side-groups at comparable concentrations, have shown similar CD traces indicative of π-stacked aggregate formation. The characteristic shape of the CD trace for NDI 2 shows that, even at 2 × 10−5 M and with 1% dioxane in TCE, nanotube formation is observed. This is attributed to the aforementioned entropic rationale, whereby the covalent linkage causes the π-stacked aggregate and random polymers to have fewer accessible conformational states, making their formation entropically unfavourable and thus nanotube formation comparatively favourable. Furthermore, a plot of the maxima at 383 nm as a function of temperature produced a curve whose sigmoidal character could be fitted to an isodesmic model to yield a Tm value of 324 K (Fig. 12). The observed trend in the CD intensity – namely that the maximum intensity decreases as temperature increases – is explained by the fact that, at higher temperatures, the entropic cost of incorporating an unaggregated NDI unit into a nanotube increases thus making the self assembly process less favourable. As a result, the CD maximum at 383 nm, which is diagnostic of nanotube formation, decreases in intensity as the temperature increases.
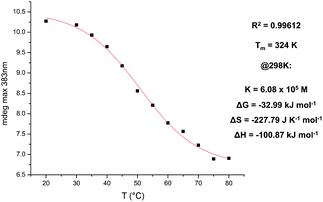 | ||
| Fig. 12 Fitting to the isodesmic model of the maxima at 383 nm in VT CD data as a function of temperature; NDI 2 at 2 × 10−5 M in 1% dioxane in TCE solvent mixture. | ||
NDI 3 also displayed a CD trace with a characteristic shape indicating the formation of nanotubes. However, a plot of the same maxima at 383 nm produced a linear trace that could not be fitted to the isodesmic model, suggesting that, in the temperature range used for VT CD (10–95 °C: a narrower range than that available for VT NMR studies due to the water-based cooling system used), nanotubes composed of 3 do not undergo the melting transition required to produce a sigmoidal trace.
To observe the melting transition within the temperature range, 3% dioxane in TCE was used as the new solvent system for 3 for VT CD studies; the increased proportion of dioxane was intended to destabilise nanotube formation and force the melting curve transition to occur within the set temperature range.
A plot of change in the CD maxima at 383 nm as a function of temperature (3 in 3% dioxane in TCE at 1.4 × 10−5 M) provided a curve that could be fitted with the isodesmic model, yielding a melting temperature value of 332 K (Fig. 13).11
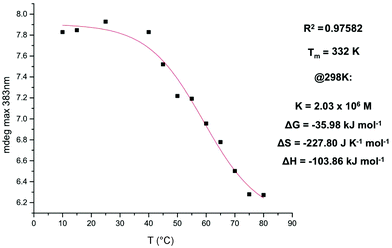 | ||
| Fig. 13 Fitting to the isodesmic model of the maxima at 383 nm as a function of temperature. NDI 3 in 3% dioxane in TCE (v/v) at 1.4 × 10−5 M. | ||
The thermodynamic functions and the Tm values determined from fitting the isodesmic model to the VT CD data were not compared with values obtained by VT NMR due to the order of magnitude difference in concentration.12
Entropy–enthalpy compensation
In the studies by the Sanders group,2 a key determinant in the supramolecular assembly mechanism of NDI nanotubes was the presence of entropy–enthalpy compensation, in which the enthalpic gain provided by either sidechain or host–guest interactions was offset by the entropic penalty of the formation of tighter nanotubes. The presence of entropy–enthalpy compensation in these systems was investigated by plotting the calculated −ΔH values as a function of their −TΔS values (at T = 298 K). In the event of entropy–enthalpy compensation being observed, the gradient of a −ΔH vs. −TΔS plot should equal unity.The results described above could be summarised graphically into a plot whose line of best fit had a gradient of 0.94 with regression value exceeding 0.93, thereby giving a statistically significant linear correlation for the −ΔH and −TΔS values. The results presented in Fig. 14 are revealing: first, a general trend in the −ΔH value – whereby the enthalpy of nanotube formation becomes less favourable as more NDI units are covalently linked – is observed. This trend is rationalised as follows: the covalent linkages rigidify the molecule, and so the NDIs are unable to access the optimum geometry for nanotube formation, resulting in molecular strain when incorporated into the nanotubular structure. As a result, there is an enthalpic penalty of incorporating covalently linked NDIs into nanotubes. However, the reverse is true for the trend in the entropy values; nanotube formation becomes less unfavourable as more NDI units are linked together. This too is consistent with expectations – as noted earlier, covalent linking both reduces the number of accessible conformational states in the π-stacked aggregates and random polymers as well as the degrees of freedom of the unaggregated NDI, thus lowering the entropy penalty of incorporating them into a nanotube. The linear correlation between the −ΔH and −TΔS values implies that the enthalpic penalty of incorporating an NDI into nanotubes originating from molecular strain is largely compensated by the reduced entropic penalty originating from the reduced degrees of freedom in the free, unaggregated state. Consequently, a substantial increase in ΔG is not observed.
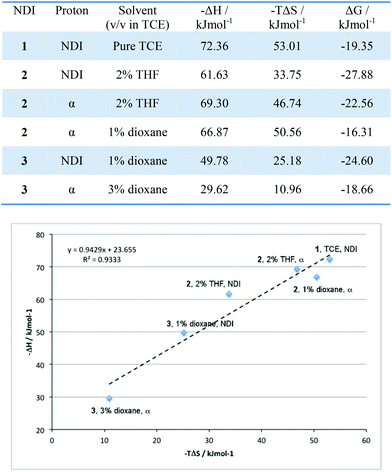 | ||
| Fig. 14 Top: table of −ΔH and −TΔS values for each solvent system. Bottom: an entropy–enthalpy plot for 1–3 in the various solvent systems used, for T = 298 K. | ||
Conclusions
The thermodynamic functions and supramolecular self-assembly mechanism of a family of homologue NDIs was investigated. The linking together of NDI subunits by terephthalate moieties had a significant positive effect on their robustness against hydrogen bond competitors. Monomeric NDI 1 was unable to form nanotubes in either 2% THF or 1% 1,4-dioxane in TCE (v/v) whilst at the opposite extreme, evidence of nanotube formation for trimeric NDI 3 was observed even when using 3% dioxane in TCE (v/v). The thermodynamic functions for all VT NMR experiments were plotted on an enthalpy–entropy graph to illustrate the presence of a large degree of entropy–enthalpy compensation in these systems.Conflict of interest
The authors declare no conflict of interest.Acknowledgements
We thank the EPSRC (K. T.) and the University of Bath (G. D. P.) for funding. We also are grateful to the National Institutes of Health (R15 GM088748), the Research Corporation for Science Advancement, and the Sydney J. Weinberg, Jr. Foundation for financial support (D. E. H.).Notes and references
- G. D. Pantoş, P. Pengo and J. K. M. Sanders, Angew. Chem., Int. Ed., 2007, 46, 194 CrossRef PubMed
.
- N. Ponnuswamy, G. D. Pantoş, M. M. J. Smulders and J. K. M. Sanders, J. Am. Chem. Soc., 2012, 134, 566 CrossRef CAS PubMed
.
- M. M. J. Smulders, M. M. L. Nieuwenhuizen, T. F. A. de Greef, P. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Chem.–Eur. J., 2010, 16, 362 CrossRef CAS PubMed
.
- D. Zhao and J. S. Moore, Org. Biomol. Chem., 2003, 1, 3471 CAS
.
- R. B. Martin, Chem. Rev., 1996, 96, 3043 CrossRef CAS PubMed
.
- Z. Chen, A. Lohr, C. R. Saha-Möller and F. Würthner, Chem. Soc. Rev., 2009, 38, 564 RSC
.
- T. F. A. de Greef, M. M. J. Smulders, M. Wolffs, A. P. H. J. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687 CrossRef CAS PubMed
.
- N. Ponnuswamy, A. R. Stefankiewicz, J. K. M. Sanders and G. D. Pantoş, Top. Curr. Chem., 2012, 322, 217 CrossRef CAS PubMed
.
- J.-C. Olsen, N. A. Batchelder, J. H. Raney and D. E. Hansen, Supramol. Chem., 2012, 24, 841 CrossRef CAS
.
- M. B. Avinash and T. Govindaraju, Nanoscale, 2011, 3, 2536 RSC
.
- As a test, a VT NMR experiment was conducted on NDI 3 in 3% dioxane in TCE and, though its Tm value was decreased as expected, the curve could still be fitted to yield a Tm value of 299 K. As a point of comparison, VT NMR studies on NDI 2 in this solvent system produced a quasi-linear plot, indicating the loss of nanotube formation.
- The lower concentrations employed in the VT CD experiments (vs. VT NMR) lead to supramolecular aggregates of lower stability, thus leading, as expected, to lower Tm values.
Footnote |
| † Electronic supplementary information (ESI) available: Complete VT NMR and VT CD data along with a full description of the algorithm for calculating the thermodynamic functions. See DOI: 10.1039/c3ob41761a |
| This journal is © The Royal Society of Chemistry 2014 |