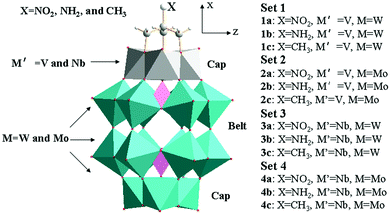
Prediction of second-order nonlinear optical properties of Wells–Dawson polyoxometalate derivatives [X–C(CH2O)3P2M′3M15O59]6− (X = NO2, NH2, and CH3, M′ = V and Nb, M = W and Mo)†
Ting
Zhang
,
Li-Kai
Yan
*,
Sha
Cong
,
Wei
Guan
and
Zhong-Min
Su
*
Institute of Functional Material Chemistry, Faculty of Chemistry, Northeast Normal University, Changchun 130024, P.R. China. E-mail: yanlk924@nenu.edu.cn; zmsu@nenu.edu.cn; Fax: +86-431-5684009
First published on 16th December 2013
Abstract
The geometrical structures of Wells–Dawson derivatives [X–C(CH2O)3P2M′3M15O59]6− (X = NO2, NH2, and CH3, M′ = V and Nb, M = W and Mo) have been calculated by the density functional theory (DFT) method. The results show that the distances of P⋯P and P⋯C are controlled by the {M′3} triads, and {M′3} triads also affect the sizes of W6 hexagonal belts. The second-order polarizabilities and origin of nonlinear optical (NLO) properties of those clusters have been investigated by a time-dependent density functional theory (TDDFT) method. The NLO property analysis reveals that [X–C(CH2O)3P2V3Mo15O59]6− (X = NH2) anions have the largest βvec values, 75.064 × 10−30 esu. Grafting electron donors to POM clusters is an efficient way to improve the NLO response. The major electron transition orbitals show that the charge transfer from the organic groups to the metal atoms is responsible for the NLO properties of these polyoxometalates.
Introduction
Polyoxometalates (POMs) are early transition metal–oxygen clusters, which have been applied in analytical chemistry, catalysis, medicine and materials science.1,2 Recent studies have shown that lacunary,3 transition metal trisubstituted POMs4 and POM-based organic–inorganic hybrids5,7 are potential candidates as novel nonlinear optical (NLO) materials.8–10 POMs reveal a large variety of shapes, sizes, and compositions and provide a good basis for molecular design. Among the members of the POMs family, Wells–Dawson (W–D) POMs are the typical and important structures. The traditional W–D POMs are centrosymmetric. However, second-order NLO materials are required to be noncentrosymmetric. In order to achieve second-order NLO responses, POMs must be arranged noncentrosymmetrically. One effective way is by the introduction of transition metals. Our previous study has shown that the trisubstituted W–D POMs α-[P2M15M′3O62]m− (M = WVI, MoVI, and M′ = VV, MoVI) display good second-order NLO properties.11 The results indicate that the transition metal trisubstituted effect of W–D POMs leads to the charge separation; the metal atoms in the cap region may be viewed as electron acceptors. And the βvec values are −35.175 × 10−30 esu and −44.287 × 10−30 esu for α-[P2W15V3O62]9− and α-[P2Mo15V3O62]9− according to the LB94 calculations. The calculated static first hyperpolarizability value of α-[P2Mo15V3O62]9− is about 5 times as large as that of the p-nitroaniline molecule.Compared with organic NLO materials, the totally inorganic NLO materials have attracted considerable attention because of their good stability. However, the relevant small photoelectric coefficients of the inorganic NLO materials are the bottleneck to practical applications. So the new materials should be explored to resolve the above problems.
During the past decade, there has been increasing interest in the functional chemistry of POMs with organic derivatives.12 The inorganic–organic hybrids of POMs have been proven to be potential NLO materials.3,5,6 The NLO properties of Lindqvist- and Keggin-type POM organoimido derivatives have been drawn increasing attention.4,13,14 The organic–inorganic hybrids of W–D POMs are also important structures, which have been continuously synthesized by Cronin15 and Hasenknopf.16 Cronin has successfully grafted tris (hydroxymethyl) aminomethane [(HOCH2)3CNH2, Tris] to a W–D cluster, [P2V3W15O62]9−, and the alkoxypolyoxometalate (TBA)4H2[H2NC(CH2O)3P2V3W15O59] derivative was synthesized.17 The structure of (TBA)4H2[H2NC(CH2O)3P2V3W15O59] can be regarded as three bridging oxygen atoms of the {V3} cap in (TBA)5[H4P2V3W15O62] cluster replaced by three alkoxy oxygen atoms of the triol moiety. Furthermore, the (TBA)4H2[O2NC(CH2O)3P2V3W15O59] and (TBA)4H2[H3CC(CH2O)3P2V3W15O59] clusters can also be obtained similarly. These organic–inorganic hybrid POMs building blocks are capable of forming fully H-bonded nanoassemblies not only in the solid sate but also in solution. Considering these reasons, those clusters may be desirable NLO materials.
In the present work, we employ time-dependent density functional theory (TDDFT) method to calculate the second-order NLO properties of W–D derivatives [X–C(CH2O)3P2M′3M15O59]6− (X = NO2, NH2, and CH3, M′ = V and Nb, M = W and Mo). The main aim of this work is to verify the relationship between second-order NLO properties and organic segments, as well as the substituted metals. The differences in second-order NLO properties and charge transfer between organic–inorganic hybrids and totally inorganic W–D POMs were also explored.
Computational methods
All of the calculations were performed at the DFT level by using the ADF2009 suite of programs.18,19 The zero-order regular approximation (ZORA) was adopted in the calculations to account for the scalar relativistic effects.20–23 The optimizations of molecular structures were carried out using the Becke and Perdew (BP86)24,25 exchange-correlation (XC) functional, and VWN local density functional26 within the framework of the generalized gradient approximation (GGA). The triple-ζ basis plus polarization Slater-type orbital basis sets were used to describe the main group elements (O, C, N, and H), whereas for transition metals V, Nb, Mo and W atoms, a frozen core composed of 1s to 2p, 1s to 3d, 1s to 3d and 1s to 4d shells was used. To reduce the discrepancy between the gas-phase calculation and the solution phase measurement, the solvent effect was employed in the calculations of geometrical optimization and excitation properties by using the conductor-like screening model (COSMO).27,28 The solvent cavity surrounding the anion was created using the solvent-excluding method with fine tesserae. The solute dielectric constant was set to 37.5 (acetonitrile). The van der Waals radii for the POM and organic ligand atoms, which actually define the cavity in the COSMO, were chosen to be 1.49, 1.41, 1.40, 1.08, 1.79, 2.07, 2.09, and 2.10 Å for C, N, O, H, V, Nb, Mo and W, respectively.29 The value of the numerical integration parameter used to determine the precision of numerical integrals was 6.0. Geometrical optimization structures are sketched in Fig. 1.TDDFT is one of the most popular methods for studying excitation properties in quantum chemistry due to its efficiency and accuracy. It has been used to investigate the electronic spectra of numerous systems, including closed- and open-shell systems.30–32 For the calculations of second-order polarizability and excitation property, the EXCITATION together with RESPONSE modules33 implemented in the ADF program were used on the basis of the optimized geometries. In this work, the asymptotically correct Van Leeuwen–Baerends (LB94) potential has been adopted to calculate the hyperpolarizabilities of all clusters. The statistical average of different model orbital potentials (SAOP) by Gritsenko, Baerends et al.34 was used to calculate the excitation energy. In previous papers,35–37 the SAOP potential has been shown to provide high quality results for a whole series of static and frequency-dependent molecular response properties and to provide a substantial improvement upon the LDA and GGA potentials. Moreover, the value of the numerical integration parameter was 6.0 to determine the precision of numerical integrals.
Results and discussion
Geometrical structure
According to the substituted transition metals, we tentatively nominate the studied POMs clusters as set 1 ([X–C(CH2O)3P2V3W15O59]6−), set 2 ([X–C(CH2O)3P2V3Mo15O59]6−), set 3 ([X–C(CH2O)3P2Nb3W15O59]6−) and set 4 ([X–C(CH2O)3P2Nb3Mo15O59]6−). Herein, the X group in each set is NO2, NH2, and CH3, respectively. The schematic diagrams for the optimized geometries are shown in Fig. 1. The important geometrical parameters of sets 1, 2, 3 and 4 are listed in Table 1 and Fig. 2. From Table 1, it can be seen that the P⋯P distances of sets 2 and 4 are longer than those of sets 1 and 3. In other words, the P⋯P distances of clusters depend on the substituted transition metal (Mo > W) and the deviation is 0.047–0.118 Å. The comparison of P⋯P distance separations by substituted {V3} triads (sets 1 and 2) or {Nb3} triads (sets 3 and 4) provides the proof, e.g., 1a > 3a, 1b > 3b, 1c > 3c, 2a > 4a, 2b > 4b and 2c > 4c (the deviation is 0.049–0.105 Å). The results show that sets 4 and 1 have the longest and shortest P⋯P distances, respectively. Actually, the same trends can be found in P⋯C distances. In addition, the distances of P⋯C for series a are shorter than those for series b and c in all sets owing to the different substituted groups (X = NO2, NH2, and CH3).| P⋯P | P⋯C | C–X (X = C and N) | |
|---|---|---|---|
| 1a | 4.052 | 5.609 | 1.524 |
| 1b | 4.049 | 5.646 | 1.474 |
| 1c | 4.044 | 5.655 | 1.539 |
| 2a | 4.165 | 5.619 | 1.526 |
| 2b | 4.167 | 5.660 | 1.474 |
| 2c | 4.166 | 5.669 | 1.540 |
| 3a | 4.157 | 5.743 | 1.532 |
| 3b | 4.151 | 5.778 | 1.476 |
| 3c | 4.149 | 5.786 | 1.543 |
| 4a | 4.258 | 5.745 | 1.531 |
| 4b | 4.248 | 5.782 | 1.477 |
| 4c | 4.250 | 5.789 | 1.543 |
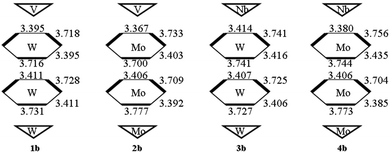
The studied systems can be viewed as an assembly of two polar {M′3} (one is {V3} or {Nb3}, the other is {W3} or {Mo3}) triads and two hexagonal belts (upper belt and lower belt). As the size differences in polar {M′3} triads are small, so the sizes of two hexagonal belts are discussed in this section. From Fig. S1,† it can be seen that the Wb⋯Wb within the same hexagonal belt in the same set is similar. Hence, the Wb⋯Wb space is not influenced by the substituted group X. And the nonbonding alternation naturally maintains as shown by the Wb⋯Wb differences inside the same belt. In the following, the series b in all sets will be selected to discuss the geometry structure. As shown in Fig. 2, the size of the upper hexagonal belt for system 1b is larger than that of lower hexagonal belts. In contrast, the lower hexagonal belt of system 3b is somewhat wide. As a result, the upper polar {M′3} triads influence the sizes of upper and lower hexagonal belts for [X–C(CH2O)3P2M′3W15O59]6− (M′ = V and Nb). This behavior cannot be verified for 2b and 4b. Specifically, the upper belt of 4b is slightly larger than that of 2b. It reflects that {M′3} triads only affect the sizes of upper hexagonal belts for [X–C(CH2O)3P2M′3Mo15O59]6− (M′ = V and Nb) anions.
Ground state properties
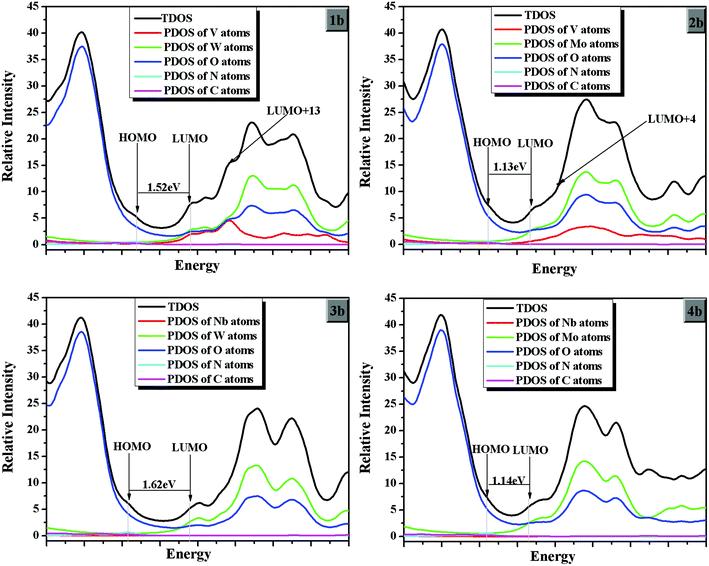
On the basis of the optimized ground state geometries of sets 1, 2, 3 and 4 clusters, the partial density of states (PDOS) were calculated and the results are presented in Fig. 3. The PDOS can provide the contributions of a group to each molecular orbital. From Fig. 3, the greatest density on HOMOs in the range from −6.58 to −5.70 eV is localized on the oxygen atoms for all clusters. From 1a, 1b, and 1c in Fig. 3, the greatest densities on LUMOs is from −4.23 to −4.17 eV. (As we know, most of the calculated LUMO energies for POM-based hybrids are below the zero value.10,38–40 Due to the calculation limitations, we only calculated the polyanions without counterions. So the energy gap is below the zero value. Although the conductor-like screening model (COSMO) could reduce the energy error, the LUMO energy is occasionally negative.) The LUMOs of 1a, 1b, and 1c are localized on the vanadium, tungsten, oxygen atoms, and the band gaps (Ebg = |ELUMO − EHOMO|) increase in the following order: 1b (1.52 eV) < 1c (1.94 eV) < 1a (2.07 eV). Usually, the NLO response is roughly inversely proportional to the HOMO–LUMO gap, so the NLO response may be decreased in the following order: 1b > 1c > 1a. For systems 2a, 2b, and 2c, the molybdenum, oxygen and vanadium (slightly) atoms contribute to the LUMOs. The energy band gaps (Ebg) of set 2 clusters are around 1.13–1.52 eV. While most densities on LUMOs for sets 3 and 4 (the energy levels around −4.2 eV for set 3 and −4.73 ∼ −4.66 eV for set 4) localize on the niobium and tungsten (or molybdenum) atoms. The band gaps are above 1.62 eV and below 1.56 eV for sets 3 and 4, respectively. In addition, most densities on HOMOs for all compounds are similar, and the energy levels of HOMOs for sets 3 and 4 are lower than those of sets 1 and 2. So the upper polar {M′3} triads play an important role on the energy levels of HOMOs for the studied clusters. The LUMO energies of sets 1 and 3 are higher than those of sets 2 and 4. It shows that the LUMO energy levels are determined by tungsten and molybdenum atoms of the present studied clusters. In conclusion, the band gaps of sets 1 and 3 are higher than those of sets 2 and 4, respectively. Thus, the band gaps increase as M changes in the order W > Mo, and the NLO response may decrease as M changes in the order Mo < W. Furthermore, considering the substituted group X, the band gaps of series b (X = NH2) in each set are lower than those of series a and c (X = NO2 and CH3). It predicts that the charge transfer is easy for series b in all sets, and the NLO response of b may be larger than others.Nonlinear optical properties
The static first hyperpolarizabilities (βvec) for all clusters have been calculated using the following equation: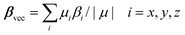 | (1) |
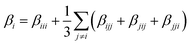 | (2) |
Our previous work has proven that the functionals LB94, BP86, and PBE0 give the same order of βvec values.11,41 Considering the computational cost, we calculated the first hyperpolarizabilities of the studied clusters by using LB94 method.3,5,7,9–11,13,14 The βvec values of the studied clusters are listed in Table 2. It can be found that the βvec values of series b in all sets possess considerably large second-order NLO responses. Among all clusters, the cluster 2b displays the largest βvec value, 75.064 × 10−30 esu, which is 4 times as large as that of cluster 2c. Moreover, the β value of cluster 1b is 71.814 × 10−30 esu, which is about 5 times larger than that of 1c. The βvec values of clusters 3b and 4b are ∼2 times larger than those of clusters 3c and 4c. In the previous work, the βvec values are −35.175 × 10−30 esu and −44.287 × 10−30 esu for α-[P2W15V3O62]9− and α-[P2Mo15V3O62]9−, which are smaller than those of systems 1b ([NH2–C(CH2O)3P2V3W15O59]6−) and 2b ([NH2–C(CH2O)3P2V3Mo15O59]6−), and larger than those of systems 1a ([NO2–C(CH2O)3P2V3W15O59]6−), 1c ([CH3–C(CH2O)3P2V3W15O59]6−) and 2a ([NO2–C(CH2O)3P2V3Mo15O59]6−), 2c ([CH3–C(CH2O)3P2V3Mo15O59]6−). It indicates that the introduction of the strong electron donor NH2 based on the transition metal substituted W–D POMs is helpful for enhancing the βvec value, and the introduction of strong electron accepter NO2 will decrease the βvec value. It is worth noting that the cap metal substitutions affect the second-order NLO responses in series b ({V3} triads vs. {Nb3} triads). In addition, the belt transition metal in W–D clusters also affect the second-order NLO response, that is, the βvec value of P2Mo15V3 is larger than that of P2W15V3.11 In the present work, the molybdenum substituted derivatives also generated larger second-order NLO responses than those of tungsten substituted derivatives (2a >1a, 2b >1b, 2c >1c, 4a >3a, 4b >3b and 4c >3c).
| β x | β y | β vec | |
|---|---|---|---|
| 1a | −2.975 | −1.065 | −2.997 |
| 1b | 71.855 | −3.349 | 71.814 |
| 1c | 14.873 | 0.065 | 14.844 |
| 2a | −8.433 | −1.720 | −8.584 |
| 2b | 75.127 | −5.653 | 75.064 |
| 2c | 20.136 | 0.337 | 20.134 |
| 3a | −1.811 | −0.894 | −1.811 |
| 3b | 21.504 | 0.165 | 21.412 |
| 3c | 13.364 | −0.01 | 13.364 |
| 4a | 10.428 | −1.157 | −10.407 |
| 4b | 46.486 | −0.412 | 46.134 |
| 4c | 23.009 | −1.535 | 22.876 |
We have performed TDDFT calculations to obtain the electronic spectrum. The TDDFT calculated transition energies, oscillator strength of the first excited state and the crucial excited state, together with the dominant molecular orbital transitions to these excited states are summarized in Table 3 and Table S1.† Taking series b as an example, the nature of the electronic transitions is analyzed.
| Systems | E ge | f os | Composition |
|---|---|---|---|
| 1b | 2.459 | 0.012 | HOMO−1 (405a′′) → LUMO+1 (406a′′) (84%) |
| 2b | 1.865 | 0.012 | HOMO (348a′) → LUMO+3 (350a′) (97%) |
| 3b | 3.170 | 0.006 | HOMO (485a′) → LUMO+5 (488a′) (98%) |
| 4b | 2.428 | 0.004 | HOMO (363a′) → LUMO+6 (366a′) (99%) |
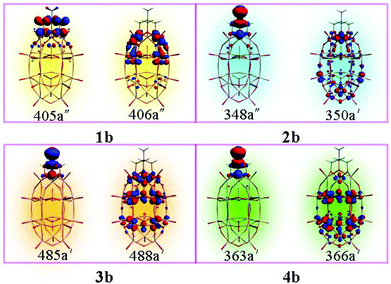
The molecular orbitals involved in the dominant electron transitions for series b are shown in Fig. 4. For cluster 1b, the transition energy is 2.459 eV, which is generated by the promotion of one electron from HOMO−1 (405a′′) to LUMO+1 (406a′′). From Fig. 4, it can be seen that the HOMO−1 localizes on the organic segment and the oxygen atoms of the cap region, and LUMO+1 localizes on the capped vanadium atoms and the tungsten atoms close to the cap region. So the charge transfer of system 1b is mainly from the organic segment and oxygen atoms of the cap region to the transition metal atoms. The transition character for clusters 2b, 3b and 4b is similar, that is, the charge transfers for these clusters are mainly from the organic segment (NH2–C(CH2O)3) to the POM. The results clearly show that the organic segment acts as an electron donor and the POM cluster acts as an electron acceptor. In a previous study, without an organic group, the transition metal substituted W–D POMs could form a D–A charge transfer model, with the charge transfer of trisubstituted W–D polyoxometalates being from oxo ligands of the cap region to V atoms and adjacent W atoms.11 The introduction of the organic group could form a different charge transfer model. It suggests that the electron-donating ability of NH2–C(CH2O)3 is stronger than that of the oxo ligands in the cap region.
It can be found that the crucial excited state is mainly composed of the HOMO−1 → LUMO+1, HOMO → LUMO+3, HOMO → LUMO+5, and HOMO → LUMO+6 for 1b, 2b, 3b, and 4b, respectively. The orbital transitions associated with the crucial excited states are allowed according to the transition selection rules, and the calculated oscillator strength of the crucial excited state is larger than that of the first excited states. The excitation would generate the charge transfer from organically grafted (X–C(CH2O)3) donor to metal acceptor (Fig. 4). The results show that the organic groups are more likely to display electron donor features than oxo ligands of the cap region in the studied clusters.
As mentioned above, the major electron transition orbitals of 1b, 2b, 3b, and 4b anions are diverse. From Fig. 4, it can be seen that the occupied orbitals (405a′′, 348a′′, 485a′, and 363a′) are similar, which mainly localize on the organic groups. Nevertheless, the unoccupied orbitals are multifarious. The unoccupied orbital of 1b (406a′′) localizes on two V atoms and adjacent W atoms. The unoccupied orbital of 2b (350a′) mainly delocalizes over one V atom and Mo atoms (lower belt and lower cap). While for 3b, the unoccupied orbital (488a′) mainly localizes on Nb atoms and two belts W atoms. For 4b, the Mo atoms impart more contributions to the unoccupied orbital 366a′. The results indicate that the grafted organic group (X–C(CH2O)3) could change the charge transfer direction.
Conclusions
In summary, systematic DFT calculations have been carried out to investigate the geometrical structure and second-order NLO properties of [X–C(CH2O)3P2M′3M15O59]6− (X = NO2, NH2, and CH3, M′ = V and Nb, M = W and Mo) clusters. Several conclusions can be drawn: (1) structural analysis shows that changing M′ metals from V to Nb, the distance of P⋯P and P⋯C become longer. As M = W, {M′3} triads influence on the sizes of upper and lower hexagonal belts. However, {M′3} triads only affect the sizes of upper hexagonal belts with M = Mo. (2) The PDOS calculations show that the upper polar {M′3} triads play an important role on the energy levels of HOMOs, and the LUMOs energy levels are determined by tungsten and molybdenum atoms of the present studied clusters. The band gaps of series b in each set are lower than those of series a and c. As a result, the charge transfer is easier for series b in all sets. (3) [X–C(CH2O)3P2V3M15O59]6− (X = NH2) cluster possesses considerably large second-order NLO responses among series b. The introduction of a strong electron donor is helpful for enhancing the βvec values of the studied clusters. TDDFT calculations suggest that the charge transfer mainly occurs from the organic groups to the metal atoms.Acknowledgements
The authors gratefully acknowledge financial support by NSFC (20971020, 21073030 and 21131001), Program for New Century Excellent Talents in University (NCET-10-318), Doctoral Fund of Ministry of Education of China (20100043120007), and the Science and Technology Development Planning of Jilin Province (20100104 and 20100320).Notes and references
- E. Antonova, C. Näther, P. Kögerler and W. Bensch, Angew. Chem., Int. Ed., 2011, 50, 764 CrossRef CAS PubMed.
- M. T. Pope and A. Müller, Angew. Chem., Int. Ed. Engl., 1991, 30, 34 CrossRef.
- M. R. S. A. Janjua, Inorg. Chem., 2012, 51, 11306 CrossRef CAS PubMed.
- W. Guan, C. G. Liu, P. Song, G. C. Yang and Z. M. Su, Theor. Chem. Acc., 2009, 122, 265 CrossRef CAS.
- M. R. S. A. Janjua, M. Amin, M. Ali, B. Bashir, M. U. Khan, M. A. Iqbal, W. Guan, L. K. Yan and Z. M. Su, Eur. J. Inorg. Chem., 2012, 705 CrossRef CAS.
- D. Wayne Demoin, Y. W. Li, S. S. Jurisson and C. A. Deakyne, Comput. Theor. Chem., 2012, 997, 34 CrossRef PubMed.
- L. K. Yan, G. C. Yang, W. Guan, Z. M. Su and R. S. Wang, J. Phys. Chem. B, 2005, 109, 22332 CrossRef CAS PubMed.
- C. Yao, L. K. Yan, W. Guan, C. G. Liu, P. Song and Z. M. Su, J. Cluster Sci., 2010, 21, 69 CrossRef CAS PubMed.
- P. Song, W. Guan, C. G. Liu, L. K. Yan, C. Yao and Z. M. Su, J. Mol. Struct. (THEOCHEM), 2010, 947, 9 CrossRef CAS PubMed.
- C. Yao, L.-K. Yan, W. Guan, C.-G. Liu, P. Song and Z.-M. Su, Dalton Trans., 2010, 39, 7645 RSC.
- C. G. Liu, W. Guan, P. Song, Z. M. Su, C. Yao and E. B. Wang, Inorg. Chem., 2009, 48, 8115 CrossRef CAS PubMed.
- P. Gouzerh and A. Proust, Chem. Rev., 1998, 98, 77 CrossRef CAS PubMed.
- L. K. Yan, M. S. Jin, J. Zhuang, C. G. Liu, Z. M. Su and C. C. Sun, J. Phys. Chem. A, 2008, 112, 9919 CrossRef CAS PubMed.
- M. R. S. A. Janjua, C. G. Liu, W. Guan, J. Zhuang, S. Muhammad, L. K. Yan and Z. M. Su, J. Phys. Chem. A, 2009, 113, 3576 CrossRef CAS PubMed.
- C. P. Pradeep, F. Y. Li, C. Lydon, H. N. Miras, D. L. Long, L. Xu and L. Cronin, Chem.–Eur. J., 2011, 17, 7472 CrossRef CAS PubMed.
- M. P. Santoni, A. K. Pal, G. S. Hanan, A. Proust and B. Hasenknopf, Inorg. Chem., 2011, 50, 6737 CrossRef CAS PubMed.
- C. P. Pradeep, D. L. Long, G. N. Newton, Y. F. Song and L. Cronin, Angew. Chem., Int. Ed., 2008, 47, 4388 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chim. Acta, 1998, 99, 391 Search PubMed.
- C. Chang, M. Pelissier and P. Durand, Phys. Scr., 1986, 34, 394 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 97832 CrossRef PubMed.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijder, Int. J. Quantum Chem., 1996, 57, 281 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224 CrossRef CAS.
- C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396 CrossRef CAS.
- S. Z. Hu, Z. H. Zhou and K. Tsai, Acta. Phys. Chim. Sin., 2003, 19, 1073 CAS.
- G. Li, G. Jia, Q. Gao, Z. Feng and C. Li, J. Phys. Chem. C, 2011, 115, 972 CAS.
- G. V. N. Rajapakse, A. V. Soldatova and M. A. J. Rodgers, J. Phys. Chem. B, 2010, 114, 14205 CrossRef CAS PubMed.
- T. F. Miao, J. Li, S. Y. Liao, K. C. Zheng and L. N. Ji, Inorg. Chim. Acta, 2010, 363, 3880 CrossRef CAS PubMed.
- S. J. A. van Gisbergen, J. G. Snijders and E. J. Baerends, Comput. Phys. Commun., 1999, 118, 119 CrossRef CAS.
- P. R. T. Schipper, O. V. Gritsenko, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2000, 112, 1344 CrossRef CAS PubMed.
- C. Dablemont, C. G. Hamaker, R. Thouvenot, Z. Sojka, M. Che, E. A. Maatta and A. Proust, Chem.–Eur. J., 2006, 12, 9150 CrossRef CAS PubMed.
- S. Romo, N. S. Antonova, J. J. Carbo and J. M. Poblet, Dalton Trans., 2008, 5166 RSC.
- U. Kortz, C. Marquer, R. Thouvenot and M. Nierlich, Inorg. Chem., 2003, 42, 1158 CrossRef CAS PubMed.
- S. Cong, L. K. Yan, S. Z. Wen, W. Guan and Z. M. Su, Theor. Chem. Acc., 2011, 130, 1043 CrossRef CAS PubMed.
- L. K. Yan, M. S. Jin, P. Song and Z. M. Su, J. Phys. Chem. B, 2010, 114, 3754 CrossRef CAS PubMed.
- X. López, C. Bo and J. M. Poblet, J. Am. Chem. Soc., 2002, 124, 12574 CrossRef PubMed.
- C. G. Liu, W. Guan, L. K. Yan, Z. M. Su, P. Song and E. B. Wang, J. Phys. Chem. C, 2009, 113, 19672 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3qi00024a |
| This journal is © the Partner Organisations 2014 |