One-dimensional GdIII–MII (M = Mn, Co) acetate chains exhibiting a large cryogenic magnetocaloric effect at ΔH = 3 T†
Yin-Yin
Pan
,
Yan
Yang
,
La-Sheng
Long
*,
Rong-Bin
Huang
and
Lan-Sun
Zheng
State Key Laboratory of Physical Chemistry of Solid Surface and Department of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China. E-mail: lslong@xmu.edu.cn
First published on 11th August 2014
Abstract
Two one-dimensional acetate chains, GdIII–MnII (1) and GdIII–CoII (2), have been prepared. Magnetic investigations indicate that the magnetic entropy changes (−ΔSm) in 1 have maximum values of 38.70 J kg−1 K−1 at ΔH = 7 T and 31.08 J kg−1 K−1 at ΔH = 3 T, while these in 2 have maximum values of 35.18 J kg−1 K−1 at ΔH = 7 T and 28.67 J kg−1 K−1 at ΔH = 3 T.
The magnetocaloric effect (MCE) is a magneto-thermodynamic phenomenon in which a change in temperature of a suitable material is caused by exposing the material to a changing magnetic field.1 Magnetic refrigeration is a cooling technology based on the MCE.2 Owing to its environmental friendliness and energy efficiency, magnetic refrigeration is regarded as the most promising technology to replace traditional refrigeration, especially for acquiring and maintaining low temperatures.3 Although the factors influencing the MCE of magnetic materials are known now, large-scale applications using magnetic refrigeration remain a great challenge. One of the obstacles to applying magnetic refrigeration is that the magnetic entropy of the magnetic materials synthesized so far is not large enough at a relatively low magnetic field.4
Coordination polymers, because of their structural diversity and controllability, have recently attracted great attention in the field of magnetic refrigeration.5–8 On one hand, their structural diversity and controllability facilitate the adjustment of the magnetic interaction between the metal ions, leading to a significantly larger MCE than that of lanthanide alloys and magnetic nanoparticles.9,10 On the other hand, when compared with metal cluster compounds, coordination polymers often possess a relatively higher density, and long-range magnetic ordering,5–8 resulting in an MCE larger than that of metal cluster compounds.4,11
The isotropic GdIII (f7) and MnII (d5) ions, which possess the largest magnetic entropy of the cations in the f and d blocks, respectively, have been widely chosen to make excellent molecular cryocoolers.4b,7b,12 Owing to their paramagnetic or weakly ferromagnetic interactions, their low-lying excited spin states are of key importance for obtaining a large MCE at a low magnetic field.7b All MnII ions should be alternately separated by GdIII ions, so as to avoid the relatively strong MnII⋯MnII magnetic coupling, when using GdIII and MnII to synthesize magnetic materials. Although some Mn–Gd species, with the MnII ions alternately separated by the GdIII ions such as MnII4GdIII6,4b MnII9GdIII94b and MnII4GdIII4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 clusters, have been synthesized, Mn–Gd coordination polymers, with the MnII ions alternately separated by the GdIII ions, remain rare.7b Herein, we report the structures and MCEs of two one-dimensional (1D) GdIII–MII acetate chains, formulated as [GdMn0.5(OAc)4(H2O)2]·3H2O (1) and [GdCo0.5(OAc)4(H2O)2]·3H2O (2). Single-crystal structural analysis reveals that the MII ions in 1 and 2 are alternately separated by GdIII ions. Magnetic investigations indicate that the magnetic entropy is up to 31.08 J kg−1 K−1 for 1 and 28.67 J kg−1 K−1 for 2 even at ΔH = 3 T.
12 clusters, have been synthesized, Mn–Gd coordination polymers, with the MnII ions alternately separated by the GdIII ions, remain rare.7b Herein, we report the structures and MCEs of two one-dimensional (1D) GdIII–MII acetate chains, formulated as [GdMn0.5(OAc)4(H2O)2]·3H2O (1) and [GdCo0.5(OAc)4(H2O)2]·3H2O (2). Single-crystal structural analysis reveals that the MII ions in 1 and 2 are alternately separated by GdIII ions. Magnetic investigations indicate that the magnetic entropy is up to 31.08 J kg−1 K−1 for 1 and 28.67 J kg−1 K−1 for 2 even at ΔH = 3 T.
Complex 1 was prepared by the reaction of Gd(OAc)3·6H2O (0.388 g, 1 mmol) and Mn(OAc)2·4H2O (0.245 g, 1 mmol) in a mixed solution of deionized water (10 mL) and anhydrous ethanol (5 mL). Complex 2 was prepared in a similar way as described for 1. As complexes 1 and 2 are isomorphous, only the structure of 1 is described in detail. Single-crystal structure analysis revealed that complex 1 crystallized in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. Each asymmetric unit in 1 consists of one Gd3+ ion, 0.5 Co2+ ions, four acetates, two coordinated water molecules and three guest water molecules. As shown in Fig. 1, each GdIII ion is located in a capped square-antiprism geometry and coordinated by two water molecules, two acetates in a chelate mode and three acetates in a monodentate mode. Each Mn(II) ion is located in an octahedron geometry and coordinated by six acetates in a monodentate mode. The two adjacent GdIII ions bridged by a pair of μ–η2:η1 acetates, and the adjacent GdIII and MnII ions bridged by one μ–η2:η1 acetate and two syn–syn acetates, generate a 1D chain structure with each MnII ion alternately separated by two GdIII ions. This 1D chain structure is very similar to that of NdCo0.5
space group. Each asymmetric unit in 1 consists of one Gd3+ ion, 0.5 Co2+ ions, four acetates, two coordinated water molecules and three guest water molecules. As shown in Fig. 1, each GdIII ion is located in a capped square-antiprism geometry and coordinated by two water molecules, two acetates in a chelate mode and three acetates in a monodentate mode. Each Mn(II) ion is located in an octahedron geometry and coordinated by six acetates in a monodentate mode. The two adjacent GdIII ions bridged by a pair of μ–η2:η1 acetates, and the adjacent GdIII and MnII ions bridged by one μ–η2:η1 acetate and two syn–syn acetates, generate a 1D chain structure with each MnII ion alternately separated by two GdIII ions. This 1D chain structure is very similar to that of NdCo0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 as reported previously. The bond lengths of Gd–O are 2.340(3)–2.731(3) Å, and the bond lengths of Mn–O are 2.173(3)–2.192(3) Å, which are comparable to the corresponding values in previously reported 3D Gd–Mn magnetic materials.7b,14 The Gd⋯Gd distance is 4.277(2) Å, and the Gd–O8–Gd angle is 114.77(1)°, which are comparable to the corresponding values in previously reported 1D Gd3+ acetate chains.5b The Gd⋯Mn distance is 4.030(6) Å, this value is smaller than that previously reported 3D Gd–Mn magnetic materials.7b,14 The Gd–O2–Mn angle is 122.42(1)°. The Gd–Mn–Gd and Gd–Gd–Mn angles are 180° and 132.56(2)°, respectively. There exist intramolecular hydrogen bonds between one coordinated water molecule and two acetate ligands (O10⋯O1 = 2.882(4) Å, H10A⋯O1 = 2.08 Å, ∠O10–H10A⋯O1 = 157.3°, O10⋯O6 = 2.827(4) Å, H10B⋯O6 = 2.00 Å, ∠O10–H10B⋯O6 = 163.6°).
13 as reported previously. The bond lengths of Gd–O are 2.340(3)–2.731(3) Å, and the bond lengths of Mn–O are 2.173(3)–2.192(3) Å, which are comparable to the corresponding values in previously reported 3D Gd–Mn magnetic materials.7b,14 The Gd⋯Gd distance is 4.277(2) Å, and the Gd–O8–Gd angle is 114.77(1)°, which are comparable to the corresponding values in previously reported 1D Gd3+ acetate chains.5b The Gd⋯Mn distance is 4.030(6) Å, this value is smaller than that previously reported 3D Gd–Mn magnetic materials.7b,14 The Gd–O2–Mn angle is 122.42(1)°. The Gd–Mn–Gd and Gd–Gd–Mn angles are 180° and 132.56(2)°, respectively. There exist intramolecular hydrogen bonds between one coordinated water molecule and two acetate ligands (O10⋯O1 = 2.882(4) Å, H10A⋯O1 = 2.08 Å, ∠O10–H10A⋯O1 = 157.3°, O10⋯O6 = 2.827(4) Å, H10B⋯O6 = 2.00 Å, ∠O10–H10B⋯O6 = 163.6°).
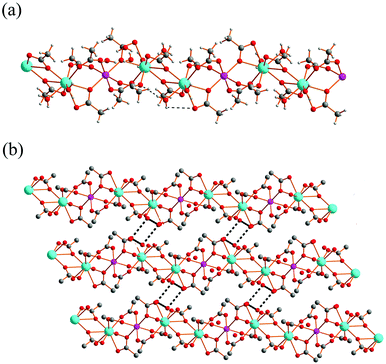 | ||
| Fig. 1 (a) The 1D chain structure of 1. (b) The 2D structure of 1. Cyan: Gd, purple: Mn, red: O, gray: C. The H atoms in the 2D network are omitted for clarity. | ||
The adjacent 1D chains extend into a 2D layer structure via water tetramers, each formed by two guest water molecules, O12 and O13 (O13⋯O12 = 2.775(6) Å, H13B⋯O12 = 1.88(9) Å, ∠O13–H13B⋯O12 = 154(6)°), which are hydrogen-bonded to the carboxylate groups of the adjacent chains (O12⋯O3 = 2.840(4) Å, H12B⋯O3 = 1.99 Å, ∠O12–H12B⋯O3 = 174.9°). The extension of the adjacent 2D layer structures via the water tetramers hydrogen-bonded to the coordinated water molecules (O13⋯O9 = 2.676(5) Å, H13A⋯O9 = 1.97 Å, ∠O13–H13A⋯O9 = 139.8°) from two adjacent 2D layer structures, generates the 3D structure of 1 (ESI Fig. S1†).
The bond lengths of Gd–O in 2 are 2.330(2)–2.732(2) Å, compared to these in 1, and the bond lengths of Co–O are 2.083(2)–2.112(2) Å. The values are comparable to the previously reported ones in a NdCo0.5 1D chain structure.13 The Gd⋯Gd distance is 4.277(9) Å, and the Gd–O–Gd angle is 114.88(8)°, comparable to those in 1. The Gd⋯Co distance and the Gd–O–Co, Gd–Co–Gd and Gd–Gd–Co angles are 4.007(5) Å, 124.01(9)°, 180° and 132.20(2)°, respectively.
The temperature dependence of the magnetic susceptibilities of 1 and 2 was measured from 2 to 300 K with an applied direct-current (dc) magnetic field of 1000 Oe. As shown in Fig. 2a and b, the χmT value of 9.84 cm3 K mol−1 for 1 at 300 K is close to the expected spin-only value of 10.07 cm3 K mol−1 for one isolated GdIII ion (S = 7/2, g = 2) and 0.5 isolated MnII ions (S = 5/2, g = 2). With the temperature decreasing, the χmT values remained essentially constant until 100 K, after which they decreased gradually as T decreased to 10 K, and then decreased rapidly to 8.92 cm3 K mol−1 at 2 K, which is probably due to the antiferromagnetic interactions of the intra-chain Gd–Gd–Mn. The χmT value of 8.82 cm3 K mol−1 for 2 at 300 K equals the expected spin-only value of 8.82 cm3 K mol−1 for one isolated GdIII ion (S = 7/2, g = 2) and 0.5 isolated CoII ions (S = 3/2). With the temperature decreasing, the χmT values stayed essentially constant until 100 K, then, they decreased gradually as T decreased to 10 K, after which they dropped rapidly to 8.22 cm3 K mol−1 at 2 K, which can probably be ascribed to the antiferromagnetic interactions of the intra-chain Gd–Gd–Co and the zero-field splitting of the ground states.15 The data obey the Curie–Weiss law with C = 9.804 cm3 K mol−1, θ = −0.34 K for 1 and C = 9.901 cm3 K mol−1, θ = −2.32 K for 2. This result indicates that 1 and 2 have weak antiferromagnetic interactions. The stronger antiferromagnetic interaction in 2 is attributed to the anisotropy of the CoII ions.16
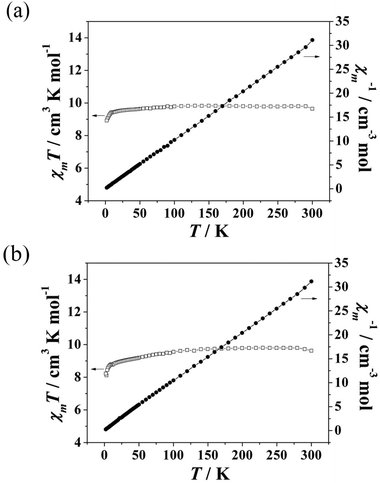 | ||
| Fig. 2 Temperature dependence of χmT and the inverse molecular susceptibility plots for 1 (a) and 2 (b). | ||
The field dependence of the magnetization of 1 and 2 was also investigated at T = 2 K. As shown in Fig. 3a and b, the magnetization M reaches a value of 9.37 NμB for 1 and 8.42 NμB for 2. The former is close to the saturated value of 9.5 NμB calculated for one isolated GdIII ion (S = 7/2) and 0.5 isolated MnII ions (S = 5/2) in 1, while the latter is higher than that of 8.2 NμB calculated for one isolated GdIII ion (S = 7/2) and 0.5 isolated CoII ions (S = 1/2) in 2. The higher experimental value of the magnetization M for 2, as compared to the calculated one, is related to the anisotropy of the CoII ions.16 For comparison, the field dependence of the magnetization for 1 and 2 at T = 2 K was calculated using the Brillouin function. As shown in Fig. S2 and S3 (ESI†), the field dependence of the magnetization calculated for 1 is slightly higher than that obtained from the experimental data, while the field dependence of the magnetization calculated for 2 is consistent with that obtained from the experimental data.
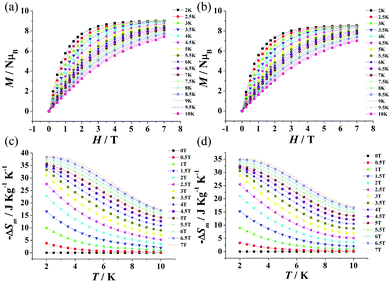 | ||
| Fig. 3 Magnetization versus applied field of 1 (a) and 2 (b) at T = 2–10 K and H = 0–7 T. Experimental −ΔSm obtained from the magnetization data of 1 (c) and 2 (d) at various fields and temperatures. | ||
The magnetic entropy changes, −ΔSm of 1 and 2 (Fig. 3c and d) for evaluating the MCEs can be calculated using the equation17 ΔSm(T, ΔH) = ∫[∂M(T,H)/∂T]HdH from the experimental magnetization data in Fig. 3a and b. The maximum value of −ΔSm for 1 is 38.70 J kg−1 K−1 (78.68 mJ cm−3 K−1) at 2.5 K and ΔH = 7 T. This is smaller than the value 48.40 J kg−1 K−1 calculated using the equation17 −ΔSm = nR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) with one isolated GdIII (S = 7/2) and 0.5 MnII (S = 5/2) ions. The maximum value of −ΔSm for 2 is 35.18 J kg−1 K−1 (72.89 mJ cm−3 K−1) at 2.5 K for ΔH = 7 T, which is also smaller than the calculated value of 44.93 J kg−1 K−1 with one isolated GdIII (S = 7/2) and 0.5 CoII (S = 3/2) ions. The experimental maximum values of −ΔSm for 1 and 2 are smaller than the theoretical values probably because of the weak antiferromagnetic interactions in 1 and 2.4c,d Surprisingly, the MCEs can also get satisfying values of 31.08 J kg−1 K−1 (63.19 mJ cm−3 K−1) for 1 and 28.67 J kg−1 K−1 (59.40 mJ cm−3 K−1) for 2 at ΔH = 3 T. These values are even higher than that for the commercial magnetic refrigerant GGG (−ΔSm ≈ 24 J kg−1 K−1, at ΔH = 3 T).18 Complexes 1 and 2 exhibit a higher MCE than that of GGG at ΔH = 3 T, which may be attributed to the weak magnetic interactions, since the magnetic interaction in GGG is paramagnetic,19 and the use of paramagnetic materials as low-temperature refrigerants often requires relatively large fields to provide a relevant cooling power.20
ln(2S + 1) with one isolated GdIII (S = 7/2) and 0.5 MnII (S = 5/2) ions. The maximum value of −ΔSm for 2 is 35.18 J kg−1 K−1 (72.89 mJ cm−3 K−1) at 2.5 K for ΔH = 7 T, which is also smaller than the calculated value of 44.93 J kg−1 K−1 with one isolated GdIII (S = 7/2) and 0.5 CoII (S = 3/2) ions. The experimental maximum values of −ΔSm for 1 and 2 are smaller than the theoretical values probably because of the weak antiferromagnetic interactions in 1 and 2.4c,d Surprisingly, the MCEs can also get satisfying values of 31.08 J kg−1 K−1 (63.19 mJ cm−3 K−1) for 1 and 28.67 J kg−1 K−1 (59.40 mJ cm−3 K−1) for 2 at ΔH = 3 T. These values are even higher than that for the commercial magnetic refrigerant GGG (−ΔSm ≈ 24 J kg−1 K−1, at ΔH = 3 T).18 Complexes 1 and 2 exhibit a higher MCE than that of GGG at ΔH = 3 T, which may be attributed to the weak magnetic interactions, since the magnetic interaction in GGG is paramagnetic,19 and the use of paramagnetic materials as low-temperature refrigerants often requires relatively large fields to provide a relevant cooling power.20
In summary, two 3d–4f acetate chains, 1 and 2, with high MCEs were reported. The MCE for complex 1 (−ΔSm = 38.70 J kg−1 K−1) is larger than that of 2 (−ΔSm = 35.18 J kg−1 K−1) at ΔH = 7 T. More importantly, the −ΔSm values for 1 and 2 at a lower and applicable field of ΔH = 3 T are up to 31.08 J kg−1 K−1 and 28.67 J kg−1 K−1, respectively. The large MCEs for 1 and 2 are attributed to the small acetate ligands, the increased dimension and the alternating M–Gd–M structure in the complexes. The preparation of other multidimensional 3d–4f structures with other small-molecule ligands and alternating arrangements is in progress.
Experimental section
Synthesis of 1
Gd(OAc)3·6H2O (0.388 g, 1 mmol) and Mn(OAc)2·4H2O (0.245 g, 1 mmol) were dissolved in a mixture of deionized water (10 mL) and anhydrous ethanol (5 mL). Then acetic acid glacial (500 μl, 8.75 mmol) was added under stirring, and a freshly prepared aqueous solution of NaOH (3 mL, 1.0 M) was added dropwise. The mixture was heated to 70 °C and refluxed for 1 day. Evaporation of the filtrate over one month under ambient conditions afforded 0.16 g of colourless cubic-shaped crystals (yield 32% based on Gd).Synthesis of 2
Gd(OAc)3·6H2O (0.194 g, 0.5 mmol) and Co(OAc)2·4H2O (0.125 g, 0.5 mmol) were dissolved in methanol (40.0 mL), then triethylamine (0.145 mL, 1.0 mmol) was added to it. The mixture was heated to 70 °C and refluxed for 1 day. Evaporation of the filtrate over one month under ambient conditions afforded 0.22 g of pink cubic-shaped crystals (yield 43% based on Gd).Crystal data for 1
GdMn0.5C8O13H22, M = 510.98, triclinic, a = 8.2014(6) Å, b = 10.2761(6) Å, c = 11.3982(10) Å, α = 111.426(7)°, β = 108.079(7)°, γ = 93.090(6)°, V = 834.76(11) Å3, T = 173 K, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Z = 2. The density was 2.033 g cm−3. 3274 reflections were measured, 3079 independent reflections (Rint = 0.0314). The final R1 value was 0.0283 (I > 2σ(I)). The final wR(F2) value was 0.0693 (I > 2σ(I)). The goodness of fit on F2 was 1.038. Anal. Calcd for 1: C, 18.79; H, 4.31; N, 0. Found: C, 18.73; H, 4.47; N, 0.091. IR (KBr pellet): 3405(b, s), 1552(s), 1432(s), 1384(w), 1022(w), 950(w), 676(m), 616(w).
, Z = 2. The density was 2.033 g cm−3. 3274 reflections were measured, 3079 independent reflections (Rint = 0.0314). The final R1 value was 0.0283 (I > 2σ(I)). The final wR(F2) value was 0.0693 (I > 2σ(I)). The goodness of fit on F2 was 1.038. Anal. Calcd for 1: C, 18.79; H, 4.31; N, 0. Found: C, 18.73; H, 4.47; N, 0.091. IR (KBr pellet): 3405(b, s), 1552(s), 1432(s), 1384(w), 1022(w), 950(w), 676(m), 616(w).
Crystal data for 2
GdCo0.5C8O13H22, M = 512.97, triclinic, a = 8.1656(5) Å, b = 10.2359(7) Å, c = 11.3405(6) Å, α = 111.699(6)°, β = 108.094(5)°, γ = 92.947(5)°, V = 822.17(8) Å3, T = 173 K, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Z = 2. The density was 2.072 g cm−3. 3218 reflections were measured, 3096 independent reflections (Rint = 0.0245). The final R1 value was 0.0203 (I > 2σ(I)). The final wR(F2) value was 0.0516 (I > 2σ(I)). The goodness of fit on F2 was 1.030. Anal. Calcd for 2: C, 18.71; H, 4.29; N, 0. Found: C, 18.67; H, 4.32; N, 0.800. IR (KBr pellet): 3392(b, s), 1547(s), 1428(s), 1384(w), 1029(w), 952(w), 680(m), 619(w).
, Z = 2. The density was 2.072 g cm−3. 3218 reflections were measured, 3096 independent reflections (Rint = 0.0245). The final R1 value was 0.0203 (I > 2σ(I)). The final wR(F2) value was 0.0516 (I > 2σ(I)). The goodness of fit on F2 was 1.030. Anal. Calcd for 2: C, 18.71; H, 4.29; N, 0. Found: C, 18.67; H, 4.32; N, 0.800. IR (KBr pellet): 3392(b, s), 1547(s), 1428(s), 1384(w), 1029(w), 952(w), 680(m), 619(w).
Acknowledgements
We thank the 973 project from MSTC (grant no. 2012CB821704 and 2014CB845601), the NNSFC (grant no. 21390391) and the Doctoral Fund of the Ministry of Education of China (20120121110012) for financial support.Notes and references
- (a) E. Warburg, Ann. Phys., 1881, 249, 141 CrossRef PubMed; (b) P. Debye, Ann. Phys., 1926, 386, 1154 CrossRef PubMed; (c) W. F. Giauque, J. Am. Chem. Soc., 1927, 49, 1864 CrossRef CAS; (d) V. K. Pecharsky and K. A. Gschneidner Jr, J. Magn. Magn. Mater., 1999, 200, 44 CrossRef CAS; (e) K. A. Gschneidner Jr and V. K. Pecharsky, Int. J. Refrig., 2008, 31, 945 CrossRef PubMed.
- (a) C. Zimm, A. Jastrab, A. Sternberg, V. Pecharsky, K. A. Gschneidner Jr, M. Osborne and I. Anderson, Adv. Cryog. Eng., 1998, 43, 1759 Search PubMed; (b) B. F. Yu, Q. Gao, B. Zhang, X. Z. Meng and Z. Chen, Int. J. Refrig., 2003, 26, 622 CrossRef; (c) V. K. Pecharsky and K. A. Gschneidner Jr, Int. J. Refrig., 2006, 29, 1239 CrossRef CAS PubMed.
- (a) B. G. Shen, J. R. Sun, F. X. Hu, H. W. Zhang and Z. H. Cheng, Adv. Mater., 2009, 21, 4545 CrossRef CAS PubMed; (b) C. Zimm, A. Jastrab, A. Sternberg, V. K. Pecharsky, K. A. Gschneidner Jr, M. Osborne and I. Anderson, Adv. Cryog. Eng., 1998, 43, 1759 Search PubMed.
- (a) J. W. Sharples, Y. Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650 RSC; (b) Y. Z. Zheng, E. M. Pineda, M. Helliwell and R. E. P. Winpenny, Chem. – Eur. J., 2012, 18, 4161 CrossRef CAS PubMed; (c) J. B. Peng, Q. C. Zhang, X. J. Kong, Y. Z. Zheng, Y. P. Ren, L. S. Long, R. B. Huang, L. S. Zheng and Z. P. Zheng, J. Am. Chem. Soc., 2012, 134, 3314 CrossRef CAS PubMed; (d) J. B. Peng, Q. C. Zhang, X. J. Kong and L. S. Long, Angew. Chem., Int. Ed., 2011, 50, 10649 CrossRef CAS PubMed.
- (a) R. Sibille, T. Mazet, B. Malaman and M. Francois, Chem. – Eur. J., 2012, 18, 12970 CrossRef CAS PubMed; (b) F. S. Guo, J. D. Leng and M. L. Tong, Inorg. Chem., 2012, 51, 405 CrossRef CAS PubMed; (c) G. Lorusso, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592 RSC.
- (a) J. M. Jia, S. J. Liu, Y. Cui, S. D. Han, T. L. Hu and X. H. Bu, Cryst. Growth Des., 2013, 13, 4631 CrossRef CAS; (b) Y. C. Chen, F. S. Guo, Y. Z. Zheng, J. L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M. L. Tong, Chem. – Eur. J., 2013, 19, 13504 CrossRef CAS PubMed; (c) G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653 CrossRef CAS PubMed; (d) Y. C. Chen, L. Qin, Z. S. Meng, D. F. Yang, C. Wu, Z. D. Fu, Y. Z. Zheng, J. L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M. L. Tong, J. Mater. Chem., 2014, 2, 9851 CAS.
- (a) P. F. Shi, Y. Z. Zheng and B. Zhao, Chem. – Eur. J., 2012, 18, 15086 CrossRef CAS PubMed; (b) F. S. Guo, Y. C. Chen, J. L. Liu, J. D. Leng, Z. S. Meng, M. Orendáč and M. L. Tong, Chem. Commun., 2012, 48, 12219 RSC.
- Y. Z. Zheng, G. J. Zhou, Z. P. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462 RSC.
- (a) M. Evangelisti, A. Candini, A. Ghirri, M. Affronte, E. K. Brechin and E. J. L. McInnes, Appl. Phys. Lett., 2005, 87, 072504 CrossRef PubMed; (b) R. Shaw, R. H. Laye, L. F. Jones, D. M. Low, C. Talbot-Eeckelaers, Q. Wei, C. J. Milios and S. J. Teat, Inorg. Chem., 2007, 46, 4968 CrossRef CAS PubMed; (c) M. Manoli, R. D. L. Johnstone, S. Parsons, M. Murrie, M. Affronte, M. Evangelisti and E. K. Brechin, Angew. Chem., Int. Ed., 2007, 46, 4456 CrossRef CAS PubMed.
- (a) G. Karotsis, S. Kennedy, S. J. Teat, C. M. Beavers, D. A. Fowler, J. J. Morales, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, J. Am. Chem. Soc., 2010, 132, 12983 CrossRef CAS PubMed; (b) Y. Z. Zheng, M. Evangelisti and R. E. P. Winpenny, Chem. Sci., 2011, 2, 99 RSC; (c) Y. Z. Zheng, M. Evangelisti and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 3692 CrossRef CAS PubMed.
- (a) M. Evangelisti, O. Roubeau, E. Palacios, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed; (b) Y. Z. Zheng, M. Evangelisti and R. E. P. Winpenny, J. Am. Chem. Soc., 2012, 134, 1057 CrossRef CAS PubMed.
- (a) G. Karotsis, M. Evangelisti and S. J. Dalgamo, Angew. Chem., Int. Ed., 2009, 48, 9928 CrossRef CAS PubMed; (b) G. Karotsis, S. Kennedy and M. Evangelisti, J. Am. Chem. Soc., 2010, 132, 12983 CrossRef CAS PubMed.
- A. Gonzalez and A. Beltran, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 1624 CrossRef.
- T. K. Prasad, M. V. Rajasekharan and J. Costes, Angew. Chem., Int. Ed., 2007, 46, 2851 CrossRef CAS PubMed.
- X. J. Kong, Y. P. Ren, W. X. Chen, L. S. Long, Z. P. Zheng, R. B. Huang and L. S. Zheng, Angew. Chem., Int. Ed., 2008, 47, 2398 CrossRef CAS PubMed.
- (a) Y. Q. Sun, S. Y. Liu, Y. Y. Xu, L. Wu, D. Z. Gao, G. Y. Zhang and D. Z. Liao, Polyhedron, 2014, 74, 39 CrossRef CAS PubMed; (b) A. V. Palii, S. M. Ostrovsky, S. I. Klokishner, I. Sophia, O. S. Reu, Z. M. Sun, A. V. Prosvirin, H. H. Zhao, J. G. Mao and K. R. Dunbar, J. Phys. Chem. A, 2006, 110, 14003 CrossRef CAS PubMed.
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672 RSC.
- B. Baudun, R. Lagnier and B. Salce, J. Magn. Magn. Mater., 1982, 27, 315 CrossRef.
- R. D. McMichael, J. J. Ritter and R. D. Shull, J. Appl. Phys., 1993, 73, 6946 CrossRef CAS PubMed.
- R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 43 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The field dependence of magnetization for 1 and 2 at T = 2 K calculated using Brillouin function, PXRD patterns, TGA diagram and CIF files. CCDC 1006167 and 1006168. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4qi00078a |
| This journal is © the Partner Organisations 2014 |
