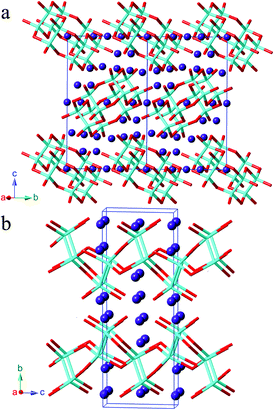
Synthesis, polymorphism, and electronic structures of Sr₃Sn₂As₄

Abstract

Two polymorphs of Sr₃Sn₂As₄ were synthesized from the Sn-flux reactions, and their structures were determined by the single-crystal X-ray diffraction technique. α-Sr₃Sn₂As₄ adopts the Sr₃Sn₂P₄ structure type with the orthorhombic space group Cmca (a = 25.798(2) Å, b = 12.8883(11) Å, c = 19.1244(16) Å, V = 6358.8(9) ų, Z = 24), whereas β-Sr₃Sn₂As₄ belongs to Ca₃Si₂As₄ structure type and crystallizes in the monoclinic crystal system P2₁/c (a = 7.7049(13), b = 19.118(3), c = 7.6877(13), β = 112.003(2)°, V = 1049.9(3), Z = 4). Despite the obvious structural differences, the polyanion units of both compounds feature similar [Sn₂As₆] octahedra. Differential thermal analysis and thermogravimetry measurements indicate that α-Sr₃Sn₂As₄ has good thermal stability and melts at 1185 K, while β-Sr₃Sn₂As₄ starts to decompose above 800 K. Diffuse reflectance spectral measurements proved that both compounds had a band gap of about 0.9 eV, supported by the density functional calculations.

---

Introduction

Zintl phases are valence precise compounds formed among metals with very different electronegativities, such as alkali metals, alkali earth metals, and group 13–15 elements.^1,2 Recently, Zintl phases have become appealing to more and more scientists due to their diverse structures and rich physical properties, including superconductivity,^3–5 magnetoresistance,^6–8 mixed valence,^9,10 thermoelectricity^11–13 and so on. Numerous studies on the crystal and electronic structures, as well as related properties have been reported in the last decade.¹⁴ Surprisingly, although so many compounds have been synthesized, the variety of such phases seems far from being exhausted.

For Zintl compounds with the general formula A₃M₂Pn₄ (A = alkaline-earth metals, Yb or Eu; M = group 12, 13 or 14 metals; Pn = pnictogen elements), various polyanion structures have been discovered, i.e. two-dimensional [Cd₂Sb₄]⁶⁻ layers in Ba₃Cd₂Sb₄,¹⁵ one-dimensional [In₂P₄]⁶⁻ chains in Eu₃In₂P₄ ¹⁶ and zero-dimensional [Sn₁₂P₂₄]³⁶⁻ clusters in Sr₃Sn₂P₄,¹⁷ which can all be rationalized using the Zintl–Klemm concept. The variety of the 3-2-4 family has aroused many studies involving the correlation between structures and properties. As part of such investigations, the A₃Tt₂Pn₄ (Tt = Si, Ge or Sn) system is of special interest due to its structural diversity. The structures of A₃Tt₂Pn₄ generally feature polyanionic rings, such as four-membered rings in Sr₃Si₂As₄,¹⁸ five-membered rings in Ca₃Si₂As₄ ¹⁹ and six-membered rings in Sr₃Sn₂P₄.¹⁷ More interestingly, all these different rings are composed of the same Tt₂Pn₆ octahedral units.

Herein, we present the flux synthesis of two new ternary Zintl polymorphs, α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄, which belong to the Sr₃Sn₂P₄ ¹⁷ and Ca₃Si₂As₄ ¹⁹ structure types, respectively. Compounds with the Ca₃Si₂As₄ structure type are very common and more than half of the A₃Tt₂Pn₄ series adopt this structure. However, for the Sr₃Sn₂P₄ structure type, only one phosphide, Sr₃Sn₂P₄, has been reported so far. By single-crystal X-ray diffraction methods, the crystal structures of α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ were determined accurately, and in cooperation with the density functional theoretical calculations their electronic structures were studied as well. The theoretical results indicated the semiconducting properties of both compounds, which were consistent with the measured optical diffuse reflectance spectral data. Thermal stability studies were performed with the aid of differential thermal analysis and thermogravimetry measurements.

Results and discussion

Structure description

Compound α-Sr₃Sn₂As₄ crystallizes in the orthorhombic Sr₃Sn₂P₄ structure type (Cmca), whereas β-Sr₃Sn₂As₄ crystallizes in the monoclinic Ca₃Si₂As₄ structure type (P2₁/c). Since the structures of both compounds have been well discussed in previous studies, only some important structural features will be discussed here. Information on data collection, structure solution and refinement is summarized in Table 1. Positional and equivalent isotropic displacement parameters, and selected bond distances are all listed in Tables S1 and S2 (ESI†).

Table 1 Selected crystal data and structure refinement parameters for two polymorphs of Sr₃Sn₂As₄

Formula	α-Sr3Sn2As4	β-Sr3Sn2As4
a R 1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo^2 − Fc^2)^2]/∑[w(Fo^2)^2]]^1/2, and w = 1/[σ^2Fo^2 + (AP)^2 + BP], P = (Fo^2 + 2Fc^2)/3; A and B are weight coefficients.
Fw/g mol^−1	799.92	799.92
T/K	296(2)	296(2)
Radiation, wavelength	Mo-Kα, 0.71073 Å
Crystal system	Orthorhombic	Monoclinic
Space group, Z	Cmca, 24	P21/c, 4
Unit cell dimensions
a/Å	25.798(2)	7.7049(13)
b/Å	12.8883(11)	19.118(3)
c/Å	19.1244(16)	7.6877(13)
β/°	—	112.003(2)
V/Å^3	6358.8(9)	1049.9(3)
ρ calc/g cm^−3	5.013	5.060
μ Mo Kα/mm^−1	31.968	32.268
Extinction coefficient	0.000069(2)	—
GOF	1.019	1.050
Final R indices^a [I > 2σ(I)]	R 1 = 0.0329	R 1 = 0.0324
	wR2 = 0.0513	wR2 = 0.0795
Final R indices^a [all data]	R 1 = 0.0610	R 1 = 0.0408
	wR2 = 0.0667	wR2 = 0.0831

---

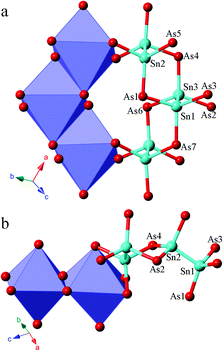
A structure comparison between α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ is provided in Fig. 1. As shown in Fig. 1, the anion structure of α-Sr₃Sn₂As₄ features an interesting [Sn₁₂As₂₄]³⁶⁻ cluster, which encapsulates a Sr²⁺ cation in the center. Each [Sn₁₂As₂₄]³⁶⁻ cluster can be viewed as composed of six [Sn₂As₆] octahedra, connected in the edge-sharing manner. Such an ethane-like [Sn₂As₆] fragment is very common in pnictide Zintl phases and similar examples have been frequently reported as in Sr₃Si₂As₄,¹⁸ Ca₃Si₂As₄ ¹⁹ and ACdGeAs₂ (A = K, Rb).²⁰ However, it is really interesting if this structure is compared with its polymorph β-Sr₃Sn₂As₄, in which the polyanion structure turns out to be a completely different infinite chain. In addition, such one-dimensional chains are also built of the same [Sn₂As₆] octahedra as in α-Sr₃Sn₂As₄ and the connection of these [Sn₂As₆] octahedral units still embodies the edge-sharing fashion. A better illustration of the difference in the anion structures of these two polymorphs is presented in Fig. 2, shown by both polyhedral and ball-and-stick fashions. In α-Sr₃Sn₂As₄, the edge-sharing connection between two neighbouring [Sn₂As₆] octahedra takes place via two As atoms shared by four different [SnAs₃] triangular pyramids. This connection pattern results in a unique [Sn₄As₂] six-membered ring, which helps build the “circle-like” anion clusters in α-Sr₃Sn₂As₄. While for β-Sr₃Sn₂As₄ the situation is a little different: these two As atoms are shared by three [SnAs₃] triangular pyramids, which are still from two different [Sn₂As₆] octahedral and in this way, polyanion chains are formed featuring new [Sn₃As₂] five-membered rings.

Fig. 1 Crystal structure of (a) α-Sr₃Sn₂As₄ and (b) β-Sr₃Sn₂As₄. Sr atoms are plotted in purple spheres, and the polyanionic framework are represented by stick mode with Sn and As atoms shown in light blue and red colors, respectively.

Fig. 2 Polyhedral and ball-and-stick view of the structure of polyanion units of (a) α-Sr₃Sn₂As₄ and (b) β-Sr₃Sn₂As₄. Sn and As atoms are plotted as light blue and red spheres, respectively. [Sn₂As₆] octahedra are emphasized in polyhedral view.

The Sr cations are six-coordinated in both compounds, which all reside in the centers of the distorted As₆ octahedra. The Sn–Sn and Sn–As bonding distances are very similar in these two polymorphs. The corresponding Sn–Sn distances are 2.7659(9) to 2.7955(12) Å in α-Sr₃Sn₂As₄, and 2.7173(9) Å in β-Sr₃Sn₂As₄. The Sn–As interatomic distances are in the range of 2.5523(10) to 2.6563(9) Å in α-Sr₃Sn₂As₄, and 2.5327(11) to 2.6362(10) Å in β-Sr₃Sn₂As₄. These results are comparable to those Zintl compounds with similar bonding patterns,^21–23 yet much shorter than the typical multicenter bonding distances.^24,25 This is consistent with the Zintl concept that the interactions of anionic structures should be localized in two-center two-electron (2c–2e) bonding. The As–Sn–Sn bonding angles are in the range of 103.59(4)° to 111.73(3)° in α-Sr₃Sn₂As₄ and 97.24(3)° to 117.87(3) ° in β-Sr₃Sn₂As₄, which suggests an obviously more distorted tetrahedral coordination geometry for the Sn atoms in β-Sr₃Sn₂As₄ due to the formation of the five-membered rings.

Thermal stability

TG-DSC measurements were performed in order to evaluate the thermal stability of both compounds, and the results are shown in Fig. S1 (ESI†). There is no obvious phase transition behavior observed between these two phases. For α-Sr₃Sn₂As₄, two sequential cycles were performed to ensure its thermal behavior and the results of the 2^nd cycle are shown in Fig. S2.† There is no significant mass loss observed in the whole measured process. Both DSC curves exhibit similar sharp endothermic peaks and exothermic peaks at 1185 K and 1160 K, respectively. Due to the good reproducibility, these two peaks should be attributed to melting and crystallization processes of this compound. Although based on the powder diffraction patterns (Fig. S3†) there are no significant impurities identified, the slight fluctuations of the curves suggest the possible existence of some uncertain amorphous impurities. A similar situation exists for β-Sr₃Sn₂As₄; however, a significant mass loss is observed at above 800 K, which evidently indicates the decomposition process of β-Sr₃Sn₂As₄. It is not surprising that both compounds have shown a distinct thermal behavior due to their different structures. The thermal behavior of the β-phase is very similar to its isostructural analogue Eu₃Ge₂As₄,²⁶ which also has a mass loss of about 7% in the range from 830 K to 1170 K.

Optical absorption spectrum

UV–vis/near-IR diffuse reflectance spectra were recorded at room temperature for both α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ and the calculated optical absorption spectra are presented in Fig. S4.† The optical absorption spectra of compounds are very similar and both suggest semiconducting characters. The room temperature band gaps evaluated for α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ are 0.86(2) and 0.87(3) eV, respectively, which are consistent with their black colour. However, as mentioned above, the existence of some uncertain amorphous impurities may also affect the absorption behavior, which exhibit a small peak around 0.9 eV as well as the fluctuant baseline. Tauc plots were also tried to evaluate the band gaps (Fig. S5†) and the results are consistent with the previous findings.

Electronic band structure

To better understand their optical properties, electronic band structure calculations based on the density functional method were carried out for both compounds and the results are shown in Fig. 3. As shown in Fig. 3, both structures clearly indicate the existence of a small band gap, 0.82 and 0.83 eV for α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄, respectively, which suggest a semiconducting character as confirmed by the optical absorption spectra above. In addition, the valence band maximum (VBM) and the conduction band minimum (CBM) of the compounds are both located at the same k-vector, a clue that these compounds should be direct band gap semiconductors. Despite the similarities, the band structures of α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ are significantly different in the band width. The bands in α-Sr₃Sn₂As₄ are obviously much narrower than those of β-Sr₃Sn₂As₄, which means the electrons are more localized in α-Sr₃Sn₂As₄ than in β-Sr₃Sn₂As₄. By taking their crystal structures into account, such discrepancies are reasonable since in α-Sr₃Sn₂As₄, the polyanion structure is basically composed of the isolated [Sn₁₂As₂₄]³⁶⁻ clusters, whereas for β-Sr₃Sn₂As₄ the Sn and As atoms form infinite chains in favor of electron transport.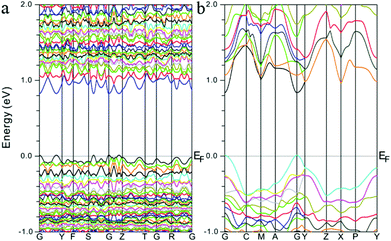

Fig. 3 Calculated electronic band structures for (a) α-Sr₃Sn₂As₄ and (b) β-Sr₃Sn₂As₄, respectively. The Fermi level is chosen as the energy reference at 0 eV.

Projections of the corresponding total and partial density of states (DOS) for both α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ are presented in Fig. 4. A qualitative comparison of the DOS between these two polymorphs reveals high similarity in the DOS curves: the conduction bands are generally composed of 4d orbitals of Sr and the antibonding states originated from the Sn–As interactions; the valence bands can be divided into two different regions—the lower region ranging from −8 to −4 eV are primarily contributed by the localized s states from As atoms and another region, which has relatively higher energy below the Fermi level, is composed mainly of Sr-4d, Sn-5s and 5p, and As-4p orbitals. The high hybridization between Sn and As orbitals in the valence band suggests strong covalent interactions within the anionic framework and the significant p–d mixing of Sr and As indicates non-negligible covalent bonding interactions between cations and anions. Although cations in Zintl phases are usually considered merely as charge suppliers and space fillers, many recent researches^27–29 indicate that they can play more important roles, such as stabilizing the structure or affecting the transport properties. Despite the similarites above, there exists a sharp shoulder peak right below the Fermi level for α-Sr₃Sn₂As₄, which predominantly consists of the 4p orbitals of As atoms and is not observed in β-Sr₃Sn₂As₄. This peak should be designated as the non-bonding electrons or a lone pair on As atoms of α-Sr₃Sn₂As₄ with the knowledge that the polyanion structure of α-Sr₃Sn₂As₄ consists of the isolated [Sn₁₂As₂₄]³⁶⁻ clusters, which should more favor the electron localization than the chain structure of β-Sr₃Sn₂As₄. These results are in accord with the electronic band structure calculations presented above and also are similar to our recent report on arsenide Zintl analogues.^30,31

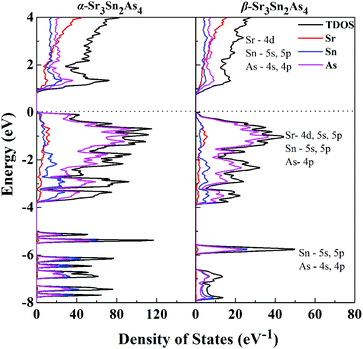Fig. 4 Calculated total DOS and projected DOS are plotted on the same energy scale for α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄. The Fermi level is selected as the energy reference.

Conclusions

In conclusion, two polymorphs of Sr₃Sn₂As₄ have been synthesized and structurally characterized. Although they feature identical [Sn₂As₆] octahedral building units, the different connection patterns lead to the significantly different polyanionic structures. For α-Sr₃Sn₂As₄, the structure can be described as made up of zero-dimensional [Sn₁₂As₂₄]³⁶⁻ clusters that are separated by the Sr cations and in the β-phase there exist one-dimensional infinite chains consisting of the edge-sharing [Sn₂As₆] octahedra. The measured optical absorption spectra for both compounds suggest a semiconducting character with band gaps of 0.86 and 0.87 eV for α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄, respectively. These results are in good agreement with the theoretical calculations.

Experimental section

Synthesis

All syntheses were performed in an argon-filled glovebox with the oxygen level below 0.1 ppm or under vacuum. The elements were commercially purchased and used as received: Sr (Alfa, granules, 99%), Sn (Alfa, shot, 99.9%), and As (Alfa, lump, 99.999%).

α-Sr₃Sn₂As₄. Single crystals of α-Sr₃Sn₂As₄ were initially prepared by using Sn as the self-flux and big single crystals of α-Sr₃Sn₂As₄ were obtained by utilizing the following procedure: Sr : Sn : As = 3 : 10 : 4 were loaded into an alumina crucible and the reaction mixture was first heated to 1000 °C at a rate of 200 °C h⁻¹, then homogenized at this temperature for 20 h, and slowly cooled down to 600 °C at a rate of 3 °C h⁻¹. At this temperature, the ampule was quickly taken out of the furnace and the excess of Sn was removed by centrifugation. The utilization of low-fold metal flux (5-fold excess of Sn) is necessary in order to synthesize α-Sr₃Sn₂As₄ and a high-fold metal flux, such as 20-fold excess or higher, will lead to another product Sr₅Sn₂As₆.²¹ Stoichiometric reactions were also performed, but the main products of such reactions were mixtures of small irregular blocks of α-Sr₃Sn₂As₄ as well as some uncertain amorphous phases.

β-Sr₃Sn₂As₄. β-Sr₃Sn₂As₄ was accidentally identified from the Sn-flux reaction aiming at synthesizing a hypothetical compound “SrSnAs₂” by using a loading ratio of Sr : Sn : As = 1 : 7 : 2. The synthesis process is similar to that of α-Sr₃Sn₂As₄ but a higher homogenization temperature (1050 °C) and lower flux separation temperature (500 °C) were applied. The products of this reaction consist of block-shaped α-Sr₃Sn₂As₄ and some plate-shaped crystals of β-Sr₃Sn₂As₄. After the crystal structure of β-Sr₃Sn₂As₄ was identified, several stoichiometric reactions attempting to synthesize β-Sr₃Sn₂As₄ were tried but the results were negative.

Single crystal structure determination

In order to avoid possible decomposition of the title compounds during the data collection, all crystals were picked in an argon-filled glovebox and cut in Paratone N oil to the desired dimensions. The X-ray diffraction data were collected on a Bruker CCD-based diffractometer at 296 K utilizing a Mo Kα radiation (0.71703 Å). Data reduction and integration, together with global unit cell refinements were done by the INTEGRATE program incorporated in the APEX2 software.³² Semi-empirical absorption corrections were applied using the SCALE program for the area detector.³² The structures were solved by direct methods and refined by full matrix least-squares methods on F² using SHELX.³³ In the last refinement cycles, the atomic positions of the two compounds were standardized using the program structure TIDY.^34,35 All structures were refined to convergence with anisotropic displacement parameters. Crystallographic data and structural refinements are summarized in Table 1. Atomic positions and anisotropic displacement parameters and selected bond lengths are given in Tables S1 and S2, respectively. Further information in the form of CIF has been deposited with Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: (49) 7247-808-666; e-mail: crysdata@fiz-karlsruhe.de) – depository CSD 428135 and 428136 for α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄, respectively.

Powder X-ray diffraction

For phase identification, powder X-ray diffraction (PXRD) patterns were taken at room temperature by a Bruker AXS X-ray powder diffractometer using Cu-Kα radiation. The data were recorded in a 2θ mode with a step size of 0.02° and a counting time of 10 s. In Fig. S3 (in ESI†), the comparison between experimental and simulated data confirms the purity of the samples.

Differential thermal analysis and thermogravimetry measurements (DTA/TG)

The thermal stabilities of α-Sr₃Sn₂As₄ and β-Sr₃Sn₂As₄ were tested using a Mettler–Toledo TGA/DSC/1600HT instrument. Thermogravimetric Analysis (TGA) and Differential Scanning Calorimetry (DSC) experiments were performed on polycrystalline material samples for the two phases under the protection of high-purity argon gas with a heating rate of 10 K min⁻¹. In order to verify the thermal behavior of the α-phase, the TGA–DSC experiments were performed twice.

UV–Vis–NIR diffuse reflectance spectrum

The optical diffuse reflectance spectrum for two polymorphs of Sr₃Sn₂As₄ was measured on polycrystalline samples at room temperature using a Shimadzu UV-3101 PC spectrometer equipped with an integrating sphere attachment and BaSO₄ as a reference. The absorption spectrum was calculated from the reflection spectrum via the Kubelka–Munk function: α/S = (1 − R)²/2R, in which α was the absorption coefficient, S was the scattering coefficient, and R was the reflectance.

Computational details

The electronic band structure calculations of Sr₃Sn₂As₄ were performed with the full potential linearized augmented plane wave method (FP-LAPW)^36,37 as implemented in the Wien2k code.³⁸ In this method, the unit cell is divided into non-overlapping muffin-tin (MT) spheres and an interstitial region. The wavefunctions in the interstitial regions are expanded in plane waves up to R_MT × K_max = 7, where R_MT is the smallest radius of all MT spheres and K_max is the plane wave cut-off. The valence wavefunctions inside the MT spheres are expanded up to l_max = 10 while the charge density was Fourier expanded up to G_max = 12 au⁻¹. The MT radii were chosen to be 2.4 Bohr for Sr and Sn atoms and 2.3 Bohr for As atoms. Calculations were performed using 1000 k-points and the exchange correlation potential was calculated using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA).³⁹ The Brillouin Zone (BZ) integration was performed using the tetrahedron method and the self-consistent calculations were considered to have converged if the total energy and the charge of the system are stable within 10⁻⁴ Ryd and 10⁻⁴ e⁻, respectively.

Acknowledgements

The authors acknowledge the financial support from the National Natural Science Foundation of China (grant no. 51271098, 51021062, 51272129), the Independent Innovation Foundation of Shandong University (IIFSDU), the Program of Introducing Talents of Disciplines to Universities in China (111 program no. b06017).

Notes and references

1. E. Zintl, Angew. Chem., 1939, 52, 1–6.
2. S. M. Kauzlarich, Chemistry, Structure and Bonding of Zintl Phases and Ions, VCH Publishers, New York, 1996.
3. M. Rotter, M. Tegel and D. Johrendt, Phys. Rev. Lett., 2008, 101, 107006.
4. X. C. Wang, Q. Q. Liu, Y. X. Lv, W. B. Gao, L. X. Yang, R. C. Yu, F. Y. Li and C. Q. Jin, Solid State Commun., 2008, 148, 538–540.
5. T. Nomura, S. W. Kim, Y. Kamihara, M. Hirano, P. V. Sushko, K. Kato, M. Takata, A. L. Shluger and H. Hosono, Supercond. Sci. Technol., 2008, 21, 125028.
6. A. M. Goforth, H. Hope, C. L. Condron, S. M. Kauzlarich, N. Jensen, P. Klavins, S. MaQuilon and Z. Fisk, Chem. Mater., 2009, 21, 4480–4489.
7. D. J. Webb, R. Cohen, P. Klavins, R. N. Shelton, J. Y. Chan and S. M. Kauzlarich, J. Appl. Phys., 1998, 83, 7192.
8. X. Ma, J. Lu, J. B. Whalen and S. E. Latturner, Inorg. Chem., 2013, 52, 3342–3348.
9. J. R. Salvador, D. Bilc, S. D. Mahanti, T. Hogan, F. Guo and M. G. Kanatzidis, J. Am. Chem. Soc., 2004, 126, 4474–4475.
10. P. H. Tobash and S. Bobev, J. Am. Chem. Soc., 2006, 128, 3532–3533.
11. F. Gascoin, S. Ottensmann, D. Stark, S. M. Haïle and G. J. Snyder, Adv. Funct. Mater., 2005, 15, 1860–1864.
12. X. J. Wang, M. B. Tang, H. H. Chen, X. X. Yang, J. T. Zhao, U. Burkhardt and Y. Grin, Appl. Phys. Lett., 2009, 94, 092106.
13. A. Zevalkink, W. G. Zeier, G. Pomrehn, E. Schechtel, W. Tremel and G. J. Snyder, Energy Environ. Sci., 2012, 5, 9121–9128.
14. E. S. Toberer, A. F. May and G. J. Snyder, Chem. Mater., 2010, 22, 624–634.
15. B. Saparov, S.-Q. Xia and S. Bobev, Inorg. Chem., 2008, 47, 11237–11244.
16. J. Jiang, M. M. Olmstead, S. M. Kauzlarich, H.-O. Lee, P. Klavins and Z. Fisk, Inorg. Chem., 2005, 44, 5322–5327.
17. B. Eisenmann and U. Röβler, Z. Anorg. Allg. Chem., 1998, 624, 406–410.
18. B. Eisenmann and H. Schäfer, Angew. Chem., Int. Ed. Engl., 1980, 19, 480–481.
19. B. Eisenman and H. Schäfer, Z. Anorg. Allg. Chem., 1982, 484, 142–152.
20. M. Khatun, S. S. Stoyko and A. Mar, Inorg. Chem., 2014, 53, 7756–7762.
21. J. Wang, S.-Q. Xia and X.-T. Tao, Inorg. Chem., 2012, 51, 5771–5778.
22. B. Eisenmann, H. Jordan and H. Schäfer, Z. Naturforsch., Teil B: Anorg. Chem., Org. Chem., 1984, 39, 1151–1153.
23. R. Lam and A. Mar, Solid State Sci., 2001, 3, 503–512.
24. G. Haegg and A. G. Hybinette, Philos. Mag., 1935, 20, 913–929.
25. W. Willott and E. Evans, Philos. Mag., 1934, 18, 114–128.
26. X. Liu, S. Xia, X. Lei, M. Pan and X. Tao, Eur. J. Inorg. Chem., 2014, 13, 2248–2253.
27. S. Xia and S. Bobev, J. Am. Chem. Soc., 2007, 129, 4049–4057.
28. S.-J. Kim, S. Ponou and T. F. Fässler, Inorg. Chem., 2008, 47, 3594–3602.
29. P. Alemany, M. Llunell and E. Canadell, Inorg. Chem., 2006, 45, 7235–7241.
30. X. Liu, N. Lin, J. Wang, M. Pan, X. Zhao, X. Tao and S. Xia, Inorg. Chem., 2013, 52, 11836–11842.
31. S. S. Stoyko and A. Mar, Inorg. Chem., 2011, 50, 11152–11161.
32. Bruker APEX2, Bruker AXS Inc., Madison, WI, 2005.
33. G. M. Sheldrick, SHELXTL, University of Göttingen, Göttingen, Germany, 2001.
34. E. Parthé and L. M. Gelato, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1984, 40, 169.
35. L. M. Gelato and E. Parthé, J. Appl. Crystallogr., 1987, 20, 139.
36. G. K. H. Madsen, P. Blaha, K. Schwarz, E. Sjostedt and L. Nordstrom, Phys. Rev. B: Condens. Matter, 2001, 64, 195134.
37. K. Schwarz, P. Blaha and G. K. H. Madsen, Comput. Phys. Commun., 2002, 147, 71–76.
38. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties, Technische Universität Vienna, Austria, 2001.
39. J. P. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.

---

Footnote

† Electronic supplementary information (ESI) available: The X-ray crystallographic file in CIF format of the title compounds; positional and equivalent isotropic displacement parameters and selected bond distances of two compounds; TG-DSC measurements on both compounds; the TG-DSC curves of 2^nd cycle for α-Sr₃Sn₂As₄; powder X-ray diffraction patterns of the polycrystalline samples of two polymorphs of Sr₃Sn₂As₄; the optical absorption spectrum measured on polycrystalline samples. See DOI: 10.1039/c4qi00106k

---