Understanding the reaction mechanisms of Pd-catalysed oxidation of alcohols and domino oxidation–arylation reactions using phenyl chloride as an oxidant

Abstract

Density functional theory calculations were carried out to study the Pd-catalysed oxidation reactions of alcohols using phenyl chloride as an oxidant. Our calculations supported that the mechanism mainly involves oxidative addition, β-hydride elimination, reductive elimination, and finally ligand substitution. Through our calculations, we have explained why oxidation of secondary alcohol was experimentally observed but not that of primary alcohol. The oxidation products (ketones) of secondary alcohols bind much more weakly than the oxidation products (aldehydes) of primary alcohols, contributing to the reactivity difference. The mechanism of the Pd-catalysed domino oxidation–arylation reactions of secondary alcohols was also studied. We have explained the experimental observation that α-arylation of the oxidation products (ketones) of secondary alcohols occurs only when the temperature was raised to 80 °C from below 40 °C.

---

Introduction

Transition metal catalysed oxidation of alcohols to carbonyl compounds, which is a fundamental reaction in organic chemistry, has attracted considerable interest over the past few years.¹ Examples of transition metals used in these oxidation reactions include iridium,² ruthenium,³ gold,⁴ copper,⁵ manganese,⁶ iron,⁷ and palladium.⁸ Of these reported oxidation reactions, catalysts based on palladium were particularly attractive and the scope of the related reactions was extensively examined. Ebner et al. found that palladium complexes are capable of catalysing enantioselective oxidation of chiral secondary alcohols.⁹ Iwasawa et al. reported Pd-catalysed aerobic oxidation of alcohols under an air atmosphere in the presence of substituted pyridines.¹⁰

Development of catalyst systems that can control the ability to selectively oxidize an alcohol in the presence of other groups susceptible to oxidation has been identified as one of the key challenges in alcohol oxidations.¹¹ In 2009, Navarro et al. found that NHC-Pd complexes were able to catalyse oxidation of secondary alcohols at mild temperatures when phenyl chloride was used as an oxidant (eqn (1)). Interestingly, the NHC-Pd complexes did not catalyse the oxidation of primary alcohols under the same reaction conditions. Although a reaction mechanism involving oxidative addition, β-hydride elimination, and reductive elimination has been proposed, it cannot account for the experimental observation that secondary alcohols are far more reactive than primary alcohols.¹² On the basis of their work, the same research group reported in 2011 the domino oxidation–arylation reactions of secondary alcohols to produce α-arylated products under the same NHC-Pd catalytic system but at a higher temperature (80 °C) and in the presence of 2.1 equivalent of the oxidant phenyl chloride (eqn (2)).¹³

Theoretical studies reported so far on metal-catalysed oxidation of alcohols are limited. Baerends et al. theoretically investigated the aerobic oxidation of primary alcohols to aldehydes, using [Cu(bipy)]²⁺, the TEMPO radical, and a strong base as the catalytic system. The most important conclusion of this work is that oxidation of alcohols to aldehydes takes place by electrophilic attack of uncoordinated TEMPO⁺ on one C–H(α) bond of a primary alcohol.¹⁴ Goddard et al. theoretically studied the reactivity of (NHC)Pd(OAc)₂ and emphasized the role played by the strong trans influence ligand NHC. They found that β-hydride elimination, in which the β-hydrogen of a palladium-bound alkoxide was transferred directly to the free oxygen of the bound carboxylate, provides the lowest-energy route.¹⁵

In this work, with the aid of DFT calculations, we will investigate the reactivity difference between primary and secondary alcohols in the Pd-catalysed oxidation reactions (eqn (1)) by studying the detailed reaction mechanisms. We hope to understand the factors affecting the reactivity difference. We will also study the mechanism related to the Pd-catalysed domino oxidation–arylation reaction shown in eqn (2) and try to understand how higher temperature promotes the α-arylation immediately after the alcohol oxidation. An understanding of the reaction mechanism is expected to lead to more efficient synthetic strategies and more efficient catalysts for the oxidation of alcohols to aldehydes or ketones.

Worth mentioning here is that in recent years, environment-friendly alcohol dehydrogenation that does not require an oxidant has been developed to synthesize amides and pyrroles.¹⁶ Wang et al. investigated the mechanism of Ru-catalysed reactions of amines with primary alcohols to produce amides.¹⁷ In these reactions, the dehydrogenation reactions normally proceed via the bifunctional double hydrogen transfer mechanism rather than the β-H elimination mechanism.

Computational details

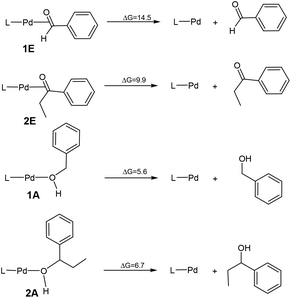
Full geometry optimizations have been performed at the Becke3LYP (B3LYP) level of the density functional theory.¹⁸ The effective core potentials (ECPs) of Hay and Wadt with a double-ζ valence basis set (LanL2DZ)¹⁹ were used to describe Pd, Cl and K. Polarization functions were added for Pd (ζ_f = 1.47), Cl (ζ_d = 0.64) and K (ζ_d = 1.00).²⁰ The 6-31G(d) basis set was used for all the other atoms. Frequency calculations were carried out to confirm the characteristics of all of the optimized structures as minima or transition states. Calculations of intrinsic reaction coordinates (IRC)²¹ were also performed to confirm that transition states connect two relevant minima. To obtain free energies in solution, the solvation-corrected relative free energies were calculated in Gaussian 09²² using the M06 DFT functional²³ with the universal solvation model (SMD).²⁴ Such an approach to obtain the solvation-corrected relative free energies has been popularly used recently in a number of theoretical studies.²⁵ Toluene was employed as the solvent (according to the reaction conditions).

To reduce the computational cost, we used 1,3-dimethylimidazol-2-ylidine as the model NHC ligand, in which the substituents at N in the experimentally used NHC ligand (IPr = 1,3-bis-(2,6-diisopropylphenyl)imidazol-2-ylidene) were replaced by CH₃. Our early work established the validity of using 1,3-dimethylimidazol-2-ylidine as a model for IPr.²⁶ To provide further support for the use of the model NHC ligand, we also calculated the reaction free energies for 1E + PhCH₂OH → 1A + PhCHO and 2E + PhEtCHOH → 2A + PhEtCO, which are important for our conclusions, with the full NHC ligand used in the experimental reactions. The results show that with the model NHC ligand the reaction free energies are 8.8 and 3.2 kcal mol⁻¹ (Fig. 1 and 3). With the full NHC model, the reaction free energies are 8.7 and 3.9 kcal mol⁻¹. We also calculated the free energy changes for 1A + PhCl → 1TS_(A–B) and 2A + PhCl → 2TS_(A–B) with the full NHC ligand. The free energy changes were calculated to be 17.0 and 17.7 kcal mol⁻¹ (Fig. S1 and S2†), compared with 20.6 and 20.8 kcal mol⁻¹ from the model NHC results. Additional comments on the relative barriers using different models are given in the ESI.†

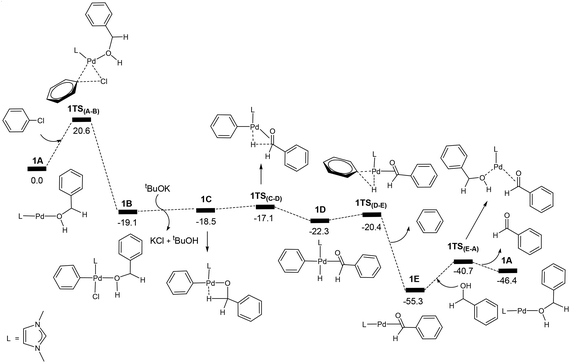Fig. 1 Energy profile calculated for the Pd-catalysed oxidation of PhCH₂OH (PhCH₂OH + PhCl + ^tBuOK → PhCHO + PhH + ^tBuOH + KCl). The relative free energies are given in kcal mol⁻¹.

Results and discussion

General mechanism of the Pd-catalysed oxidation reactions of alcohols

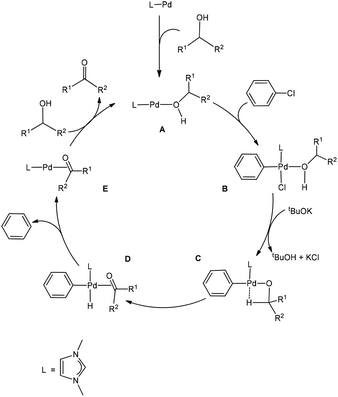
As mentioned in the Introduction, the reaction mechanism proposed for the Pd-catalysed oxidation reactions of alcohols involves oxidative addition, β-hydride elimination, and reductive elimination. Based on our calculation results, a version of the proposal providing all the relevant details of the nature of the species involved is given in Scheme 1. An alcohol molecule first coordinates to the Pd centre to form the two-coordinate active species LPd(0)(alcohol) A, which is a 14e Pd(0) complex. 14e Pd(0) complexes are normally considered to be the active species for oxidation addition of aryl halides.²⁷ We consider the two-coordinate active species A containing an alcohol molecule, instead of a phenyl chloride as a ligand of the starting species because an alcohol molecule is expected to be more strongly coordinating.

Scheme 1 The proposed mechanism of the Pd-catalysed oxidation reactions of alcohols.

Oxidative addition of phenyl chloride to complex A gives a four-coordinate, square planar Pd(II) complex (B).²⁸ The complex B reacts with ^tBuOK to give ^tBuOH, KCl and the intermediate C containing an agostic interaction. The intermediate C then undergoes β-hydride elimination to give complex D, which is a precursor complex ready to undergo reductive elimination to give the co-product benzene molecule, and complex E in which the carbonyl product molecule acts as a ligand. Finally, a ligand substitution of substrate (alcohol) for product (aldehyde/ketone) occurs to regenerate the active species A and complete the catalytic cycle.

Oxidation of primary alcohols

Fig. 1 shows the energy profile calculated for the Pd-catalysed oxidation reaction of PhCH₂OH, a primary alcohol, (PhCH₂OH → PhCHO), on the basis of the reaction mechanism illustrated in Scheme 1. In Fig. 1, oxidative addition of phenyl chloride to the two-coordinate complex active species 1A occurs as the first step via the transition state 1TS_(A–B) to give the square-planar Pd(II) intermediate 1B with a barrier of 20.6 kcal mol⁻¹. Here, 1A + PhCl, instead of the van der Waals complex of the two, were set as the energy reference point, considering the entropy contribution. In fact, the van der Waals complex of the two is lying higher in free energy than 1A + PhCl. Then the base ^tBuOK neutralizes HCl eliminated from the intermediate 1B to give ^tBuOH + KCl and the intermediate 1C which contains an agostic interaction. Next, β-hydride elimination gives the hydride intermediate 1D. Then, reductive elimination takes place to release a benzene molecule and form the intermediate 1E. In the intermediate 1E, the carbonyl product molecule is coordinated to the metal centre as a ligand through an η²-coordination of the C=O bond. We can see that once the intermediate 1B is formed, the steps followed leading to 1E are all very facile. Finally, a ligand substitution gives the final aldehyde product PhCHO and regenerates the active species 1A. Here, 1E is the resting state of the catalytic cycle on the basis of our theoretical calculations.

The energy profile shown in Fig. 1 indicates that the overall reaction is highly exergonic with a reaction free energy of −46.4 kcal mol⁻¹ (PhCH₂OH + PhCl + ^tBuOK → PhCHO + PhH + ^tBuOH + KCl). The highest energy structure in the energy profile corresponds to the transition state 1TS_(A–B) which lies 20.6 kcal mol⁻¹ higher in energy than the energy reference point (1A + PhCH₂OH + PhCl + ^tBuOK). From the energy profile shown in Fig. 1, one may rush to conclude that the overall barrier for the catalytic reaction corresponds to the barrier calculated for the oxidative addition of PhCl to 1A, which is 20.6 kcal mol⁻¹. This is not the case because the lowest energy point in the catalytic cycle corresponds to the intermediate 1E, not the end point of the catalytic cycle. We can see that 1E + PhCH₂OH is more stable than 1A + PhCHO by 8.9 kcal mol⁻¹ (Fig. 1). In fact, the overall barrier for the catalytic reaction should be 20.6 + 8.9 = 29.5 (kcal mol⁻¹) according the energetic span model developed by Kozuch et al.²⁹

To further elaborate the application of the energetic span model to the case here, we have depicted the schematic energy profile diagram in Fig. 2 by extending the energy profile to an additional catalytic cycle. In Fig. 2, RDTS and RDI stand for rate-determining transition state and intermediate, respectively. ΔG_R is the reaction free energy for the catalytic reaction under consideration. From Fig. 2, we can also view the first RDI to the second RDI as a catalytic cycle. In this view, we can easily come to the conclusion that the overall barrier is ΔG₁ + ΔG₂, not a simple addition of the two relevant barriers (ΔG₁ + ΔG₃). In Fig. 1, we have that ΔG₁ = 20.6 kcal mol⁻¹ and ΔG₂ = 8.9 kcal mol⁻¹.

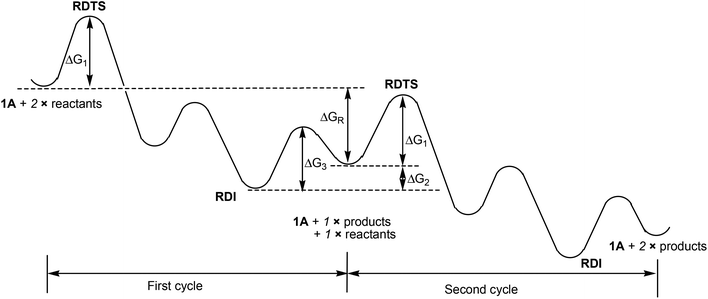Fig. 2 Schematic illustration of the energy profile given in Fig. 1, which includes the energy profile for an additional catalytic cycle.

Oxidation of secondary alcohols

For comparison, we also calculated the energy profile for the corresponding catalysed oxidation reaction of the secondary alcohol PhEtCHOH (PhEtCHOH → PhEtCO) on the basis of the reaction mechanism shown in Scheme 1. Fig. 3 shows the calculated energy profile. From Fig. 3, we see that the energy profile is very similar to that calculated for the catalysed oxidation of PhCH₂OH shown in Fig. 1. The transition state 2TS_(A–B) corresponds to the highest energy structure in the energy profile, which lies 20.8 kcal mol⁻¹ above the energy reference point. 2TS_(A–B) is in fact the transition state for the oxidative addition of PhCl to 2A. Clearly, the barrier (20.8 kcal mol⁻¹) calculated for the oxidative addition of PhCl to 2A is approximately the same as that (20.6 kcal mol⁻¹, Fig. 1) calculated for the oxidative addition of PhCl to 1A.

Similar to what we found for the reaction of the primary alcohol PhCH₂OH, the intermediate 2E having the product molecule PhEtCO as a ligand also corresponds to the lowest energy point in the energy profile. However, 2E + PhEtCHOH is more stable than 2A + PhEtCO by 3.2 kcal mol⁻¹ only. In the reaction of the primary alcohol PhCH₂OH, 1E + PhCH₂OH is more stable than 1A + PhCHO by 8.9 kcal mol⁻¹. Thus, the overall barrier for the catalytic reaction of the secondary alcohol PhEtCHOH is 20.8 + 3.2 = 24.0 (kcal mol⁻¹). The overall reaction (PhEtCHOH + PhCl + ^tBuOK → PhEtCO + PhH + ^tBuOH + KCl) is exergonic with a reaction free energy of −47.6 kcal mol⁻¹.

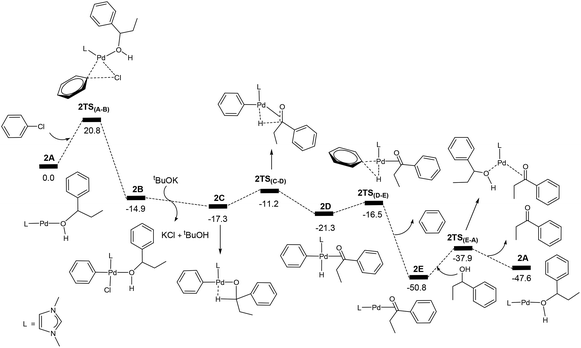Fig. 3 Energy profile calculated for the Pd-catalysed oxidation of PhEtCHOH (PhEtCHOH + PhCl + ^tBuOK → PhEtCO + PhH + ^tBuOH + KCl). The relative free energies are given in kcal mol⁻¹.

Reactivity difference between primary and secondary alcohols

The calculation results described above indicate that the Pd-catalysed oxidation reaction of the secondary alcohol PhEtCHOH is kinetically more favorable than that of the primary alcohol PhCH₂OH by 5.5 kcal mol⁻¹. The barrier difference (5.5 kcal mol⁻¹) can give a multiplicative difference of about 10⁵ in the reaction rate if we assume an Arrhenius expression for the rate constant and similar pre-exponential factors. Experimentally, the oxidation reaction of the secondary alcohol PhEtCHOH was carried out at 25 °C and took 11 hours to achieve a yield of 91%.¹³ Given the difference in the reaction rate, it is expected that the oxidation reaction of the corresponding primary alcohol PhCH₂OH was not observed experimentally.

The analysis given above indicates that the overall barrier for the catalysed oxidation of a given alcohol substrate molecule is the sum of (1) the barrier (ΔG₁) for oxidative addition of PhCl to the active species LPd(0)(substrate) (1A or 2A) and (2) the reaction free energy (ΔG₂) for the ligand substitution of an alcohol substrate molecule for an aldehyde or ketone product molecule in LPd(0)(product) to regenerate the active species.

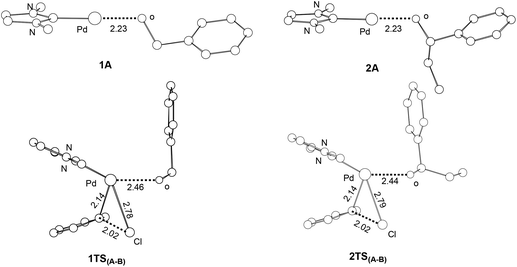
Our calculations show that the barriers (ΔG₁) for the oxidative additions of phenyl chloride to 1A and 2A are approximately the same. Examining the structures of 1A, 2A and the corresponding oxidative addition transition states 1TS_(A–B) and 2TS_(A–B) (Fig. 4), we see that the optimized structures of 1A and 2A as well as 1TS_(A–B) and 2TS_(A–B) are similar to each other. The results are consistent with the fact that approximately the same barriers were calculated for the two oxidative additions.

Fig. 4 Selected bond distances (Å) calculated for the active species 1A and 2A and the oxidative addition transition states 1TS(A–B) and 2TS(A–B). Hydrogen atoms have been omitted for the purpose of clarity.

As discussed above, the ligand substitution of an alcohol substrate molecule for an aldehyde or a ketone product molecule is another step that contributed to the overall barrier. The energetics (ΔG₂) associated with the ligand substitution step reflects how relatively easily an aldehyde or a ketone product molecule, once it is formed, is released from the catalyst to which it is coordinated. The calculation results show that 1E + PhCH₂OH → 1A + PhCHO is more endergonic than 2E + PhEtCHOH → 2A + PhEtCO by 5.5 kcal mol⁻¹. Here, we can see that it is the difference in (ΔG₂) that contributes to the significant reactivity difference of the two substrate molecules.

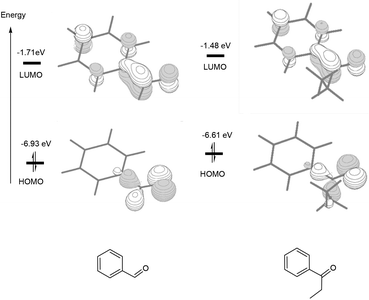
Scheme 2 compares the binding energies of the alcohol substrate molecules and the corresponding aldehyde/ketone product molecules with the Pd(0) metal centre. A relatively small difference in the binding energy was calculated between the two alcohol substrate molecules. However, a noticeably significant difference in the binding energy can be found between the two product molecules. Clearly, the product molecule PhCHO derived from the former alcohol substrate molecule binds much more strongly to the Pd(0) metal centre than the product molecule PhEtCO derived from the latter alcohol substrate molecule. The stronger η²-binding of PhCHO versus PhEtCO with Pd(0) can be attributed to both steric and electronic effects. PhCHO is less sterically hindered than PhEtCO when it is η²-coordinated to the metal centre. Electronically, PhCHO has a lower lying C=O π* orbital when compared with PhEtCO (Fig. 5), giving rise to greater Pd(0)-to-CO(π*) back-bonding interaction. In the calculated structures shown in Fig. 6, 1E gives a shorter Pd–C(O) distance than 2E.

Fig. 5 The HOMO and LUMO calculated for PhCHO and PhEtCO. The orbital energies are given in eV.

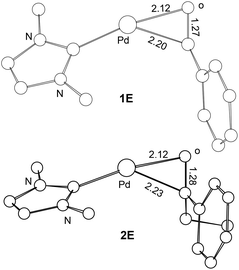Fig. 6 Selected bond distances (Å) calculated for the ligand substitution intermediates 1E and 2E. Hydrogen atoms have been omitted for the purpose of clarity.

Scheme 2 The binding energies of the alcohol substrate molecules and the corresponding aldehyde/ketone product molecules with the Pd(0) metal centre.

[LPd(O^tBu)]⁻ as the active species

In the presence of ^tBuOK, one might argue that the anionic species [LPd(O^tBu)]⁻, instead of LPd(0)(alcohol) A, acted as the active species for the catalytic process. Considering this anionic species as the active species, we also calculated the energy profile for the catalysed oxidation reaction of the primary alcohol PhCH₂OH. The detailed energy profile (Fig. S3†) and the mechanistic cycle (Scheme S1†), which is very similar to Scheme 1 except for the active species, are given in the ESI.† Interestingly, the overall reaction barrier was found to be only 17.3 kcal mol⁻¹. With such a small overall reaction barrier, one would expect that the reaction could occur easily and quickly. However, the experimental finding is that the reaction occurs at the elevated temperature of 25–40 °C and takes hours to complete. Therefore, in the actual reaction, the anionic species [LPd(O^tBu)]⁻ is unlikely to be involved as the active species in the catalytic cycle.

A plausible explanation for the anionic species [LPd(O^tBu)]⁻ not being involved as the active species is given as follows. Experimentally, tertbutoxide has very poor solubility in toluene, which is the solvent used in the reactions. Alcohol and the catalyst are much more soluble in toluene than tertbutoxide. Therefore, it is reasonable to assume that formation of LPd(0)(alcohol) is much faster than that of [LPd(O^tBu)]⁻.

With LPd(0)(alcohol) as the active species, oxidative addition of PhCl has a reasonably small barrier and is expected to have a fast step also. Once LPd(II)Ph(Cl)(alcohol) is formed from the oxidative addition, the coordinated alcohol in this Pd(II) complex is much more acidic (when compared with the coordinated alcohol in LPd(0)(alcohol)) and easily deprotonated by tertbutoxide as proposed in Scheme 1.

Decarbonylation of LPd(0)(PhCHO) (1E)

Another possible reason for the oxidation reaction of primary alcohol PhCH₂OH not being observed could be due to decarbonylation of LPd(0)(PhCHO) (1E) via C–H oxidative addition. We studied this possibility (see ESI† for the calculated energy profile). From 1E, oxidative addition of the C–H bond to the Pd centre occurs to give a hydride intermediate. Then α-phenyl migration to the metal centre gives a four-coordinate complex (LPd(II)H(CO)Ph), in which CO is a ligand. Finally, the reductive elimination takes place to release a benzene molecule and form a two-coordinate complex containing the NHC ligand and CO. An overall free energy barrier of 41.3 kcal mol⁻¹ was calculated for the α-phenyl migration. With such an inaccessibly high barrier, we cannot argue that decarbonylation is responsible for the oxidation reaction of primary alcohol PhCH₂OH not being observed.

Mechanism of the Pd-catalysed domino oxidation–arylation of secondary alcohols

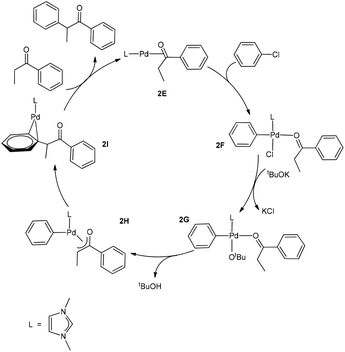
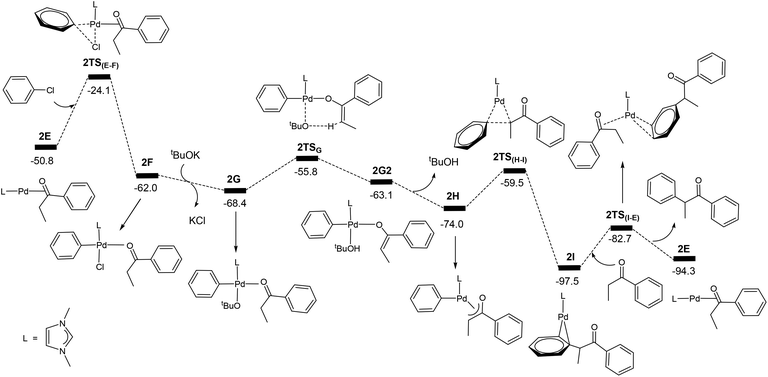
Now we come to understanding the Pd-catalysed domino oxidation–arylation reactions of secondary alcohols shown in eqn (2) in which α-arylated products were produced when two equivalents of the oxidant phenyl chloride were used in the reaction. Here, we can reasonably hypothesize that the secondary alcohols were first oxidized to their corresponding ketones and then further reacted with the second equivalent of the oxidant phenyl chloride at a higher temperature to finally produce the α-arylated products. Indeed, experimental evidence supports this hypothesis. Experimentally, α-arylated products were produced when ketones derived from eqn (1) were allowed to react with phenyl chloride at 80 °C under the same catalytic system.¹³ In other words, the key to understanding the reaction mechanism for eqn (2) is to understand how a ketone molecule reacts with phenyl chloride.

Here, we use the product molecule PhEtCO (discussed above) as a substrate ketone to react with phenyl chloride (the α-arylation reaction). Fig. 3 shows that the last step 2E + PhEtCHOH → 2A + PhEtCO, which is a ligand substitution process, is reversible. Therefore, instead of undergoing the ligand substitution, 2E can further react with PhCl via oxidative addition to give a four-coordinate, square planar Pd(II) species 2F (Scheme 3). From the species 2F, a ligand substitution of ^tBuO⁻ for Cl⁻ gives the intermediate 2G. Subsequently, deprotonation at the α-carbon by the ^tBuO⁻ ligand produces the η³ intermediate 2H and ^tBuOH. Then, reductive elimination in the 2H takes place to give the intermediate 2I in which the α-arylated product molecule acts as a ligand. Finally, a ligand substitution of a ketone molecule for the α-arylated product molecule regenerates the active catalytic species 2E and completes the α-arylation reaction.

Scheme 3 The proposed mechanism of the Pd-catalysed α-arylation reaction of PhEtCO.

Fig. 7 shows the energy profile calculated for the Pd-catalysed α-arylation reaction of PhEtCO based on the mechanism proposed in Scheme 3. The first step is the oxidative addition of phenyl chloride to the two-coordinate complex 2E to give the intermediate 2Fvia the transition state 2TS_(E–F). The free energy barrier calculated for this step is 26.7 kcal mol⁻¹. From 2F, a ligand substitution of ^tBuO⁻ for Cl⁻ occurs to give the intermediate 2G, in which the ^tBuO⁻ ligand coordinates to the metal centre. The deprotonation from 2G proceeds to 2G2via the transition state 2TS_G, which involves migration of one proton at the coordinated-PhEtCO α-carbon to the ^tBuO⁻ ligand. In the 2G2 intermediate, ^tBuOH is easily dissociated to form the more stable intermediate 2H. Reductive elimination in 2H occurs to give the two-coordinated intermediate 2Ivia the transition state 2TS_(H–I), in which the α-arylated product molecule is coordinated as a ligand to the metal centre in an η² coordination mode. In the final step, a ligand substitution of PhEtCO for the α-arylation product regenerates the active catalytic species 2E and completes the α-arylation reaction.

Fig. 7 Energy profile calculated for the Pd-catalysed α-arylation reaction of PhEtCO. The relative free energies are given in kcal mol⁻¹.

The energy profile shown in Fig. 7 indicates that the overall reaction PhEtCO + PhCl + ^tBuOK → CH₃CH(Ph)C(O)Ph + ^tBuOH + KCl is exergonic with a reaction free energy of −43.5 kcal mol⁻¹. The highest energy structure in the energy profile corresponds to the transition state 2TS_(E–F) which lies 26.7 kcal mol⁻¹ higher in energy than the energy reference point (2E + PhEtCO + PhCl + ^tBuOK). The lowest energy structure corresponds to the intermediate 2I. 2I + PhEtCO is more stable than 2E + CH₃CH(Ph)C(O)Ph by 3.2 kcal mol⁻¹. As mentioned above, the overall barrier for the α-arylation reaction is 29.9 kcal mol⁻¹, the sum of 26.7 kcal mol⁻¹ and 3.2 kcal mol⁻¹ according to what we discussed above (Fig. 2).

The calculation results indicate that the α-arylation of the oxidation product PhEtCO has a higher overall free energy barrier than the oxidation of PhEtCHOH. Therefore, it is expected that at a lower temperature, the reaction stops at the oxidation reaction while at a higher temperature the reaction can continue to give the α-arylated product. These results well explain that the oxidation reaction occurs below 40 °C and further reaction (α-arylation reaction) of the oxidation product occurs when the temperature was raised to 80 °C. We would like to point out here that the ability of a ketone to be enolized (formation of 2H), but not benzaldehyde, contributes to the fact that the secondary alcohols can further react with one more equivalent of PhCl leading to α-arylation.

Conclusion

The Pd-catalysed oxidation reactions of primary and secondary alcohols to the corresponding aldehydes and ketones, respectively, by phenyl chloride have been investigated with the aid of DFT calculations. The results of the calculations support that the mechanism mainly involves oxidative addition, β-hydride elimination, reductive elimination, and finally ligand substitution.

Experimentally, selective oxidation of secondary alcohols versus primary alcohols has been observed. Consistent with this experimental observation, the oxidation reaction of the secondary alcohol PhEtCHOH was calculated to be kinetically more favorable than that of the primary alcohol PhCH₂OH. Our detailed mechanistic analysis indicates that the overall reaction barrier for the oxidation of a given alcohol substrate molecule is the sum of (1) the barrier for oxidative addition of phenyl chloride to the active species LPd(0)(alcohol) and (2) the reaction free energy for the ligand substitution of the alcohol substrate molecule for the aldehyde or ketone product molecule in LPd(0)(aldehyde) or LPd(0)(ketone) to regenerate the active species LPd(0)(alcohol). We found that a ketone product molecule binds much more weakly to the Pd(0) metal centre than an aldehyde product molecule, explaining that oxidation of secondary alcohols, but not primary alcohols, occurs under the catalytic conditions.

The Pd-catalysed domino oxidation–arylation reactions of secondary alcohols have also been investigated. Our calculation results support that the secondary alcohols were first oxidized by phenyl chloride to their corresponding ketones according the mechanism summarized above and then further reacted with the second equivalent of the oxidant phenyl chloride at a higher temperature to finally produce the α-arylated products. In the α-arylation reaction of the ketone product molecule, we have established that the mechanism involves (1) oxidative addition of PhCl to LPd(0)(ketone), (2) ligand substitution of ^tBuO⁻ for Cl⁻, (3) deprotonation of an α-H of the coordinated ketone molecule by the ^tBuO⁻ ligand, (4) reductive elimination to give a species which contains the α-arylated product molecule as a ligand, and (5) finally a ligand substitution of a ketone molecule for the α-arylated product molecule to regenerate the active species LPd(0)(ketone). The overall barrier calculated for the α-arylation of the oxidation product PhEtCO was found to be higher than the oxidation of the secondary alcohol PhEtCHOH. These results explain the experimental observation that α-ketone arylation occurs when the temperature was raised to 80 °C from below 40 °C.

As a final note to readers, we would like to point out that the conclusions summarized above are based on the assumption that LPd(0)(alcohol) is the active species for the catalytic cycle. In the presence of ^tBuOK, one would expect that the anionic species [LPd(0)(O^tBu)]⁻ is likely the active species. However, our calculations show that the anionic species [LPd(0)(O^tBu)]⁻ gives an overall reaction barrier of 17.3 kcal mol⁻¹ for the catalysed oxidation of PhCH₂OH, which is too small to account for the oxidation reactions observed experimentally (slow and with elevated temperature). We argue that the poor solubility of the tertbutoxide and the solvent used (toluene) prevents the fast formation of the anionic species. We also examined whether decarbonylation is responsible for the oxidation reaction of primary alcohol PhCH₂OH not being observed. Our calculation results do not support this. We hope that this work will invite more research on these reactions to gain more insights into the reaction mechanism.

Acknowledgements

This work was supported by the Research Grants Council of Hong Kong (HKUST603711, HKUST603313 and CUHK7/CRF/12G).

Notes and references

1. (a) Y. M. A. Yamada, C. K. Jin and Y. Uozumi, Org. Lett., 2010, 12, 4540; (b) F. Hanasaka, K. Fujita and R. Yamaguchi, Organometallics, 2004, 23, 1490; (c) A. S. Guram, X. Bei and H. W. Turner, Org. Lett., 2003, 5, 2485.
2. (a) A. V. Polukeev, P. V. Petrovskii, A. S. Peregudov, M. G. Ezernitskaya and A. A. Koridze, Organometallics, 2013, 32, 1000; (b) R. Kawahara, K. Fujita and R. Yamaguchi, J. Am. Chem. Soc., 2012, 134, 3643; (c) B. Jiang, Y. Feng and E. A. Ison, J. Am. Chem. Soc., 2008, 130, 14462.
3. (a) S. Manzini, C. A. Urbina-Blanco and S. P. Nolan, Organometallics, 2013, 32, 660; (b) A. J. A. Watson, A. C. Maxwell and J. M. J. Williams, Org. Lett., 2010, 12, 3856; (c) B.-Z. Zhan, M. A. White, T.-K. Sham, J. A. Pincock, R. J. Doucet, K. V. R. Rao, K. N. Robertson and T. S. Cameron, J. Am. Chem. Soc., 2003, 125, 2195.
4. B. Guan, D. Xing, G. Cai, X. Wan, N. Yu, Z. Fang, L. Yang and Z. Shi, J. Am. Chem. Soc., 2005, 127, 18004.
5. (a) X. Liu, Q. Xia, Y. Zhang, C. Chen and W. Chen, J. Org. Chem., 2013, 78, 8531; (b) I. E. Markó, A. Gautier, R. Dumeunier, K. Doda, F. Philippart, S. M. Brown and C. J. Urch, Angew. Chem., Int. Ed., 2004, 43, 1588.
6. M. K. Brown, M. M. Blewett, J. R. Colombe and E. J. Corey, J. Am. Chem. Soc., 2010, 132, 11165.
7. J. Liu and S. Ma, Org. Lett., 2013, 15, 5150.
8. (a) K. Mori, T. Hara, T. Mizugaki, K. Ebitani and K. Kaneda, J. Am. Chem. Soc., 2004, 126, 10657; (b) J. A. Mueller, D. R. Jensen and M. S. Sigman, J. Am. Chem. Soc., 2002, 124, 8202.
9. D. C. Ebner, R. M. Trend, C. Genet, M. J. McGrath, P. O'Brien and B. M. Stoltz, Angew. Chem., Int. Ed., 2008, 47, 6367.
10. T. Iwasawa, M. Tokunaga, Y. Obora and Y. Tsuji, J. Am. Chem. Soc., 2004, 126, 6554.
11. J. Muzart, Tetrahedron, 2003, 59, 5789.
12. C. Berini, D. F. Brayton, C. Mocka and O. Navarro, Org. Lett., 2009, 11, 4244.
13. B. Landers, C. Berini, C. Wang and O. Navarro, J. Org. Chem., 2011, 76, 1390.
14. C. Michel, P. Belanzoni, P. Gamez, J. Reedijk and E. J. Baerends, Inorg. Chem., 2009, 48, 11909.
15. R. J. Nielsen and W. A. Goddard III, J. Am. Chem. Soc., 2006, 128, 9651.
16. (a) C. Gunanathan, Y. Ben-David and D. Milstein, Science, 2007, 317, 790; (b) B. Kang, X. Huang, L. Xie and N. Maulide, J. Am. Chem. Soc., 2013, 135, 11704; (c) S. Michlik and R. Kempe, Nat. Chem., 2013, 5, 140; (d) D. Srimani, Y. Ben-David and D. Milstein, Angew. Chem., Int. Ed., 2013, 52, 4012; (e) H. Li, X. Wang, F. Huang, G. Lu, J. Jiang and Z. Wang, Organometallics, 2011, 30, 5233; (f) G. Zeng and S. Li, Inorg. Chem., 2011, 50, 10572; (g) G. B. Hall, R. Kottani, G. A. N. Felton, T. Yamamoto, D. H. Evans, R. S. Glass and D. L. Lichtenberger, J. Am. Chem. Soc., 2014, 136, 4012.
17. (a) C. Song, S. Qu, Y. Tao, Y. Dang and Z. Wang, ACS Catal., 2014, 4, 2854; (b) H. Li, G. Lu, J. Jiang, F. Huang and Z. Wang, Organometallics, 2011, 30, 2349.
18. (a) P. J. Stephens, F. J. Devlin, C. F. Chaobalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (c) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200; (d) C. Lee, W. Yang and G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785.
19. (a) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284; (b) P. J. Hays and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
20. (a) A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmenn and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114; (b) A. Höllwarth, M. Böhme, S. Dapprich, A. W. Ehlers, A. Gobbi, V. Jonas, K. F. Köhler, R. Stegmenn, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 237.
21. (a) K. Fukui, Acc. Chem. Res., 1981, 14, 363–375; (b) K. Fukui, J. Phys. Chem., 1970, 74, 4161.
22. M. J. Frisch, et al.Gaussian 09, revision D. 01, Gaussian, Inc., Pittsburgh, PA, 2009.
23. (a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
24. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
25. (a) F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642; (b) N. Lo, H. Chen, W. Chuang, C. Lu, P. Chen and P. Chen, J. Phys. Chem. B, 2013, 117, 13899; (c) Y. Li and Z. Lin, J. Org. Chem., 2013, 78, 11357; (d) Q. Xu, H. Gao, M. Yousufuddin, D. H. Ess and L. Kürti, J. Am. Chem. Soc., 2013, 135, 14048.
26. (a) L. Dang, Z. Lin and T. B. Marder, Organometallics, 2010, 29, 917; (b) L. Dang, Z. Lin and T. B. Marder, Chem. Commun., 2009, 3987; (c) H. T. Zhao, L. Dang, T. B. Marder and Z. Lin, J. Am. Chem. Soc., 2008, 130, 5586; (d) L. Dang, H. T. Zhao, Z. Lin and T. B. Marder, Organometallics, 2008, 27, 1178; (e) H. T. Zhao, Z. Lin and T. X. B. Marder, J. Am. Chem. Soc., 2006, 128, 15637.
27. (a) A. A. C. Braga, N. H. Morgon, G. Ujaque and F. Maseras, J. Am. Chem. Soc., 2005, 127, 9298; (b) R. B. Bedford and C. S. J. Cazin, Organometallics, 2003, 22, 987; (c) E. Galardon, S. Ramdeehul, J. M. Brown, A. Cowley, K. K. Hii and A. Jutand, Angew. Chem., Int. Ed., 2002, 41, 1760.
28. (a) M. García-melchor, A. A. C. Braga, A. Lledós, G. Ujaque and F. Maseras, Acc. Chem. Res., 2013, 46, 2626; (b) L. Xue and Z. Lin, Chem. Soc. Rev., 2010, 39, 1692; (c) U. Christmann and R. Vilar, Angew. Chem., Int. Ed., 2005, 44, 366; (d) G. B. Smith, G. C. Dezeny, D. L. Hughes, A. O. King and T. R. Verhoeven, J. Org. Chem., 1994, 59, 8151.
29. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4qo00214h

---