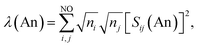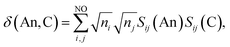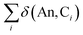Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
f-Orbital covalency in the actinocenes (An = Th–Cm): multiconfigurational studies and topological analysis†
Andrew
Kerridge
*
Department of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: a.kerridge@ucl.ac.uk
First published on 18th February 2014
Abstract
The CASSCF methodology is used to calculate the ground state electron densities of a series of seven actinocenes, AnCOT2 (An = Th–Cm, COT = η8-C8H8). The multiconfigurational character of these complexes is found to be substantial and topological analysis of the electron density via the QTAIM approach is therefore chosen in order to investigate the electronic structure in more detail. Topological analysis reveals increased values of the electron density at the An–C bond critical point for An = Pa–Pu, suggesting enhanced covalent character in metal–ligand bonding for these complexes. In order to investigate the origins of this covalency, integrated one- and two-electron properties are evaluated. A trend for increased electronic charge, spin density and electron localisation on the An centre as one traverses the actinide series is found. The difference between atomic number and the electron localisation index is considered and found to correlate well with the expected oxidation state in these complexes, with a tendency towards trivalent character for the later actinides. Total and orbitally resolved delocalisation indices are evaluated, and increased electron delocalisation is found for the complexes containing Pa–Pu centres. It is shown that, while 5f contributions to covalency in these complexes are smaller in magnitude than 6d contributions, the variation in covalency is almost entirely accounted for by the variation in the 5f contribution.
Introduction
The quantification of covalency in f-element complexes is of both fundamental scientific interest and critical industrial importance. In the nuclear power industry, the remediation of spent nuclear fuel is based on the chemical separation of minor actinides from lanthanides.1,2 That this separation is possible is believed to be due to the more radially extended nature of the 5f shell of the former, resulting in enhanced covalent interactions with soft donor ligands3 when compared to those of the latter, which are characterised by a contracted, core-like, 4f shell. Advantage can be taken of the stability afforded by this enhanced covalent interaction in order to design ligands which are strongly selective for actinides over lanthanides,1,4 from which separation processes follow. The presence of strong electron correlation, however, makes metal–ligand covalency difficult to quantify in complexes containing open shell ions.5,6 Whilst the identification of near-degeneracy between actinide 5f and carbon 2p orbitals in a variety of complexes7,8 has shown promise in developing our understanding of the role of the 5f orbitals in bonding, static correlation, manifesting itself in the form of multiconfigurational character in the electronic wavefunction, results in the failure of these traditional views of covalency due to the breakdown of the independent particle approximation. In order to allow the question of covalency in such multiconfigurational systems to be considered, one can instead turn to the physically observable total electron density. When this is taken as the fundamental property to be analysed, advantage can be taken of topological analysis through the application of the quantum theory of atoms in molecules9 (QTAIM), which allows for the decomposition of a molecule into a space-filling and contiguous set of open quantum systems, or ‘atomic basins’. This topological analysis can be used to infer details of the nature of bonding interactions within the system of interest and can be extended to also consider integrated one- and two-electron properties.Computational chemical approaches are established as important tools in developing our understanding of fundamental actinide chemistry10 and in this work, the covalent contribution to bonding in the prototypical actinide organometallic sandwich complexes, AnCOT2 (COT = η8-C8H8), is investigated. Since the first synthesis of uranocene (UCOT2) was reported by Streitwieser and Müller-Westerhoff in 1968,11 a significant amount of effort has been expended by the actinide chemistry community in order to elucidate the chemical properties of the actinocenes. In addition to uranocene, a number of other AnCOT2 (An = Th, Pa, Np, Pu, Am) complexes have been synthesised,12–15 the latter as the trivalent potassium salt. Whilst there is a significant body of experimental literature relating to the actinocenes, the high (D8h) symmetry of these complexes (see Fig. 1) has made them particularly amenable to theoretical studies, which have demonstrated the need for a multiconfigurational description of the wavefunction.16–22 Here, electron densities derived from complete-active-space self-consistent-field (CASSCF) calculations are used as the basis for topological investigations using QTAIM. A trend in covalency is established across the series, indicating maximum covalent character in the U, Np and Pu complexes. Novel analysis based on the orbital decomposition of integrated electronic properties is employed in order to show that although actinide 5f orbital contributions to covalent character are not the dominant contributions in these complexes, the variation in covalency found across the series is commensurate with the variation in An 5f contributions.
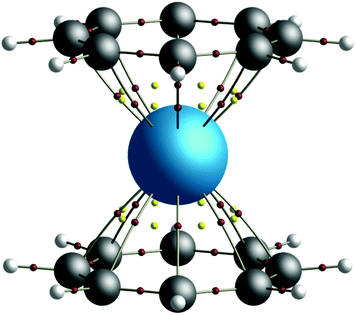 | ||
| Fig. 1 QTAIM calculated molecular graph of the D8h symmetry thorocene complex, ThCOT2. Bond critical points (BCPs) are shown in red, ring critical points (RCPs) in yellow. | ||
Computational details
Complete-active-space self-consistent-field (CASSCF)23 calculations were performed using version 7.6 of the MOLCAS quantum-chemical software package.24,25 Throughout, ANO-RCC basis sets of polarised triple-zeta quality were used.26–28 Molecular geometries were obtained by optimising the distance between the An ion and the ring centroid of the COT dianion with respect to complete active space second order perturbation theory (CASPT2)29 calculated energies. In all calculations, the geometric structure of the COT ligand was held at the geometry used in previous studies.18,20–22 CASPT2 calculations employed an imaginary level shifting technique in order to minimise the effect of intruder states. The value of this level shift was 0.2. Topological analysis employing QTAIM was performed using the AIMAll30 and Multiwfn31 codes. Whilst there are numerous examples in the literature of other analytical approaches, such as Mulliken, NBO or energy decomposition analysis, being used in attempts to deepen our understanding of bonding in f-element complexes, such approaches have not been employed in this study. Mulliken analysis is well known as providing only a qualitative description of atomic populations in actinide complexes,32 whereas NBO and energy decomposition approaches can give somewhat contradictory results when applied to the question of covalency.33 While QTAIM is, like any approach, open to a degree of interpretation, previous work has shown it to be a robust tool in the analysis of f-block compounds, exhibiting trends commensurate with chemical intuition.6,22 QTAIM also has the advantage of being easily applicable to multiconfigurational systems, and it has therefore been chosen as the method of analysis employed in this study.Although all complexes considered here possess D8h point group symmetry, restrictions of the MOLCAS code require that calculations were performed using its highest abelian subgroup, D2h. Bearing this in mind, irreducible representations (irreps) of D2h will be used in the discussion.
Throughout the bonding analysis performed in this study, the effects of dynamical correlation and spin-orbit coupling (SOC) are neglected. Whilst the former could be included via multiconfigurational second-order perturbation theory (e.g. via the CASPT2 approach employed in the geometry optimisations) and the latter via the restricted-active space state interaction (RASSI) approach, it was not possible to generate total electron densities in a manner amenable to QTAIM analysis. Inclusion of dynamical correlation effects would not be expected to significantly affect the results presented here since the important electron interactions associated with the bonding between ion and ligand are incorporated within the chosen active spaces: all electrons included in the active spaces are explicitly correlated. Whilst the effects of SOC can be significant in actinide complexes, they are again expected to have little effect on bonding character. It has previously been shown21 that although the effects of SOC on the energetics of UCOT2 and PuCOT2 are pronounced, they have virtually no effect on the calculated geometries of these complexes, implying little effect on the character of the bonding interaction. This is unsurprising since, within the RASSI formalism, SOC states are constructed from a basis of CASSCF-states calculated in the absence of SOC, and the CASSCF basis states only differ in the occupation of non-bonding 5f-orbitals.
Active spaces
In all AnCOT2 calculations, a 16 orbital active space was constructed, as used previously.22 This active space incorporates the highest occupied π-orbitals of au, b1u, ag and b1g symmetry (in keeping with previous work18,20–22) along with the seven f-orbitals of au (fδ), b1u (fσ, fδ), b2u (fπ, fφ) and b3u (fπ, fφ) symmetry and the five d-orbitals of ag (dσ, dδ), b1g (dδ), b2g (dπ) and b3g (dπ) symmetry. Adopting the CASSCF(n, m) notation to indicate a calculation incorporating an active space explicitly correlating n electrons in m orbitals, this selection results in CASSCF(n, 16) calculations, with n ranging from 8 (Th) to 14 (Cm).Results
Geometry optimisations
For each complex, the electronic ground state was identified by evaluating the CASPT2-calculated energy of the lowest lying state of each of the eight irreducible representations of the D2h point group. Ground state total energies were then calculated at a series of ring centroid-metal separations between 1.700 and 2.300 Å. In total, approximately 20 data points were obtained for each complex. These data were fitted with a sixth-order polynomial in order to obtain equilibrium ring-metal separations. The results of these calculations are given in Fig. 2, along with the ground electronic states of each complex. Of the seven complexes considered here only three, ThCOT2, UCOT2 and NpCOT2 have been structurally characterised,34,35 with experimentally determined ring-metal separations (rRM) of 2.004, 1.926 and 1.909 Å, respectively. The present calculations give optimised rRM of 2.002, 1.907 and 1.890 Å, in good agreement with the experimental data. Table 1 compares rRM with ionic radii (IR) taken from the literature.36 There is, in general, good agreement between the two, particularly in relation to the significant reduction in both rRM and IR when moving from Th to Pa. As one looks further across the series however, an interesting trend appears: the ratio rRM/IR gradually increases, which may be indicative of increased charge concentration on the An ion and/or a reduction in covalent interaction between ligand and ion. The small increase in rRM of 0.021 Å when comparing CmCOT2 to AmCOT2 may therefore be a manifestation of the same effect, and will be investigated in more detail in the following sections.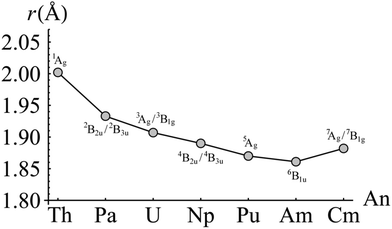 | ||
| Fig. 2 CASPT2-calculated AnCOT2 ring-metal separations. The electronic state for which the geometry was optimised is indicated above and below the corresponding data point. | ||
| Complex | r RM (Å) | IR (Å) | r RM/IR |
|---|---|---|---|
| ThCOT2 | 2.002 | 0.94 | 2.130 |
| PaCOT2 | 1.933 | 0.90 | 2.148 |
| UCOT2 | 1.907 | 0.89 | 2.143 |
| NpCOT2 | 1.890 | 0.87 | 2.172 |
| PuCOT2 | 1.870 | 0.86 | 2.174 |
| AmCOT2 | 1.861 | 0.85 | 2.189 |
| CmCOT2 | 1.882 | 0.85 | 2.214 |
Natural orbital analysis
In order to better understand the electronic structure of the metallocenes, the natural spin-orbitals (NOs) and corresponding occupations (NOOs) were evaluated for each complex. The natural orbitals, introduced by Löwdin,37 are obtained via the diagonalisation of the first order reduced density matrix (RDM), and therefore provide an unambiguous orbital decomposition of the electron density. The NOs also have the property that they are maximum-occupancy orbitals and are thus a basis for the most compact CI description of the wavefunction. It follows that, for an electronic state constructed from a monodeterminantal wavefunction, every NOO will take a value of 0, 1 or 2. For a multiconfigurational electronic state, the deviation of the NOOs from integer values can be taken as a measure of multiconfigurational character.38 Occupation numbers close to integer values correspond to ‘strongly’ occupied orbitals, whereas occupation numbers close to zero correspond to ‘weakly’ occupied orbitals.The D8h point group symmetry and η8 hapticity of AnCOT2, combined with the fact that the highest lying π-orbitals of the (COT2−)2 ligand system span the e2g and e2u irreps,‡ allows for the possible participation of the An 6dδ (e2g symmetry) and 5fδ (e2u symmetry) orbitals in delta-type metal–ligand bonding,14,39–43 respectively. The natural orbital analysis therefore begins with consideration of these orbitals. Bearing in mind that calculations are performed in D2h symmetry, Fig. 3 presents the natural orbitals occupations (NOOs) for the strongly and weakly occupied orbitals of (a) ag ⊕ b1g and (b) au ⊕ b1u symmetry. Fig. 3a shows that the NOOs corresponding to the gerade orbitals show little variation when moving across the actinide series and are very closer to integer values. The strongly occupied orbitals have NOOs ranging from 3.904 (ThCOT2) to 3.964 (CmCOT2) whilst the weakly occupied orbitals have NOOS ranging from 0.024 (ThCOT2) to 0.040 (PuCOT2). These NOOs indicate a degree of multiconfigurational character and justify the inclusion of these orbitals in the active spaces employed here. Visualisation of the orbitals reveals a degree of metal–ligand hybridisation, with the strongly (weakly) occupied orbitals exhibiting bonding (antibonding) character: the question of whether this corresponds to An 6d covalency will be considered in later sections. Fig. 3b presents the corresponding data for the ungerade orbitals. Here, a more pronounced trend is apparent. There is a reduction in the occupation of the strongly occupied orbitals when moving across the series from Th (3.896) to Am (3.652), along with a concomitant increase in occupation of the weakly occupied orbitals, 0.016 for ThCOT2, 0.340 for AmCOT2. This trend has been reported previously for a subset of the complexes considered here21 and indicates a degree of multiconfigurational character in PuCOT2 and AmCOT2 comparable to that previously reported in several related Ce complexes.20,44,45
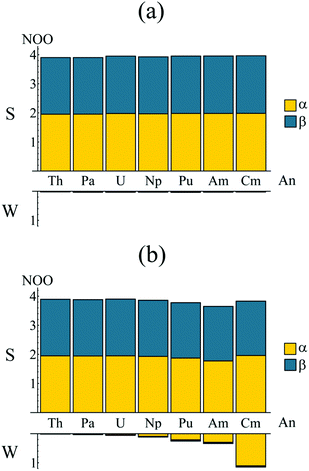 | ||
| Fig. 3 Natural orbital occupations of the strongly (S) and weakly (W) occupied orbitals of (a) ag/b1g symmetry and (b) au/b1u symmetry. Occupations are summed since in the full (D8h) symmetry of the complexes considered here ag/u ⊕ b1g/1u spans e2g/2u. See Table S1† for numerical data. | ||
Fig. 3b shows almost equal spin-up (α) and spin-down (β) occupation of the strongly occupied au/b1u natural orbitals, mirroring the ag/b1g orbital occupations presented in Fig. 3a. The weakly occupied au/b1u orbitals, however, exhibit a strong preference for occupation of the α-orbital, increasing the spin density associated with the 5fn occupation of the An ions.
Whilst the trend from Th–Am is quite clear, there is a marked deviation between the Am and Cm complexes. The trend towards lower occupations of the strongly occupied au/b1u orbitals is reversed in the latter, with an occupation of 3.832 being comparable to that of the early actinide complexes. There is also a substantial increase in occupation of the weakly occupied au/b1u orbitals (1.149 compared to 0.340 in AmCOT2). This is, however, to be expected. Whilst the An 5fδ orbitals form (anti-)bonding linear combinations with the ligand π2u HOMO, the 5fσ, 5fπ and 5fϕ orbitals are essentially non-bonding. These non-bonding orbitals become fully occupied in the 5f5 Am complex and so the 5f6 configuration of CmCOT2 must, by necessity, involve occupation of the energetically unfavourable antibonding π2u–5fδ orbital: this corresponds to the NOO of the ‘weakly’ occupied orbital of Fig. 3b. The occupation of this antibonding orbital is commensurate with the increased ring-metal separation of CmCOT2 over AmCOT2. Furthermore, the occupation number of 3.832 found in CmCOT2 has the same origin. Since only one antibonding orbital is now available for (weak) occupation, so only one strongly occupied orbital has a commensurate reduced occupation number. Since the value of 3.832 is in fact the sum of occupations of two orbitals it is, as expected, higher than that of the other later actinides considered here.
Finally, the An non-bonding 5f NOOs are given in Table 2. From these, the leading 5fn configurations can be derived, indicating a preference for occupation of the (presumably near-degenerate) 5fπ and 5fϕ orbitals over occupation of 5fσ. The degree to which these orbitals can be considered as non-bonding and localised on the An centre will be discussed later in this study. As would be expected, the total non-bonding 5f orbital occupation increases by approximately integer amounts as the actinide series is crossed.
| Complex | Configuration | 5fσ | 5fπ | 5fϕ | 5fNB |
|---|---|---|---|---|---|
| ThCOT2 | 5f0 | — | — | — | 0 |
| PaCOT2 | 5f1φ | — | — | 0.980 | 0.980 |
| UCOT2 | 5f1π5f1φ | — | 0.995 | 0.993 | 1.988 |
| NpCOT2 | 5f2π5f1φ | — | 1.956 | 0.982 | 2.938 |
| PuCOT2 | 5f2π5f2φ | — | 1.946 | 1.924 | 3.870 |
| AmCOT2 | 5f1σ5f2π5f2φ | 0.983 | 1.972 | 1.962 | 4.917 |
| CmCOT2 | 5f1σ5f2π5f1δ5f2φ | 0.984 | 1.969 | 1.969 | 4.922 |
Topological analysis
As previously discussed, the strong static correlation present in the complexes under consideration (as evidenced by the increasing NOOs of the weakly occupied orbitals of au/b1u symmetry highlighted in Fig. 3b) makes covalency measures based on orbital mixing due to energetic near-degeneracy at best ambiguous. As an alternative, the total electron density can be investigated by employing the Quantum Theory of Atoms in Molecules (QTAIM). The topological analysis afforded by this approach allows for a molecule to be divided into a contiguous set of space-filling atomic basins, the surfaces of which satisfy the condition ∇ρ(r)·n(r) = 0. Evaluation of ∇ρ(r) = 0 reveals the set of critical points associated with the molecule. Each atomic basin (typically) contains a single nuclear critical point (NCP) at the position of the nuclear centre. A bond critical point (BCP) is found when the uniquely defined line of maximum density between two atoms has its minimum at the interatomic surface joining the two atomic basins: in this situation, the atoms are considered to be bonded to one another.46 The nature of this bonding can be characterised by the values of the density and its Laplacian at the BCP: as a general rule, ρBCP > 0.20 a.u. and ∇2ρBCP < 0 for a covalent bond, whilst ρBCP < 0.10 a.u. and ∇2ρBCP > 0 indicates an ionic bond. More broadly, increasing values of ρBCP indicate increasing covalent character of the bonding interaction.Fig. 4 shows the value of ρBCP and its Laplacian at the metal–carbon critical point for each complex considered here. Values of ρBCP are ∼0.04 a.u., with the Laplacian being small and positive in all cases. This is indicative of a predominantly ionic interaction, as would be expected. However, whilst the Laplacian slowly increases across the series from Th–Am (with a small reduction upon moving to Cm), the density itself exhibits a pronounced maximum between Pa and Pu, with a maximum value of ρBCP = 0.476 a.u. found in UCOT2. This suggests that the early actinides, with the exception of Th, exhibit a more covalent interaction with the COT ligand than those occurring later in the series. The low value associated with the formally 5f0 thorium complex may indicate the involvement of the 5fδ orbitals in the covalent interaction of the other complexes. Moreover, the maximum value found in UCOT2 is consistent with the results obtained from density functional theoretical studies of AnCp3.47
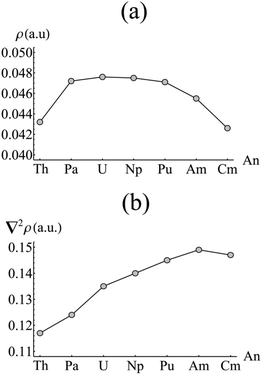 | ||
| Fig. 4 Values of (a) the electron density (ρ) and (b) its Laplacian (∇2ρ) evaluated at the metal–carbon bond critical point in AnCOT2 (An = Th–Cm). See Table S2† for numerical data. | ||
Integrated one- and two-electron properties
Whilst the topological analysis discussed in the previous section suggests enhanced covalency amongst the Pa, U, Np and Pu actinocenes, more detailed information is required in order to identify its origin. The atomic basins identified previously can again be employed. Integrating the electron density over an atomic basin ΩA gives the atomic population N(A) from which the atomic charge q(A) can be derived. If instead one considers the exchange–correlation component of the electron pair density, two further properties can be defined: the localisation index, λ(A), obtained by integration of both components of the pair density over the same atomic basin ΩA, and the delocalisation index, δ(A, B), obtained by integrating one component over ΩA and one over ΩB. λ(A) corresponds to the average number of electrons localised upon a given atom, while δ(A, B) quantifies the average number of electrons shared between two atoms and can be considered as an unambiguous and quantitative measure of covalency. Formally, the evaluation of two-electron properties requires explicit knowledge of the 2nd order RDM. Construction of this matrix, however, is computationally demanding, and so approximate methods have been developed based on the 1st order RDM. In this work, the approximate form of the 2nd order RDM proposed by Müller48 is employed.Fig. 5 shows the atomic populations N(An) and atomic charges q(An) of the metal centre of each complex considered in this study. The element-by-element increase in N(An) is highlighted in yellow. For the elements Pa–Am, this increase is slightly greater than unity, and manifests itself in a steadily decreasing atomic charge, as shown in Fig. 3b. The difference in actinide charge between ThCOT2 to AmCOT2 is 0.704 a.u., evident of strong trivalent character in the latter. This is not unexpected for the later actinides, the chemistry of which bears strong similarities to that of the lanthanides.
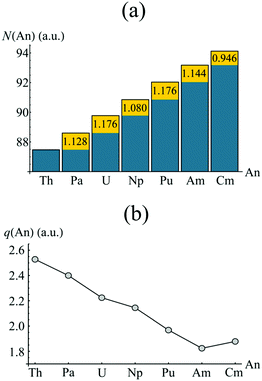 | ||
| Fig. 5 QTAIM calculated atomic populations (a) and atomic charges (b) of the An centres in AnCOT2 (An = Th–Cm). The yellow regions in (a) show the increase of electron density in ΩAn when compared to the previous element. See Table S3† for numerical data. | ||
The increase in atomic population when moving from Am to Cm deviates from the trend discussed above. Here, the increase is marginally less than unity, resulting in a Cm charge slightly higher than that of Am. As previously discussed, CmCOT2 is the only complex considered here which exhibits occupation of anything other than a nonbonding 5f orbital, namely an antibonding π2u–5fδ orbital. The fact that this orbital has a degree of ligand character explains this deviation from the Th–Am trend.
In order to investigate the increased trivalent character suggested by analysis of the atomic charges, the localisation indices λ(An) were evaluated, and are presented in Fig. 6a. Again the element-by-element increase is highlighted in yellow. In each case (except that of Th & Pa), λ(An) increases by an amount greater than unity, this being most pronounced between Np & Pu and Pu & Am. This has a cumulative effect as one traverses the actinide series, as can be seen in Fig. 6b. Here, the difference between the atomic number, Z, and λ(An) is given for An = Th–Cm. λ(An) is a measure of the number of electrons localised on An, and so Z(An)–λ(An), which therefore gives the number of electrons donated and/or shared by the An atom, might be expected to give a measure of formal oxidation state. Z(An)–λ(An) ∼ +4 for An = Th–Np, mirroring the expected value. For later actinides, however, electron localisation increases: in CmCOT2, Z(Cm)–λ(Cm) = 3.270, implying a trivalent oxidation state. The same assignment can be made for AmCOT2, with PuCOT2 appearing to be best described as mixed valent according to this criterion. This latter conclusion is in accord with previous findings.22
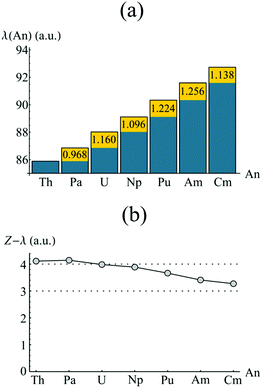 | ||
| Fig. 6 QTAIM calculated localisation indices (a) and differences between atomic number and λ(An) (b) of the An centres in AnCOT2 (An = Th–Cm). The yellow regions in (a) show the increase of electron localisation in ΩAn when compared to the previous element. See Table S4† for numerical data. | ||
Assuming the Müller approximation to the 2nd order RDM, λ(An) and δ(An, C) can be decomposed into orbital contributions:49
where ni is the NOO of the natural orbital φi, Sij(A) is the overlap integral between NOs φi and φj evaluated over the atomic basin ΩA, and the summation runs over all NOs. Advantage can be taken of these definitions in order to obtain orbital contributions to electron (de)localisation. In particular, 5f and 6d contributions can be evaluated for the MCOT2 complexes considered in this study. This is possible due to the high symmetry of these complexes. The central atomic basin ΩAn will have the same symmetry as the molecule and, since the 5f and 6d have ungerade and gerade parity, respectively, the overlap integrals S5f,6d(An) will be equal to zero. The decomposition of the (de)localisation index into orbital contributions as used in this study is depicted schematically in Fig. 7. In addition to the total (de)localisation indices, the contributions from the π-electron subsystem (λπ/δπ), the 5fδ and π2u orbitals (λ5fδ/δ5fδ) and the 6dδ and π2g orbitals (λ6dδ/δ6dδ) are also evaluated.
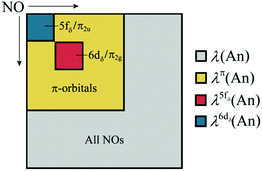 | ||
| Fig. 7 Schematic showing the various contributions to the orbitally resolved localisation indices evaluated in this study. | ||
Firstly, the π-orbital, 5fδ and 6dδ contributions to the localisation index are considered. In the case of the 5fδ (6dδ) contribution, the ligand π2u (π2g) orbitals (which are able to mix with the respective metal orbitals) are also included in the summation. Fig. 8a presents the orbitally resolved localisation indices. There is a substantial increase in An localisation amongst the π-electron subsystem as one moves from Th to Am, and this localisation is almost entirely due to increased localisation amongst the 5fδ and π2u orbitals, with contributions from 6dδ and π2g orbitals remaining approximately constant across the series. The substantial increase in the case of CmCOT2 is again due to the occupation of the antibonding π2u–5fδ orbital. Fig. 8b reveals that the degree of electron localisation amongst the non-bonding 5f orbitals is, as expected, almost total, with localisation indices ranging from 92.0% (Pa) to 98.6% (Cm) of the total nonbonding 5f populations (N(An) in Fig. 8b).
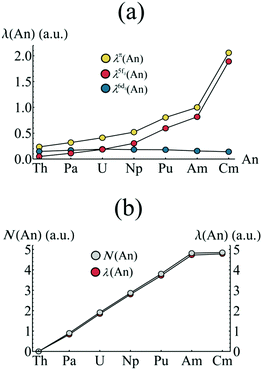 | ||
| Fig. 8 (a) Orbitally resolved localisation indices and (b) comparison of nonbonding 5f occupation and localisation for AnCOT2 (An = Th–Cm). See Table S5† for numerical data. | ||
In order to quantify An–C covalency in these complexes, delocalisation indices δ(An, C) were evaluated in analogy with the orbitally resolved localisation indices. These delocalisation indices are presented in Fig. 9. The trend in total delocalisation index from Th to Cm mirrors the trend in ρBCP (cf.Fig. 2a). As previously discussed, an increase in ρBCP corresponds to an increase in covalent bonding character and so a commensurate increase in electron delocalisation would be expected. That this increase is found strongly supports the view that there is indeed enhanced covalent character in the complexes of the early actinides, Pa–Pu. Whilst the magnitude of delocalisation indices is quite modest, δ(An, C) taking a maximum value of 0.220 a.u. in UCOT2, it should be borne in mind that this value corresponds to the average number of electrons shared between the An centre and a single carbon centre. Since there are sixteen carbons atoms in AnCOT2, the total number of electrons shared is significantly larger and is listed in Table 3.
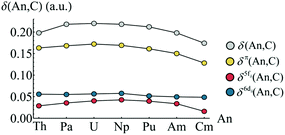 | ||
| Fig. 9 Total and orbitally resolved delocalisation indices for AnCOT2 (An = Th–Cm). See Table S6† for numerical data. | ||
The trend in delocalisation indices is mirrored by the contribution from the π-electron subsystem, which accounts for approximately 77% of the total value, on average. This implies a not insignificant contribution from NOs with σ-character, although the orbital decomposition here means that contributions from terms involving the overlap integrals Sσπ are neglected. Since the contribution from terms involving Sππ are so substantial, it would seem reasonable to suggest that contribution from terms Sπσ are more significant than those involving Sσσ.
Fig. 9 also shows that the 6dδ/π2g contributions to the delocalisation index are approximately constant across the series, with a mean value of 0.054 and a standard deviation of just 0.004. This consistency across the series suggests that, while there is a non-negligible An 6dδ contribution to covalency in these systems, its existence does not explain the variation observed in the delocalisation indices. Looking instead at the 5fδ/π2u contributions, a trend mirroring that of the total delocalisation indices is found. In particular, there is a pronounced reduction in f-electron delocalisation in CmCOT2. This can again be rationalised in terms of the antibonding π2u–5fδ orbital. Occupation of this orbital would, due to its antibonding character, be expected to reduce the covalent character of the Cm–C bond. This manifests itself in the calculated reduction in the delocalisation index.
Overall, whilst the magnitude of the 5fδ contribution is found to be smaller than the 6dδ contribution, the trend observed in the former strongly follows that of the total delocalisation indices and therefore provides strong evidence for the variation in covalency across the An series found here as having its origin in covalent 5fδ contributions to the An–COT bond.
Summary and conclusions
In this study, the ring-metal separations of AnCOT2 (An = Th–Cm) complexes were optimised at the CASPT2 level of theory, where good agreement was found with experimentally determined structural data. A trend of reducing separation was found, but this reduction was not as great as might be expected from consideration of the ionic radii of the An(IV) ions, suggesting possible increasing trivalent character as one moves across the series. Analysis of CASSCF-calculated natural orbitals was performed, and strong multiconfigurational character was found to be associated with the occupation of the 5fδ and π2u orbitals. These orbitals both exhibited a strong degree of ligand–metal hybridisation and, coupled with the strong multiconfigurational character, suggested that orbital-based measures of covalency would prove ambiguous. In order to quantify covalency in an unambiguous manner, QTAIM analysis was employed. Firstly, topological properties of the electron density were considered and, in particular, the values of ρ and its Laplacian at the An–C bond critical points (BCPs) were assessed: here a significant trend in ρ was found. Initially increasing, it reached a maximum for the elements Pa–Pu before decreasing for the later actinides. An increase in ρ at the BCP is considered an indicator of increased covalent interaction, since this corresponds to an accumulation of electronic charge density in the bonding region. This analysis therefore provides evidence of enhanced covalency in the early actinides, excluding thorium. Since thorium has an empty 5f shell in its tetravalent oxidation state, it would suggest that the enhanced covalency in Pa–Pu has its origin in An 5f contributions. In order to investigate this further, integrated one- and two-electron properties were investigated, namely the atomic electron population, N(An), and the (de)localisation indices λ(An) and δ(An, C). The atomic population increased by an amount slightly greater than unity for each step across the actinide series, suggesting increased electron localisation on the An centre. There was a small deviation from this trend when considering the Cm complex, due to occupation of an antibonding orbital exhibiting a degree of ligand character. Total and orbitally resolved localisation indices were evaluated in order to further asses the degree of electron localisation on the An centre as one traverses the actinide series. Here the degree of electron localisation derived from occupation of 6dδ and π2g orbitals was found to be approximately constant across the series. The total electron localisation exhibited an increasing trend as the actinide series was traversed, and this was found to be mirrored in the variation of the contribution of the 5fδ and π2u orbitals to the localisation index. Occupied nonbonding 5f orbitals were calculated to be almost entirely localised on the actinide centre. Comparison of localisation index with atomic number reveals a correlation with the expected oxidation state of the complexes.The trend in the total delocalisation index was found to be strongly reminiscent of that found for the values of ρ at the M–C BCPs, supporting the view that increased values of ρBCP are associated with increased covalency. Again, 6dδ and π2g contributions were found to be approximately constant, whereas the 5fδ and π2u contributions mirrored the trend in the total delocalisation index. This therefore provides strong evidence that, while 5f contributions to covalency in these complexes are smaller in magnitude than 6d contributions, the variation in covalency is almost entirely accounted for by the variation in the 5f contribution.
This study demonstrates that the combination of multiconfigurational quantum chemical simulations with topological analysis of the resulting electron density provides a powerful and unambiguous method for assessing and characterising covalency in high symmetry actinide complexes. That this study has been able to show that variation in covalency is almost completely accounted for by considering An 5f contributions has important implications for the design of novel ligands suitable for the challenging technological problem of An/Ln separation.
Acknowledgements
The author would like to thank the EPSRC for the award of a career acceleration fellowship (grant EP/J002208/1), UCL research computing for access to the Legion and Unity HPC facilities, the National Service for Computational Chemistry Software (NSCCS) for access to the Columbus HPC facility and the support of the Thomas Young Centre for the theory and simulation of materials.References
- H. H. Dam, D. N. Reinhoudt and W. Verboom, Chem. Soc. Rev., 2007, 36, 367–377 RSC.
- Z. Kolarik, Chem. Rev., 2008, 108, 4208–4252 CrossRef PubMed.
- M. P. Jensen and A. H. Bond, J. Am. Chem. Soc., 2002, 124, 9870–9877 CrossRef PubMed.
- F. Lewis, M. Hudson and L. Harwood, Synlett, 2011, 2011, 2609–2632 CrossRef PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef PubMed.
- J. R. Walensky, R. L. Martin, J. W. Ziller and W. J. Evans, Inorg. Chem., 2010, 49, 10007–10012 CrossRef PubMed.
- W. W. Lukens, N. M. Edelstein, N. Magnani, T. W. Hayton, S. Fortier and L. A. Seaman, J. Am. Chem. Soc., 2013, 135, 10742–10754 CrossRef PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- D. Wang, W. F. van Gunsteren and Z. Chai, Chem. Soc. Rev., 2012, 41, 5836–5865 RSC.
- A. Streitwieser and U. Müeller-Westerhoff, J. Am. Chem. Soc., 1968, 90, 7364 CrossRef.
- A. Streitwieser and N. Yoshida, J. Am. Chem. Soc., 1969, 91, 7528 CrossRef.
- D. F. Starks, T. C. Parsons, A. Streitwieser and N. Edelstein, Inorg. Chem., 1974, 13, 1307–1308 CrossRef.
- D. G. Karraker, J. A. Stone, E. R. Jones and N. Edelstein, J. Am. Chem. Soc., 1970, 92, 4841–4845 CrossRef.
- D. G. Karraker, in Proceedings of the 4th International Transplutonium Symposium, ed. W. Muller, North-Holland, Amsterdam, 1975, vol. II Search PubMed.
- A. H. H. Chang and R. M. Pitzer, J. Am. Chem. Soc., 1989, 111, 2500–2507 CrossRef.
- A. H. H. Chang, K. Zhao, W. C. Ermler and R. M. Pitzer, J. Alloys Compd., 1994, 213–214, 191–195 CrossRef.
- M. Dolg, P. Fulde, H. Stoll, H. Preuss, A. Chang and R. M. Pitzer, Chem. Phys., 1995, 195, 71–82 CrossRef.
- W. Liu, M. Dolg and P. Fulde, J. Chem. Phys., 1997, 107, 3584 CrossRef PubMed.
- A. Kerridge, R. Coates and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 2896–2905 CrossRef PubMed.
- A. Kerridge and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 8737–8745 CrossRef PubMed.
- A. Kerridge, Dalton Trans., 2013, 42, 16428–16436 RSC.
- B. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- F. Aquilante, L. D. E. Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. P. Nák, M. Reiher, B. O. Roos, L. Serrano-andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef PubMed.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, Chem. Phys. Lett., 2005, 409, 295–299 CrossRef PubMed.
- K. Anderson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinskit, J. Phys. Chem., 1990, 5483–5488 CrossRef.
- T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overl. Park KS, USA, 2013 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef PubMed.
- A. E. Clark, J. L. Sonnenberg, P. J. Hay and R. L. Martin, J. Chem. Phys., 2004, 121, 2563–2570 CrossRef PubMed.
- L. Petit, C. Adamo and P. Maldivi, Inorg. Chem., 2006, 45, 8517–8522 CrossRef PubMed.
- A. Avdeef, K. N. Raymond, K. O. Hodgson and A. Zalkin, Inorg. Chem., 1972, 11, 1083–1088 CrossRef.
- D. J. A. De Ridder, J. Rebizant, C. Apostolidis, B. Kanellakopulos and E. Dornberger, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 597–600 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- P. Löwdin, Phys. Rev., 1955, 376, 1474–1489 CrossRef.
- M. W. Schmidt and M. S. Gordon, Annu. Rev. Phys. Chem., 1998, 49, 233–266 CrossRef CAS PubMed.
- A. Streitwieser, D. Dempf, G. N. La Mar, and N. Edelstein, 1971, 93, 7343–7344.
- K. D. Warren, Inorg. Chem., 1975, 14, 3095–3103 CrossRef CAS.
- J. P. Clark and J. C. Green, Dalton Trans., 1977, 505–508 RSC.
- P. M. Boerrigter, E. J. Baerends and J. G. Snijders, Chem. Phys., 1988, 122, 357–374 CrossRef CAS.
- J. G. Brennan, J. C. Green, and C. M. Redfern, 1989, 111, 2373–2377.
- R. Coates, M. Coreno, M. DeSimone, J. C. Green, N. Kaltsoyannis, A. Kerridge, N. Narband and A. Sella, Dalton Trans., 2009, 5943–5953 RSC.
- A. Kerridge and N. Kaltsoyannis, C. R. Chim., 2010, 13, 853–859 CrossRef CAS PubMed.
- R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396 CrossRef CAS PubMed.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
- A. M. K. Müller, Phys. Lett. A, 1984, 105, 446–452 CrossRef.
- F. Feixas, J. Vandenbussche, P. Bultinck, E. Matito and M. Solà, Phys. Chem. Chem. Phys., 2011, 13, 20690–20703 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra47088a |
| ‡ In the subduction from D8h to (the working symmetry) D2h, e2g/2u → ag/u ⊕ b1g/1u. |
| This journal is © The Royal Society of Chemistry 2014 |